שאלה 1: חשבונות שדה
הפתרונות המלאים זמינים בתרגול 6.
שאלה 2: אנרגיה, פוטנציאל ותנועה במערכת מטענים על משולש שווה־צלעות
על קודקודיו של משולש שווה צלעות שאורך צלעו הוא $a$ ממקמים שלושה מטנים חשמליים. שניים חיובים זהים בגודל $q$ השלישי מטען שלילי $-Q$ ומסתו $m$. המשולש כולו מונח על משטח אופקי כך שהכבידה לא משחק תפקיד בבעייה.
סעיף א: מציאת גודל מטען שנדרש לאיפוס המערכת
מה צריך להיות גודלו של המטען השלילי כדי שהאנגיה האלקטוסטאלית של כל המערכת תהיה בדיוק אפס?
צריך לעשות סופר פוזיציה על כל הזוגות (שלושה):
\[U_{tot} = \frac{kq^2}{a} + \frac{kq(-Q)}{a} + \frac{kq(-Q)}{a}\] \[= \frac{kq}{a}(q-2Q)\]אז בשביל שיתאפס:
\[q-2Q = 0 \implies Q = -\frac{1}{2}\]שאלו על גודל אז עקרונית הסימן לא משנה.
סעיף ב: חישוב הפוטנציאל בנקודת הקודקוד המכילה את המטען השלילי
מהו הפוטנציאל בנקודת הקודקוד המכילה את המטען השלילי?

אלה ההשפעות של שני החיוביים עליה:
\[V = \frac{2kq}{a}\]טעויות אפשריות:
- המטען השלילי $(-Q)$ לא נכנס כאן לחישוב! סוכמים רק את המטענים החיוביים, כאשר הפוטנציאל שלהם הוא פשוט פוטנציאל נקודתי כמו להביא את המטען הנקודתי מאינסוף.
הערה כללית: הפוטנציאל חיובי כי הוא נוצר על ידי מטענים חיוביים.
סעיף ג: חישוב הפוטנציאל במרכז המשולש
מה הפוטנציאל במרכז המשולש הנגרם על ידי שני המטענים החיוביים?
המרחק בין מרכז משולש שווה צלעות עם צלע $a$ לקודקוד הוא:
\[d = \frac{a}{\sqrt{3}}\]אז הפוטנציאל במרכז הוא:
\[V_{center} = \frac{2kq}{\frac{a}{\sqrt{3}}} = \frac{2\sqrt{3}kq}{a}\]סעיף ד: חישוב מהירות, תאוצה ועבודה על המטען השלילי
מאפשרים למטען השלילי חופש תנועה וכתוצאה מכך הוא מאיץ לעבר מרכז המשולש.
1. מה תהיה המהירות שלו במרכז המשלוש?
אפשר להיעזר בפוטנציאלים שמצאנו ובשימור אנרגיה:
\[U_i + \cancel{\frac{1}{2}mv_i^2} = U_f + \frac{1}{2}mv^2\] \[\frac{1}{2}mv^2 = (-Q)V_i - (-Q)V_f\] \[\frac{1}{2}mv^2 = - Q \frac{2kq}{a} + Q \frac{2\sqrt{3}kq}{a}\] \[v^2 = \frac{Q4k}{am}( - 1 + \sqrt{3})\] \[v = \sqrt{\frac{Q4k}{am}(\sqrt{3} - 1)}\]טעויות שהיו לי:
השתמשתי במטען $q$ במקום $-Q$ כשחישבתי את האנרגיה הפוטנציאלית. כלומר, הנה דוגמה לטעות:
\[\frac{1}{2}mv^2 = qV_i - qV_f\] \[\frac{1}{2}mv^2 = q \frac{2kq}{a} - q \frac{2\sqrt{3}kq}{a}\] \[v^2 = \frac{q4k}{am}(1 - \sqrt{3})\] \[v = \sqrt{\frac{q4k}{am}(1 - \sqrt{3})}\]
2. מה תהיה התאוצה שלו במרכז המשולש?
אני חושב שאפשר לפתור עם ניוטון:
\[F = mA\]מצד שני
\[F = QE\]והשדה במרכז דורש חישוב.
משיקולי סימטריה רק הרכיבים בכיוון הציר של המרכז שורדים (נניח מעלה).
בלי הכיוון:
\[E_1 = E_2 = \frac{kq}{d^2} = \frac{kq}{\left(\frac{a}{\sqrt{3}}\right)^2} = \frac{3kq}{a^2}\]לאחר הכיוון הם נסכמים - יש לי כאן טעות, זה לא קוסינוס שישים הזווית כנראה יותר קשורה לשלושים. אתקן בהמשך.
\[E = \frac{6kq}{a^2} \cos(60) = \frac{6kq}{a^2} \cdot \frac{1}{2}\]אז:
\[\frac{6kq}{a^2} = mA\] \[A = \frac{6kq}{ma^2}\]להזהר לא להתבלבל בסימונים: $a$ קטנה משמש כאן לצלע.
3. כמה עבודה נדרשת על מנת להחזירו ממרכז המשולש לקודקוד בו היה ממוקם מראש?
\[W = (-Q)\left(V_f - V_i\right)\] \[W = (-Q)\left(\frac{2kq}{a} - \frac{2\sqrt{3}kq}{a}\right)\] \[W = \frac{-2Qkq}{a}\left(1 - \sqrt{3}\right)\]זאת האנרגיה הקינטית שהרוויח בנפילה, והיא חיובית.
\[\boxed{W = \frac{2Qkq}{a}(\sqrt{3} - 1)}\]שאלה 3: פוטנציאל חשמלי בגליל מוליך עם מעטפת גלילית מוארקת
גליל מוליך ארוך מאוד אשר רדיוסו הוא $a$ טעון בצפיפות מטען אורכית $\lambda$ קולון ליחידת אורך של הגליל. סביב הגליל מונחת מעטפת גלילית דקה ומוארקת ברדיוס $b>a$, כך שציר הגליל וציר המעטפת הגלילית מתלכדים. מהו הפוטנציאל החשמלי בכל המרחב?
הנחייה: מיצאו את השדה והביאו חלקיק מן האינסוף כנגד (או עם) השפעת השדה.

גם לתרגיל הזה קיים פתרון מפורט בתרגול 6. להלן פתרון נוסף:
נתחיל מחישוב פוטנציאל.
בתוך מוליך פוטנציאל אפס:
\[E(r<a) = 0\]על המוליך עצמו יש נוחסה:
בין המוליך למעטפת - יש נוסחה:
\[E(a<r<b) = \frac{\lambda}{2\pi\epsilon_0 r}\]מחוץ - המעטפת מוארקת ולהבנתי השדה מנוטרל:
\[E(r<b)=0\]מציאת הפוטנציאל - מבחוץ לבפנים:
\[V(b)=0\]בגלל הארקה.
אזור $a < r < b$:
\[V(a < r < b) = -\int_b^r E \, dr' = -\int_b^r \frac{\lambda}{2\pi\varepsilon_0 r'} dr' = \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{r}\right)\]אזור $r < a$:
פוטנציאל קבוע בתוך מוליך, שווה לערך על השפה:
\[V = V(a) = \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{a}\right)\]סיכום:
\[V(r) = \begin{cases} \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{a}\right) & r < a \\ \frac{\lambda}{2\pi\varepsilon_0} \ln\left(\frac{b}{r}\right) & a < r < b \\ 0 & r > b \end{cases}\]
שאלה 4: כדור מוליך עם הארקות
גם לתרגיל הזה קיים פתרון מפורט בתרגול 6.
שאלה 5: אנרגיה פוטנציאלית של קונפיגורציות מטענים בקובייה
נתונה קוביה אשר אורך צלעה הוא $a$.
במקרה ראשון מניחים מטען חשמלי $+q$ על כל אחד מקוקודי הקוביה. מהי האנרגיה הפוטנציאלית האגורה בקונפיגורציית מטענים זו?
במקרה השני מניחים על ארבעת הקודקודים העליונים מטען חשמלי שלילי שגודלו הוא $-q$ ועל ארבעת הקוקודים התחתונים מטען חשמלי חיובי שגודלו הוא $+q$. מהי האנרגיה הפוטנציאלית האגורה בקונפיגורציית מטענים זו?

סעיף 1 - רק מטענים חיוביים
קצת קומבינטוריקה. בקובייה יש:
- זוגות שנוצרים מהצלעות - 12 כאלה, במרחק $a$
- זוגות שנוצרים מאלכסונים על פאות - 12 כאלה במרחק $\sqrt{2}a$
- זוגות שנוצרים מאלכסונים בתוך הקובייה - 4 כאלה במרחק $\sqrt{3}a$
אפשר לוודא שזה נסכם למספר הזוגות שמתקבלים מבירה של 8 על 2:
\[\binom{8}{2} = \frac{8!}{6!\cdot 2} = 7 \cdot 4 = 28\]
עכשיו נסכום:
\[U_{tot} = 12 \frac{kq^2}{a} + 12 \frac{kq^2}{\sqrt{2}a} + 4 \frac{kq^2}{\sqrt{3}a}\] \[= 4 \frac{kq^2}{a} \left(3 + 3 \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}}\right)\]או בצורה מסודרת:
\[\boxed{U = \frac{4kq^2}{a} \left(3 + \frac{3\sqrt{2}}{2} + \frac{\sqrt{3}}{3}\right)}\]סעיף 2 - שינוי המטען
מסתבר שזה לא מתאפס - למרות שיש ארבעה חיוביים וארבעה שליליים המרחקים שונים.
התאצלתי לסכום, להלן פתרון מג׳ונרט:
בסעיף 2 צריך לבדוק את הסימנים של כל סוג זוג:
צלעות (12 זוגות, מרחק $a$):
- צלעות אופקיות (על הפאה העליונה): 4 זוגות $(-q)(-q) = +q^2$
- צלעות אופקיות (על הפאה התחתונה): 4 זוגות $(+q)(+q) = +q^2$
- צלעות אנכיות: 4 זוגות $(+q)(-q) = -q^2$
סה”כ צלעות: $4 + 4 - 4 = 4$ זוגות “חיוביים”
אלכסוני פאות (12 זוגות, מרחק $\sqrt{2}a$):
- על הפאה העליונה: 2 זוגות $(-q)(-q) = +q^2$
- על הפאה התחתונה: 2 זוגות $(+q)(+q) = +q^2$
- על 4 הפאות האנכיות: 8 זוגות $(+q)(-q) = -q^2$
סה”כ אלכסוני פאות: $2 + 2 - 8 = -4$ זוגות
אלכסוני קובייה (4 זוגות, מרחק $\sqrt{3}a$):
כל אלכסון מחבר קודקוד עליון לתחתון: $(+q)(-q) = -q^2$
סה”כ: $-4$ זוגות
נסכום:
\[U = \frac{kq^2}{a}\left(4 \cdot 1 - 4 \cdot \frac{1}{\sqrt{2}} - 4 \cdot \frac{1}{\sqrt{3}}\right)\] \[= \frac{4kq^2}{a}\left(1 - \frac{1}{\sqrt{2}} - \frac{1}{\sqrt{3}}\right)\]המספר בסוגריים הוא בערך $1 - 0.707 - 0.577 \approx -0.28$
אז האנרגיה שלילית, מה שהגיוני - יש יותר זוגות של מטענים מנוגדים (שמושכים) מאשר זוגות של מטענים זהים (שדוחים).
שאלה 6
גם לתרגיל הזה קיים פתרון מפורט בתרגול 6.
שאלה 7: מטענים ופוטנציאל במערכת כדור מוליך וקליפה כדורית מוליכה קונצנטרית
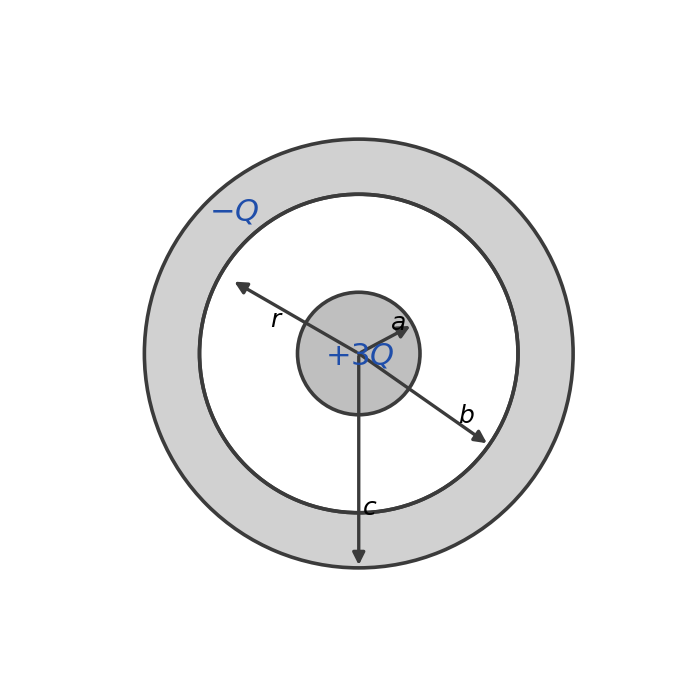
כדור מוליך בעל רדיוס $a$ טעון במטען חיובי $+3Q$ ומצא בתוך קליפה כדורית מוליכה בעלת רדיוס פנימי $b$ ורדיוס חיצוני $c$, הטעונה במטען $-Q$. לכדור ולקליפה הכדורית יש מרכז משותף.
מהו המטען על השפה החיצונית $(r=c)$ של הקליפה הכדורית?
מהו הפוטנציאל החשמלי על השפה הפנימית $(r=b)$ של הקליפה הכדורית? הנח שהפוטנציאל באינסוף הוא אפס.
מהו הפוטנציאל החמשלי במרכז הכדור $(r=0)$ ? הנח שהפוטנציאל באינסוף הוא אפס.
סעיף 1 - המטען על השפה החיצונית של הקליפה
הכדור מוליך אז המטענים יהיו על המעטפת שלו.
גם הקליפה הכדורית אבל להבנתי זה יתחלק כך שחלק אולי יתאזנו עם האמצע?
נכון, בדיוק!
העיקרון: בתוך מוליך השדה חייב להיות אפס. לכן אם ניקח משטח גאוסי בתוך החומר של הקליפה ($b < r < c$), השדה שם אפס, ולכן המטען הכלוא חייב להיות אפס.
מה קורה:
על השפה הפנימית ($r=b$) יישב מטען $-3Q$ כדי לאזן את השדה מהכדור הפנימי.
המטען הכולל על הקליפה הוא $-Q$, אז משימור מטען:
\[Q_{inner} + Q_{outer} = -Q\] \[-3Q + Q_{outer} = -Q\] \[Q_{outer} = +2Q\]
הפוטנציאל החשמלי על השפה הפנימית
דרך מקוצרת:
בתוך מוליך הפוטנציאל קבוע, ושווה לפוטנציאל על השפה החיצונית שלו. במקרים שאין השפעה מבחוץ מה שבפנים כנראה מתבטל, להבנתי. אולי אפשר לחשוב על זה כעבודה להבאת מטען יחיד מאינסוף לנקודה.
במקרה שלנו השפה החיצונית במרחק $c$ ובמטען $+2Q$, לכן:
\[V(r=b) = \frac{2kQ}{c}\]
להלן גם חישוב מלא.
לחישוב פוטנציאל משתמשים במרחק מהמרכז, לא במרחק מהשפה!
הפוטנציאל בנקודה $r=b$ נוצר מכל התפלגויות המטען. עבור קליפות כדוריות וכדורים:
- מטען על כדור/קליפה ברדיוס $R$: אם אנחנו בחוץ ($r > R$), הפוטנציאל הוא $\frac{kQ}{r}$
- אם אנחנו בפנים ($r < R$), הפוטנציאל הוא $\frac{kQ}{R}$ (קבוע!)
בנקודה $r = b$ יש שלוש תרומות:
-
הכדור הפנימי ($+3Q$ על $r=a$): אנחנו בחוץ, אז $\frac{k(+3Q)}{b}$
-
השפה הפנימית של הקליפה ($-3Q$ על $r=b$): אנחנו בדיוק עליה, אז $\frac{k(-3Q)}{b}$
-
השפה החיצונית ($+2Q$ על $r=c$): אנחנו בפנים, אז $\frac{k(+2Q)}{c}$
דוגמה לטעות שלי - חישוב ההשפעה מהקצה במקום מהמרכז:
יש עליה השפעה מבפנים ומבחוץ וצריך לסכום:
- ההשפעה של הקליפה החיצונית - במרחק של $c-r$ ממנה - טעות! המרחק הוא מהמרכז!
- ההשפעה של הפנימית במרחק של $b-a$ - טעות! רק b.
- גם פספסתי את ההשפעה של הצד הפנימי של הקליפה החיצונית (שלמעשה מתבטל עם הפנימי).
הפוטנציאל החשמלי במרכז הכדור
השדה אפס אבל הפוטנציאל לא. במקרה הזה יש השפעות חיצוניות שלא מתבטלות וצריך לסכום. אפשר לחשוב על להביא חלקיק מהאינסוף?
נסכום:
- החיצונית משפיעה $\frac{2kQ}{c}$
- החלק הפנימי של החיצונית: $\frac{-3kQ}{b}$
- החלק החיצוני של הפנימי: $\frac{3kQ}{a}$
סך הכל:
\[V_{ball} = k\left(\frac{3Q}{a}+\frac{-3Q}{b}+\frac{2Q}{c}\right)\] דור פסקל