חלק א’: מוליכים והתנהגות מטענים
עקרון יסוד: אין הצטברות מטען בתוך מוליך
בתוך מוליך לא יכולה להיות הצטברות של מטענים (למעט הצטברות שמייצרת שדה אפס)
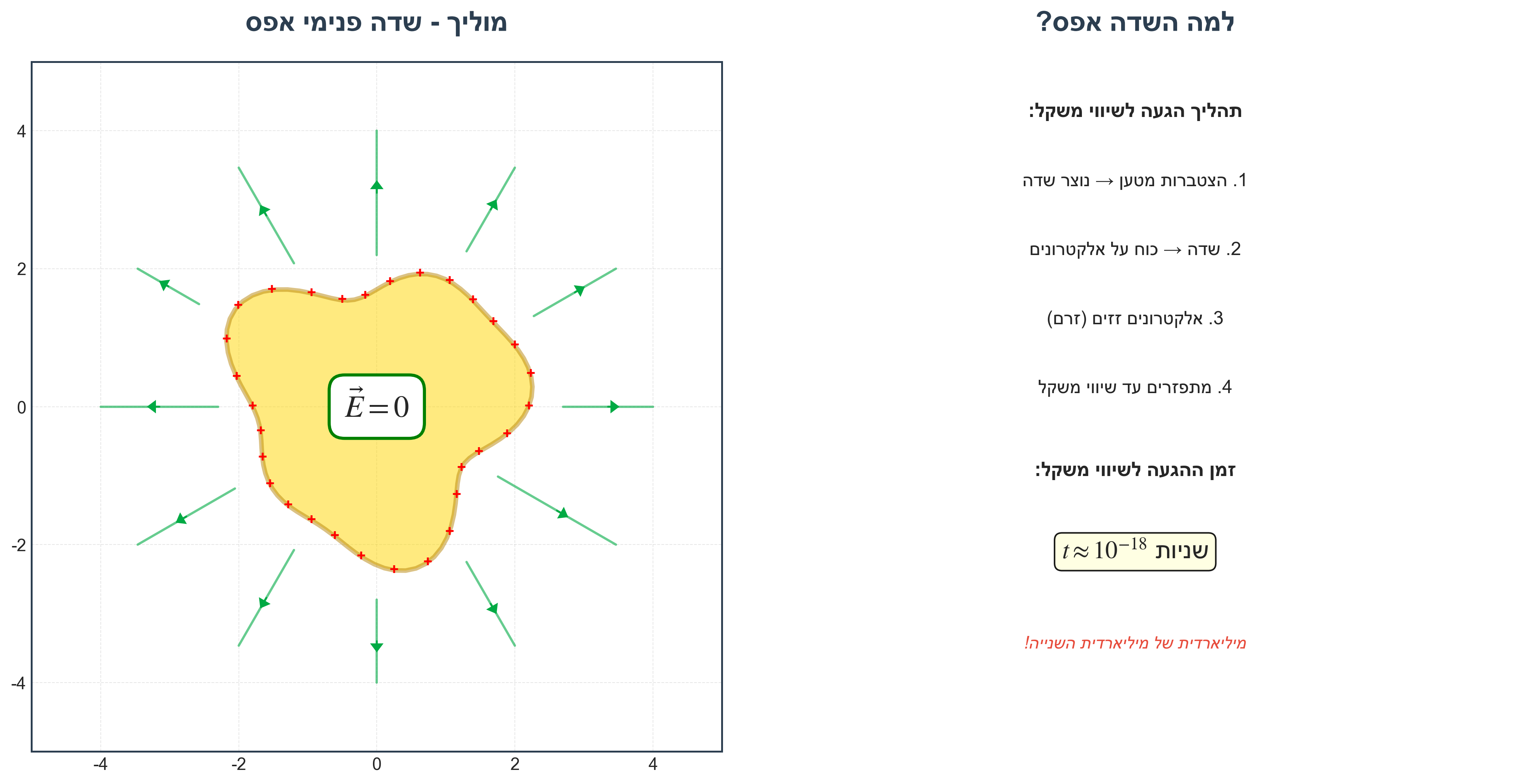
הסיבה הפיזיקלית
- יש הצטברות מטען ← נוצר שדה בתוך המוליך
- שדה ← כוח על מטענים ← המטענים זזים (זרם)
- המטענים מתפזרים עד להגעה לשיווי משקל
- שיווי משקל = המטענים על קליפות המוליך
זמן ההגעה לשיווי משקל
\[t \approx 10^{-18} \, \mathrm{ s}\]להמחשה:
- $10^{-9}$ = מיליארדית השנייה
- $10^{-18}$ = מיליארדית של מיליארדית השנייה
מאפייני מוליכים
- מכילים גז של אלקטרונים כמעט חופשיים
- האלקטרונים אחוזים לאטומים באחיזה חלשה מאוד
- יכולים לקפוץ מאטום לאטום בקלות
- בכל אזור במוליך - המטען הכולל ניטרלי (בקירוב)
חלק ב’: מוליך כדורי חלול - ניתוח מפורט
תיאור המערכת
מוליך כדורי עם:
- רדיוס פנימי: $R_1$
- רדיוס חיצוני: $R_2$
- חלל פנימי (ריק)
- שכבת מתכת בין $R_1$ ל-$R_2$
מקרה 1: מטען $Q$ במרכז החלל
השאלה: איך מתפלג המטען על המוליך? כלומר, מה המטען על הקליפה הפנימית ומה המטען על הקליפה החיצונית?
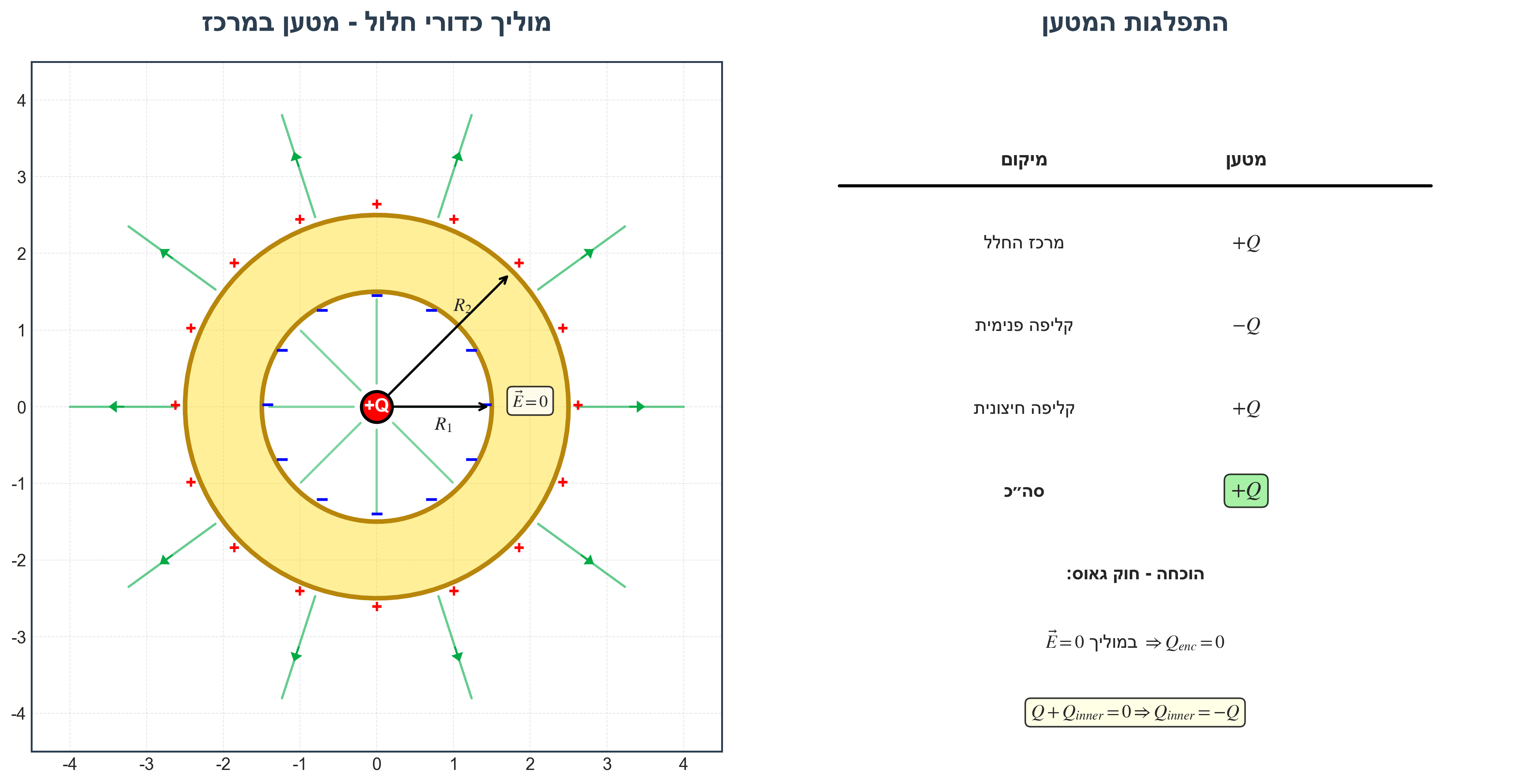
מה קורה?
- המטען $+Q$ במרכז יוצר שדה רדיאלי
- דרישה: שדה אפס בתוך המוליך
- פתרון: על הקליפה הפנימית מצטבר $-Q$
הוכחה באמצעות חוק גאוס
בונים קליפה גאוסית בתוך המוליך (בין $R_1$ ל-$R_2$):
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\varepsilon_0}\]- השדה בתוך המוליך: $\vec{E} = 0$
- לכן: $Q_{\text{enc}} = 0$
- המסקנה: $Q_{\text{inner}} + Q_{\text{inner shell}} = 0$
- לכן: $Q_{\text{inner shell}} = -Q$
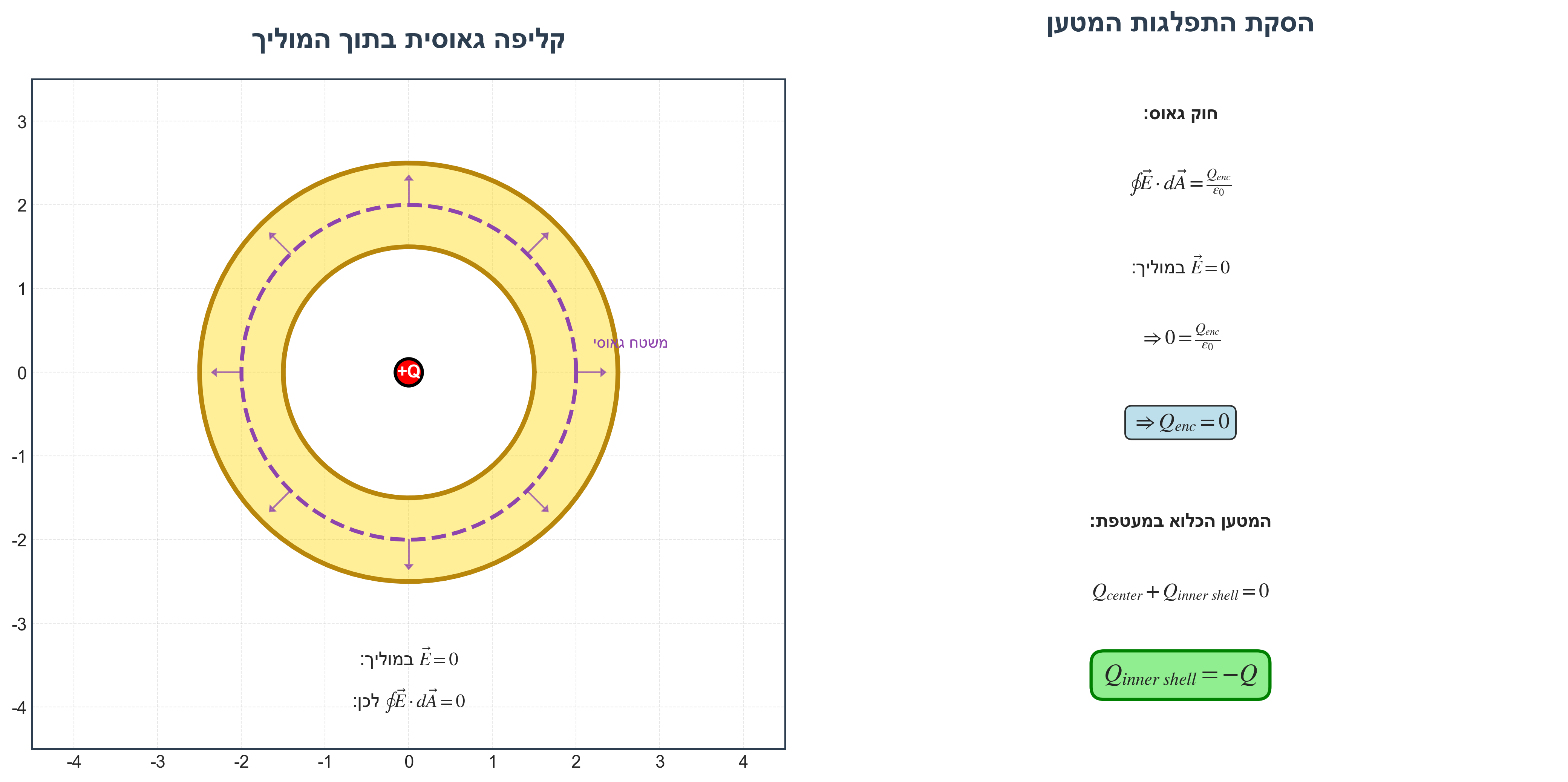
שימור מטען
- המוליך היה ניטרלי
- אם נלקח $-Q$ לקליפה הפנימית
- חייב להישאר $+Q$ על הקליפה החיצונית
סיכום התפלגות המטען
| מיקום | מטען |
|---|---|
| מרכז החלל | $+Q$ |
| קליפה פנימית | $-Q$ |
| קליפה חיצונית | $+Q$ |
| סה”כ | $+Q$ |
מקרה 2: מטען $Q_{big}$ על המוליך (ללא מטען בפנים)
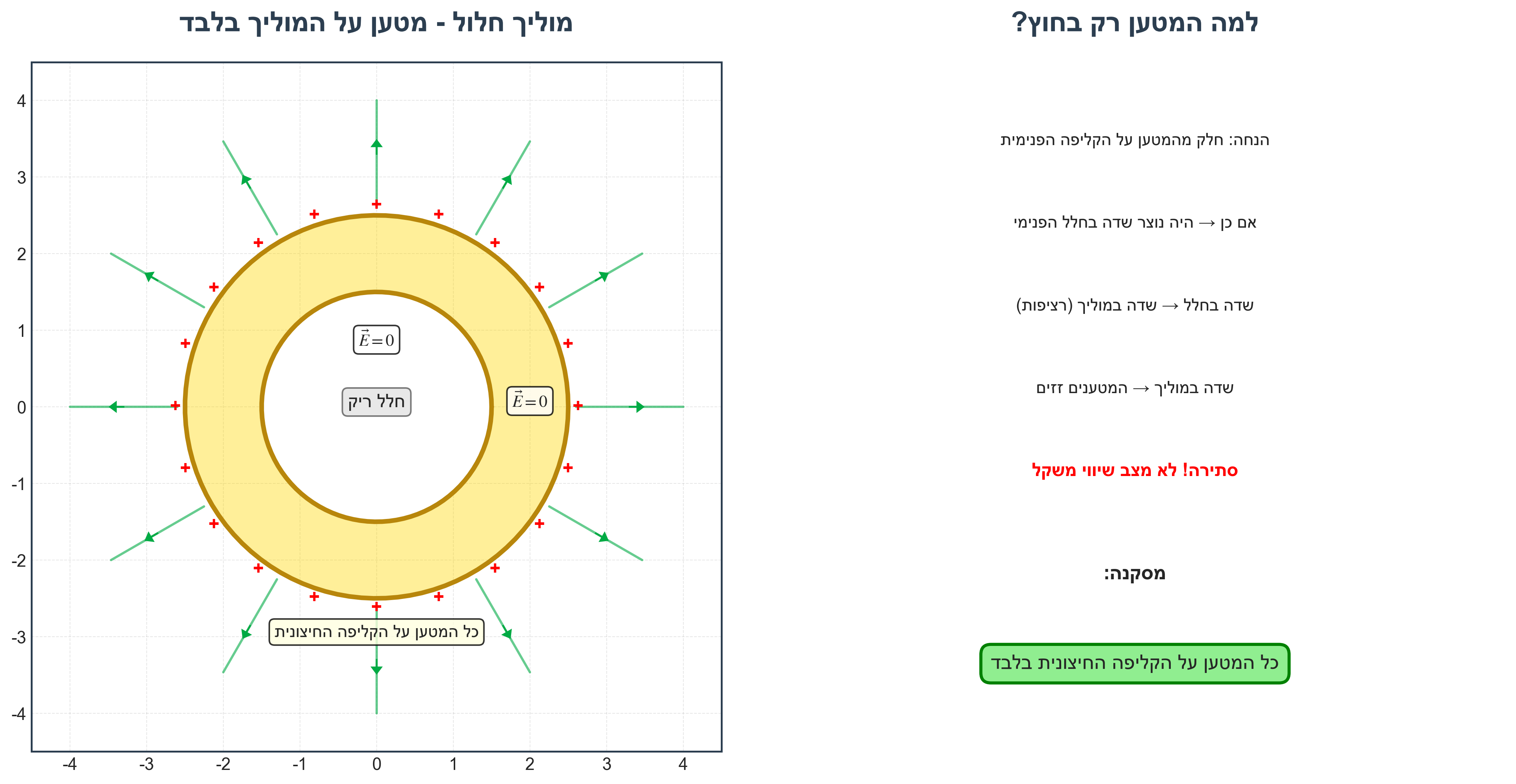
שאלה: איך מתפלג המטען? כלומר, מהו המטען על הקליפה הפנימית ועל הקליפה החיצונית?
תשובה: כל המטען מתרכז על הקליפה החיצונית בלבד
הסבר
- אם חלק מהמטען היה על הקליפה הפנימית ← היה שדה בתוך המוליך
- שדה בתוך המוליך ← המטענים היו זזים (לא מצב סטטי)
- מסקנה: במצב של שיווי משקל, כל המטען בחוץ
מקרה 3: מטען $q$ במרכז ועוד מטען $Q$ על המוליך
- מה התפלגות המטען במוליך?
- מה השדה מחוץ למוליך?
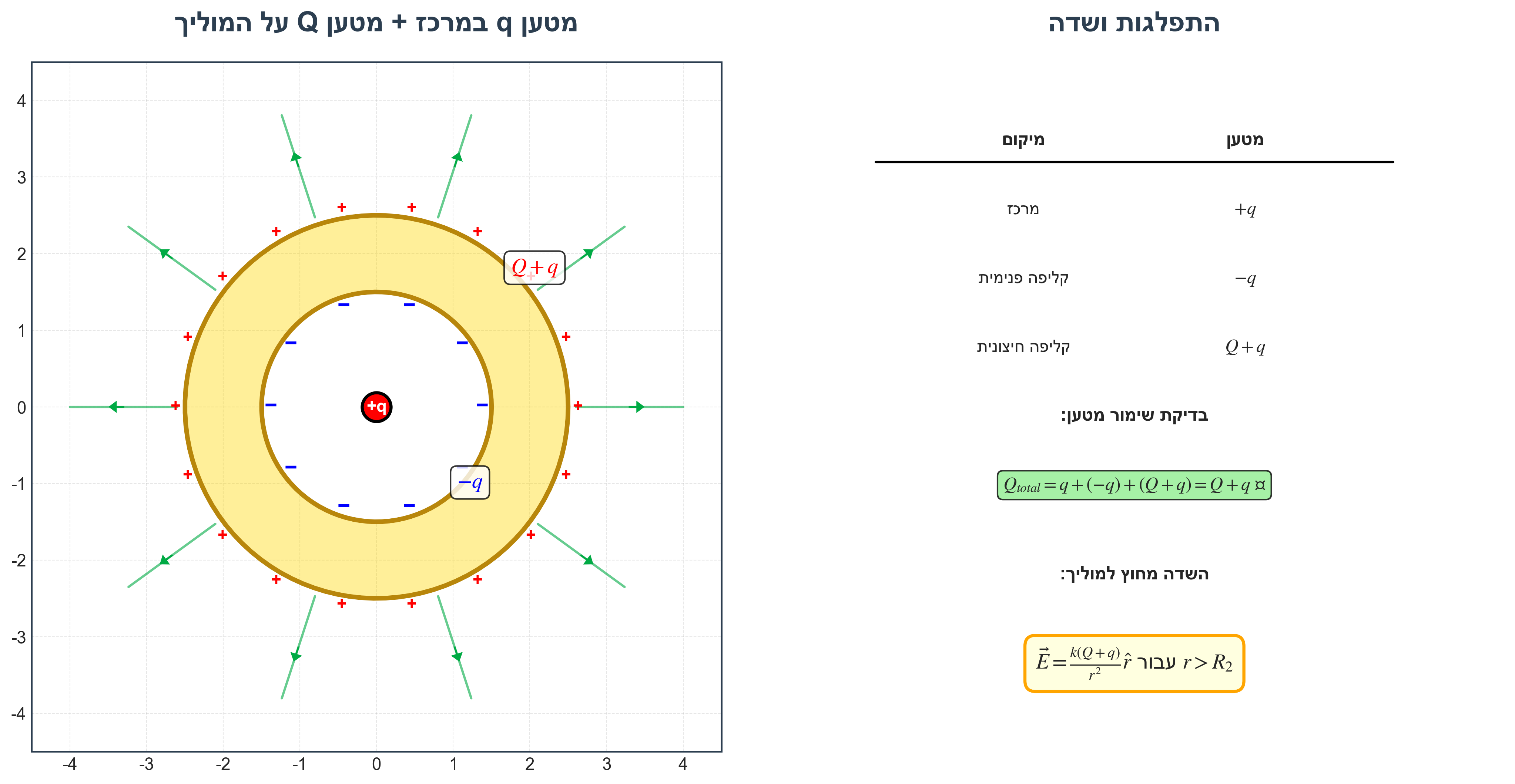
התפלגות המטען
| מיקום | מטען | הסבר |
|---|---|---|
| מרכז | $+q$ | נתון |
| קליפה פנימית | $-q$ | כדי שהשדה בתוך המוליך יהיה אפס |
| קליפה חיצונית | $Q + q$ | שימור מטען: $Q + q - q = Q$ על המוליך |
בדיקת שימור מטען
\[Q_{total} = q + (-q) + (Q+q) = Q + q\]זה נכון! שמנו $q$ במרכז ו-$Q$ על המוליך.
השדה מחוץ למוליך
\[\vec{E} = \frac{k(Q+q)}{r^2}\hat{r} \quad \text{for } r > R_2\]חלק ג’: עקרונות חשובים
עיקרון 1: השדה בתוך מוליך תמיד אפס
\[\vec{E}_{\text{inside a conductor}} = 0\]עיקרון 2: המטען מתרכז על פני השטח
- כל המטען העודף במוליך נמצא על פני השטח בלבד
- אין מטען נטו בנפח הפנימי של המוליך
עיקרון 3: שימור מטען
\[\sum Q = \text{const}\]- מטען לא יכול להיעלם או להיווצר יש מאין
- חשבונות המטען חייבים להישמר (כמו חשבונות מסה)
עיקרון 4: קליפה גאוסית בתוך מוליך
- אם $\vec{E} = 0$ על הקליפה ← $Q_{enc} = 0$
- זה קובע את התפלגות המטען על פני השטח
חלק ד’: מבוא לעבודה ולאנרגיה (יושלם בשיעור הבא)
נושאים שיילמדו
- עבודה בשדה חשמלי - הגדרה וחישוב
- אנרגיה אלקטרוסטטית - אנרגיה הנובעת מתצורת מטענים
- אנרגיה מכנית - קשר לאנרגיה קינטית ופוטנציאלית
- פוטנציאל חשמלי - מושג מרכזי בשיעור הבא
סיכום נקודות מפתח
| נושא | נקודה מרכזית |
|---|---|
| מוליך | שדה פנימי = 0 תמיד |
| מטען במוליך | מתרכז על פני השטח בלבד |
| זמן שיווי משקל | $\sim 10^{-18}$ שניות |
| קליפה גאוסית במוליך | רואה מטען אפס בפנים |
| שימור מטען | חוק שימור בסיסי |
נניח שבמקום מסוים במרחב מרוכז מטען שגודלו $Q$. המטען הזה מייצר במרחב שדה שדועך ביחס $1/r^2$.
נניח שיש לי מטען קטן באינסוף $q$
נניח ש $q$ מטען חיובי ו-$Q$ מטען חיובי.
$Q$ מפעיל שדה שמושך את $q$ לכיוון $Q$.
השאלה: איזה עבודה מבצע $Q$ על $q$ כאשר $q$ נע מאינסוף למרחק $R$ מ-$Q$?
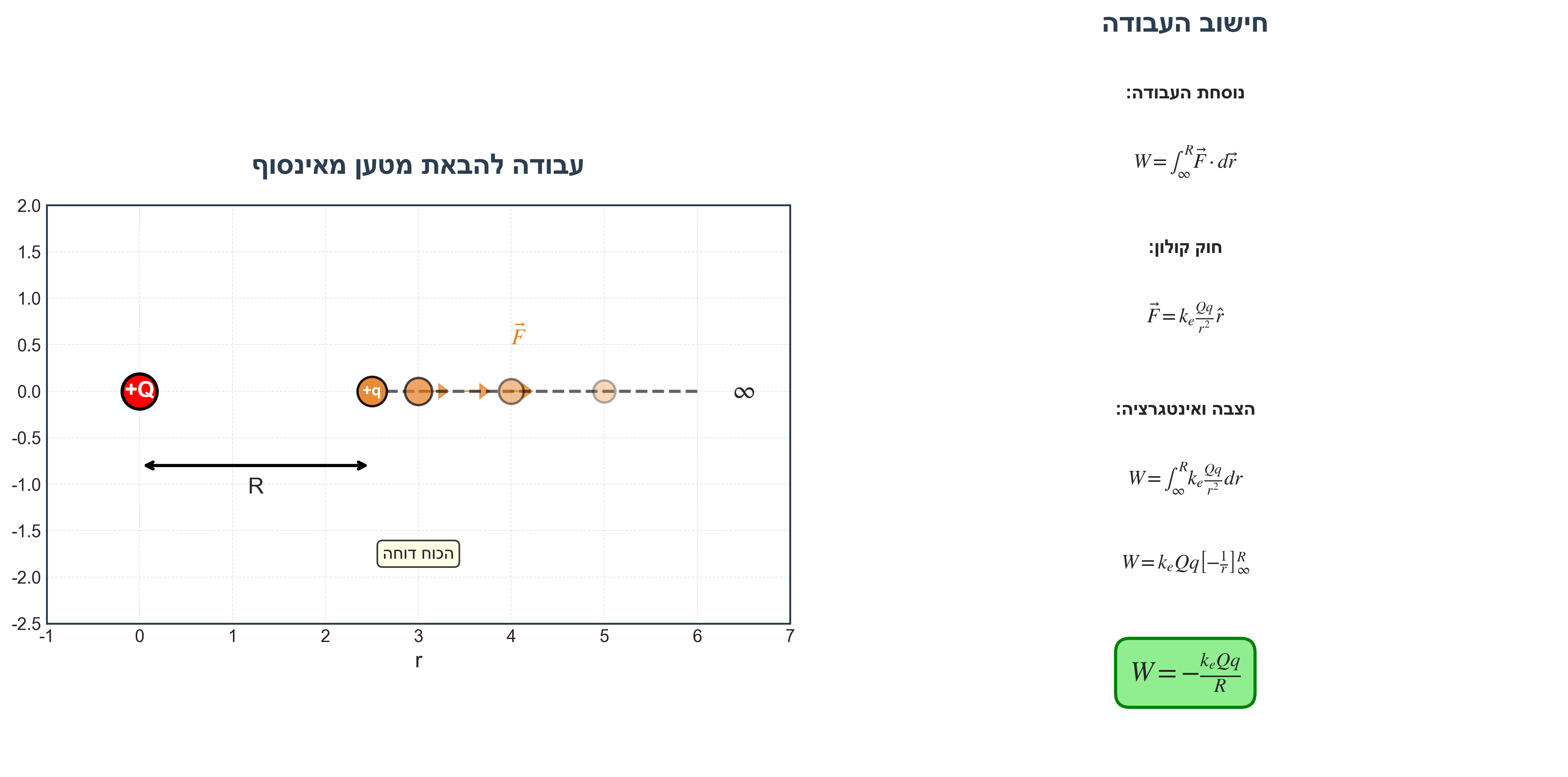
פתרון:
ניעזר בנוסחת העבודה:
\[W = \int_{\infty}^{r=R} \vec{F} \cdot d\vec{r}\]לפי חוק קולון:
\[\vec{F} = k_e \frac{Qq}{r^2} \hat{r}\]כשהסימן שלילי כוח מושך $(-\vec{r})$.
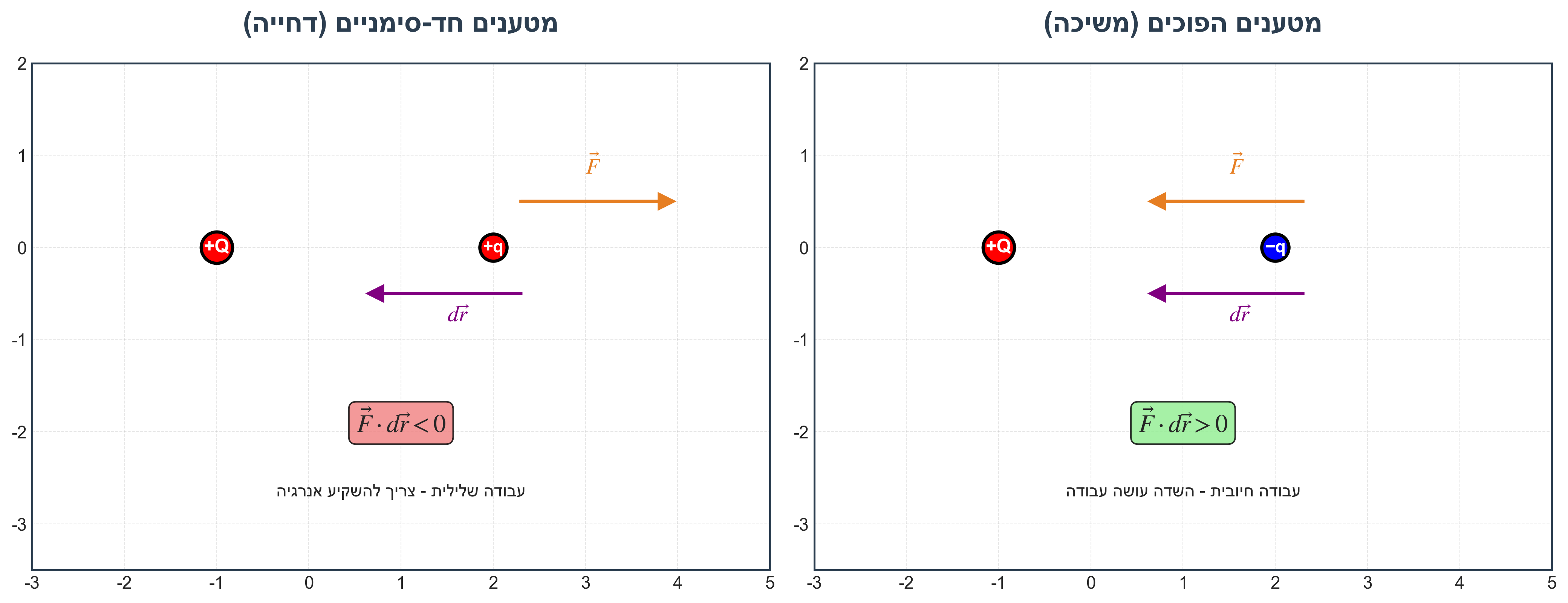
נחזור ונציב באינטגרל:
\[W = \int_{\infty}^{R} k_e \frac{Qq}{r^2} dr\] \[W = k_e Qq \left[ -\frac{1}{r} \right]_{\infty}^{R}\] \[W = k_e \frac{Qq}{R}\] \[= - \frac{K_e Qq}{R} + \cancel{\frac{K_e Qq}{\infty}}\]סך הכל:
\[\boxed{W = - k_e \frac{Qq}{R}}\]דור פסקל