שאלה 1: גוף במישור משופע
גוף בעל מסה $m$ נמצא על משטח משופע בזווית $\theta$ ביחס לאופק. מקדם החיכוך הסטטי בין הגוף למשטח הוא $\mu_s$.
- באילו זוויות הגוף ישאר במקומו ולא יחליק?
- במידה שהזווית גדולה יותר, מהו המרחק שהגוף יעבור ב-$t$ שניות?
- מהי הזווית עבורה הגוף ינוע במהירות קבועה במורד?
- האם הוא יכול לנוע במהירות קבועה במעלה המישור המשופע?
פתרון מפורט
חלק א: תנאי שיווי משקל
נבחר מערכת צירים: ציר $x$ במקביל למשטח (חיובי במורד), ציר $y$ ניצב למשטח.
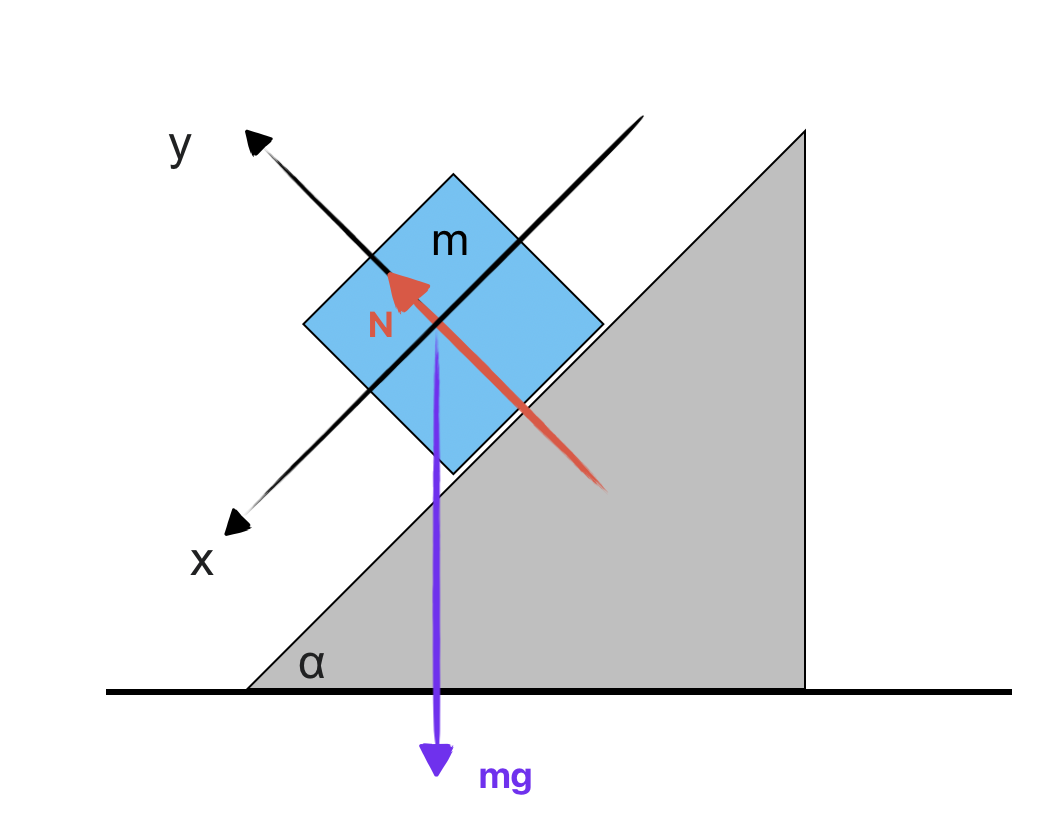
משוואות שיווי משקל בכיוון $y$:
\[\sum F_y = N - mg\cos\theta = 0\]לכן הכוח הנורמלי:
\[\boxed{N = mg\cos\theta}\]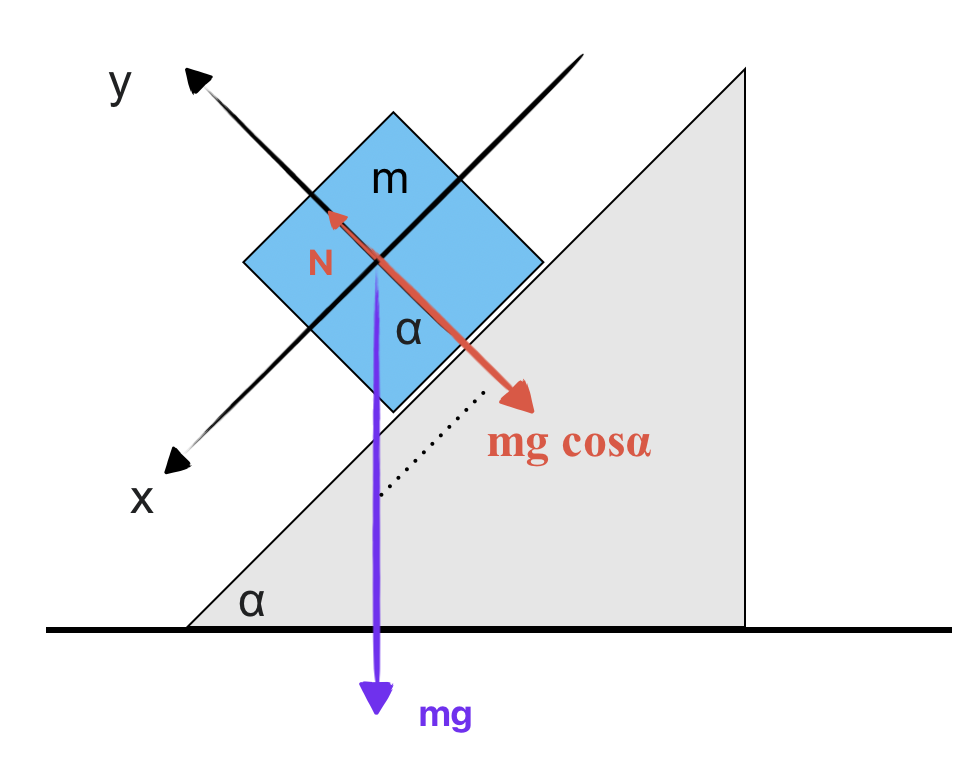
משוואות שיווי משקל בכיוון $x$:
\[\sum F_x = mg\sin\theta - f_s = 0\]כאשר $f_s \leq \mu_s N$, סכום הכוחות שווה לאפס מכיוון שבתחילה הגוף במנוחה. כלומר:
\[\begin{aligned} mg\sin\theta - f_s &\leq 0 \\[10pt] mg\sin\theta &\leq f_s \\[10pt] &\leq \mu_s N \end{aligned}\]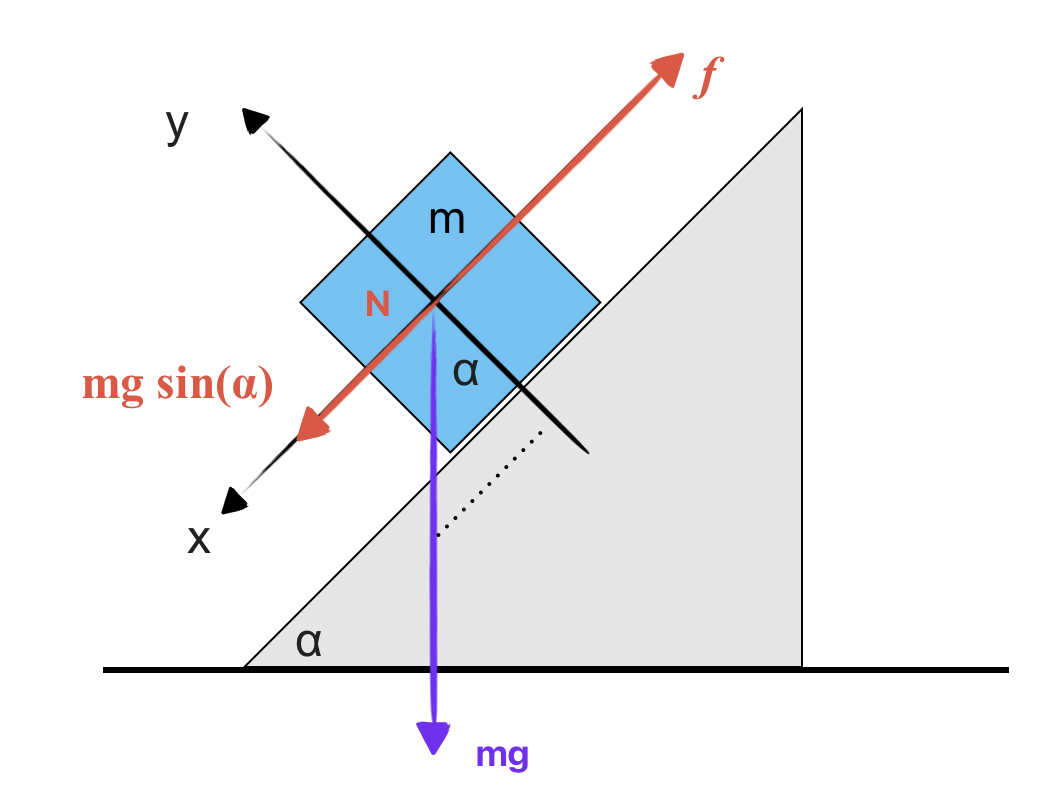
נציב את $N$ שמצאנו, אז לאחר שהעברנו את $f_s$ אגף:
\[\begin{aligned} mg\sin\theta &\leq \mu_s mg\cos\theta \\[10pt] \tan\theta &\leq \mu_s \\[10pt] \implies \theta &\leq \arctan(\mu_s) \end{aligned}\]$\tan(\theta)$ פונציה עולה ולכן:
\[\implies 0 \leq \theta \leq \arctan(\mu_s)\]כלומר, הגוף יישאר במקומו כאשר הזווית $\theta$ קטנה או שווה לזווית הקריטית:
\[\boxed{\theta \leq \arctan(\mu_s)}\]המרחק כאשר הגוף מתחיל להחליק
כאשר $\theta > \arctan(\mu_s)$, הגוף מתחיל להחליק במורד המישור, ואז יש להשתמש בחיכוך קינטי $f_k = \mu_k N$. מכאן:
\[\begin{aligned} \sum F_x &= mg\sin\theta - \mu_k mg\cos\theta = ma_x \\[10pt] & \cancel{m}g \sin\theta - \mu_k \cancel{m}g\cos\theta = \cancel{m}a_x \\[10pt] \implies a_x &= g(\sin\theta - \mu_k\cos\theta) \end{aligned}\]כלומר, התאוצה של הגוף במורד המישור היא:
\[\boxed{a_x = g(\sin\theta - \mu_k\cos\theta)}\]זוהי תאוצה קבועה, ולכן לפי נוסחת מיקום בתאוצה קבועה נוכל לקבל את המרחק שהגוף עובר לאחר זמן $t$:
\[\begin{aligned} x(t) - x(0) &= \Delta x = v_0 t + \frac{1}{2}a_x t^2 = \frac{g(\sin\theta - \mu_k\cos\theta)}{2} t^2 \\[10pt] \implies \Delta x &= \frac{g}{2}(\sin\theta - \mu_k\cos\theta)t^2 \end{aligned}\]כלומר, המרחק שהגוף עובר לאחר זמן $t$ הוא:
\[\boxed{\Delta x = \frac{g}{2}(\sin\theta - \mu_k\cos\theta)t^2}\]מה הזווית עבורה הגוף ינוע במהירות קבועה במורד המישור?
השאלה השקולה היא באיזו זווית התאוצה $a_x = 0$
\[\begin{aligned} \sin(\theta_0) &= \mu_k\cos(\theta_0) \\[10pt] \implies \tan(\theta_0) &= \mu_k \\[10pt] \implies \theta_0 &= \arctan(\mu_k) \end{aligned}\]כלומר, הגוף ינוע במהירות קבועה במורד המישור כאשר הזווית היא:
\[\boxed{\theta_0 = \arctan(\mu_k)}\]האם הגוף יכול לנוע במהירות קבועה במעלה המישור?
לא. בתנועה במעלה המישור כוח החיכוך הקינטי פועל כלפי מטה, ויצטרף לכוח הכובד. $\sum F_x$ חיובי ממש, שגורם לתאוצה חיובית בכיוון המורד ולא תתקיים מהירות קבועה.
שאלה 2: תנועה הרמונית פשוטה
גוף בעל מסה $m = 0.1 \mathrm{kg}$ נע בתנועה הרמונית לאורך ציר $x$ עם:
- משרעת התנודה: $C = 0.25 \mathrm{[m]}$
- זמן המחזור: $T = 2 \mathrm{[s]}$
- מיקום התחלתי: $x_0 = x(t=0) = 0.12 \mathrm{[m]}$
נדרש למצוא:
- את הכוח הפועל על הגוף בזמן $t = \frac{1}{3}$ שנייה
- את המהירות בזמן $t = 0$
- את המהירות כשהגוף עובר בנקודת שיווי המשקל
פתרון מפורט
הגדרת משוואת התנועה
התנועה ההרמונית מתוארת על ידי:
\[x(t) = A\cos(\omega t + \phi)\]כאשר $A$ היא האמפליטודה, $\omega$ התדירות הזוויתית, ו-$\phi$ הפאזה ההתחלתית.
מהנתונים נוכל לקבל את ערכי $A$, $\omega$ ו-$\phi$:
\[A = C = 0.25 \mathrm{[m]}\]מהנתון על זמן המחזור $T$:
\[\begin{aligned} T &= 2 \mathrm{[s]} \\[10pt] &\implies f = \frac{1}{T} = \frac{1}{2} \mathrm{[Hz]} \\[10pt] &\implies \omega = 2\pi f = 2\pi \cdot \frac{1}{2} = \pi \mathrm{ [rad/s]} \end{aligned}\]כלומר:
- $\omega = \frac{2\pi}{T} = \frac{2\pi}{2} = \pi$ רד/שנייה
מציאת הפאזה ההתחלתית $\phi$
מתנאי ההתחלה $x(0) = 0.12 \mathrm{[m]}$:
\[\begin{aligned} x(0) &= A\cos(\omega \cdot 0 + \phi) = 0.12 \\[10pt] &= A\cos(\phi) \\[10pt] &= 0.25\cos(\phi) \end{aligned}\] \[0.25\cos(\phi) = 0.12\] \[\begin{aligned} \cos(\phi) &= \frac{0.12}{0.25} \\[10pt] \implies \phi &= \arccos\left(0.48\right) = 1.07 \mathrm{[rad]} \end{aligned}\]משוואת המיקום המלאה:
\[\boxed{x(t) = 0.25\cos(\pi t + 1.07)}\]חלק א: הכוח בזמן $t = \frac{1}{3}$ שנייה
המהירות:
\[\dot{x}(t) = -0.25\pi\sin(\pi t + 1.07)\]התאוצה:
\[\ddot{x}(t) = -0.25\pi^2\cos(\pi t + 1.07)\]בזמן $t = \frac{1}{3}$:
\[x\left(\frac{1}{3}\right) = 0.25\cos\left(\frac{\pi}{3} + 1.07\right) = 0.25\cos(2.12) \approx -0.125 \mathrm{[m]}\]הכוח:
\[F = m\ddot{x} = 0.1 \times (-\pi^2) \times (-0.125) = 0.1 \times 9.87 \times 0.125\] \[\boxed{F\left(\frac{1}{3}\right) = 0.123 \mathrm{[N]}}\]חלק ב: המהירות ההתחלתית
\[v(0) = \dot{x}(0) = -0.25\pi\sin(1.07)\] \[\boxed{v(0) = -0.69 \mathrm{[m/s]}}\]חלק ג: המהירות בנקודות שיווי המשקל
הגוף עובר בנקודת שיווי המשקל כאשר $x = 0$:
\[\cos(\pi t + 1.07) = 0\] \[\pi t + 1.07 = \frac{\pi}{2} + n\pi\]לכן:
\[t_n = \frac{1}{\pi}\left(\frac{\pi}{2} + n\pi - 1.07\right)\]המהירות בזמנים אלו:
\[v(t_n) = -0.25\pi\sin\left(\frac{\pi}{2} + n\pi\right) = (-1)^{n+1} \times 0.25\pi\]עבור $n = 0$:
\[t_0 = 0.16 \mathrm{[s]}\] \[\boxed{v(t_0) = -\frac{\pi}{4} = -0.785 \mathrm{[m/s]}}\]שאלה 3: תנועה מעגלית עם תאוצה זוויתית משתנה
ילד עומד במרחק $R$ ממרכז קרוסלה. הקרוסלה מתחילה ממנוחה עם תאוצה זוויתית:
\[a_t = (1 - e^{-t})\]תנאי התחלה: $v(0) = 0$, $\theta(0) = 0$
נדרש למצוא:
- את התאוצה הזוויתית ($\ddot{\theta}$)
- את המהירות הזוויתית ($\omega(t)$) כפונקציה של הזמן
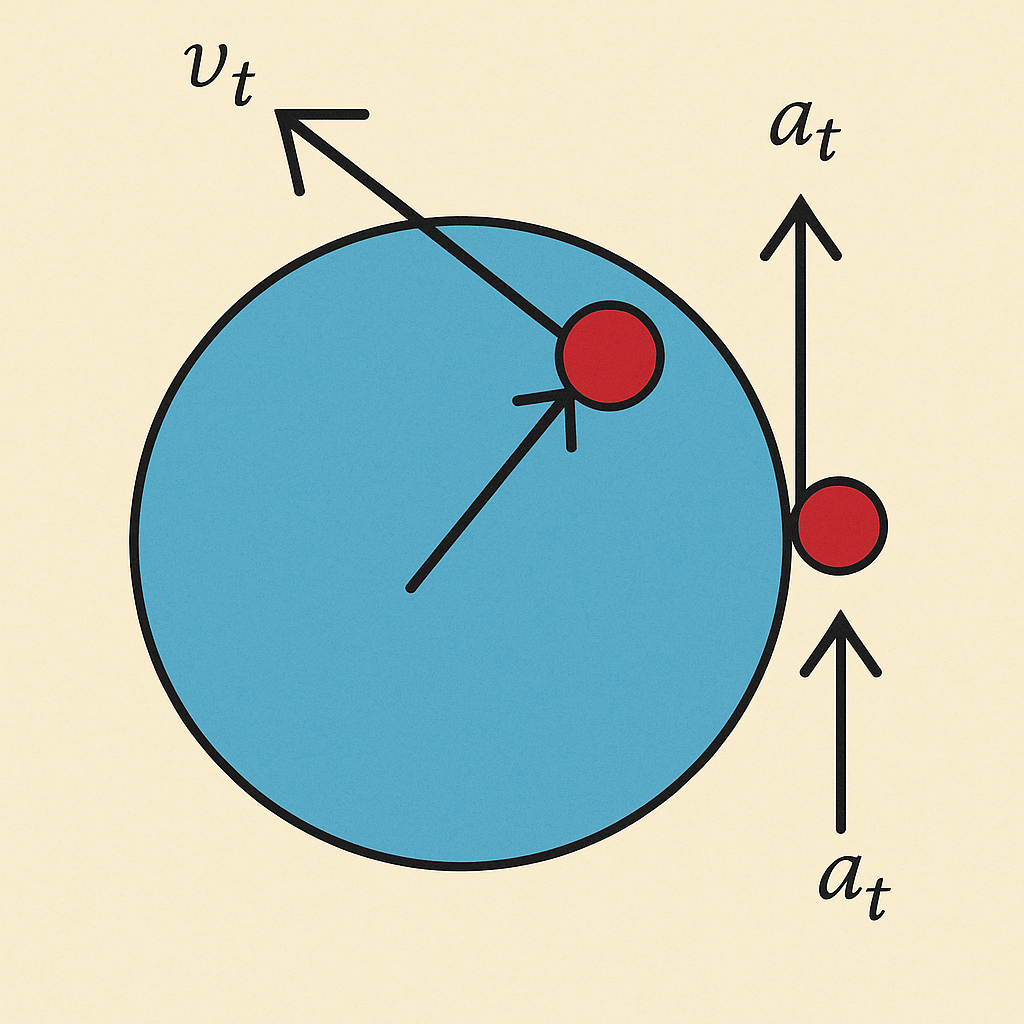
פתרון מפורט
הערה: הסימונים הבאים שקולים:
\[a_t = a_\theta = a_{\text{tangential}}\]
נזכר בנוסחאות שפיתחנו בשיעור:
\[\begin{aligned} \vec{a} &= a_r \hat{r} + a_\theta \hat{\theta} \\[10pt] &= \underbrace{\left(\ddot{r} - r\dot{\theta}^2\right)}_{a_r}\hat{r} + \underbrace{\left(2\dot{r}\dot{\theta} + r\ddot{\theta}\right)}_{a_\theta}\hat{\theta} \end{aligned}\]במקרה הזה אין לנו תאוצה רדיאלית - כי מדובר בקרוסלה, כלומר:
\[\vec{a} = a_\theta \hat{\theta}\]ניעזר בפיתוח של וקטור התאוצה בקואורדינטות פולריות:
\[a_\theta = \left(\cancel{2\underbrace{\dot{r}}_{=0}\dot{\theta}} + r\ddot{\theta}\right) = R\ddot{\theta}\]הביטוי שמתקבל הוא $R\ddot{\theta}$, בגלל שבקרוסלה הילד לא משנה את הרדיוס, כלומר $\dot{r} = 0$.
מציאת התאוצה הזוויתית ($\ddot{\theta}$)
\[\boxed{\ddot{\theta}(t) = \frac{a_\theta}{R} = \frac{\left(1-e^{-t}\right)}{R}}\]מציאת המהירות הזוויתית ($\omega = \dot{\theta}$)
המהירות הזוויתית קשורה לתאוצה הזוויתית על ידי:
\[\ddot{\theta} = \frac{d\dot{\theta}}{dt} = \frac{d\omega}{dt}\]נוכל להוציא את $\omega$ על ידי אינטגרציה של $\ddot{\theta}$:
\[\implies \omega(t)-\underbrace{\omega(0)}_{=0} = \int_0^t \ddot{\theta}(s) ds\]נציב את התאוצה שמצאנו ונפתור את האינטגרל לקבלת המהירות הזוויתית:
\[\begin{aligned} \implies \omega(t) &= \int_0^t \frac{1-e^{-s}}{R} ds = \frac{1}{R}\left[s + e^{-s}\right]_0^t \\[10pt] &= \frac{t+ e^{-t} - 1}{R} \end{aligned}\]המהירות הזוויתית:
\[\boxed{\omega(t) = \frac{t + e^{-t} - 1}{R} \mathrm{[rad/s]}}\]מציאת הזווית הכוללת ($\theta(t)$)
\[\begin{aligned} \theta(t) &= \int_0^t \omega(s) ds \\[10pt] &= \frac{1}{R}\int_0^t (s + e^{-s} - 1) ds \\[10pt] &= \frac{1}{R}\left[\frac{s^2}{2} - e^{-s} - s\right]_0^t \end{aligned}\] \[\boxed{\theta(t) = \frac{1}{R}\left(\frac{t^2}{2} + 1 - e^{-t} - t\right) \mathrm{[rad]}}\]וקטור התאוצה בקואורדינטות פולריות
בקואורדינטות פולריות, התאוצה הכוללת:
\[\vec{a} = (a_r)\hat{r} + (a_\theta)\hat{\theta}\]כאשר:
-
התאוצה הרדיאלית (צנטריפטלית), ממה שמצאנו קודם על המהירות הזוויתית:
\[a_r = -R\omega^2 = -R\left(\frac{t + e^{-t} - 1}{R}\right)^2\] -
התאוצה המשיקית, מהנתון:
\[a_\theta = R\alpha = 1 - e^{-t}\]
לכן:
\[\boxed{\vec{a}(t) = -\frac{(t + e^{-t} - 1)^2}{R}\hat{r} + (1 - e^{-t})\hat{\theta}}\]וקטור המהירות
הנוסחה לחישוב וקטור המהירות בקואורדינטות פולריות:
\[\vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta}\]כאמור הנגזרת של הרדיוס היא אפס, כלומר $\dot{r} = 0$. לכן:
\[\vec{v} = R\dot{\theta}\hat{\theta} = R\left(\frac{t + e^{-t} - 1}{R}\right)\hat{\theta}\] \[\boxed{\vec{v}(t) = (t + e^{-t} - 1)\hat{\theta}}\]וקטור המיקום בקואורדינטות קרטזיות
בהנחה שבזמן $t = 0$ הילד נמצא על ציר $x$ החיובי:
\[\begin{aligned} \vec{r}(t) &= R\cos[\theta(t)]\hat{x} + R\sin[\theta(t)]\hat{y} \\[10pt] &= R\cos\left[\frac{t^2/2 + 1 - e^{-t} - t}{R}\right]\hat{x} \\[10pt] &+ R\sin\left[\frac{t^2/2 + 1 - e^{-t} - t}{R}\right]\hat{y} \end{aligned}\]סיכום עקרונות מרכזיים
1. ניתוח כוחות במישור משופע
- תמיד יש לפרק את כוח הכובד לרכיבים מקבילים וניצבים למשטח
- הזווית הקריטית תלויה רק במקדם החיכוך ולא במסה
- $\tan\theta_c = \mu_s$ היא נוסחה אוניברסלית
2. תנועה הרמונית פשוטה
- הכוח פרופורציונלי להעתק: $F = -kx$
- התדירות אינה תלויה באמפליטודה
- המהירות המקסימלית: $v_{max} = A\omega$
3. תנועה מעגלית
- בתנועה מעגלית תמיד קיימת תאוצה צנטריפטלית: $a_r = -R\omega^2$
- כאשר המהירות הזוויתית משתנה, קיימת גם תאוצה משיקית: $a_\theta = R\alpha$
- וקטור התאוצה הכולל הוא סכום וקטורי של שני הרכיבים
חזור לתרגול 8
עבור לשיעור 9