רקע היסטורי
המכניקה הניוטונית, נושא הלימוד בקורס זה, פותחה במאה ה-17 על ידי שני ענקי המדע: גוטפריד וילהלם לייבניץ ואיזק ניוטון. שני אישים אלה, שהיו יריבים מפורסמים, תרמו כל אחד בדרכו להתפתחות הפיזיקה המודרנית.
לייבניץ (1716-1646) היה איש אשכולות במלוא מובן המילה - פילוסוף דגול שרעיונותיו נלמדים עד היום, מתמטיקאי שפיתח את החשבון האינפיניטסימלי, ואף המציא את רוב הסימונים המתמטיים שבהם אנו משתמשים כיום.
ניוטון (1727-1643), יריבו הגדול, היה לא רק מדען אלא גם תיאולוג שעסק רבות בפרשנות המקרא, במיוחד בנבואות אחרית הימים. הוא שלט בעברית והותיר אחריו כתבים רבים העוסקים בפענוח ספרי דניאל ויחזקאל. מעניין לציין שניוטון עסק גם באלכימיה וניסה להפוך חומרים פשוטים לזהב - משימה שהטבע אכן מבצע בליבות כוכבים כבדים, שם יסודות קלים הופכים ליסודות כבדים יותר.
 |  |
|---|---|
| ניוטון (1727-1643) | לייבניץ (1716-1646) |
המכניקה הניוטונית בפרספקטיבה
ניוטון הצליח לנסח את הדינמיקה והקינמטיקה של גופים באמצעות מערכת חוקים ומשוואות דיפרנציאליות. הישגו המרכזי היה ההבנה שאותם חוקים פיזיקליים השולטים בתנועת גופים במעבדה שולטים גם בתנועת גרמי השמיים.
כעבור כ-200 שנה, איינשטיין הראה שהמכניקה הניוטונית היא קירוב מצוין לתיאור הטבע, אך לא התיאור המלא. באנלוגיה: כשם שהסביבה הקרובה נראית לנו שטוחה אף שאנו חיים על כדור, כך המכניקה הניוטונית היא קירוב מצוין למציאות ברוב המצבים היומיומיים, אך היא חלק מתיאוריה רחבה יותר - תורת היחסות.
למרות שתורת היחסות היא “הדבר האמיתי והיפה”, כל פיזיקאי מתחיל את דרכו בלימוד המכניקה הניוטונית, שמהווה את הבסיס להבנת הפיזיקה המודרנית.
כלים מתמטיים נדרשים
לימוד הפיזיקה דורש כלים מתמטיים מתקדמים מעבר לחשבון האינפיניטסימלי הבסיסי. בקורס זה נזדקק למשוואות דיפרנציאליות ברמת מבוא, אלגברה לינארית, פונקציות מרובות משתנים, משוואות דיפרנציאליות חלקיות, ואופרטורי גזירה דיפרנציאליים וקטוריים. כלים אלה יילמדו תוך כדי הקורס בהתאם לצורך.
המרחב התלת-ממדי וחשבון וקטורים
המציאות הפיזיקלית שלנו היא תלת-ממדית. כדי לקבוע מיקום מדויק של נקודה במרחב, נדרשים שלושה מספרים. לשם כך אנו משתמשים במערכת של שלושה צירים ניצבים זה לזה, עם ראשית משותפת המשמשת כנקודת ייחוס.
מערכת צירים ימנית
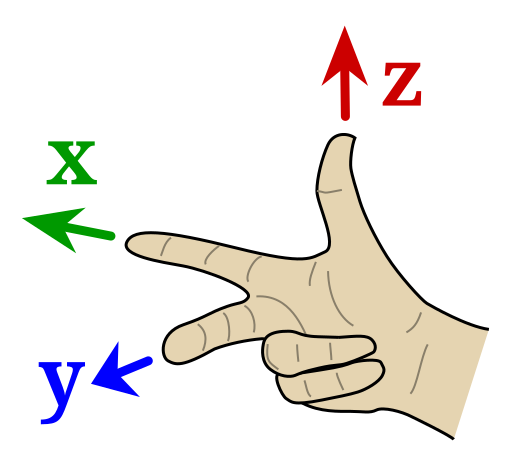
מערכת הצירים הסטנדרטית בפיזיקה מאורגנת כ”שלשה ימנית” על פי כלל יד ימין (כלל בורג ימני): כאשר אצבעות יד ימין מתכופפות מציר x לציר y, האגודל מצביע בכיוון ציר z.
 | |
|---|---|
| כלל יד ימין | מערכת צירים תלת-ממדית ימנית (מימין) ושמאלית (משמאל) |
הגדרת וקטור
וקטור הוא ישות מתמטית שמתארת גודל וכיוון במרחב. ברמה האלמנטרית, וקטור מסומן באמצעות אות עם חץ מעליה (למשל $\vec{v}$), ובספרות מקצועית לעתים משתמשים באות מודגשת ($\mathbf{v}$).
במרחב תלת-ממדי, וקטור מיוצג על ידי שלשה סדורה של מספרים, למשל $(2,1,3)$, כאשר כל מספר מייצג את הרכיב בכיוון הציר המתאים.
מאפייני וקטור
וקטור מאופיין על ידי שני גדלים בסיסיים:
- גודל - אורך הוקטור
- כיוון - האוריינטציה שלו במרחב
ייצוג גרפי של וקטור
וקטור מיוצג גרפית כחץ. לדוגמה, הוקטור $(2,1,3)$ מתקבל על ידי תזוזה של 2 יחידות בכיוון ציר $x$, יחידה אחת בכיוון ציר $y$, ו-3 יחידות בכיוון ציר $z$. החץ המייצג את הוקטור נמתח מראשית הצירים לנקודה הסופית.
וקטורי יחידה
וקטור יחידה הוא וקטור שאורכו שווה בדיוק לאחד. לכל וקטור $\vec{r}$ ניתן להגדיר וקטור יחידה בכיוונו:
\[\hat{r} = \frac{\vec{r}}{\vert\vec{r}\vert}\]כאשר $\vert\hat{r}\vert = 1$.
במערכת צירים קרטזית מוגדרים שלושה וקטורי יחידה בסיסיים:
- $\hat{x}$ (או $\hat{i}$) = $(1,0,0)$ - וקטור יחידה בכיוון ציר x
- $\hat{y}$ (או $\hat{j}$) = $(0,1,0)$ - וקטור יחידה בכיוון ציר y
- $\hat{z}$ (או $\hat{k}$) = $(0,0,1)$ - וקטור יחידה בכיוון ציר z
וקטורי יחידה אלה מהווים בסיס סטנדרטי למרחב התלת-ממדי. כל וקטור ניתן לפירוק לרכיביו באמצעותם:
\[\vec{a} = a_x\hat{x} + a_y\hat{y} + a_z\hat{z}\]שיטות לתיאור וקטורים
תיאור קרטזי
בתיאור קרטזי, וקטור מיוצג על ידי הקואורדינטות שלו ביחס לצירים:
\[\vec{a} = (a_x, a_y, a_z)\]תיאור פולרי (דו-ממדי)
במישור דו-ממדי, ניתן לתאר וקטור באמצעות אורכו והזווית שהוא יוצר עם ציר $x$ החיובי. הקשר בין שני התיאורים נתון על ידי:
- $\tan \theta = \frac{a_y}{a_x}$
- $\theta = \arctan(\frac{a_y}{a_x})$
- $\vert\vec{a}\vert = \sqrt{a_x^2 + a_y^2}$
אורך וקטור
אורך (או גודל) של וקטור מחושב באמצעות הכללה של משפט פיתגורס:
\[\vert \vec{a}\vert = \sqrt{a_x^2 + a_y^2 + a_z^2}\]נוסחה זו ניתנת להכללה למרחב $n$-ממדי:
\[\vert \vec{a}\vert = \sqrt{a_1^2 + a_2^2 + \ldots + a_N^2}\]פעולות על וקטורים
מכפלת סקלר בווקטור
סקלר הוא גודל המתואר על ידי מספר בלבד, ללא כיוון. כאשר כופלים סקלר $\alpha$ בווקטור $\vec{a} = (a_x, a_y, a_z)$, מתקבל:
\[\alpha \vec{a} = (\alpha a_x, \alpha a_y, \alpha a_z)\]המשמעות הגיאומטרית של פעולה זו:
- אם $\alpha > 1$: מתיחת הוקטור
- אם $0 < \alpha < 1$: כיווץ הוקטור
- אם $\alpha < 0$: היפוך כיוון הוקטור (בנוסף לשינוי האורך)
דוגמה 1
נתון $\vec{a} = (3, 2, -1)$. נחשב:
- $2\vec{a} = 2(3, 2, -1) = (6, 4, -2)$
- $\vert\vec{a}\vert = \sqrt{3^2 + 2^2 + (-1)^2} = \sqrt{14}$
- $\vert2\vec{a}\vert = \sqrt{6^2 + 4^2 + (-2)^2} = \sqrt{56} = 2\sqrt{14}$
שימו לב שאורך הוקטור הוכפל בדיוק באותו גורם.
חיבור וחיסור וקטורים
חיבור וקטורים מבוצע רכיב-רכיב:
\[\vec{a} + \vec{b} = (a_x + b_x, a_y + b_y, a_z + b_z)\]באופן דומה, חיסור וקטורים:
\[\vec{a} - \vec{b} = (a_x - b_x, a_y - b_y, a_z - b_z)\]דוגמה 2
נתונים:
- $\vec{a} = (2, 2) = 2\hat{x} + 2\hat{y}$
- $\vec{b} = (1, 3) = \hat{x} + 3\hat{y}$
חיבורם:
\[\vec{a} + \vec{b} = (2,2) + (1,3) = (3,5)\]המשמעות הגיאומטרית של חיבור וקטורים
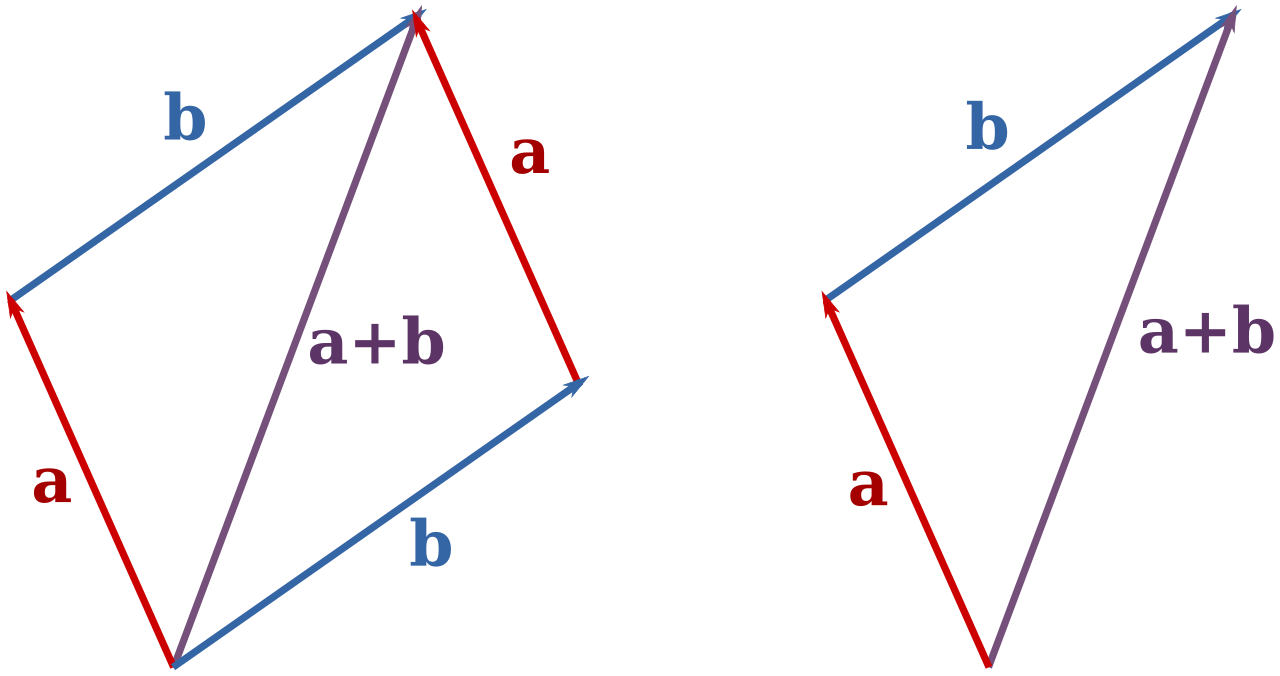
גיאומטרית, סכום של שני וקטורים הוא האלכסון הגדול במקבילית ששני הווקטורים פורשים. הסכום הזה נקרא השקול הווקטורי. האלכסון הקטן במקבילית מייצג את ההפרש בין הוקטורים.
 |
|---|
| מקבילית הוקטורים - הסכום הוא האלכסון הגדול |
משפט פיתגורס במרחב תלת-ממדי
נרחיב את משפט פיתגורס למרחב תלת-ממדי:
\[\vert \vec{a}\vert = \sqrt{a_x^2 + a_y^2 + a_z^2}\]ניתן לצייר נקודה במרחב תלת-ממדי ולהשתמש במשפט פיתגורס פעמיים כדי לחשב את המרחק שלה מהראשית.
\[\begin{aligned} \vec{a} &= (a_x, a_y, a_z) \\[10pt] \vert \vec{a}| &= \sqrt{a_x^2 + a_y^2 + a_z^2} \end{aligned}\]אפשר להרחיב את משפט פיתגורס לכל מספר ממדים:
דור פסקל“ב-N ממדים, הגודל של $\vec{a}$… יהיה שווה ל-$\sqrt{a_1^2 + a_2^2 + \ldots + a_N^2}$”