פיזיקה לרפואנים - שיעור 9

חלק א: וקטורים בקואורדינטות גליליות

בשיעור הקודם סיימנו עם וקטורי המקום, המהירות והתאוצה בקואורדינטות גליליות.

נזכיר את הביטויים שפיתחנו:

וקטור המקום:

וקטור המהירות:

וקטור התאוצה:

הביטויים האלו מבטאים את וקטור המקום, המהירות והתאוצה של גוף שנע במישור, כאשר מבטאים אותם בקואורדינטות גליליות (פולריות).

מה הן קואורדינטות גליליות?

קואורדינטות גליליות (פולריות) מורכבות מ:

• מעגלים קונצנטריים
• קרניים היוצאות מהמרכז

הקרניים הן הקואורדינטות הרדיאליות, והפריסה של הקרן מציר ה-x היא הקואורדינטה הזוויתית.

אם אני נמצא בנקודה מסוימת במישור, אני יכול לפרוש שני וקטורי יחידה:

• $\hat{r}$ - וקטור יחידה בכיוון הרדיאלי
• $\hat{\theta}$ - וקטור יחידה בכיוון המשיק למעגל (ניצב לכיוון הרדיאלי)

וקטורי היחידה האלו תלויים בזמן, מכיוון שהגוף מבצע תנועה כלשהי במישור. כלומר, בכל נקודה במסלול, המישור נפרס על ידי שני וקטורי יחידה שתלויים במקום (וכתוצאה מכך בזמן).

מקרה פרטי: תנועה מעגלית קצובה

במקרה של תנועה מעגלית קצובה:

• $r = \text{constant}$ (כלומר $\dot{r} = 0$)
• $\dot{\theta} = \omega = \text{constant}$ (כלומר $\ddot{\theta} = 0$)

מכאן נקבל:

כלומר, התאוצה בתנועה מעגלית קצובה היא תמיד לכיוון מרכז המעגל.

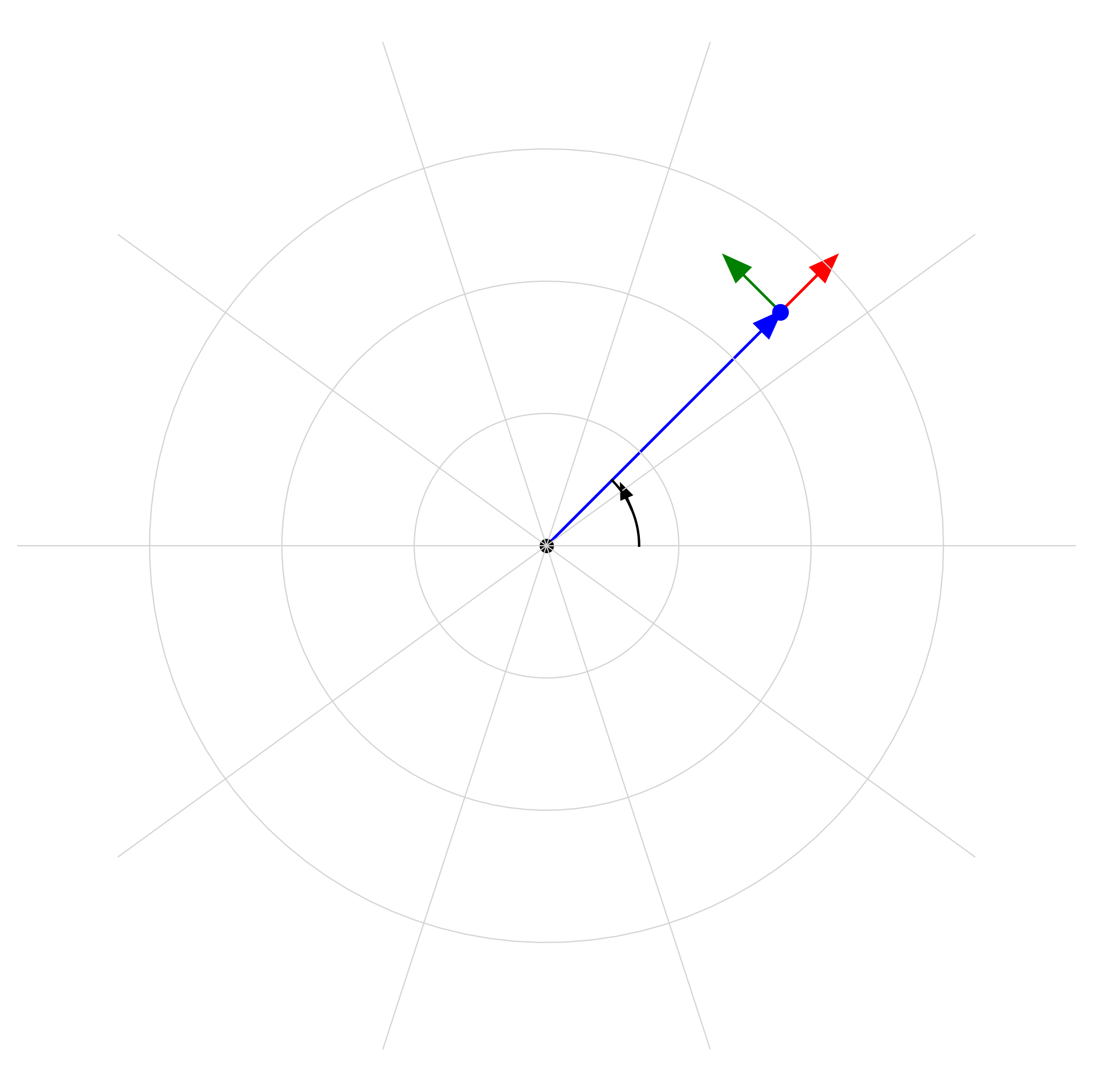
חלק ב: המטוטלת המתמטית

עכשיו ניקח דוגמה מהחיים האמיתיים ונתאר את תנועת המטוטלת באמצעות קואורדינטות פולריות.

מה היא מטוטלת מתמטית?

מטוטלת מתמטית היא מודל פשוט שבו:

• יש חוט מתוח שתלוי מתקרה
• בקצה החוט יש מסה נקודתית $m$
• אורך החוט הוא $L$
• החוט תמיד נשאר מתוח

כאשר מושכים את המטוטלת לזווית מסוימת $\theta$ ומשחררים, היא מתחילה להתנדנד בצורה שבה החוט נשאר מתוח.

מדוע להשתמש בקואורדינטות פולריות?

המטוטלת היא דוגמה קלאסית למערכת עם סימטריה פולרית:

• הרדיוס של התנועה קבוע (אורך החוט $L$)
• מספיק לדעת את הזווית $\theta$ כדי לתאר את מיקום המסה במלואו

אם היינו משתמשים בקואורדינטות קרטזיות, היינו צריכים לטפל בשני משתנים ($x$ ו-$y$), והביטויים היו מסובכים יותר. בנוסף, המערכת הייתה מאיצה גם בכיוון $x$ וגם בכיוון $y$.

מטוטלת פיזיקלית לעומת מטוטלת מתמטית

בחיים האמיתיים אין מטוטלות מתמטיות, אלא מטוטלות פיזיקליות:

• המסה אינה נקודתית
• לחוט יש מסה
• יכולות להיות דרגות חופש נוספות (כמו סיבוב הגוף סביב מרכז הכובד שלו)
• יכול להיות איבוד אנרגיה

מטוטלת פיזיקלית היא מערכת מורכבת יותר עם מספר דרגות חופש.

דרגות חופש

דרגת חופש היא משתנה בלתי תלוי שחוקי הפיזיקה מכתיבים את התפתחותו בזמן.

• מטוטלת מתמטית פשוטה: דרגת חופש אחת (הזווית $\theta$)
• מטוטלת כפולה: שתי דרגות חופש (שתי זוויות, $\theta$ ו-$\phi$)
• בעיה בתלת-מימד: שלוש דרגות חופש ($x(t)$, $y(t)$, $z(t)$)

חלק ג: ניתוח המטוטלת המתמטית

אפיון המערכת

ראשית, נזהה את הפרמטרים של הבעיה:

• מסת המטוטלת $m$
• אורך החוט $L$
• תאוצת הכבידה $g$

נשתמש בקואורדינטות פולריות עם הזווית $\theta(t)$ כמשתנה שמתאר את מצב המערכת.

הכוחות במערכת

יש שני כוחות שפועלים על המסה:

1. כוח המשיכה $mg$ שפועל כלפי מטה (בכיוון שלילי של ציר $y$)
2. מתיחות החוט $T$ שפועלת לאורך החוט (בכיוון $-\hat{r}$)

כדי לבנות את משוואות התנועה בקואורדינטות פולריות, נפרק את כוח הכבידה למרכיבים בכיוונים הרדיאלי והמשיקי:

• המרכיב הרדיאלי: $mg\cos\theta$ בכיוון $\hat{r}$
• המרכיב המשיקי: $mg\sin\theta$ בכיוון $\hat{\theta}$

משוואות התנועה

נשתמש בחוק השני של ניוטון: $\vec{F} = m\vec{a}$

בכיוון הרדיאלי:

מכיוון שבמטוטלת מתמטית הרדיוס קבוע ($r = L$), נוכל לכתוב:

בכיוון המשיקי (הזוויתי):

או:

זאת משוואת התנועה של המטוטלת המתמטית. מדובר במשוואה דיפרנציאלית לא לינארית מסדר שני, שאין לה פתרון אנליטי מדויק במקרה הכללי.

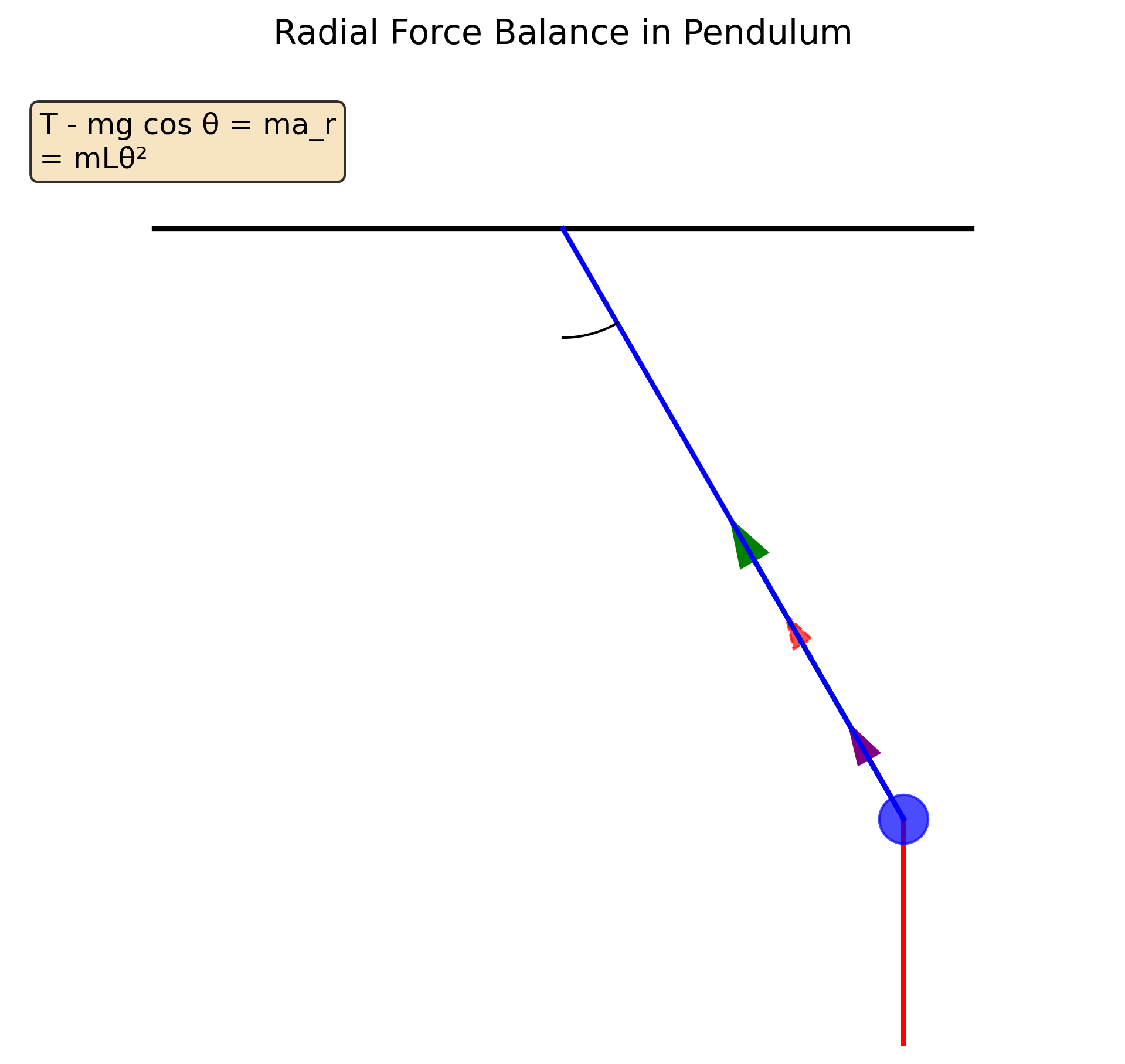
תזכורת מפיזיקה בתיכון

בתיכון למדנו:

כאשר $r$ במקרה שלנו הוא $L$ (אורך המטוטלת). קראנו לביטוי $mr\omega^2$ התאוצה הצנטריפטלית $a_c$.

נזכור ש:

התאוצה הצנטריפטלית שקשורה בתנועה המעגלית שווה לשקול הכוחות בכיוון הרדיאלי. זה מה שלמדנו בתיכון.

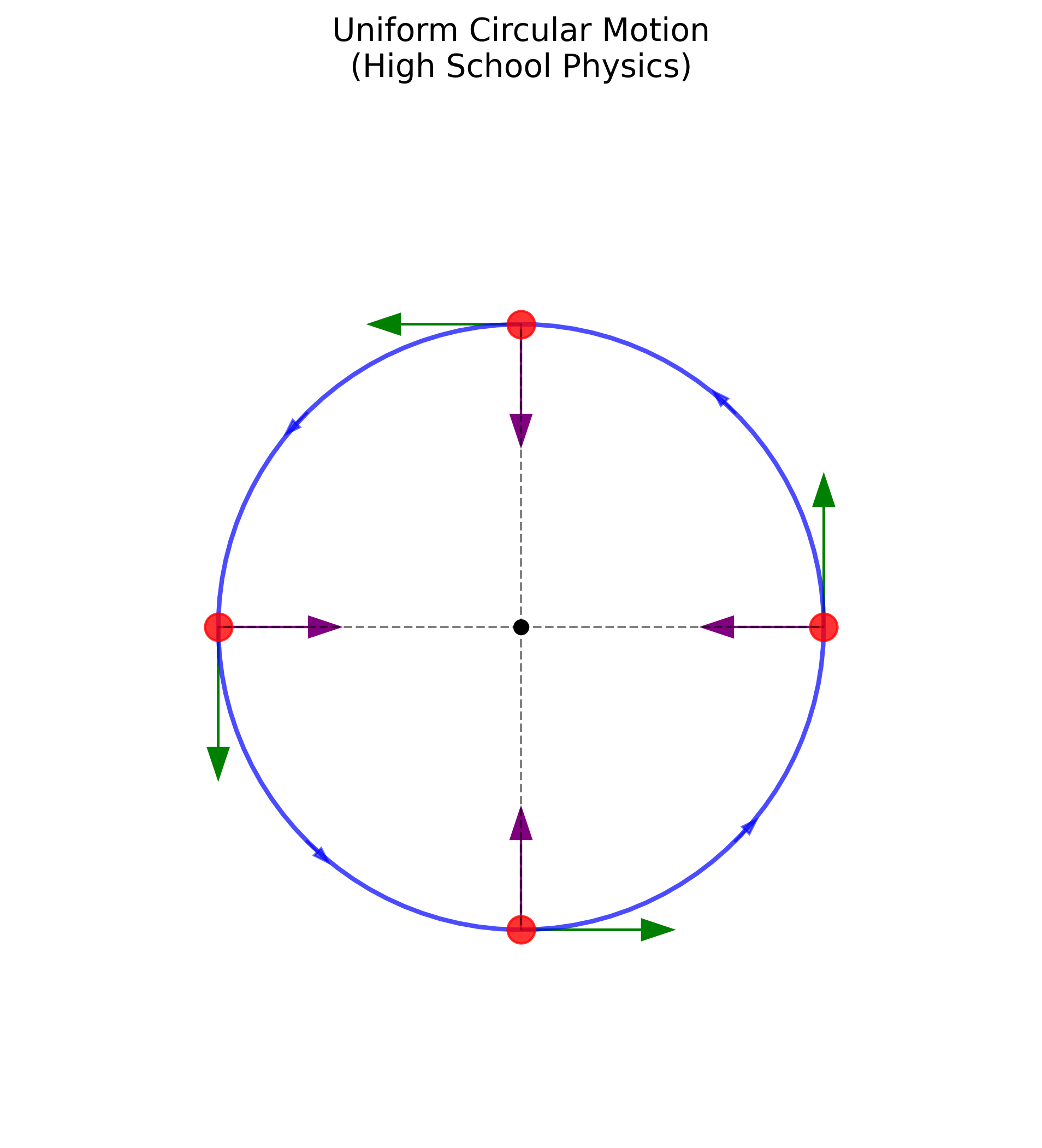
הבנה מעמיקה של התנועה המעגלית

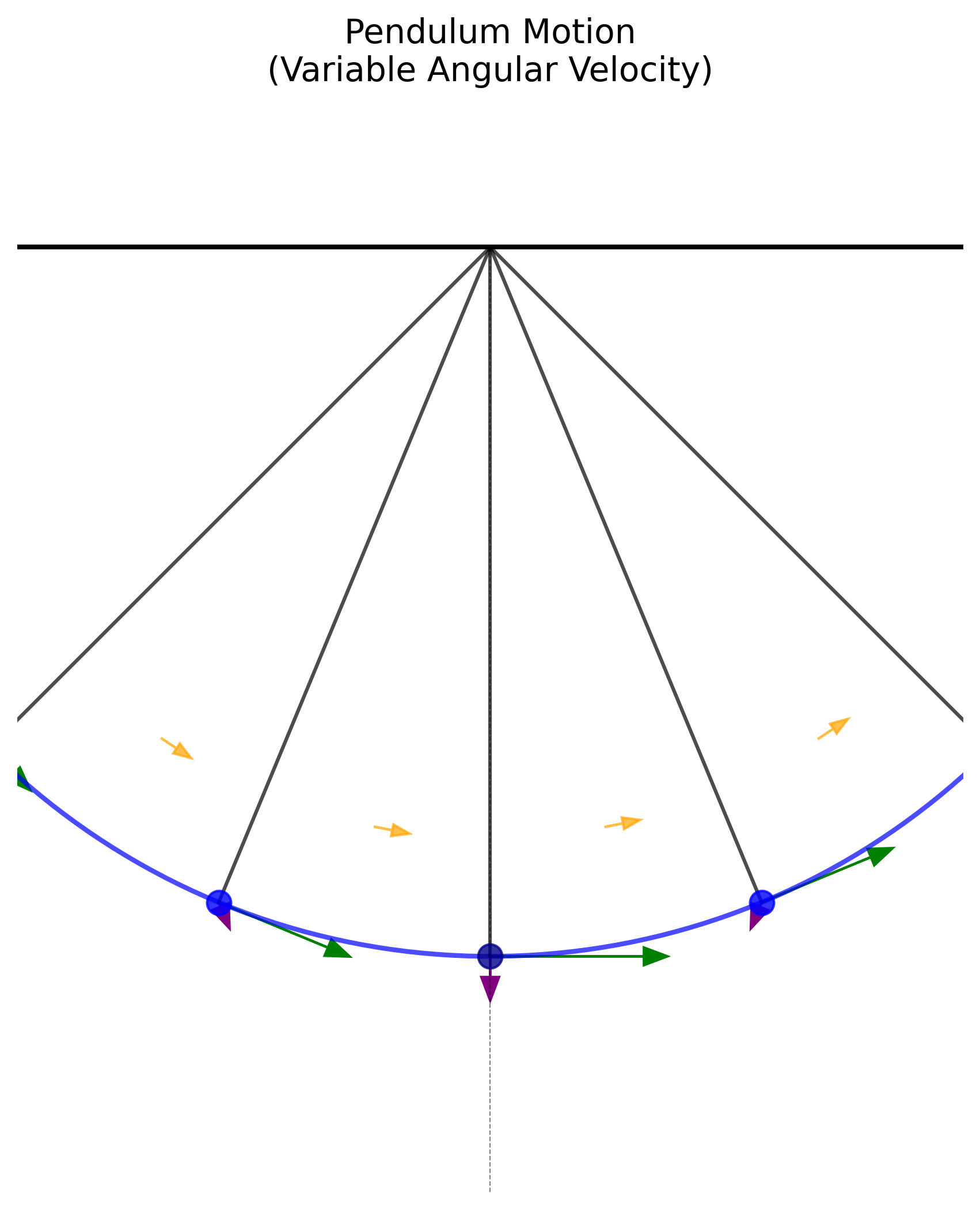
הביטוי שלנו יותר אלגנטי ונותן ראייה רחבה יותר של המציאות. חשוב לשים לב:

1. בתיכון קראנו למהירות הזוויתית $\omega$ והתייחסנו אליה כקבועה (בתנועה מעגלית קצובה).
2. אך במטוטלת, $\omega$ (או $\dot{\theta}$) תלויה בזמן - עובדה שבתיכון התעלמו ממנה.
3. התאוצה הרדיאלית היא למעשה פונקציה של הזמן כי המהירות הזוויתית משתנה.

לכן, יותר הגיוני להסתכל על התאוצה הרדיאלית (או צנטריפטלית) כך:

ומשוואת התנועה בכיוון הרדיאלי:

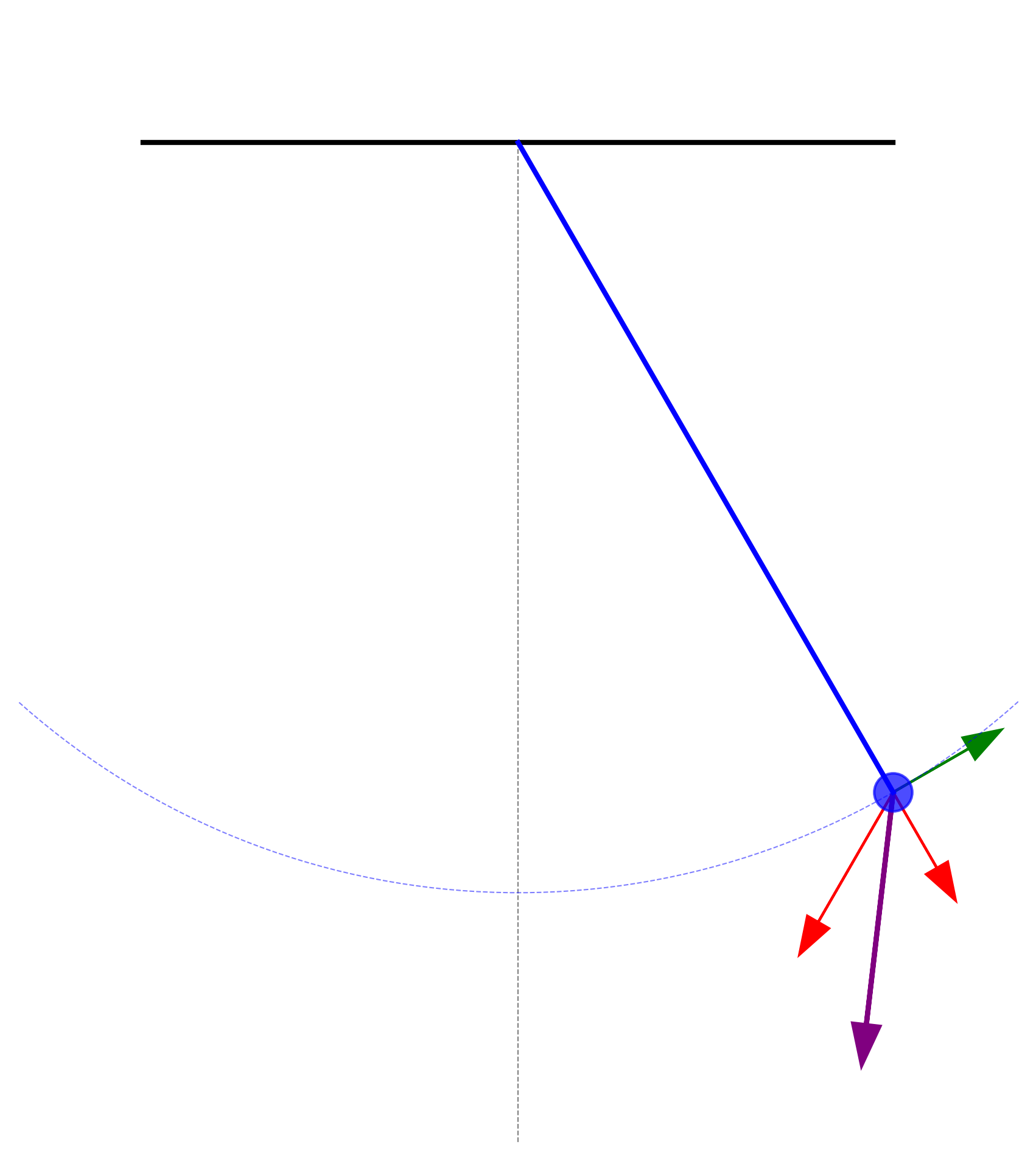
המתיחות בחוט

חשוב להבין שהמתיחות בחוט היא לא קבועה! טעות שעושים תלמידי תיכון היא לחשוב ש:

זו טעות! החוק הראשון של ניוטון ($\sum F = 0, \text{when no a}$) אינו תקף כאן כי יש תנועה מעגלית. החוק השני תקף ($\sum F = ma$), ולכן המתיחות תלויה גם במהירות הזוויתית של המטוטלת ($\dot{\theta}$).

כלומר, המתיחות בחוט מורכבת משני מרכיבים:

1. $mr\dot{\theta}^2$ - הכוח הצנטריפטלי הנדרש לשמירה על התנועה המעגלית
2. $mg\cos\theta$ - איזון מרכיב הכבידה בכיוון הרדיאלי (שפועל החוצה)

תלמידי תיכון מפספסים את המרכיב הראשון ולא מבינים שגם בתנועה מעגלית במהירות קבועה יש תאוצה צנטריפטלית ($a_r = r\dot{\theta}^2$) שדורשת כוח צנטריפטלי.

נקודות מיוחדות במסלול המטוטלת

• בנקודה התחתונה ($\theta = 0$): המתיחות היא מקסימלית כי:
  • $\cos(0) = 1$ - מרכיב הכבידה מקסימלי
  • $\dot{\theta}$ מקסימלי - התאוצה הצנטריפטלית מקסימלית
• בנקודות הקיצוניות של התנועה: המהירות הזוויתית $\dot{\theta} = 0$, ולכן התאוצה הצנטריפטלית מתאפסת, והמתיחות קטנה יותר.

משוואות התנועה של המטוטלת

לסיכום, שתי המשוואות שמתארות את תנועת המטוטלת הן:

1. בכיוון הרדיאלי:

   \[ma_r = T - mg\cos\theta\]

2. בכיוון הזוויתי (טנגנציאלי):

   \[mL\ddot{\theta} = -mg\sin\theta\]

המשוואה השנייה היא המשוואה החשובה לתיאור התנועה. נוכל לכתוב אותה בצורה:

נסמן $\omega_0^2 = \frac{g}{L}$ ונקבל:

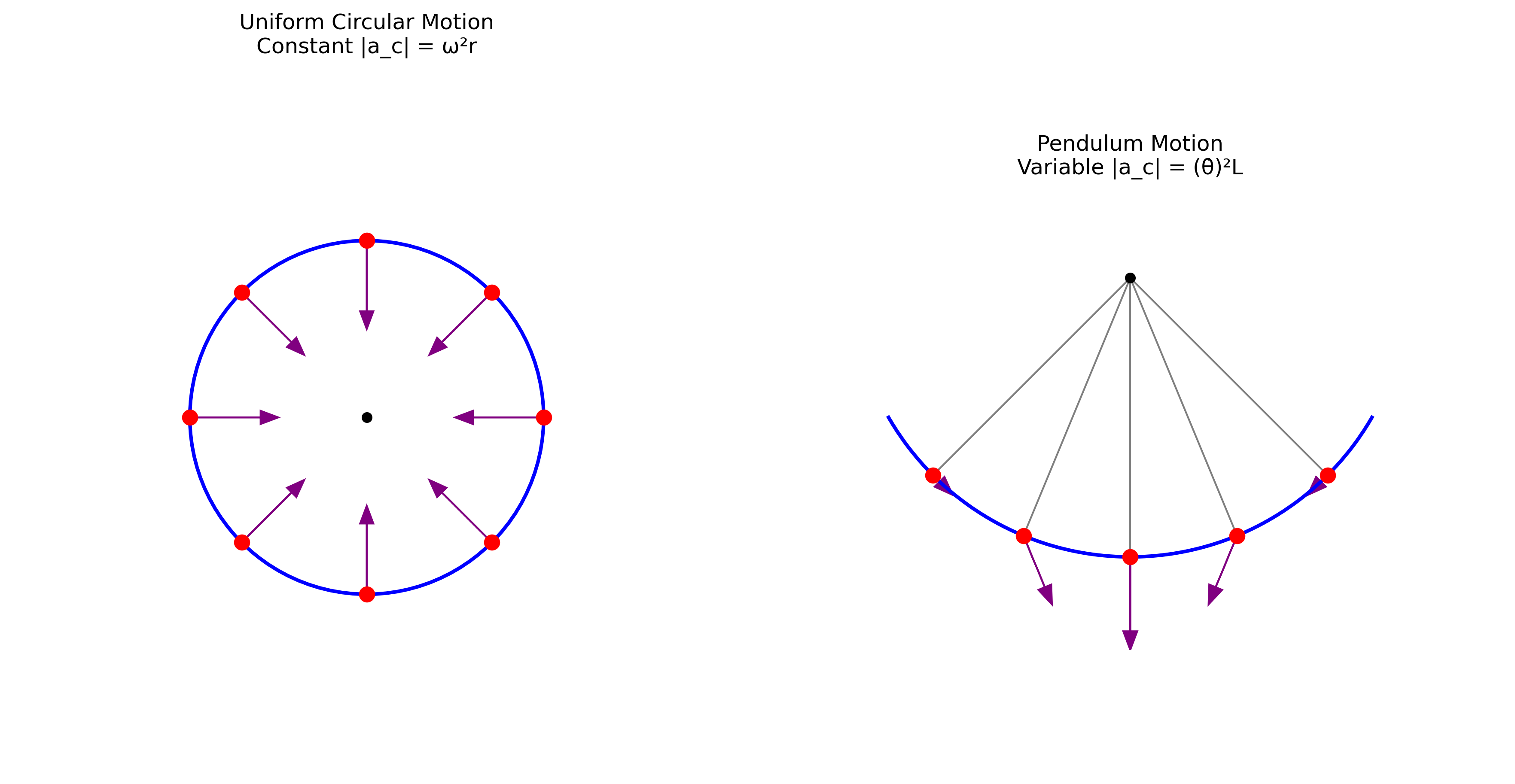
פתרון משוואת המטוטלת

משוואה זו היא משוואה דיפרנציאלית אליפטית שאין לה פתרון אנליטי מדויק. אפשר לפתור אותה:

1. בשיטות נומריות
2. בקירוב לזוויות קטנות

קירוב לזוויות קטנות

לזוויות קטנות, נוכל לפתח את $\sin\theta$ בטור טיילור:

אם נתעלם מכל האיברים מלבד הראשון, נקבל:

זוהי משוואת התנודד ההרמוני הפשוט, שהפתרון שלה הוא:

כאשר $C$ ו-$\phi$ הם קבועים שנקבעים על ידי תנאי ההתחלה.

פתרון עם תנאי התחלה

נניח שיש לנו:

• $\theta(t=0) = \theta_0$ (זווית התחלתית)
• $\dot{\theta}(t=0) = \alpha$ (מהירות זוויתית התחלתית)

אזי:

נציב את תנאי ההתחלה:

מחלוקת המשוואה השנייה בראשונה:

ומכאן:

במקרה המיוחד שבו $\alpha = 0$ (מהירות התחלתית אפס), מקבלים $\phi = 0$, ולכן:

זו תנועה הרמונית פשוטה עם אמפליטודה $\theta_0$, והמטוטלת מתנודדת בין $\theta_0$ ל-$-\theta_0$ סביב מצב שיווי המשקל $\theta = 0$.

הפתרון הכללי עם תנאי התחלה שונים

הפתרון שקיבלנו קודם ($\theta(t) = \theta_0\cos(\omega_0 t)$) תקף רק למקרה שבו המהירות הזוויתית ההתחלתית היא אפס ($\alpha = 0$).

במבחן כמובן, לא אשאל תמיד על המקרה הפרטי הזה. אוכל למשל לשאול על מצב שבו מושכים את המטוטלת למטה ($\theta_0 = 0$) ונותנים לה “קיק” (דחיפה) התחלתי, כלומר $\alpha \neq 0$.

הפתרון הכללי של משוואת המטוטלת (בקירוב לזוויות קטנות) הוא:

כאשר:

• $C = \sqrt{\theta_0^2 + \frac{\alpha^2}{\omega_0^2}}$ (האמפליטודה)
• $\phi = \arctan\left(-\frac{\alpha}{\omega_0\theta_0}\right)$ (הפאזה)
• $\omega_0 = \sqrt{\frac{g}{L}}$ (התדירות הזוויתית הטבעית)

מקרה מיוחד: $\theta_0 = 0$ ו-$\alpha \neq 0$

במקרה שבו מתחילים בתחתית ($\theta_0 = 0$) עם מהירות זוויתית התחלתית $\alpha$:

1. $\phi = \arctan\left(-\frac{\alpha}{0}\right) = -\frac{\pi}{2}$ (כי טנגנס של $\frac{\pi}{2}$ הוא אינסוף)
2. $C = \frac{\alpha}{\omega_0}$

ולכן הפתרון הוא:

שכן $\cos(\omega_0 t - \frac{\pi}{2}) = \sin(\omega_0 t)$

תקופת התנודות של המטוטלת

זמן המחזור של המטוטלת הוא הזמן שלוקח לה להשלים תנודה שלמה ולחזור לאותו מצב. כאשר:

ולכן:

ככל שהחוט ארוך יותר, זמן המחזור ארוך יותר.

המהירות בנקודות מיוחדות במסלול

המהירות בתחתית המסלול (רבע זמן מחזור)

ברבע זמן מחזור ($t = \frac{T}{4} = \frac{\pi}{2\omega_0}$), המהירות הזוויתית היא:

זו המהירות הזוויתית המקסימלית (בערך מוחלט), כי $\sin(\frac{\pi}{2}) = 1$.

המהירות בנקודות אחרות

• בשמינית זמן מחזור ($t = \frac{T}{8}$): המהירות היא פחות מהמקסימום
• בשלושת רבעי זמן מחזור ($t = \frac{3T}{4}$): המהירות זהה בגודלה למהירות ברבע זמן מחזור, אך בכיוון ההפוך

הקשר בין המהירות הזוויתית והמהירות המשיקית

בתנועה מעגלית, אנו יודעים ש:

• אורך הקשת: $s = L\theta$
• המהירות המשיקית: $v_\theta = L\dot{\theta}$
• התאוצה המשיקית: $a_\theta = L\ddot{\theta}$

נתייחס לתכונה משיקית (tangential) בעזרת הסימונים הבאים:

\[a_T = a_\parallel = a_{\theta}\]

במקרה של המטוטלת המתמטית כאשר $\theta(t) = \theta_0\cos(\omega_0 t)$:

• $v_\theta = -L\omega_0\theta_0\sin(\omega_0 t)$
• $a_\theta = -L\omega_0^2\theta_0\cos(\omega_0 t)$

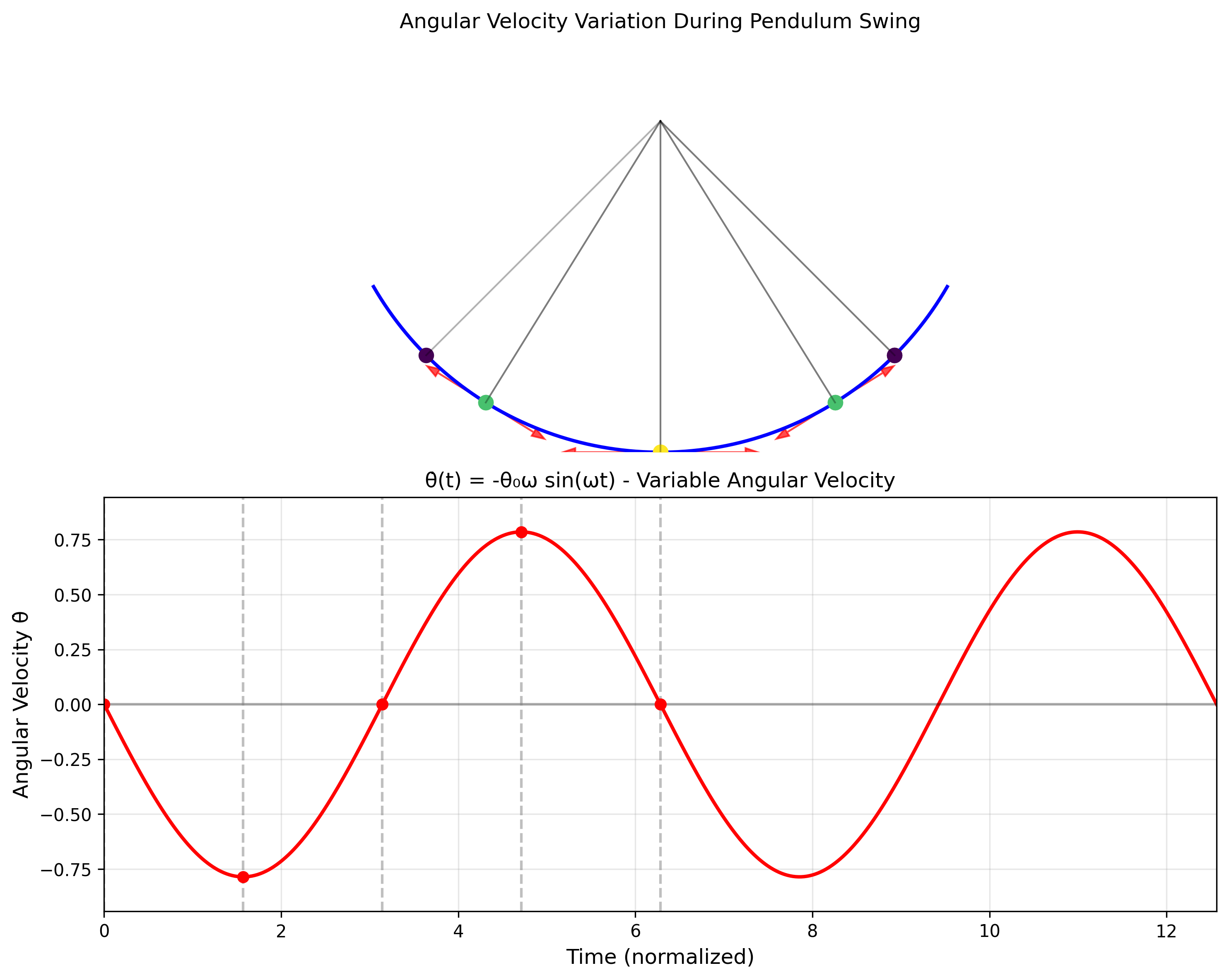
התאוצה הצנטריפטלית והמתיחות בחוט

משוואת התנועה בכיוון הרדיאלי:

או:

בנקודות קיצוניות של התנועה

• בנקודות הקיצוניות (כאשר $\theta = \theta_0$ או $\theta = -\theta_0$):
  • $v_\theta = 0$ (המהירות המשיקית מתאפסת)
  • $a_{\text{צנטריפטלית}} = \frac{v_\theta^2}{L} = 0$ (התאוצה הצנטריפטלית מתאפסת)
  • $T = mg\cos\theta_0$ (המתיחות בחוט היא הקטנה ביותר)
• בתחתית המסלול (כאשר $\theta = 0$):
  • $v_\theta = L\omega_0\theta_0$ (המהירות המשיקית מקסימלית)
  • $a_{\text{צנטריפטלית}} = \frac{v_\theta^2}{L} = L\omega_0^2\theta_0^2$ (התאוצה הצנטריפטלית מקסימלית)
  • $T = mg + mL\omega_0^2\theta_0^2$ (המתיחות בחוט היא הגדולה ביותר)

בנקודות ביניים במסלול, וקטור התאוצה הכולל אינו מכוון אל מרכז המעגל ואינו בכיוון המשיק בלבד, אלא יש לו מרכיב בשני הכיוונים.