מבנה לואיס
לואיס היה הראשון שהחליט שהוא רוצה לראות או להבין קישורים בכימיה.
העיקרון של לואיס היה מאוד פשוט. לואיס אמר את הדבר הבא: אלקטרונים של אטומים משתפים ביניהם אלקטרונים, שהכלל שדוחף אותם לעשות זאת הוא “כלל האוקטט” (Octet Rule), שכל אחד רוצה שיהיה מסביבו אוקטט.
בעצם אנחנו מתעסקים רק עם אלקטרוני הערכיות. מה זה אלקטרוני ערכיות? אלה האלקטרונים ברמה הקוונטית האחרונה (ולא ברמת תת-קוונטית). לדוגמה, עבור $\text{2s}$ ו- $\text{2p}$, אלקטרוני ה-$\text{p}$ וה-$\text{s}$ נחשבים יחד כאלקטרוני ערכיות.
למשל, לחנקן $\text{N}$ יש חמישה אלקטרוני ערכיות. כל אלקטרון מסומן כנקודה, והמטרה בסופו של דבר היא ליצור שיתוף קשרים. הקשרים יכולים להיות יחידים, כפולים, או משולשים. לדוגמה, עבור מימן $\text{H}$ מתקיים “כלל הדובלט” במקום כלל האוקטט, כך שמספיקים שני אלקטרונים סביבו.
\[\begin{array}{cccccc} \text{H} & \text{C} & \text{N} & \text{O} & \text{F} & \text{Se} \\ 1 & 4 & 5 & 6 & 7 & 6 \end{array}\] \[\begin{array}{@{}c@{}c@{}c@{}} & \Large{\cdot\cdot} & \\[-6pt] & \Large{\cdot} \text{N} \Large{\cdot} \\[-6pt] & \Large{\cdot} & \end{array}\] \[\begin{array}{@{}c@{}c@{}c@{}} & \Large{\cdot\cdot} & \\[-6pt] & \Large{\cdot} \text{Se} \mathbf{:} \\[-6pt] & \Large{\cdot} & \end{array}\]דיברנו על קשרים פולאריים ואיך מוצאים אותם לפי טבלת אלקטרונגטיביות. שלב נוסף הוא חישוב אחוז יוני של קשרים. התחלנו גם לדבר על איך יוצרים מבנה לואיס.
שלבים לכתיבת מבנה לואיס
- ספירת אלקטרוני ערכיות.
- זיהוי האטום המרכזי - בדרך כלל האטום בעל האלקטרושליליות הנמוכה ביותר. פחמן $\text{C}$ בדרך כלל יהיה אטום מרכזי. אטומי מימן $\text{H}$ תמיד יהיו בקצוות.
- יצירת מבנה שלד וחיבור האטומים במבנה על ידי קשרים קוולנטיים יחידים.
- חישוב מספר האלקטרונים שנשארו (שניים יורדים על כל קשר קוולנטי)
- השלמת האלקטרונים שנשארו - תחילה אוקטטים של אטומי הקצה ואז של האטומים המרכזיים אם אפשר.
- אם לאטום המרכזי חסר אוקטט - נשתמש בזוגות של אלקטרונים בלתי קושרים מהאטומים שבקצה ליצירת קשרים קוולנטיים כפולים עם האטום המרכזי. נחזור על כך עד שלכולם יהיה אוקטט (למעט מקרים חריגים).
חריגות לכלל האוקטט
אלקטרון לא משובץ - רדיקלים
מבנה לואיס נוצר כך: לוקחים את כל האלקטרונים הוולנסיים, ומפזרים אותם בזוגות מסביב לאטום המרכזי. אם נשאר אלקטרון לא משובץ, זה נקרא “רדיקל”, שהוא מצב נדיר.
$\text{CH}_3$
\[\begin{array}{ccc} & \text{H} & \\[-6pt] & | & \\ \text{H} & - \text{C} - & \text{H} \\[-6pt] & \Large{\cdot} & \\ \end{array}\]לדוגמה, עבור $\text{CH}_3$, נותר אלקטרון לא משובץ, מה שיוצר רדיקל חופשי. רדיקלים הם חומרים פעילים במיוחד, שמגיבים מהר ליצירת קשרים חדשים. רדיקלים נפוצים במצבים כמו חשיפה לקרינה אולטרה-סגולה או רדיואקטיבית.
אוקטט לא מושלם
עוד חריגה מכלל האוקטט היא “אוקטט לא מושלם”, לדוגמה $\text{BF}_3$, שבו האטום המרכזי בור (B) נותר עם שישה אלקטרונים בלבד.
$\text{BF}_3$
\[\begin{array}{ccc} & \Large{\cdot\cdot} & \\[-16pt] & \mathbf{:} \text{F} \mathbf{:}& \\[-6pt] & | & \\ & \text{B} & \\[-6pt] & / \ \ \backslash & \\ \mathbf{:}\text{F}\mathbf{:} & & \mathbf{:}\text{F}\mathbf{:} \\[-16pt] \Large{\cdot\cdot} & & \Large{\cdot\cdot} \end{array}\]אוקטט מורחב
$\text{SF}_6$
חריגה נוספת היא “אוקטט מורחב”, הנפוצה עבור אטומים עם אורביטלי $d$, כמו ב-$\text{SF}_6$, שבו הגופרית חורגת ל-12 אלקטרונים מסביבה.
\[\begin{array}{ccc} \Large{\cdot\cdot} & \Large{\cdot\cdot} & \Large{\cdot\cdot} \\[-16pt] \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} \\[-16pt] & \backslash \ \ | \ \ / & \\ & \text{S} & \\[-6pt] & / \ \ \ | \ \ \ \backslash & \\ \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} \\[-16pt] \Large{\cdot\cdot} & \Large{\cdot\cdot} & \Large{\cdot\cdot} \end{array}\]מבנה רזוננס
בנושא רזוננס (Resonance): במקרים שבהם לא ניתן להכריע בין מבנים, אנו מתייחסים אליהם כמצבים רזונטיביים. דוגמה לכך היא מולקולת האוזון ($\text{O}_3$), שבה יש שני מבנים שקולים, והמבנה בפועל הוא ממוצע רזונטיבי ביניהם.
אוזון $\text{O}_3$
\[:\overset{\cdot\cdot}{\text{O}} = \overset{\cdot\cdot}{\text{O}} - \overset{\cdot\cdot}{\underset{\cdot\cdot}{\text{O}}}: \quad \leftrightarrow \quad :\overset{\cdot\cdot}{\underset{\cdot\cdot}{\text{O}}} - \overset{\cdot\cdot}{\text{O}} = \overset{\cdot\cdot}{\text{O}}:\]מטען פורמאלי
לסיכום, כשבונים מבנה לואיס, עדיף למזער את המטענים הפורמליים (Formal Charge) במולקולה. מטען פורמלי מחושב כך:
נוסחה לחישוב מטען פורמאלי
\[\begin{aligned} \text{Formal Charge} &= \\ & \text{Electrons in Free Atom} \\ &- \text{Non-bonding Electrons} \\ &- \frac{1}{2} \times \text{Bonding Electrons} \end{aligned}\]VSEPR וצורות של מולקלות
מבנים רזונטיביים ואי-שוויון במטענים מובילים להבנה מעמיקה יותר של יציבות ואינטראקציות כימיות.
| מספר הקבוצות סביב האטום המרכזי | צורת מולקולה | זווית | דוגמה |
|---|---|---|---|
| 2 | Linear | $180^\circ$ | $\text{BeCl}_2$ |
| 3 | Trigonal planar | $120^\circ$ | $\text{BF}_3$ |
| 4 | Tetrahedral | $109.5^\circ$ | $\text{CH}_4$ |
| 5 | Trigonal bipyramidal | $90^\circ$ | $\text{PF}_5$ |
| 6 | Octahedral | $90^\circ$ | $\text{SF}_6$ |
לינארי $\text{AX}_2$
כל המולקולות שהן נקראות $\text{AX}_2$, עשיתם איזשהו מבנה, יש לכם $A$ מרכזי ו-$X_2$, אטום מרכזי ושניים קשורים אליו. למשל בריליום כלוריד: $ֿ\text{BeCl}_2$.
$\text{BeCl}_2$
\[\begin{array}{ccc} \Large{\cdot\cdot} & & \Large{\cdot\cdot} \\[-16pt] \mathbf{:}\text{Cl} & - \text{Be} - & \text{Cl}\mathbf{:} \\[-6pt] \Large{\cdot\cdot} & & \Large{\cdot\cdot} \\[-16pt] \end{array}\]אם עשיתם בריליום כלוריד, אתם תראו שיש בריליום במרכז קשור לכלור. זה בעצם מערכת של $\text{AX}_2$. הדרך היחידה שהחומרים האלה יצרו היא במקסימום דחייה (balance repulsion), ואמרנו שזה נעשה על ידי יצירת זווית של $180^\circ$.
רק ב-$180^\circ$ בין אלקטרוני הקשר מתקיים מקסימום דחייה. זה מבנה מאוד פשוט ולכן נותן מבנה לינארי. כל המולקולות שהיו לכם מהמבנה הזה $\text{AX}_2$ הן בעלות נוטציה של $\text{AX}_2$, ללא זוגות אלקטרוניים לא קושרים. ל-$A$ אין זוגות אלקטרוניים לא קושרים, הוא מסר אותם לכלור ונשאר בלי אלקטרונים לא קושרים. המבנה הוא לינארי.
מיד תראו כי ל-$\text{AX}_2\text{E}_2$ עם זוגות אלקטרונים לא קושרים, כמו מולקולת מים, נוצר מבנה שונה. מבנה כזה נראה כ”שפנפן” ($\text{bent}$).
$\text{AX}_3$
משולש מישורי - trigonal planar
השלב הבא: משפחת חומרים שנקראת $\text{AX}_3$. לדוגמה, $\text{BF}_3$. זהו אטום מרכזי $\text{B}$ שקשור לשלושה אטומים $\text{F}$. כל אחד מה-$\text{F}$ מקיים את כלל האוקטט, אך ל-$\text{B}$ לא מתקיים כלל האוקטט (לא נורא).
$\text{BF}_3$ - אוקטט לא מושלם
\[\begin{array}{ccc} & \Large{\cdot\cdot} & \\[-16pt] & \mathbf{:} \text{F} \mathbf{:}& \\[-6pt] & | & \\ & \text{B} & \\[-6pt] & / \ \ \backslash & \\ \mathbf{:}\text{F}\mathbf{:} & & \mathbf{:}\text{F}\mathbf{:} \\[-16pt] \Large{\cdot\cdot} & & \Large{\cdot\cdot} \end{array}\]החומרים האלה צריכים ליצור מבנה במרחב עם מקסימום תחייה, וזהו מבנה של $120^\circ$, כמו צורה של “משולש מישורי” ($\text{Trigonal Planner}$), הדומה לסימן של “מרצדס”.
$\text{AX}_2\text{E}$
bent
$\text{SO}_2$
\[\begin{array}{ccc} & \Large{\cdot\cdot} & \\[-16pt] & \text{S} & \\[-6pt] & \diagup\diagup \quad \diagdown\diagdown & \\[-6pt] \mathbf{:}\text{O} & & \text{O}\mathbf{:} \\[-16pt] \Large{\cdot\cdot} & & \Large{\cdot\cdot} \end{array}\]לעיתים החומר ייצור מבנה $\text{AX}_2\text{E}$ עם זוג אלקטרונים לא קושר. לדוגמה, המולקולה $\text{SO}_2$: כשיוצרים מבנה לואיס ל-$\text{SO}_2$, הגופרית חורגת מכלל האוקטט, ויש לה זוג אלקטרונים לא קושר. המבנה הזה נקרא $\text{AX}_2\text{E}$, עם זוויות מעט קטנות מ-$120^\circ$, בשל דחיפת זוג האלקטרונים הלא קושר.
$\text{AX}_4$
טטרהדרים
מבנים נוספים כוללים $\text{AX}_4$ – המבנה הטטראדרי. לדוגמה, $\text{CH}_4$: מבנה רגיל שבו יש $109^\circ$ בין הקשרים.
$\text{CH}_4$
\[\begin{array}{ccc} & \text{H} & \\[-6pt] & \vert & \\ \text{H} & - \text{C} - & \text{H} \\[-6pt] & \vert & \\ & \text{H} & \end{array}\]$\text{AX}_3\text{E}$
trigonal pyramidal
כאשר יש זוג אלקטרונים לא קושר, כמו באמוניה ($\text{NH}_3$), המבנה עדיין טטראדרי, אך הזוויות קטנות ל-$107^\circ$.
$\text{NH}_3$
\[\begin{array}{ccc} & \text{H} & \\[-6pt] & | & \\ & \text{N}\mathbf{:} & \\[-6pt] & / \ \backslash & \\ & \text{H} \ \ \ \ \ \ \text{H} &\\[-16pt] \end{array}\]$\text{AX}_2\text{E}_2$
bent - שפנפן
במולקולת מים ($\text{H}_2\text{O}$) הזוויות קטנות עוד יותר ל-$104^\circ$ בשל שני זוגות אלקטרונים לא קושרים. למרות שמבנה לואיס לכאורה נראה סימטרי, מודל VSEPR מראה שהמולקולה עצמה היא לא לינארית.
$\text{H}_2\text{O}$
\[\begin{array}{ccc} & \text{: O :} & \\[-6pt] & / \quad \backslash & \\[-6pt] \text{H} & & \text{H} \end{array}\]$\text{AX}_5$
trigonal bipyramidal - ביפירמידה טריגונלית
מבנה נוסף: $\text{AX}_5$, ביפירמידה טריגונלית, או דו-פירמידה משולשת (דור: לא סגור על התרגום)($\text{Trigonal Bipyramidal}$). לדוגמה, $\text{PCl}_5$, שבו שלושה אטומים במישור וזוויות של $120^\circ$, ושני אטומים נוספים בזוויות של $90^\circ$ ו-$180^\circ$. תשומת הלב שבמולקולת $\text{PCl}_5$ יש חריגה מכלל האוקטט מהסוג של אוקטט מורחב - הגופרית חורגת ל-10 אלקטרונים. ככלל, חריגות כאלה מתקיימות ביסודות מהשורה השלישית ומעלה.
$\text{PCl}_5$
\[\begin{array}{ccc} \Large{\cdot\cdot} & \Large{\cdot\cdot} & \Large{\cdot\cdot} \\[-16pt] \mathbf{:}\text{Cl}\mathbf{:} & \mathbf{:}\text{Cl}\mathbf{:} & \mathbf{:}\text{Cl}\mathbf{:} \\[-16pt] & \backslash \ \ | \ \ / & \\ & \text{P} & \\[-6pt] & / \ \ \ \ \ \ \backslash & \\ \mathbf{:}\text{Cl}\mathbf{:} & & \mathbf{:}\text{Cl}\mathbf{:} \\[-16pt] \Large{\cdot\cdot} & & \Large{\cdot\cdot} \end{array}\]$\text{AX}_4\text{E}$
seesaw
במולקולות מורכבות יותר, כמו $\text{SF}_4$, המבנה הוא $\text{AX}_4\text{E}$, עם זוג אלקטרונים לא קושר, והמבנה נותר דו-פירמידלי.
$\text{AX}_6$
מבנים אוקטהדרליים
לבסוף, מבנים אוקטהדרליים ($\text{AX}_6$), כמו $\text{SF}_6$, כוללים שישה קשרים בזוויות של $90^\circ$. גם כאן יש חריגה מכלל האוקטט מהסוג של אוקטט מורחב - הגופרית חורגת ל-12 אלקטרונים.
$\text{SF}_6$ - אוקטהדר
\[\begin{array}{ccc} \Large{\cdot\cdot} & \Large{\cdot\cdot} & \Large{\cdot\cdot} \\[-16pt] \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} \\[-16pt] & \backslash \ \ | \ \ / & \\ & \text{S} & \\[-6pt] & / \ \ \ | \ \ \ \backslash & \\ \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} & \mathbf{:}\text{F}\mathbf{:} \\[-16pt] \Large{\cdot\cdot} & \Large{\cdot\cdot} & \Large{\cdot\cdot} \end{array}\]$\text{AX}_4\text{E}_2$
$\text{Square Planar}$
מבנה כזה יכול לכלול זוגות אלקטרונים לא קושרים, כמו $\text{AX}_4\text{E}_2$, שבו המבנה הופך לשטוח מרובע ($\text{Square Planar}$).
מציאת מבנה
התהליך למציאת מבנה כולל:
- יצירת מבנה לואיס
- קביעת נוטציית $\text{AXE}$
- קביעת הגיאומטריה בהתאם למודל $\text{VSEPR}$
האסטרטגיה: תחילה מבצעים מבנה לואיס ולאחר מכן מפרקים כל אטום לבחון את הגיאומטריה סביבו. כעת ניגע במושג נוסף שחשוב להבין: “מומנט דיפול” או “כותביות”.
מומנט דיפול $\left( \mu \right)$
כאשר מולקולה מקבלת צורה מרחבית, מומנט דיפול (Dipole Moment) נובע מהפרש באלקטרונגטיביות בין האטומים. אם יש הפרש כזה, האלקטרונים נמשכים לאטום בעל האלקטרונגטיביות הגבוהה יותר. לדוגמה, בחיבור בין מימן לכלור, האלקטרונים נמצאים יותר זמן סביב הכלור: $\text{H} \mapsto \text{Cl}$
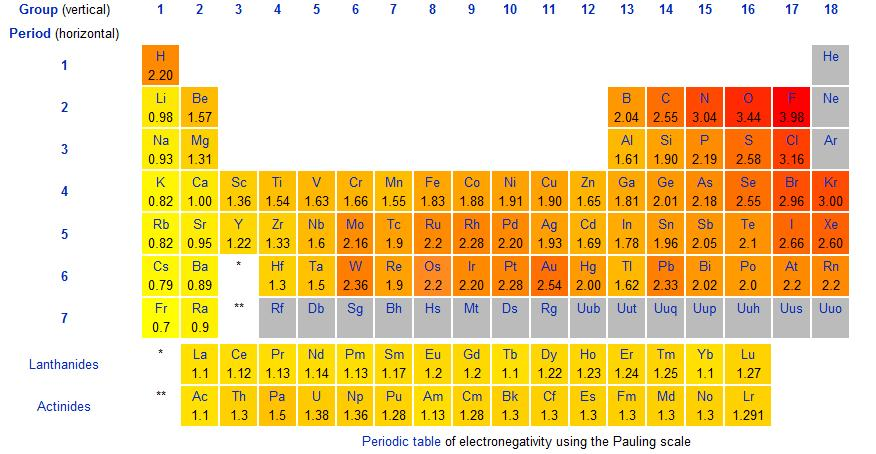\[\begin{array}{ccc} & \delta^{-} & \\[-16pt] & \Large{\cdot\cdot} & \\[-16pt] & \mathbf{:} \text{Cl} \mathbf{:}& \\[-6pt] & | & \\ & \text{H} & \\[-6pt] & \delta^{+} & \\[-16pt] \end{array}\] \[\mu = \delta \times d\] The extent of the charge displacement in a polar covalent bond is given by the dipole moment, m. The dipole moment is the product of a partial charge 1d2 and distance (d).
$\text{HCl}$
CO₂
היחידות למדידת מומנט דיפול הן “Debye”, אך ניתוח הכותביות חשוב יותר להבנה מרחבית. לדוגמה, במולקולה $\text{CO}_2$: חמצן מושך אלקטרונים חזק יותר מפחמן, כך שקיים מומנט דיפול בכל קשר. עם זאת, הוקטורים של מומנט הדיפול שווים בגודלם ובכיוונים מנוגדים, ולכן המולקולה אינה כותבית. למרות קיומו של מומנט דיפול בכל קשר, חיבור וקטורי מבטל את הכותביות של המולקולה.
\[\begin{array}{ccc} \Large{\cdot\cdot} & & \Large{\cdot\cdot} \\[-16pt] \text{O} & \overset{\leftarrow}{=}\text{C}\overset{\rightarrow}{=}& \text{O} \\[-6pt] \Large{\cdot\cdot} & & \Large{\cdot\cdot} \end{array}\]$\text{CCl}_4$
דוגמה נוספת: $\text{CCl}_4$. כאן, הפחמן נמצא במרכז, וארבעת הכלורים מסודרים בצורה טטראדרלית. אף שקיים הפרש באלקטרונגטיביות בין פחמן לכלור, המולקולה אינה כותבית משום שהוקטורים של מומנט הדיפול מתבטלים. אם מחליפים אחד מהכלורים במימן, מתקבלת מולקולה כותבית, שכן המבנה אינו סימטרי עוד.
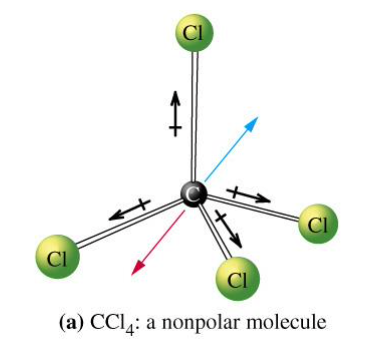
דוגמאות אלו מדגישות כיצד צורת המולקולה משפיעה על הכותביות. חישוב וקטורי של מומנט דיפול מאפשר לקבוע האם המולקולה כותבית או לא. לדוגמה:
- $\text{H}_2$ – אין מומנט דיפול ואין כותביות (אטומים זהים).
- $\text{H}_2\text{O}$ – מולקולה כותבית בשל המבנה הטטראדרלי ושני זוגות אלקטרונים לא קושרים.
- $\text{N}_2$ ו-$\text{O}_2$ – אין מומנט דיפול, משום שמדובר באטומים זהים.
אורך קשר ($\text{pm}$)
עכשיו נעבור למושג “אורך קשר”. אורך קשר תלוי בחוזק הקשר. קשרים כפולים או משולשים קצרים וחזקים יותר מקשרים יחידים. לדוגמה:
- קשר פחמן-פחמן יחיד: $154 \, \text{pm}$.
- קשר פחמן-פחמן כפול: $134 \, \text{pm}$.
- קשר פחמן-פחמן משולש: $120 \, \text{pm}$.
חוזק קשר ואורכו מאפשרים לחשב את אנתלפיית הריאקציה ($\Delta H$) לפי משוואה פשוטה:
\[\Delta_{rxn} H = \Delta H(\text{bond breakage}) - \Delta H(\text{bond formation})\] \[= \sum \text{BE(reactants)} - \sum \text{BE(products)}\]| קשר | אנרגית קשר (בקילו-ג׳ול למול) |
|---|---|
| $\text{C-C}$ | $347$ |
| $\text{C=C}$ | $614$ |
| $\text{C≡C}$ | $839$ |
| $\text{C-H}$ | $413$ |
| $\text{C-Cl}$ | $330$ |
| $\text{Cl-Cl}$ | $243$ |
לדוגמה, בריאקציה של $\text{CH}_4 + \text{Cl}_2 \to \text{HCl} + \text{CH}_3\text{Cl}$, ניתן לחשב את $\Delta H$ על ידי סכימת אנרגיות הקשרים שנשברו ונוצרו: $\text{CH}_4 + \text{Cl}_2 \to \text{HCl} + \text{CH}_3\text{Cl}$
\[\begin{array}{ccc} & \text{H} & \\[-6pt] & | & \\ & \text{H} - \text{C} - \text{H} & \\[-6pt] & | & \\ & \text{H} & \\[-6pt] \end{array} \ \text{Cl}-\text{Cl} \ \ \to \ \ \begin{array}{ccc} & \text{H} & \\[-6pt] & | & \\ & \text{H} - \text{C} - \text{Cl} & \\[-6pt] & | & \\ & \text{H} & \\[-6pt] \end{array} \ \ \ \text{H}-\text{Cl}\] \[\Delta H = \left( 4 \times 414 \right) + \left( 1 \times 243 \right) - \left( 1 \times 431 \right) - \left( 1 \times 339 \right) = - 113 \, \text{kJ/mol}\]לסיכום, מבנה לואיס הוא מודל ראשוני ומאוד אינטואיטיבי, אך הוא אינו מתאר את המציאות במלואה. לשם כך נעבור למודל אורביטלי המאפשר ניתוח מעמיק יותר של קשרים וחפיפת אורביטלים.
דור פסקל