מטרת השיעור
בשיעור זה נלמד כיצד לתאר תנועה במערכת קואורדינטות פולאריות, נגזור את הביטויים למהירות ותאוצה, ונחיל זאת על דוגמה קונקרטית של תנועה מעגלית.
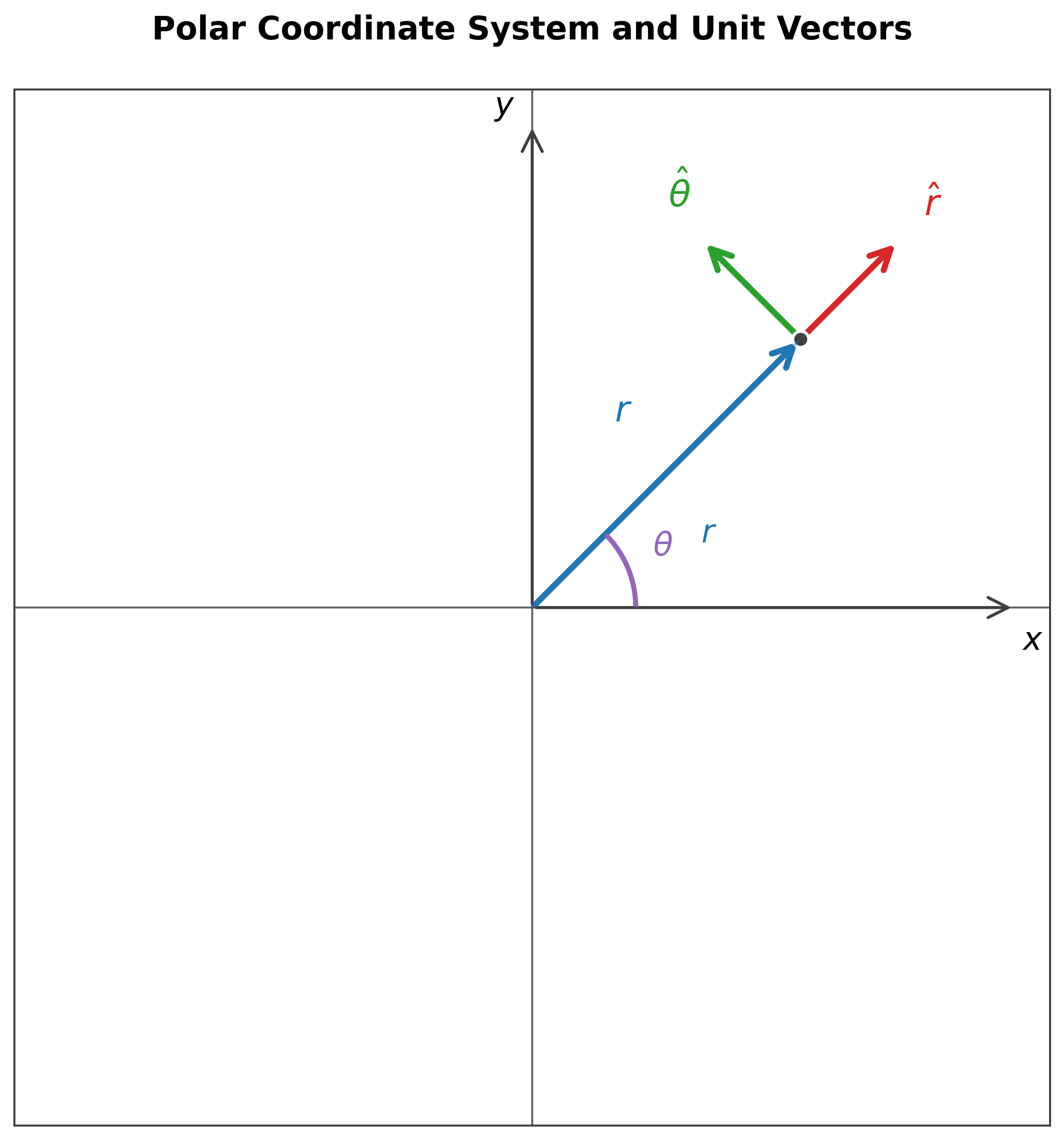
וקטורי יחידה בקואורדינטות פולאריות
הגדרת וקטורי היחידה
בקואורדינטות פולאריות יש לנו שני וקטורי יחידה:
\[\begin{align} \hat{r} &= \cos\theta \, \hat{x} + \sin\theta \, \hat{y} \tag{1} \\ \hat{\theta} &= -\sin\theta \, \hat{x} + \cos\theta \, \hat{y} \tag{2} \end{align}\]- $\hat{r}$ הוא וקטור היחידה בכיוון הרדיאלי (מהמרכז החוצה)
- $\hat{\theta}$ הוא וקטור היחידה בכיוון המשיקי - טנגנציאלי (ניצב ל-$\hat{r}$) (בכיוון התנועה סביב המעגל)
נגזרות וקטורי היחידה
נקודת מפתח חשובה: וקטורי היחידה $\hat{r}$ ו-$\hat{\theta}$ תלויים בזמן כאשר הזווית $\theta$ משתנה עם הזמן.
נגזור את וקטור היחידה של הציר הרדיאלי ($\hat{r}$) שבהגדרה $(1)$ לפי הזמן $t$:
\[\begin{align} \frac{d\hat{r}}{dt} &= \frac{d}{dt}(\cos\theta \, \hat{x} + \sin\theta \, \hat{y}) \\ &= -\sin\theta \cdot \frac{d\theta}{dt} \, \hat{x} + \cos\theta \cdot \frac{d\theta}{dt} \, \hat{y} \\ &= \dot{\theta}(-\sin\theta \, \hat{x} + \cos\theta \, \hat{y}) \\ &= \dot{\theta} \, \hat{\theta} \end{align}\]באופן דומה נגזור את וקטור היחידה המשיקי $\hat{\theta}$ שבהגדרה $(2)$:
\[\begin{align} \frac{d\hat{\theta}}{dt} &= \frac{d}{dt}(-\sin\theta \, \hat{x} + \cos\theta \, \hat{y}) \\ &= -\cos\theta \cdot \dot{\theta} \, \hat{x} - \sin\theta \cdot \dot{\theta} \, \hat{y} \\ &= -\dot{\theta}(\cos\theta \, \hat{x} + \sin\theta \, \hat{y}) \\ &= -\dot{\theta} \, \hat{r} \end{align}\]תוצאות מרכזיות - הנגזרות של וקטורי היחידה בקואורדינטות פולאריות:
\[\begin{align} \dot{\hat{r}} &= \dot{\theta} \, \hat{\theta} \tag{3} \\ \dot{\hat{\theta}} &= -\dot{\theta} \, \hat{r} \tag{4} \end{align}\]התוצאות האלה יסייעו לנו להגיע לנוסחת התאוצה והמהירות בקואורדינטות פולאריות. החשיבות היא שבניגוד למערכות אחרות, וקטורי היחידה כאן הם פונקציה - הם משתנים עם הזמן.
וקטור המהירות בקואורדינטות פולאריות
גזירת וקטור המקום
וקטור המקום הוא המרחק מהמרכז לכיוון הנקודה במערכת קואורדינטות פולאריות. הוא מוגדר כ:
\[\vec{r} = r \, \hat{r} \tag{5}\]הערה: נראה שבחלק מהמקומות מסמנים $R$ במקום $r$.
המהירות היא הנגזרת של וקטור המקום ($5$) לפי הזמן. וקטור המקום עצמו כאמור תלוי בזמן, ולכן נשתמש בכלל השרשרת:
\[\begin{align} \vec{v} &= \frac{d\vec{r}}{dt} \\ &\overset{(5)}{=} \frac{d}{dt}(r \, \hat{r}) \\ &= \frac{dr}{dt} \, \hat{r} + r \, \frac{d\hat{r}}{dt} \tag{$\text{chain rule}$} \\ &= \dot{r} \, \hat{r} + r \, \dot{\theta} \, \hat{\theta} \tag{6} \end{align}\]הביטוי האחרון במשוואה $(6)$ התקבל מהצבת הנגזרת של וקטור היחידה $\hat{r}$ מהתוצאה $(3)$. סך הכל מצאנו שוקטור המהירות בקואורדינטות פולאריות הוא:
\[\boxed{\vec{v} = \dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta}} \tag{7}\]
פרשנות פיזיקלית
- $v_r = \dot{r}$: רכיב המהירות הרדיאלי (שינוי המרחק מהמרכז)
- $v_{\theta} = r\dot{\theta}$: רכיב המהירות המשיקי (תנועה לאורך העיגול)
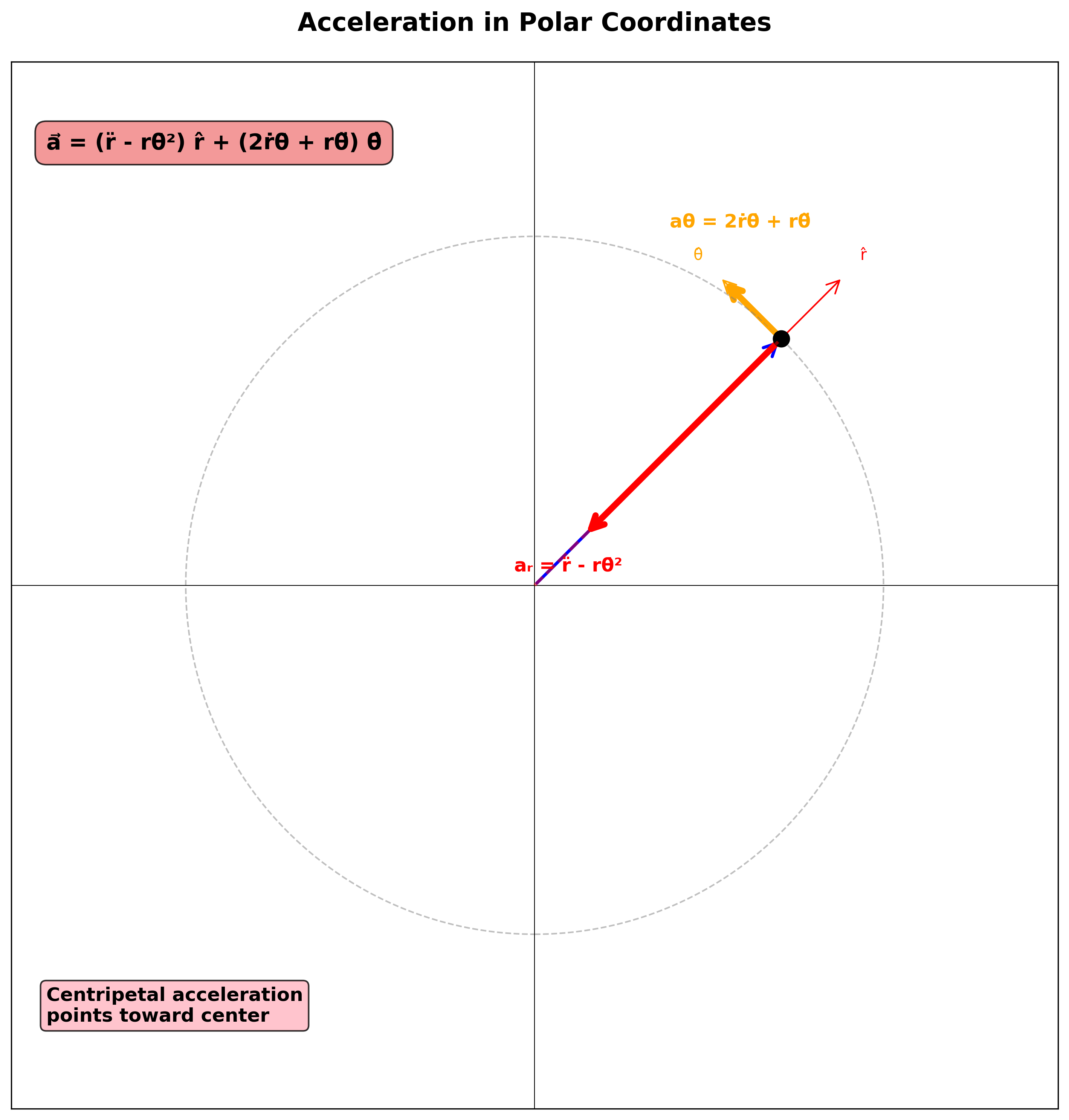
וקטור התאוצה בקואורדינטות פולאריות
גזירת וקטור המהירות
התאוצה היא נגזרת וקטור המהירות לפי הזמן ($7$):
\[\begin{align} \vec{a} &= \frac{d\vec{v}}{dt} \\ &\overset{(7)}{=} \frac{d}{dt}(\dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta}) \\ &= \ddot{r} \, \hat{r} + \dot{r} \, \frac{d\hat{r}}{dt} + \dot{r}\dot{\theta} \, \hat{\theta} + r\ddot{\theta} \, \hat{\theta} + r\dot{\theta} \, \frac{d\hat{\theta}}{dt} \end{align}\]החלפת הנגזרות של וקטורי היחידה:
\[\begin{align} \vec{a} &= \ddot{r} \, \hat{r} + \dot{r} \cdot \overbrace{\dot{\theta} \, \hat{\theta}}^{(3)} + \dot{r}\dot{\theta} \, \hat{\theta} + r\ddot{\theta} \, \hat{\theta} + r\dot{\theta} \cdot (-\dot{\theta} \, \hat{r}) \\ &= \ddot{r} \, \hat{r} - r\dot{\theta}^2 \, \hat{r} + 2\dot{r}\dot{\theta} \, \hat{\theta} + r\ddot{\theta} \, \hat{\theta} \end{align}\]ביטוי התאוצה בקואורדינטות פולאריות:
\[\boxed{\vec{a} = (\ddot{r} - r\dot{\theta}^2) \, \hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta}) \, \hat{\theta}} \tag{8}\]רכיבי התאוצה
- $a_r = \ddot{r} - r\dot{\theta}^2$: תאוצה רדיאלית
- $a_{\theta} = 2\dot{r}\dot{\theta} + r\ddot{\theta}$: תאוצה משיקית
דוגמה 1: נמלה על תקליט מסתובב
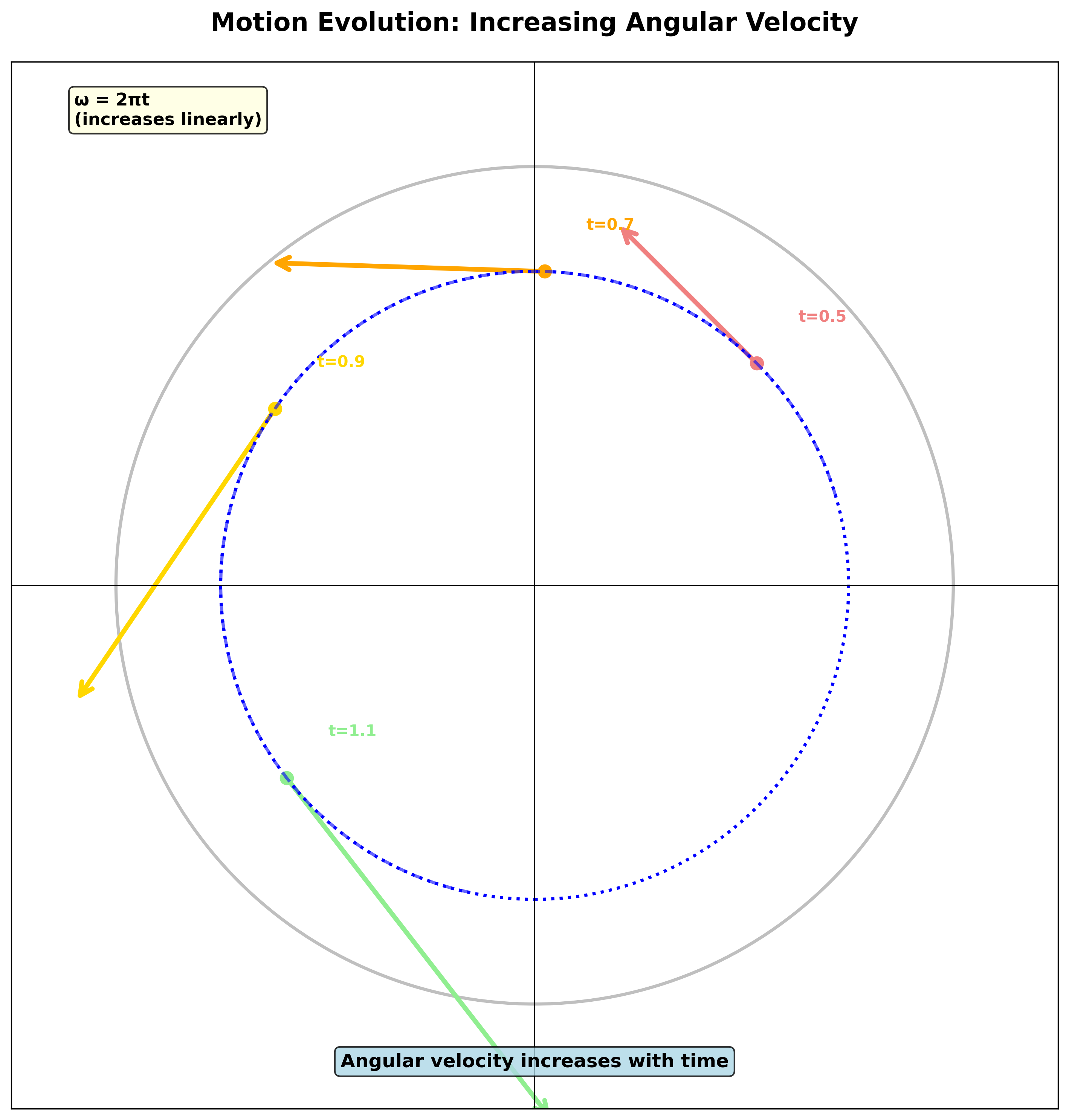
נמלה יושבת על התקליט במרחק קבוע $R$ מהמרכז. תקליט מסתובב כך שהזווית משתנה לפי: $\theta(t) = \pi t^2$. כלומר, כך שהמהירות הזוויתית הולכת וגדלה.
- מה מיקום הנמלה בקוארדינטות קרטזיות?
- וקטור המהירות והתאוצה
- הזווית בין מיקום הנמלה לבין כיוון תנועת הנמלה
- מהי התאוצה הרדיאלית והמשיקית והזוויתית?
ניתוח התנועה
נתחיל בניתוח התנועה של הנמלה על התקליט המסתובב. נשתמש בקואורדינטות פולאריות כדי לתאר את התנועה.
וקטור המקום:
\[\vec{r}(t) = R \, \hat{r}\]נמצא את הביטוי לנגזרות של וקטור המקום לפי הזמן. מאחר ש-$R$ קבוע:
\[\begin{align} \dot{r} &= 0 \\ \ddot{r} &= 0 \end{align}\]המהירות הזוויתית:
ניעזר בנתון $\theta(t) = \pi t^2$ כדי לחשב את המהירות הזוויתית - נגזרת הזווית לפי הזמן:
\[\begin{align} \omega = \dot{\theta} &= \frac{d}{dt}(\pi t^2) = 2\pi t \end{align}\]התאוצה הזוויתית:
זו הנגזרת השנייה של הזווית לפי הזמן:
\[\begin{align} \alpha = \ddot{\theta} &= \frac{d\omega}{dt} = 2\pi \end{align}\]
סעיף 1: מיקום הנמלה בקואורדינטות קרטזיות
בכתה פתרנו את התרגיל בלי להיעזר בקואורדינטות קרטזיות, עם התמקדות בסעיפים 2 ו-4. ככל הנראה לא מומלץ להתבסס על קואורדינטות קרטזיות במקרה זה, מאחר שהבעיה מתאימה יותר לקואורדינטות פולאריות. לשלמות התמונה התשובה לסעיף 1 היא:
\[\begin{align} x(t) &= R \cos(\pi t^2) \\ y(t) &= R \sin(\pi t^2) \end{align}\]סעיף 2: וקטור המהירות והתאוצה
חישוב המהירות
מאחר שזו תנועה מעגלית ($r = R$ קבוע), אין רכיב רדיאלי של המהירות ($\dot{r} = 0$). נשתמש בנוסחה הכללית לתנועה מעגלית:
\[\vec{v} = r\omega \, \hat{\theta}\]כאשר $\omega = \dot{\theta}$. נציב את הערכים $r= R$ ו-$\omega = 2\pi t$ ונקבל:
\[\vec{v} = R \cdot 2\pi t \, \hat{\theta} = 2\pi Rt \, \hat{\theta}\]זו התשובה - וקטור המהירות הוא:
\[\boxed{\vec{v} = 2\pi Rt \, \hat{\theta}} \tag{9}\]תוצאה: המהירות המשיקית גדלה ליניארית עם הזמן.
הערה: אם $R$ היה משתנה, היינו צריכים לחשב גם את רכיב המהירות הרדיאלי $\dot{r} \, \hat{r}$, אך מאחר ש-$R$ קבוע, רכיב זה הוא אפס. הנוסחה הכללית הייתה:
\[\vec{v} = \dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta}\]
חישוב התאוצה
נשתמש בנוסחה הכללית לתאוצה בקואורדינטות פולאריות $(8)$:
\[\begin{align} \vec{a} &= (0 - R(2\pi t)^2) \, \hat{r} + (0 + R \cdot 2\pi) \, \hat{\theta} \\ &= -4\pi^2 Rt^2 \, \hat{r} + 2\pi R \, \hat{\theta} \end{align}\]וקטור התאוצה הוא:
\[\boxed{\vec{a} = -4\pi^2 Rt^2 \, \hat{r} + 2\pi R \, \hat{\theta}}\]
סעיף 3: הזווית בין מיקום הנמלה לכיוון תנועתה
המרצה לא התמקד בסעיף הזה בכתה. בכל מקרה, להלן הצעת פתרון:
הזווית בין וקטור המקום $\vec{r}$ לכיוון התנועה $\vec{v}$ ניתנת על ידי:
\[\begin{align} \cos\phi &= \frac{\vec{r} \cdot \vec{v}}{|\vec{r}| |\vec{v}|} \\ &= \frac{R \hat{r} \cdot (2\pi Rt \, \hat{\theta})}{R \cdot 2\pi Rt} \\ &= \frac{R \cdot 2\pi Rt \cdot 0}{R \cdot 2\pi Rt} = 0 \end{align}\]הזווית $\phi$ היא:
\[\phi = \frac{\pi}{2} \text{ radian} = 90^\circ\]סעיף 4: תאוצה רדיאלית ומשיקית
פרשנות פיזיקלית לתרגיל הנמלה
רכיב רדיאלי
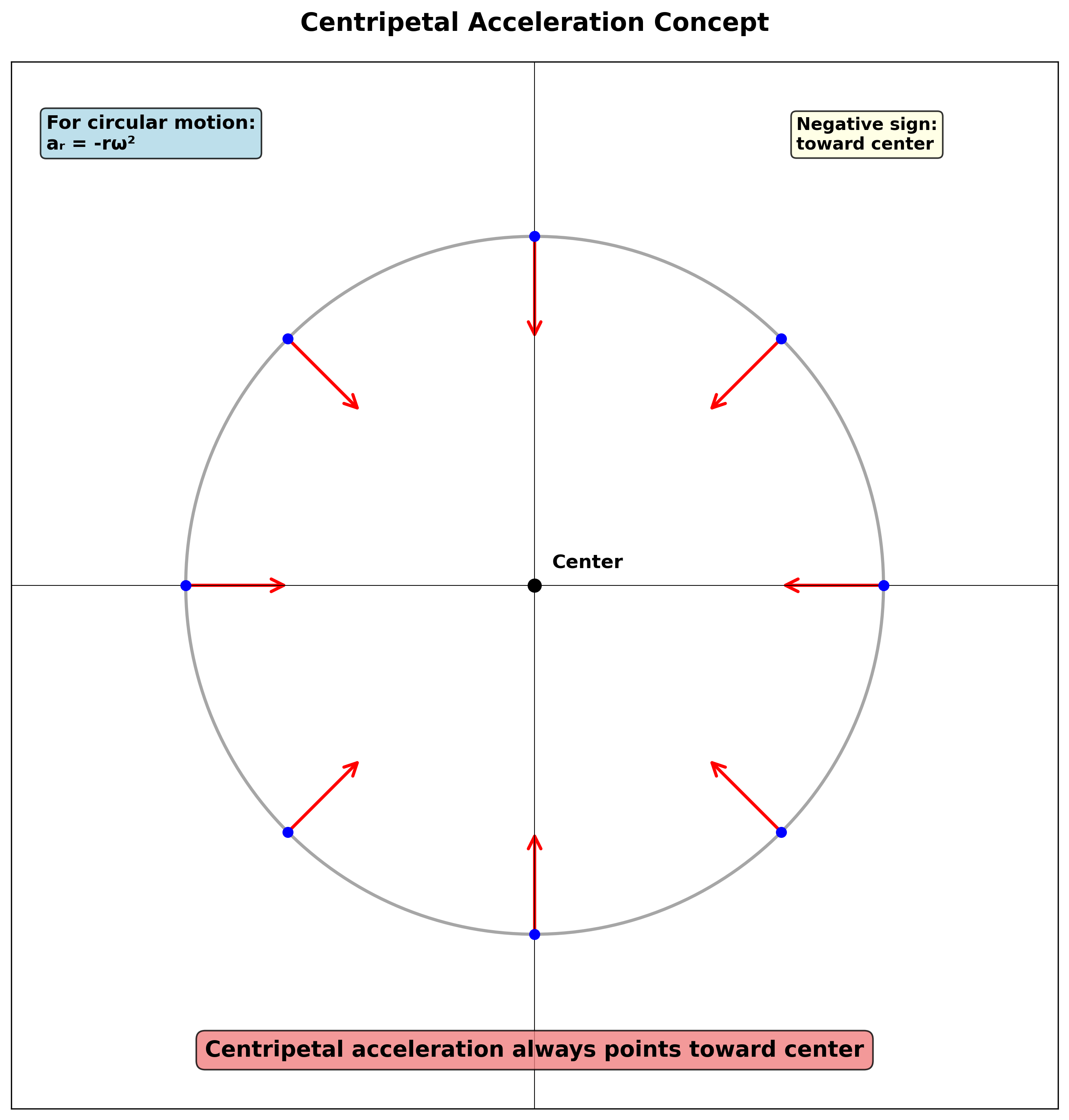
\[a_r = -4\pi^2 Rt^2\]- הסימן השלילי מציין שהתאוצה פונה לעבר המרכז
- זוהי תאוצה צנטריפטלית (centripetal acceleration)
- גודלה גדל כ-$t^2$ - ככל שהמהירות הזוויתית עולה, התאוצה הצנטריפטלית גדלה
רכיב משיקי
\[a_{\theta} = 2\pi R\]- זוהי תאוצה קבועה בכיוון המשיקי
- גורמת להאצת התנועה המעגלית
דוגמה 2: מטוטלת במעלית מואצת
יש לנו מעלית עם מטוטלת באורך $L$. המעלית מואצת כלפי מעלה בתאוצה $A$.
השאלה המרכזית: איך משפיעה תאוצת המעלית על תנועת המטוטלת?
הערה: השאלה המלאה מתרגול אחר הייתה למצוא את שיווי המשקל ביחס לצופה מהמערכת, תדירות התנודות ואת זמן המחזור ($T$) במצבים הבאים:
- המערכת נמצאת בתוך מעלית הנעה בתאוצה קבועה $A$ כלפי מעלה.
- המערכת נמצאת ברכבת הנעה בתאוצה קבועה $A$ ימינה.
- המערכת נמצאת ברכבת הנעה במהירות קבועה ימינה.
סעיף 1
כוחות מדומים
כאשר המעלית מואצת כלפי מעלה, מתבוננים במטוטלת ממערכת הייחוס של המעלית ורואים כוח פיקטיבי נוסף.
על הכדור פועלים שני כוחות:
- כוח הכבידה: $mg$ כלפי מטה
- כוח מדומה: $mA$ כלפי מטה
הכלל: הכוח המדומה הוא תמיד מסה כפול תאוצה המערכת בכיוון הפוך.
כוח הכבידה האפקטיבי
במעלית מואצת, כוח הכבידה האפקטיבי הוא:
\[F_{\text{effective}} = m(g + a)\]זה בדיוק כמו מטוטלת רגילה, רק שכוח הכבידה חזק יותר.
\[F_{\text{imaginary}} = ma \quad \text{(downward)}\]המהירות הזוויתית החדשה
במטוטלת רגילה, המהירות הזוויתית של תנודות קטנות היא:
\[\omega = \sqrt{\frac{g}{L}}\]במעלית מואצת, מחליפים את $g$ ב-$(g+a)$:
\[\boxed{\omega = \sqrt{\frac{g+a}{L}}}\]
משוואת התנועה
נשתמש בקואורדינטות פולאריות ובחוק השני של ניוטון ($F = ma$) כדי למצוא את משוואת התנועה של המטוטלת.
בכיוון המשיקי
התאוצה המשיקית היא: $a_{\theta} = L\ddot{\theta}$
הכוח המשיקי הוא הרכיב המשיקי של כוח הכבידה האפקטיבי:
\[F_{\theta} = -m(g+a)\sin\theta \tag{1}\]בתנודות קטנות: $\sin\theta \approx \theta$. נציב את השקילות הזאת ב-($1$) ונקבל:
\[F_{\theta} \approx -m(g+a)\theta \tag{2}\]נשתמש בחוק השני של ניוטון בכיוון המשיקי:
\[-m(g+a)\theta = mL\ddot{\theta}\]נחליף בין הצדדים לנוחות ונבודד את $\ddot{\theta}$:
\[\begin{align} mL\ddot{\theta} &= -m(g+a)\theta \tag{$\div mL$} \\ \ddot{\theta} &= -\frac{(g+a)}{L}\theta \end{align}\]סך הכל, משוואת התנועה של המטוטלת במעלית מואצת היא:
\[\boxed{\ddot{\theta} = -\frac{g+a}{L}\theta}\]זו משוואת תנועה הרמונית פשוטה עם תדירות זוויתית $\omega = \sqrt{\frac{g+a}{L}}$.
בכיוון הרדיאלי
גם בכיוון הרדיאלי יש תאוצה צנטריפטלית: $a_r = -L\dot{\theta}^2$
החוק השני בכיוון הרדיאלי:
\[T - m(g+a)\cos\theta = mL\dot{\theta}^2\]לכן מתיחות החוט היא:
\[\boxed{T = mL\dot{\theta}^2 + m(g+a)\cos\theta}\]
ההבחנה בין קואורדינטות
מדוע קואורדינטות פולאריות?
במטוטלת, התנועה היא מעגלית. בקואורדינטות פולאריות:
- כיוון רדיאלי: אין תנועה (המרחק $L$ קבוע)
- כיוון משיקי: יש תנועה (הזווית $\theta$ משתנה)
זה יותר פשוט מקואורדינטות קרטזיות שבהן שני הצירים משתנים.
הקשר לתורת היחסות
רעיון מעניין: תופעה זו הובילה את איינשטיין לפתח את תורת היחסות(?).
עקרון השקילות: אדם במעלית סגורה לא יכול להבחין בין:
- מעלית נייחת בכוח כבידה $g$
- מעלית מואצת בתאוצה $A$ במרחב ללא כבידה
בשני המקרים הוא חש “כוח כבידה” של $g+A$.
במעלית נופלת חופשית ($A = -g$): הכוח האפקטיבי הוא אפס - כולם “צפים” כמו אסטרונאוטים.
תשובה פורמאלית לסעיף 1
נקודת שיווי המשקל נמצאת כשהכדור והחוט מאונחים לקרקע.
\[\sum F_r = ma_r\]נציב את הכוחות בכיוון הרדיאלי:
\[(mg + mA)\cos\theta - T = mL\dot{\theta}^2\]נציב את הכוחות בכיוון המשיקי:
\[\sum F_{\theta} = ma_{\theta}\] \[-(mg + mA)\sin\theta = mL\ddot{\theta}\]בקירוב של זוויות קטנות ($\sin\theta \approx \theta$):
\[-(mg + mA)\theta = mL\ddot{\theta}\]מכאן נובע ש:
\[\ddot{\theta} = -\frac{(g + A)}{L}\theta\] \[\omega = \sqrt{\frac{g + A}{L}}\]זמן המחזור של המטוטלת הוא:
\[T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{L}{g + A}}\]סעיף 2 - מטוטלת ברכבת מואצת ימינה
הפתרון לתרגיל הופיע בשיעור תגבור.
סיכום מושגים עיקריים
נגזרות וקטורי יחידה
\[\begin{align} \dot{\hat{r}} &= \dot{\theta} \, \hat{\theta} \\ \dot{\hat{\theta}} &= -\dot{\theta} \, \hat{r} \end{align}\]מהירות ותאוצה כלליות
\[\begin{align} \vec{v} &= \dot{r} \, \hat{r} + r\dot{\theta} \, \hat{\theta} \\ \vec{a} &= (\ddot{r} - r\dot{\theta}^2) \, \hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta}) \, \hat{\theta} \end{align}\]מקרה מיוחד: תנועה מעגלית ($r =$ קבוע)
\[\begin{align} \vec{v} &= r\omega \, \hat{\theta} \\ \vec{a} &= -r\omega^2 \, \hat{r} + r\alpha \, \hat{\theta} \end{align}\]כאשר:
- $\omega = \dot{\theta}$ - מהירות זוויתית
- $\alpha = \ddot{\theta}$ - תאוצה זוויתית
- $-r\omega^2 \, \hat{r}$ - תאוצה צנטריפטלית
- $r\alpha \, \hat{\theta}$ - תאוצה משיקית
מינוח
- תאוצה צנטריפטלית: תאוצה הפונה לעבר מרכז העיגול
- תאוצה צנטריפוגלית: תאוצה הפונה החוצה ממרכז העיגול
- תאוצה רדיאלית: תאוצה בכיוון הרדיאלי (יכולה להיות לכיוון המרכז או ממנו)
הערה חשובה: קואורדינטות פולאריות מאפשרות תיאור אלגנטי של תנועה מעגלית וספירלית, כאשר הסימטריה הטבעית של הבעיה מתבטאת במשוואות פשוטות יותר מאשר בקואורדינטות קרטזיות.
חזור לתרגול 7
עבור לשיעור 9