להלן שאלות התרגול:
1. תנועה בשני ממדים עם כוח תלוי זמן
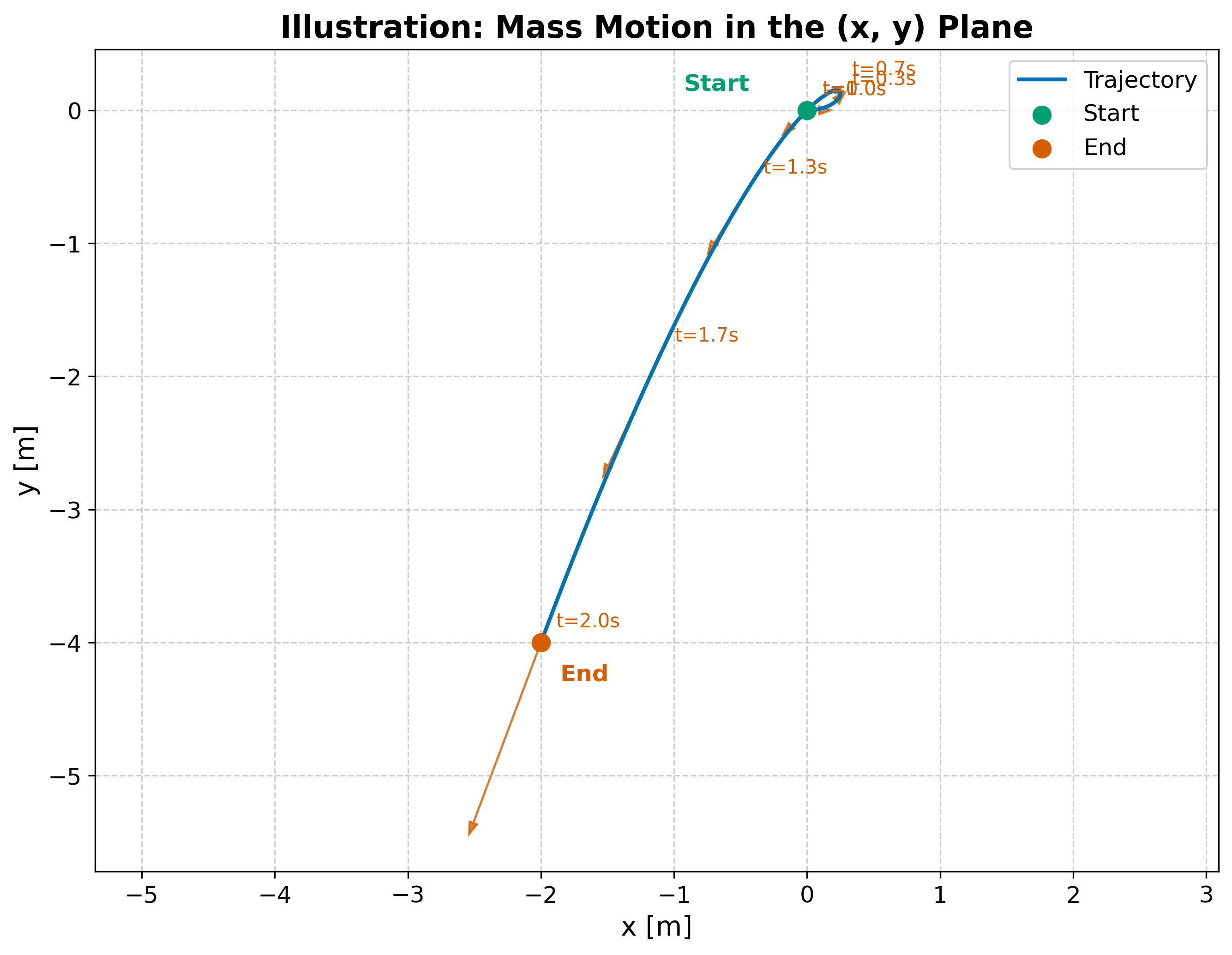
נתון גוף בעל מסה $m = 1.5 \, \mathrm{kg}$ הנע במישור $(x,y)$ מתחיל בתנועתו מהנקודה $(0,0)$. המישור חסר חיכוך.
וקטור מהירות הגוף נתון ביחידות של מטר לשנייה:
\[\mathbf{v}(t) = (1 - 2t)\hat{\mathbf{x}} + (2t - 3t^2)\hat{\mathbf{y}}\]
- חשבו את מהירות הגוף כאשר הוא מגיע בחזרה לנקודת המוצא $(0,0)$.
- חשבו את הזמן $t_m$ שבו גודל הכוח הפועל על הגוף הוא מינימלי.
- כמה עבודה עשה הכוח הפועל על הגוף מתחילת התנועה עד לזמן $t = 2 \, \mathrm{s}$?
- האם הכוח הפועל על הגוף הוא כוח משמר? נמקו בצורה ברורה ותמציתית.
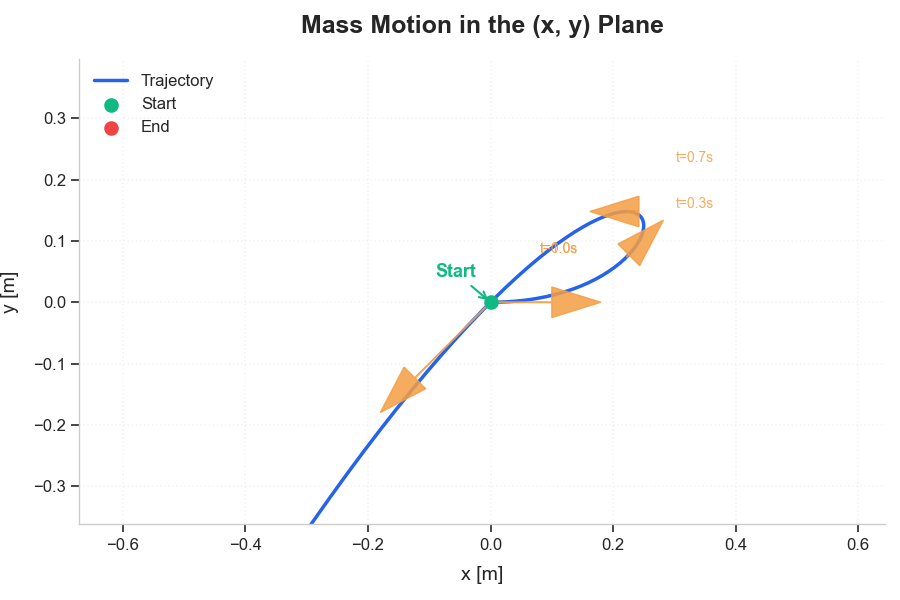
1.1 מציאת המהירות כאשר הגוף חוזר לנקודת המוצא
נמצא את הזמן שבו הגוף חוזר לראשית, ואז נוכל לחשב את מהירותו באותו זמן.
לא תמיד מובטח שיש זמן $t \ne 0$ שבו $\mathbf{r}(t) = \left(x(t), y(t)\right) = (0, 0)$, אבל במקרה הזה זה עולה מהשאלה.
נחשב את וקטור המיקום $\mathbf{r}(t)$ על ידי אינטגרציה של $\mathbf{v}(t)$.
עבור רכיב $x$:
\[x(t) = x(0) + \int_0^t v_x(s)\,ds = 0 + \int_0^t (1 - 2s)\,ds = t - t^2\]עבור רכיב $y$:
\[y(t) = y(0) + \int_0^t v_y(s)\,ds = 0 + \int_0^t (2s-3s^2)\,ds = t^2 - t^3\]מציאת זמן החזרה לראשית:
הגוף חוזר לראשית כאשר $x(t) = 0$ וגם $y(t) = 0$ (עבור $t > 0$).
מהתנאי $x(t) = 0$:
\[t - t^2 = 0 \implies t(1 - t) = 0\]הפתרונות הם $t = 0$ או $t = 1$.
מהתנאי $y(t) = 0$:
\[t^2 - t^3 = 0 \implies t^2(1 - t) = 0\]הפתרונות הם $t = 0$ או $t = 1$.
לכן, הגוף חוזר לראשית בזמן $t = 1 \, \mathrm{s}$.
המהירות בזמן החזרה:
נחשב את וקטור המהירות בזמן $t = 1$:
\[\begin{aligned} \mathbf{v}(1) &= \left(1 - 2(1)\right)\hat{\mathbf{x}} + \left(2(1) - 3(1)^2\right)\hat{\mathbf{y}} \\[5pt] &= (-1)\hat{\mathbf{x}} + (-1)\hat{\mathbf{y}} \\[5pt] &= -\hat{\mathbf{x}} - \hat{\mathbf{y}} \end{aligned}\]גודל המהירות:
\[|\mathbf{v}(1)| = \sqrt{(-1)^2 + (-1)^2} = \sqrt{2} \, \mathrm{m/s}\]השאלה ביקשה את “מהירות הגוף”, שלרוב מתכוונת לווקטור המהירות.
\[\boxed{\mathbf{v}(t=1) = (-1, -1) \, \mathrm{m/s}}\]1.2 הזמן שבו גודל הכוח מינימלי
לפי החוק השני של ניוטון, $\mathbf{F} = m\mathbf{a}$. כיוון שהמסה קבועה, הכוח פרופורציונלי לתאוצה, שהיא נגזרת המהירות לפי הזמן.
\[\begin{aligned} \mathbf{a}(t) &= \frac{d\mathbf{v}}{dt} = \frac{d}{dt}\left[(1 - 2t)\hat{\mathbf{x}} + (2t - 3t^2)\hat{\mathbf{y}}\right] \\[5pt] &= -2\hat{\mathbf{x}} + (2 - 6t)\hat{\mathbf{y}} \end{aligned}\]גודל הכוח:
\[|\mathbf{F}(t)| = m|\mathbf{a}(t)| = m\sqrt{(-2)^2 + (2 - 6t)^2} = m\sqrt{4 + (2 - 6t)^2}\]גודל הכוח $\vert \mathbf{F}(t)\vert $ הוא מינימלי כאשר הביטוי שבתוך השורש, $4 + (2 - 6t)^2$, הוא מינימלי. זה קורה כאשר $(2 - 6t)^2 = 0$, כלומר:
\[2 - 6t = 0 \implies \boxed{t_m = \frac{1}{3} \, \mathrm{s}}\]1.3 העבודה שביצע הכוח
העבודה שביצע הכוח מ-$t = 0$ עד $t = 2 \, \mathrm{s}$ ניתנת על ידי משפט עבודה-אנרגיה:
\[W = \Delta E_k = \frac{1}{2}m|\mathbf{v}(2)|^2 - \frac{1}{2}m|\mathbf{v}(0)|^2\]נחשב את המהירויות:
\[\mathbf{v}(0) = (1 - 0)\hat{\mathbf{x}} + (0 - 0)\hat{\mathbf{y}} = \hat{\mathbf{x}}\]לכן
\[|\mathbf{v}(0)|^2 = 1^2 = 1\]נחשב את $\mathbf{v}(2)$:
\[\mathbf{v}(2) = (1 - 4)\hat{\mathbf{x}} + (4 - 12)\hat{\mathbf{y}} = -3\hat{\mathbf{x}} - 8\hat{\mathbf{y}}\]לכן
\[|\mathbf{v}(2)|^2 = (-3)^2 + (-8)^2 = 9 + 64 = 73\]נציב את הערכים:
\[W = \frac{1}{2}m(73 - 1) = \frac{1}{2}(1.5)(72) = \boxed{54 \, \mathrm{J}}\]דרך חלופית (מסובכת יותר) היא לחשב את העבודה בעזרת אינטגרל מסלולי:
\[W = \int_{t=0}^{t=2} \mathbf{F}(t) \cdot \mathbf{v}(t) \, dt\]כאשר $\mathbf{F}(t) = m\mathbf{a}(t) = m(-2, 2 - 6t)$ ו-$\mathbf{v}(t) = (1 - 2t, 2t - 3t^2)$.
\[W = m \int_{0}^{2} \left[ -2(1 - 2t) + (2 - 6t)(2t - 3t^2) \right] dt\]לאחר פתיחת סוגריים ואינטגרציה, מתקבלת אותה תוצאה: $W = 54 \, \mathrm{J}$.
1.4 האם הכוח משמר?
כוח משמר מוגדר ככוח שעבודתו על מסלול סגור כלשהו שווה לאפס. במקרה שלנו, הגוף יוצא מנקודת המוצא $(0,0)$ בזמן $t=0$ וחוזר אליה בזמן $t=1$. זהו מסלול סגור. נחשב את העבודה על מסלול זה:
\[W_{0\to1} = \Delta E_k = \frac{1}{2}m\left(|\mathbf{v}(1)|^2 - |\mathbf{v}(0)|^2\right)\]כבר חישבנו:
\[\begin{aligned} |\mathbf{v}(1)|^2 &= (-\hat{\mathbf{x}} - \hat{\mathbf{y}}) \cdot (-\hat{\mathbf{x}} - \hat{\mathbf{y}}) = 2 \\[5pt] |\mathbf{v}(0)|^2 &= (\hat{\mathbf{x}}) \cdot (\hat{\mathbf{x}}) = 1 \end{aligned}\]לכן:
\[W_{0\to1} = \frac{1}{2}(1.5)(2 - 1) = 0.75 \, \mathrm{J}\]מסקנה: מכיוון שהעבודה על מסלול סגור ($W_{0\to1} = 0.75 \, \mathrm{J}$) אינה שווה לאפס, הכוח אינו משמר.
דרך נוספת להראות זאת היא לבדוק אם הכוח תלוי רק במיקום. הכוח $\mathbf{F}(t) = m\mathbf{a}(t)$ תלוי מפורשות בזמן, ולכן אינו יכול להיות משמר (כוח משמר תלוי במיקום בלבד).
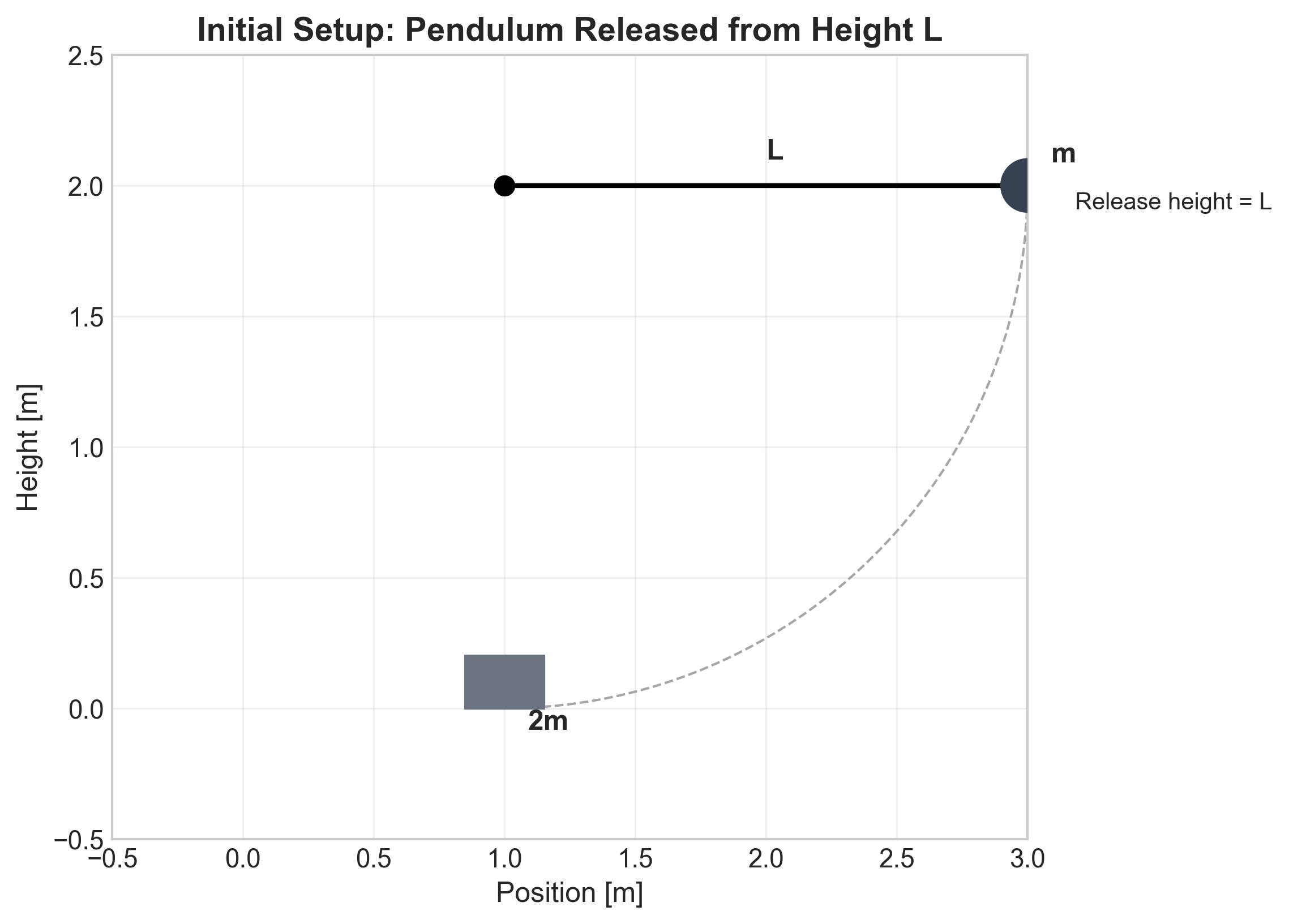
2. התנגשויות במערכת מטוטלת
משקולת בעלת מסה $m$ מחוברת למטוטלת בעלת חוט באורך $\ell$. המשקולת משוחררת ממנוחה מגובה $\ell$ (כלומר, כשהחוט אופקי) ופוגעת בקוביה במנוחה בעלת מסה $2m$ הנמצאת בנקודה הנמוכה ביותר של המסלול. לאחר הפגיעה, המטוטלת והקוביה נעות.
לאיזה גובה תעלה המטוטלת ($m$) לאחר הפגיעה בכל אחד מהמקרים הבאים?
- ההתנגשות אלסטית לחלוטין.
- ההתנגשות אינה אלסטית, והקוביה נעה לאחר ההתנגשות במהירות השווה למהירות המטוטלת לפני ההתנגשות.
- ההתנגשות פלסטית לחלוטין (הכדור והקוביה נדבקים זה לזה).
2.1 התנגשות אלסטית
שלב א׳: מציאת מהירות המטוטלת לפני ההתנגשות
משימור אנרגיה מכנית במהלך נפילת המטוטלת מגובה $h=\ell$ לנקודה הנמוכה ביותר: האנרגיה הפוטנציאלית ההתחלתית הופכת לאנרגיה קינטית.
\[mg\ell = \frac{1}{2}mv_1^2\]מכאן, מהירות המטוטלת רגע לפני הפגיעה היא:
\[\boxed{v_1 = \sqrt{2g\ell}}\]שלב ב׳: ניתוח ההתנגשות האלסטית
בהתנגשות אלסטית חד-ממדית בין מסה $m_1=m$ למסה $m_2=2m$ (שנמצאת במנוחה), נשמרים גם התנע וגם האנרגיה הקינטית. נסמן את מהירות המטוטלת לאחר ההתנגשות ב-$u_1$ ואת מהירות הקוביה ב-$u_2$.
-
שימור תנע:
\[\begin{aligned} mv_1 + (2m) \cdot 0 &= mu_1 + (2m)u_2 \\[5pt] \implies v_1 &= u_1 + 2u_2 \quad (1) \end{aligned}\] -
שימור אנרגיה קינטית:
\[\begin{aligned} \frac{1}{2}mv_1^2 + 0 &= \frac{1}{2}mu_1^2 + \frac{1}{2}(2m)u_2^2 \\[5pt] \implies v_1^2 &= u_1^2 + 2u_2^2 \quad (2) \end{aligned}\]
מפתרון מערכת המשוואות (1) ו-(2) עבור $u_1$ (מהירות המטוטלת לאחר ההתנגשות), מקבלים:
\[u_1 = \frac{m_1 - m_2}{m_1 + m_2} v_1 = \frac{m - 2m}{m + 2m} v_1 = -\frac{1}{3}v_1\]הסימן השלילי מציין שהמטוטלת נעה בכיוון ההפוך (אחורה).
שלב ג׳: מציאת הגובה המקסימלי לאחר ההתנגשות
משימור אנרגיה עבור המטוטלת לאחר ההתנגשות, האנרגיה הקינטית שלה הופכת לאנרגיה פוטנציאלית:
\[\begin{aligned} \frac{1}{2}mu_1^2 &= mgh_{\text{max}} \\[5pt] \implies h_{\text{max}} &= \frac{u_1^2}{2g} \end{aligned}\]נציב את $u_1 = -\frac{1}{3}v_1$ ואת $v_1 = \sqrt{2g\ell}$:
\[h_{\text{max}} = \frac{\left(-\frac{1}{3}\sqrt{2g\ell}\right)^2}{2g} = \frac{\frac{1}{9}(2g\ell)}{2g} = \frac{\ell}{9}\] \[\boxed{h_{\text{max}} = \frac{\ell}{9}}\]2.2 התנגשות לא-אלסטית עם תנאי מיוחד
נתון שלאחר ההתנגשות, מהירות הקוביה ($u_2$) שווה למהירות המטוטלת לפני ההתנגשות ($v_1$).
\[u_2 = v_1 = \sqrt{2g\ell}\]נשתמש בשימור תנע כדי למצוא את מהירות המטוטלת לאחר ההתנגשות, $u_1$:
\[mv_1 = mu_1 + (2m)u_2\]נציב $u_2 = v_1$:
\[\begin{aligned} mv_1 &= mu_1 + 2mv_1 \\[5pt] \implies u_1 &= v_1 - 2v_1 \\[5pt] &= -v_1 \end{aligned}\]המטוטלת נעה אחורה במהירות שגודלה שווה למהירות הפגיעה. משימור אנרגיה, היא תגיע בחזרה בדיוק לגובה ההתחלתי.
\[h_{\text{max}} = \frac{u_1^2}{2g} = \frac{(-v_1)^2}{2g} = \frac{v_1^2}{2g} = \frac{2g\ell}{2g} = \ell\] \[\boxed{h_{\text{max}} = \ell}\]הערה: מצב זה אינו פיזיקלי, מכיוון שהאנרגיה הקינטית לאחר ההתנגשות גדולה מהאנרגיה הקינטית לפניה, מה שסותר את חוק שימור האנרגיה.
2.3 התנגשות פלסטית
בהתנגשות פלסטית, שני הגופים נדבקים ונעים יחד לאחר ההתנגשות במהירות משותפת $\mathbf{u}$.
שלב א׳: שימור תנע
\[mv_1 = (m + 2m)u = 3mu\]מכאן, המהירות המשותפת לאחר ההתנגשות היא:
\[u = \frac{mv_1}{3m} = \frac{v_1}{3} = \frac{\sqrt{2g\ell}}{3}\]שלב ב׳: מציאת הגובה המקסימלי
משימור אנרגיה עבור המערכת המאוחדת (מסה $3m$) לאחר ההתנגשות:
\[\frac{1}{2}(3m)u^2 = (3m)gh_{\text{max}} \implies h_{\text{max}} = \frac{u^2}{2g}\]נציב את $u$:
\[h_{\text{max}} = \frac{\left(\frac{\sqrt{2g\ell}}{3}\right)^2}{2g} = \frac{\frac{2g\ell}{9}}{2g} = \frac{\ell}{9}\] \[\boxed{h_{\text{max}} = \frac{\ell}{9}}\]שאלה 3 מתרגול 11:
מערכת של שני קיפצים
מערכת של שני קיפצים, כל אחד בעל אורך $a$, בשיווי משקל וקבוע קפיץ $k$. הקיפצים מחוברים זה לזה ומקובעים בקצה האחר בנקודות $(-a, 0)$, $(a, 0)$. נניח שהקיפצים יכולים להתכווץ או להתרחב, אך לא להתכופף.
הראה שהפוטנציאל של המערכת, עבור העברת נקודת החיבור מ$(0,0)$ ל-$(x, y)$ כלשהי, הוא:
\[\phi = \frac{k}{2} \left[ \sqrt{(x + a)^2 + y^2} - a \right]^2 + \frac{k}{2} \left[ \sqrt{(x - a)^2 + y^2} - a \right]^2\]כיוון שהפוטנציאל תלוי ב-$x$ וב-$y$, נצטרך להשתמש בנגזרות חלקיות על מנת למצוא את הכוחות. זכור שנגזרת חלקית של פונקציה $f(x,y)$ מוגדרת בעזרת הנגזרת המלאה כך:
\[\frac{\partial f (x,y)}{\partial x}= \frac{df(x,y=\text{const})}{dx}\] \[\frac{\partial f (x,y)}{\partial y}= \frac{df(x=\text{const},y)}{dy}\]מצא את הכוח $\vec{F}_x$ והראה שעבור $\mathbf{r}=0$ מתקיים $\vec{F}_x = 0$.
מצא את הכוח $\vec{F}_y$ עבור $x=0$. בדוק שסימן התוצאה (חיובית או שלילית) הגיוני.
סעיף 1 - פוטנציאל המערכת בעת הזזה
הרעיון הוא להבין כיצד כל הזזה משפיעה על אורך הקפיצים. נעביר מערכת צירים במצב המאוזן ונבדוק בכמה מתארך או מתכווץ כל קפיץ $\Delta \ell_1$ ו-$\Delta \ell_2$. מכאן $\phi = \frac{k}{2}(\Delta \ell_1^2 + \Delta \ell_2^2)$.
\[\ell_1 = \sqrt{(a+x)^2 + y^2}\] \[\ell_2 = \sqrt{(a-x)^2 + y^2}\] \[\Delta \ell_1^2 = \left(\ell_{1 f} - \ell_{1 i}\right)^2 = \left(\sqrt{(a+x)^2 + y^2} - a\right)^2\] \[\Delta \ell_2^2 = \left(\ell_{2 f} - \ell_{2 i}\right)^2 = \left(\sqrt{(a-x)^2 + y^2} - a\right)^2\] \[\boxed{\phi = \frac{k}{2} \left[ \sqrt{(a+x)^2 + y^2} - a \right]^2 + \frac{k}{2} \left[ \sqrt{(a-x)^2 + y^2} - a \right]^2}\]סעיף 2 - כוח $\vec{F}_x$ בנקודה $(0,0)$
כוח הוא נגזרת של פוטנציאל:
\[\vec{F}_x = -\frac{\partial \Phi}{\partial x}\]נחשב את הנגזרת החלקית של $\Phi$ לפי $x$:
\[\begin{aligned} \frac{\partial \Phi}{\partial x} &= \frac{k}{2} \frac{\partial}{\partial x} \left[ \sqrt{(a+x)^2 + y^2} - a \right]^2 + \frac{k}{2} \frac{\partial}{\partial x} \left[ \sqrt{(a-x)^2 + y^2} - a \right]^2 \\[5pt] &= k \left[ \frac{(a+x)}{\sqrt{(a+x)^2 + y^2}} \right] \left[ \sqrt{(a+x)^2 + y^2} - a \right] - k \left[ \frac{(a-x)}{\sqrt{(a-x)^2 + y^2}} \right] \left[ \sqrt{(a-x)^2 + y^2} - a \right] \end{aligned}\]כעת נציב $x=0$:
\[\begin{aligned} \frac{\partial \Phi}{\partial x} &= k \left[ \frac{a}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] - \frac{a}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] \right] \\[5pt] &= k \left[ \frac{a}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a - \sqrt{a^2 + y^2} + a \right] \right] \\[5pt] &= k \left[ \frac{a}{\sqrt{a^2 + y^2}} \cdot 0 \right] = 0 \end{aligned}\]לכן, הכוח $\vec{F}_x$ בנקודה $(0,0)$ הוא:
\[\boxed{\vec{F}_x = 0}\]סעיף 3 - כוח $\vec{F}_y$ עבור $x=0$
כעת נחשב את הכוח $\vec{F}_y$ עבור $x=0$:
\[\vec{F}_y = -\frac{\partial \Phi}{\partial y}\]נחשב את הנגזרת החלקית של $\Phi$ לפי $y$:
\[\begin{aligned} \frac{\partial \Phi}{\partial y} &= \frac{k}{2} \frac{\partial}{\partial y} \left[ \sqrt{(a+x)^2 + y^2} - a \right]^2 + \frac{k}{2} \frac{\partial}{\partial y} \left[ \sqrt{(a-x)^2 + y^2} - a \right]^2 \\[5pt] &= k \left[ \frac{y}{\sqrt{(a+x)^2 + y^2}} \right]\left[ \sqrt{(a+x)^2 + y^2} - a \right] + k \left[ \frac{y}{\sqrt{(a-x)^2 + y^2}} \right]\left[ \sqrt{(a-x)^2 + y^2} - a \right] \end{aligned}\]נציב $x=0$:
\[\begin{aligned} \frac{\partial \Phi}{\partial y} &= k \left[ \frac{y}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] + \frac{y}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a \right] \right] \\[5pt] &= k \left[ \frac{y}{\sqrt{a^2 + y^2}} \left[ \sqrt{a^2 + y^2} - a + \sqrt{a^2 + y^2} - a \right] \right] \\[5pt] &= k \left[ \frac{y}{\sqrt{a^2 + y^2}} \cdot 2\left(\sqrt{a^2 + y^2} - a\right) \right] \end{aligned}\]לכן, הכוח $\vec{F}_y$ עבור $x=0$ הוא:
\[\vec{F}_y = -k \left[ \frac{y}{\sqrt{a^2 + y^2}} \cdot 2\left(\sqrt{a^2 + y^2} - a\right) \right]\] \[\boxed{\vec{F}_y = -2k \left[ \frac{y}{\sqrt{a^2 + y^2}} \left(\sqrt{a^2 + y^2} - a\right) \right]}\]אפשר לראות שהכיוון של הכוח תלוי בסימן של $y$ ובניגוד לכיוון של הווקטור $\hat{\mathbf{y}}$:
- אם $y > 0$, אז $\vec{F}_y < 0$ (כוח כלפי מטה).
- אם $y < 0$, אז $\vec{F}_y > 0$ (כוח כלפי מעלה).
כלומר, הקפיץ ״רוצה״ לחזור את המערכת למצב שיווי המשקל, שבו $y=0$.
תודה למתרגל על טיוטת הפתרון הבהירה.
תרגול מיום 26 ביוני 2025.
מהירות בריחה
אנרגיית הכבידה הפועלת בין שני גופים מחוץ לכדור הארץ היא:
\[\phi(r) = -\frac{G M m}{r}\]כאשר $r$ הוא המרחק בין הגופים, $m$ מסת הגוף הנמשך, $M$ מסת הגוף המושך ו- $G=6.67\tfrac{\mathrm{m}^3}{\mathrm{s}^2 \cdot \mathrm{kg}}$ הוא קבוע הכבידה.
- מה הסיבה לסימן השלילי? כיצד הוא מבטא את העובדה שכוח הכבידה הוא כוח משיכה?
הראו שכוח הכבידה הנגזר מאנרגיה זו הוא:
\[\mathbf{F}(r) = -\frac{G M m}{r^2} \hat{\mathbf{r}}\]הראו שסמוך לפני כדור הארץ, כוח הכבידה הוא בקירוב:
\[\mathbf{F} \approx -mg \hat{\mathbf{r}}\]כאשר $R_E \approx 6400 \, \mathrm{km}$ הוא רדיוס כדור הארץ, $M_E \approx 6 \times 10^{24} \, \mathrm{kg}$ היא מסת כדור הארץ, ו-$g \approx 10 \, \mathrm{m/s^2}$.
- מצאו את השינוי באנרגיה הדרוש להעביר גוף מפני כדור הארץ למרחק אינסופי ממנו. מהי מהירות המילוט מפני כדור הארץ?
- ציירו גרף של האנרגיה הפוטנציאלית כתלות במרחק $r$. מה מייצגת בגרף האנרגיה הקינטית המינימלית הדרושה לגוף כדי להימלט מכוח המשיכה של הפלנטה?
סעיף 1 - הסיבה לסימן השלילי
אינטואיטיבית, כדי להרחיק 2 גופים מסיביים נדרשת עבודה חיובית.
הסבר מקלוד:
הסימן השלילי באנרגיה הפוטנציאלית $\phi(r) = -\frac{GMm}{r}$ משקף את העובדה שכוח הכבידה הוא כוח משיכה:
הסבר פיזיקלי:
- אנרגיה פוטנציאלית מוגדרת כך ש-$U(\infty) = 0$ (נקודת ייחוס)
- כאשר מקרבים שני גופים מאינסוף, כוח הכבידה עושה עבודה חיובית
- לפי משפט העבודה-אנרגיה: $W_{gravity} = -\Delta U > 0$
- לכן $U(r) - U(\infty) < 0$, כלומר $U(r) < 0$
הסבר מתמטי נוסף (מהתרגול):
דרך נוספת לראות את זה היא מהגדרת העבודה כאינטגרל:
\[W_{r_0 \to \infty} = \int_{r_0}^{\infty} \mathbf{F}_{\text{ext}} \cdot d\mathbf{r} = -\int_{r_0}^{\infty} \mathbf{F}_g \cdot d\mathbf{r} = -\int_{r_0}^{\infty} \left(-\frac{G M m}{r^2}\right) dr\] \[= \Delta U = U(\infty) - U(r_0) = 0 - \left(-\frac{G M m}{r_0}\right) = \frac{G M m}{r_0} > 0\]סעיף 2 - גזירת כוח הכבידה
נדרש להראות שכוח הכבידה הוא
\[\mathbf{F} = -\frac{G M m}{r^2} \hat{\mathbf{r}}\]הכוח נגזר מהאנרגיה הפוטנציאלית: $\mathbf{F} = -\nabla U$. במקרה של סימטריה כדורית, כאשר $U$ תלוי רק ב-$r$:
\[\mathbf{F}(r) = -\frac{dU}{dr}\hat{\mathbf{r}} = -\frac{d}{dr}\left(-\frac{G M m}{r}\right)\hat{\mathbf{r}} = - \left(G M m \cdot \left(-\frac{1}{r^2}\right)\right)\hat{\mathbf{r}} = -\frac{G M m}{r^2}\hat{\mathbf{r}}\]פעולה מ-$\phi$ ל-$\mathbf{F}$ היא הגרדינט של $\phi$:
\[\mathbf{F} = -\nabla U = -\left(\frac{\partial U}{\partial x}, \frac{\partial U}{\partial y}, \frac{\partial U}{\partial z}\right)\]בשאלה הזאת היה ניתן גם לסמן $\phi = U(r)$, ואז $\mathbf{F} = -\nabla \phi$.
סעיף 3 - כוח הכבידה סמוך לפני כדור הארץ
גודל הכוח הוא:
\[|\mathbf{F}\vert = \frac{G M m}{r^2}\]סמוך לפני כדור הארץ ($r=R_E$), גודל הכוח הוא:
\[|\mathbf{F}\vert = \frac{G M_E m}{R_E^2}\]אנו מגדירים את תאוצת הכובד $g$ כ-$g = \frac{G M_E}{R_E^2}$. לכן, $\vert \mathbf{F}\vert = mg$.
נציב ערכים:
$g = \frac{(6.674 \times 10^{-11})(6 \times 10^{24})}{(6.4 \times 10^6)^2} \approx 9.8 \, \mathrm{m/s^2}$.
לכן, סמוך לפני כדור הארץ:
\[\mathbf{F} = -mg \hat{\mathbf{r}}\](כיוון הכוח לכיוון מרכז כדור הארץ)
סעיף 4 - השינוי באנרגיה ומהירות המילוט
סעיף 4 - מציאת השינוי באנרגיה ומהירות המילוט.
השינוי באנרגיה הפוטנציאלית להעברת גוף מפני כדור הארץ ($r=R_E$) לאינסוף ($r \to \infty$):
\[\Delta U = U(\infty) - U(R_E) = 0 - \left(-\frac{G M_E m}{R_E}\right) = \frac{G M_E m}{R_E}\]כדי שהגוף יגיע לאינסוף עם מהירות אפס (התנאי המינימלי למילוט), האנרגיה הקינטית ההתחלתית שלו צריכה להיות שווה בדיוק לשינוי באנרגיה הפוטנציאלית.
לפי שימור אנרגיה: $E_k + U = 0$.
\[\frac{1}{2}mv_{\text{esc}}^2 - \frac{G M_E m}{R_E} = 0 \implies \frac{1}{2}mv_{\text{esc}}^2 = \frac{G M_E m}{R_E}\] \[v_{\text{esc}} = \sqrt{\frac{2G M_E}{R_E}}\]מאחר ש-$g = \frac{G M_E}{R_E^2}$, נוכל לכתוב $G M_E = g R_E^2$. נציב זאת:
\[v_{\text{esc}} = \sqrt{\frac{2(gR_E^2)}{R_E}} = \sqrt{2gR_E} \approx \sqrt{2 \cdot 9.8 \cdot 6.4 \times 10^6} \approx 11.2 \times 10^3 \, \mathrm{m/s} \approx 11.2 \, \mathrm{km/s}\]סעיף 5 - גרף האנרגיה הפוטנציאלית
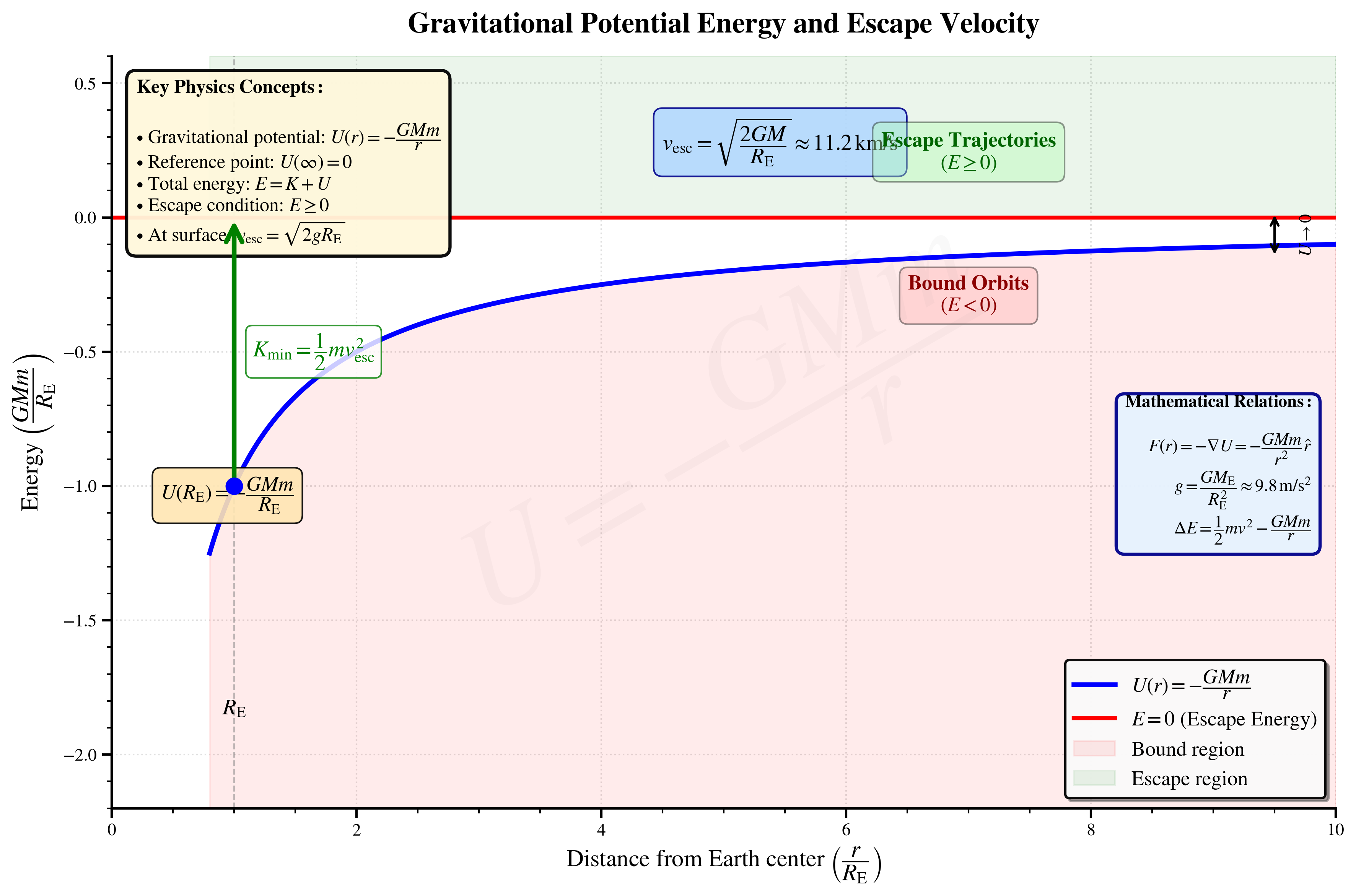
- העקומה הכחולה מייצגת את האנרגיה הפוטנציאלית $U(r) = -\frac{GMm}{r}$
- היא שלילית לכל $r$ סופי
- שואפת ל-0 כאשר $r \to \infty$
- הערך המינימלי הוא ב-$r = R_E$
- הקו האדום ($E = 0$) מייצג את האנרגיה הכוללת המינימלית למילוט
- תנאי המילוט: $E_{total} = K + U \geq 0$
- במקרה הגבולי: $E_{total} = 0$
-
החץ הירוק מייצג את האנרגיה הקינטית המינימלית הדרושה למילוט:
\[K_{min} = -U(R_E) = \frac{GMm}{R_E} = \frac{1}{2}mv_{esc}^2\]
משמעות פיזיקלית:
- אם $E_{total} < 0$: הגוף חסום במסלול סגור (אליפסה)
- אם $E_{total} = 0$: הגוף בדיוק מסוגל להימלט (מסלול פרבולי)
- אם $E_{total} > 0$: הגוף נמלט עם מהירות עודפת (מסלול היפרבולי)
סיכום התוצאות
| גודל | ערך |
|---|---|
| תאוצת הכובד | $g = 9.8 \, \mathrm{m/s^2}$ |
| מהירות המילוט | $v_{esc} = 11.2 \, \mathrm{km/s}$ |
| אנרגיה נדרשת למילוט | $\Delta U = \frac{GMm}{R_E}$ |
שאלה 2 - חישוב עבודה
נתון גרף של כוח (בניוטון) הפועל בכיוון $x$ על גוף, כתלות במיקום הגוף $x$ (במטרים). הגוף נע מ-$x=1 \, \mathrm{m}$ ל-$x=2 \, \mathrm{m}$.
העריכו את העבודה שנעשתה על הגוף.
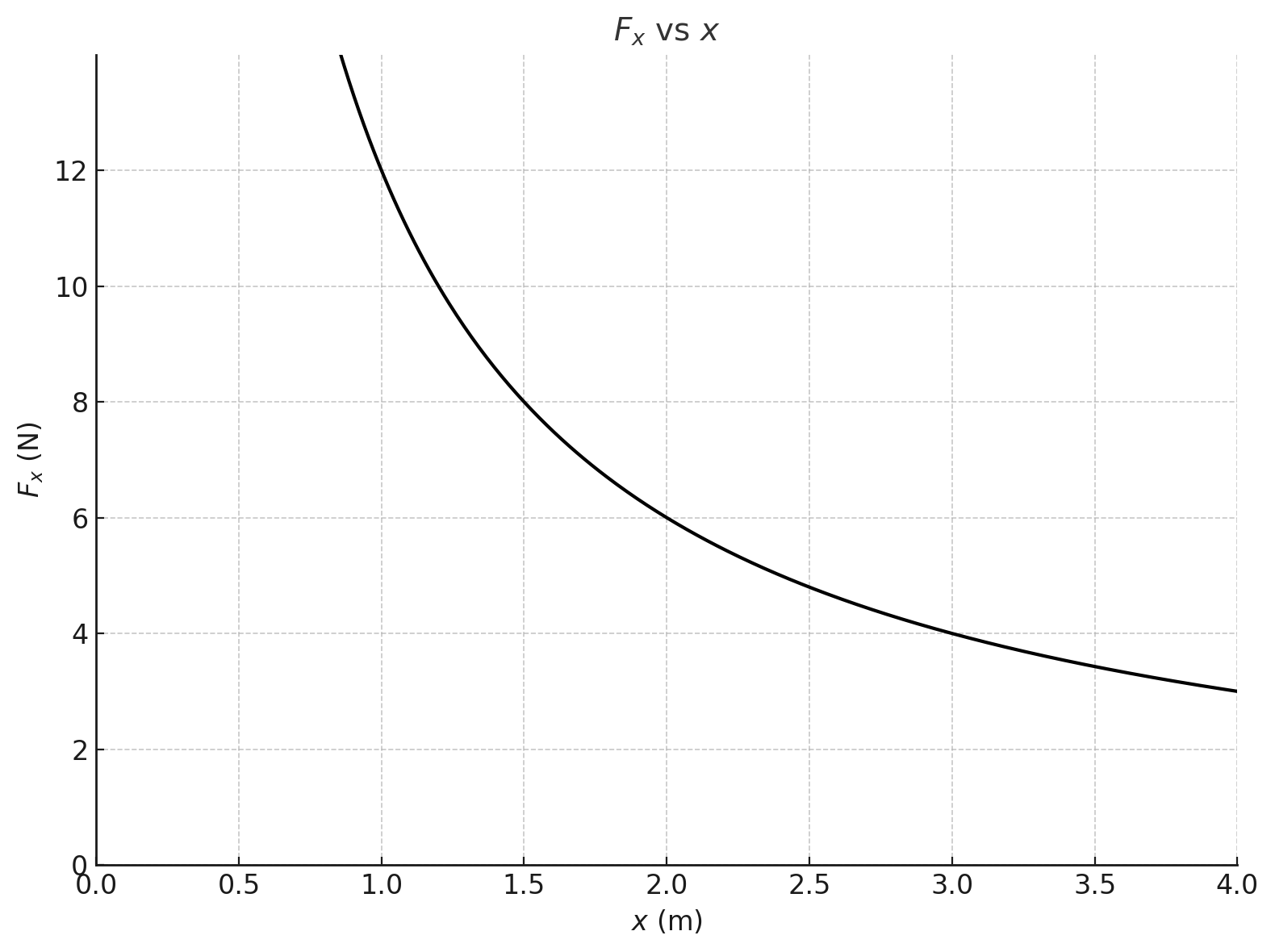
העבודה שנעשית על ידי כוח משתנה לאורך מסלול ישר היא השטח שמתחת לגרף הכוח כפונקציה של המיקום.
\[W = \int_{x_0}^{x_1} F(x) \, dx\]כדי להעריך את העבודה, יש לחשב את השטח מתחת לעקומת הגרף בין $x=1$ ל-$x=2$.
שאלה 3 - שימוש במשפט עבודה אנרגיה
כדור בעל מסה $m$ מחליק על מסילה חלקה המתוארת באיור, למעט קטע באורך $L$ עם מקדם חיכוך קינטי $\mu_k$. בסוף המסילה ישנו קפיץ בעל קבוע $k$. הכדור מתחיל ממנוחה בנקודה השמאלית ביותר, בגובה $H$.
- מהי המהירות ההתחלתית המינימלית שיש להקנות לכדור כדי שיגיע למישור המחוספס?
- עבור הנתונים הקודמים, בכמה הקפיץ מתכווץ? אם ההתנגשות היא אלסטית (משמרת אנרגיה), הנח שהכדור פוגע נע ביחד עם הקפיץ עד קצה הכיווץ.
- האם האנרגיה נשמרת במקרה בו הכדור מתגלגל ולא מחליק על המשטח על החיכוך? נמק.
Ball Peak starts here (3H/2) ∧ ● / \ ┌─┐ / \ Friction H | \______/ \ μ_k, L Spring _|_____________________[========] ╲╱╲╱╲╱│
סעיף 1: המהירות ההתחלתית המינימלית
כדי למצוא את המהירות המינימלית, נשתמש בשימור אנרגיה מכנית. הכדור צריך להגיע לפחות לנקודה הגבוהה ביותר במסילה כדי להמשיך הלאה.
נסמן את המהירות ההתחלתית ב-$v_0$. האנרגיה הכוללת בהתחלה היא:
\[E_{i} = \frac{1}{2}mv_0^2 + mgH\]בנקודה הגבוהה ביותר, המהירות המינימלית היא אפס (תנאי קריטי), לכן:
\[E_{\text{peak}} = mg \cdot \frac{3H}{2}\]משימור אנרגיה:
\[\frac{1}{2}mv_0^2 + mgH = mg \cdot \frac{3H}{2}\]נפתור עבור $v_0$:
\[\begin{aligned} \frac{1}{2}mv_0^2 &= mg \cdot \frac{3H}{2} - mgH \\[10pt] &= \frac{mgH}{2} \\[10pt] v_0^2 &= gH \\[10pt] &\implies \boxed{v_0 = \sqrt{gH}} \end{aligned}\]סעיף 2: כיווץ הקפיץ
נחשב את כיווץ הקפיץ. הכדור מתחיל עם המהירות שמצאנו ועובר את כל המסלול.
שלב א׳: מהירות הכדור לפני אזור החיכוך
כשהכדור מגיע לאזור החיכוך (בגובה 0), נשתמש בשימור אנרגיה:
\[\frac{1}{2}mv_0^2 + mgH = \frac{1}{2}mv_1^2\]כאשר $v_1$ היא המהירות בכניסה לאזור החיכוך.
\[\begin{aligned} \frac{1}{2}m(gH) + mgH &= \frac{1}{2}mv_1^2 \\[10pt] \frac{3}{2}mgH &= \frac{1}{2}mv_1^2 \\[10pt] 3gH &= v_1^2 \\[10pt] v_1 &= \boxed{\sqrt{3gH}} \end{aligned}\]שלב ב׳: אובדן אנרגיה עקב חיכוך
העבודה שעושה כוח החיכוך היא:
\[W_{\text{friction}} = -\mu_k mg L\]הסימן השלילי מציין שהחיכוך מתנגד לתנועה.
שלב ג׳: מהירות הכדור כשהוא פוגע בקפיץ
נשתמש במשפט עבודה-אנרגיה $\text{II}$:
\[W_{\text{NC}} = \Delta E_{\text{tot}}\] \[\begin{aligned} W_{\text{friction}} &= \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2 \\[10pt] \frac{1}{2}mv_2^2 &= \frac{1}{2}m(3gH) - \mu_k mg L \\[10pt] v_2^2 &= 3gH - 2\mu_k g L \\[10pt] v_2 &= \boxed{\sqrt{3gH - 2\mu_k g L}} \end{aligned}\]שלב ד’: כיווץ הקפיץ
כשהכדור פוגע בקפיץ ונע איתו, כל האנרגיה הקינטית הופכת לאנרגיה פוטנציאלית אלסטית:
\[\frac{1}{2}mv_2^2 = \frac{1}{2}kx^2\]כאשר $x$ הוא כיווץ הקפיץ.
\[x^2 = \frac{m}{k}v_2^2 = \frac{m}{k}(3gH - 2\mu_k g L)\] \[\boxed{x = \sqrt{\frac{m}{k}(3gH - 2\mu_k g L)}}\]הפתרון תקף רק אם $3gH > 2\mu_k g L$, אחרת הכדור לא יגיע לקפיץ.
סעיף 3: שימור אנרגיה בגלגול ללא החלקה
הערה: השאלה לא ברורה לי, ונראה שלא הייתה ברורה גם לחברים בכתה. מתי למשל כדור מחליק ומתי הוא מתגלגל?
לפי פתרון המתרגל הנוסף, במקרה של גלגל גלגול (גלגל ללא החלקה) - חיכוך סטטי לא תורם עבודה, ולכן יש שימור אנרגיה.
החלקה - חיכוך קינטי (אבל להבנתי המרצה לא הדגיש את ההבדלים בין חיכוך קינטי לחיכוך סטטי).
עגלה ותיבה - מע׳ רב גופית
תיבה שמסתה $m$ מונחת על עגלה שמסתה $M$ היכולה לנוע ללא חיכוך על משטח אופקי (ראו איור). מעניקים לתיבה מהירות התחלתיחת $v=v_0$.
- מה הגובה המינימלי $h_{\text{min}}$ של העגלה שימנע את מעבר התיבה לצידה השני?
- אם גובה העגלה גדול מ-$h_{\text{min}}$, שחושב בסעיף א, מהן מהירויות העגלה והתיבה כאשר התיבה חוזרת לתחתית העגלה?
נתון: $M = 10 \, \mathrm{kg}$, $m = 1 \, \mathrm{kg}$, $v_0 = 5 \, \mathrm{m/s}$.
╭───┐ v₀ → ╱ | ↑ ■ ╱ | h ┌──────╯ | ↓ ╰─●──────────●─╯ ──────────────────────
הערה מקדימה: רוב הפיתרון שלהלן נכתב בעזרת LLM, קחו אותו בערבון מוגבל.
נתונים
- $m = 1 \, \text{kg}$ (מסת התיבה)
- $M = 10 \, \text{kg}$ (מסת העגלה)
- $v_0 = 5 \, \text{m/s}$ (מהירות התחלתית של התיבה)
- $g \approx 10 \, \text{m/s}^2$ (תאוצת הכבידה)
- העגלה נעה ללא חיכוך על משטח אופקי
חלק א׳: הגובה המינימלי $h_{\text{min}}$
הרעיון הפיזיקלי
התיבה “מטפסת” על העגלה בזמן שהעגלה מאיצה. הגובה המינימלי הוא הגובה שבו התיבה תעצור בדיוק בראש העגלה ולא תמשיך לצדה השני. ברגע זה, מהירות התיבה והעגלה זהות (אין תנועה יחסית ביניהן).
שלב 1: מציאת המהירות המשותפת באמצעות שימור תנע
מושג - שימור תנע: במערכת סגורה (ללא כוחות חיצוניים), התנע הכולל נשמר.
תנע התחלתי:
- התיבה: $p_{m} = mv_0 = 1 \times 5 = 5 \, \text{kg⋅m/s}$
- העגלה: $p_{M} = M \times 0 = 0$
- תנע כולל: $p_{i} = 5 \, \text{kg⋅m/s}$
תנע סופי (כאשר שתיהן נעות במהירות זהה $v$):
\[p_{f} = (m + M)v = 11v\]מעקרון שימור התנע:
\[5 = 11v\] \[v = \frac{5}{11} \approx 0.45 \, \text{m/s}\]זוהי המהירות המשותפת של שני הגופים ברגע שהתיבה מגיעה לגובה המקסימלי.
שלב 2: מציאת הגובה באמצעות שימור אנרגיה
מושג - שימור אנרגיה: האנרגיה הכוללת במערכת נשמרת (קינטית + פוטנציאלית).
אנרגיה התחלתית:
\[E_{i} = \frac{1}{2}mv_0^2 = \frac{1}{2} \times 1 \times 5^2 = 12.5 \, \text{J}\]אנרגיה סופית:
- אנרגיה קינטית של שני הגופים: $\frac{1}{2}(m + M)v^2$
- אנרגיה פוטנציאלית של התיבה: $mgh_{\text{min}}$
מעקרון שימור אנרגיה:
\[12.5 = \frac{25}{22} + 10h_{\text{min}}\] \[10h_{\text{min}} = 12.5 - \frac{25}{22} = \frac{275 - 25}{22} = \frac{250}{22}\] \[h_{\text{min}} = \frac{250}{220} = \frac{25}{22} \approx 1.14 \, \text{m}\]נוסחה כללית
\[h_{\text{min}} = \frac{v_0^2 M}{2g(m + M)}\]חלק ב׳: מהירויות כאשר התיבה חוזרת לתחתית
הרעיון הפיזיקלי
כאשר גובה העגלה גדול מ-$h_{\text{min}}$, התיבה “מגלשת” חזרה למטה. המצב דומה להתנגשות אלסטית - האנרגיה הפוטנציאלית הרוכשת התיבה בגובה מתמירה חזרה לאנרגיה קינטית.
מערכת המשוואות
שימור תנע אופקי:
\[mv_0 = mv_m + Mv_M\] \[5 = v_m + 10v_M \quad \text{...(1)}\]שימור אנרגיה (האנרגיה הפוטנציאלית = 0 בתחתית):
\[\frac{1}{2}mv_0^2 = \frac{1}{2}mv_m^2 + \frac{1}{2}Mv_M^2\] \[25 = v_m^2 + 10v_M^2 \quad \text{...(2)}\]פתרון המערכת
מהמשוואה (1):
\[v_m = 5 - 10v_M\]נציב במשוואה (2):
\[25 = (5 - 10v_M)^2 + 10v_M^2\] \[25 = 25 - 100v_M + 100v_M^2 + 10v_M^2\] \[0 = 110v_M^2 - 100v_M\] \[0 = v_M(110v_M - 100)\]הפתרונות:
- $v_M = 0$ (מצב התחלתי)
- $v_M = \frac{100}{110} = \frac{10}{11} \approx 0.91 \, \text{m/s}$
מהירות העגלה הסופית:
\[v_M = \frac{10}{11} \approx 0.91 \, \text{m/s}\]מהירות התיבה הסופית:
\[v_m = 5 - 10 \times \frac{10}{11} = 5 - \frac{100}{11} = \frac{55 - 100}{11} = -\frac{45}{11} \approx -4.09 \, \text{m/s}\]משמעות התוצאות
- מהירות התיבה שלילית - התיבה נעה בכיוון הנגדי למהירות ההתחלתית
- מהירות העגלה חיובית - העגלה נעה באותו כיוון של המהירות ההתחלתית של התיבה
- סכום המהירויות המשוקללות שומר על התנע הכולל: $1 \times (-4.09) + 10 \times 0.91 = 5$
תשובות סופיות
א) הגובה המינימלי
\[\boxed{h_{\text{min}} = 1.14 \, \text{m}}\]ב) מהירויות כאשר התיבה חוזרת לתחתית
- מהירות התיבה: $\boxed{v_m = -4.09 \, \text{m/s}}$ (לאחור)
- מהירות העגלה: $\boxed{v_M = 0.91 \, \text{m/s}}$ (קדימה)
בדיקת תוצאות
- שימור תנע: $1 \times (-4.09) + 10 \times 0.91 = 5.01 \approx 5$ ✓
- שימור אנרגיה: $\frac{1}{2} \times 1 \times 4.09^2 + \frac{1}{2} \times 10 \times 0.91^2 = 12.5$ ✓