מבוא לבדיקת השערות (חזרה)
בדיקת השערות היא אחד הכלים המרכזיים בסטטיסטיקה היסקית. השיטה מאפשרת לנו לקבל החלטות מבוססות נתונים לגבי אוכלוסיות על סמך מדגמים (קבוצה שדגמנו מתוך האוכלוסייה), תוך כדי כימות רמת הוודאות בהחלטותינו.
מושג ה-P-value: הגדרה ומשמעות
הגדרה פורמלית
ה-P-value מוגדר כהסתברות לקבל את הערך הנצפה של הסטטיסטי הנבחן או ערך קיצוני ממנו, בהינתן שהשערת האפס נכונה. באופן מתמטי:
\[P\text{-value} = P(T \geq t_{obs} | H_0)\]כאשר $T$ הוא הסטטיסטי, $t_{obs}$ הוא הערך הנצפה, ו-$H_0$ היא השערת האפס.
משמעות אינטואיטיבית
P-value נמוך מהווה ראיה נגד השערת האפס. כאשר אנחנו מקבלים P-value נמוך מאוד, אנחנו למעשה אומרים: “אם השערת האפס הייתה נכונה, הסיכוי לראות תוצאה קיצונית כמו זו שראינו (או יותר קיצונית) הוא נמוך מאוד”. זה מוביל אותנו לפקפק בנכונות השערת האפס.
קביעת כיוון הקיצוניות
כיוון הקיצוניות נקבע לפי ההשערה האלטרנטיבית. נזכיר ש-$\mu$ מייצג את תוחלת האוכלוסייה, ו-$\mu_0$ הוא ערך התוחלת תחת השערת האפס:
- אם $H_1: \mu > \mu_0$ — ערכים קיצוניים הם ערכים גדולים מהערך שנצפה
- אם $H_1: \mu < \mu_0$ — ערכים קיצוניים הם ערכים קטנים מהערך שנצפה
- אם $H_1: \mu \neq \mu_0$ — ערכים קיצוניים הם ערכים ש-מרחקם מ-$\mu_0$ שווה או גדול מהמרחק של הערך שנצפה
רמת מובהקות וקבלת החלטות
הגדרת רמת המובהקות
רמת המובהקות, המסומנת ב-$\alpha$, היא הסף שאנחנו קובעים מראש לדחיית השערת האפס. זו ההסתברות המקסימלית שאנחנו מוכנים לקבל לטעות מסוג $\text{I}$ (דחיית השערת אפס נכונה).
במדעי החיים והרפואה, הערך המקובל הוא $\alpha = 0.05$. בתחומים הדורשים דיוק רב יותר (כגון פיזיקת חלקיקים), משתמשים בערכי $\alpha$ נמוכים בהרבה.
כללי החלטה
- אם $P\text{-value} < \alpha$: דוחים את השערת האפס ברמת מובהקות $\alpha$
- אם $P\text{-value} \geq \alpha$: לא דוחים את השערת האפס
חשוב להדגיש: אי-דחיית השערת האפס אינה מהווה “קבלה” של השערת האפס. אנחנו פשוט לא מצליחים להפריך אותה על סמך הנתונים הקיימים.
סיכום השלבים בבדיקת השערה
הערה: אני חושב שהייתה בשיעור חזרתיות מסוימת. ניסיתי לאחד את הדברים, ייתכן שחלק מהפרטים נשמטו. ככל הנראה השלבים הבאים הם התהליך מבחן Z למדגם אחד (One-Sample Z Test), שמופיע גם בהמשך בפירוט נפרד.
-
שלב 1: ניסוח המבחן במונחים של השערת אפס והשערה אלטרנטיבית
נניח $H_0: \mu = \mu_0$ כאשר $\mu_0$ הוא הערך הידוע או המצופה.
- השערת האפס ($H_0$): מייצגת את המצב הדיפולטי, “אין שינוי” או “אין הבדל”
- ההשערה האלטרנטיבית ($H_1$): מייצגת את מה שאנחנו מעוניינים להוכיח
-
שלב 2: קביעת רמת מובהקות ($\alpha$) מראש - בדרך כלל $\alpha = 0.05$.
יש לקבוע את $\alpha$ לפני איסוף הנתונים. זאת פרקטיקה חיונית למניעת הטיית תוצאות.
-
שלב 3: חישוב ממוצע המדגם (או סטטיסטי אחר) ותקנונו. במדגם גדול, ממוצע המדגם מתפלג:
\[\bar{X} \sim \mathcal{N}\left(\mu_0, \frac{\sigma^2}{n}\right)\] -
שלב 4: חישוב P-value באמצעות פייתון (או בכל דרך אחרת), בעזרת הצבת סטיית התקן המתוקננת.
\[Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]חישוב ההסתברות לקבל ערך קיצוני כמו הערך שנצפה או יותר, תחת השערת האפס.
- אם $H_1: \mu > \mu_0$: $\text{P-value} = P(Z > z_{obs})$
- אם $H_1: \mu < \mu_0$: $\text{P-value} = P(Z < z_{obs})$
- אם $H_1: \mu \neq \mu_0$: $\text{P-value} = 2 \cdot P(Z > \vert z_{obs}\vert)$
-
שלב 5: החלטה האם השערת האפס נדחית - השוואת ה-P-value לרמת המובהקות וקבלת החלטה האם לדחות את השערת האפס.
מבחן Z למדגם יחיד
תנאי יישום המבחן
מבחן Z למדגם יחיד מתאים כאשר:
- גודל המדגם גדול ($n \geq 30$), מה שמבטיח תחולת משפט הגבול המרכזי
- סטיית התקן באוכלוסייה ($\sigma$) ידועה
מבנה המבחן
נניח שיש לנו מדגם בגודל $n$ מאוכלוסייה עם תוחלת לא ידועה $\mu$ וסטיית תקן ידועה $\sigma$. ממוצע המדגם הוא $\bar{X}$.
תחת השערת האפס $H_0: \mu = \mu_0$, ממוצע המדגם מתפלג נורמלית:
\[\bar{X} \sim \mathcal{N}\left(\mu_0, \frac{\sigma^2}{n}\right)\]הסטטיסטי המתוקנן:
\[Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]מתפלג התפלגות נורמלית תקנית תחת $H_0$.
דוגמה: בדיקת רמות LDL במעשנים
נתון כי רמת ה-LDL הממוצעת באוכלוסייה הכללית היא 120 מ”ג/ד”ל עם סטיית תקן של 80 מ”ג/ד”ל.
במדגם של 64 מעשנים נמצא ממוצע LDL של 130 מ”ג/ד”ל.
האם רמת ה-LDL במעשנים גבוהה באופן מובהק מהרמה באוכלוסייה הכללית?
נסמן ב-$\mu$ את תוחלת רמת ה-LDL באוכלוסיית המעשנים.
ניסוח ההשערות
\[H_0: \mu = 120\]כלומר, שהתוחלת של המעשנים היא כמו באוכלוסייה הכללית.
\[H_1: \mu > 120\]כלומר, שהתוחלת של המעשנים גבוהה מהאוכלוסייה הכללית.
קביעת רמת המובהקות
נקבע $\alpha = 0.05$ (הערך הסטנדרטי במחקר ביו-רפואי).
חישובים
הססטיסטי הוא ממוצע המדגם:
\[\bar{X} = 130\]תחת השערת האפס, ממוצע המדגם מתפלג נורמלית.
התוחלת של ממוצע המדגם תחת השערת האפס היא:
\[\mu = 120\]סטיית התקן של ממוצע המדגם היא:
\[\frac{\sigma}{\sqrt{n}} = \frac{80}{\sqrt{64}} = \frac{80}{8} = 10\]יכולנו לקבל את החישובים האלה בגלל שהמדגם גדול, משפט הגבול המרכזי מאפשר לנו להתייחס לממוצע המדגם כאל משתנה מקרי מתפלג נורמלית.
סך הכל:
\[\bar{X} \sim \mathcal{N}\left(120, 10^2\right) = \mathcal{N}(120, 100)\]ציון התקן (Z-score או הסטטיסטי המתוקנן) הוא:
חישוב P-value
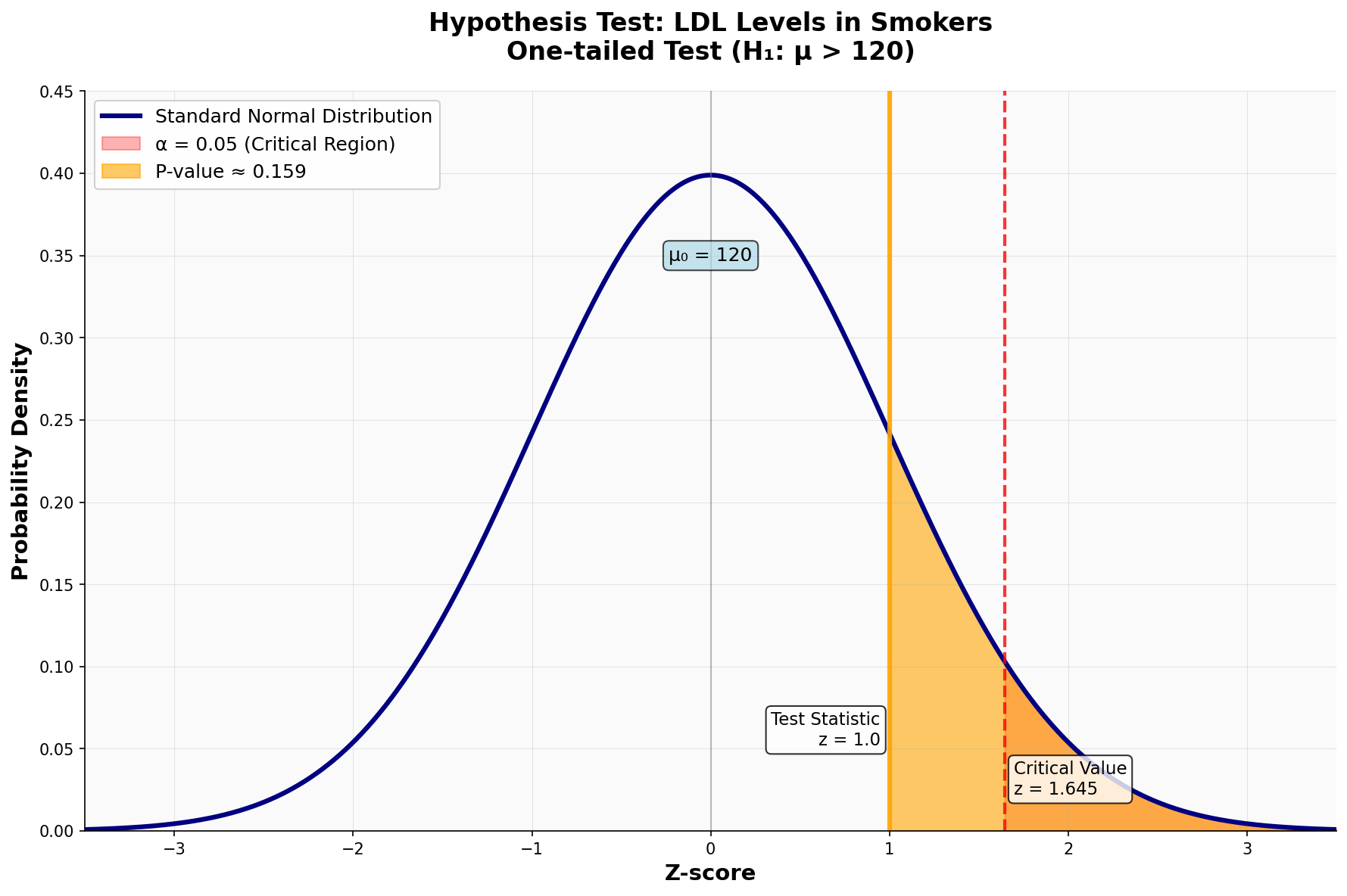
\[P\text{-value} = P(Z \geq 1) = 1 - \Phi(1) \approx 0.16\]כאשר $\Phi$ היא פונקציית ההתפלגות המצטברת של ההתפלגות הנורמלית התקנית.
הערה: נראה שזאת פונקציית ההשרדות (
Survival Function) של ההתפלגות הנורמלית, שהיא $1 - \Phi(z)$. בשאלות במטלה 2 שקיבלנו התבקשנו להציג את התשובות בצורתSF...
את התוצאה אפשר לקבל מפייתון, למשל:
from scipy.stats import norm
z_score = 1
p_value = norm.sf(z_score)
print(f"P-value: {p_value:.4f}")
הפלט:
P-value: 0.1587
מסקנה
מכיוון ש-$P\text{-value} = 0.16 > 0.05 = \alpha$, אנחנו לא דוחים את השערת האפס. אין ראיות מספיקות לטעון שרמת ה-LDL במעשנים גבוהה באופן מובהק מהרמה באוכלוסייה הכללית.
השפעת גודל המדגם על עוצמת המבחן
ניתוח תאורטי
כאשר המדגם ($n$) גדל, סטיית התקן של ממוצע המדגם קטנה:
\[\text{SE} = \frac{\sigma}{\sqrt{n}}\]זה מוביל לכך שאותו הפרש בין ממוצע המדגם לערך תחת השערת האפס מתבטא במספר גדול יותר של סטיות תקן, מה שמגדיל את ציון התקן ומקטין את ה-P-value.
דוגמה
נניח שבמקום 64 מעשנים, דגמנו 256 מעשנים וקיבלנו אותו ממוצע של 130 מ”ג/ד”ל. כלומר כעת:
\[n = 256\]סטיית התקן של ממוצע המדגם:
\[\text{SE} = \frac{80}{\sqrt{256}} = \frac{80}{16} = \boxed{5}\]ציון התקן:
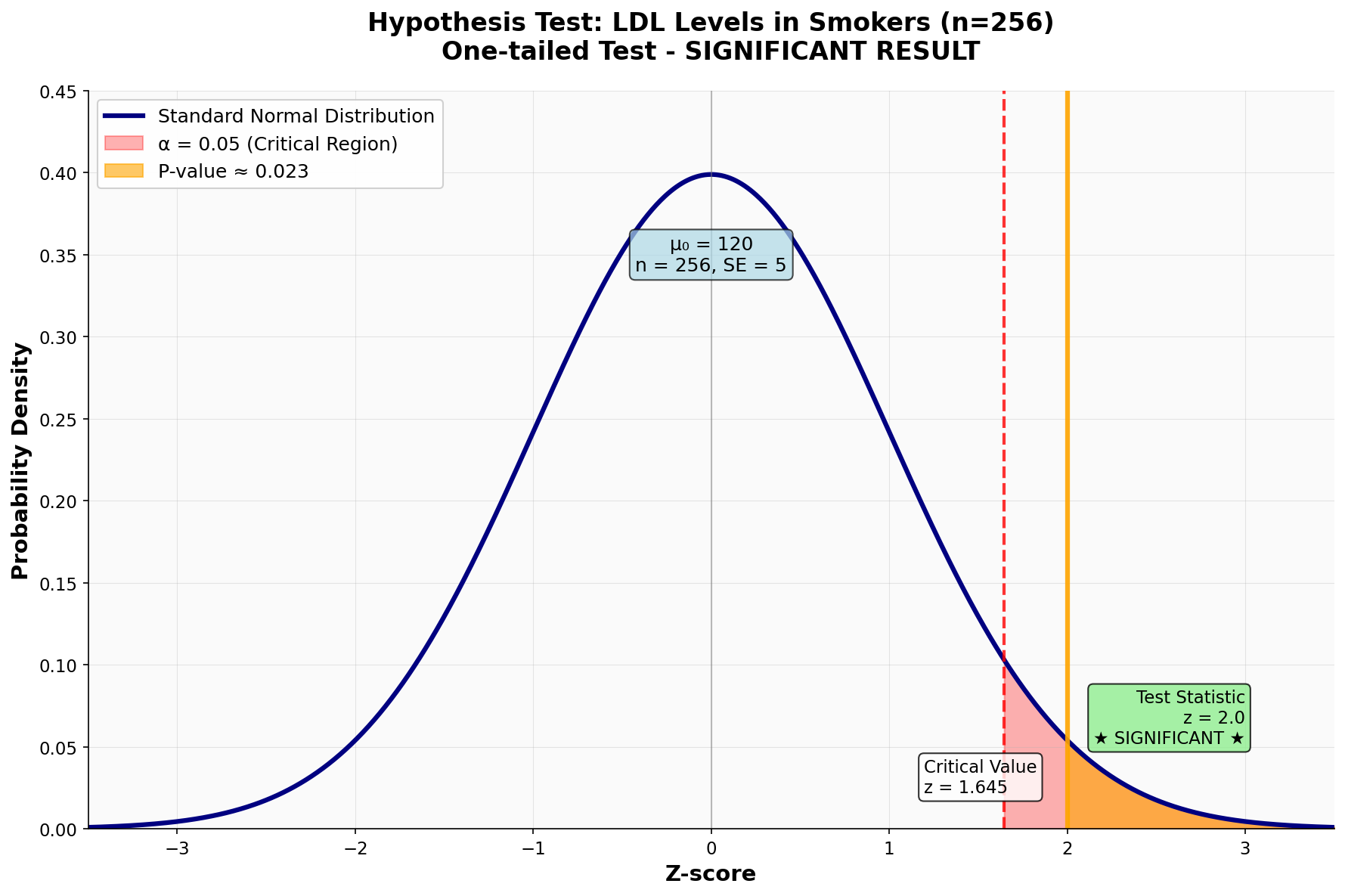
\[Z = \frac{130 - 120}{\mathbf{5}} = 2\]P-value:
\[P\text{-value} = P(Z \geq 2) \approx 0.023\]כעת $P\text{-value} = 0.023 < 0.05 = \alpha$, ולכן דוחים את השערת האפס. כלומר, יש ראיות סטטיסטיות לכך שרמת ה-LDL במעשנים גבוהה באופן מובהק מהרמה באוכלוסייה הכללית.
מסקנה חשובה: אותו גודל אפקט (הפרש של 10 מ”ג/ד”ל) יכול להיות לא מובהק במדגם קטן אך מובהק במדגם גדול. זה ממחיש את החשיבות של תכנון גודל מדגם מתאים למחקר.
אתם יכולים לייצר את הגרף בעצמכם בסביבת הפייתון שבאתר:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Set up the figure with a clean, modern style
fig, ax = plt.subplots(figsize=(12, 8))
plt.rcParams['font.size'] = 11
# Generate x values for the normal distribution
x = np.linspace(-4, 4, 1000)
y = norm.pdf(x)
# Plot the main normal distribution curve
ax.plot(x, y, 'navy', linewidth=3, label='Standard Normal Distribution')
# Critical value for α = 0.05 (one-tailed)
alpha = 0.05
z_critical = norm.ppf(1 - alpha) # ≈ 1.645
# Test statistic (with n=256, SE=5)
z_test = 2.0
# Fill the alpha region (critical region)
x_alpha = x[x >= z_critical]
y_alpha = norm.pdf(x_alpha)
ax.fill_between(x_alpha, y_alpha, alpha=0.3, color='red',
label=f'α = {alpha} (Critical Region)')
# Fill the p-value region
x_pvalue = x[x >= z_test]
y_pvalue = norm.pdf(x_pvalue)
ax.fill_between(x_pvalue, y_pvalue, alpha=0.6, color='orange',
label=f'P-value ≈ 0.023')
# Add vertical lines
ax.axvline(z_critical, color='red', linestyle='--', linewidth=2, alpha=0.8)
ax.axvline(z_test, color='orange', linestyle='-', linewidth=3, alpha=0.9)
ax.axvline(0, color='gray', linestyle='-', linewidth=1, alpha=0.5)
# Add text annotations
ax.text(z_critical - 0.45, 0.02, f'Critical Value\nz = {z_critical:.3f}',
fontsize=11, ha='left', va='bottom',
bbox=dict(boxstyle='round,pad=0.3', facecolor='white', alpha=0.8))
ax.text(z_test + 1, 0.05, f'Test Statistic\nz = {z_test}\n★ SIGNIFICANT ★',
fontsize=11, ha='right', va='bottom',
bbox=dict(boxstyle='round,pad=0.3', facecolor='lightgreen', alpha=0.8))
ax.text(0, 0.35, 'μ₀ = 120\nn = 256, SE = 5', fontsize=12, ha='center', va='center',
bbox=dict(boxstyle='round,pad=0.3', facecolor='lightblue', alpha=0.7))
# Styling
ax.set_xlim(-3.5, 3.5)
ax.set_ylim(0, 0.45)
ax.set_xlabel('Z-score', fontsize=14, fontweight='bold')
ax.set_ylabel('Probability Density', fontsize=14, fontweight='bold')
ax.set_title('Hypothesis Test: LDL Levels in Smokers (n=256)\nOne-tailed Test - SIGNIFICANT RESULT',
fontsize=16, fontweight='bold', pad=20)
# Legend
ax.legend(loc='upper left', fontsize=12, framealpha=0.9)
# Grid styling
ax.grid(True, alpha=0.3, linestyle='-', linewidth=0.5)
ax.set_facecolor('#fafafa')
fig.patch.set_facecolor('white')
# Remove top and right spines
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.tight_layout()
plt.show()
סוגי טעויות בבדיקת השערות
טעות מסוג $\text{I}$ (Type I Error)
טעות מסוג $\text{I}$ מתרחשת כשדוחים את השערת האפס למרות שבפועל היא נכונה. בטרמינולוגיה הרפואית, זאת תוצאה חיובית כוזבת (False Positive).
ההסתברות לטעות מסוג $\text{I}$ מסומנת ב-$\alpha$ ושווה בדיוק לרמת המובהקות שנקבעה מראש:
\[P(\text{Reject } H_0 | H_0 \text{ is true}) = \alpha\]טעות מסוג $\text{II}$ (Type II Error)
טעות מסוג $\text{II}$ מתרחשת כאשר לא דוחים את השערת האפס בעוד שהיא למעשה שגויה. בטרמינולוגיה הרפואית, זאת תוצאה שלילית כוזבת (False Negative).
ההסתברות לטעות מסוג $\text{II}$ מסומנת ב-β:
\[P(\text{Fail to reject } H_0 | H_1 \text{ is true}) = \beta\]טבלת סיכום הטעויות
ניתן לסכם את כל האפשרויות בטבלה הבאה:
| המציאות | החלטה: דחיית $H_0$ | החלטה: אי-דחיית $H_0$ |
|---|---|---|
| $H_0$ נכונה | טעות מסוג $\text{I}$ ($\alpha$) | החלטה נכונה (1-$\alpha$) |
| $H_1$ נכונה | החלטה נכונה (1-β) | טעות מסוג $\text{II}$ (β) |
הערך (1-β) נקרא עוצמת המבחן (Power) ומייצג את ההסתברות לזהות אפקט אמיתי כאשר הוא קיים.
הגורמים המשפיעים על עוצמת המבחן
ניתוח הסטטיסטי המתוקנן
הסטטיסטי המתוקנן במבחן Z מוגדר כך:
\[Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]כדי להגדיל את הסיכוי לדחות השערת אפס שגויה (כלומר, להגדיל את עוצמת המבחן), אנחנו רוצים שערכו המוחלט של Z יהיה גדול. יש שלוש דרכים להשיג זאת:
1. הגדלת גודל האפקט
גודל האפקט מוגדר כהפרש בין הממוצע האמיתי באוכלוסייה לבין ערכו תחת השערת האפס:
\[\text{Effect size} = |\mu - \mu_0|\]ככל שהאפקט גדול יותר, כך קל יותר לזהות אותו סטטיסטית. לדוגמה, אם רמת ה-LDL במעשנים היא 200 מ”ג/ד”ל במקום 130, האפקט של 80 יחידות יהיה קל מאוד לזיהוי.
2. הקטנת השונות באוכלוסייה
השונות באוכלוסייה (σ²) משפיעה ישירות על סטיית התקן של ממוצע המדגם:
\[\text{SE} = \frac{\mathbf{\sigma}}{\sqrt{n}}\]ככל שהשונות קטנה יותר, כך ההתפלגות של ממוצע המדגם מרוכזת יותר סביב התוחלת, מה שמקל על זיהוי סטיות מהערך הצפוי.
בפועל, ניתן להקטין שונות על ידי:
- תכנון ניסוי מבוקר היטב
- בחירת אוכלוסיית מחקר הומוגנית
- שימוש בשיטות מדידה מדויקות
3. הגדלת המדגם
השפעת גודל המדגם על עוצמת המבחן היא דרמטית. סטיית התקן של ממוצע המדגם קטנה ביחס ל-$\sqrt{n}$:
\[\text{SE} = \frac{\sigma}{\mathbf{\sqrt{n}}}\]לדוגמה:
- עבור n = 100: סטיית התקן מוקטנת פי 10
- עבור n = 10,000: סטיית התקן מוקטנת פי 100
דוגמה: השוואת גדלי מדגם שונים
(החלק הזה חוזר על הדוגמה הקודמת, אולי ירד בעריכה)
נחזור לדוגמת ה-LDL ונבחן את ההשפעה של גודל המדגם:
מדגם קטן (n = 64)
- סטיית תקן של ממוצע המדגם: $\text{SE} = \frac{80}{8} = 10$
- ציון תקן: $Z = \frac{130-120}{10} = 1$
- P-value ≈ 0.16
- מסקנה: לא דוחים את $H_0$
מדגם גדול (n = 256)
- סטיית תקן של ממוצע המדגם: $\text{SE} = \frac{80}{16} = 5$
- ציון תקן: $Z = \frac{130-120}{5} = 2$
- P-value ≈ 0.023
- מסקנה: דוחים את $H_0$
אותו הפרש של 10 מ”ג/ד”ל מתגלה כמובהק במדגם הגדול אך לא במדגם הקטן.
חשיבות קביעת רמת המובהקות מראש
העיקרון הבסיסי
רמת המובהקות ($\alpha$) חייבת להיקבע לפני איסוף הנתונים וביצוע הניתוח. זהו עיקרון מתודולוגי קריטי שמונע מניפולציה של תוצאות.
הבעייתיות ב”דיג נתונים”
קביעת רמת המובהקות לאחר חישוב ה-P-value (למשל, קביעת $\alpha = 0.06$ כאשר התקבל P-value = 0.055) מהווה הטיה חמורה ופוגעת בתקפות המסקנות הסטטיסטיות.
המשמעות המעשית של תוצאות סטטיסטיות
הבחנה בין מובהקות סטטיסטית למובהקות קלינית
מובהקות סטטיסטית אינה מעידה בהכרח על חשיבות מעשית. הפרש של 10 מ”ג/ד”ל ברמת LDL עשוי להיות מובהק סטטיסטית במדגם גדול, אך השאלה הקלינית היא האם הפרש זה משמעותי מבחינה רפואית.
תכנון גודל מדגם
בתכנון מחקר, יש לקחת בחשבון:
- גודל האפקט המינימלי בעל משמעות מעשית
- השונות הצפויה באוכלוסייה
- רמת המובהקות הרצויה ($\alpha$)
- העוצמה הרצויה ($1 - \beta$)
נוסחאות לחישוב גודל מדגם נדרש יוצגו בפרקים מתקדמים יותר.
הגורמים המשפיעים על יכולת זיהוי אפקטים
הבנת המנגנון הסטטיסטי
כדי להבין לעומק כיצד ניתן לשפר את יכולתנו לזהות הבדלים אמיתיים באוכלוסייה, נחזור לנוסחת הסטטיסטי המתוקנן:
\[Z = \frac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]ערכו המוחלט של סטטיסטי זה קובע את עוצמת הראיות נגד השערת האפס. ככל שערך זה גדול יותר, כך סביר יותר שנדחה השערת אפס שגויה.
שלושת המרכיבים המרכזיים
1. גודל האפקט הממשי
גודל האפקט מתבטא במונה של הסטטיסטי - ההפרש $\vert \bar{X} - \mu_0 \vert$. זהו הגורם היחיד שאנחנו לא יכולים לשלוט בו ישירות, שכן הוא משקף את המציאות הביולוגית או הרפואית שאנחנו חוקרים.
משמעות מעשית: אם ההבדל האמיתי בין אוכלוסיות הוא זעיר, נזדקק למאמץ רב יותר (מדגם גדול או שונות קטנה) כדי לזהותו. לעומת זאת, אפקטים דרמטיים (כגון הבדל של 100 ml/dl ברמת קולסטרול) יהיו קלים לזיהוי גם במדגמים קטנים יחסית.
2. השונות באוכלוסייה
השונות $\sigma^2$ משפיעה באופן הפוך על יכולתנו לזהות הבדלים. שונות גבוהה “מטשטשת” את האפקט האמיתי ומקשה על זיהויו.
אסטרטגיות להקטנת שונות:
- ריבוד האוכלוסייה: חלוקה לתת-קבוצות הומוגניות (לדוגמה, ניתוח נפרד לגברים ונשים)
- בקרת משתנים מתערבים: שמירה על תנאי ניסוי אחידים
- שיפור דיוק המדידה: שימוש במכשירי מדידה מדויקים יותר
דוגמה: נניח שאנחנו בוחנים השפעת תרופה על לחץ דם. 80-20, השונות תהיה עצומה. אם נצמצם לטווח גילים 50-40, השונות תקטן משמעותית.
3. גודל המדגם
השפעת גודל המדגם על דיוק האומדן היא דרמטית אך מתונה על ידי פונקציית השורש:
\[\text{Reduction of standard deviation} = \frac{1}{\sqrt{n}}\]השלכות מעשיות:
- הכפלת גודל המדגם מקטינה את סטיית התקן רק פי $\sqrt{2} \approx 1.41$
- כדי להקטין את סטיית התקן פי 2, יש להגדיל את המדגם פי 4
- כדי להקטין את סטיית התקן פי 10, יש להגדיל את המדגם פי 100
זאת הסיבה שמחקרים קליניים גדולים דורשים משאבים כה רבים - השיפור בדיוק גדל באופן תת-ליניארי עם גודל המדגם.
מבחנים דו-צדדיים: כאשר הכיוון אינו ידוע
הרציונל למבחן דו-צדדי
במקרים רבים במחקר הביו-רפואי, כיוון ההשפעה הצפויה אינו ידוע מראש. לדוגמה:
- בדיקת איכות תרופות: ריכוז חומר פעיל גבוה מדי מסוכן (רעילות), ונמוך מדי אינו יעיל
- השפעות לא ידועות: תרופה חדשה עשויה להעלות או להוריד ערך ביוכימי
- מחקר גישוש: כאשר אין לנו השערה מוקדמת לגבי כיוון ההשפעה
המבנה המתמטי של מבחן דו-צדדי
בהשערה דו-צדדית, אנחנו בודקים:
\[H_0: \mu = \mu_0\] \[H_1: \mu \neq \mu_0\]הגדרת “קיצוניות” כוללת כעת שני כיוונים. עבור ערך נצפה $\bar{x}$, ערכים קיצוניים הם:
- כל ערך $\geq \bar{x}$ (אם $\bar{x} > \mu_0$)
- כל ערך $\leq 2\mu_0 - \bar{x}$ (הערך הסימטרי בצד השני)
חישוב P-value במבחן דו-צדדי
תהליך החישוב כולל שלושה שלבים:
שלב 1: חישוב הסטייה מהערך הצפוי
\[\text{deviation} = |\bar{x} - \mu_0|\]שלב 2: חישוב ההסתברות בכל זנב
\[P_{\text{one tail}} = P(|\bar{X} - \mu_0| \geq |\bar{x} - \mu_0|)\]שלב 3: הכפלה לקבלת P-value הכולל
\[\text{P-value} = 2 \times P_{\text{one tail}}\]עבור התפלגות נורמלית תקנית:
\[\text{P-value} = 2 \times P(Z > |z|) = 2 \times [1 - \Phi(|z|)]\]דוגמה: בקרת איכות של תרופות
יצרן תרופות בודק תבליות שאמורות להכיל $100 \, \mathrm{mg}$ חומר פעיל.
סטיית התקן הידועה בתהליך הייצור היא $5 \, \mathrm{mg}$.
במדגם של $50$ תבליות נמצא ממוצע של $102 \, \mathrm{mg}$.
האם הטבליות פגומות? האם יש להן תוחלת חומר פעיל שונה מ- $100 \, \mathrm{mg}$?
ניסוח ההשערות
מכיוון שסטייה בכל כיוון מהווה בעיה (מינון יתר או חסר), נשתמש במבחן דו-צדדי:
\[H_0: \mu = 100\] \[H_1: \mu \neq 100\]חישוב הסטטיסטי
סטיית התקן של ממוצע המדגם:
\[\text{SE} = \frac{5}{\sqrt{50}} = \frac{5}{7.07} \approx 0.71\]ציון התקן:
\[Z = \frac{102 - 100}{0.71} = 2.83\]חישוב P-value
ההסתברות בזנב העליון:
\[P(Z > 2.83) \approx 0.0023\]בשל הסימטריה של ההתפלגות הנורמלית:
\[P(Z < -2.83) \approx 0.0023\]לכן:
\[\text{P-value} = 2 \times 0.0023 = \boxed{0.0046}\]מסקנה
מכיוון ש-$\text{P-value} = 0.0046 < 0.05 = \alpha$, דוחים את השערת האפס. כלומר, קיימת ראיה מובהקת שתהליך הייצור אינו מכויל כראוי.
השוואה בין מבחנים חד-צדדיים ודו-צדדיים
המחיר של אי-ודאות כיוונית
כשאנחנו עוברים ממבחן חד-צדדי לדו-צדדי, ה-P-value מוכפל. זה “המחיר” שאנחנו משלמים על אי-הוודאות לגבי כיוון האפקט.
דוגמה להמחשה:
נניח שקיבלנו $Z = 1.76$ במבחן כלשהו.
במבחן חד-צדדי:
\[\text{P-value} = P(Z > 1.76) \approx 0.039\]מכיוון ש-$0.039 < 0.05$, נדחה את $H_0$.
במבחן דו-צדדי:
\[\text{P-value} = 2 \times 0.039 = 0.078\]מכיוון ש-$0.078 > 0.05$, לא נדחה את $H_0$.
אותם נתונים מובילים להחלטות שונות בהתאם לאופי ההשערה.
הנחיות לבחירת סוג המבחן
השתמש במבחן חד-צדדי כאשר:
- יש בסיס תיאורטי חזק לכיוון מסוים
- האפקט בכיוון ההפוך אינו סביר או חסר משמעות
- קיים מידע מוקדם התומך בכיוון ספציפי
השתמש במבחן דו-צדדי כאשר:
- אין השערה מוקדמת לגבי הכיוון
- שני הכיוונים אפשריים ובעלי משמעות
- מדובר במחקר גישוש ראשוני
החשיבות של קביעה מראש
כמו רמת המובהקות, גם סוג המבחן (חד או דו-צדדי) חייב להיקבע לפני איסוף הנתונים. שינוי סוג המבחן לאחר ראיית התוצאות (“אני רואה שהאפקט חיובי, אז אעבור למבחן חד-צדדי”) מהווה מניפולציה סטטיסטית חמורה.
סיכום: אינטגרציה של המושגים
התמונה המלאה של בדיקת השערות כוללת הבנה עמוקה של הקשרים בין:
- גודל האפקט הממשי באוכלוסייה
- השונות הטבעית בנתונים
- גודל המדגם שברשותנו
- סוג המבחן (חד או דו-צדדי)
- רמת המובהקות שנקבעה
כל אחד מהגורמים האלה משפיע על היכולת שלנו להגיע למסקנות מבוססות. הבנת האינטראקציות ביניהם חיונית לתכנון מחקרים יעילים ולפרשנות נכונה של תוצאות סטטיסטיות.
בפרקים הבאים נרחיב את הדיון למצבים מציאותיים יותר, כמו מקרים שבהם השונות אינה ידועה, ונלמד על מבחנים מזווגים שמאפשרים הקטנת שונות באמצעות תכנון ניסוי חכם.
דור פסקל