מבוא
בשיעור זה נסגור את הנושאים התיאורטיים ונתחיל לעסוק בפתרון בעיות מעשיות. בשיעורים הקרובים נפתור קונפיגורציות אלקטרומגנטיות שונות תוך שימוש במשוואות שפיתחנו.
חלק א’: משוואות מקסוול - סיכום
ארבע משוואות מקסוול
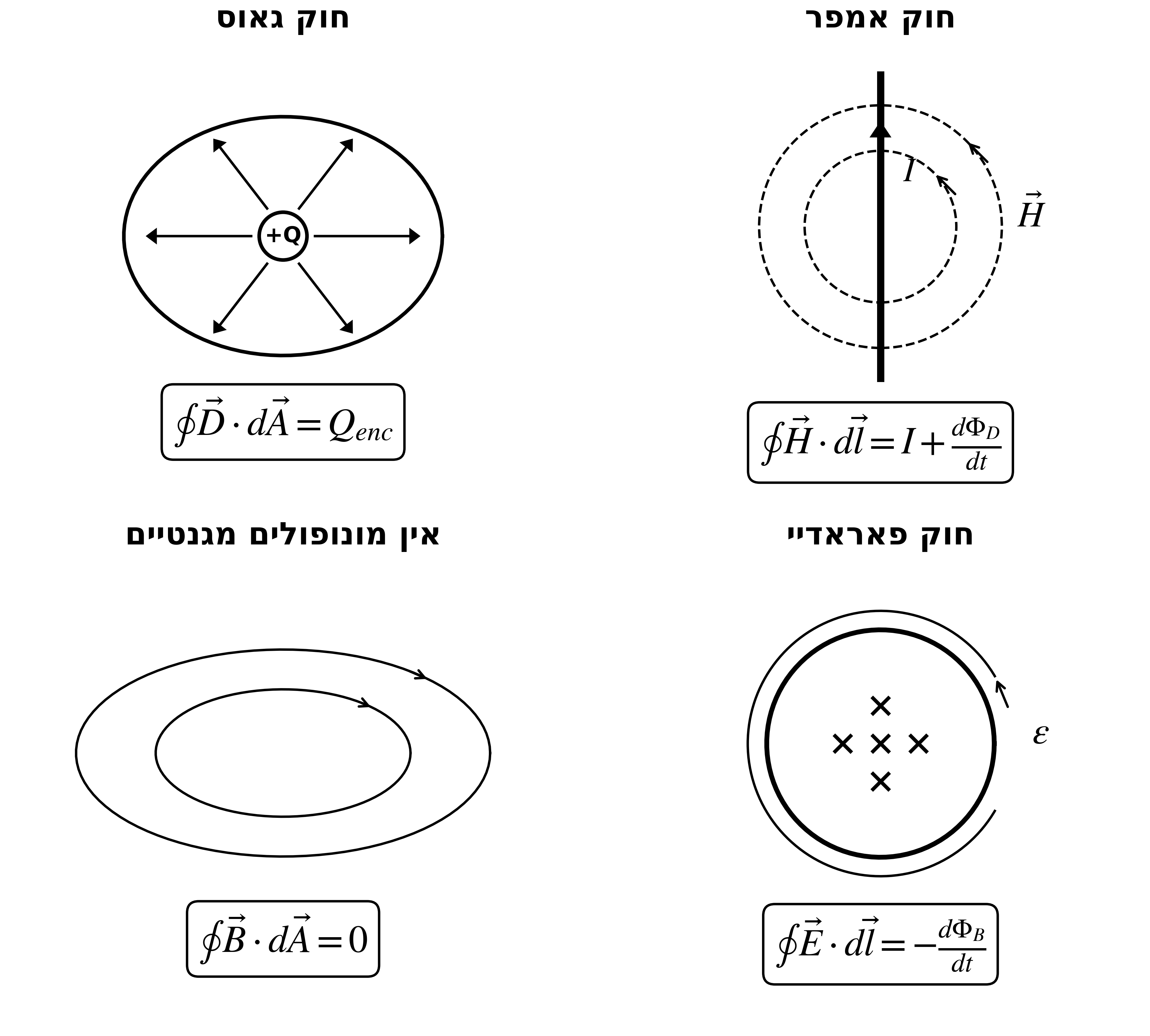
משוואה ראשונה: חוק גאוס
צורה דיפרנציאלית: - משוואת מקסוול הראשונה
\[\vec{\nabla} \cdot \vec{D} = \rho\]צורה אינטגרלית: - חוק גאוס
\[\oint_{\partial\Omega} \vec{D} \cdot d\vec{s} = Q_{enc}\]המשמעות: השטף של שדה ההסטה החשמלית $\vec{D}$ דרך מעטפת סגורה שווה למטען הכלוא בתוכה.
הערה: נראה שהמרצה משתמש בסימון $\Sigma$ כדי לתאר $enc$ - ראו להלן.
משוואה שנייה: חוק אמפר
צורה דיפרנציאלית: - משוואת מקסוול השנייה (עם תיקון מקסוול)
\[\vec{\nabla} \times \vec{H} - \frac{\partial \vec{D}}{\partial t} = \vec{j}\]צורה אינטגרלית: - חוק אמפר-מקסוול (בשיעור נקרא תחילה ״חוק אמפר המוכלל״ ואז עודכן ל״חוק אמפר״):
\[\oint_{\partial\Sigma} \vec{H} \cdot d\vec{r} = \frac{d}{dt}\int_\Sigma \vec{D} \cdot d\vec{s} + I\]כאשר:
- $\vec{j} = \rho\vec{v}$ היא צפיפות הזרם
- $I = \int_\Sigma \vec{j} \cdot d\vec{s}$ הוא הזרם החשמלי (נמדד באמפר = קולון/שנייה)
משוואה שלישית: אין מונופולים מגנטיים
אין לה שם מיוחד (חוק ״אין שם״).
צורה דיפרנציאלית: - משוואת מקסוול השלישית
\[\vec{\nabla} \cdot \vec{B} = 0\]צורה אינטגרלית: - חוק ״אין שם״:
\[\oint_{\partial\Omega} \vec{B} \cdot d\vec{s} = 0\]המשמעות: אין מטענים מגנטיים בטבע. קווי השדה המגנטי תמיד סגורים.
משוואה רביעית: חוק פאראדיי
צורה דיפרנציאלית: - משוואת מקסוול הרביעית
\[\vec{\nabla} \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}\]צורה אינטגרלית: - חוק פאראדיי
\[\oint_{\partial\Sigma} \vec{E} \cdot d\vec{r} = -\frac{d}{dt}\int_\Sigma \vec{B} \cdot d\vec{s}\]המשמעות טרם ברורה לי.
הבחנה חשובה: $\Sigma$ לעומת $\Omega$
| סימון | משמעות | דוגמה |
|---|---|---|
| $\Sigma$ | משטח פתוח עם שפה | דיסקה, משטח שרירותי |
| $\partial\Sigma$ | השפה של המשטח | מעגל, עקומה סגורה |
| $\Omega$ | נפח סגור | כדור, קובייה |
| $\partial\Omega$ | המעטפת של הנפח | משטח סגור |
נקודת מפתח: משטח שסוגר נפח ($\partial\Omega$) הוא תמיד חסר גבול, כי “הגבול של גבול שווה לקבוצה ריקה”.
חלק ב’: פתרון משוואות מקסוול בוואקום
יחסי החומר בוואקום
בוואקום מתקיים:
\[\vec{D} = \epsilon_0 \vec{E}\] \[\vec{H} = \frac{\vec{B}}{\mu_0}\]הקבועים $\epsilon_0$ ו-$\mu_0$ הם הברקוד האלקטרומגנטי של הוואקום - הם מאפיינים את התכונות האלקטרומגנטיות של החלל הריק.
ערכים:
\[\frac{1}{4\pi\epsilon_0} = 9 \times 10^9 \, \frac{N \cdot m^2}{C^2}\] \[\mu_0 = 4\pi \times 10^{-7} \, \frac{N \cdot s^2}{C^2}\]משוואות מקסוול בוואקום
בוואקום אין מקורות: $\rho = 0$ ו-$\vec{j} = 0$. המשוואות הופכות ל:
\[\begin{aligned} &\vec{\nabla} \cdot \vec{E} = 0 \\[6pt] &\vec{\nabla} \cdot \vec{B} = 0 \\[6pt] &\vec{\nabla} \times \vec{H} = \frac{\partial \vec{D}}{\partial t} \\[6pt] &\vec{\nabla} \times \vec{E} = -\frac{\partial \vec{B}}{\partial t} \\[6pt] \end{aligned}\]גזירת משוואת הגלים
על ידי הצבה ומניפולציות מתמטיות, מקבלים את משוואות הגלים:
\[\nabla^2 \vec{E} = \frac{1}{c^2}\frac{\partial^2 \vec{E}}{\partial t^2}\] \[\nabla^2 \vec{B} = \frac{1}{c^2}\frac{\partial^2 \vec{B}}{\partial t^2}\]כאשר:
\[c = \frac{1}{\sqrt{\epsilon_0 \mu_0}} = 3 \times 10^8 \, \frac{\mathrm{m}}{\mathrm{s}}\]זוהי מהירות האור!
חלק ג’: גלים אלקטרומגנטיים
הפתרון הגלי
פתרון משוואות הגלים:
\[\vec{E} = \vec{E}_k \, \cos\,(\vec{k} \cdot \vec{r} - \omega t)\] \[\vec{B} = \vec{B}_k \, \cos\,(\vec{k} \cdot \vec{r} - \omega t)\]כאשר:
- $\vec{E}_k$ ו-$\vec{B}_k$ הן האמפליטודות (קבועים)
- $\vec{k}$ הוא וקטור הגל
- $\omega$ היא התדירות הזוויתית
הוכחה דרך הצבה
נציב את הפתרון במשוואת הגלים ונקבל (בתקווה) פסוק אמת.
אגף שמאל - הלפלסיאן:
\[\nabla^2 E = \frac{\partial^2 E}{\partial x^2} + \frac{\partial^2 E}{\partial y^2} + \frac{\partial^2 E}{\partial z^2}\]כאשר $\vec{k} \cdot \vec{r} = k_x x + k_y y + k_z z$:
- גזירה ראשונה לפי $x$: מוציאה $k_x$, קוסינוס הופך למינוס סינוס
- גזירה שנייה לפי $x$: מוציאה עוד $k_x$, מינוס סינוס הופך למינוס קוסינוס
התוצאה:
\[\nabla^2 E = -(k_x^2 + k_y^2 + k_z^2) \cdot E = -k^2 E\]אגף ימין - נגזרת לפי זמן פעמיים:
\[\frac{1}{c^2}\frac{\partial^2 E}{\partial t^2} = -\frac{\omega^2}{c^2} E\]יחס הנפיצה (Dispersion Relation)
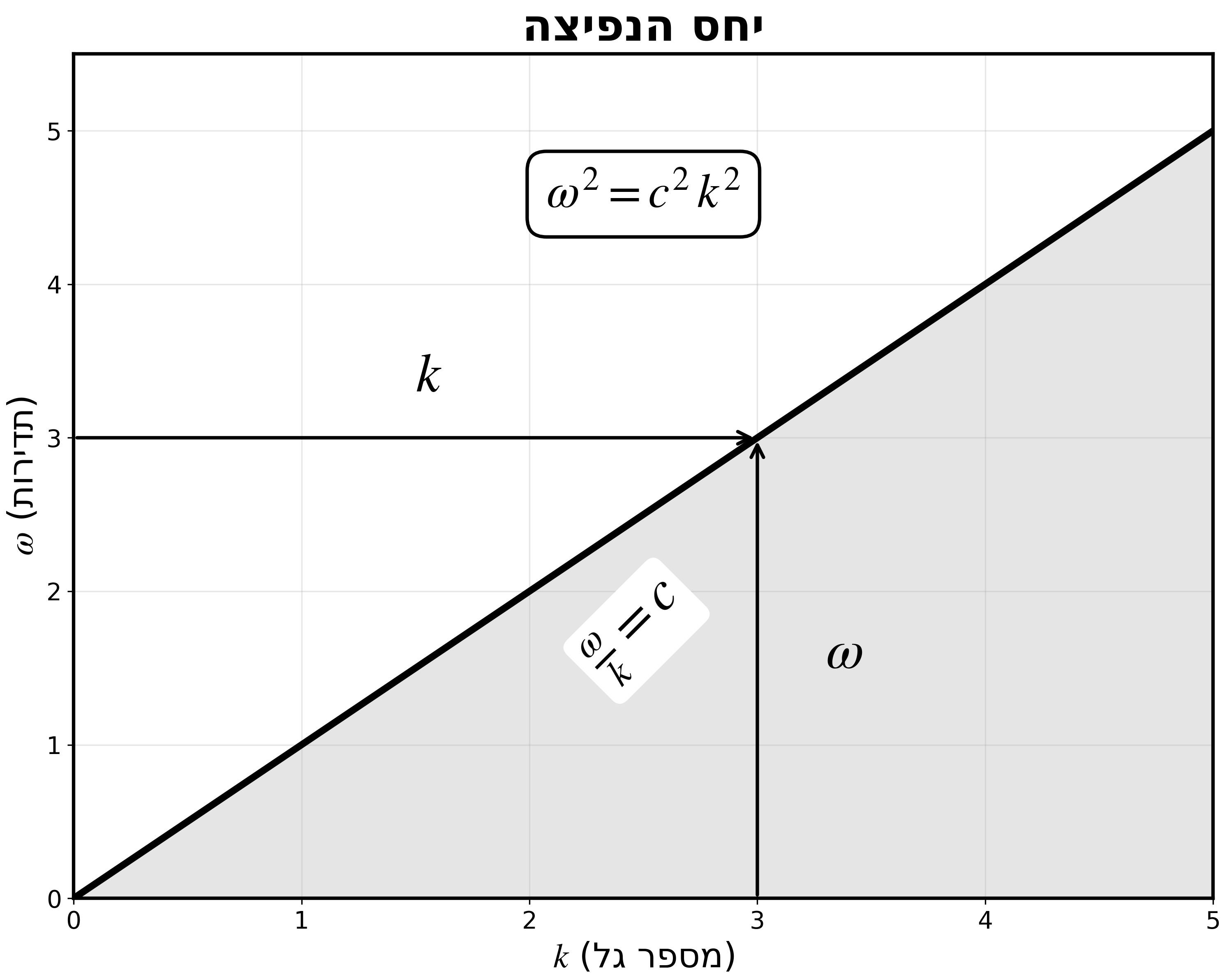
משוואת הגלים מתקיימת אם ורק אם:
\[\boxed{k^2 = \frac{\omega^2}{c^2}}\]או באופן שקול:
\[\omega^2 = k^2 \cdot c^2\]מספר הגל ואורך הגל
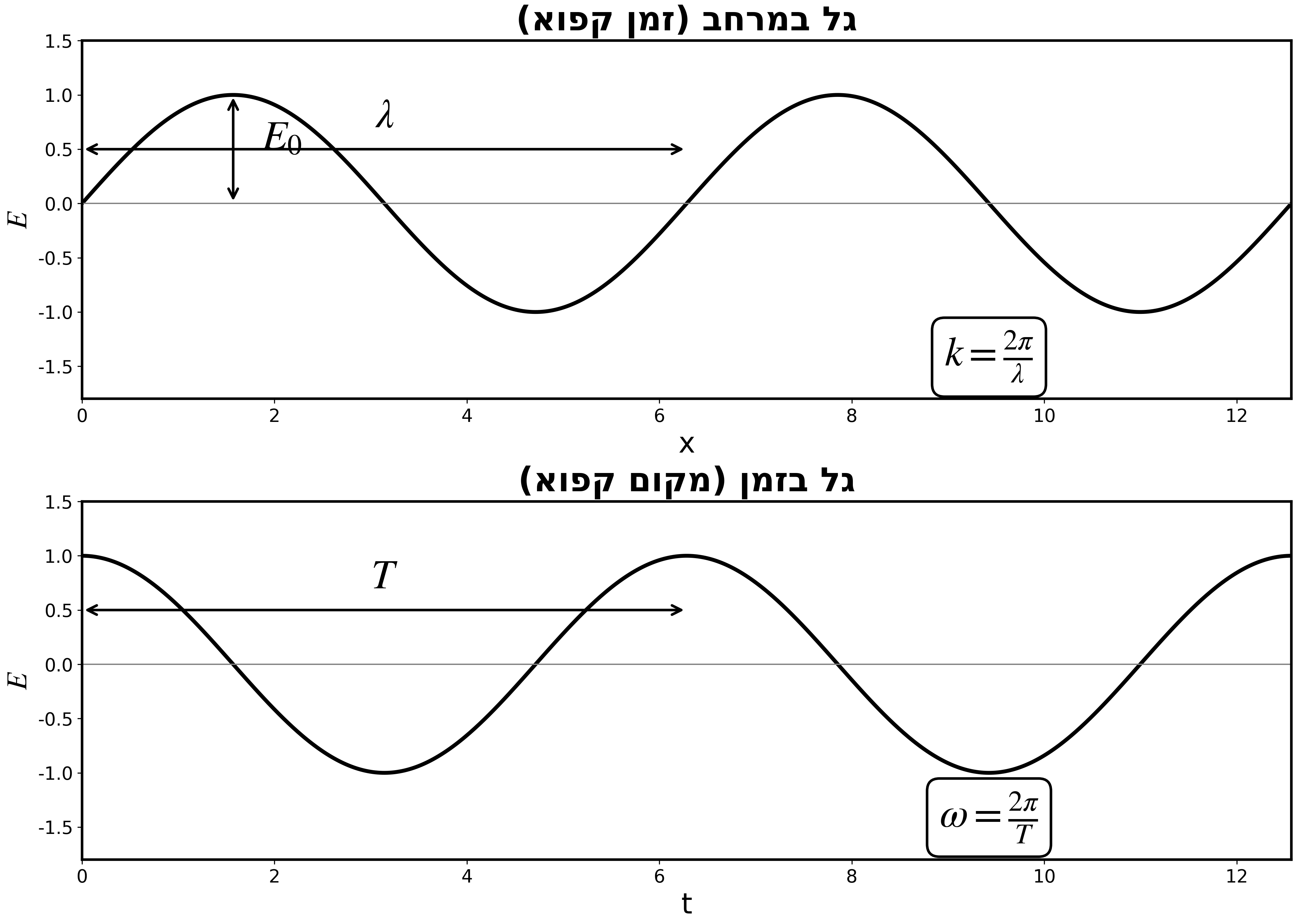
ניתוח במרחב (הקפאת הזמן)
נקבע $t = 0$:
\[E \propto \cos(kx)\]הקוסינוס חוזר על עצמו כל $2\pi$. אם $\lambda$ הוא אורך הגל:
\[k\lambda = 2\pi\] \[\boxed{k = \frac{2\pi}{\lambda}}\]$k$ נקרא מספר הגל.
ניתוח בזמן (הקפאת המקום)
נקבע $x = 0$:
\[E \propto \cos(\omega t)\]אם $T$ הוא זמן המחזור:
\[\omega T = 2\pi\] \[\boxed{\omega = \frac{2\pi}{T}}\]$\omega$ נקראת תדירות זוויתית (מוכרת ממכניקה כמהירות זוויתית).
הקשר למהירות הגל
\[c = \frac{\omega}{k} = \frac{2\pi/T}{2\pi/\lambda} = \frac{\lambda}{T}\]המשמעות: המהירות היא המרחק שהגל עובר ($\lambda$) חלקי הזמן שלוקח לו לעבור מחזור אחד ($T$).
מבנה גל אלקטרומגנטי
כאשר מציבים את הפתרונות הגליים בכל משוואות מקסוול, מתקבל:
- $\vec{E}$ ו-$\vec{B}$ ניצבים זה לזה
- שניהם ניצבים לכיוון ההתקדמות $\vec{k}$
- הם באותה פאזה (מתאפסים ומגיעים למקסימום יחד)
- יש להם אותו $\vec{k}$ ואותו $\omega$
איור סכמטי:
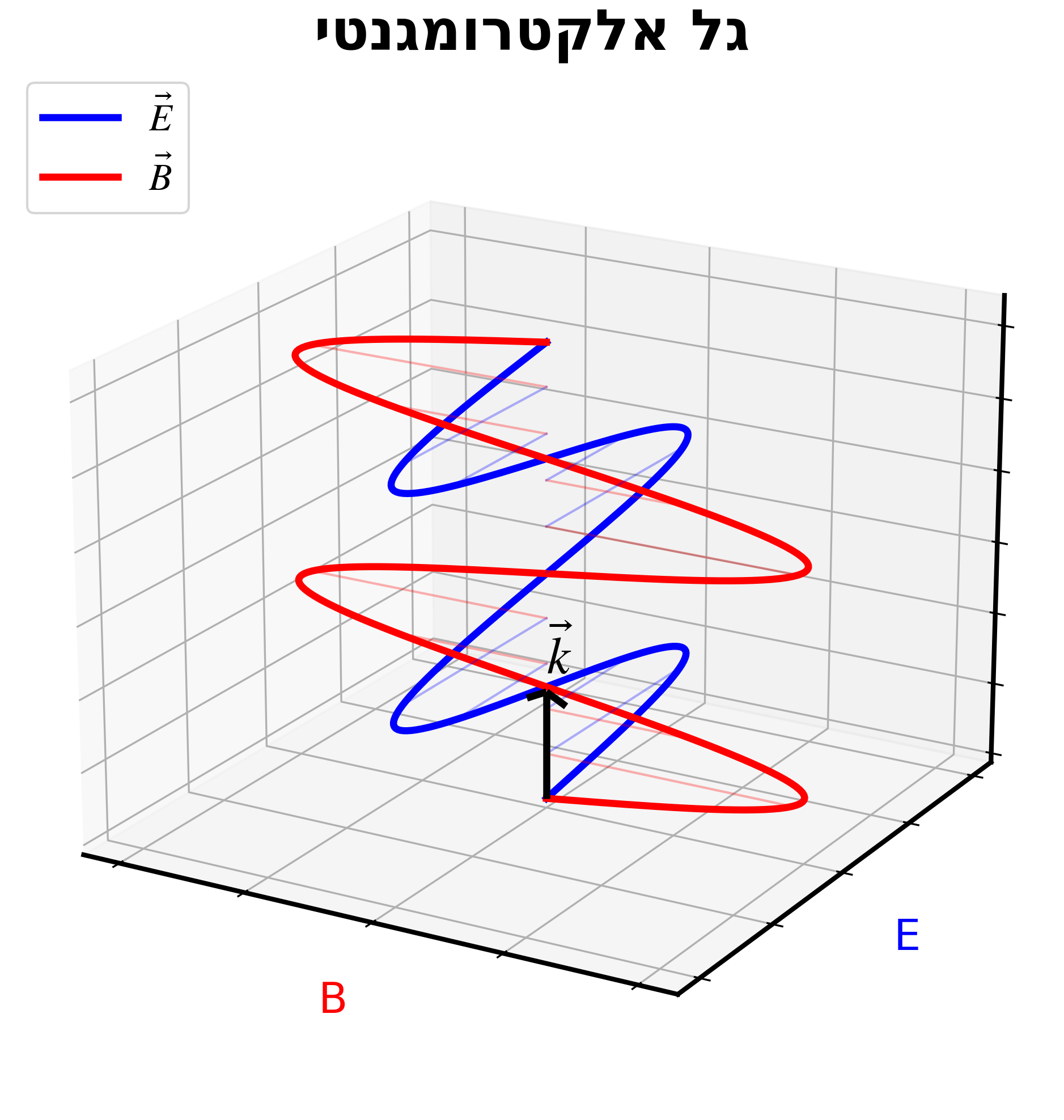
זהו גל אור! האור הוא הפרעות המתפשטות בשדות האלקטרומגנטיים של הוואקום.
חלק ד’: הספקטרום האלקטרומגנטי
אור נראה
העין האנושית רגישה לאורכי גל בטווח צר מאוד:
| אורך גל (nm) | צבע |
|---|---|
| 450 | סגול |
| 500 | כחול |
| 550 | ירוק |
| 600 | כתום |
| 650 | כתום-אדום |
| 700 | אדום |
כל הצבעים שאנחנו רואים הם גלים אלקטרומגנטיים בתדירויות שונות!
מעבר לאור הנראה
גלים אלקטרומגנטיים קיימים בכל אורכי הגל:
| סוג קרינה | אורך גל | אנרגיה | שימושים/תכונות |
|---|---|---|---|
| גלי רדיו | מטרים עד ק”מ | נמוכה מאוד | תקשורת, שידורים |
| מיקרוגל | ס”מ | נמוכה | תנורים, WiFi |
| אינפרא-אדום | מיקרומטרים | נמוכה-בינונית | חום, שלטים |
| אור נראה | 400-700 nm | בינונית | ראייה |
| אולטרא-סגול | 10-400 nm | גבוהה | כוויות שמש |
| קרני X (רנטגן) | ננומטרים בודדים | גבוהה מאוד | צילום רפואי |
| קרני גמא | פיקומטרים | גבוהה ביותר | קרינה גרעינית |
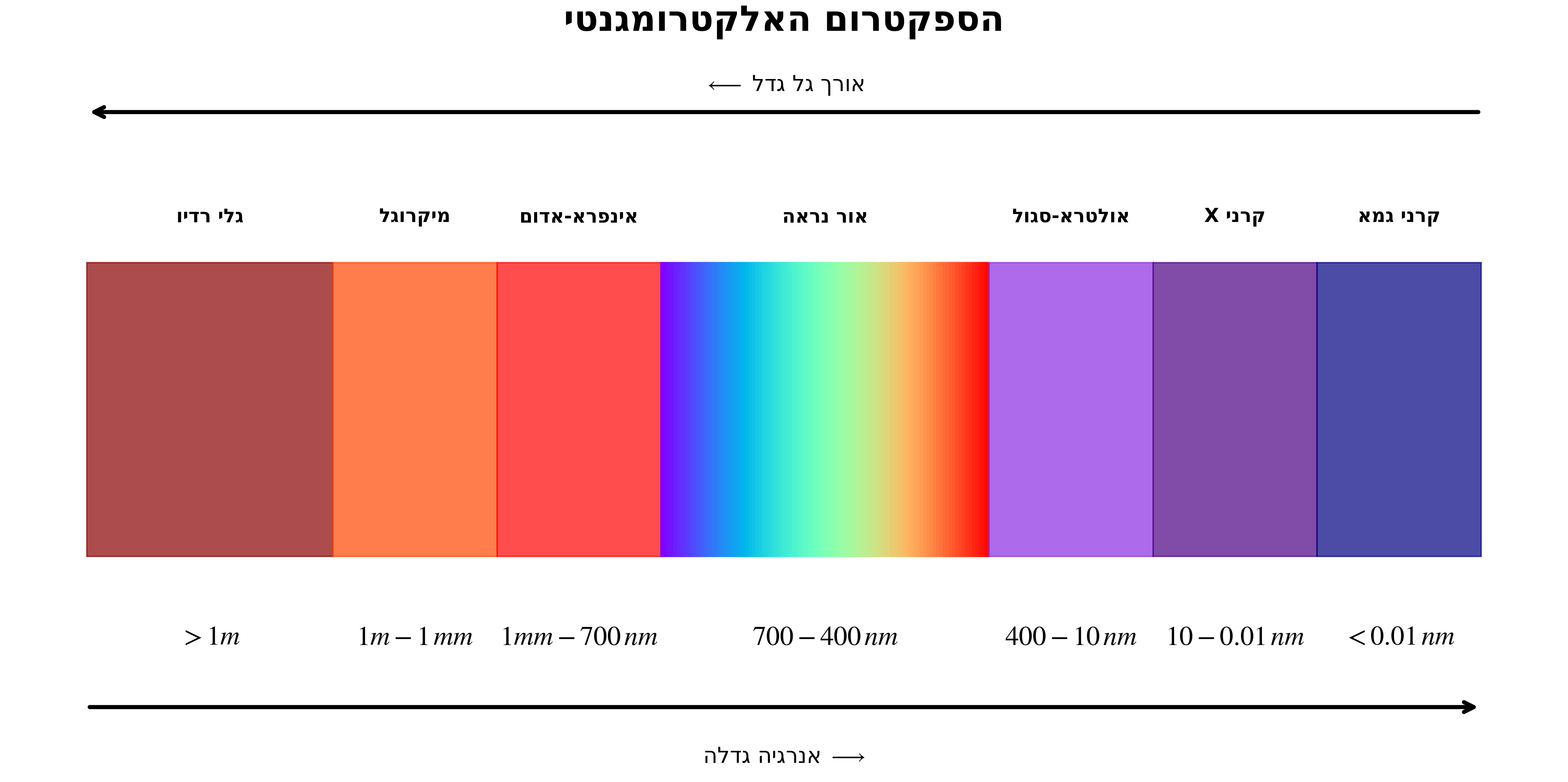
עקרון חשוב: אנרגיה ואורך גל
\[\text{The shorter the wavelength} \;\Leftrightarrow\; \text{the radiation is more energetic}\]השלכות רפואיות:
- קרני X חודרות לגוף אך נעצרות בעצמות ← צילומי רנטגן
- קרינה אנרגטית מאוד יכולה לשבור קשרים מולקולריים ב-DNA ← מוטציות
- שימוש מופרז בצילומי רנטגן מסכן את המטופל
לגבי רכבים חשמליים ותדרים נמוכים: השדות האלקטרומגנטיים ברכב חשמלי הם בתדירות נמוכה מאוד (אורך גל ארוך מאוד), הרבה פחות אנרגטיים מאור נראה. לכן אין סכנה בריאותית.
חלק ה’: הפוטנציאלים האלקטרומגנטיים
פוטנציאל מגנטי $\vec{A}$
מהמשוואה $\vec{\nabla} \cdot \vec{B} = 0$ (אין מונופולים מגנטיים):
הפתרון הלא-טריוויאלי: אם הדיברגנס של $\vec{B}$ הוא אפס, אז $\vec{B}$ הוא שדה ערבולי, ולכן:
\[\boxed{\vec{B} = \vec{\nabla} \times \vec{A}}\]$\vec{A}$ נקרא הפוטנציאל המגנטי (פוטנציאל וקטורי).
למה קוראים לזה פוטנציאל? כי $\vec{B}$ נגזר מ-$\vec{A}$, בדיוק כמו שכוח משמר נגזר מאנרגיה פוטנציאלית.
גזירת הצורה הכללית של השדה החשמלי
נציב $\vec{B} = \vec{\nabla} \times \vec{A}$ בחוק פאראדיי:
\[\vec{\nabla} \times \vec{E} = -\frac{\partial \vec{B}}{\partial t} = -\frac{\partial}{\partial t}(\vec{\nabla} \times \vec{A})\]מכיוון שנגזרות מרחביות וזמניות מתחלפות:
\[\vec{\nabla} \times \vec{E} = -\vec{\nabla} \times \frac{\partial \vec{A}}{\partial t}\] \[\vec{\nabla} \times \left(\vec{E} + \frac{\partial \vec{A}}{\partial t}\right) = 0\]זהות וקטורית: אם הרוטור של משהו שווה אפס, אז הוא חייב להיות גרדיאנט של פונקציה סקלרית:
\[\vec{E} + \frac{\partial \vec{A}}{\partial t} = -\vec{\nabla}\phi\]הצורה הכללית של השדה החשמלי
\[\boxed{\vec{E} = -\vec{\nabla}\phi - \frac{\partial \vec{A}}{\partial t}}\]שני רכיבים:
| רכיב | מקור | תכונה |
|---|---|---|
| $-\vec{\nabla}\phi$ | פוטנציאל אלקטרוסטטי | משמר (אינטגרל על מסלול סגור = 0) |
| $-\frac{\partial \vec{A}}{\partial t}$ | שינוי בפוטנציאל המגנטי | לא משמר (מקורו בשדות מגנטיים משתנים) |
זהויות וקטוריות חשובות
\[\begin{aligned} &\vec{\nabla} \cdot (\vec{\nabla} \times \vec{A}) = 0 \quad &\text{(The divergence of a curl (rotor) is always zero)} \\[6pt] &\vec{\nabla} \times (\vec{\nabla}\phi) = 0 \quad &\text{(The curl of a gradient is always zero)} \end{aligned}\]חלק ו’: חוק פאראדיי - כא”מ מושרה
הנוסחה
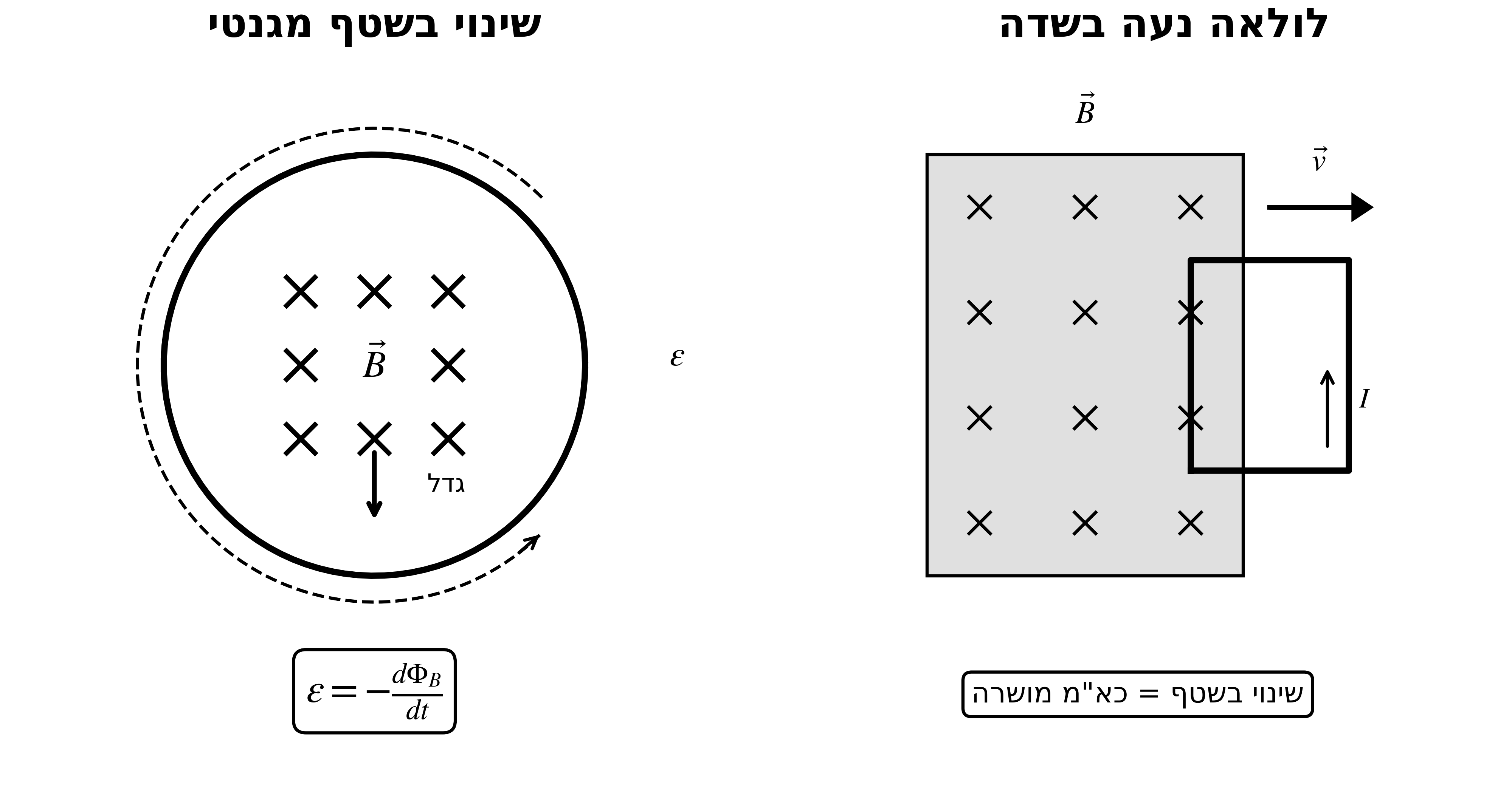
\[\boxed{\varepsilon = \oint \vec{E} \cdot d\vec{l} = -\frac{d\Phi_B}{dt}}\]כאשר השטף המגנטי הוא:
\[\Phi_B = \int_\Sigma \vec{B} \cdot d\vec{A}\]המשמעות הפיזיקלית
שינוי בשטף המגנטי דרך משטח יוצר כוח אלקטרומוטורי (כא”מ) על שפת המשטח.
זהו העיקרון שעומד בבסיס:
- גנרטורים - תרגום אנרגיה מכנית לאנרגיה חשמלית
- שנאים - העברת אנרגיה חשמלית בין סלילים
- אינדוקציה - יצירת זרם מושרה
חלק ז’: דוגמה מפורטת
הבעיה
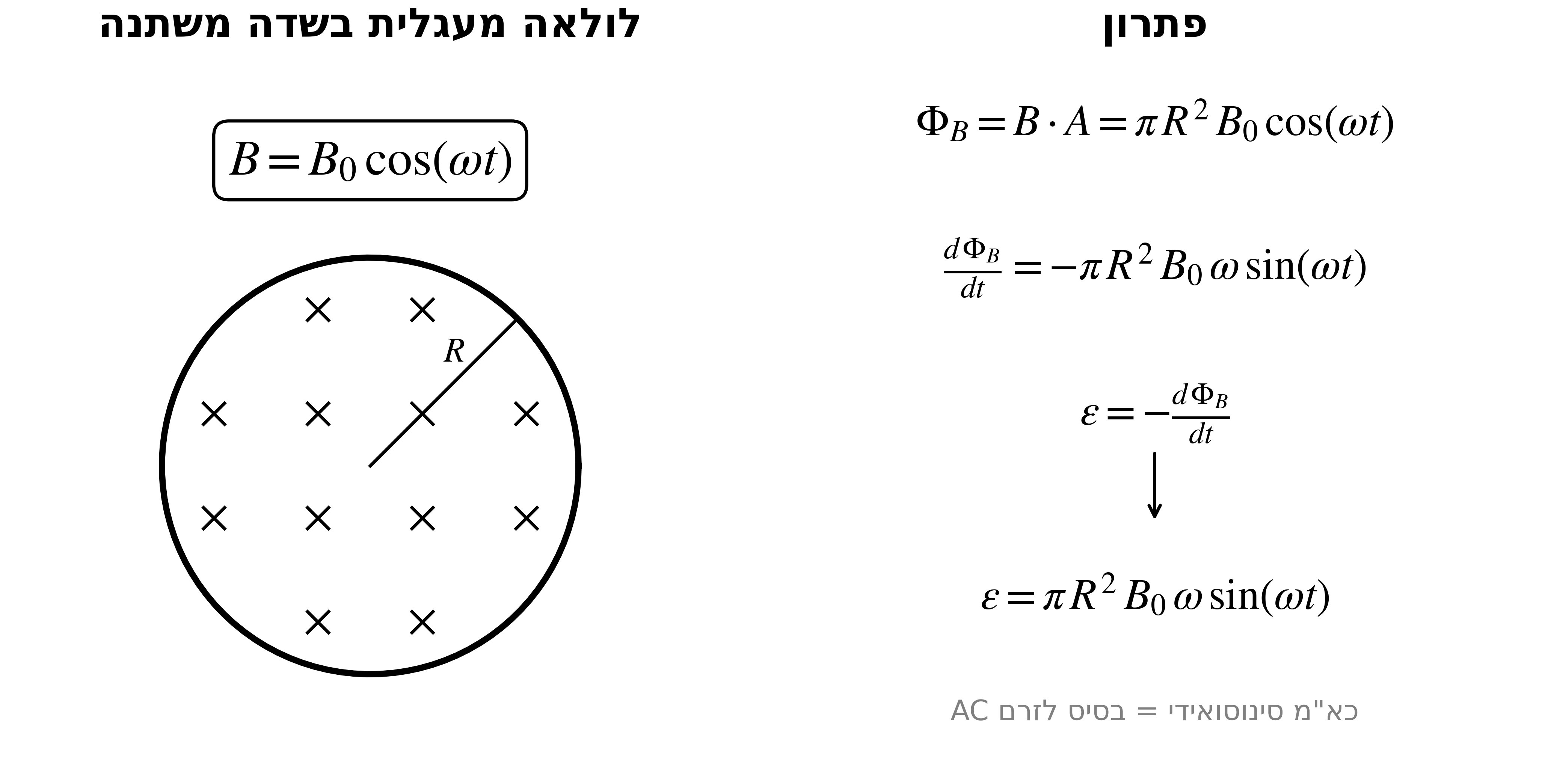
לולאה מעגלית ברדיוס $R$ נמצאת בשדה מגנטי אחיד הניצב למישור הלולאה.
השדה המגנטי משתנה בזמן:
\[B = B_0 \cos(\omega t)\]מצא: את הכא”מ המושרה על הלולאה.
הפתרון
שלב 1: חישוב השטף המגנטי
השדה אחיד וניצב למשטח, לכן:
\[\Phi_B = \vec{B} \cdot \vec{A} = B \cdot A = B_0 \cos(\omega t) \cdot \pi R^2\]שלב 2: גזירה לפי הזמן
\[\begin{aligned} \frac{d\Phi_B}{dt} &= \pi R^2 \cdot \frac{d}{dt}[B_0 \cos(\omega t)] \\[6pt] &= \pi R^2 \cdot (-B_0 \omega \sin(\omega t)) \\[6pt] &= -\pi R^2 B_0 \omega \sin(\omega t) \end{aligned}\]שלב 3: הכא”מ המושרה
\[\varepsilon = -\frac{d\Phi_B}{dt} = \pi R^2 B_0 \omega \sin(\omega t)\]התוצאה
\[\boxed{\varepsilon = \pi R^2 B_0 \omega \sin(\omega t)}\]זהו כא”מ שמתנדנד סינוסואידית - הבסיס לזרם חילופין (AC) שמגיע לבתים שלנו!
חלק ח’: חוק לנץ
הניסוח
כיוון הזרם המושרה הוא תמיד כזה שהוא מתנגד לשינוי בשטף שיצר אותו.
המינוס בחוק פאראדיי ($\varepsilon = -\frac{d\Phi_B}{dt}$) נקרא חוק לנץ.
ההסבר הפיזיקלי
נניח שהזרם המושרה היה מחזק את השינוי בשטף:
- שינוי בשטף ← זרם מושרה
- זרם ← שדה מגנטי נוסף
- שדה נוסף מחזק את השטף ← שינוי גדול יותר
- שינוי גדול יותר ← זרם גדול יותר
- … וחוזר חלילה ← אנרגיה יש מאין!
זה בלתי אפשרי (מפר את חוק שימור האנרגיה), ולכן הזרם חייב להתנגד לשינוי.
חלק ט’: כלל יד ימין
הכלל
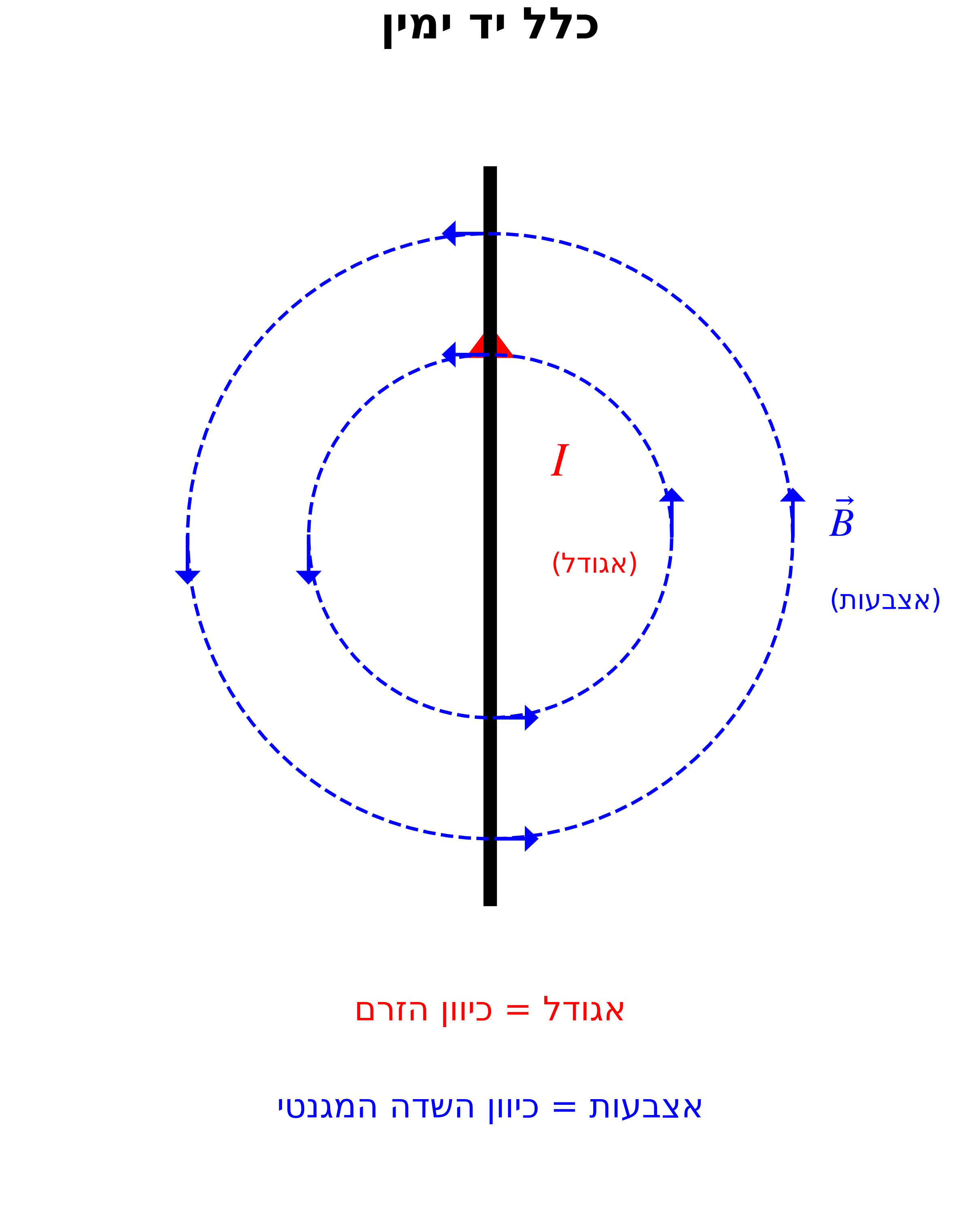
כשזרם $I$ זורם בתייל, הוא יוצר סביבו שדה מגנטי ערבולי.
הכלל:
- האגודל מצביע בכיוון זרימת הזרם
- האצבעות המתעגלות מראות את כיוון השדה המגנטי
↑ I (זרם)
|
←────●────→ B (שדה מגנטי מעגלי)
|
↓
שימוש בחוק לנץ
בדוגמה שלנו:
- שדה מגנטי חיצוני נכנס לדף (⊗)
- כשהשטף גדל, הזרם המושרה ייצור שדה יוצא מהדף (להתנגד לגידול)
- לפי יד ימין: אם השדה יוצא מהדף, הזרם זורם נגד כיוון השעון
⊗ ⊗ ⊗ ⊗ ⊗
⊗ ⊗
⊗ ⊙ ⊗ שדה חיצוני: ⊗ (נכנס)
⊗ (⟲) ⊗ שדה מושרה: ⊙ (יוצא, בתוך הלולאה בלבד)
⊗ ⊗ זרם: נגד כיוון השעון
⊗ ⊗ ⊗ ⊗ ⊗
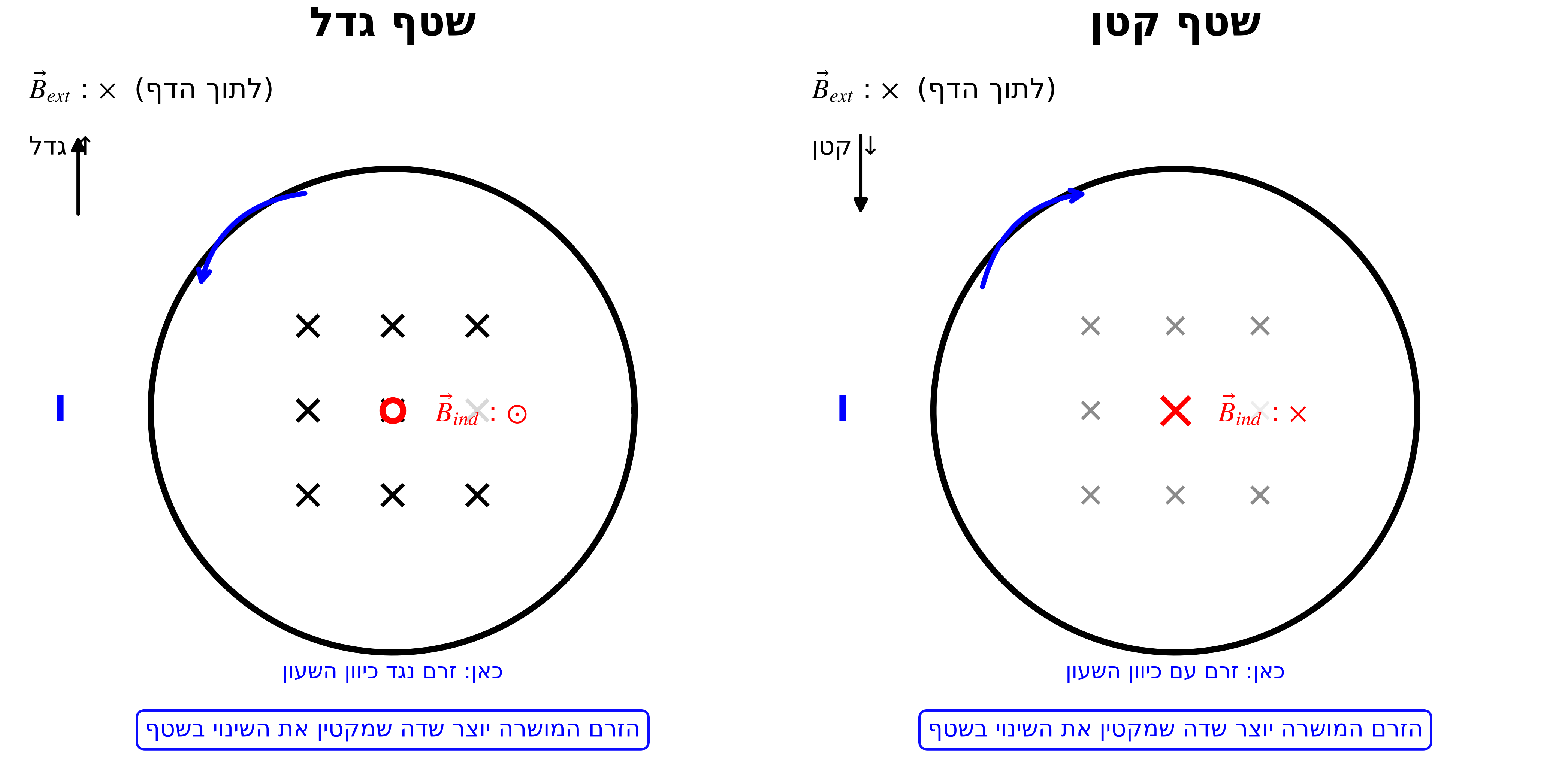
נקודה חשובה: מה שקובע הוא השדה בתוך הלולאה (במשטח שהיא סוגרת), לא מחוצה לה!
חלק י’: תורת היחסות הפרטית - הערה
הרקע
משוואות מקסוול כוללות גדלים שנראים תלויי צופה (כמו צפיפות זרם $\vec{j}$).
אבל $\epsilon_0$ ו-$\mu_0$ הם אוניברסליים - הם מתארים את הוואקום, והוואקום זהה לכל הצופים.
המסקנה של איינשטיין
אם $\epsilon_0$ ו-$\mu_0$ אוניברסליים, אז גם:
\[c = \frac{1}{\sqrt{\epsilon_0 \mu_0}}\]מהירות האור זהה לכל הצופים, ללא קשר לתנועתם!
המשמעות
אם מישהו עומד ומודד מהירות האור - הוא יקבל $3 \times 10^8 \mathrm{m/s}$.
אם מישהו אחר נע ב-99% ממהירות האור ומודד את אותו האור - גם הוא יקבל $3 \times 10^8 \mathrm{m/s}$.
זה לא טריוויאלי! במכניקה קלאסית, מהירויות מתחברות. אבל מהירות האור לא.
כדי שזה יתקיים, המושגים של מרחב וזמן חייבים להיות תלויי צופה. צופים שונים מודדים אורכים וזמנים שונים - אבל חוקי הפיזיקה (ומהירות האור) זהים לכולם.
“אילו התיאוריה שלי לא הייתה נכונה, היה מספיק מדען אחד להפריך אותה. לא צריך מאה.” - איינשטיין
סיכום נקודות מפתח לבחינה
-
משוואות מקסוול - דעו את ארבעתן בשתי הצורות (דיפרנציאלית ואינטגרלית)
-
משוואת הגלים בוואקום ומהירות האור $c = 1/\sqrt{\epsilon_0\mu_0}$
-
יחס הנפיצה: $\omega = ck$ או $k^2 = \omega^2/c^2$
- קשרים:
- $k = 2\pi/\lambda$ (מספר גל)
- $\omega = 2\pi/T$ (תדירות זוויתית)
- $c = \lambda/T = \omega/k$
- פוטנציאלים:
- $\vec{B} = \vec{\nabla} \times \vec{A}$
- $\vec{E} = -\vec{\nabla}\phi - \partial\vec{A}/\partial t$
-
חוק פאראדיי: $\varepsilon = -d\Phi_B/dt$
-
חוק לנץ: הזרם המושרה מתנגד לשינוי שיצר אותו
- כלל יד ימין: אגודל = זרם, אצבעות = שדה מגנטי