כימיה כללית ופיזיקלית

תמיסות

בפרק זה נעסוק בתמיסות, שמהוות חלק מרכזי בעולם הביולוגיה. כל התהליכים הביולוגיים מתרחשים בתמיסות, במיוחד תמיסות מימיות \( \left(\text{Aqueous Solutions}\right) \). לכן, נדבר כאן על סוגי תמיסות, מאפייניהן, והיחידות השונות המשמשות למדידת ריכוזים בתמיסות.

תמיסות הן בדרך כלל תערובות הומוגניות, שבהן ריכוז החומרים אחיד לאורך כל הנפח. בתמיסות ניתן להבחין בין ממס \( \left(\text{Solvent}\right) \) ומומס \( \left(\text{Solute}\right) \). הממס הוא בדרך כלל הנוזל שנמצא בריכוז הגבוה ביותר, למשל מים. המומס הם החומרים המומסים בממס: מלחים, סוכרים, חלבונים, הורמונים, ועוד.

ריכוז התמיסה נמדד בדרכים שונות, ובבתי חולים לדוגמה, משתמשים ביחידות בינלאומיות לתרופות, אנטיביוטיקה וויטמינים. בכימיה ישנן דרכים נוספות למדידת ריכוזים:

אחוז מסה/מסה: למשל, 5 גרם מומס ב-95 גרם ממס, כלומר \( \frac{5}{100} \times 100\% = 5\% \).
אחוז נפח/נפח (\( V/V \)): למשל, 25 מיליליטר מומס ב-100 מיליליטר תמיסה.
מסה/נפח: יחידה נפוצה בבתי חולים. לדוגמה, תמיסת סליין 0.9% מכילה 0.9 גרם מלח בליטר אחד של מים.

המעבר בין היחידות השונות דורש חישובים והמרות יחידות. יחידות נוספות כוללות:

PPM (חלקים למיליון): חלק אחד של חומר מומס במיליון חלקים של ממס. למשל, 1 מיליגרם מומס בליטר מים הוא \( 1 \, \text{ppm} \), כי \( 1 \, \text{mg} = 10^{-3} \, \text{g} \), וליטר מים שוקל \( 10^3 \, \text{g} \).
PPB (חלקים לביליון): יחידת ריכוז קטנה יותר.
PPT (חלקים לטריליון): יחידת ריכוז נדירה למדידות זעירות.

תלמיד: איך אני עובר בין יחידות?

מורה: באמצעות חישובים והמרות יחידות. חשוב להבין את ההגדרות וליישם את הכללים המתמטיים הנדרשים.

שבר מולארי \(\left( X_i \right)\)

השבר המולארי (\(X_i\)) הוא היחס בין כמות המולים של חומר מסוים לכמות המולים הכוללת במערכת. זוהי דרך נוספת לבטא ריכוז של חומר בתמיסה, והיא שימושית במצבים מסוימים.

לדוגמה, אם יש לכם תמיסה שמכילה 2 מול סוכר ו-8 מול מים, השבר המולארי של הסוכר הוא: \[ X_{\text{sugar}} = \frac{\text{moles of sugar}}{\text{total moles}} = \frac{2}{2+8} = 0.2 \] כלומר, 20% מהמולים בתמיסה הם של סוכר.

חשוב לזכור כי סכום השברים המולאריים של כל \( \text{n} \) הרכיבים בתמיסה תמיד יהיה שווה ל-1: \[ \sum_{i=1}^{n} X_i = 1 \]

מולליות \(\left( m \right)\)

המולליות (\(m\)) היא מדד נוסף לריכוז, המוגדר כמספר המולים של המומס חלקי המסה של הממס בקילוגרמים: \[ m = \frac{n}{m_{\text{solvent}}} = \frac{\text{moles of solute}}{\text{mass of solvent (kg)}} \]

\[ m = \frac{\text{mol}}{\text{kg}} = \frac{\text{mol}}{1000\text{g}} \]

בניגוד למולריות (\(M\)), שמודדת את מספר המולים ביחס לנפח התמיסה (בליטרים), המולליות אינה תלויה בנפח ומשמשת לעיתים קרובות כאשר רוצים להימנע משינויים שנגרמים כתוצאה משינויים בטמפרטורה.

לדוגמה: אם יש לכם 10 גרם אתנול (צפיפות 0.789 גרם/מ"ל) ואתם מוסיפים מים עד שנפח התמיסה הכולל מגיע ל-100 מ"ל, תוכלו לחשב את הנפח, המסה, השבר המולארי, המולריות והמולליות.

המולליות שימושית במיוחד במעבדות ובבתי חולים, שבהם שינויים בטמפרטורה יכולים להשפיע על הנפח אך לא על המסה, ולכן נוח להשתמש במדד זה לצורך חישובים מדויקים.

כוחות בין תמיסות

כשמדברים על כוחות בין תמיסות, אנו מתמקדים בהתנהגות של חומרים כאשר הם מעורבבים. לדוגמה, אם מערבבים שני נוזלים \(A\) ו-\(B\), כמו מים ואלכוהול, יש לבחון את סוגי האינטראקציות הבין-מולקולריות:

כוחות בין מולקולות \(A-A\).
כוחות בין מולקולות \(B-B\).
כוחות בין מולקולות \(A-B\).

אם הכוחות \(A-A\) ו-\(B-B\) חזקים יותר מ-\(A-B\), אזי התמיסות לא יתערבבו בקלות. בדומה ליחסי קבוצות שונות באוכלוסייה: כמו שחרדים יעדיפו להיות עם חרדים וחילונים יעדיפו להיות עם חילונים, כך גם מולקולות יעדיפו אינטראקציות עם בני-מינן.

לעומת זאת, כאשר הכוחות בין \(A-B\) דומים לאלו שבין \(A-A\) ו-\(B-B\), התמיסה היא אידיאלית. כלומר, החומרים מתערבבים בקלות ואפשר לנבא את תכונות התמיסה על סמך תכונות הרכיבים בנפרד.

דוגמה לתמיסה אידיאלית היא תערובת של בנזן (\(C_6H_6\)) וטולואן (\(C_6H_5CH_3\)). מכיוון שיש להם מבנה כימי דומה, הם מתערבבים היטב בכל יחס ויוצרים תמיסה אחידה.

תמיסות אידיאליות מתקיימות כאשר: \[ \Delta \text{H}_{\text{soln}} = 0 \] כלומר, אין שינוי באנרגיה בעת ערבוב החומרים.

תמיסות לא אידיאליות

בתמיסות לא אידיאליות, האינטראקציות בין \(A-B\) עשויות להיות חזקות או חלשות יותר מהאינטראקציות \(A-A\) ו-\(B-B\). כתוצאה מכך, מתקיימת סטייה חיובית או שלילית מהתנהגות אידיאלית:

סטייה חיובית: אינטראקציות \(A-B\) חלשות, ולכן הנפח הסופי של התמיסה גדול מהצפוי.
סטייה שלילית: אינטראקציות \(A-B\) חזקות, ולכן הנפח הסופי של התמיסה קטן מהצפוי.

לדוגמה, תערובת של אתנול (\(C_2H_5OH\)) ומים יוצרת סטייה שלילית. האינטראקציות החזקות בין אתנול למים גורמות לנפח התמיסה להיות קטן מהצפוי.

\[ V_{\text{solution}} \lt V_A + V_B \]

תלמיד: למה הנפח קטן?

מורה: בגלל שהמולקולות של אתנול ומים נמשכות חזק אחת לשנייה, הן מסתדרות קרוב יותר זו לזו, וכך הנפח קטן.

באופן כללי, אם רוצים להבין את תכונות התמיסה, יש לבחון את סוגי האינטראקציות הקיימות בין החומרים ולחשב את תרומתן לתכונות הכוללות.

איזומרים והאינטראקציה שלהם

איזומרים הם מולקולות שיש להן את אותה נוסחה כימית אך מבנה שונה. לדוגמה, ריח של תפוז וריח של לימון נגרמים על ידי איזומרים אופטיים - חומרים שהאף שלנו יכול להבדיל ביניהם למרות הדמיון הכימי.

תלמיד: איך האף שלנו מזהה את ההבדל?

מורה: האף יודע להבחין בין איזומרים אופטיים בגלל מבנה מולקולרי שונה שמשפיע על קולטנים באף.

דוגמה נוספת: אננטיומרים הם סוג של איזומרים אופטיים שיש להם תכונות כימיות דומות אך אינטראקציות ביולוגיות שונות. זו הסיבה שחומר מסוים יכול להריח כמו תפוז בעוד שאיזומר שלו יריח כמו לימון.

תמיסות לא אידיאליות ואינטראקציות כימיות

תלמיד: אפשר לחזור על התמיסה הלא אידיאלית?

מורה: כמובן. תמיסה לא אידיאלית נוצרת כאשר הכוחות בין המולקולות השונות בתמיסה אינם זהים. לדוגמה, בחומר כמו כלורופורם (טריכלורומתאן) (\(CHCl_3\)) או אצטון \(\left( {\left( \text{CH}_3 \right)}_2 \text{CO} \right)\), יש אינטראקציות ייחודיות. למשל, מולקולות אצטון יכולות ליצור קשרי מימן עם טריכלורומתאן, ולכן נוצרת תמיסה עם חוזק יחסי גבוה.

תמיסה כזו לא תהיה אידיאלית, כיוון שהאינטראקציה \(A-B\) חזקה יותר מהאינטראקציות \(A-A\) או \(B-B\), והנפח הכולל של התמיסה יהיה קטן מהצפוי: \[ V_{\text{solution}} \lt V_A + V_B \]

תלמיד: אז מתי תמיסה נחשבת אידיאלית?

מורה: תמיסה אידיאלית מתקיימת כאשר האינטראקציות בין כל המולקולות זהות לחלוטין. דוגמה לכך היא בנזן וטולואן: שני חומרים עם מבנים כימיים דומים מאוד, שמתערבבים ללא שינוי בתכונות הפיזיקליות.

דוגמאות לערבוביות (Solution formation)

תלמיד: מה קובע אם שני חומרים יתערבבו?

מורה: הכלל המרכזי הוא "דומה מתמסס בדומה" (Like dissolves like). חומרים עם מבנים כימיים דומים נוטים להתערבב זה עם זה. לדוגמה:

\(C_6H_{14}\) (הקסאן) ו-\(C_8H_{18}\) (אוקטאן): מתערבבים היטב כי שניהם פחמימנים דומים.
מים ואתנול (\(C_2H_5OH\)): יוצרים תמיסה עם קשרי מימן, אך לא אידיאלית.
מים ושמן: אינם מתערבבים כלל כי הם בעלי תכונות כימיות שונות מאוד.

תמיסות אידיאליות נוצרות כאשר אין שינוי בתכונות הפיזיקליות: \[ \Delta H_{\text{mix}} = 0 \quad \text{ו-} \quad V_{\text{solution}} = V_A + V_B \]

לעומת זאת, בתמיסות לא אידיאליות, הנפח או האנרגיה יכולים לסטות מהצפוי, תלוי באופי האינטראקציות בין המולקולות.

מסיסות בתמיסות מימיות

מה במיוחד בתמיסות מימיות? יכולות להמיס הרבה. אמרנו על זה: יכולות להמיס הרבה מאוד יונים בתוכן, בגלל שמים הם ממס קוטבי, עם דיפול. מים יכולים לפרק מלחים, להמיס פנימה ולייצב אטומים ויונים. לא כל חומר יכול לעשות זאת.

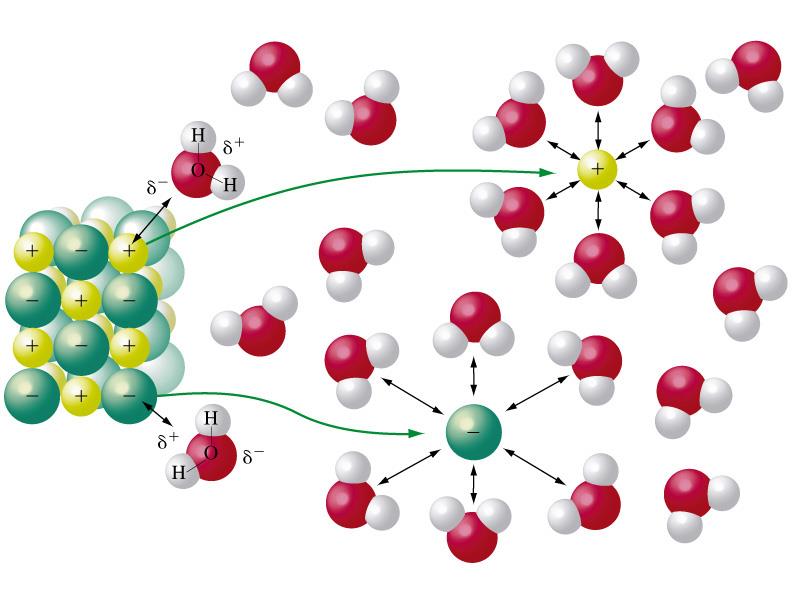
באופן כללי, מה אנחנו יודעים לגבי תמיסות מימיות? ככלל, בתמיסות מימיות, אם מחממים את המים, המסיסות גדלה. לדוגמה, אם תמיס בכוס מים בטמפרטורת החדר, תוכל להמיס אולי 3 כפיות מלח. אם תחמם את המים ל-70°C, תוכל להמיס 6 כפיות מלח.

עקומות מסיסות

מסיסות במים היא פונקציה של הטמפרטורה. לכל חומר יש גבול מסיסות בטמפרטורה נתונה, מעבר אליו החומר לא יתמוסס וישקע. לדוגמה, אפשר להמיס סוכר במאה מיליליטר מים כך:

ב-20°C: עד 5 כפיות סוכר.
ב-70°C: עד 10 כפיות סוכר.

מעבר לכמות זו, החומר יתחיל לשקוע.

מסיסות מלחים

לדוגמה, NaCl (מלח שולחן) מתמוסס היטב במים. בטמפרטורה של 0°C אפשר להמיס עד 40 גרם NaCl במאה מיליליטר מים, וגם ב-30°C המסיסות דומה.

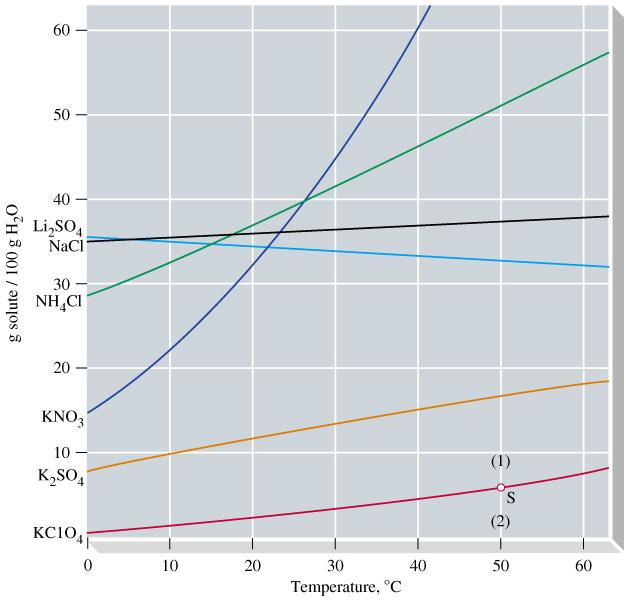
ככלל, מסיסות של חומרים יוניים עולה עם הטמפרטורה. אך יש יוצאים מן הכלל, ותלוי גם בדרגת הרוויה.

עקומות המסיסות והנקודות החשובות

(2) Unsaturated: תמיסה שבה ניתן להמיס עוד חומר, כל עוד הטמפרטורה לא עברה את הגבול.
Saturated: תמיסה רוויה בנקודה המדויקת שלה על העקומה.
(1) Supersaturated: תמיסה שבה כמות החומר עברה את הגבול, והוא יתחיל לשקוע.

השפעת הטמפרטורה על מסיסות

לא רק חומרים יוניים מתמוססים במים, גם גזים כמו O₂ ו-CO₂. אולם, בניגוד לחומרים יוניים, מסיסות גזים במים יורדת עם העלייה בטמפרטורה.

לדוגמה, באוקיינוסים, אם הטמפרטורה עולה ב-2°C בלבד, מסיסות הגזים במים משתנה, מה שיכול להשפיע על בעלי חיים שתלויים בריכוזי ה-O₂ ו-CO₂.

מסקנות:

המסיסות תלויה בטמפרטורה: ככל שהטמפרטורה עולה, המסיסות של רוב החומרים במים גדלה.
יש גבול מסיסות לכל חומר, מעבר לו החומר לא יתמוסס.
מסיסות גזים פועלת הפוך: ככל שהטמפרטורה עולה, מסיסות הגזים קטנה.

חוק הנרי ומסיסות גזים (השפעת הלחץ על מסיסות)

מסיסות של גזים במים מושפעת מהלחץ. חוק הנרי קובע שהמסיסות של גז היא קבוע \( k \) כפול לחץ הגז: \[ \underbrace{C}_{\text{solubility}} = k \cdot \underbrace{P_{\text{gas}}}_{\text{Partial pressure}} \]

לדוגמה, אם המסיסות של גז מסוים היא 23.54 מ"ל בלחץ של 1 אטמוספירה בטמפרטורה מסוימת (לצורך הדוגמה - במים ב \( 0^{\circ} \) מעלות), ניתן לחשב את קבוע הנרי כך:

\[ k = \frac{C}{P_{\text{gas}}} = \frac{23.54 \text{mL N}_2 / L}{1.00 \text{ atm}} \]

אם רוצים להעלות את המסיסות ל- \( 100.0 \ \text{mL per L}\), ניתן לחשב את הלחץ הדרוש: \[ P_{\text{gas}} = \frac{C}{k} = \frac{100.0 \text{ mL}}{23.54 \text{mL N}_2 / \text{atm}} \approx 4.25 \text{ atm} \]

מסקנה: ככל שהלחץ עולה, כך עולה מסיסות הגז במים.

צלילה ומסיסות גזים - העקרונות של חוק הנרי

בעת צלילה, הלחץ האטמוספרי עולה, ולכן מסיסות הגזים בדם עולה. אם הצולל עולה מהר מדי לפני המים, הגזים עשויים להשתחרר מהר מדי וליצור בועות קטלניות בדם.

תופעה זו דומה לפתיחת בקבוק קולה: כאשר פותחים את הפקק, משתחרר הלחץ, מולקולות גז משתחררות מהנוזל ונוצרות בועות.

סיכום:

מסיסות גזים במים עולה עם העלייה בלחץ, אך פוחתת עם העלייה בטמפרטורה.
צלילה בעומק רב דורשת הקפדה על איזון בלחצים כדי למנוע שחרור פתאומי של גזים בדם.

חוק ראול ולחץ אדים של תמיסות

נעסוק בתמיסות של שני רכיבים: \( A \) הממס, ו-\( B \) המומס.

ראול גילה שהוספת חומר לתמיסה מורידה את לחץ האדים של הממס \( \left( \text{A} \right) \).

הירידה בלחץ האדים נובעת מהנוסחה ללחץ האדים החלקי: \[ P_{\text{A}} = \underbrace{X_{\text{A}}}_{\lt1} \cdot P^\circ_{\text{A}} \] כאשר \( P_{\text{A}} \) הוא הלחץ החלקי של רכיב A, \( X_{\text{A}} \) השבר המולי שלו A בתמיסה, ו-\( P^\circ_{\text{A}} \) לחץ האדים שלו בתמיסה טהורה.

הסיבה לירידה בלחץ האדים, כלומר \( P_{\text{A}} \lt P^\circ_{\text{A}} \), היא העובדה שהשבר המולי קטן מ-1, שכן: \[ X_{\text{A}} + X_{\text{B}} = 1.00 \]

כמו כן, לחץ האדים הכולל של תמיסה ניתן על ידי סכום הלחצים החלקיים: \[ P_{\text{total}} = P_{\text{A}} + P_B = X_{\text{A}} \cdot P^\circ_{\text{A}} + X_{\text{B}} \cdot P^\circ_B \]

לחץ אדים בתמיסות מושפע מהרכב התמיסה. לפי חוקי התמיסות האידיאליות, הלחץ החלקי של רכיב A בתמיסה ניתן על ידי הנוסחה: \[ P_{\text{A}} = X_{\text{A}} \cdot P^\circ_{\text{A}} \] כאשר:

\( P_{\text{A}} \): לחץ האדים החלקי של רכיב A.
\( X_{\text{A}} \): השבר המולי של רכיב A בתמיסה.
\( P^\circ_{\text{A}} \): לחץ האדים של רכיב A כשהוא טהור.

ניתן לחשב את הלחץ האדים הכולל לפי סכום הלחצים החלקיים: \( P_\text{total} = P_{\text{A}} + P_B \).

שימוש בחוק ראול בחישובים

חוק ראול קובע כי הלחץ החלקי של רכיב מסוים בתמיסה, שווה לשבר המולי של הרכיב בתמיסה, כפול לחץ האדים הטהור של הרכיב.

דוגמה:

נתונים:

ב-25 מעלות צלזיוס:
- לחץ האדים של בנזן (\( P_{\text{benzene}}^\circ \)) = 95.1 מ"מ כספית.
- לחץ האדים של טולואן (\( P_{\text{toluene}}^\circ \)) = 28.4 מ"מ כספית.
תמיסה עם שבר מולי חצי-חצי:
- \( X_{\text{benzene}} = 0.5 \)
- \( X_{\text{toluene}} = 0.5 \)

חישוב הלחץ החלקי של כל רכיב בתמיסה:

\( P_{\text{benzene}} = X_{\text{benzene}} \cdot P_{\text{benzene}}^\circ = 0.5 \cdot 95.1 = 47.6 \, \text{mm Hg} \)
\( P_{\text{toluene}} = X_{\text{toluene}} \cdot P_{\text{toluene}}^\circ = 0.5 \cdot 28.4 = 14.2 \, \text{mm Hg} \)

הלחץ הכולל: \[ P_{\text{total}} = P_{\text{benzene}} + P_{\text{toluene}} = 47.6 + 14.2 = 61.8 \, \text{mm Hg} \]

חישוב הרכב הגז בשיווי משקל:

נשתמש בחוק ראול כדי לחשב את השבר המולי של כל רכיב בפאזה הגזית: \[ X_{\text{component}} = \frac{P_{\text{component}}}{P_{\text{total}}} \]

\( X_{\text{benzene}} = \frac{P_{\text{benzene}}}{P_{\text{total}}} = \frac{47.6}{61.8} = 0.77 \)
\( X_{\text{toluene}} = \frac{P_{\text{toluene}}}{P_{\text{total}}} = \frac{14.2}{61.8} = 0.23 \)

מדוע השבר המולי של הבנזן גבוה יותר בפאזה הגזית?

למרות שהתמיסה היא חצי-חצי מבחינת השבר המולי, בפאזה הגזית הלחץ של הבנזן גבוה יותר משל הטולואן. זאת, מכיוון שלבנזן יש לחץ אדים טבעי גבוה יותר, ולכן הוא נוטה להתנדף יותר.

\( P_{\text{benzene}} \) תורם כ-77% מהלחץ הכולל.
\( P_{\text{toluene}} \) תורם כ-23% מהלחץ הכולל.

כך שאתם רואים, בחוק ראול:
חוק ראול מתאר מצב שבו, בתמיסה, השבר המולי של רכיב מסוים כפול לחץ האדים הטבעי שלו קובע את הלחץ החלקי של הרכיב בפאזה הגזית. לדוגמה, אם מתחילים מתמיסה שבה השבר המולי הוא חצי-חצי עבור בנזן ותולווין, בפאזה הגזית השבר המולי עשוי להיות שונה, לדוגמה 70% עבור בנזן ו-30% עבור תולווין.

חוק ראול ותהליך הזיקוק

חוק ראול מאפשר להבין כיצד תמיסות מתנהגות בפאזה הגזית, ומשמש רבות ב:

תהליכי זיקוק: הפרדת חומרים על בסיס לחץ האדים שלהם.
תעשייה: טיהור וניקוי חומרים.
רפואה: יישומים בתמיסות רוויות.

מה קורה בזיקוק?
מתחילים מתמיסה בעלת הרכב מסוים, לדוגמה: 30% בנזן ו-70% תולווין. מחממים את התמיסה, ומה שנוצר בפאזה הגזית הוא הרכב חדש, לדוגמה 50%-50%. לוקחים את הפאזה הגזית, מקררים אותה, ומקבלים תמיסה חדשה. החימום והקירור החוזרים גורמים להפרדה הדרגתית, כאשר כל פעם מאשירים את הגז הנדיף יותר בפאזה הגזית.

זיקוק למקוטעים

זהו תהליך המשמש בתי זיקוק להפרדת תערובות על בסיס לחצים חלקיים. התהליך מבוצע כך:

חימום התמיסה למעבר לפאזה הגזית.
הפרדת רכיבי הגז לפי נדיפותם.
קירור הפאזה הגזית והפיכתה לנוזל חדש.

כך נוצרות תמיסות חדשות בהרכבים שונים.

אתגרים בזיקוק

מצב אזאוטרופי

מצב שבו הרכב הפאזה הגזית והרכב התמיסה זהים. לדוגמה, תערובת אתנול ומים (90% אתנול, 10% מים). במצב זה אי אפשר להפריד באמצעות זיקוק רגיל. ניתן להפריד בדרכים אחרות:

הוספת חומר שלישי שמאפשר הפרדה.
שימוש בממברנה המאפשרת מעבר של רכיב אחד בלבד.

לחץ אוסמוטי \(\pi\)

לחץ אוסמוטי הוא הלחץ שנוצר כתוצאה מהפרשי ריכוזים של מומסים משני צידי ממברנה חדירה-בררנית. הממברנה מאפשרת מעבר של ממס (כמו מים) אך מונעת מעבר של המומס, מה שמוביל לתנועה של מים בין שתי התמיסות כדי להשוות את הריכוזים.

עקרון האוסמוזה

כאשר קיימת ממברנה שמפרידה בין תמיסות עם ריכוזים שונים:

מים עוברים מתמיסה מהולה (ריכוז נמוך של מומסים) אל תמיסה מרוכזת (ריכוז גבוה של מומסים).
תנועה זו נמשכת עד להשוואת הריכוזים משני צידי הממברנה.

אם הממברנה אינה חדירה למומסים, נוצר לחץ על התמיסה המרוכזת עקב כניסת המים. לחץ זה נקרא לחץ אוסמוטי.

משוואת הלחץ האוסמוטי

הלחץ האוסמוטי מחושב בעזרת המשוואה:

\[ \pi = MRT \]

כאשר:

\(M\): ריכוז התמיסה במולריות (\(\text{mol/L}\)).
\(R\): קבוע הגזים האידיאליים (\(0.0821 \, \text{L·atm/(mol·K)}\)).
\(T\): הטמפרטורה בקלווין (\(K\)).

התוצאה מתקבלת ביחידות אטמוספרות (\(\text{atm}\)).

דוגמה לניסוי

דמיינו שקית חדירה-בררנית עם ריכוז גבוה של סוכר, המונחת במים:

הסוכר אינו יכול לעבור דרך הממברנה.
מים נכנסים לתוך השקית כדי לדלל את ריכוז הסוכר.
כתוצאה מכך, מפלס המים בתוך השקית עולה, ונוצר לחץ אוסמוטי.

השפעת המומסים על תכונות פיזיקליות

הוספת מומסים לממס משנה את תכונותיו הפיזיקליות, כולל:

ירידת נקודת הקיפאון: המומס מפריע להיווצרות מבנה גבישי מסודר של הממס.
עליית נקודת הרתיחה: המומס מחזק את הכוחות בין מולקולות הממס, ודורש יותר אנרגיה להפרדתן.

לדוגמה:

מפזרים מלח על כבישים בחורף כדי למנוע קיפאון.
מרססים אתילן גליקול על כנפי מטוסים כדי למנוע היווצרות קרח.

למה תהליכים אלו מתרחשים?

הוספת יונים לתמיסה משנה את כוחות האינטראקציה:

בנוזלים, יונים יוצרים קשרים חזקים יותר עם המים מאשר מים לבד, ולכן נדרשת יותר אנרגיה כדי להרתיח את התמיסה.
לגבי קיפאון, היונים מפריעים למולקולות המים להסתדר במבנה גבישי, ולכן נקודת הקיפאון יורדת.

לחץ אוסמוטי, שינוי בנקודת קיפאון, ושינוי בנקודת רתיחה הם חלק ממה שנקרא תכונות קוליגטיביות, שתלויות בריכוז המומסים ולא בסוגם.

שינויים בנקודת הקיפאון \(\Delta T_f\)

מהו שינוי נקודת הקיפאון?

שינוי נקודת הקיפאון הוא ירידה בטמפרטורה שבה נוזל קופא, כתוצאה מהוספת מומס. תהליך זה מתואר בעזרת משוואת ואן 'ט הוף:

\[ \Delta T_f = -K_f \cdot m \]

כאשר:

\(\Delta T_f\): שינוי נקודת הקיפאון (במעלות צלזיוס).
\(K_f\): הקבוע הקריאוסקופי של הממס (תלוי בסוג הנוזל).
\(m\): מולליות (מספר המולים של המומס לכל קילוגרם ממס).

תכונה קוליגטיבית

שינוי נקודת הקיפאון הוא תכונה קוליגטיבית, כלומר הוא תלוי רק במספר החלקיקים המומסים ולא בסוגם. לדוגמה:

תמיסה של מלח (\(\text{NaCl}\)) תוריד את נקודת הקיפאון יותר מתמיסה של סוכר באותו ריכוז, כיוון שמלח מתפרק ליונים (\(\text{Na}^+\) ו-\(\text{Cl}^-\)).
חומר כמו \(\text{CaCl}_2\), שמתפרק לשלושה יונים (\(\text{Ca}^{2+}\) ו-2\(\text{Cl}^-\)), יוריד את נקודת הקיפאון פי שלושה יותר מתמיסה של \(\text{NaCl}\).

שימושים מעשיים

תופעת ירידת נקודת הקיפאון משמשת במגוון תחומים:

בכבישים: פיזור מלח כדי למנוע קיפאון של מים בשלג או קרח.
במטוסים: ריסוס אתילן גליקול או פרופילן גליקול על הכנפיים למניעת הצטברות קרח.
ברדיאטור של רכב: הוספת תערובת של אתילן גליקול ומים כדי למנוע קיפאון ולשמור על תקינות המנוע במזג אוויר קר.
בהקפאת תאים: הוספת חומרים שמונעים היווצרות גבישי קרח שעלולים לפגוע בממברנות התאים.

דוגמאות מהטבע

בטבע, בעלי חיים החיים במים קפואים משתמשים בחלבונים מיוחדים שמונעים היווצרות גבישי קרח גדולים. חלבונים אלו נקשרים לגבישי הקרח הקטנים ומונעים מהם לגדול, כך שהתאים אינם נפגעים.

דוגמה חישובית

נניח שיש תמיסה של \(\text{NaCl}\) בריכוז של \(1 \, \text{mol/kg}\) במים:

\(K_f\) של מים הוא \(1.86 \, \text{°C·kg/mol}\).
\(i\), מקדם ונט הוף, שווה ל-2 עבור \(\text{NaCl}\) (מכיוון שהוא מתפרק לשני יונים).

\[ \Delta T_f = -i \cdot K_f \cdot m = -(2)(1.86)(1) = -3.72 \, \text{°C} \]

נקודת הקיפאון החדשה של המים תהיה:

\[ 0 - 3.72 = -3.72 \, \text{°C} \]

Using Freezing Point Depression Data (\(K_f\)) - Example

Nicotine extracted from tobacco leaves is a liquid completely miscible with water at temperatures below 60°C.

(a) What is the molality of nicotine in an aqueous solution that starts to freeze at -0.450°C?

(b) If this solution is obtained by dissolving 1.921 g of nicotine in 48.92 g of H₂O, what must be the molar mass of nicotine?

To find the molality: \[ \Delta T_f = -0.450^\circ C, \quad K_f = -1.86^\circ C \cdot m^{-1} \] \[ \text{molality} = \frac{\Delta T_f}{-K_f} = \frac{-0.450}{-1.86} = 0.242 \, m \]

To find the molar mass: \[ \text{molality} = \frac{\text{moles of solute}}{\text{kg of solvent}} \] \[ \text{moles of solute} = 0.242 \cdot 0.04892 \, \text{kg water} = 0.01183 \, \text{mol} \] \[ \text{Molar mass (M)} = \frac{\text{mass of nicotine}}{\text{moles of nicotine}} = \frac{1.921 \, \text{g}}{0.01183 \, \text{mol}} = 162 \, \text{g/mol} \]

Thus, the molar mass of nicotine is approximately \(162 \, \text{g/mol}\).

שימוש בנתונים על נקודת קיפאון (\(k_f\)) - שאלה לדוגמה

ניקוטין שמופק מעלי טבק הוא נוזל המתמוסס לחלוטין במים בטמפרטורות מתחת ל-60°C.

(א) מה המולליות של ניקוטין בתמיסה מימית שמתחילה לקפוא ב-\(-0.450^\circ C\)?

(ב) אם התמיסה הוכנה על ידי המסת \(1.921 \, \text{g}\) ניקוטין ב-\(48.92 \, \text{g}\) מים, מהו המשקל המולקולרי של ניקוטין?

לחישוב המולליות: \[ \Delta T_f = -0.450^\circ C, \quad K_f = -1.86^\circ C \cdot m^{-1} \] \[ \text{molality} = \frac{\Delta T_f}{-K_f} = \frac{-0.450}{-1.86} = 0.242 \, m \]

לחישוב המשקל המולקולרי: \[ \text{molality} = \frac{\text{moles of solute}}{\text{kg of solvent}} \] \[ \text{moles of solute} = 0.242 \cdot 0.04892 \, \text{kg water} = 0.01183 \, \text{mol} \] \[ \text{Molar mass (M)} = \frac{\text{mass of nicotine}}{\text{moles of nicotine}} = \frac{1.921 \, \text{g}}{0.01183 \, \text{mol}} = 162 \, \text{g/mol} \]

לכן, המשקל המולקולרי של ניקוטין הוא כ-\(162 \, \text{g/mol}\).

הסבר לדוגמה

ניקוטין, שמופק מעלי טבק, מתמוסס במים בטמפרטורות מתחת ל-60°C. בדוגמה זו, עלינו לחשב את המולליות של ניקוטין בתמיסה, וכן את המשקל המולקולרי שלו, בהתבסס על נתוני ירידת נקודת הקיפאון.

חישוב המולליות: ירידת נקודת הקיפאון היא \(-0.450^\circ C\), וה-\(K_f\) של מים הוא \(-1.86^\circ C \cdot m^{-1}\). בעזרת המשוואה: \[ \Delta T_f = -K_f \cdot m \] ניתן למצוא את המולליות: \[ m = \frac{\Delta T_f}{-K_f} = \frac{-0.450}{-1.86} = 0.242 \, \text{mol/kg}. \]

חישוב המשקל המולקולרי: התמיסה נוצרה על ידי המסת \(1.921 \, \text{g}\) ניקוטין ב-\(48.92 \, \text{g}\) מים. המולליות מחושבת כך: \[ \text{molality} = \frac{\text{moles of nicotine}}{\text{kg of water}} \implies \text{moles of nicotine} = m \cdot \text{kg of water}. \] נציב את הערכים: \[ \text{moles of nicotine} = 0.242 \cdot 0.04892 = 0.01183 \, \text{mol}. \] כעת נמצא את המשקל המולקולרי: \[ \text{Molar mass} = \frac{\text{mass of nicotine}}{\text{moles of nicotine}} = \frac{1.921}{0.01183} = 162 \, \text{g/mol}. \]

לכן, המשקל המולקולרי של ניקוטין הוא כ-\(162 \, \text{g/mol}\).

פקטור דיסוציאציה \( \left(i\right) \)

מהו פקטור התמוססות?

ואן הוף מצא שיש גורם \( i \) שמהווה יחס בין טמפרטורת הקיפאון בפועל, לבין זו שציפינו לה. בהמשך, התיאוריה של החוקר ארניוס על דיסוציאציה הבהירה את הפער: שכשמלחים מתמוססים בתמיסה, הם לא תמיד מתפרקים במלואם ליונים, ולכן החישובים דורשים התאמה.

מדוע יש פער במדידות?

כאשר מחשבים תכונות קוליגטיביות, כמו שינוי נקודת הקיפאון (\(\Delta T_f\)) או נקודת הרתיחה (\(\Delta T_b\)), המשוואות מתבססות על מספר החלקיקים המתמוססים. עם זאת, במציאות:

מלחים לא תמיד מתמוססים לחלוטין (התפרקות יונית חלקית).
לדוגמה, \(\text{NaCl}\) אמור להתפרק לשני יונים (\(\text{Na}^+\) ו-\(\text{Cl}^-\)), אך \(i\) בפועל עשוי להיות 1.9 ולא 2.
באופן דומה, \(\text{K}_2\text{SO}_4\) שאמור להתפרק לשלושה יונים (\(2\text{K}^+\) ו-\(\text{SO}_4^{2-}\)), עשוי לתת \(i = 2.6\).

משוואות מעודכנות

כדי לדייק את החישובים, הוכנס פקטור \(i\) למשוואות הקוליגטיביות:

 לחץ אוסמוטי: \(\pi = i \cdot c \cdot RT\)
שינוי נקודת הקיפאון: \(\Delta T_f = -i \cdot K_f \cdot m\)
שינוי נקודת הרתיחה: \(\Delta T_b = i \cdot K_b \cdot m\)
 

במשוואות אלו:

\(i\): מידת הפירוק של המלח.
\(c\): ריכוז התמיסה במולריות.
\(K_f\) ו-\(K_b\): קבועי הקיפאון והרתיחה, בהתאמה.
\(m\): מולליות (מול לכל קילוגרם ממס).

דוגמה חישובית למציאת \(i\)

נניח שאורניוס בדק תמיסה מימית של \(\text{NaCl}\) בריכוז של \(0.01 \, \text{mol/L}\):

היינו מצפים לתוצאה הבאה: \[ {\Delta T}_f = -1.86 \, \text{°C·kg/mol} \cdot 0.01 \, \text{mol/L} = -0.0186 \, \text{°C} \]

אך במדידות נמצא ש-\(\Delta T_f = -0.0361 \, \text{°C}\).

חישוב \( i \) נעשה בעזרת היחס בין מדידת התכונה הקוליגטיבית בפועל, לבין זו המצופה. למשל, עבור \(\text{NaCl}\): \[ i = \frac{\text{mesured} \, \Delta T_f}{\text{expected} \, \Delta T_f} = \frac{-0.0361}{-0.0186} = \boxed{1.94} \]

לערך הזה אנחנו קוראים קבוע דיסוציאציה, או קבוע פירוק של היונים, במקרה הזה של \(\text{NaCl}\).

דור פסקל

16 בדצמבר 2024

חזור לחלק הקודם
המשך לשיווי משקל