פתיח - אנושיות לפני נוסחאות
לתיעוד - ההרצאה הועברה במהלך מלחמת חרבות ברזל, מבצע עם כלביא 2025. המרצה גילה אמפתיה רבה.
מקווה שאתם בטוחים בין האזעקות. אם קשה - יש פסיכולוגית בפקולטה, וגם אני פה לשיחה.
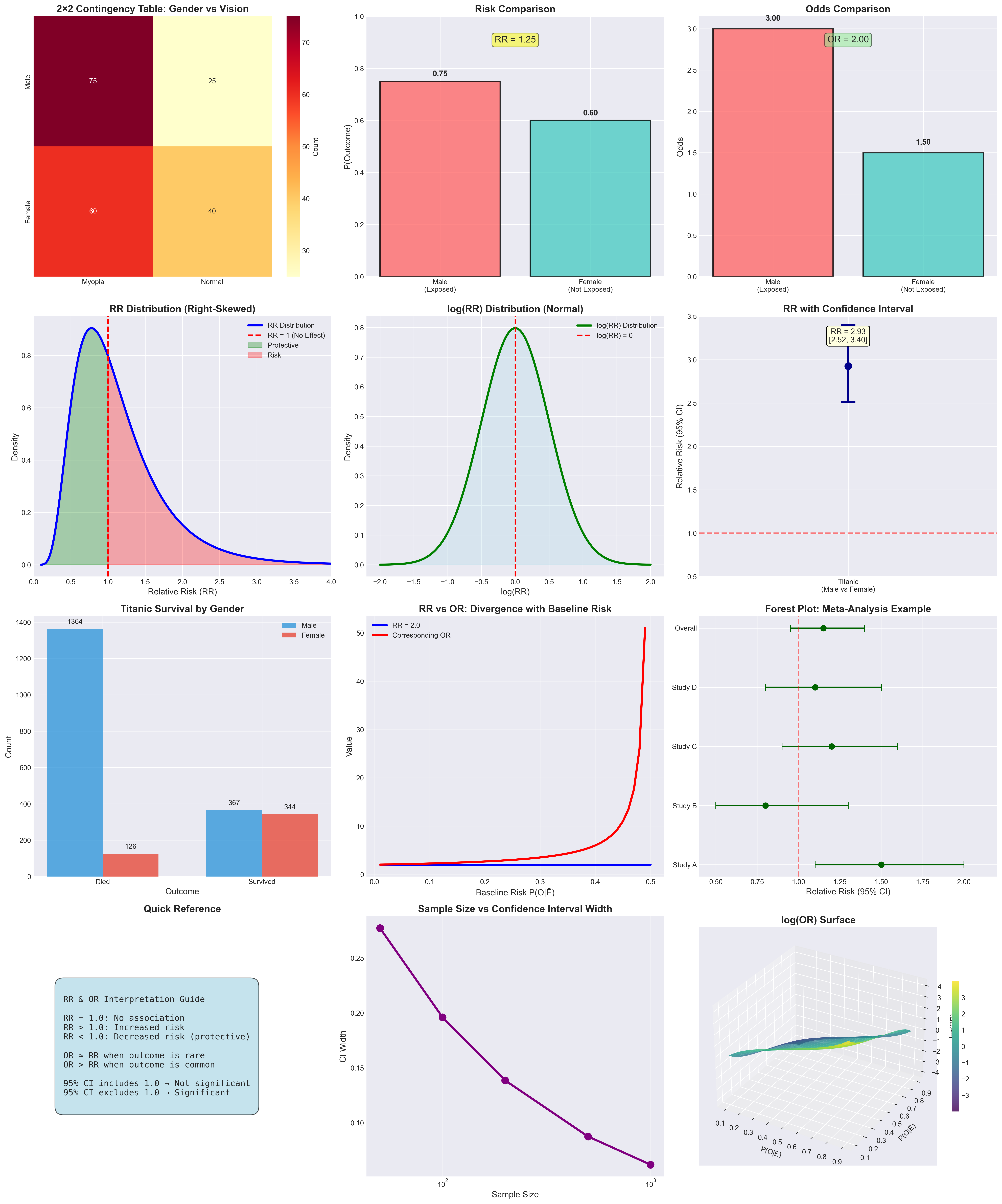
למה בכלל צריך מדדי סיכון?
כאשר שני המשתנים שלנו קטגוריאליים (למשל עישון כן/לא ו‑סרטן יש/אין) - לא מספיק לבדוק “הפרש”; אנחנו רוצים יחס שמעיד בכמה משתנה אחד מגדיל (או מקטין) את ההסתברות להשתנות השני.
| סמל | מהות | דוגמאות |
|---|---|---|
| $E$ | Exposure - גורם סיכון (מחלק לחשופים / לא חשופים) | עישון, מגדר, תואר אקדמי |
| $O$ | Outcome - תוצאה | סרטן, קוצר‑ראייה, תמותה |
| RR | Relative Risk | $\dfrac{P(O\mid E)}{P(O\mid \bar E)}$ |
| OR | Odds Ratio | $\dfrac{\text{odds}(O\mid E)}{\text{odds}(O\mid \bar E)}$ |
- RR = 1 ← אין קשר;
- RR > 1 ← החשיפה מסוכנת (גורם הסיכון מעלה את הסיכון);
- RR < 1 ← החשיפה מגנה
Relative Risk (RR)
אינטואיציה
“פי‑3 סיכון” נקלט מיידית; ההפרש בין $1/10{,}000$ ל‑$1/1{,}000{,}000$ - הרבה פחות.
טבלת 2 × 2 והנוסחה
| Outcome = 1 | Outcome = 0 | סה”כ | |
|---|---|---|---|
| Exposure = 1 | $A$ | $B$ | $A+B$ |
| Exposure = 0 | $C$ | $D$ | $C+D$ |
דוגמה 1 - קוצר‑ראייה
| קוצר‑ראייה | ראייה תקינה | סה”כ | |
|---|---|---|---|
| גברים | 75 | 25 | 100 |
| נשים | 60 | 40 | 100 |
הערה: לא בודקים חולים / לא חולים - אלא חשופים / לא חשופים.
האם יש קשר בין מין לבין קוצר ראייה? נשלים את הטבלה:
| קוצר‑ראייה | ראייה תקינה | סה”כ | |
|---|---|---|---|
| גברים | 75 | 25 | 100 |
| נשים | 60 | 40 | 100 |
| סה”כ | 135 | 65 | 200 |
הסיכון בגברים:
\[P(O\mid E) = \frac{75}{100} = 0.75\]הסיכון בנשים:
\[P(O\mid \bar E) = \frac{60}{100} = 0.6\]הסיכון היחסי:
\[RR = \frac{P(O\mid E)}{P(O\mid \bar E)} = \frac{0.75}{0.6} = 1.25\]כאן המין היה החשיפה.
באופן ככלי:
\[RR_\text{Male} = \tfrac{75/100}{60/100}=1.25\]להיות
גברמעלה את הסיכון לקוצר‑ראייה ב‑$25 \%$.
מגבלה מובנית - צריך קוהורט (עוקבה)
מחקר עוקבה (קוהורט - Cohort study) הוא שיטה למחקר מדעי בשימוש בענפים כגון רפואה, מדעי החברה, אקטואריה, סיעוד, אקולוגיה, ניתוח עסקי ועוד. זהו סוג של מחקר תצפיתי ולא מחקר התערבותי. במחקר מתרחש מעקב אחר קבוצת אנשים ותיעוד של מאפיינים או אירועים רלוונטיים למחקר. מחקרים אלו נחשבים ל״תקן הזהב״ (Gold standard) של המחקרים התצפיתיים בהם מחפשים יחסים אטיולוגיים, כמו למשל האם יש קשר בין חשיפה לגורם כלשהו למחלה או תופעת לוואי מסוימת והאם הקשר יכול להיות סיבתי (אם כי לא ניתן לקבוע סיבתיות על סמך מחקר עוקבה). פירוש המונח ״עוקבה״ הוא קבוצת אנשים בעלי אפיון סטטיסטי או דמוגרפי משותף, כגון שנת לידה, מצב משפחתי וכו׳, הנתונה למעקב ולמחקר. קבוצת העוקבה בהכרח תהיה קבוצת אנשים אשר לא חולים במחלה הנבדקת. ויקיפדיה
כדי ש‑RR יהיה תקף חייבים לדגום על‑פי החשיפה ולעקוב בזמן. במחקר מקרה-ביקורת אי‑אפשר להעריך RR ישירות.
דוגמה 2 - הטיטאניק
| מת | חי | סה”כ | |
|---|---|---|---|
| גברים | 1364 | 367 | 1731 |
| נשים | 126 | 344 | 470 |
הסיכון בגברים:
\[P(O\mid E) = \frac{1364}{1731} \approx 0.79\]הסיכון בנשים:
\[P(O\mid \bar E) = \frac{126}{470} \approx 0.27\]הסיכון היחסי:
\[RR = \frac{0.79}{0.27}\approx 2.926\]סיכון המוות לגבר היה גבוה פי‑3 לעומת אישה.
רווח סמך לסיכון יחסי
רווח סמך ללוגריתם ה‑RR:
תחת השערת האפס, הסיכון היחסי בעל התפלגות א-סימטרית ימנית כאשר השכיר הוא 1
הלוגריתם של הסיכון היחסי מתפלג נורמלית בקרוב, עם שכיח (וממוצע) של $\log RR = 0$.
נוכל לתקנן מ״מ זה להיות נורמלי סטנדרטי:
\[Z = \frac{\log RR}{\sigma_{\log RR}} \sim \mathcal{N}(0, 1)\]
- מחשבים $\log RR$ (הופך את ההתפלגות לסימטרית).
-
שונות:
\[\mathrm{Var}(\log(RR))=\tfrac{1}{A}-\tfrac{1}{A+B}+\tfrac{1}{C}-\tfrac{1}{C+D}\] -
נמצא רווח סמך של $95 \%$ סביב $\log RR$:
\[\log RR \pm 1.96 \cdot \sqrt{\tfrac{1}{A}-\tfrac{1}{A+B}+\tfrac{1}{C}-\tfrac{1}{C+D}}\] - אם נרצה רווחי סמך אחרים נחליף את $1.96$ ב‑$Z$ המתאים.
דוגמה - טיטאניק
לוגריתם הסיכון היחסי של גברים (חשיפה) לעומת נשים (לא חשיפה):
\[\log RR = \log(2.926) \approx 1.073\]סטיית התקן היא:
\[\sigma_{\log RR} = \sqrt{\tfrac{1}{1364}+\tfrac{1}{126}-\tfrac{1}{1731}+\tfrac{1}{470}} \approx 0.077\]רווח סמך של $95 \%$ סביב $\log RR$:
\[\log RR \pm 1.96 \cdot \sigma_{\log RR} = 1.073 \pm 1.96 \cdot 0.077\]כלומר:
\[\boxed{\log RR \in [0.92, 1.22]}\]נחזור לסיכון היחסי על ידי העלאה בחזקה (אקספוננט):
\[RR \in [e^{0.92}, e^{1.22}] \approx [2.514, 3.404]\]חשוב לחזור מאקספוננט.
דוגמה 3 - COVID‑19 בהריון
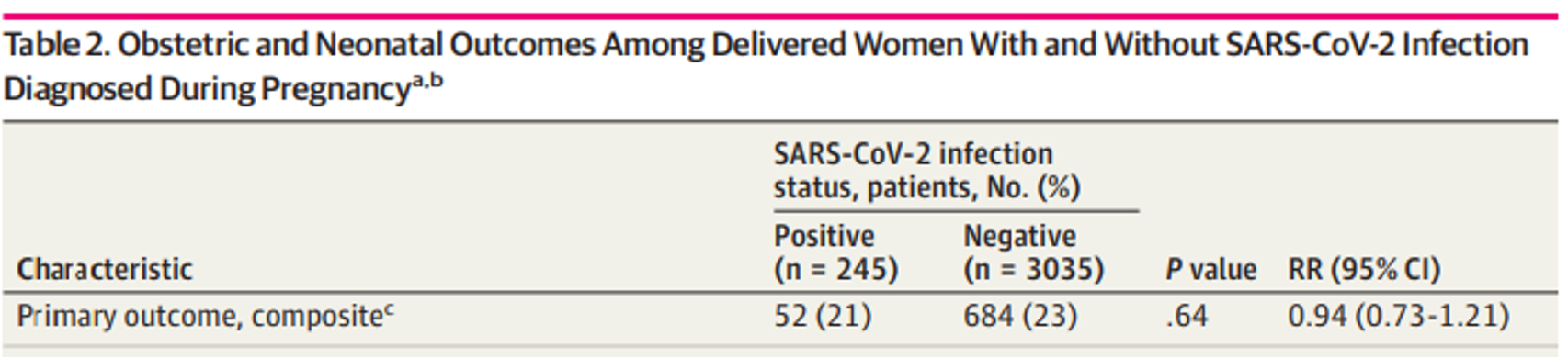
$RR = 0.94$, 95% CI [$0.63$, $1.33$] - אין עדות סטטיסטית לכך ש‑COVID-19 מעלה את הסיכון ל‑Outcome המשולב.
Odds Ratio (OR)
| פיתחו תוצא (מחלה) - כן | פיתחו תוצא - לא | odds | |
|---|---|---|---|
| חשופים | $A$ | $B$ | $\frac{A}{B}$ |
| לא חשופים | $C$ | $D$ | $\frac{C}{D}$ |
השונות של $\log(\text{OR})$ היא:
\[\text{Var}(\log(\text{OR})) = \frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}\]נמצא רווח סמך ברמת סמך של 95% עבור $\log(\text{OR})$:
\[\left[\log(\text{OR}) \pm 1.96 \cdot \sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}\right]\]הסטטיסטי הנורמלי הסטנדרטי הוא:
\[Z_0 = \frac{\ln(\hat{\text{OR}})}{\sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}}\]ולכן ערך ה-P-value הוא:
\[P(Z < Z_0)\]לכן, רווח הסמך ל-$\text{OR}$ ב-95% הוא:
\[e^{\left(\log(\text{OR}) \pm 1.96 \cdot \sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}\right)}\]רווחי סמך אחרים יימצאו באותה דרך — רק נחליף את 1.96 בערך z המתאים לרמת הסמך הרצויה.
הגדרת Odds
\[\text{odds} = \frac{\text{Happening}}{\text{Not happening}}\]נסמן ב-$P(O)$ את ההסתברות לתוצאה $O$.
\[\text{odds}(O)=\frac{P(O)}{1-P(O)}\]ה-odds שאם נבחר יום אקראי בשבוע נקבל יום של סופ”ש (שישי או שבת):
\[\text{odds}(P=2/7)=\frac{2/7}{1-2/7}=\frac{2/7}{5/7}=\boxed{\frac{2}{5}}\]לפעעמים גם נכתב כך:
\[2:5\]המשמעות:
- $\text{Odds} < 1$ יותר סביר שהמאורע לא יקרה מאשר יקרה.
- $\text{Odds} > 1$ יותר סביר שהמאורע יקרה מאשר לא יקרה.
- $\text{Odds} = 1$ סיכוי שווה.
נוסחת ה‑OR בטבלת 2×2
\[OR = \frac{A/B}{C/D}=\frac{AD}{BC}\]דוגמה - קוצר‑ראייה שוב
מתוך 100 גברים, 75 סובלים מקוצר ראיה והשאר לא:
\[\text{odds}(O\mid E) = \frac{75}{25} = 3\]עבור נשים:
\[\text{odds}(O\mid \bar E) = \frac{60}{40} = 1.5\]ה-Odds Ratio (OR) הוא היחס בין שני ה-odds:
\[OR = \frac{3}{1.5} = 2\]נקרא גם יחס הסיכויים או יחס צולב.
למה OR כל‑כך חשוב?
- נחשב בכל עיצוב מחקר (כולל מקרה-ביקורת).
- קל להשוות בין מאמרים.
- מופיע ברגרסיה לוגיסטית.
CI ל‑OR
\[\sigma^2\_{\log OR}=\frac{1}{A}+\frac{1}{B}+\frac{1}{C}+\frac{1}{D}\]בדיוק כמו RR, רק עם סכום הפוכים.
דוגמה - אחות גילברט
| מוות | אין מוות | סה”כ | |
|---|---|---|---|
| נוכחת | 40 A | 217 B | 257 |
| לא‑נוכחת | 34 C | 1350 D | 1384 |
\[OR = \frac{AD}{BC}\]\[OR=\frac{40\times1350}{217\times34}\approx7.3\]
כדי לבדוק רווח סמך ברמת מובהקות של $95\%$ נחשב את סטיית התקן:
\[\sigma^2\_{\log OR}=\frac{1}{40}+\frac{1}{217}+\frac{1}{34}+\frac{1}{1350}\approx0.053\] \[\sigma\_{\log OR}=\sqrt{0.053}\approx0.232\]נחשב את $Z$:
\[Z=\frac{\log(7.3)}{0.232}\approx9.4\]נחשב את ה-$p$-value:
import scipy.stats as stats
import numpy as np
or_val = 40 * 1350 / (217 * 34)
sigma_log_or = (1/40 + 1/217 + 1/34 + 1/1350) ** 0.5
z = np.log(or_val) / sigma_log_or
p_value = 1 - stats.norm.cdf(z) # One-tailed test
print(f"OR: {or_val:.4f}, Z: {z:.2f}, P-value: {p_value:.16f}")
# OR: 7.3191, Z: 8.14, P-value: 0.0000000000000002
CI 95% לא כולל 1 ← $P≈10^{-20}$ ← קשר סטטיסטי רצחני; עדיין לא הוכחת גורם (לי יצא $10^{-16}$).
טרנספורמציה לוגריתמית - מהות ולא קישוט
- התפלגויות RR ו‑OR ימניות וארוכות‑זנב.
- $\log$ מקרב אותן ← Z‑critical.
- טעות נפוצה: לשכוח לחזור מאקספוננט ← תקבלו CI שגוי סביב $\log RR$ ולא סביב RR.
קשר ≠ סיבתיות
“איך מבודדים גורם שלישי?” - שאלה מצוינת. תשובה קצרה: בנתונים תצפיתיים אי‑אפשר בלי הנחות. גם בניסוי אקראי - צריך להאמין שהאקראיות שוברת Confounders סמויים.
סיכום מהיר
| מדד | מתי משתמשים | יתרון | חסרון |
|---|---|---|---|
| RR | מחקרי עוקבה, ניסויי התערבות | פירוש אינטואיטיבי | דורש מעקב לפי חשיפה |
| OR | עוקבה, מקרה-ביקורת, לוגיסטית | ניתן לחישוב תמיד | פחות אינטואיטיבי |
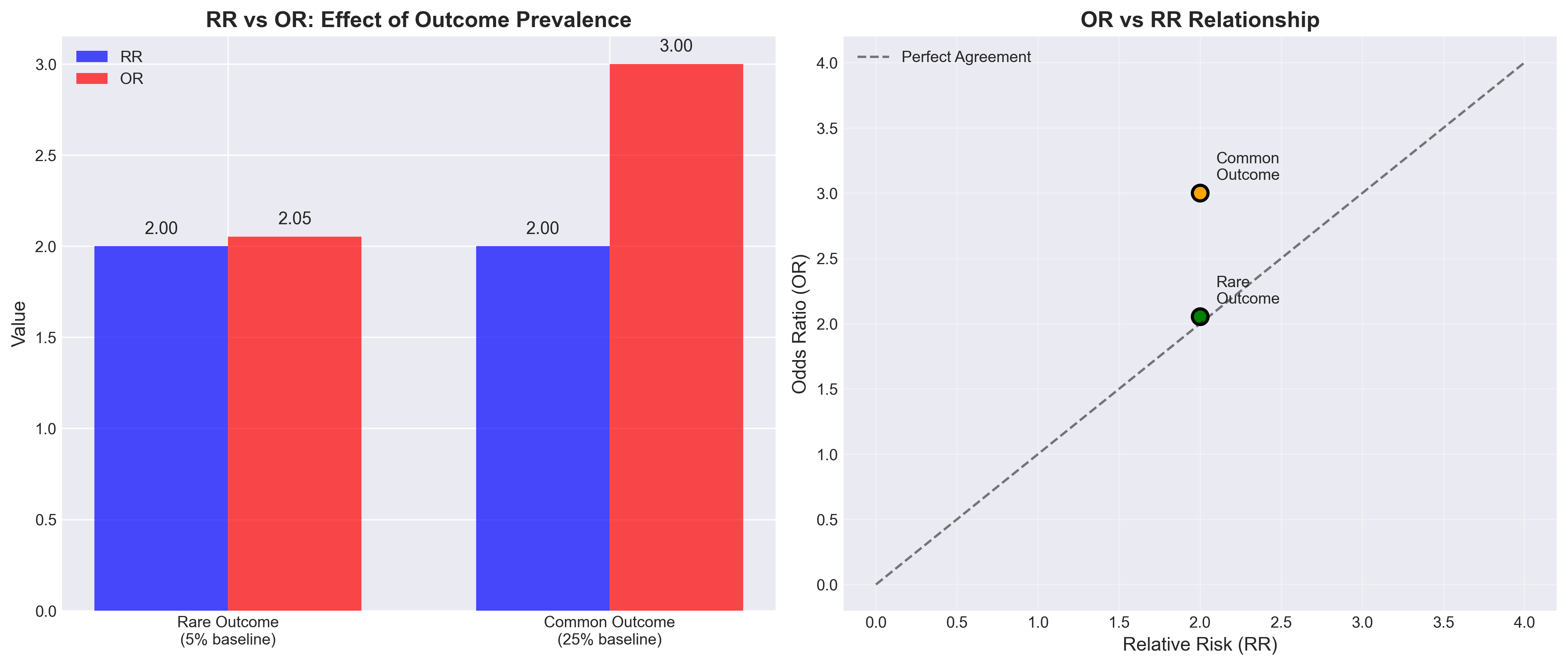
בשיעור הבא: Fisher Exact, וספוילר - $OR$ עם דגימות קטנות.
תרגול שאלות:
\[OR = \frac{AD}{BC} = \frac{72 \cdot 55}{219 \cdot 58} \approx \boxed{0.3117}\]שאלה 1 (קשר שלילי בין החשיפה לתוצאה) - (OR) מאמר על השפעת צריכת תה ירוק על הישנות סרטן הערמונית (Jian et al., 2004)
מחקר מקרה-ביקורת לבדיקת הקשר בין צריכת תה ירוק ובין סרטן הערמונית.
נדגמה קבוצה של חולים בסרטן הערמונית וקבוצה של בריאים. עבור כל משתתף נאסף מידע על אודות צריכת התה שלו.
להלן התוצאות:
Drink Green Tea? cases controls Yes 72 A 219 B No 58 C 55 D האם על פי המדגם ניתן להסיק ששתיית תה ירוק מגנה מפני סרטן הערמונית?
נחשב את $Z$:
\[Z = \frac{\log(0.3117)}{\sigma_{\log OR}}\] \[\sigma^2_{\log OR} = \frac{1}{72} + \frac{1}{219} + \frac{1}{58} + \frac{1}{55} \approx 0.0539\] \[\implies \sigma_{\log OR} = \sqrt{0.0539} \approx \boxed{0.2321}\]נציב את הערכים:
\[Z = \frac{\log(OR=-1.165)}{\sigma_{\log OR}} = \frac{-1.165}{0.2321} \approx -5.02\]נחשב עם פייתון:
import scipy.stats as stats
import numpy as np
or_val = 72 * 55 / (219 * 58)
sigma_log_or = (1/72 + 1/219 + 1/58 + 1/55) ** 0.5
z = (np.log(or_val)) / sigma_log_or
p_value = stats.norm.cdf(z)
print(f"OR: {or_val:.4f}, Z: {z:.2f}, P-value: {p_value:.7f}")
#OR: 0.3118, Z: -5.02, P-value: 0.0000003