תרגיםים:
- תרגיל 1: מספר כוחות פועלים על תיבה
- תרגיל 2: אדם מושך ארגז
- תרגיל 3: יחסי תאוצות
- תרגיל 4: חישוב כוח קבוע
תרגיל 1: מספר כוחות פועלים על תיבה
- מצא את הכח השקול, בהצגה קרטזית ופולארית.
- מה התאוצה הפועלת על התיבה אם משקלה 2 קילוגרם?
- מהו הכח המינימלי שיש להפעיל (גודל וכיוון) על מנת שהתיבה תעמוד במקום?
פתרון
חלק 1: מציאת הכח השקול
נתונים בשרטוט כוחות של 6N בזווית 60° מעל הציר האופקי, כוח של 6N בזווית 60° מתחת לציר האופקי, וכוח אנכי כלפי מטה של 4N.
תזכורת לזוויות טריגונומטריות חשובות:
\[\boxed{ \begin{aligned} \sin(60°) &= \frac{\sqrt{3}}{2} \approx 0.866 \\ \cos(60°) &= \frac{1}{2} = 0.5 \\ \tan(60°) &= \sqrt{3} \approx 1.732 \\ \sin(30°) &= \frac{1}{2} = 0.5 \\ \cos(30°) &= \frac{\sqrt{3}}{2} \approx 0.866 \end{aligned}}\]
נחשב את רכיבי הכוחות. בציר $x$ נשתמש ב-$\cos(60°)$ ובציר $y$ נשתמש ב-$\sin(60°)$.
ציר $x$:
\[\begin{aligned} F_{xT} &= \sum F_x = 6 \cdot \cos(60°) + 6 \cdot \cos(60°) \\[5pt] &= 6 \cdot \frac{1}{2} + 6 \cdot \frac{1}{2} \\[5pt] &= 6 \, \mathrm{[N]} \end{aligned}\]ציר $y$:
\[\begin{aligned} F_{yT} &= \sum F_y = 6 \cdot \sin(60°) - 6 \cdot \sin(60°) - 4 \\[5pt] &= 6 \cdot \frac{\sqrt{3}}{2} - 6 \cdot \frac{\sqrt{3}}{2} - 4 \\[5pt] &= 0 - 4 \\[5pt] &= -4 \, \mathrm{[N]} \end{aligned}\]לכן הכח השקול בצורה קרטזית הוא:
\[\boxed{\vec{F_T} = \left(6, -4\right)}\]הגודל של הכח השקול:
\[|\vec{F_T}| = \sqrt{6^2 + 4^2} = \sqrt{36 + 16} = \sqrt{52} \approx 7.21 \, \mathrm{[N]}\]מכאן האורך שלו, או הרדיוס, הוא:
\[\boxed{r = 7.21}\]הזווית של הכח השקול ביחס לציר ה-x החיובי:
\[\theta = \arctan\left(\frac{F_y}{F_x}\right) = \arctan\left(\frac{-4}{6}\right) \approx -33.7\]לכן הכח השקול בצורה פולרית הוא:
\[\boxed{\vec{F_T}(r, \theta) = (7.21, -33.7)}\]חלק 2: חישוב התאוצה
מהחוק השני של ניוטון:
\[\vec{a} = \frac{\vec{F_T}}{m} = \frac{[6, -4](N)}{2[kg]} = [3, -2] \mathrm{[\frac{m}{s^2}]}\]או בצורה פולרית:
\[\vec{a} = \frac{|\vec{F_T}|}{m} \angle \theta = \frac{7.21[N]}{2[kg]} \angle -33.7° = 3.61[\frac{m}{s^2}] \angle -33.7°\]חלק 3: הכח המינימלי להחזקת התיבה במקום
כדי שהתיבה תעמוד במקום, יש להפעיל כח שהוא שווה בגודלו והפוך בכיוונו לכח השקול:
\[\vec{F} = -\vec{F_T} = [-6, 4]\]או בצורה פולרית:
\[\vec{F} = 7.21\mathrm{[N]} \angle 146.3°\]
תרגיל 2: אדם מושך ארגז
אדם גורר ארגז שמשקלו 50 ק”ג. הוא מפעיל כוח של 196 ניוטון בזוויות שונות:
בהנחה שהארגז נגרר על גבי משטח חסר חיכוך והחבל אופקי, מה תהיה תאוצת הארגז? מה יהיה כוח הנורמל?
בהנחה שהארגז נגרר על גבי משטח חסר חיכוך והחבל בזווית של 32 מעלות לכיוון האופקי, מה תהיה תאוצת הארגז? מה יהיה כוח הנורמל?
עבור אותו הכוח מסעיף ב’, בהנחה שהארגז נע במהירות קבועה, מה גודלו של כוח החיכוך הפועל באופן מנוגד לכיוון התנועה?
פתרון
חלק א: החבל אופקי
במקרה זה, הכוח פועל רק בכיוון האופקי:
\[F_{Tx} = F = 196 \, \mathrm{[N]}\]הכוחות בכיוון האנכי מאוזנים (הארגז לא מתרומם או שוקע) $N=mg$.
התאוצה בכיוון האופקי:
\[a_x = \frac{F_{Tx}}{m} = \frac{196\mathrm{[N]}}{50\mathrm{[kg]}} = 3.92 \mathrm{[\frac{m}{s^2}]}\]חלק ב: החבל בזווית 32°
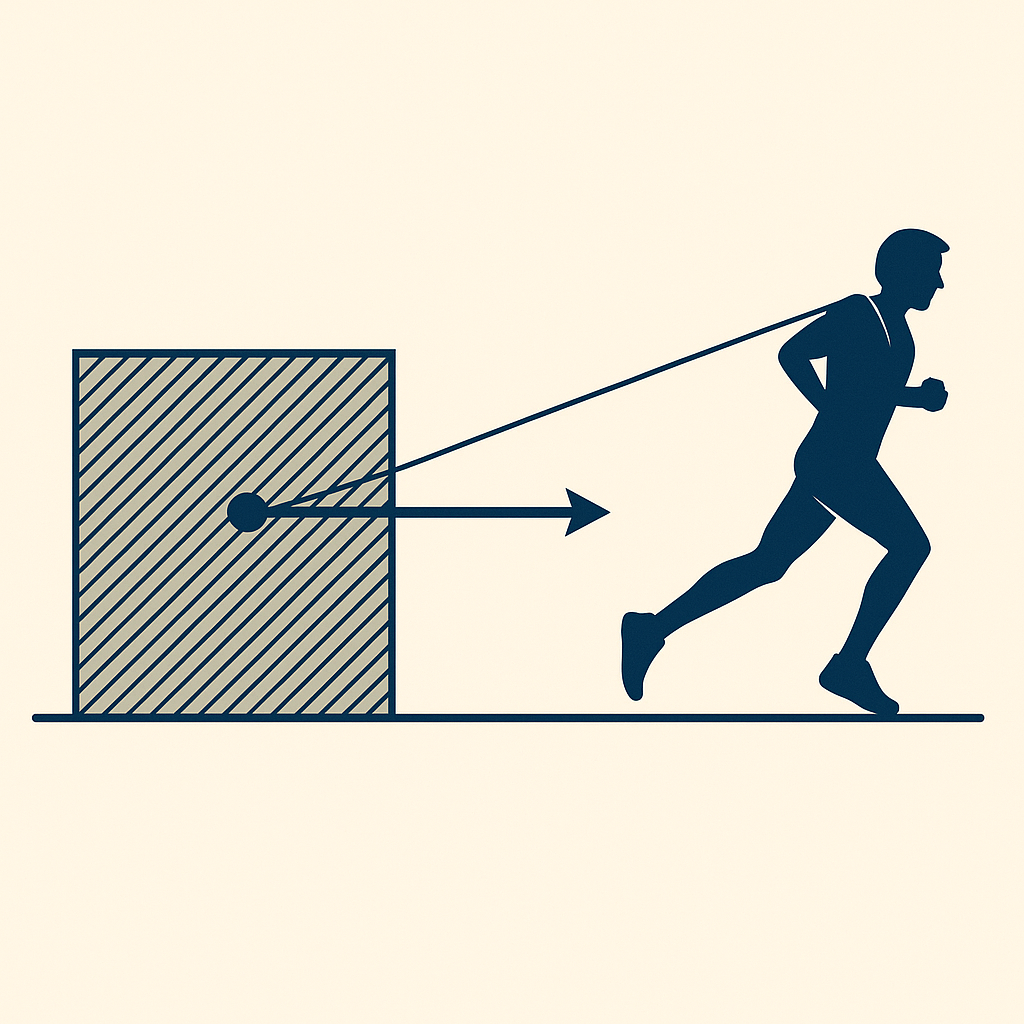
במקרה הזה הכוח מתפצל לרכיבים:
\[F_x = F \cdot \cos(32°) = 196 \cdot 0.848 = 166.2 \mathrm{[N]}\] \[F_y = F \cdot \sin(32°) = 196 \cdot 0.53 = 103.9 \mathrm{[N]}\]הכוחות בכיוון האנכי:
\[\begin{aligned} F_y + N - mg &= 0 \\ N &= mg - F_y \end{aligned}\]כאשר $m = 50 \, \mathrm{[kg]}$ ו-$g = 9.8 \, \mathrm{[\frac{m}{s^2}]}$, נקבל את הנורמאל:
\[\begin{aligned} F_y + N - mg &= 0 \\ N &= mg - F_y \\ N &= 50 \cdot 9.8 - 103.9 \\ N &= 490 - 103.9 \\ N &= 386.1 \, \mathrm{[N]} \end{aligned}\]התאוצה בכיוון האופקי:
\[a_x = \frac{F_x}{m} = \frac{166.2\mathrm{[N]}}{50\mathrm{[kg]}} = 3.32 \mathrm{[\frac{m}{s^2}]}\]חלק ג: תנועה במהירות קבועה
אם הארגז נע במהירות קבועה, אז התאוצה היא אפס, ולכן סך הכוחות האופקיים הוא אפס:
\[F_x - F_{friction} = 0 \Rightarrow F_{friction} = F_x = 166.2 \mathrm{[N]}\]תרגיל 3: יחסי תאוצות
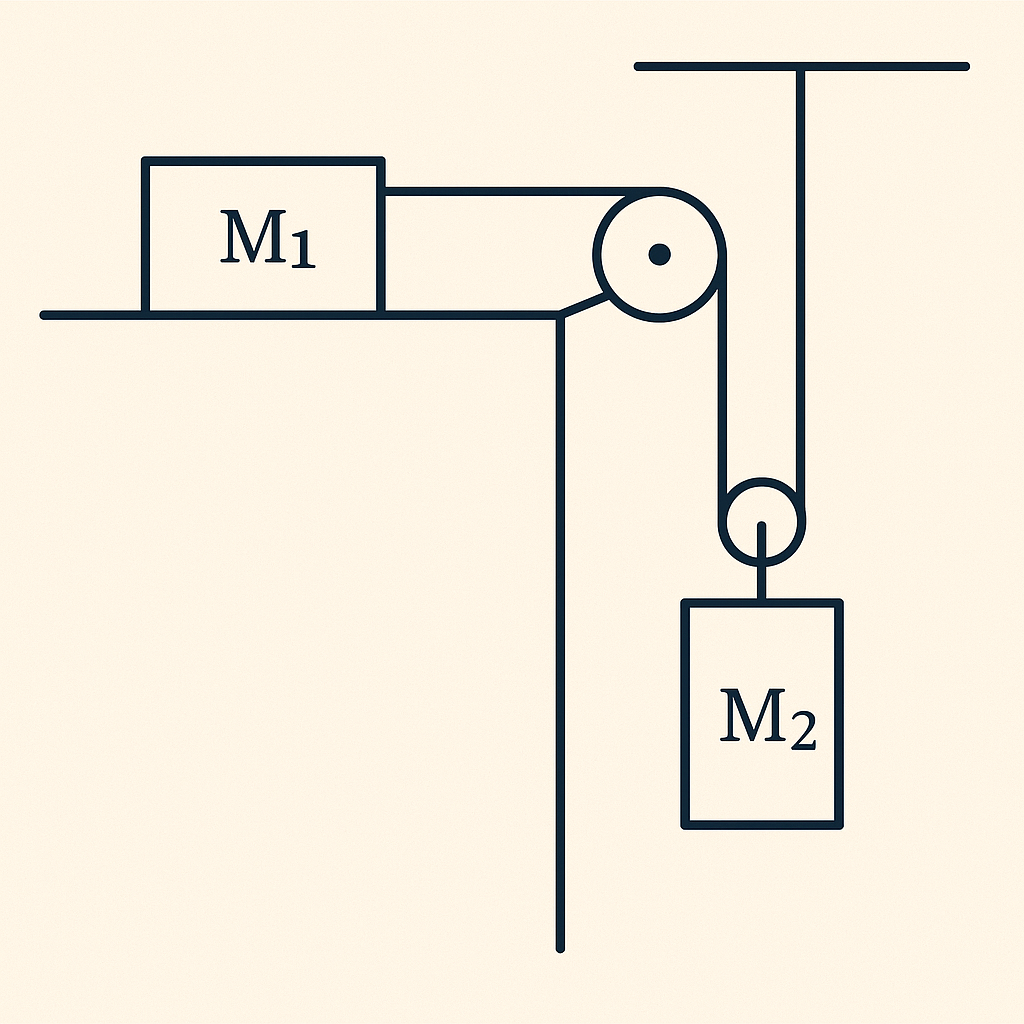
בתרגיל זה מוצגת מערכת גלגלות עם שני גופים בעלי מסות M1 ו-M2. מה יחס התאוצות של שני הגופים?
נבחן את היחס בין תזוזות ומהירויות במערכת:
\[v_{2y} = \frac{\Delta x}{\Delta t} = \frac{v_{1x}}{2}\]וכן את היחס בין התאוצות:
\[a_{2y} = \frac{\Delta v_{2y}}{\Delta t} = \frac{1}{2}a_{1x}\]כלומר:
\[\frac{a_{1x}}{a_{2y}} = 2\]
תרגיל 4: חישוב כוח קבוע
מצאו את הכוח הקבוע הדרוש להאיץ מסה של עשרה טון לאורך קו ישר ממהירות של 54 קמ״ש למהירות של 108 קמ״ש במשך חמש דקות.
פתרון
נשתמש בנוסחה $F = ma = m\frac{\Delta v}{\Delta t}$:
\[F = m \cdot \frac{v_2 - v_1}{\Delta t} = 10 \cdot 1000[kg] \cdot \frac{\frac{108 \cdot 1000[m]}{3600[s]} - \frac{54 \cdot 1000[m]}{3600[s]}}{5 \cdot 60[s]}\] \[= 10000[kg] \cdot \frac{30 - 15[\frac{m}{s}]}{300[s]} = 10000[kg] \cdot \frac{15[\frac{m}{s}]}{300[s]} = 500 \mathrm{[N]}\] דור פסקל