מה צריך לדעת בקינטיקה?
- לחשב קבועי זמנים - קבועי קצב של ריאקציות
- למצוא סדר של ריאקציה - כולל משוואת הקצב שלה
- לזהות סוג ריאקציה ממשוואת הקצב (סדר אפס, ראשון או שני)
- להשתמש במשוואות האינטגרטיביות
- לחשב ריכוזים בזמנים שונים
- מחציות הזמן
- לחשב אנרגיית אקטיבציה לריאקציות כימיות בהתאם לקבועים ולהשתנות שלהם עם הזמן
קינטיקה
קינטיקה כימית עוסקת במהירות של ריאקציות כימיות ובהשפעת גורמים שונים על קצב הריאקציה. במקום להתמקד רק בשאלה אם ריאקציה מתרחשת או מה האנרגיה המעורבת בה, קינטיקה חוקרת את המהירות שבה מתרחשים שינויים כימיים.
התחום כולל ניתוח פרמטרים כמו מהירות ריאקציה, וההשפעה של משתנים כמו טמפרטורה וריכוז על קצב הריאקציה. לדוגמה, ריאקציות מסוימות עשויות להתרחש תוך שניות, בעוד אחרות נמשכות שנים.
קינטיקה היא נושא מרכזי בתהליכים ביוכימיים, שבהם חשוב להבטיח שריאקציות יתרחשו בקצב מתאים. לדוגמה, פירוק חלבונים בכבד או עיכול מזון דורשים מהירות ריאקציה גבוהה. עיכובים בתהליכים אלה עלולים לגרום לבעיות רפואיות חמורות.
בתחום הביוכימיה קיים ענף ייחודי בשם “קינטיקה של ריאקציות אנזימטיות,” המתמקד במהירויות של תהליכים ביוכימיים. עם זאת, בפרק זה נתרכז בקינטיקה של ריאקציות כימיות כלליות.
קצב תגובה
\[a A + b B \rightarrow c C + d D \\\] \[\text{Rate of reaction} = \text{rate of disappearance of reactants} \\\] \[= \frac{-1}{a} \frac{d\left[A\right]}{dt} = \frac{-1}{b} \frac{d\left[B\right]}{dt} \\\] \[= \text{rate of appearance of products} \\\] \[= \frac{1}{c} \frac{d\left[C\right]}{dt} = \frac{1}{d} \frac{d\left[D\right]}{dt}\]ריאקציה לדוגמה:
\[\ce{2[Fe^3+](aq) + [Sn^2+](aq) -> 2[Fe^2+](aq) + [Sn^4+](aq)}\]בריאקציה זו מתרחש תהליך של חיזור חמצון: $\ce{[Fe^3+]}$ עובר חיזור ל-$\ce{[Fe^2+]}$, ו-$\ce{[Sn^2+]}$ עובר חמצון ל-$\ce{[Sn^4+]}$. החומרים בתחילת התהליך נקראים מגיבים, והתוצרים הסופיים הם תוצרים.
קצב התגובה מוגדר כשינוי בריכוז המגיבים או התוצרים כפונקציה של זמן. לדוגמה, אם ריכוז $\ce{[Fe^2+]}$ שנמצא לאחר $38.5 \, \text{s}$ הוא $0.001 \, \text{M}$, ניתן לחשב את קצב היצירה שלו:
\[\Delta \ce{[Fe^2+]} = 0.0010 \, \text{M} - 0 \, \text{M} = 0.0010 \, \text{M} \\\] \[\Delta t = 38.5 \, \text{s} \\\] \[\text{rate of formation of Fe}^{2+} = \frac{\Delta \ce{[Fe^2+]}}{\Delta t} = \frac{0.0010 \, \text{M}}{38.5 \, \text{s}} = 2.6 \times 10^{-5} \, \text{M s}^{-1}\]חשוב לציין שניתן לחשב את קצב התגובה גם באמצעות המגיבים. כמות המולים של $\ce{[Fe^3+]}$ שהתפרקה בתהליך זהה במקרה הזה לכמות המולים של $\ce{[Fe^2+]}$ שנוצרה. כלומר, $\Delta \ce{[Fe^3+]} = -0.0010 \, \text{M}$. בהצבה במשוואה מתקבל:
\[\frac{\Delta \ce{[Fe^3+]}}{\Delta t} = -\frac{-0.0010 \, \text{M}}{38.5 \, \text{s}} = -2.6 \times 10^{-5} \, \text{M s}^{-1}\]קצב השינוי של $\ce{[Fe^3+]}$ שלילי מפני שכמות החומר פוחתת לאורך זמן. לכן, ניתן לכתוב את קצב ההיעלמות שלו באופן הבא:
\[\text{rate of disappearance of Fe}^{3+} = -\frac{\Delta \ce{[Fe^3+]}}{\Delta t} = 2.6 \times 10^{-5} \, \text{M s}^{-1}\]כדי לקבל מספר חיובי אחד לכל התוצרים והמגיבים, הקצב מחושב לפי היחסים הסטויכיומטריים של המגיבים והתוצרים:
\[\text{Rate of reaction} = -\frac{1}{a} \frac{\Delta \left[A\right]}{\Delta t} = -\frac{1}{b} \frac{\Delta \left[B\right]}{\Delta t} = \frac{1}{c} \frac{\Delta \left[C\right]}{\Delta t} = \frac{1}{d} \frac{\Delta \left[D\right]}{\Delta t}\]באופן כללי, קצב התגובה מתקבל בעזרת השינוי במגיב $\text{A}$ באופן הבא:
\[r = -\frac{1}{a}\frac{\Delta \left[A\right]}{\Delta t}\]או בעזרת תוצר $\text{C}$:
\[r = \frac{1}{c}\frac{\Delta \left[C\right]}{\Delta t}\]לדוגמה, בריאקציה שהוצגה לעיל:
\[-\frac{\Delta \ce{[Sn^4+]}}{\Delta t} = -\frac{1}{2} \frac{\Delta \ce{[Fe^3+]}}{\Delta t}\] \[= \frac{1}{2} \frac{\Delta \ce{[Fe^2+]}}{\Delta t} = \frac{\Delta \ce{[Sn^2+]}}{\Delta t}\] \[= 1.3 \times 10^{-5} \, \text{M s}^{-1}\]מדידת קצב הריאקציה
התפרקות מי חמצן
\[\ce{H2O2(aq) -> H2O(l) + 1/2 O2(g)}\]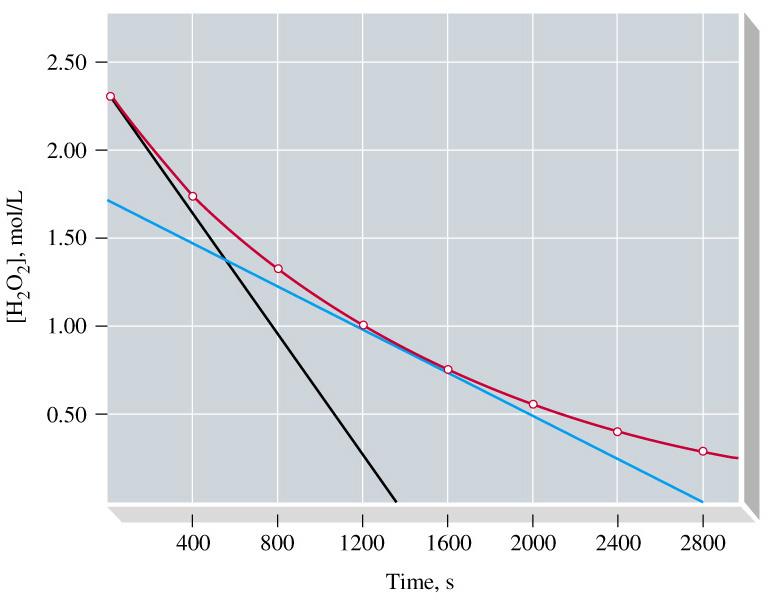
מי חמצן $\ce{H2O2}$ מתפרקים באופן טבעי למים $\ce{H2O}$ ולמולקולת חמצן $\ce{O2}$. ניתן לעקוב אחרי הריאקציה לאורך זמן בכמה דרכים:
- מעקב אחר היווצרות החמצן באמצעות איסוף החמצן ומדידת הכמות שלו.
- מעקב אחר היעלמות החמצן באמצעות תגובה עם פרמנגנט (אשלגן פרמנגנט).
הבחירה בין החלופות תלויה בנוחות. למשל, מעקב אחר העלמות של מי חמצן קלה יותר מאשר איסוף כל החמצן ומדידתו. להלן נתונים על התפרקות מי החמצן לאורך זמן:
| Time (s) | $\Delta t \, (\text{s})$ | $\ce{[H2O2]} \, (\text{M})$ | $\Delta \ce{[H2O2]} \, (\text{M})$ | Reaction Rate $\left(-\frac{\Delta \ce{[H2O2]}}{\Delta t} \right) \, (\text{M s}^{-1})$ |
|---|---|---|---|---|
| $\mathbf{0}$ | - | $\mathbf{2.32}$ | - | - |
| $\mathbf{400}$ | $400$ | $\mathbf{1.72}$ | $-0.60$ | $15.0 \times 10^{-4}$ |
| $\mathbf{800}$ | $400$ | $\mathbf{1.30}$ | $-0.42$ | $10.5 \times 10^{-4}$ |
| $\mathbf{1200}$ | $400$ | $\mathbf{0.98}$ | $-0.32$ | $8.0 \times 10^{-4}$ |
| $\mathbf{1600}$ | $400$ | $\mathbf{0.73}$ | $-0.25$ | $6.3 \times 10^{-4}$ |
| $\mathbf{2000}$ | $400$ | $\mathbf{0.54}$ | $-0.19$ | $4.8 \times 10^{-4}$ |
| $\mathbf{2400}$ | $400$ | $\mathbf{0.39}$ | $-0.15$ | $3.8 \times 10^{-4}$ |
| $\mathbf{2800}$ | $400$ | $\mathbf{0.28}$ | $-0.11$ | $2.8 \times 10^{-4}$ |
הקושי בקביעת הקצב הוא שהקצב משתנה לאורך התגובה. בתגובת מי החמצן, למשל, הקצב יורד במהירות גדולה בהתחלה ואז מתמתן: בהתחלה $2.32$ יורד ל-$2.00$, כלומר $0.32$, ואחרי זה $0.65$, וניכרת התמתנות. באופן כללי, הקצבים הראשוניים עשויים להיות גבוהים מאוד ולאחר מכן מתמתנים.
כדי לקבוע את הקצב, ניתן לקחת קו משיק לעקומה שמייצג את השינוי בריכוז כפונקציה של זמן. חישוב כזה נקרא קצב רגעי - instantaneous rate of reaction, עבור הרגע שבו נבחר להעביר את המשיק.
קצב ריאקציה דומה למד מהירות של מכונית, הקצב הרגעי אינו אחיד. כאשר מתקבלת ריאקציה, המטרה היא לקבוע לריאקציה קצב ממוצע.
בטבלה ניתן לראות שהקצבים אינם אחידים. משמעות הדבר היא השתנות ריכוז $C$ כפונקציה של זמן. הקצב הראשוני בהתחלה הוא השתנות מאוד מהירה - יורד ריכוז של $0.6$ ב-$400$ שניות, המקנה $15 \times 10^{-4}$. לעומת זאת אחרי $2,800$ שניות זה $0.1$.
לאחר קביעת קבוע קצב הריאקציה, ניתן לנבא את השינוי בריכוזים. קצב ריאקציה ומשוואות הקצב - מטרתם לנבא מה יהיו הריכוזים בדם, מה יהיו הריכוזים בריאקציה, ומה יהיו הריכוזים בכלי כפונקציה של זמן.
למשל, בהקשר רפואי, כאשר ניתנת תרופה לחולה, חשוב לדעת כיצד הריכוז שלה משתנה בדם של החולה לאורך זמן, ולחזות מה יהיה הריכוז אחרי 12 שעות או 18 שעות.
קינטיקה נלמדת כדי לקבל משוואת קצב, ומתוך משוואת הקצב לנבא ריכוזים בעתיד.
בספר מסבירים שהנקודה המתאימה לחישוב המשיק היא לאחר 1400 שניות, ומבחינים בין חישוב של קצב רגעי - instantaneous rate, כלומר קצב שמחושב ברגע מסוים, לבין חישוב קצב כללי או ממוצע.
קביעה ושימוש בקצבים ראשוניים
לעיתים נרצה לקבוע את הקצב הראשוני של התגובה - initial rate of reaction. הקצב הראשוני מתקבל בעזרת העברת משיק לגרף זמן-ריכוזים כאשר $t=0$.
לחלופין, ניתן למדוד את הריכוז של אחד המגיבים מוקדם ככל הניתן, לאורך פרק זמן קצר מאוד. השינוי הקצר הזה מתלכד עם המשיק לפרק זמן קצר לאחר $t=0$. בגרף על התפרקות מי החמצן אפשר לראות את ההתלכדות במשך 200 השניות הראשונות (הקו השחור).

דוגמה: קבע את (1) הקצב הראשוני של התגובה, ו-(2) את קצב התגובה ב-$t=100 \,\text{s}$
ניתן להניח שהקצב הראשוני קבוע למשך 100 שניות לפחות. נזכיר את התגובה:
\[\ce{H2O2 -> H2O + 1/2 O2}\]דרך אחת לחישוב הקצב הראשוני מתבססת על שיפוע המשיק בנקודה $t=0$ (הקו השחור בגרף). השיפוע מתקבל מהנוסחה הבאה:
\[t=0\,\ce{[H2O2]} = 2.32 \, \text{M}; \, t=1360\,\text{s} \, \ce{[H2O2]} = 0.\] \[\text{Initial rate of reaction} = -\left(\text{slope of tangent}\right) = -\frac{\left(0-2.32\right)\text{M}}{\left(1360-0\right)\text{s}} = \textcolor{red}{1.71 \times 10^{-3} \, \text{M s}^{-1}}\]לחלופין, ניתן לחשב את הקצב הראשוני לפי השינוי בריכוז מי החמצן במהלך 200 השניות הראשונות, לפי הנתונים בטבלת המדידות:
\[\ce{[H2O2]} = 2.32 \, \text{M at } t=0, \text{ and} \ce{[H2O2]} = 2.01 \, \text{M at } t=200 \, \text{s}\] \[\text{initial rate} = \frac{-\Delta \ce{[H2O2]}}{\Delta t} = -\frac{\left(2.01-2.32\right)\text{M}}{200\text{s}} = \textcolor{red}1.55 \times 10^{-3} \, \text{M s}^{-1}\]לחישוב קצב התגובה ב-$t=100 \, \text{s}$ משתמשים בנוסחה:
\[\text{rate of reaction} = \frac{-\Delta \ce{[H2O2]}}{\Delta t}\]בהנחה שקצב התגובה הוא $1.71 \times 10^{-3} \, \text{M s}^{-1}$ ובהצבת הנתונים כדי לבודד את הריכוז:
\[1.71 \times 10^{-3} \, \text{M s}^{-1} = \frac{-\ce{[H2O2]}}{100 \, \text{s}}\] \[-\left(1.71 \times 10^{-3} \, \text{M s}^{-1}\right) \left(100 \, \text{s}\right) = \ce{[H2O2]} = \ce{[H2O2]}_{t} - \ce{[H2O2]}_{0}\] \[-1.71 \times 10^{-1} \, \text{M} = \ce{[H2O2]}_{t} - 2.32 \, \text{M}\] \[\ce{[H2O2]}_{t} = 2.32 \, \text{M} - 1.71 \times 10^{-1} \, \text{M} = 2.15 \, \text{M}\]משוואת הקצב - The Rate Law
השפעת הריכוזים על קצב הריאקציה
\[a \, \text{A} + b \, \text{B} + \dots \rightarrow g \, \text{G} + h \, \text{H} + \dots\] \[\text{rate of reaction} = k[A]^m[B]^n+ \dots\] \[k = \text{Rate Constant}\] \[\text{Order of Reaction} = m + n\]משוואת הקצב שווה לקבוע הקצב $k$, כפול המולריות (ריכוז) של המגיבים בחזקת האקספוננטים המתאימים, לצורך העניין $\left[\text{A}\right]^{m} \, \left[B\right]^{n}$. לגבי כל ריאקציה יש לבצע ניסויים כדי למצוא את משוואת הקצב. היא תלויה בטמפרטורות ובסוגי הריאקציות.
$k$ נקרא קבוע קצב. הוא מקשר בין הריכוזים לזמן. ככל ש-$k$ גדול יותר, כך הריאקציה מהירה יותר.
$m$ ו-$n$ הם האקספוננטים בחזקות, והם נקראים סדר הריאקציה. הם משמשים לתיאור שני דברים: (1) אם $m=1$ נגיד שהריאקציה היא מסדר ראשון ב $\text{A}$, ואם $n=2$ נגיד שהריאקציה היא מסדר שני ב $\text{B}$. (2) סכום הסדרים $m+n$ קובע את סדר הריאקציה הכולל.
$m$ ו-$n$ יכולים להיות מספרים שלמים כמו $1, 2, 3, \dots$. הסכום שלהם הוא סדר הריאקציה הכולל. הלימוד יתמקד בריאקציות מסדר $0$, $1$, ו-$2$ בלבד.
הערה כללית על נגזרות
\[\lim_{\Delta t \to 0} \frac{-\Delta \left[ \text{A} \right]}{\Delta t} = \frac{d\left[ \text{A} \right]}{dt}\]בספר מסבירים שניתן להבחין בין קצב הריאקציה הכולל לקצב רגעי בעזרת החלפת $\Delta \left[ \text{A} \right]$ ו-$\Delta t$ במשוואה:
\[\frac{-d\left[ \text{A} \right]}{dt}\]הסימון $\Delta$, למעט בסימון השאיפה מתחת לגבול, מתייחס לקצב ממוצע, וסימון הנגזרת מתייחס לקצב רגעי.
שיטת הקצבים הראשונים למציאת משוואת הקצב
\[\ce{2 HgCl2(aq) + C2O4^{2-}(aq) -> 2 Cl- + 2 Hg^{2+} + 2 CO2(g)}\] \[\text{Rate of Reaction} = k \ce{[HgCl2]}^m \ce{[C2O4^{2-}]}^n\]קיימת שיטה הנקראת שיטת הקצבים הראשונים.
הריאקציה בדוגמה זו לוקחת פעמיים כסף כלוריד במים $\ce{(HgCl2)}$ פלוס אוקסלט $\ce{C2O4^{2-}}$ ליצירת כלוריד $\ce{(Cl-)}$, כספית $\ce{Hg^{2+}}$, ופחמן דו-חמצני $\ce{CO2}$. חשוב לציין שקצב הריאקציה תלוי בריכוזים, ולא במקדמים הסטויכיומטריים. כלומר, $m$ ו-$n$ אינם קשורים למקדמים הסטויכיומטריים בתגובה!
לצורך מציאת משוואת הקצב של הריאקציה:
\[\text{Rate} = k\ce{[HgCl2]}^m\ce{[C2O4^{2-}]}^n\]כאשר $k$ הוא קבוע הקצב, ו-$m$ ו-$n$ הם החזקות שאותן יש למצוא.
| Experiment | $\ce{[HgCl2]} \, (\text{M})$ | $\ce{[C2O4^{2-}]} \, (\text{M})$ | Initial Rate $\left(\text{M min}^{-1}\right)$ |
|---|---|---|---|
| 1 | $\ce{[HgCl2]}_1 = 0.105$ | $\ce{[C2O4^{2-}]}_1 = 0.15$ | $1.8$ |
| 2 | $\ce{[HgCl2]}_2 = 0.105$ | $\ce{[C2O4^{2-}]}_2 = 0.30$ | $7.1$ |
| 3 | $\ce{[HgCl2]}_3 = 0.052$ | $\ce{[C2O4^{2-}]}_3 = 0.30$ | $3.5$ |
על מנת למצוא את $m$ ו-$n$, משתמשים בניסויים. הניסוי הראשון מתבצע עם הריכוזים $\ce{[HgCl2]}_1 = 0.105$ ו-$\ce{[C2O4^{2-}]}_1 = 0.15$, והקצב ההתחלתי נמדד כ-$1.8 \, \text{M/min}$.
בניסוי השני, הריכוז של $\ce{HgCl2}$ נשמר קבוע, בעוד שריכוז $\ce{C2O4^{2-}}$ מוכפל.
יחס בין הקצבים בניסוי הראשון והשני:
\[\frac{\text{Rate}_2}{\text{Rate}_1} = \frac{\ce{[HgCl2]}_2^m\ce{[C2O4^{2-}]}_2^n}{k\ce{[HgCl2]}_1^m\ce{[C2O4^{2-}]}_1^n}\]מכיוון ש-$\ce{[HgCl2]}_2 = \ce{[HgCl2]}_1$, ניתן לפשט ל:
\[\frac{\text{Rate}_2}{\text{Rate}_1} = \frac{\ce{[C2O4^{2-}]}_2^n}{\ce{[C2O4^{2-}]}_1^n}\]\(\frac{7.1}{1.8} = \frac{0.30^n}{0.15^n} = 2^n\) לכן:
\[2^n = \frac{7.1}{1.8} \approx 4 \quad \Rightarrow \quad n = 2\]באותו אופן, משווים את הניסויים השני והשלישי כדי למצוא את $m$, כאשר $\ce{[C2O4^{2-}]}$ נשמר קבוע:
\[\frac{\text{Rate}_3}{\text{Rate}_2} = \frac{k\ce{[HgCl2]}_3^m\ce{[C2O4^{2-}]}_3^n}{k\ce{[HgCl2]}_2^m\ce{[C2O4^{2-}]}_2^n}\]מכיוון ש-$\ce{[C2O4^{2-}]}_3 = \ce{[C2O4^{2-}]}_2$, מתקבל:
\[\frac{\text{Rate}_3}{\text{Rate}_2} = \frac{\ce{[HgCl2]}_3^m}{\ce{[HgCl2]}_2^m}\] \[\frac{3.5}{7.1} = \frac{0.052^m}{0.105^m} = \left(\frac{0.052}{0.105}\right)^m\] \[0.5 = \left(\frac{1}{2}\right)^m \quad \Rightarrow \quad m = 1\]מכאן ניתן לקבוע את משוואת הקצב:
\[\text{Rate} = k\ce{[HgCl2]}^1\ce{[C2O4^{2-}]}^2\]הריאקציה היא מסדר ראשון ביחס ל-$\ce{HgCl2}$, מסדר שני ביחס ל-$\ce{C2O4^{2-}}$, וסדר כולל של 3.
ריאקציות מסדר אפס $\text{rate of reaction} = k$
בריאקציות מסדר אפס, האקספוננטים שווים לאפס. למשל, פירוק מלא של מגיב לתוצרים בקצב קבוע:
\[\ce{A -> products}\]בריאקציות כאלו הקצב אינו תלוי בריכוז המגיבים, אלא בגורם קבוע. משוואת הקצב היא:
\[\text{rate of reaction} = k\ce{[A]}^0 = k = \text{constant}\]מתקיים:
- גרף הזמן-ריכוזים הוא קו ישר עם שיפוע שלילי
- קצב התגובה שווה ל-$k$ ונשאר קבוע לאורך התגובה, הוא הנגדי לשיפוע הקו הזה
- היחידות של $k$ הן בהתאם ליחידות הזמן של הריאקציה: $\text{mol L}^{-1}$ כמו $\text{ mol M s}^{-1}$
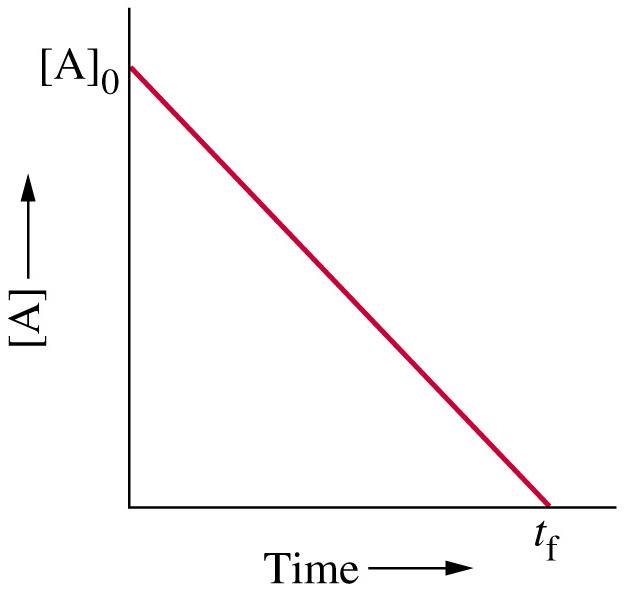
משוואת הקצב האינטגרטיבית של ריאקציות מסדר אפס
משוואה חשובה נוספת פרט למשוואת הקצב, היא משוואת הקצב האינטגרטיבית. המשוואה הזו מייצגת את האינטגרל של הריכוז של המגיב בזמן. בגלל שהגרף של ריאקציות מסדר כזה הן קו ישר יורד $\left(y=mx+n\right)$, המשוואה האינטגרטיבית היא:
\[\ce{[A]}_t = - kt + \ce{[A]}_0\]כאשר
- $y=\ce{[A]}_t$ הוא ריכוז המגיב
- $m=-k$ הוא השיפוע של הקו, שמתקבל מהאינטגרל של המשוואה $\left( \int -k \, dt = -kt \right)$
- $x=t$ הוא זמן הריאקציה
- $n=\ce{[A]}_0$ הוא הריכוז ההתחלתי של המגיב בזמן $t=0$
זמן מחצית החיים של תגובות מסדר אפס $t_{1/2} = \frac{\ce{[A]}_0}{2ak}$
עבור תגובות מסדר אפס, זמן מחצית החיים (ראו הסבר להלן) תלוי ישירות בריכוז ההתחלתי ונוסחת החישוב היא:
\(t_{1/2} = \frac{\ce{[A]}_0}{2k}\) t_{1/2} = \frac{\ce{[A]}_0}{2k} $$
ריאקציות מסדר ראשון $\text{rate of reaction} = k\left[\text{A}\right]$
משוואות שבהן סכום האקספוננטים הוא אחד. הריאקציות מסוג זה כוללות פירוק של חומר אחד לתוצרים, כדוגמת הפירוק של מי חמצן לחמצן ומים:
\[\ce{H2O2(aq) -> H2O(l) + 1/2 O2(g)}\]קצב הריאקציה במקרה זה תלוי בריכוז של $\ce{H2O2}$ בחזקת אחת:
\[\text{Rate} = k\ce{[H2O2]}^1\]באופן כללי:
\[\text{rate of reaction} = -\frac{\Delta\ce{[A]}}{\Delta t} = k\ce{[A]}\]ניתן להגיע למסקנה זו באמצעות שיטת הקצבים הראשוניים או בדרכים אחרות.
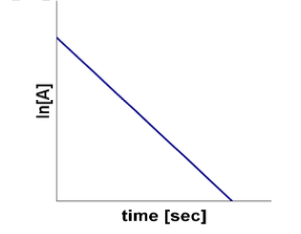
משוואת הקצב האינטגרטיבית של ריאקציות מסדר ראשון
המשוואה האינטגרטיבית נובעת מהאינטגרל של משוואת הקצב:
\[\ln \frac{\ce{[A]}_t}{\ce{[A]}_0} = -kt\]או:
\[\underbrace{\ln\ce{[A]}_t}_{y} = \underbrace{\left(-k\right)t}_{m\cdot x} + \underbrace{\ln\ce{[A]}_0}_{b}\]כדי למצוא ריכוז של מגיב בזמן $t$, אפשר להעלות את שני הצדדים ב-$e$:
\[\ce{[A]}_t = e^{-kt} \ce{[A]}_0\]שימוש במשוואת הקצב האינטגרטיבית של ריאקציות מסדר ראשון
מי חמצן $\ce{H2O2}$ בריכוז ראשוני של 2.32 מולר מתפרקים.
לחישוב $\ce{[H2O2]}$ לאחר 1200 שניות, כאשר $k = 7.30 \times 10^{-4} \, \text{s}^{-1}$, נשתמש במשוואה האינטגרטיבית עם הנתונים:
\[\ce{[H2O2]}_0 = 2.32 \, \text{M}\] \[k = 7.30 \times 10^{-4} \, \text{s}^{-1}\] \[t = 1200 \, \text{s}\] \[\ce{[H2O2]}_t = ?\]נציב את הנתונים במשוואה:
\[\ln\ce{[H2O2]}_t = -kt + \ln\ce{[H2O2]}_0\] \[= -\left(7.30 \times 10^{-4} \, \text{s}^{-1}\right) \left(1200 \, \text{s}\right) + \ln\left(2.32 \, \text{M}\right)\] \[= -0.876 + 0.841 = -0.035\]מכאן:
\[\ce{[H2O2]}_t = e^{-0.035} = 0.966 \, \text{M}\]דרך נוספת לזיהוי ריאקציות מסדר ראשון היא לשרטט את הלוגריתם הטבעי של גרף הזמן-ריכוז של התגובה ולבחון האם מתקבל קו ישר.
ניתן גם להציב ערכים עבור נקודות זמן שונות במשוואה האינטגרטיבית ולפתור עבור $k$.
במקום לעבוד עם מולריות $\text{(M)}$, לעיתים ניתן לעבוד ישירות עם מסת המגיבים או עם שברי מגיבים שהתפרקו - גישה המובילה לעקרון של מחצית החיים.
זמן מחצית החיים
חצי חיים של ריאקציה מסדר ראשון $t_{1/2} = \frac{0.693}{k}$
חצי החיים של ריאקציה מסדר ראשון מוגדר כזמן שבו ריכוז המגיב יורד לחצי מערכו ההתחלתי:
\[t_{1/2} = \frac{\ln 2}{k} = \frac{0.693}{k}\]עבור ריאקציות מסדר ראשון, ערכי מחצית חיים הם קבועים ואינם תלויים בריכוז ההתחלתי $\ce{[A]}_0$ (בניגוד לריאקציות מסדר אפס או מסדר שני).
לדוגמה, זמן מחצית החיים לפירוק של מי חמצן מתקבל על-ידי:
\[t_{1/2} = \frac{0.693}{k} = \frac{0.693}{7.30 \times 10^{-4}\, \text{s}^{-1}} = 949 \, \text{s}\]חשוב לציין שהיעדר התלות בריכוז המגיב משפיע גם על המשך התגובה: בתום זמן מחצית חיים נוסף יהיה ריכוז המגיב $\ce{[A]}$ חצי מהערך הקודם:
\[\ce{[A]}_{t_{1/2}} = \frac{1}{2} \ce{[A]}_{0}\]לאחר שני זמני מחצית חיים - כלומר $t=2t_{1/2}$ - הריכוז יהיה $\frac{1}{4} \ce{[A]}_0$, וכן הלאה:
\[\left\{ \ce{[A]}_{3t_{1/2}} = \frac{1}{8}\ce{[A]}_0, \ce{[A]}_{4t_{1/2}} = \frac{1}{16}\ce{[A]}_0, \dots \right \}\]תכונת מחצית החיים הקבועה משמשת כמבחן לזיהוי ריאקציות מסדר ראשון. למשל, בפירוק מי חמצן מריכוז התחלתי $\ce{[H2O2]}_0 = 2.32 \, \text{M}$, ניתן לבחון מתי הריכוז יהיה $\ce{[H2O2]} = 1.16 \, \text{M}, \, 0.58 \, \text{M}$ וכן הלאה.
השפעת המקדמים הסטויכיומטריים
עבור מקדמים סטויכיומטריים שונים, ניתן להכליל את המשוואות:
\[\text{rate} = - \frac{1}{a} \frac{\Delta\ce{[A]}}{\Delta t} = k\ce{[A]}\] \[\Rightarrow \frac{\Delta \ce{[A]}}{\Delta t} = a \cdot k \ce{[A]}\]המשוואה האינטגרטיבית וזמן מחצית החיים מותאמים בהתאם:
\[\ln \ce{[A]}_t = -a \cdot k \cdot t + \ln \ce{[A]}_0\] \[t_{1/2} = \frac{0.693}{a \cdot k}\]חשוב להדגיש כי המקדמים הסטויכיומטריים לא משפיעים על צורת משוואת הקצב, כלומר על $r=k\ce{[A]}^a\ce{[B]}^b\ce{[C]}^c$.
מגיבים גזים $\ln \frac{\left(P\right)_t}{\left(P\right)_0} = -kt$
\[\ce{(CH3)3COOC(CH3)3 -> 2 C3H6O + C2H6}\]התגובה המופיעה היא של DTBP, המתפרק לאצטון ואתן:
\[\ce{C8H18O2(g) -> 2 CH3COCH3(g) + CH3CH3(g)}\]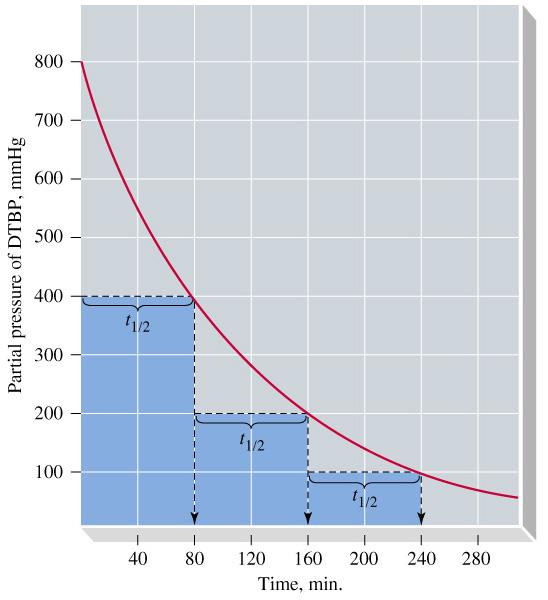
בתגובות של גזים ניתן לעבוד עם לחצים במקום עם מולריות:
\[\ln \frac{\left(P\right)_t}{\left(P\right)_0} = -kt\]דוגמה: עבור תגובה שבה הלחץ ההתחלתי הוא 800 mmHg וזמן מחצית החיים $t_{1/2} = 80$ דקות, קבוע הקצב יהיה:
\[k = \frac{0.693}{t_{1/2}} = \frac{0.693}{80} = 8.7 \times 10^{-3} \text{ min}^{-1}\]לחישוב הזמן הדרוש עד שהלחץ ירד ל-50 mmHg:
\[t = 4 \times t_{1/2} = 4 \times 80 = 320 \text{ minutes}\]חישוב לחץ חלקי
בתגובות עם גזים, הלחץ הכולל מחושב כפונקציה של זמן. בכל זמן $t$, הלחץ הכולל הוא:
\[\left(P_{\text{total}}\right)_t = \left(P_{\text{reactant}}\right)_t + \left(P_{\text{products}}\right)_t\]בתגובת ההתפרקות של DTBP:
\[\ce{C8H18O2(g) -> 2 CH3COCH3(g) + CH3CH3(g)}\]הלחץ הכולל מחושב:
\[\left(P_{\text{total}}\right)_t = \left(P_{\text{DTBP}}\right)_t + 2\left(P_{\text{acetone}}\right)_t + \left(P_{\text{ethane}}\right)_t\]עבור לחץ ראשוני $P_0$ של DTBP, הלחץ החלקי של DTBP הוא $P_{\text{DTBP}} = \left(P_0 - P_{\text{ethane}} \right)$ מאחר שעל כל מול DTBP שמתפרק נוצר מול אחד של אתן. מכאן, הלחץ החלקי של אצטון הוא $P_{\text{acetone}} = 2P_{\text{ethane}}$.
בהתאם למקדמים הסטויכיומטריים, הלחץ הכולל הוא:
\[\left(P_{\text{total}}\right)_t = \left(P_0 - \left(P_{\text{ethane}}\right)_t\right) + 2P_{\text{ethane}} + P_{\text{ethane}} = P_0 + 2P_{\text{ethane}}\]וכן:
\[\left(P_{\text{acetone}}\right)_t = \frac{P_{\text{total}} - P_0}{2}\]מכאן:
\[P_{\text{DTBP}} = \left(P_0 - P_{\text{ethane}} \right) = \frac{2P_0 - \left(P_{\text{total}} - P_0 \right)}{2} = \frac{3P_0 - P_{\text{total}}}{2}\] דור פסקל