מבוא
שיעור זה עוסק בשדות סקלריים ווקטוריים ובאופרטורים דיפרנציאליים הפועלים עליהם. נושאים אלו מהווים את הבסיס המתמטי להבנת תופעות אלקטרומגנטיות ופיזיקליות אחרות.
שדות (Fields)
הגדרה
שדה הוא ישות מתמטית שממלאת את המרחב או את המישור, ומקבלת ערך בכל נקודה ונקודה.
שדה סקלרי (Scalar Field)
הגדרה: שדה שמצמיד לכל נקודה במרחב מספר (סקלר).
סימון: $\phi(x,y,z)$ או $\phi(\vec{r})$
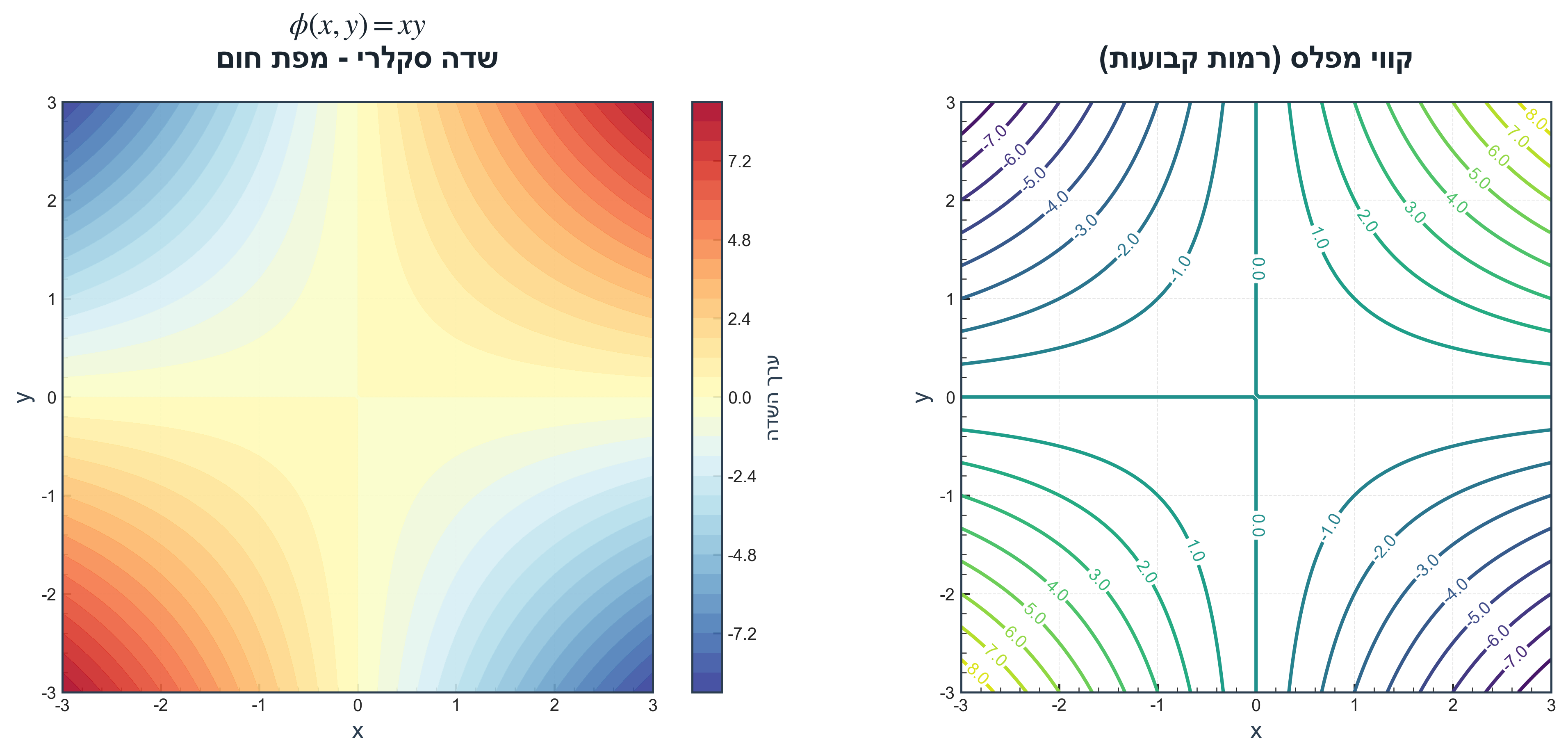
דוגמה: טמפרטורה בחדר - לכל נקודה $(x,y,z)$ בחדר מתאים ערך טמפרטורה.
דוגמאות מתמטיות:
-
שדה שמתאים לכל נקודה סקאלר שהוא מכפלת איברי הווקטור:
\[\phi(x,y,z) = xyz\] -
שדה שמתאים לכל נקודה סכום של רכיב ליניארי ואקספוננציאלי:
\[\chi(x,y,z) = x + e^{yz}\]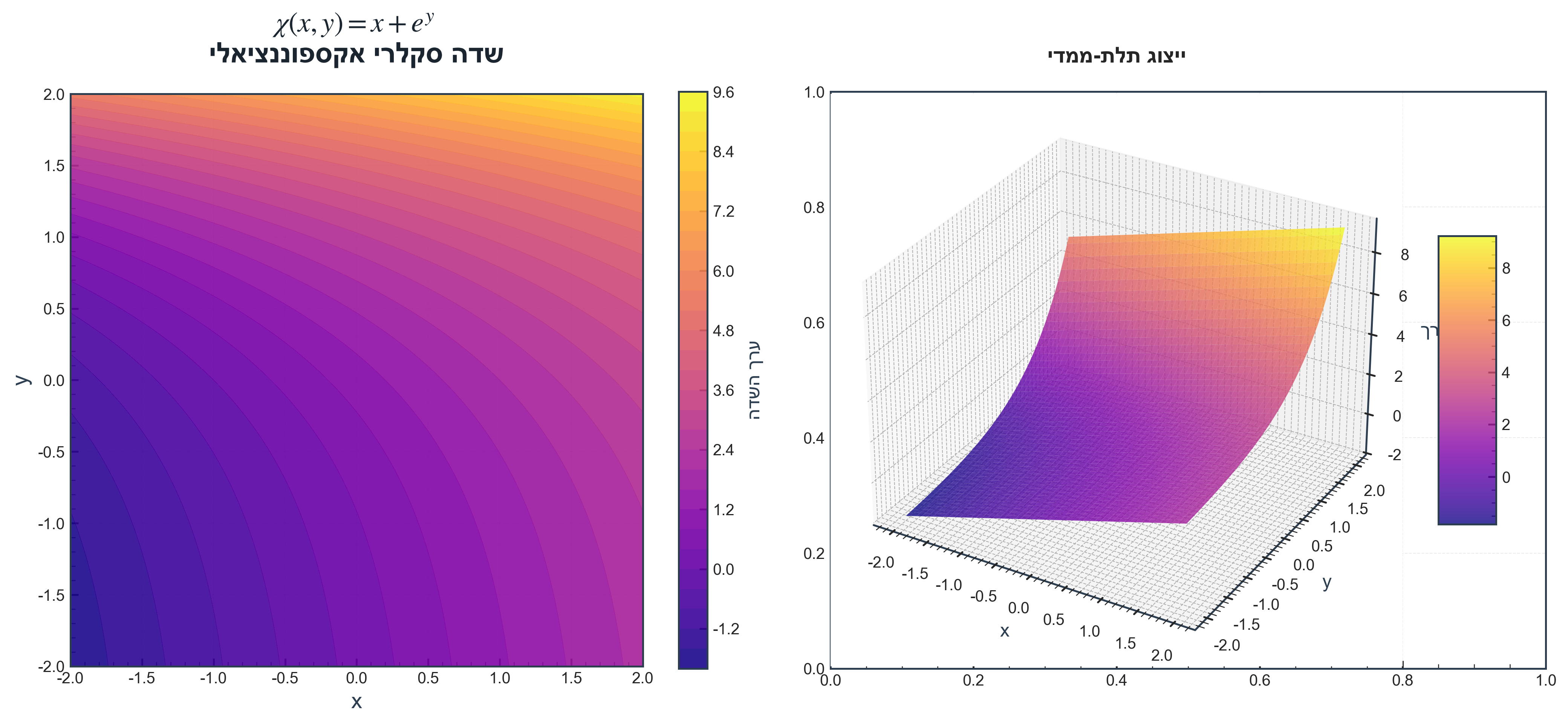
שדה וקטורי (Vector Field)
הגדרה: שדה שמצמיד לכל נקודה במרחב וקטור.
סימון: $\vec{v}(x,y,z)$ או $\vec{v}(\vec{r})$
דוגמאות:
- מהירות וכיוון זרימת אוויר בחדר
- כיוון השיערות על הקרקפת (שדה רדיאלי)
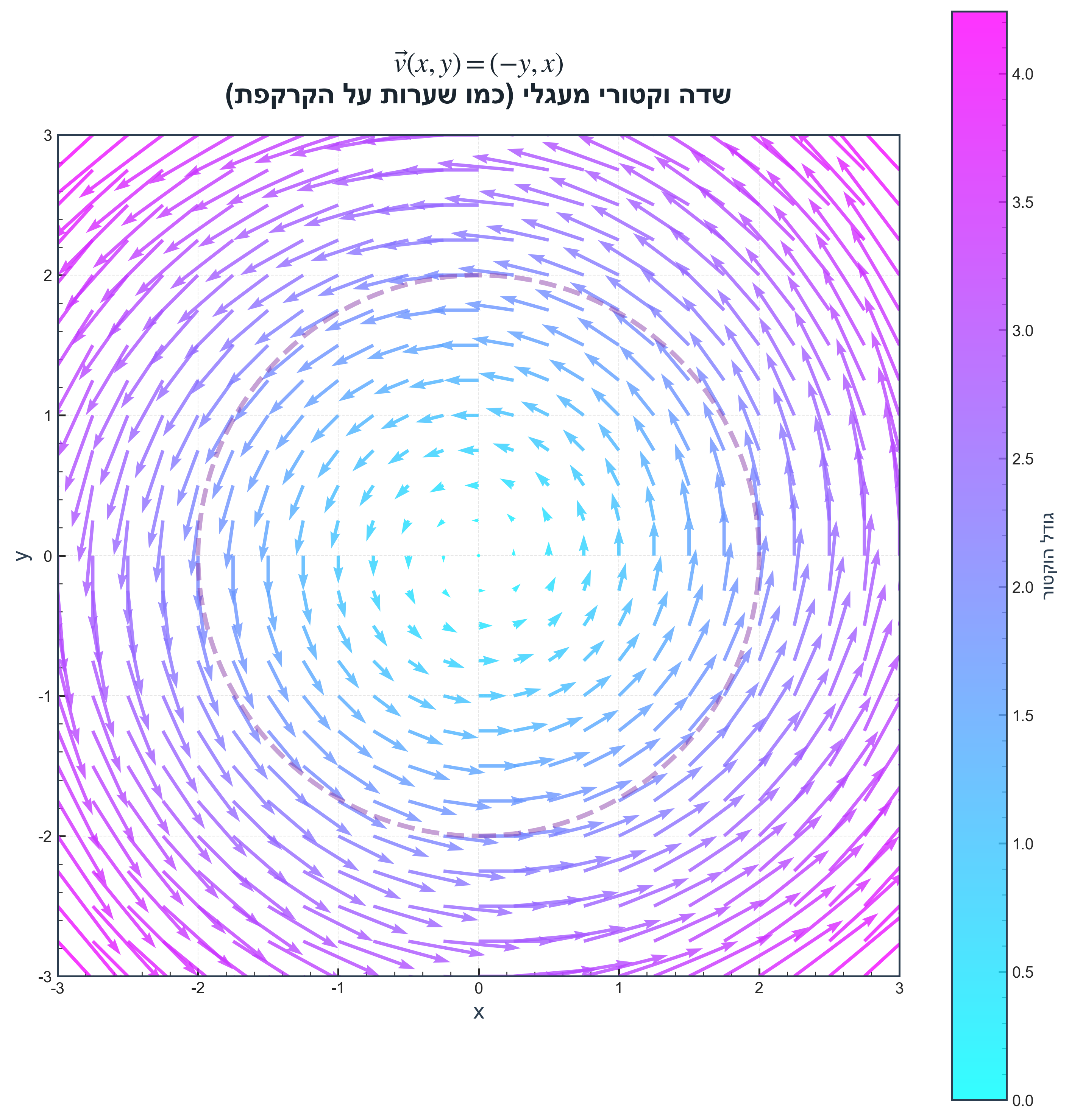
ייצוג מתמטי:
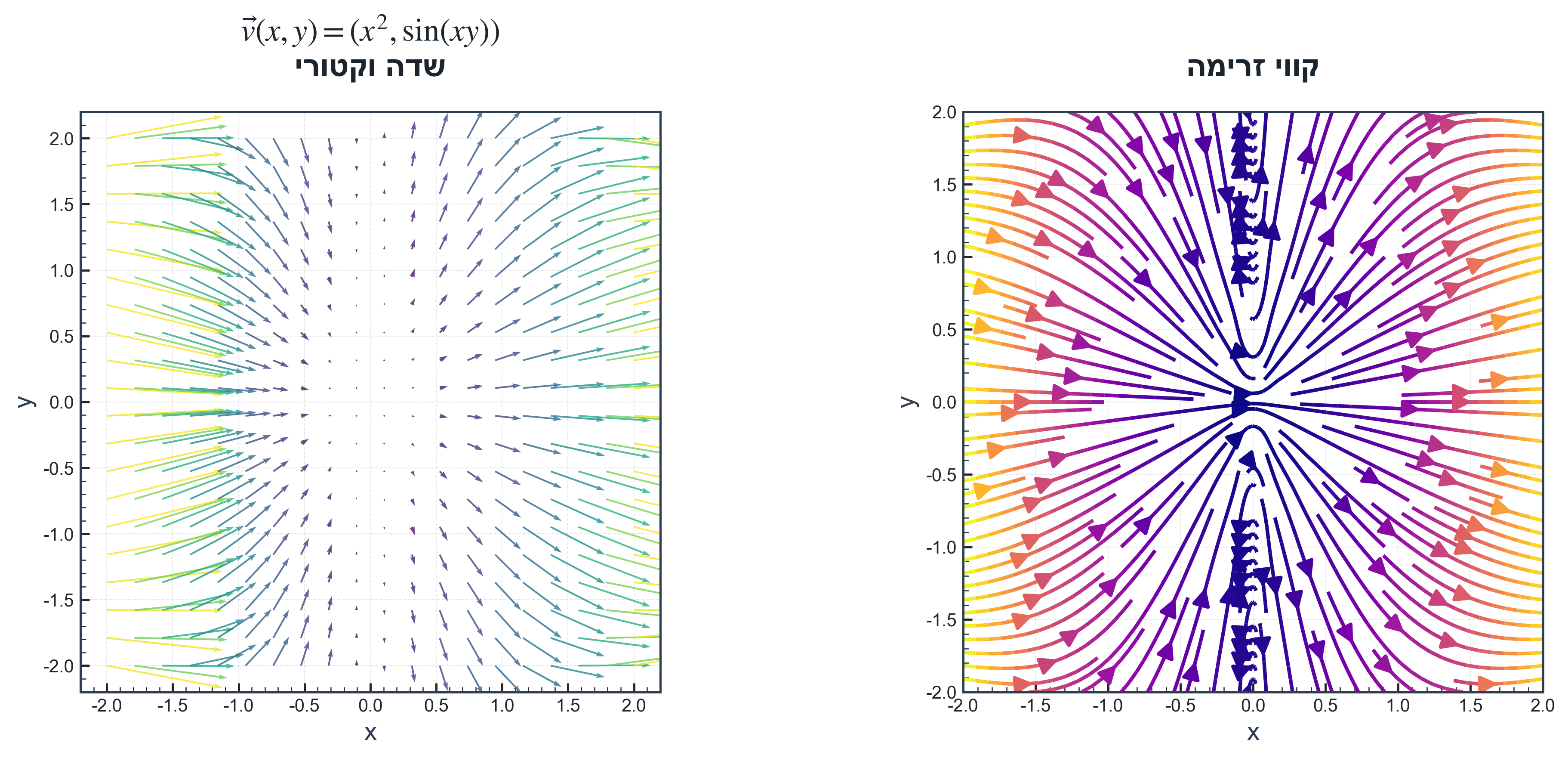
\[\vec{v}(x,y,z) = v_x(x,y,z)\hat{x} + v_y(x,y,z)\hat{y} + v_z(x,y,z)\hat{z}\]דוגמה קונקרטית:
\[\vec{v}(x,y,z) = x^2\hat{x} + \sin(xy)\hat{y} + e^{xyz}\hat{z}\]כאשר:
- $v_x(x,y,z) = x^2$
- $v_y(x,y,z) = \sin(xy)$
- $v_z(x,y,z) = e^{xyz}$
אופרטורים דיפרנציאליים
אופרטור הגרדיאנט (Gradient/Del/Nabla)
הגדרה: אופרטור וקטורי המסומן ב-$\nabla$ (נבלא), $\text{grad}$ או $\text{del}$:
\[\vec{\nabla} = \hat{x}\frac{\partial}{\partial x} + \hat{y}\frac{\partial}{\partial y} + \hat{z}\frac{\partial}{\partial z}\]פעולה על שדה סקלרי (על פונקציה $\phi(x,y,z)$, להבנתי):
\[\vec{\nabla}\phi = \hat{x}\frac{\partial\phi}{\partial x} + \hat{y}\frac{\partial\phi}{\partial y} + \hat{z}\frac{\partial\phi}{\partial z}\]תוצאה: שדה וקטורי
דוגמאות:
-
עבור $\phi(x,y,z) = xyz$:
\[\vec{\nabla}\phi = \hat{x}(yz) + \hat{y}(xz) + \hat{z}(xy)\]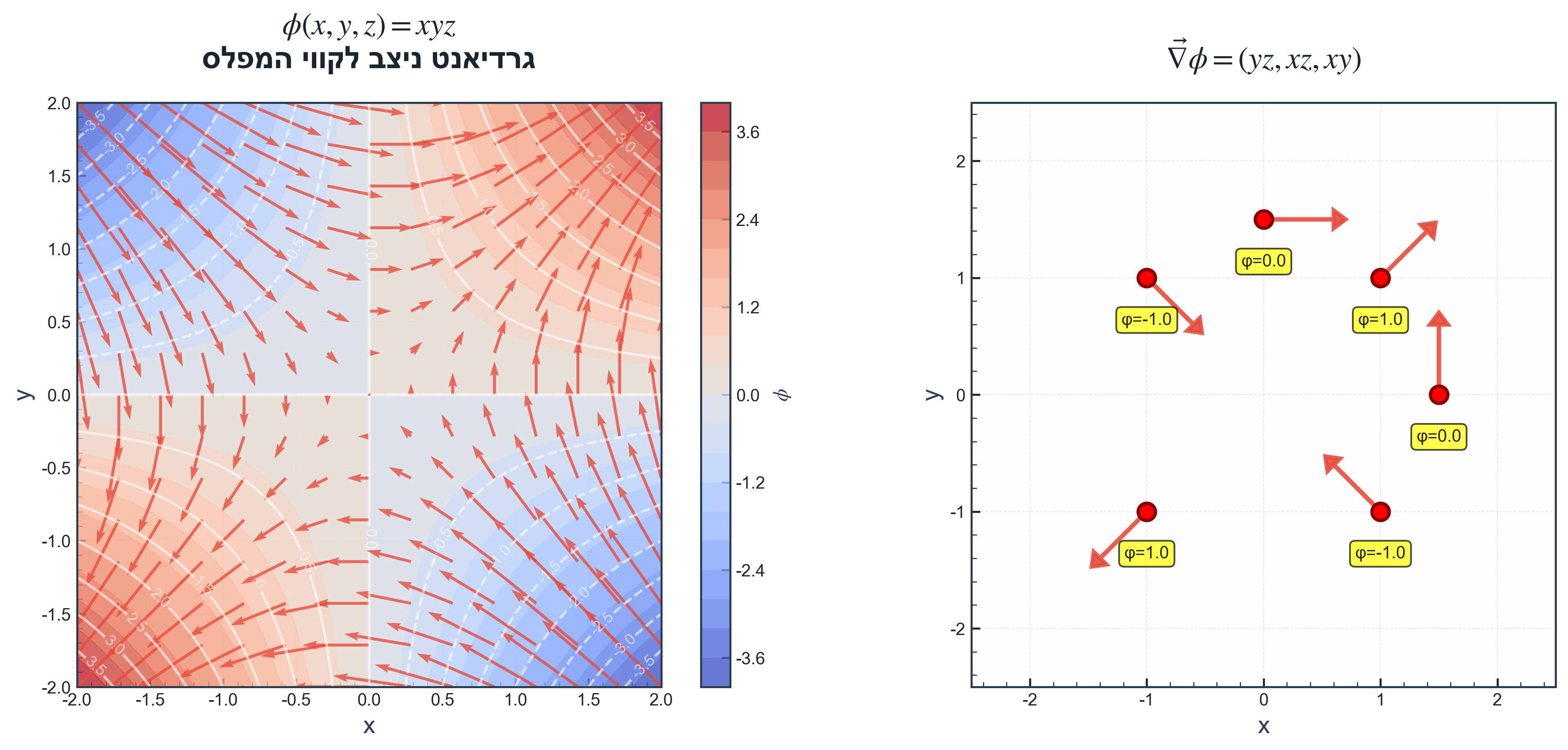
-
עבור $\chi(x,y,z) = x + e^{yz}$:
\[\vec{\nabla}\chi = \hat{x} + \hat{y}(ze^{yz}) + \hat{z}(ye^{yz})\]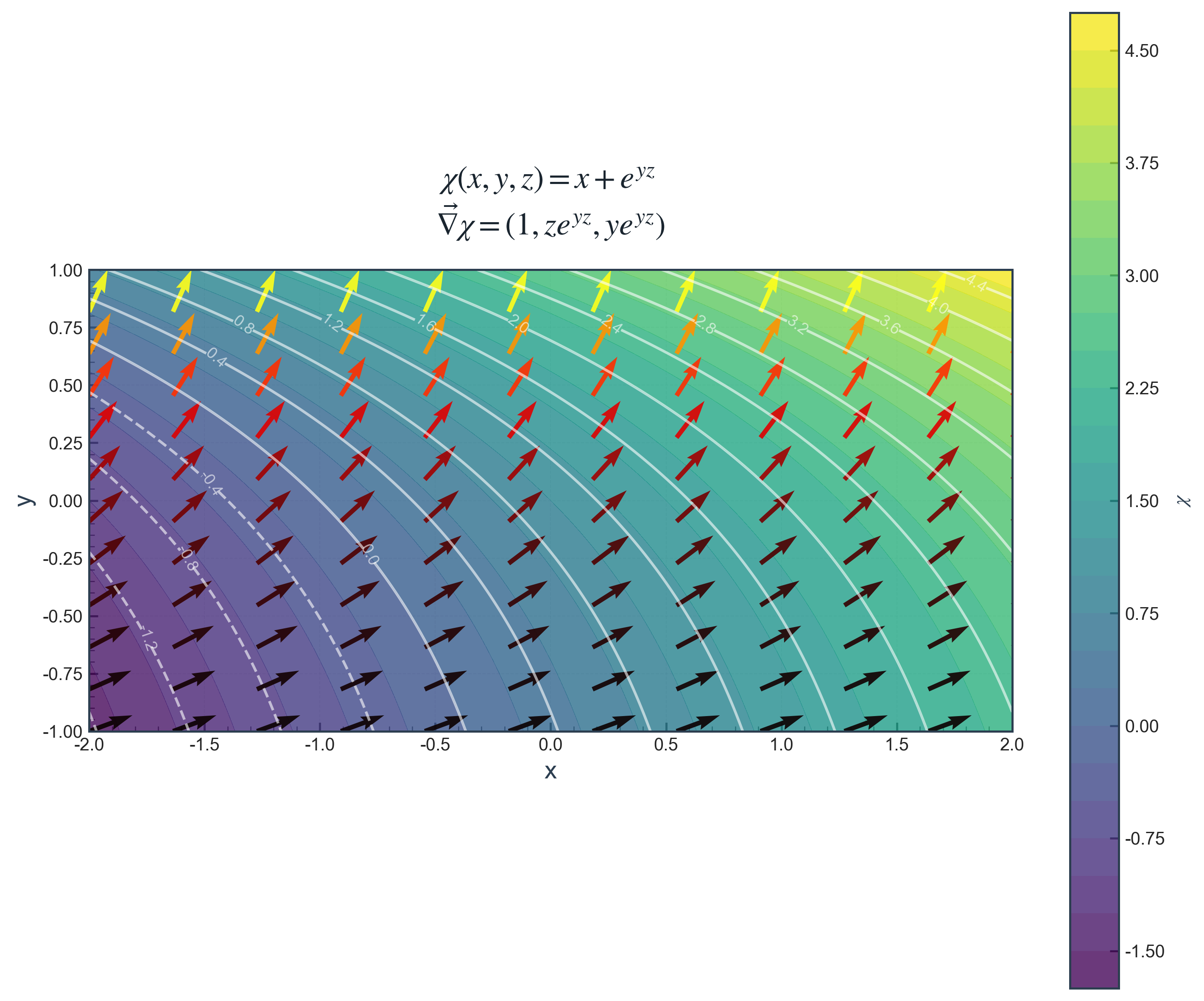
משמעות גיאומטרית
הגרדיאנט מתאר את כיוון השיפוע המרבי של השדה הסקלרי:
- מצביע בכיוון שבו השדה גדל במהירות הגבוהה ביותר
- ניצב למשטחים קבועים של השדה
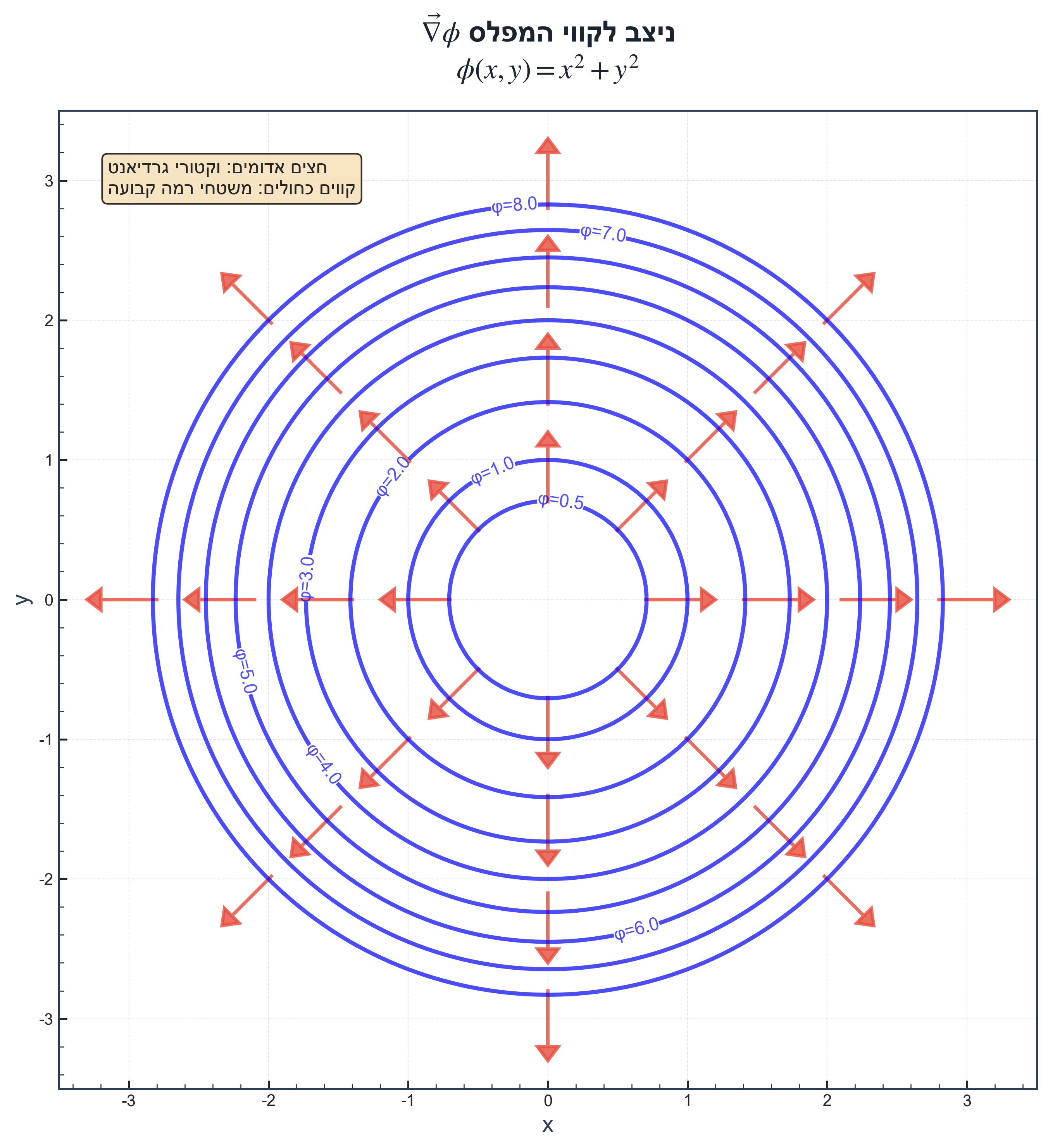
דוגמה: במפה טופוגרפית, הגרדיאנט מצביע בכיוון המורד/עלייה התלול ביותר.
שדה נורמלי למשטח
עבור משטח המוגדר על ידי $\phi(x,y,z) = c$:
\[\hat{n}(\vec{r}) = \frac{\vec{\nabla}\phi}{|\vec{\nabla}\phi|}\]וקטור היחידה הניצב למשטח.
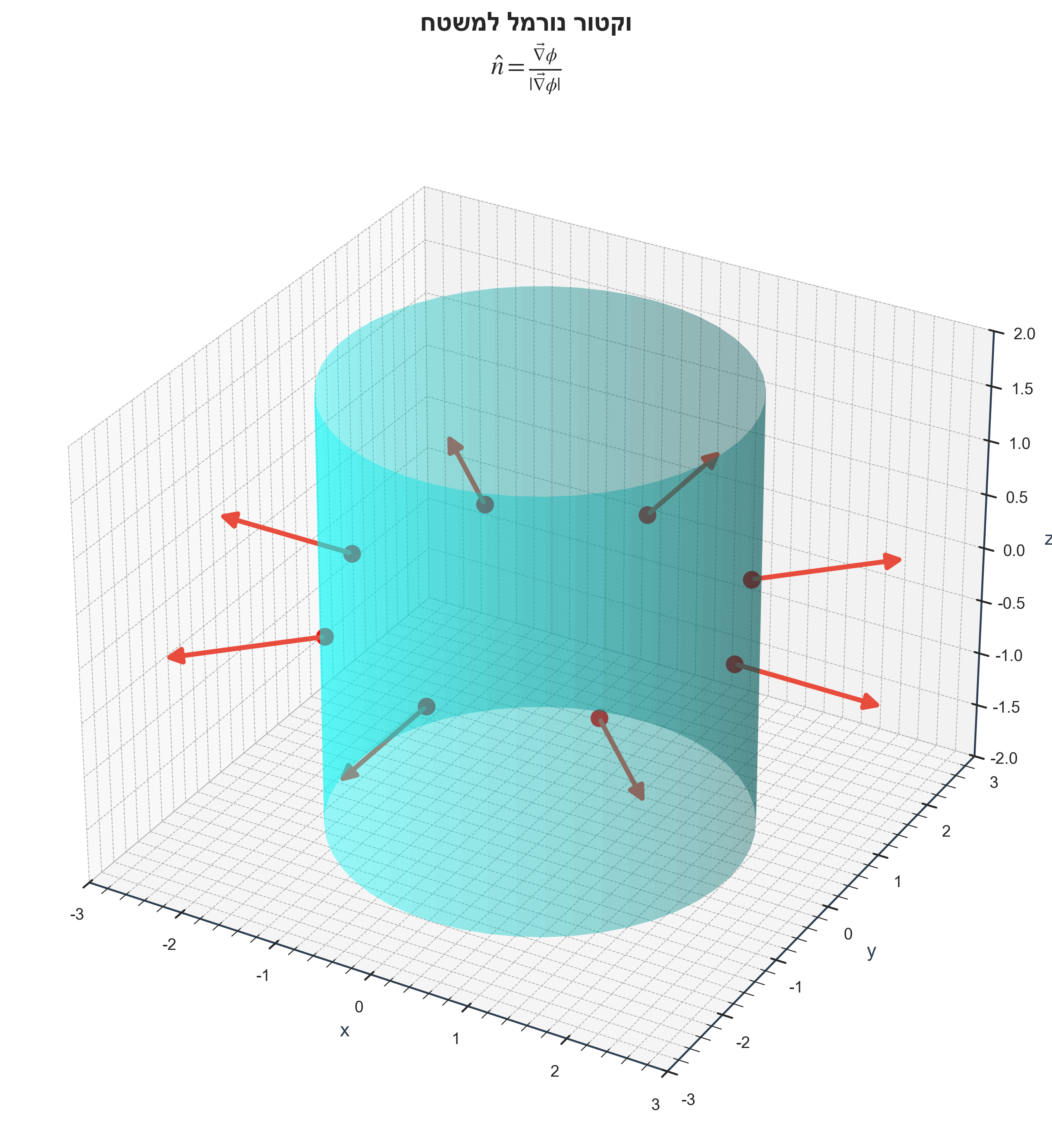
הוכחה (סקיצה):
- עבור משטח $\phi(x,y,z) = c$ (קבוע)
- הדיפרנציאל: $d\phi = 0$
- $d\phi = \nabla\phi \cdot d\vec{r} = 0$
- $\nabla\phi \perp d\vec{r}$
כיוון ש-$d\vec{r}$ שוכב על המשטח, $\nabla\phi$ ניצב למשטח.

אופרטור הדיברגנס (Divergence)
הגדרה: מכפלה סקלרית של $\nabla$ עם שדה וקטורי:
\[\boxed{\text{div}\,\vec{v} = \vec{\nabla} \cdot \vec{v} = \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z}}\]תוצאה: שדה סקלרי
דוגמה: עבור השדה הוקטורי
\[\vec{v}(x,y,z) = x^2\hat{x} + \sin(xy)\hat{y} + e^{xyz}\hat{z}\]הדיברגנס הוא:
\[\nabla \cdot \vec{v} = 2x + x\cos(xy) + xye^{xyz}\]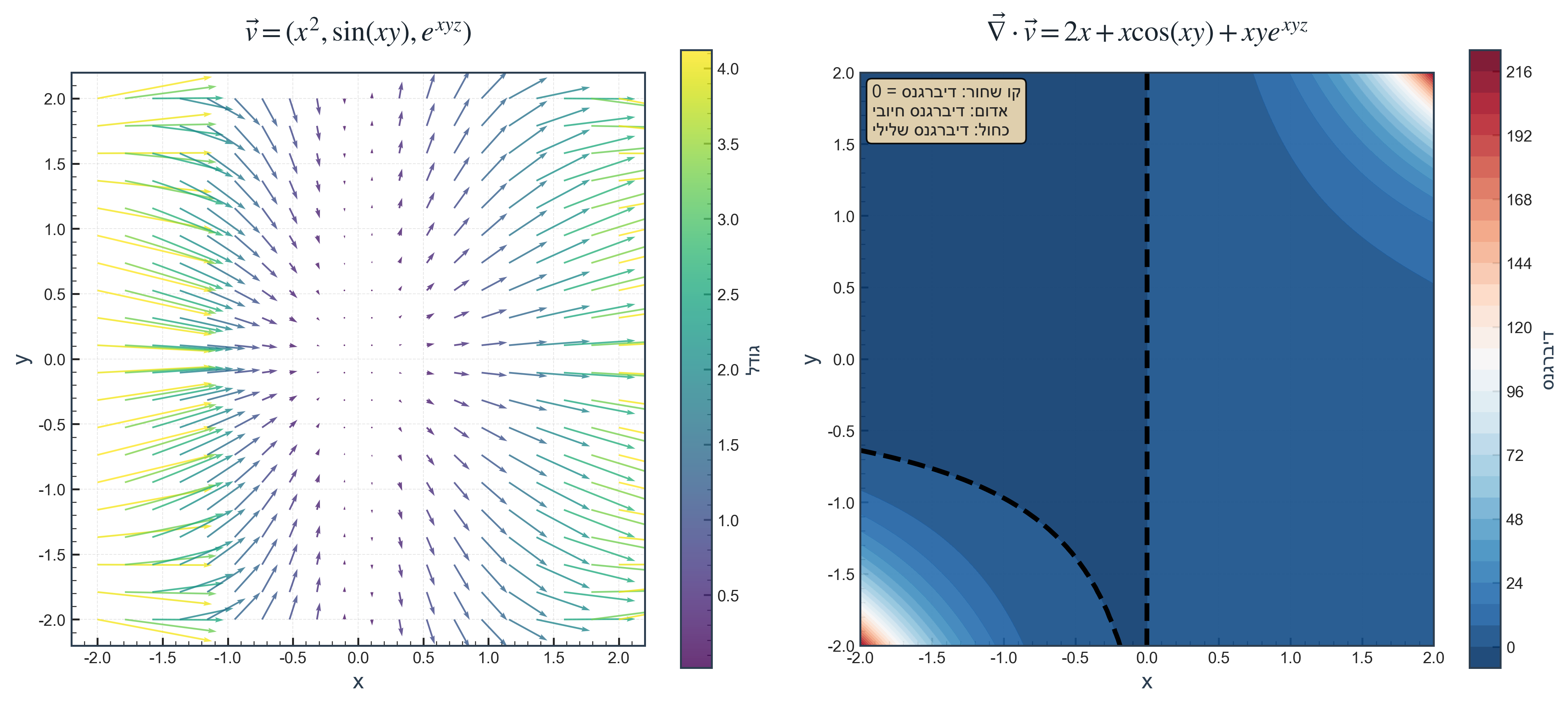
משמעות פיזיקלית
הדיברגנס מודד את עוצמת השפיעה של השדה הוקטורי:
- $\nabla \cdot \vec{v} > 0$: מקור (source) - השדה שופע החוצה מהנקודה
- $\nabla \cdot \vec{v} < 0$: בולען (sink) - השדה נכנס פנימה לנקודה
- $\nabla \cdot \vec{v} = 0$: אין שפיעה נטו
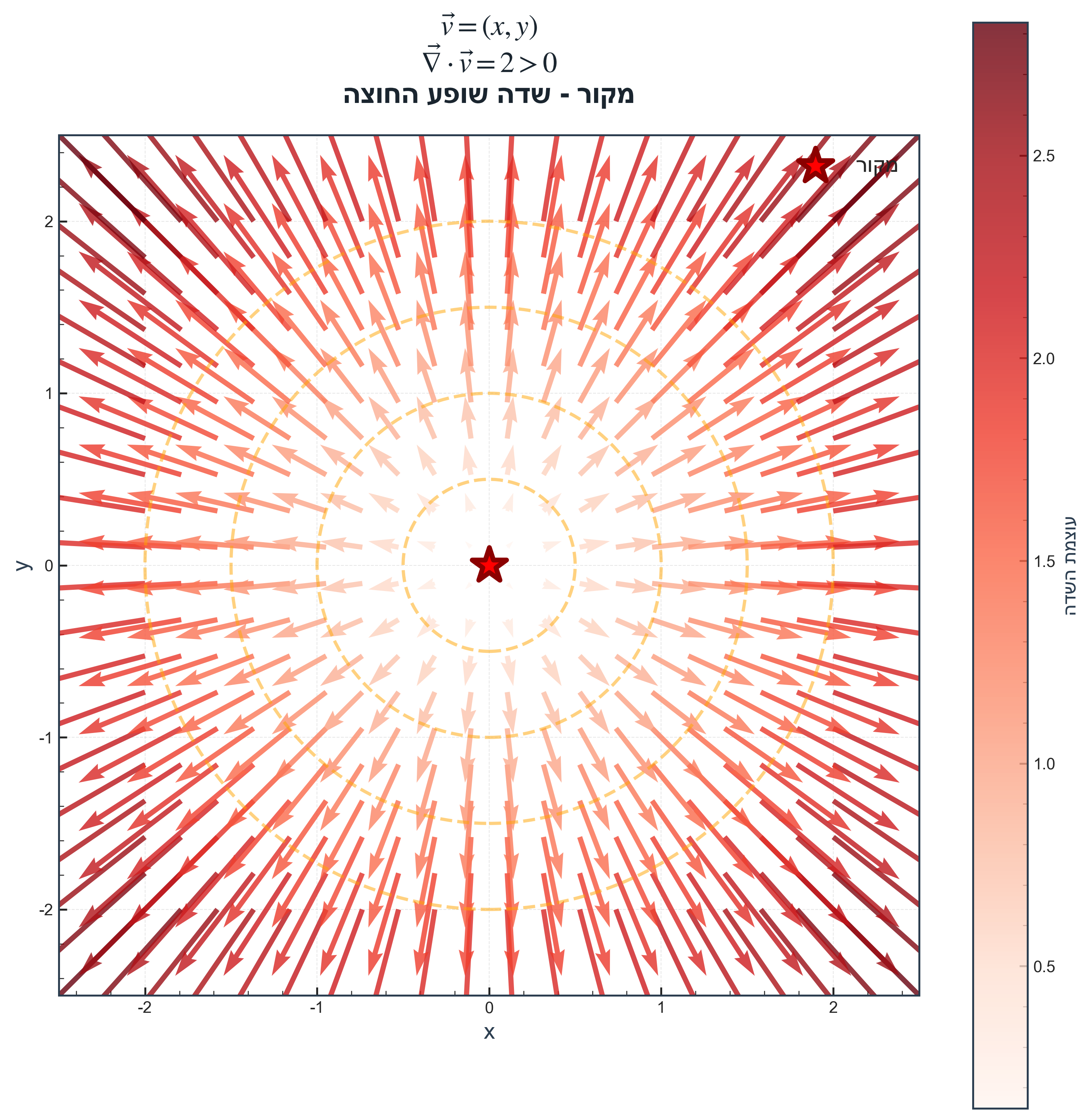 | 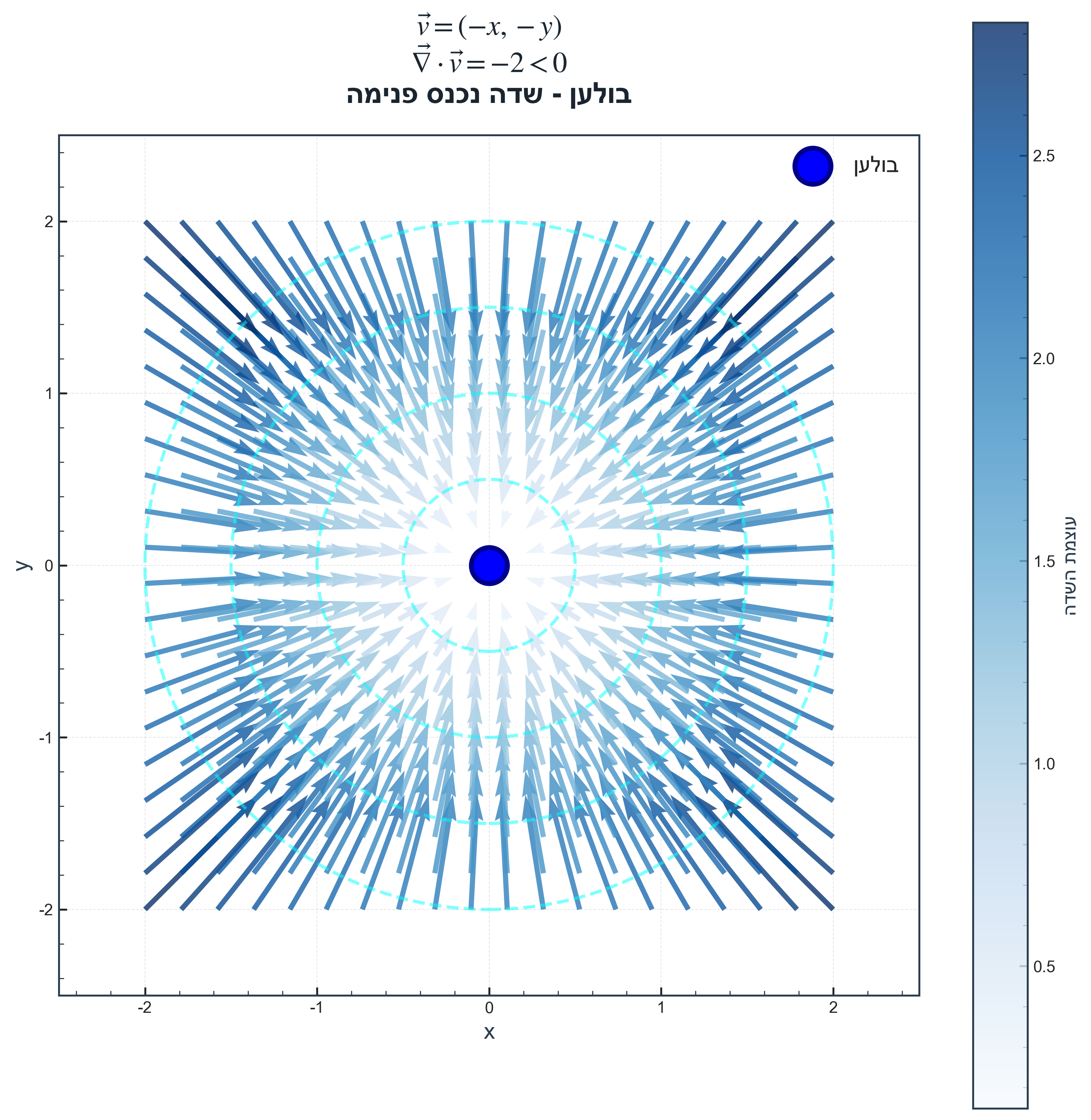 | 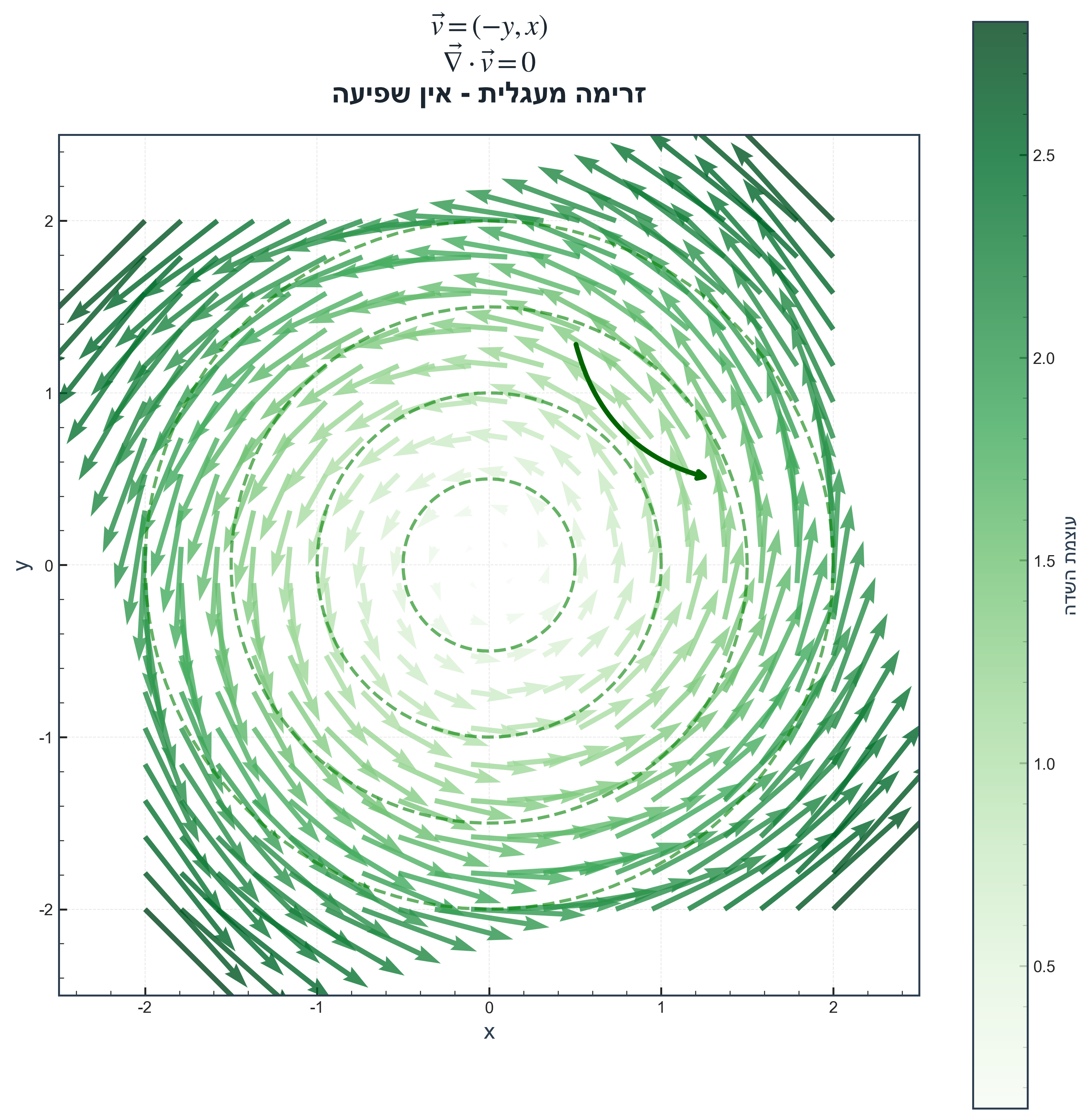 |
דוגמאות:
- מעיין מים: דיברגנס חיובי
- קיור מים: דיברגנס שלילי
- זרימה מעגלית טהורה: דיברגנס אפס
אופרטור הרוטור (Curl/Rotation)
הגדרה: מכפלה וקטורית של $\nabla$ עם שדה וקטורי:
\[\text{curl}\,\vec{v} = \vec{\nabla} \times \vec{v} = \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ v_x & v_y & v_z \end{vmatrix}\]פירוט:
\[\vec{\nabla} \times \vec{v} = \hat{x}\left(\frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z}\right) - \hat{y}\left(\frac{\partial v_z}{\partial x} - \frac{\partial v_x}{\partial z}\right) + \hat{z}\left(\frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}\right)\]תוצאה: שדה וקטורי
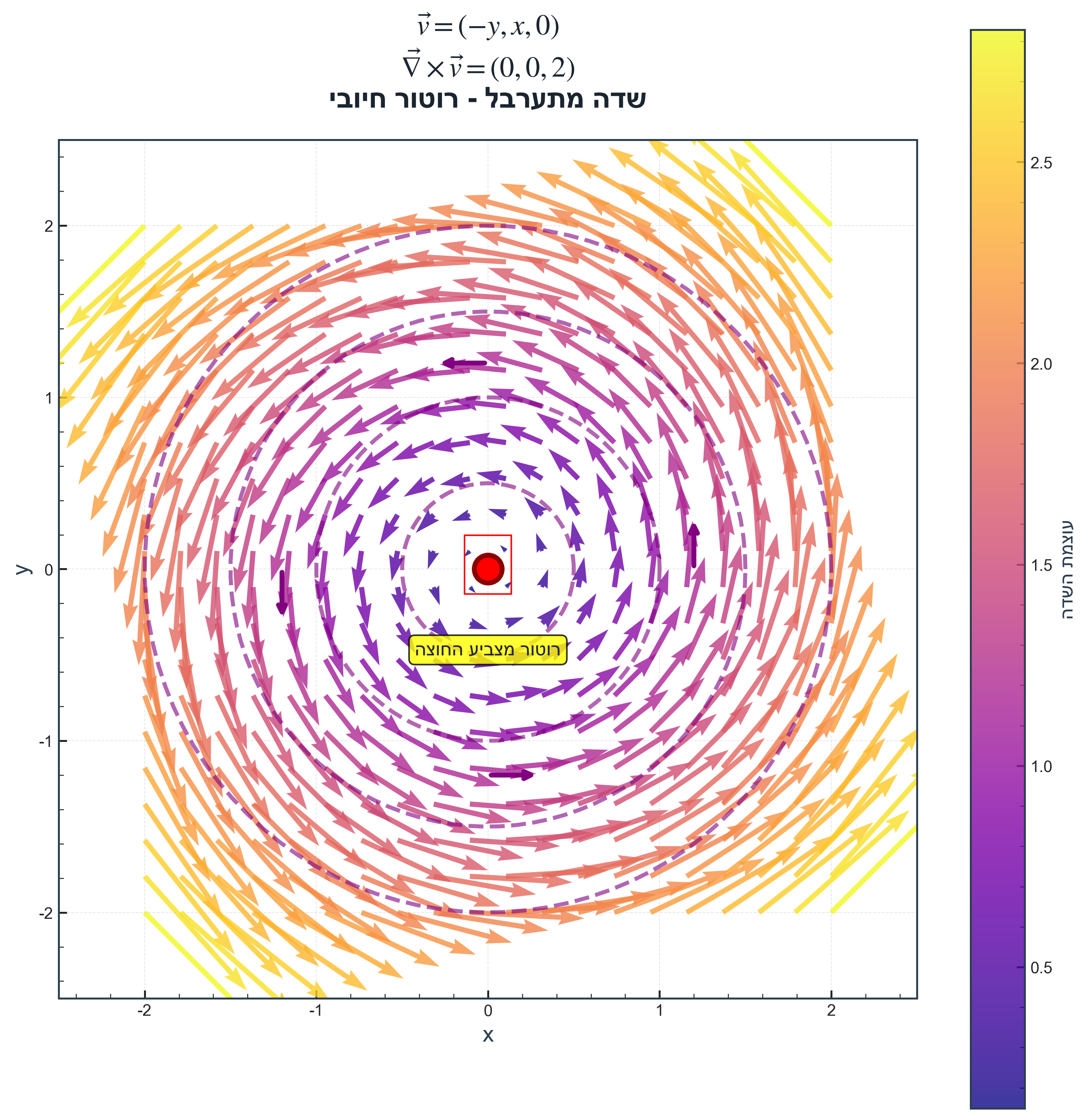
משמעות פיזיקלית של הרוטור
הרוטור מודד את עוצמת הערבוליות של השדה:
- $\nabla \times \vec{v} \neq \vec{0}$: השדה מתערבל (יש רוטציה מקומית)
- $\nabla \times \vec{v} = \vec{0}$: השדה ללא ערבוליות (irrotational)
כיוון הרוטור:
- ערבול נגד כיוון השעון: רוטור חיובי
- ערבול עם כיוון השעון: רוטור שלילי
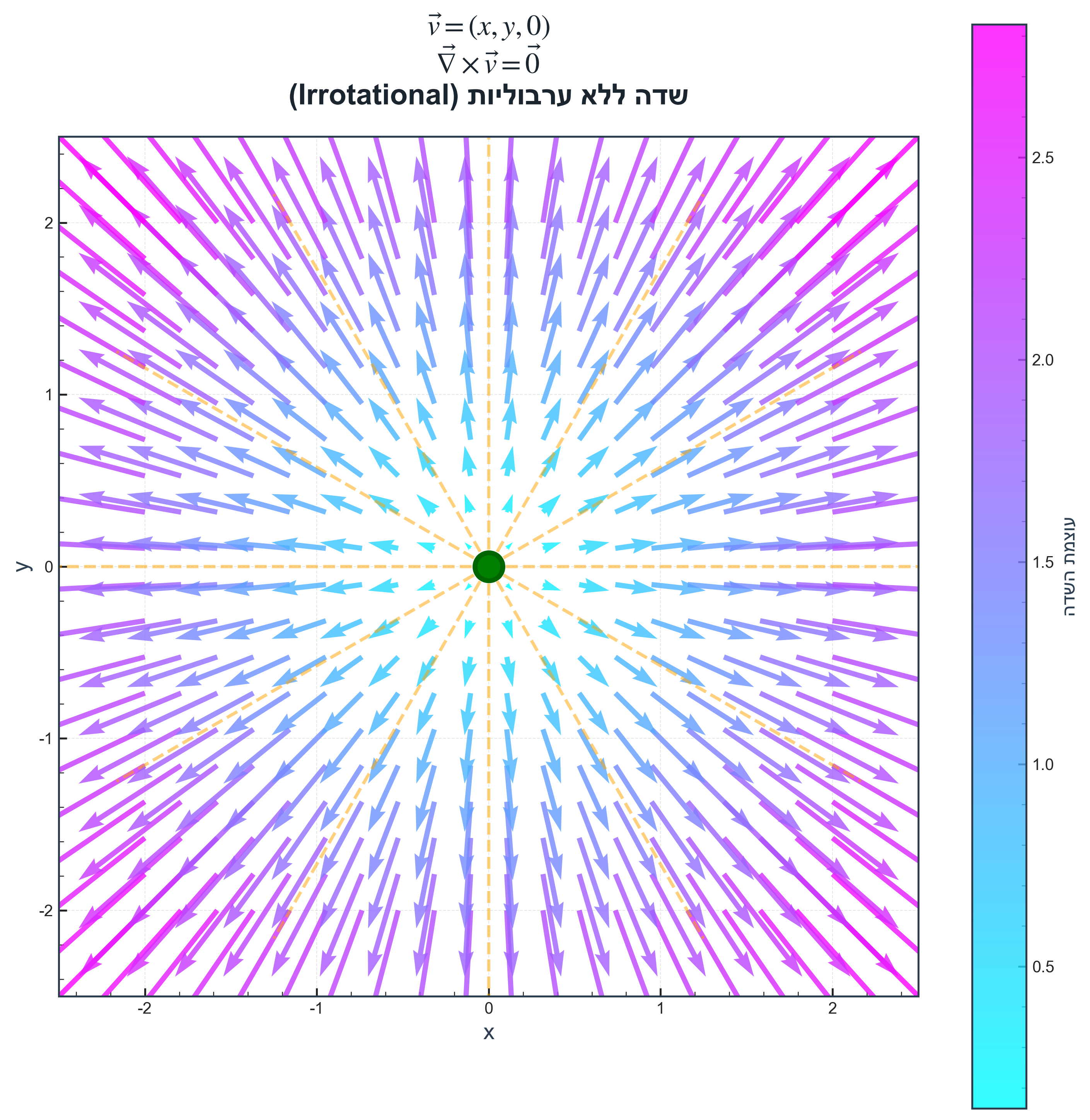
דוגמאות:
- הוריקן: רוטור גדול באזור המרכז
- שדה רדיאלי טהור: רוטור אפס
זהויות וקטוריות חשובות
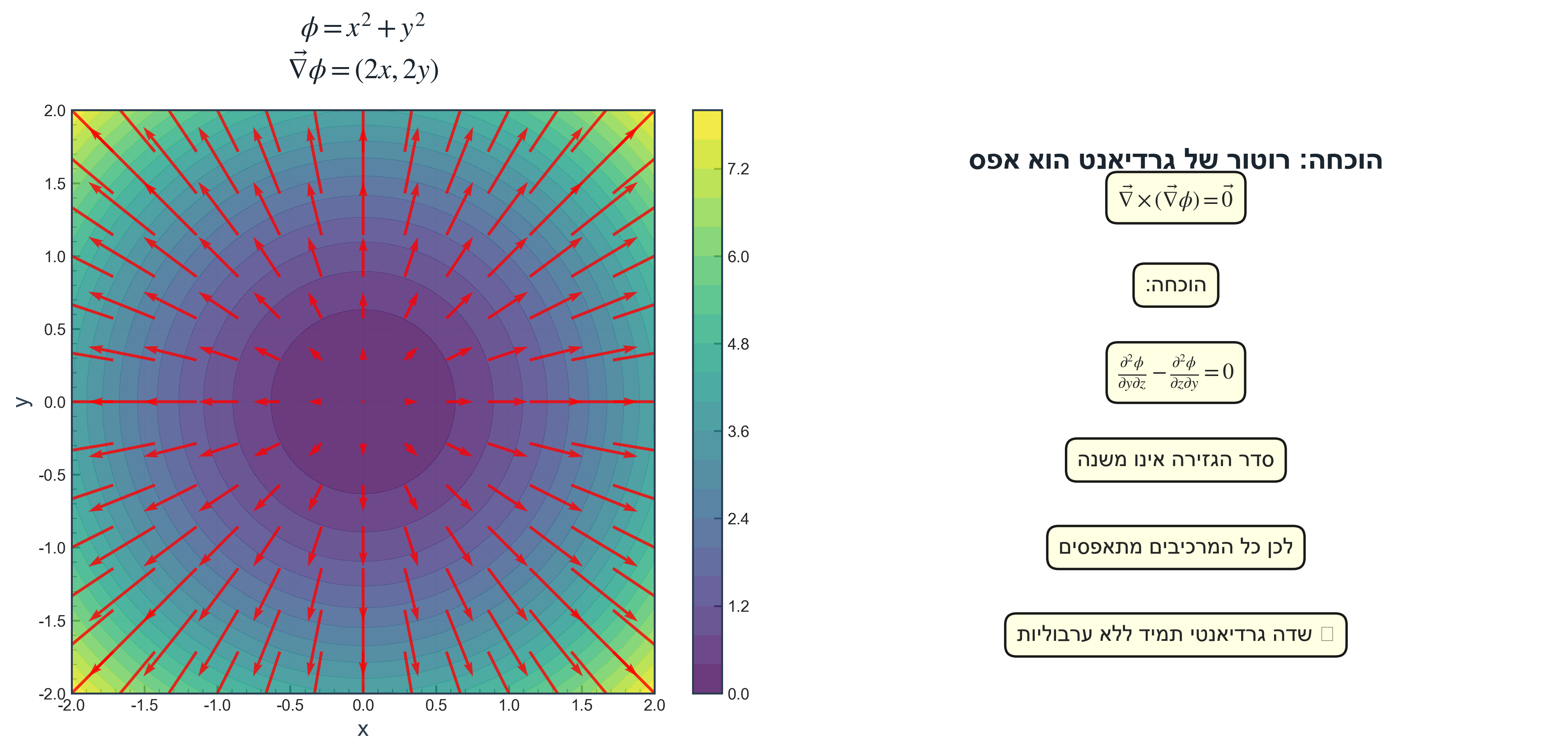
רוטור של גרדיאנט
משפט: עבור כל שדה סקלרי $\phi$:
\[\vec{\nabla} \times (\vec{\nabla} \phi) = \vec{0}\]הוכחה:
\[\vec{\nabla} \times (\vec{\nabla} \phi) = \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \frac{\partial\phi}{\partial x} & \frac{\partial\phi}{\partial y} & \frac{\partial\phi}{\partial z} \end{vmatrix}\]המרכיב ב-$\hat{x}$:
\[\frac{\partial}{\partial y}\left(\frac{\partial\phi}{\partial z}\right) - \frac{\partial}{\partial z}\left(\frac{\partial\phi}{\partial y}\right) = \frac{\partial^2\phi}{\partial y\partial z} - \frac{\partial^2\phi}{\partial z\partial y} = 0\]עקרון: סדר הגזירה בנגזרות חלקיות אינו משנה.
באופן דומה, כל המרכיבים מתאפסים.
מסקנה: שדה גרדיאנטי הוא תמיד ללא ערבוליות.
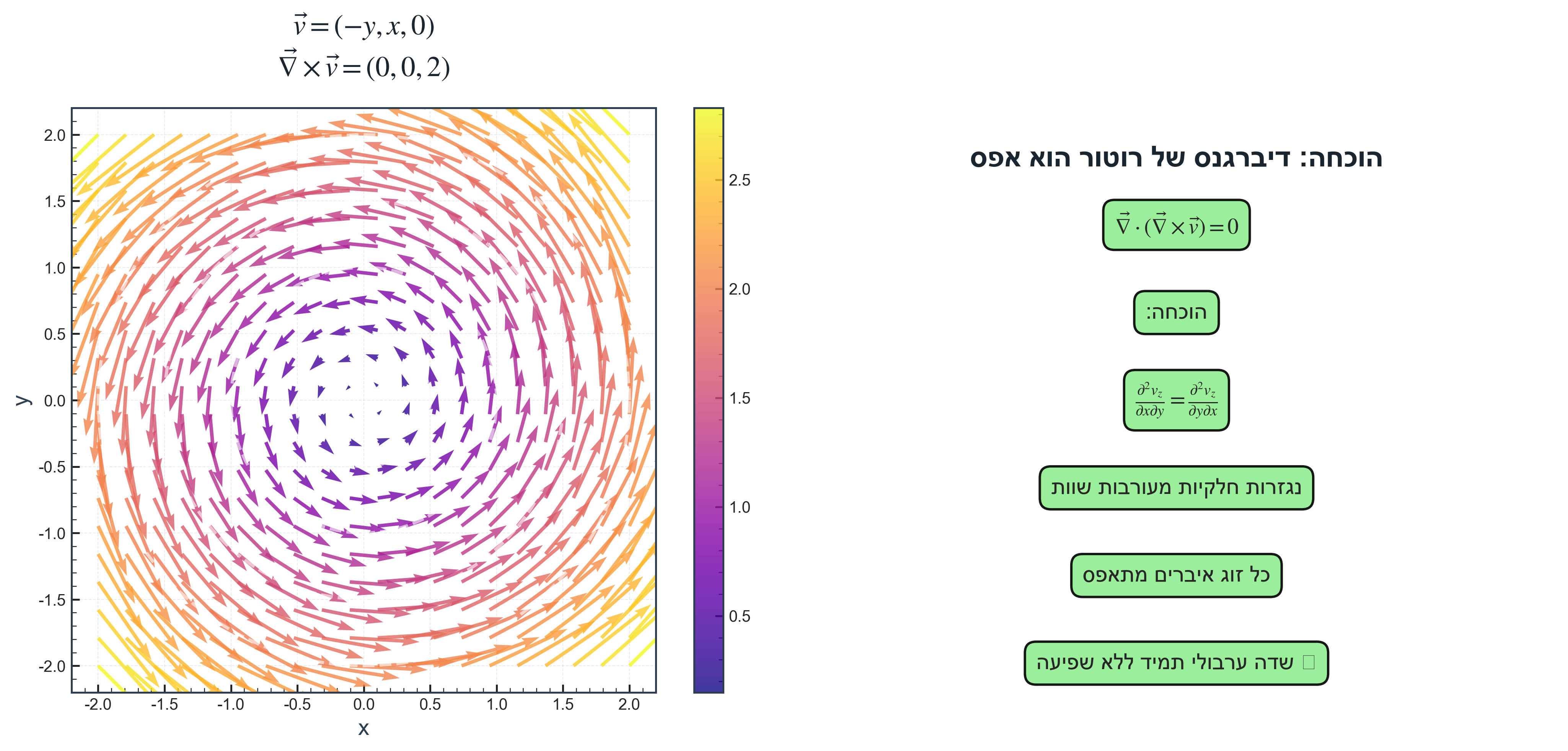
דיברגנס של רוטור
משפט: עבור כל שדה וקטורי $\vec{v}$:
\[\vec{\nabla} \cdot (\vec{\nabla} \times \vec{v}) = 0\]הוכחה:
\[\vec{\nabla} \cdot (\vec{\nabla} \times \vec{v}) = \frac{\partial}{\partial x}\left(\frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z}\right) + \frac{\partial}{\partial y}\left(\frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x}\right) + \frac{\partial}{\partial z}\left(\frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y}\right)\]פתיחת הסוגריים:
\[= \frac{\partial^2 v_z}{\partial x\partial y} - \frac{\partial^2 v_y}{\partial x\partial z} + \frac{\partial^2 v_x}{\partial y\partial z} - \frac{\partial^2 v_z}{\partial y\partial x} + \frac{\partial^2 v_y}{\partial z\partial x} - \frac{\partial^2 v_x}{\partial z\partial y}\]כל זוג איברים מתאפס בגלל שוויון נגזרות חלקיות מעורבות:
\[\frac{\partial^2 v_z}{\partial x\partial y} = \frac{\partial^2 v_z}{\partial y\partial x}, \quad \text{etc.}\]מסקנה: שדה ערבולי הוא תמיד ללא שפיעה (דיברגנס אפס).
שטף (Flux)
הגדרה אינטואיטיבית
שטף מודד את כמות השדה הוקטורי העוברת דרך משטח נתון.
אנלוגיה: גשם היורד דרך חלון:
- כאשר החלון ניצב לכיוון הגשם ← שטף מקסימלי
- כאשר החלון מקביל לכיוון הגשם ← שטף אפס
- במצבים ביניים ← שטף תלוי בזווית
תלות בזווית
עבור שדה $\vec{v}$ ומשטח עם נורמל $\hat{n}$:
- $\vec{v} \parallel \hat{n}$: שטף מקסימלי
- $\vec{v} \perp \hat{n}$: שטף אפס
- זווית כללית: השטף תלוי ב-$\vec{v} \cdot \hat{n}$
המרכיב התורם לשטף: רק המרכיב של $\vec{v}$ בכיוון הנורמל $\hat{n}$ תורם לשטף.
הגדרה מתמטית
השטף של שדה וקטורי $\vec{v}$ דרך משטח $S$ עם אלמנט שטח $d\vec{A} = \hat{n}dA$:
\[\Phi = \int_S \vec{v} \cdot d\vec{A} = \int_S \vec{v} \cdot \hat{n}\,dA\]כאשר $\hat{n}$ הוא וקטור הנורמל למשטח.
משפט הדיברגנס (Divergence Theorem)
משפט הדיברגנס, המכונה גם משפט גאוס או משפט גרין, קושר בין אינטגרל נפחי של הדיברגנס לבין אינטגרל משטחי של השטף:
\[\int_V (\nabla \cdot \vec{v})\,dV = \oint_S \vec{v} \cdot d\vec{A}\]כאשר:
- $V$ - נפח סגור
- $S$ - המשטח הסגור התחום את הנפח
- $d\vec{A}$ - אלמנט שטח מכוון כלפי חוץ
פרשנות פיזיקלית:
- אגף שמאל: סך כל המקורות (שפיעה נטו) בתוך הנפח
- אגף ימין: סך כל השטף היוצא דרך המשטח החיצוני
משמעות: מה שנוצר בפנים (מקורות) חייב לצאת החוצה (שטף).
סיכום
| אופרטור | קלט | פלט | סימון | משמעות |
|---|---|---|---|---|
| Gradient | שדה סקלרי | שדה וקטורי | $\vec{\nabla}\phi$ | כיוון השיפוע המרבי |
| Divergence | שדה וקטורי | שדה סקלרי | $\vec{\nabla} \cdot \vec{v}$ | עוצמת השפיעה |
| Curl | שדה וקטורי | שדה וקטורי | $\vec{\nabla} \times \vec{v}$ | עוצמת הערבוליות |
זהויות יסודיות:
- $\nabla \times (\nabla\phi) = \vec{0}$ - לגרדיאנט אין ערבוליות
- $\nabla \cdot (\nabla \times \vec{v}) = 0$ - לרוטור אין שפיעה
בשיעורים הבאים נשתמש במושגים האלו כדי לתאר תופעות אלקטרומגנטיות.
דור פסקל