הקדמה לבעיית המטוטלת בקרון מואץ
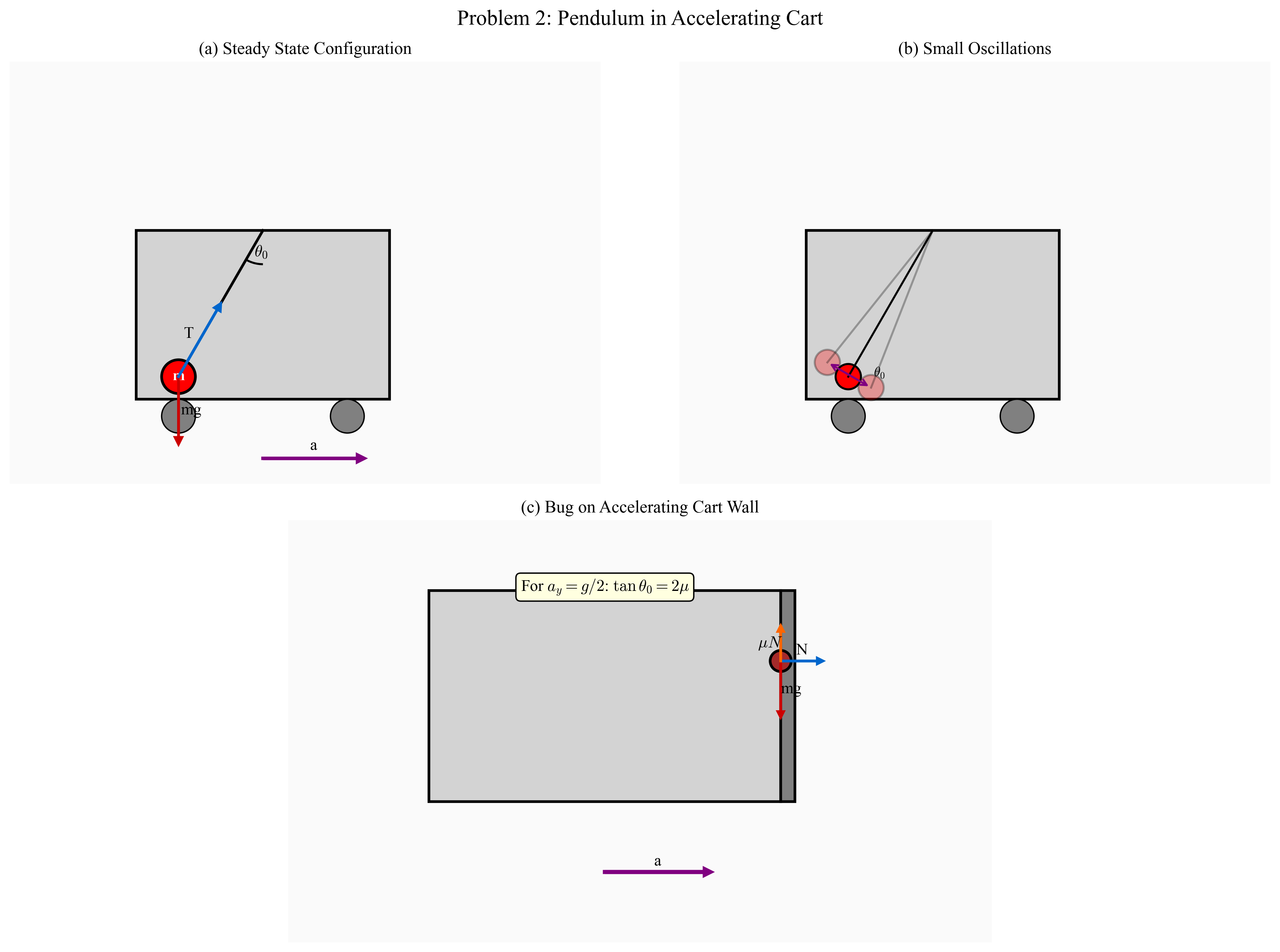
מסה $m$ מחוברת לתקרה של קרון עם חוט באורך $\ell$. הקרון מאיץ ימינה בתאוצה $A$. אנחנו צריכים לחקור את המערכת הזאת.
משחררים את המטוטלת כך שהחוט נפרש בזווית פרישה מסוימת $\theta_0$ הנשמרת כל העת במהלך התנועה. מהי התאוצה במונחים של הפרמטרים בבעיה?
שימו לב שהביטוי שקיבלתם משמש מעין “מד תאוצה”.
מסיטים את המסה $m$ למצב אנכי ומשחררים ממנוחה. מיד לאחר מכן היא מבצעת תנודות הרמוניות סביב הזווית $\theta_0$ (נקודת שיווי המשקל של המערכת).
מהי תדירות התנודות ומהי המשרעת שלהן בהנחה של זוויות קטנות (כלומר כאשר $sin \theta \approx \theta$)?
תוך כדי תנועת הקרון ימינה נצמד חרק לדופן הימנית (חזית הקרון המאיץ) והוא מחליק מטה בתאוצה בהיותו צמוד לדופן.
מקדם החיכוך בין החרק לדופן הוא $\mu$.
מה צריכה להיות זווית הפרישה $\theta_0$ כדי שתאוצתו של החרק מטה תהיה בדיוק $A = g/2$?
במהלך התנודה נקרע לפתע החוט כשהוא מתוח בזווית $\theta = 0^\circ$ ביחס לאנך. ציירו סקיצה כיצד ייראה מסלול הנפילה של המסה מנקודת המבט של צופה הנמצא בתוך העגלה.
אפיינו את הציר באמצעות צירים וזוויות והסבירו אותו.
שלב ראשון: מציאת זווית שיווי המשקל
ניתוח מתוך הקרון (מערכת ייחוס מואצת)
השלב הראשון הוא לקבוע את זווית שיווי המשקל. אנחנו נמצאים בתוך הקרון, מחזיקים את המסה, ובעדינות רבה מביאים אותה למקום שבו היא נשארת יציבה במצבה הנוכחי. זה בזווית $\theta_0$ (זווית שיווי המשקל).
השאלה: מה הקשר בין $\theta_0$ ל-$A$? והאם אפשר להשתמש ב-$\theta_0$ כדי למצוא את תאוצת הקרון?
התשובה: בוודאי שכן!
כוחות במערכת המואצת
כשאנחנו נמצאים בתוך הקרון, מבחינתנו הכל במנוחה, למרות שאנחנו מואצים. אנחנו נמצאים במערכת ייחוס לא אינרציאלית ומרגישים כוחות מדומים.
הכוחות הפועלים על המסה:
- $\downarrow mg$ כלפי מטה (כוח הכבידה)
- $\leftarrow mA$ שמאלה (כוח מדומה, הפוך לכיוון התאוצה)
משוואות שיווי המשקל
בשיווי משקל, שקול הכוחות שווה לאפס (החוק הראשון של ניוטון במערכת מואצת):
הערה: לכאורה אפשר להגיע לאותן משוואות משני החוקים - זה רלוונטי לשאלות נוספות שבהן גוף שנמצא בתוך מערכת מואצת מרגיש כוחות מדומים, כמו בעיית מד המשקל וסיבוב כדור הארץ. השאלה איך מסתכלים על הבעיה ככל הנראה תלויה בשיטת הלימוד.
המרצה ככל הנראה מבחין ביין המצבים הבאים:
כשמסתכלים על הרכבת מבחוץ (מערכת אינרציאלית, כלומר מערכת התמד או מערכת לא מואצת) - חוק שני של ניוטון (כוחות):
\[T\sin(\theta_0) = mA\]כשמסתכלים על הרכבת מבפנים (מערכת לא אינרציאלית, כלומר מערכת מואצת) - חוק ראשון של ניוטון (שיווי משקל), עם תיקון לכוחות מדומים.
\[T\sin(\theta_0) - mA = 0\]
בכיוון האנכי: (רדיאלי - באיור ↗)
\[T \cos(\theta_0) -mg = 0\] \[\boxed{T \cos(\theta_0) = mg} \tag{1}\]בכיוון האופקי: (משיקי - באיור ↘)
\[T \sin(\theta_0) - mA = 0\] \[\boxed{T \sin(\theta_0) = mA} \tag{2}\]
הערה: בשיעור נעשה תיקון בגרף שקצת בלבל אותי ביחס לזוויות ההתחלה. מאיור מעלה מציג את התיקון.
מציאת הקשר בין התאוצה לזווית
חילוק שתי המשוואות $(1)$ ו$(2)$:
\[\frac{T \sin(\theta_0)}{T \cos(\theta_0)} = \frac{mA}{mg}\] \[\tan(\theta_0) = \frac{A}{g}\]לכן:
\[\boxed{A = g \tan\left(\theta_0\right) \, \mathrm{[m/s^2]}}\]זהו מד תאוצה (אקסלרומטר)! אם אני נמצא בתוך המערכת המואצת ואני מודד את הזווית $\theta_0$, אני יודע בדיוק באיזה תאוצה המערכת שלי מתנועת.
שלב שני: דינמיקה של התנודות
הבעיה הדינמית
עכשיו אני לוקח את המסה, מוריד אותה למטה ומשחרר. היא תרצה לחזור למצב שיווי המשקל ותתחיל להתנדד סביב הזווית $\theta_0$.
ניתוח הכוחות במהלך התנועה
הכוח השקול הפועל על המסה:
\[\vec{F} = mA \hat{x} - mg \hat{y}\]גודל הכוח השקול:
\[|\vec{F}| = \sqrt{(m\underbrace{A}_{g\tan^2(\theta_0)})^2 + (-mg)^2} = mg\sqrt{1 + \tan^2(\theta_0)}\]מהזהות הטריגונומטריות:
\[1 + \tan^2(\theta_0) = \frac{1}{\cos^2(\theta_0)}\]נקבל:
\[|\vec{F}| = \frac{mg}{\cos(\theta_0)}\]פירוק לקואורדינטות פולאריות
בקואורדינטות פולאריות (רדיאלי ומשיקי):
בכיוון הרדיאלי: (רדיאלי - באיור ↗)
\[T - F\cos(\theta) = m\frac{v^2_{\theta}}{\ell}\]כאשר $F\cos(\theta)$ הוא ההיטל של הכוח השקול על הכיוון הרדיאלי.
בכיוון המשיקי: (משיקי - באיור ↘)
\[mL\ddot{\theta} = -F\sin(\theta)\]קירוב לזוויות קטנות
עבור זוויות קטנות, $\sin(\theta) \approx \theta$:
\[mL\ddot{\theta} = -F\theta\] \[\ddot{\theta} = -\frac{F}{mL}\theta\]מאחר ש-$F = \frac{mg}{\cos(\theta_0)}$:
\[\boxed{\ddot{\theta} = -\frac{g}{\ell\cos(\theta_0)}\theta} \tag{3}\]זוהי משוואת תנודה הרמונית פשוטה מהצורה:
\[\ddot{\theta} = -\omega^2 \theta\]כאשר המהירות הזווית $\omega=\dot{\theta}$ היא:
\[\boxed{\omega = \sqrt{\frac{g}{\ell\cos(\theta_0)}} \,\mathrm{[rad/s]}}\]תדירות התנודות והמשרעת
ניזכר בהגדרה של תדירות התנודות $f$:
\[\boxed{f = \frac{\omega}{2\pi} = \frac{1}{2\pi}\sqrt{\frac{g}{\ell\cos(\theta_0)}} \,\mathrm{[Hz]}}\]משרעת התנודות
המשרעת של התנודות היא הזווית ההתחלתית ביחס לזווית שיווי המשקל $\theta_0$. אם המסה משוחררת ממצב אנכי, המשרעת תהיה:
\[\boxed{\theta_{0} \,\mathrm{[rad]}}\]פתרון משוואת התנודות
הפתרון הכללי של משוואת התנודות הרמונית הוא, ובפרט למשוואה (3):
\[\theta(t) = \theta_{0} \cos(\omega t)\]כאשר $\theta_{0}$ הוא הזווית ההתחלתית ביחס לזווית שיווי המשקל $\theta_0$.
המהירות המשיקית
נגזור את הפתרון כדי למצוא את המהירות המשיקית:
\[v_{\theta} = \ell\dot{\theta} = -\ell\omega \theta_{0} \sin(\omega t)\]המתיחות כפונקציה של הזמן
\[T(t) = F\cos(\theta) + m\frac{v^2_{\theta}}{\ell}\]זוהי פונקציה מתנדנדת של הזמן.
שלב שלישי: בעיית החיכוך
תיאור הבעיה
עכשיו אני (בעל מסה $M$) נמצא על דופן הקרון. הרכבת נעה בתאוצה $A$, ויש מקדם חיכוך $\mu$ ביני לבין הדופן.
השאלה: מה צריכה להיות זווית הנטייה $\theta_0$ כדי שאני אחליק כלפי מטה בתאוצה של $\frac{g}{2}$?
ניתוח הכוחות
הכוחות הפועלים עליי:
- $Mg$ כלפי מטה (כבידה)
- $N$ כלפי חוץ מהדופן (כוח נורמלי)
- $\mu N$ כלפי מעלה (חיכוך, נגד כיוון התנועה)
משוואות תנועה
בכיוון האופקי:
\[N = MA \tag{1}\]בכיוון האנכי:
\[M \cdot \frac{g}{2} = Mg - \mu N \tag{2}\]פתרון
מהמשוואה הראשונה והביטוי שקיבלנו ל-$A$:
\[N = MA = Mg\tan(\theta_0)\]נציב את $N$ במשוואה השנייה:
\[M \cdot \frac{g}{2} = Mg - \mu \cdot Mg\tan(\theta_0)\]נחלק ב-$Mg$:
\[\frac{1}{2} = 1 - \mu\tan(\theta_0)\] \[\mu\tan(\theta_0) = \frac{1}{2}\] \[\tan(\theta_0) = \frac{1}{2\mu}\] \[\boxed{\theta_0 = \arctan\left(\frac{1}{2\mu}\right) \,\mathrm{[rad]}}\]שלב רביעי: נפילה חופשית לאחר קריעת החוט
לאחר שהחוט נקרע, המסה נופלת חופשית בתוך הקרון המואץ.
ניתוח התנועה
בתוך הקרון, המסה מרגישה:
- תאוצה $g$ כלפי מטה
- תאוצה $A$ בכיוון האופקי
מסלול התנועה
מאחר ששתי התאוצות קבועות:
\[\begin{align} \Delta x &= \frac{1}{2}At^2 \\ \Delta y &= \frac{1}{2}gt^2 \end{align}\]המסלול הוא קו ישר בזווית $\phi$ מתחת לאופק:
\[\tan(\phi) = \frac{\Delta y}{\Delta x} = \frac{g}{A}\]סיכום
המטוטלת בקרון מואץ מדגימה עקרונות חשובים בפיזיקה:
- כוחות מדומים במערכות ייחוס מואצות - הכוח $mA$ שמאלה
- מד תאוצה - $A = g\tan(\theta_0)$
- תנודות הרמוניות במערכת מואצת - $\omega = \sqrt{\frac{g}{\ell\cos(\theta_0)}}$
- חיכוך במערכות מואצות
- תנועה פרבולית במערכת ייחוס מואצת
הערה חשובה: כל הניתוחים נעשו מתוך מערכת הייחוס המואצת (הקרון), תוך התחשבות בכוחות המדומים המתאימים.
דור פסקל