תוכן עניינים
- מתמטיקה בסיסית וטריגונומטריה
- וקטורים ומערכות צירים
- קינמטיקה - תורת התנועה
- דינמיקה - חוקי ניוטון וכוחות
- תנועה הרמונית ואוסצילציות
- בעיות מרכזיות ודוגמאות
- טכניקות פתרון ואלגוריתמים
- נוסחאות מהירות לבחינה
מתמטיקה בסיסית וטריגונומטריה
זוויות נפוצות
\[\boxed{ \begin{aligned} \sin(30°) &= \frac{1}{2} = 0.5 \\[5pt] \cos(30°) &= \frac{\sqrt{3}}{2} \approx 0.866 \\[5pt] \tan(30°) &= \frac{1}{\sqrt{3}} \approx 0.577 \\[5pt] \\[5pt] \sin(45°) &= \cos(45°) = \frac{1}{\sqrt{2}} \approx 0.707 \\[5pt] \tan(45°) &= 1 \\[5pt] \\[5pt] \sin(60°) &= \frac{\sqrt{3}}{2} \approx 0.866 \\[5pt] \cos(60°) &= \frac{1}{2} = 0.5 \\[5pt] \tan(60°) &= \sqrt{3} \approx 1.732 \end{aligned}}\]זהויות טריגונומטריות
\[\boxed{ \begin{aligned} \sin(90° - \theta) &= \cos\theta \\[5pt] \cos(90° - \theta) &= \sin\theta \end{aligned}}\] \[\boxed{ \begin{aligned} \sin^2\theta + \cos^2\theta &= 1 \\[5pt] 1 + \tan^2\theta &= \frac{1}{\cos^2\theta} \\[5pt] \\[5pt] \sin(2\theta) &= 2\sin\theta\cos\theta \\[5pt] \cos(2\theta) &= \cos^2\theta - \sin^2\theta \\[5pt] &= 2\cos^2\theta - 1 \\[5pt] &= 1 - 2\sin^2\theta \\[5pt] \\[5pt] \tan(2\theta) &= \frac{2\tan\theta}{1 - \tan^2\theta} \end{aligned}}\]פונקציות היפרבוליות
\[\boxed{ \begin{aligned} \sinh(x) &= \frac{e^x - e^{-x}}{2} \\[5pt] \cosh(x) &= \frac{e^x + e^{-x}}{2} \\[5pt] \tanh(x) &= \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} \\[5pt] \end{aligned}}\]קירוב בזוויות קטנות (ברדיאנים)
\[\boxed{ \begin{aligned} \sin\theta &\approx \theta \\[5pt] \tan\theta &\approx \theta \\[5pt] \cos\theta &\approx 1 - \frac{\theta^2}{2} \end{aligned}}\]נוסחאות טריגונומטריות שימושיות
חיבור זוויות:
\[\boxed{ \begin{aligned} \sin(a + b) &= \sin a \cos b + \cos a \sin b \\[5pt] \cos(a + b) &= \cos a \cos b - \sin a \sin b \end{aligned}}\]חוקי הסינוסים והקוסינוסים:
\[\boxed{ \begin{aligned} \sin A &= \frac{a \sin B}{b} \\[5pt] \sin B &= \frac{b \sin A}{a} \\[5pt] \sin C &= \frac{c \sin A}{a} \\[5pt] \cos C &= \frac{a^2 + b^2 - c^2}{2ab} \end{aligned}}\]יחידות והמרות
יחידות סטדנרטיות:
\[\boxed{ \begin{aligned} \left[\mathrm{m}\right] &= \mathrm{meter} \\[5pt] \left[\mathrm{s}\right] &= \mathrm{second} \\[5pt] \left[\mathrm{kg}\right] &= \mathrm{kilogram} \\[5pt] \left[\mathrm{N}\right] &= \mathrm{Newton} = \mathrm{kg \cdot m/s^2} \\[5pt] \end{aligned}}\] \[\boxed{ \begin{aligned} \left[\omega\right] &= \mathrm{rad/s} \\[5pt] \left[\theta\right] &= \mathrm{rad} \\[5pt] \left[\alpha\right] &= \mathrm{rad/s^2} \\[5pt] \left[\tau\right] &= \mathrm{N \cdot m} = \mathrm{J} \\[5pt] \left[\mathrm{F}\right] &= \mathrm{N} = \mathrm{kg \cdot m/s^2} \\[5pt] \left[\mathrm{p}\right] &= \mathrm{kg \cdot m/s} \\[5pt] \left[\mathrm{E}\right] &= \mathrm{J} = \mathrm{N \cdot m} = \mathrm{kg \cdot m^2/s^2} \\[5pt]\left[\mathrm{V}\right] &= \mathrm{m^3} \\[5pt] \end{aligned}}\] \[\boxed{ \begin{aligned} 1 \, \mathrm{N} &= 1 \, \mathrm{kg} \cdot \mathrm{m/s^2} \\[5pt] 1 \, \mathrm{J} &= 1 \, \mathrm{N} \cdot \mathrm{m} = 1 \, \mathrm{kg} \cdot \mathrm{m^2/s^2} \\[5pt] g &\approx 10 \, \mathrm{m/s^2} \\[5pt] \end{aligned}}\] \[\boxed{ \begin{aligned} 1 \mathrm{ m} &= 100 \, \mathrm{ cm} \\[5pt] &= 1000 \, \mathrm{ mm} \\[5pt] &= 10^6 \, \mathrm{ μm} \\[5pt] &= 10^9 \, \mathrm{ nm} \\[5pt] \\[5pt] 1 \mathrm{ km} &= 1000\, \mathrm{ m} = 10^3 \mathrm{ m} \\[5pt] \\[5pt] 1 \mathrm{ m} &= 1000 \, \mathrm{ mm} \\[5pt] 1 \mathrm{ m} &= 10^9 \, \mathrm{ nm} \\[5pt] 1 \mathrm{ m} &= 0.001\, \mathrm{ km} \\[5pt] \\[5pt] 1 \mathrm{ s} &= 1000 \, \mathrm{ ms} \\[5pt] &= 10^6 \, \mathrm{ μs} \\[5pt] &= 10^9 \, \mathrm{ ns} \\[5pt] \\[5pt] 1 \mathrm{ min} &= 60 \, \mathrm{ s} \\[5pt] 1 \mathrm{ h} &= 3600 \, \mathrm{ s} = 3.6 \times 10^3 \, \mathrm{ s} \\[5pt] \\[5pt] 1 \mathrm{ knot} &= 1.852 \, \mathrm{ km/h} \\[5pt] \end{aligned}}\]וקטורים ומערכות צירים
פעולות בסיסיות על וקטורים
גודל (אורך) וקטור
\[\vert\vec{v}\vert = \sqrt{v_x^2 + v_y^2 + v_z^2}\]נרמול וקטור (יצירת וקטור יחידה)
\[\hat{v} = \frac{\vec{v}}{\vert\vec{v}\vert}\]מכפלה סקלרית
\[\mathbf{a} \cdot \mathbf{\vec{b}} = \vert\mathbf{a}\vert\vert\mathbf{\vec{b}}\vert\cos\theta = a_xb_x + a_yb_y + a_zb_z\]זווית בין וקטורים
\[\cos\theta = \frac{\mathbf{a} \cdot \mathbf{\vec{b}}}{\vert\mathbf{a}\vert\vert\mathbf{\vec{b}}\vert}\]תנאי ניצבות
\[\mathbf{a} \perp \mathbf{\vec{b}} \Leftrightarrow \mathbf{a} \cdot \mathbf{\vec{b}} = 0\]חיבור וקטורים (שקול כוחות)
\[\mathbf{F}_{\text{net}} = \mathbf{F}_1 + \mathbf{F}_2 + \ldots + \mathbf{F}_n\]זווית של וקטור במישור
זווית בין וקטור לבין ציר ה-$x$ (נגד כיוון השעון):
\[\boxed{ \theta = \atan 2(y,x) = \begin{cases} \arctan \left(\frac{v_y}{v_x}\right) & \text{if } v_x > 0 \\[5pt] \arctan \left(\frac{v_y}{v_x}\right) + \pi & \text{if } v_x < 0 \text{ and} v_y \geq 0 \\[5pt] \arctan \left(\frac{v_y}{v_x}\right) - \pi & \text{if } v_x < 0 \text{ and} v_y < 0 \\[5pt] \frac{\pi}{2} & \text{if } v_x = 0 \text{ and } v_y > 0 \\[5pt] -\frac{\pi}{2} & \text{if } v_x = 0 \text{ and } v_y < 0 \\[5pt] \text{undefined} & \text{if } v_x = 0 \text{ and } v_y = 0 \end{cases} }\]מערכות קואורדינטות
קואורדינטות קרטזיות
\[\vec{r} = x\mathbf{\hat{x}} + y\mathbf{\hat{y}} + z\mathbf{\hat{z}}\]קואורדינטות פולריות (2D)
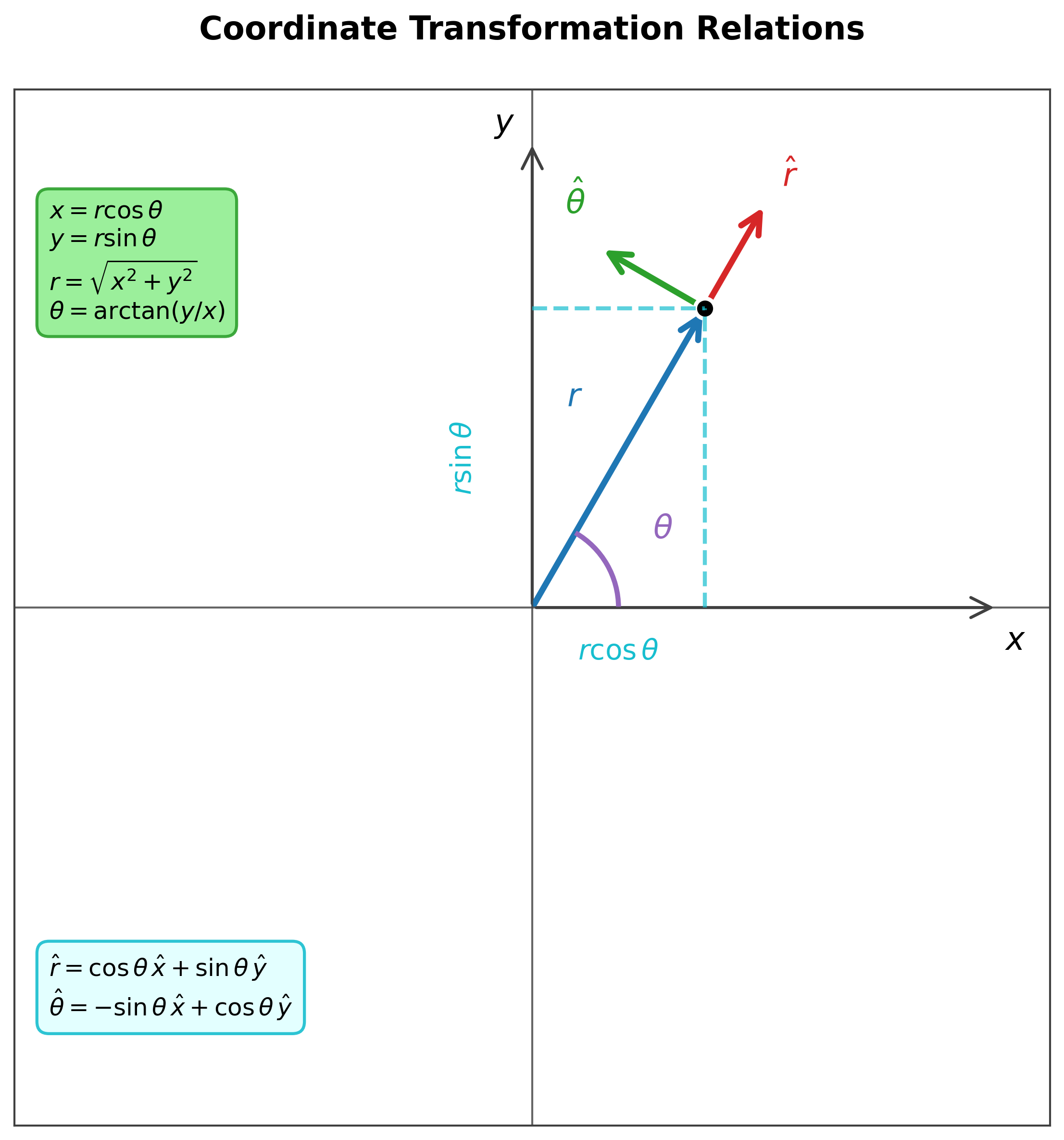
המרה מקרטזיות לפולריות:
\[\boxed{ \begin{aligned} r &= \sqrt{x^2 + y^2} \\[5pt] \theta &= \atan 2(y,x) \end{aligned}}\]המרה מפולריות לקרטזיות:
\[\boxed{ \begin{aligned} x &= r\cos\theta \\[5pt] y &= r\sin\theta \end{aligned}}\]וקטורי יחידה פולריים:
\[\boxed{ \begin{aligned} \mathbf{\hat{r}} &= \cos\theta \mathbf{\hat{x}} + \sin\theta \mathbf{\hat{y}} \\[5pt] \mathbf{\hat{\theta}} &= -\sin\theta \mathbf{\hat{x}} + \cos\theta \mathbf{\hat{y}} \end{aligned}}\]נגזרות וקטורי היחידה:
\[\boxed{ \begin{aligned} \dot{\mathbf{\hat{r}}} &= \dot{\theta}\mathbf{\hat{\theta}} \\[5pt] \dot{\mathbf{\hat{\theta}}} &= -\dot{\theta}\mathbf{\hat{r}} \end{aligned}}\]מהירות ותאוצה בפולריות:
\[\boxed{ \begin{aligned} \vec{v} &= \dot{r}\mathbf{\hat{r}} + r\dot{\theta}\mathbf{\hat{\theta}} = \dot{r}\mathbf{\hat{r}} + r\omega\mathbf{\hat{\theta}} \\[5pt] \mathbf{a} &= (\ddot{r} - r\dot{\theta}^2)\mathbf{\hat{r}} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\mathbf{\hat{\theta}} \end{aligned}}\]בתאוצה מעגלית קצובה:
\[\boxed{ \begin{aligned} \vec{v} &= R\omega\mathbf{\hat{\theta}} \\[5pt] \vec{a} &= -R\omega^2\mathbf{\hat{r}} \end{aligned}}\]קואורדינטות גליליות (3D)
המרה מקרטזיות לגליליות:
\[\boxed{ \begin{aligned} x &= r\cos\theta \\[5pt] y &= r\sin\theta \\[5pt] z &= z \end{aligned}}\] \[\boxed{ \begin{aligned} r &= \sqrt{x^2 + y^2} \\[5pt] \theta &= \arctan\left(\frac{y}{x}\right) \text{adjusted for quadrant} \\[5pt] z &= z \end{aligned}}\]קואורדינטות כדוריות (3D)
המרה מקרטזיות לכדוריות:
- $r = \sqrt{x^2 + y^2 + z^2}$
- $\theta$ = זווית מציר z
- $\varphi$ = זווית במישור xy
המרה מכדוריות לקרטזיות:
- $x = r\sin\theta\cos\varphi$
- $y = r\sin\theta\sin\varphi$
- $z = r\cos\theta$
קינמטיקה - תורת התנועה
הגדרות בסיסיות
וקטור מיקום
\[\vec{r} = x\mathbf{\hat{x}} + y\mathbf{\hat{y}} + z\mathbf{\hat{z}}\]וקטור העתק
\[\boxed{ \begin{aligned} \Delta \vec{r} &= \vec{r}_2 - \vec{r}_1 \\[5pt] &=\vec{r}(t + \Delta t) - \vec{r}(t) \\[5pt] &= \Delta x\mathbf{\hat{x}} + \Delta y\mathbf{\hat{y}} + \Delta z\mathbf{\hat{z}} \end{aligned}}\]מהירות ממוצעת
\[\vec{v}_{\text{avg}} = \frac{\Delta \vec{r}}{\Delta t} = \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{\Delta t}\]מהירות רגעית
\[\vec{v} = \lim_{\Delta t \to 0} \frac{\Delta \vec{r}}{\Delta t} = \frac{d\vec{r}}{dt}\]גודל המהירות (סקלר)
\[v = \vert\vec{v}\vert = \sqrt{v_x^2 + v_y^2 + v_z^2} \, \mathrm{m/s}\]תאוצה
\[\mathbf{a} = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2} = \frac{\Delta \vec{v}}{\Delta t} = \frac{\vec{v}(t+\Delta t) - \vec{v}(t)}{\Delta t}\]מהירות יחסית
איך גוף $A$ רואה את גוף $B$:
\[\vec{v}_{A\to B} = \vec{v}_B - \vec{v}_A\]תנועה בקו ישר עם תאוצה קבועה
\[\boxed{ \begin{aligned} x(t) &= x_0 + v_0t + \frac{1}{2}at^2 \\[5pt] v(t) &= v_0 + at \\[5pt] v^2 &= v_0^2 + 2a\Delta x \end{aligned}}\]צניחה חופשית (תנועה אנכית)
\[\boxed{ \begin{aligned} y(t) &= y_0 + v_0t - \frac{1}{2}gt^2 \\[5pt] v_y(t) &= v_0 - gt \\[5pt] v_y^2 &= v_0^2 - 2g\Delta y \end{aligned}}\]תנועה בליסטית (תנועת קליע)
רכיב אופקי (ללא תאוצה):
\[x(t) = x_0 + v_{0x}t\]רכיב אנכי (עם תאוצת כובד):
\[y(t) = y_0 + v_{0y}t - \frac{1}{2}gt^2\]טווח מקסימלי:
\[R = \frac{v_0^2\sin(2\alpha)}{g}\]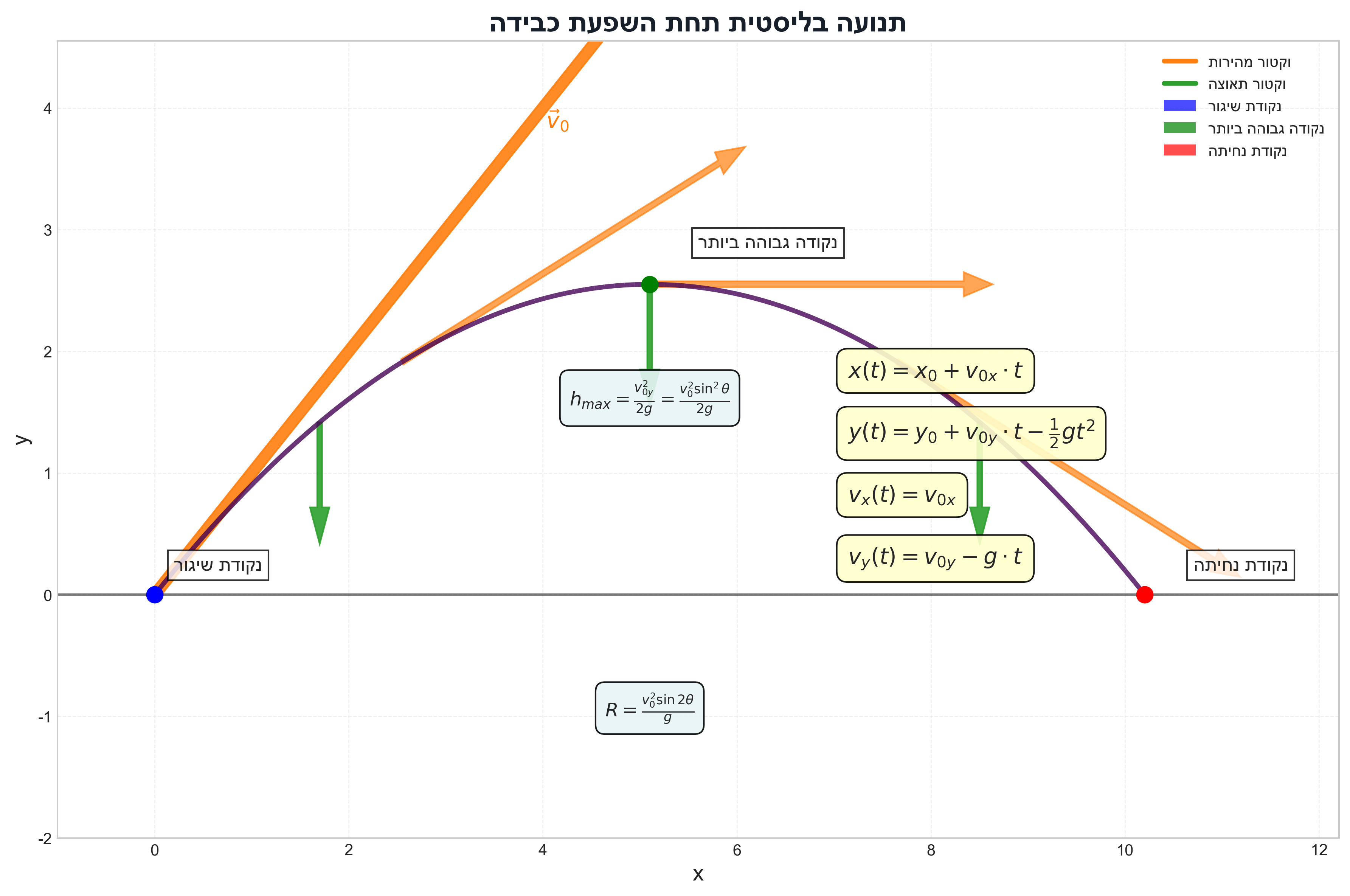
תנועה מעגלית
תנועה מעגלית קצובה (מהירות זוויתית קבועה)
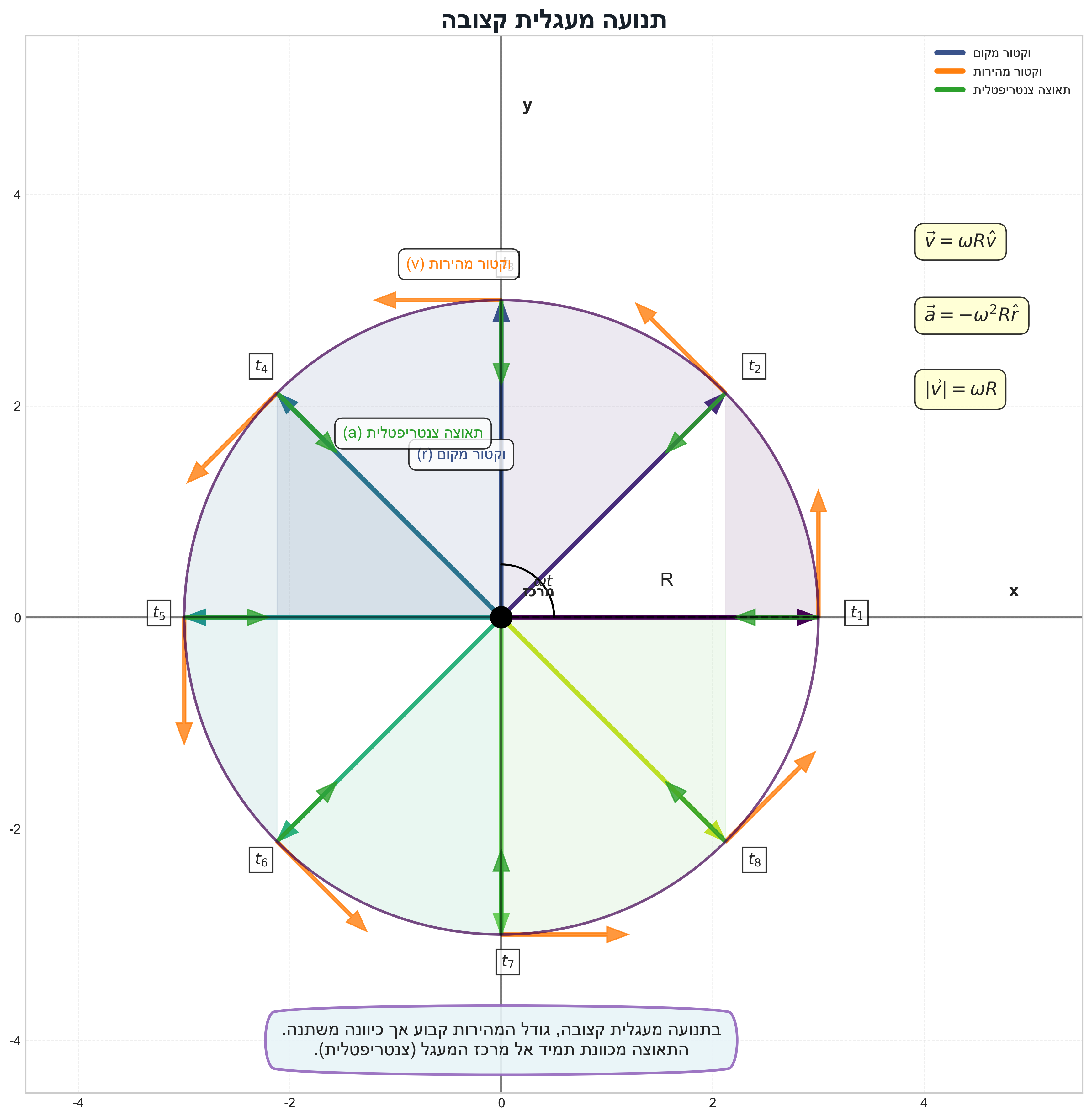
וקטור המיקום:
\[\vec{r}(t) = r[\cos(\omega t)\mathbf{\hat{x}} + \sin(\omega t)\mathbf{\hat{y}}]\]מהירות זוויתית:
\[\omega = \frac{d\theta}{dt} = \frac{2\pi}{T}\]מהירות משיקית:
\[v = r\omega\]תאוצה צנטריפטלית (כלפי המרכז):
כוח צנטריפוגלי - מהמרכז החוצה:
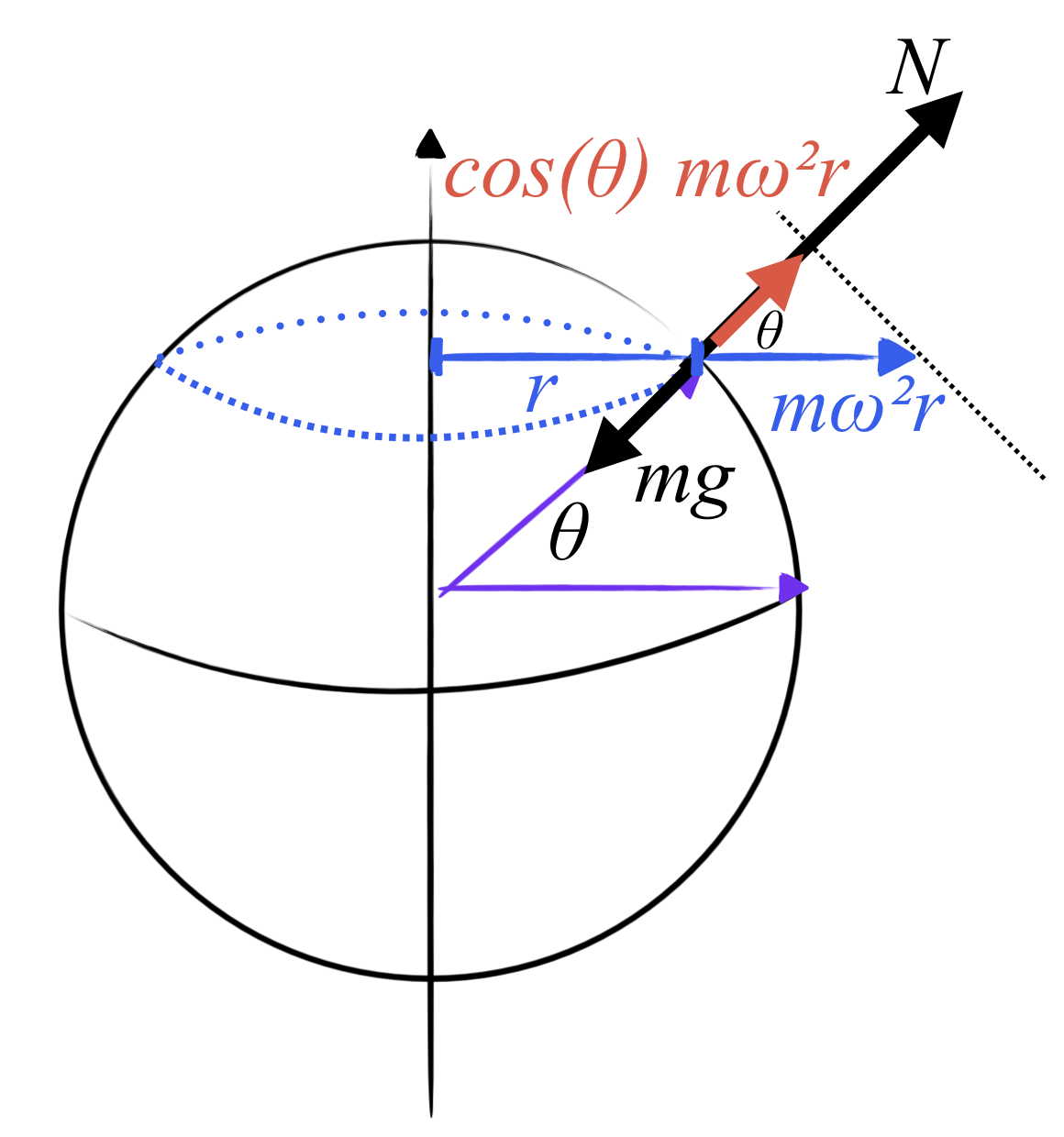
תנועה מעגלית כללית
תאוצה זוויתית:
\[\alpha = \frac{d\omega}{dt} = \frac{d^2\theta}{dt^2}\]תאוצה משיקית:
\[a_t = r\alpha\]תאוצה כוללת:
\[\mathbf{a} = -a_c\mathbf{\hat{r}} + a_t\mathbf{\hat{\theta}}\]תנועה ספירלית
תנועה מעגלית עם רדיוס משתנה (למשל אקספוננציאלית):
\[r(t) = r_0 e^{\alpha t}\]- אם $\alpha > 0$ — התנועה מתפשטת החוצה
- אם $\alpha < 0$ — התנועה מתכווצת פנימה
דינמיקה - חוקי ניוטון וכוחות
חוקי ניוטון
חוק ראשון (חוק ההתמדה)
\[\sum \mathbf{F} = 0 \Rightarrow \vec{v} = \text{const}\]גוף יישאר במנוחה או בתנועה ישרה קצובה כל עוד לא פועל עליו כוח שקול
חוק שני (חוק התנועה)
\[\sum \mathbf{F} = m\mathbf{a}\]התאוצה של גוף פרופורציונית לכוח השקול הפועל עליו
דוגמה - מישור משופע:
- ציר ניצב למישור: $N = mg\cos\alpha$ (אין תאוצה)
- ציר מקביל למישור: $mg\sin\alpha = ma$ (יש תאוצה)
חוק שלישי (חוק הפעולה והתגובה)
\[\mathbf{F}_{12} = -\mathbf{F}_{21}\]לכל פעולה יש תגובה שווה בגודלה והפוכה בכיוונה
סוגי כוחות
כוח כבידה (משקל)
\[\mathbf{F}_g = -mg\hat{j}\]כיוון: תמיד כלפי מטה
כוח נורמלי
\[N\]כיוון: תמיד ניצב למשטח המגע
כוח חיכוך
חיכוך סטטי (מנוחה):
\[f_s \leq \mu_s N\]חיכוך קינטי (תנועה):
\[f_k = \mu_k N\]כיוון: תמיד מנוגד לכיוון התנועה (או התנועה הצפויה)
הערה: במערכת עם תנועה שנובעת מכוח מדומה החיכוך להבנתי דווקא עם כיוון התנועה, כי הוא מונע את התנועה המדומה. ראו את שאלת הפשפש על תקליט משיעור 13.
כוח קפיץ (חוק הוק)
\[F = -kx\]- $k$ - קבוע הקפיץ [N/m]
- $x$ - הסטייה ממצב שיווי משקל
- הסימן השלילי מציין כוח מחזיר
כוח גרר (התנגדות תווך)
גרר ליניארי (מהירויות נמוכות):
\[F_d = -\beta v\]גרר ריבועי (מהירויות גבוהות):
\[F_d = -\beta v^2\]כוחות מדומים (במערכות לא אינרציאליות)
\[\mathbf{F}_{\text{pseudo}} = -m\mathbf{a}_{\text{frame}}\]
- מערכת לא אינרציאלית: מערכת ייחוס שנמצאת בתאוצה (ליניארית או זוויתית), ולכן יש בה צורך להוסיף כוחות מדומים (פסאודו-כוחות) כדי שחוקי ניוטון “יעבדו” בה.
- מערכת אינרציאלית: מערכת ייחוס שאינה מואצת (כלומר נעה במהירות קבועה או נחה), ובה חוקי ניוטון תקפים כפי שהם – בלי להוסיף כוחות מדומים.
מערכת, מבחינתנו, היא מערכת הצירים הרלוונטית.
תנע ומתקף
תנע:
\[\vec{p} = m\vec{v}\]מתקף:
\[\vec{J} = \int \mathbf{F} dt = \Delta \vec{p}\]שימור תנע:
\[\sum \vec{p}_{\text{before}} = \sum \vec{p}_{\text{after}}\]בדרך כלל תסייע לנו לנתח התנגשויות בין גופים. נניח שיש שני גופים במסות של $m$ ו-$M$ אז אם הגוף הקטן מתנגש פלסטית במהירות $v_0$ עם הגוף הגדול במנוחה, אז:
\[mv_0 = (m + M)V \implies V = \frac{mv_0}{m + M}\]הערה חשובה: המהירות של הדבוקה קטנה יותר כי התנע נשמר אבל האנרגיה הקינטית לא נשמרת בהתנגשות פלסטית. חלק מהאנרגיה הקינטית הופכת לחום, עיוות ורעש.
השוואת אנרגיות:
- אנרגיה התחלתית: $K_i = \frac{1}{2}mv_0^2$
- אנרגיה סופית: $K_f = \frac{1}{2}(m + M)V^2 = \frac{1}{2}\frac{m^2v_0^2}{m + M}$
- תמיד: $K_f < K_i$ (אובדן אנרגיה!)
סוגי התנגשויות:
- אלסטית: נשמרים תנע ואנרגיה קינטית
- פלסטית: נשמר תנע בלבד, אנרגיה קינטית לא נשמרת
עבודה ואנרגיה
עבודה בסיסית:
\[W = \int \mathbf{F} \cdot d\vec{r}\]עבודה במימד אחד (כוח קבוע):
\[W = F \cdot d \cdot \cos\theta\]אנרגיה קינטית:
\[K = \frac{1}{2}mv^2\]אנרגיה פוטנציאלית כבידתית:
\[U_g = mgh\]אנרגיה מכנית כוללת:
\[E = K + U\]משפטי עבודה-אנרגיה
משפט עבודה-אנרגיה הבסיסי:
\[W_{\text{net}} = \Delta K = K_f - K_i\]משפט עבודה-אנרגיה עם כוחות משמרים ולא משמרים:
\[W_{\text{non-conservative}} = \Delta E = E_f - E_i\]כאשר:
- $W_{\text{non-conservative}}$ = עבודת כוחות לא משמרים (כמו חיכוך)
- $E = K + U$ = אנרגיה מכנית כוללת
שימור אנרגיה
עם כוחות משמרים בלבד:
\[E_i = E_f \quad \text{or} \quad K_i + U_i = K_f + U_f\]עם כוחות לא משמרים (חיכוך):
\[E_i + W_{\text{non-conservative}} = E_f\]או בצורה מפורשת:
\[K_i + U_i + W_{\text{friction}} = K_f + U_f\]עבודת חיכוך
עבודת חיכוך (תמיד שלילית):
\[W_{\text{friction}} = -f_k \cdot d = -\mu_k mg \cdot d\]חישוב עבודת חיכוך מאנרגיות:
\[W_{\text{friction}} = E_f - E_i = (K_f + U_f) - (K_i + U_i)\]אנרגיה שאבדה בחיכוך:
\[\Delta E_{\text{lost}} = |W_{\text{friction}}\vert = E_i - E_f\]דוגמאות יישום
גוף גולש במדרון עם חיכוך:
- אנרגיה התחלתית: $E_i = mgh_i$ (אם מתחיל ממנוחה)
- אנרגיה סופית: $E_f = \frac{1}{2}mv_f^2 + mgh_f$
- עבודת חיכוך: $W_{\text{friction}} = E_f - E_i$
התנגשויות:
- אלסטית: נשמרת אנרגיה קינטית ותנע
- פלסטית: נשמר תנע בלבד, אנרגיה קינטית לא נשמרת
נוסחאות נוספות
עבודה מגרף כוח-מקום:
\[W = \text{area under the curve } F(x)\]כוח ממשיק עקומת אנרגיה פוטנציאלית:
\[F = -\frac{dU}{dx}\]אנרגיה פוטנציאלית כללית:
\[\Delta U = -W_{\text{conservative}}\]עקרונות חשובים
- כוחות משמרים: עבודתם לא תלויה במסלול (כבידה, אלסטי)
- כוחות לא משמרים: עבודתם תלויה במסלול (חיכוך, התנגדות אוויר)
- חיכוך תמיד מקטין אנרגיה מכנית: $W_{\text{friction}} < 0$
- שימור תנע: תמיד נשמר כאשר אין כוחות חיצוניים נטו
תנועה הרמונית ואוסצילציות
אוסצילטור הרמוני פשוט
משוואת התנועה
\[m\ddot{x} + kx = 0\]או בצורה סטנדרטית:
\[\ddot{x} + \omega^2 x = 0\]פתרון כללי
\[x(t) = A\cos(\omega t + \phi)\]כאשר:
- $A$ - משרעת התנודה
- $\omega$ - תדירות זוויתית
- $\phi$ - פאזה התחלתית
מכאן שכאשר משחררים ממנוחה, הפתרון הוא:
\[x(t) = A\cos(\omega t)\]פתרון ברישום נוסף:
\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]כאשר $A$ ו-$B$ הם קבועים שנקבעים על פי תנאי ההתחלה.
בדרך כלל יצא לי:
\[x(t) = x_0 \cos(\omega t) + \frac{v_0}{\omega} \sin(\omega t)\]תדירות זוויתית
\[\omega = \sqrt{\frac{k}{m}}\]זמן מחזור
\[T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{m}{k}}\]תדירות
\[f = \frac{1}{T} = \frac{\omega}{2\pi} = \frac{1}{2\pi}\sqrt{\frac{k}{m}}\]אנרגיה באוסצילטור הרמוני
אנרגיה קינטית:
\[K = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2 A^2 \sin^2(\omega t + \phi)\]אנרגיה פוטנציאלית:
\[U = \frac{1}{2}kx^2 = \frac{1}{2}kA^2 \cos^2(\omega t + \phi)\]אנרגיה כוללת (קבועה):
\[E = K + U = \frac{1}{2}kA^2\]מטוטלת מתמטית
משוואת תנועה (זוויות קטנות)
\[\ddot{\theta} + \frac{g}{L}\theta = 0\]תדירות זוויתית
\[\omega = \sqrt{\frac{g}{L}}\]זמן מחזור
\[T = 2\pi\sqrt{\frac{L}{g}}\]אוסצילטור במערכות מואצות
במעלית מואצת כלפי מעלה בתאוצה $A$
- תאוצה אפקטיבית: $g_{\text{eff}} = \sqrt{g^2 + A^2}$
- אם תאוצה $A$ היא תאוצה של המעלית כלפי מעלה: $g_{\text{eff}} = g + A$
- תדירות זוויתית: $\omega = \sqrt{\frac{g + A}{L}}$
- זמן מחזור: $T = 2\pi\sqrt{\frac{L}{g + A}}$
ברכבת מואצת אופקית בתאוצה $A$
- זווית שיווי משקל: $\theta_0 = \arctan\left(\frac{A}{g}\right)$
- תדירות: $\omega = \sqrt{\frac{g}{L\cos\theta_0}}$
בעיות מרכזיות ודוגמאות
1. בעיית הטריז והגליל
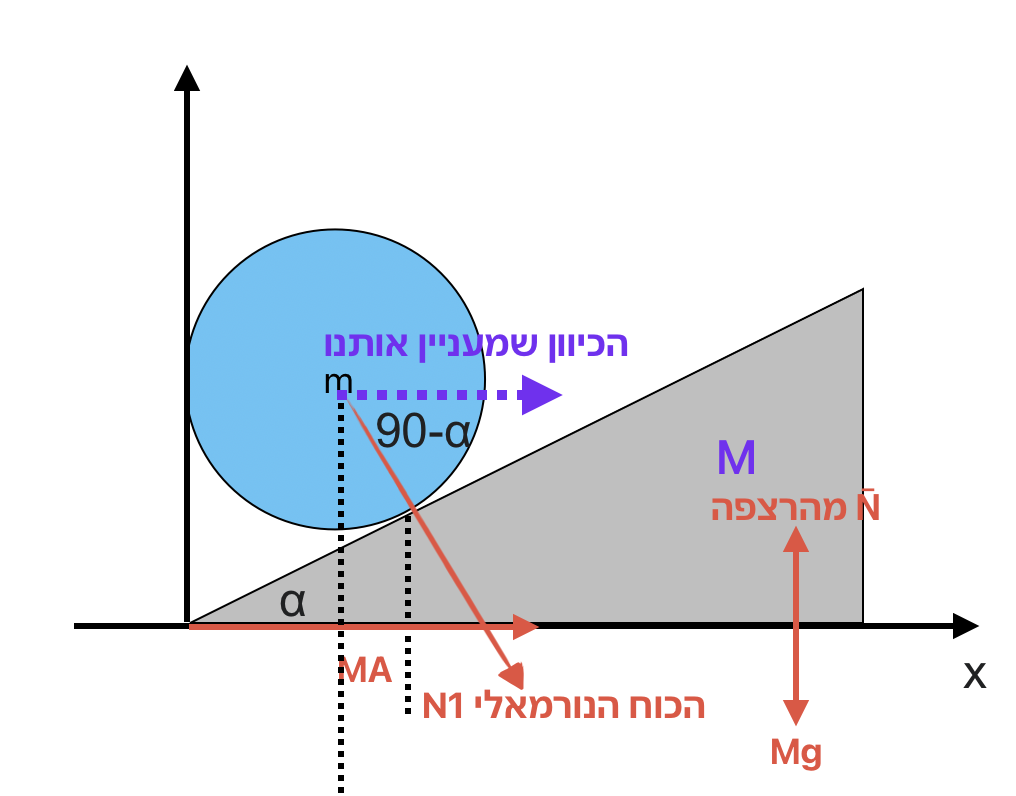
נתונים:
- גליל מסה $m$ על טריז מסה $M$
- זווית הטריז $\alpha = 30°$
- אין חיכוך
פתרון:
\[N_m = \frac{2gMm\sqrt{3}}{3M + m}\] \[a_x = \frac{10m\sqrt{3}}{3M + m}\] \[a_y = \frac{10m}{3M + m}\]2. צנחנית עם התנגדות אוויר
כוח גרר: $F = \beta v^2$
משוואת התנועה:
\[mg - \beta v^2 = m\frac{dv}{dt}\]מהירות טרמינלית:
\[v_T = \sqrt{\frac{mg}{\beta}}\]פתרון כללי:
\[v(t) = v_T \tanh\left(\frac{gt}{v_T}\right)\]3. גוף על מישור משופע
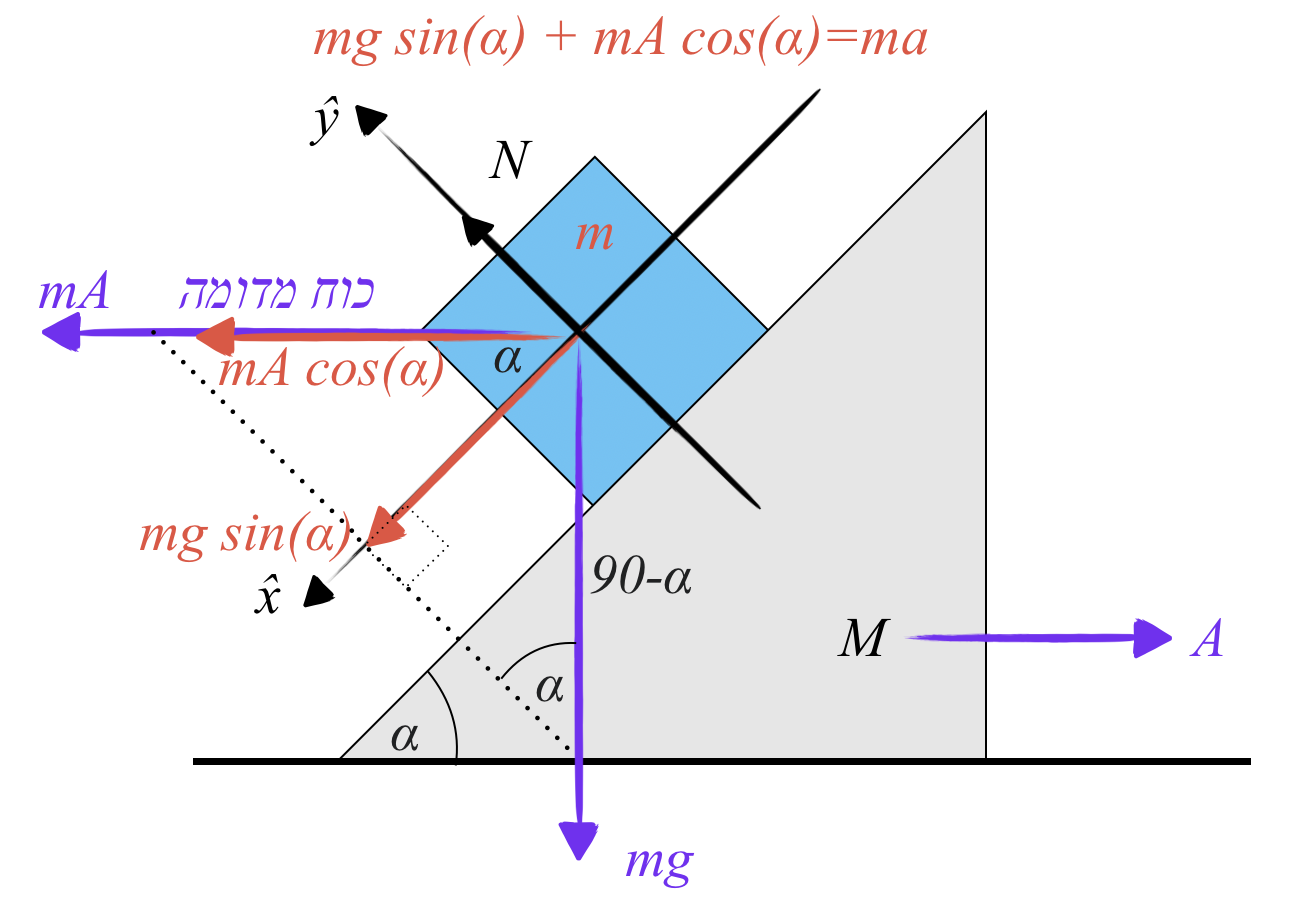
זווית קריטית (ללא החלקה):
\[\theta_{\max} = \arctan(\mu_s)\]תאוצה בהחלקה:
\[a = g(\sin\theta - \mu_k\cos\theta)\]תנועה במהירות קבועה:
\[\theta = \arctan(\mu_k)\]4. מכונת אטווד עם זבוב
תאוצה כשהזבוב על מסה:
\[a = \frac{mg}{2M+m}\]תאוצה ללא זבוב:
\[a = 0\]5. תנועה יחסית - הולך רגל וקרוסלה
- הולך רגל: $x(t) = 4 + 4t$ (תנועה ישרה)
- נער על קרוסלה: $\vec{r}(t) = (2\sin(3t), 2\cos(3t))$ (תנועה מעגלית)
-
מהירות יחסית:
\[\vec{v}_{\text{rel}} = \vec{v}_{\text{boy}} - \vec{v}_{\text{man}}\]
טרנספורמציית גליליית:
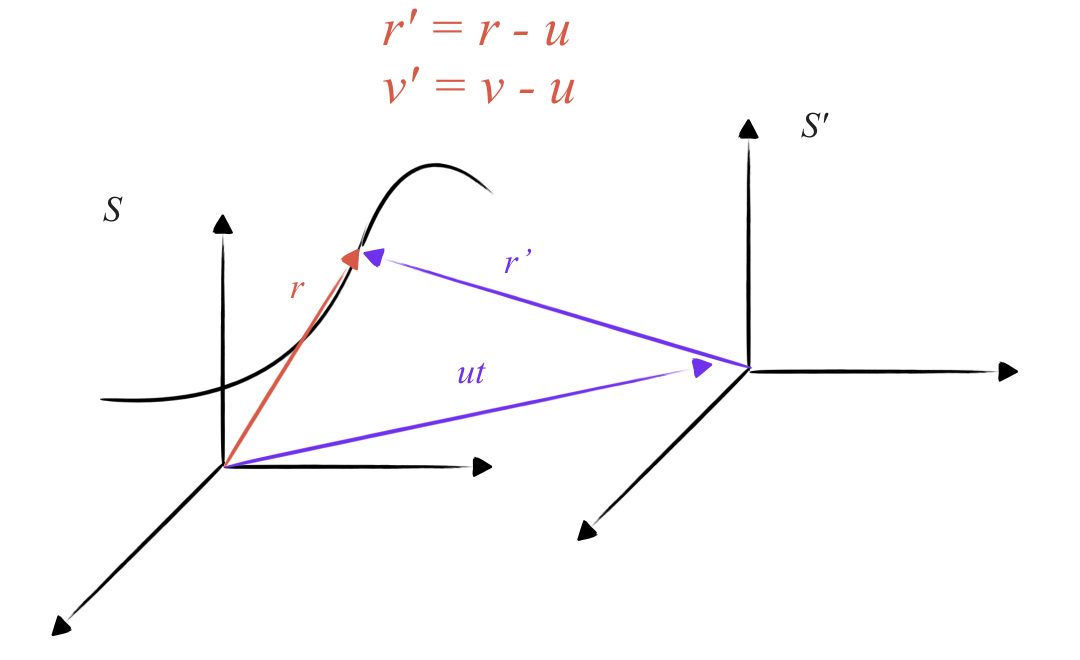
6. תנועה ספירלית מתכנסת
דוגמה: $\vec{r}(t) = e^{-\alpha t}[\cos(\omega t)\mathbf{\hat{x}} + \sin(\omega t)\mathbf{\hat{y}}]$
- המרחק דועך: $\vert\vec{r}(t)\vert = e^{-\alpha t}$
- הזווית גדלה: $\theta(t) = \omega t$
- גודל המהירות: $\vert\vec{v}(t)\vert = e^{-\alpha t}\sqrt{\alpha^2 + \omega^2}$
7. מערכות מצומדות
שתי מסות עם קפיץ על מישור משופע:
תדירות מותאמת:
\[\omega = \sqrt{\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}}\]טכניקות פתרון ואלגוריתמים
אלגוריתם כללי לפתרון בעיות
- תרשים כוחות
- צייר דיאגרמת גוף חופשי לכל גוף
- סמן את כל הכוחות הפועלים
- ודא שלא שכחת כוחות
- בחירת מערכת צירים
- בחר צירים נוחים (לרוב לאורך התנועה)
- במישור משופע: ציר אחד לאורך המישור
- בתנועה מעגלית: צירים פולריים
- כתיבת משוואות תנועה
- כתוב $\sum F_x = ma_x$ לכל ציר
- כתוב עבור כל גוף בנפרד
- שים לב לסימנים
- הוספת אילוצים
- קשרים גיאומטריים (חוט לא נמתח)
- קשרים קינמטיים (תאוצות זהות)
- תנאי התחלה
- פתרון מערכת המשוואות
- ספור משתנים ומשוואות
- פתור באלגברה או דיפרנציאלית
- בדוק סבירות התוצאה
משוואות דיפרנציאליות נפוצות ופתרונותיהן
אוסצילטור הרמוני
משוואה: $\ddot{x} + \omega^2 x = 0$
פתרון: $x(t) = A\cos(\omega t) + B\sin(\omega t)$
אוסצילטור עם הסטה
משוואה: $\ddot{x} + \omega^2 x = C$
פתרון: $x(t) = A\cos(\omega t) + B\sin(\omega t) + \frac{C}{\omega^2}$
דעיכה אקספוננציאלית
משוואה: $\dot{x} = -\gamma x$
פתרון: $x(t) = x_0 e^{-\gamma t}$
גידול אקספוננציאלי
משוואה: $\ddot{x} = \omega^2 x$
פתרון: $x(t) = A\cosh(\omega t) + B\sinh(\omega t)$
בדיקות חשובות
- בדיקת יחידות
- ודא שהיחידות מתאימות בשני צדי המשוואה
- כוח: [N] = [kg⋅m/s²]
- אנרגיה: [J] = [kg⋅m²/s²]
- בדיקת גבולות
- מה קורה כש $m \to 0$ או $m \to \infty$?
- מה קורה כש $\theta \to 0$ או $\theta \to 90°$?
- בדיקת סימטריות
- האם הבעיה סימטרית?
- האם אפשר לפשט?
- בדיקת שימור
- האם האנרגיה נשמרת?
- האם התנע נשמר?
נוסחאות מהירות לבחינה
כוחות וחוקי ניוטון
\[\boxed{ \begin{aligned} \sum \mathbf{F} &= m\mathbf{a} \\[5pt] \mathbf{F}_g &= mg \\[5pt] f_s &\leq \mu_s N \\[5pt] f_k &= \mu_k N \\[5pt] \mathbf{F}_{\text{spring}} &= -kx \end{aligned}}\]קינמטיקה - תאוצה קבועה
\[\boxed{ \begin{aligned} v &= v_0 + at \\[5pt] x &= x_0 + v_0t + \frac{1}{2}at^2 \\[5pt] v^2 &= v_0^2 + 2a\Delta x \end{aligned}}\]תנועה מעגלית
\[\boxed{ \begin{aligned} v &= r\omega \\[5pt] a_c &= \frac{v^2}{r} = r\omega^2 \\[5pt] T &= \frac{2\pi}{\omega} \end{aligned}}\]תנועה הרמונית
\[\boxed{ \begin{aligned} \omega &= \sqrt{\frac{k}{m}} \\[5pt] T &= 2\pi\sqrt{\frac{m}{k}} \\[5pt] E &= \frac{1}{2}kA^2 \end{aligned}}\]מטוטלת
\[\boxed{ \begin{aligned} \omega &= \sqrt{\frac{g}{L}} \\[5pt] T &= 2\pi\sqrt{\frac{L}{g}} \end{aligned}}\]- קרא את השאלה פעמיים לפני שמתחיל
- צייר תמיד דיאגרמת כוחות
- בדוק יחידות בכל שלב
- השתמש בערכי קירוב: $g = 10$, $\pi \approx 3$, $\sqrt{3} \approx 1.7$
- רשום תשובות ביניים
טעויות נפוצות להימנע מהן
- אל תשכח לפרק וקטורים לרכיבים
- שים לב לכיוון הכוחות (סימנים!)
- חיכוך תמיד נגד כיוון התנועה
- בתנועה מעגלית, תאוצה צנטריפטלית פנימה
- אל תערבב בין מסה למשקל
אסטרטגיה לפתרון
- 5 דקות ראשונות: קרא את כל המבחן
- התחל מהקל: פתור קודם שאלות שאתה בטוח בהן
- הקצה זמן: חלק את הזמן לפי ניקוד
- בדיקה: השאר 10 דקות בסוף לבדיקה