מבוא לכוח לורנץ
הצימוד המינימלי
כשנתונה לנו צפיפות מטען $\rho$ שנמצאת בשדה אלקטרוסטטי, הכוח שפועל עליה ועל צפיפות הזרם מוגדר על ידי צימוד מינימלי:
\[\vec{f} = \rho \vec{E} + \vec{j} \times \vec{B}\]כאשר $\vec{f}$ היא צפיפות כוח (לא כוח על חלקיק בודד), ו-$\vec{j}$ היא צפיפות הזרם. היחידות הן של צפיפות כוח - כוח ליחידת נפח.
להרחבה על הדרך שבה מקבלים זאת מוזמנים לקרוא על לגראנז׳יאן ולחלץ את הלגרנג׳יאן של התורה האלקטרו מגנטית (ככל הנראה אפשר לבנות משוואות תנועה, בדומה לניוטון, ואז לגזור את הכוח שפועל על צפיפויות מטען וזרם).
מעבר למטען נקודתי
כדי לעבור מצפיפות כוח לכוח על חלקיק בעל מטען סופי $q$, יש לבצע אינטגרציה מרחבית. כשמדובר במטען נקודתי, האינטגרציה נעשית באמצעות פונקציית דלתא של דיראק - לא למדנו אותה והיא לא נדרשת ברמת הקורס. התוצאה היא כוח לורנץ.
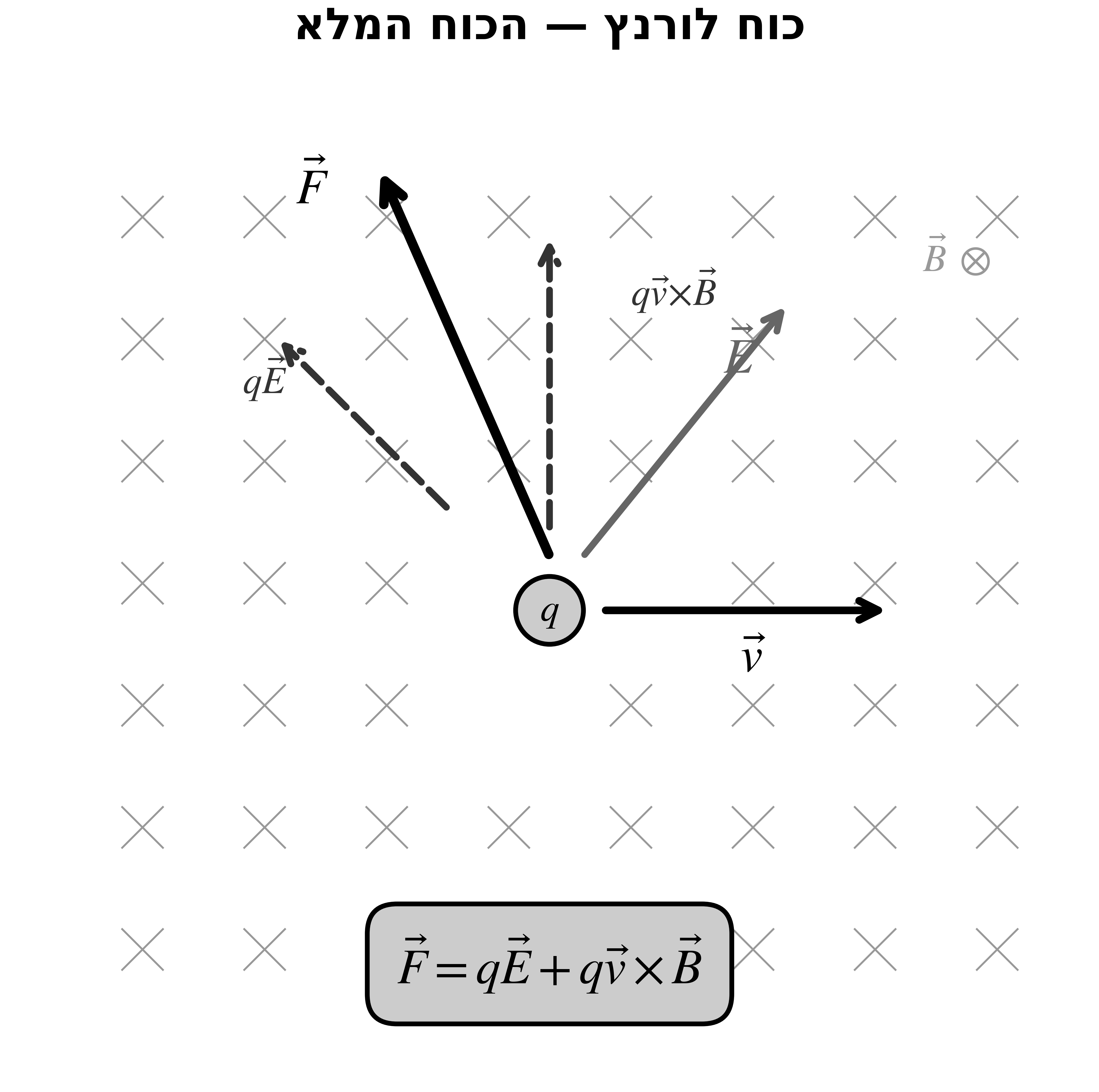
כוח לורנץ המלא
\[\boxed{\vec{F} = \underbrace{q \, \vec{E}}_{F_e} + \underbrace{q \, \vec{v} \times \vec{B}}_{F_m}}\]כאשר:
- $q$ - מטען החלקיק
- $\vec{E}$ - השדה החשמלי
- $\vec{B}$ - השדה המגנטי
- $\vec{v}$ - מהירות החלקיק
הרכיב הראשון ($\vec{F}_e = q \, \vec{E}$) הוא כוח קולון מהשדה החשמלי, במקרה ש-$E=\frac{qQ}{r^2}$ קיבלנו את חוק קולון.
הרכיב השני ($\vec{F}_m = q \, \vec{v} \times \vec{B}$) הוא הכוח המגנטי - הוא מופיע רק כשיש מטענים בתנועה.
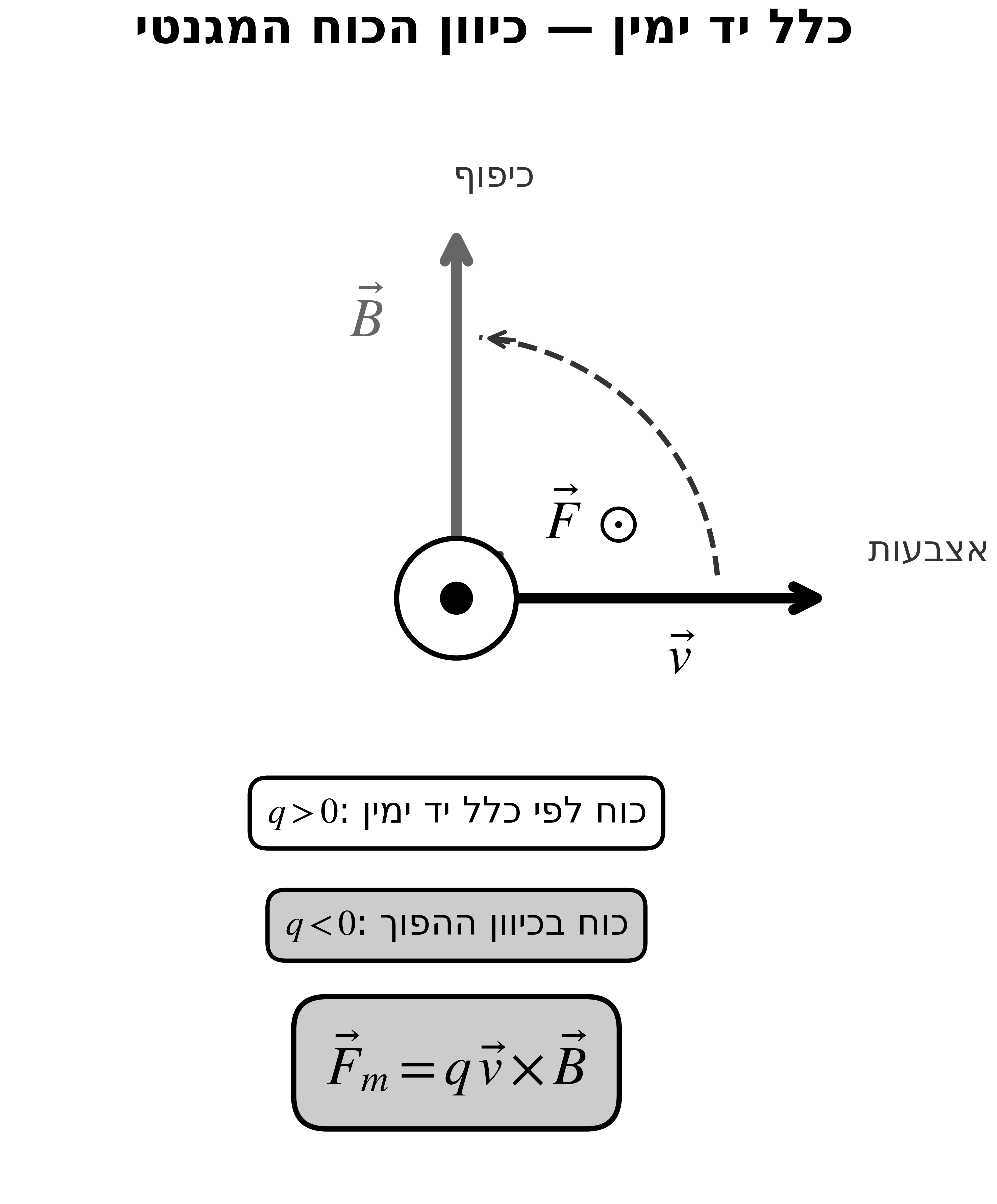
הכוח המגנטי
תכונות הכוח המגנטי
\[\vec{F}_m = q \, \vec{v} \times \vec{B}\]זה כוח מיוחד מכיוון שהוא תלוי במהירות של החלקיק (זאת פעם ראשונה שאנחנו נתקלים בזה, למעט צורה אחרת של כוח תלוי מהירות בהקשר של חיכוך).
שלושה תנאים הכרחיים לקיום כוח מגנטי:
- חייב להיות שדה מגנטי ($\vec{B} \neq 0$)
- החלקיק חייב לנוע ($\vec{v} \neq 0$)
- למהירות חייב להיות רכיב ניצב לשדה המגנטי (אם $\vec{v} \parallel \vec{B}$ אז $\vec{F}_m = 0$)
חשוב מאוד: חלקיק טעון במנוחה בתוך שדה מגנטי לא מרגיש שום כוח מגנטי! רק הרכיב המאונך לשדה המגנטי “רואה” את השדה - המכפלה הוקטורית של שני וקטורים מקבילים היא אפס.
כיוון הכוח
- הכוח תמיד ניצב למהירות (כתוצאה מהמכפלה הוקטורית)
- הכוח תמיד ניצב לשדה המגנטי
- כיוון הכוח נקבע לפי כלל יד ימין, עד כדי סימן המטען
אם המטען חיובי: $\vec{F} = \vec{v} \times \vec{B}$ (כפי שנותן כלל יד ימין)
אם המטען שלילי: הכוח בכיוון ההפוך לתוצאת $\vec{v} \times \vec{B}$
תנועה מעגלית בשדה מגנטי אחיד
הגדרת הבעיה
חלקיק טעון במטען $q$ ומסה $m$ נכנס בניצב לשדה מגנטי אחיד $\vec{B} = B\hat{z}$ במהירות התחלתית $v_0$ במישור $xy$.
גזירת משוואות התנועה
מהחוק השני של ניוטון ומפיתוח המכפלה הוקטורית בעזרת דטרמיננטה, נקבל:
\[\begin{aligned} m\vec{a} &= q \, \vec{v} \times \vec{B} \\[6pt] \vec{a} &= \frac{q}{m} \left(\vec{v} \times \vec{B}\right) \\[6pt] \vec{a} &= \frac{q}{m} \begin{pmatrix} \hat{x} & \hat{y} & \hat{z} \\ v_x & v_y & v_z \\ 0 & 0 & B \end{pmatrix} \\[6pt] &= \frac{q}{m} \left(v_y B\,\hat{x} - v_x B\,\hat{y}\right) \\[6pt] &= \frac{qB}{m} \begin{pmatrix} v_y \\ -v_x \\ 0 \end{pmatrix} \end{aligned}\]משוואות התנועה המצומדות
השוואת מקדמים נותנת:
\[\boxed{a_x = \frac{qB}{m}v_y}\] \[\boxed{a_y = -\frac{qB}{m}v_x}\] \[a_z = 0\]אלו משוואות מצומדות: $a_x$ תלוי ב-$v_y$, ו-$a_y$ תלוי ב-$v_x$. המינוס במשוואה השנייה הוא קריטי - הוא זה שיוצר את התנועה המעגלית.
התדירות הגירוסקופית (ציקלוטרונית)
נגדיר:
\[\boxed{\omega = \frac{qB}{m}}\]זאת התדירות הגירוסקופית או התדירות הציקלוטרונית - התדירות הזוויתית של התנועה המעגלית.
פתרון המשוואות הדיפרנציאליות
נרשום $a_x = \dot{v}_x$ ו-$a_y = \dot{v}_y$:
\[\dot{v}_x = \omega v_y\] \[\dot{v}_y = -\omega v_x\]שלב 1: נגזור את המשוואה הראשונה שוב לפי הזמן:
\[\ddot{v}_x = \omega \dot{v}_y\]שלב 2: נציב את המשוואה השנייה ($\dot{v}_y = -\omega v_x$):
\[\ddot{v}_x = \omega \cdot (-\omega v_x) = -\omega^2 v_x\]שלב 3: זוהי משוואת אוסילטור הרמוני!
\[\boxed{\ddot{v}_x + \omega^2 v_x = 0}\]הפתרון הכללי:
\[v_x(t) = C\cos(\omega t + \varphi)\]שלב 4: מהמשוואה $\dot{v}_y = -\omega v_x$:
\[\dot{v}_y = -\omega C\cos(\omega t + \varphi)\]אינטגרציה:
\[v_y(t) = -C\sin(\omega t + \varphi)\]מיקום כפונקציה של הזמן
אינטגרציה של המהירויות:
\[x(t) = \frac{C}{\omega}\sin(\omega t + \varphi)\] \[y(t) = \frac{C}{\omega}\cos(\omega t + \varphi)\]הוכחת התנועה המעגלית
\[x^2 + y^2 = \left(\frac{C}{\omega}\right)^2[\sin^2(\omega t + \varphi) + \cos^2(\omega t + \varphi)] = \left(\frac{C}{\omega}\right)^2 = R^2\]זוהי משוואת מעגל ברדיוס $R = \frac{C}{\omega}$.
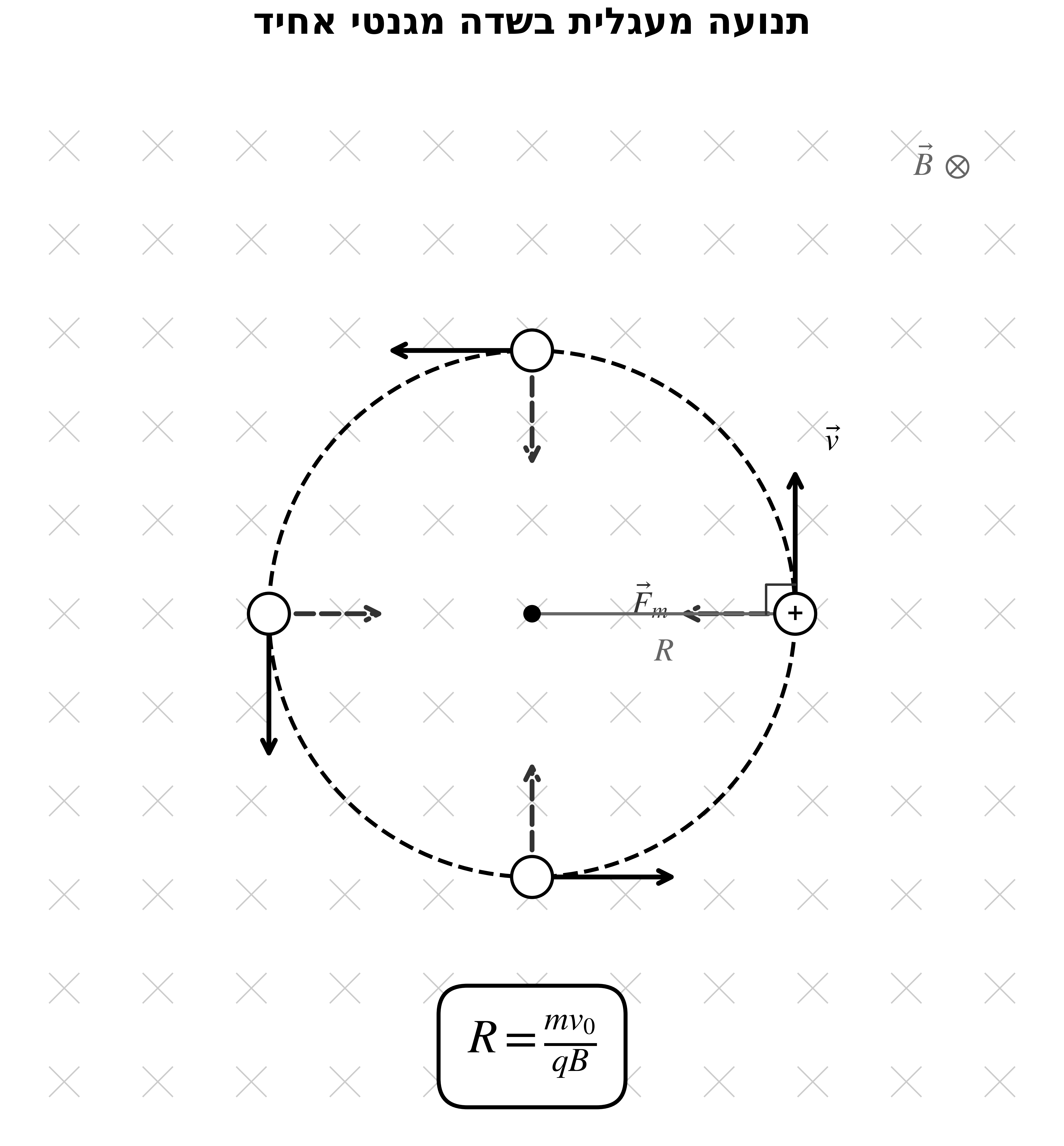
קביעת הקבוע מתנאי ההתחלה
אם החלקיק נכנס במהירות $v_0$, אז $C = v_0$, ולכן:
\[\boxed{R = \frac{C}{\omega} = \frac{v_0}{\omega} = \frac{v_0}{\frac{qB}{m}} = \frac{mv_0}{qB}}\]אימות מתנועה מעגלית (דרך חלופית)
בתנועה מעגלית קצובה, הכוח הצנטריפטלי שווה ל:
\[F_c = \frac{mv_0^2}{R}\]הכוח המגנטי (כשהמהירות ניצבת לשדה):
\[F_m = qv_0B\]השוואה ($F_c = F_m$):
\[qv_0B = \frac{mv_0^2}{R}\]פתרון עבור $R$:
\[R = \frac{mv_0}{qB} \checkmark\]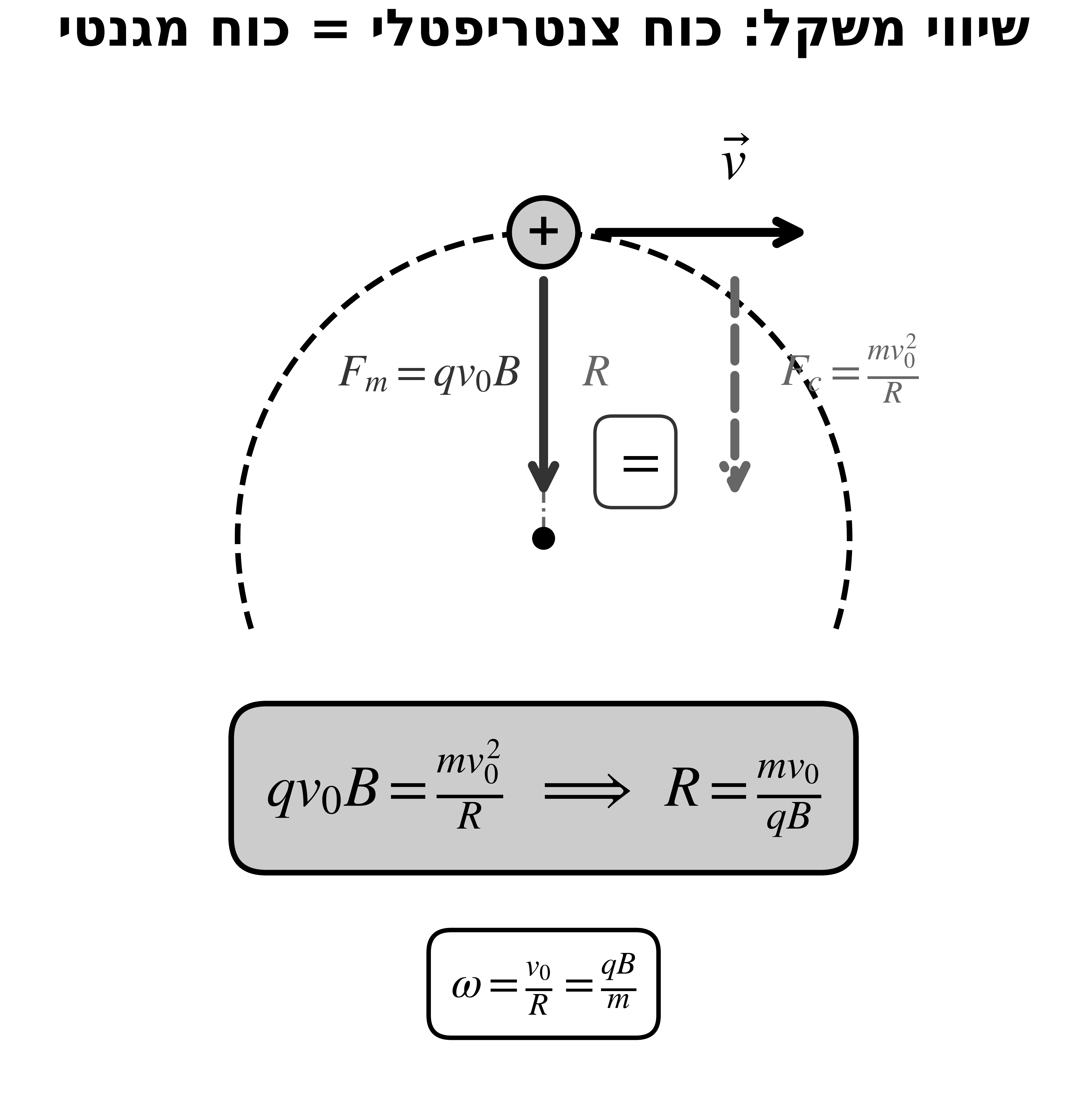
תנועה ספירלית - כניסה בזווית לשדה
המקרה הכללי
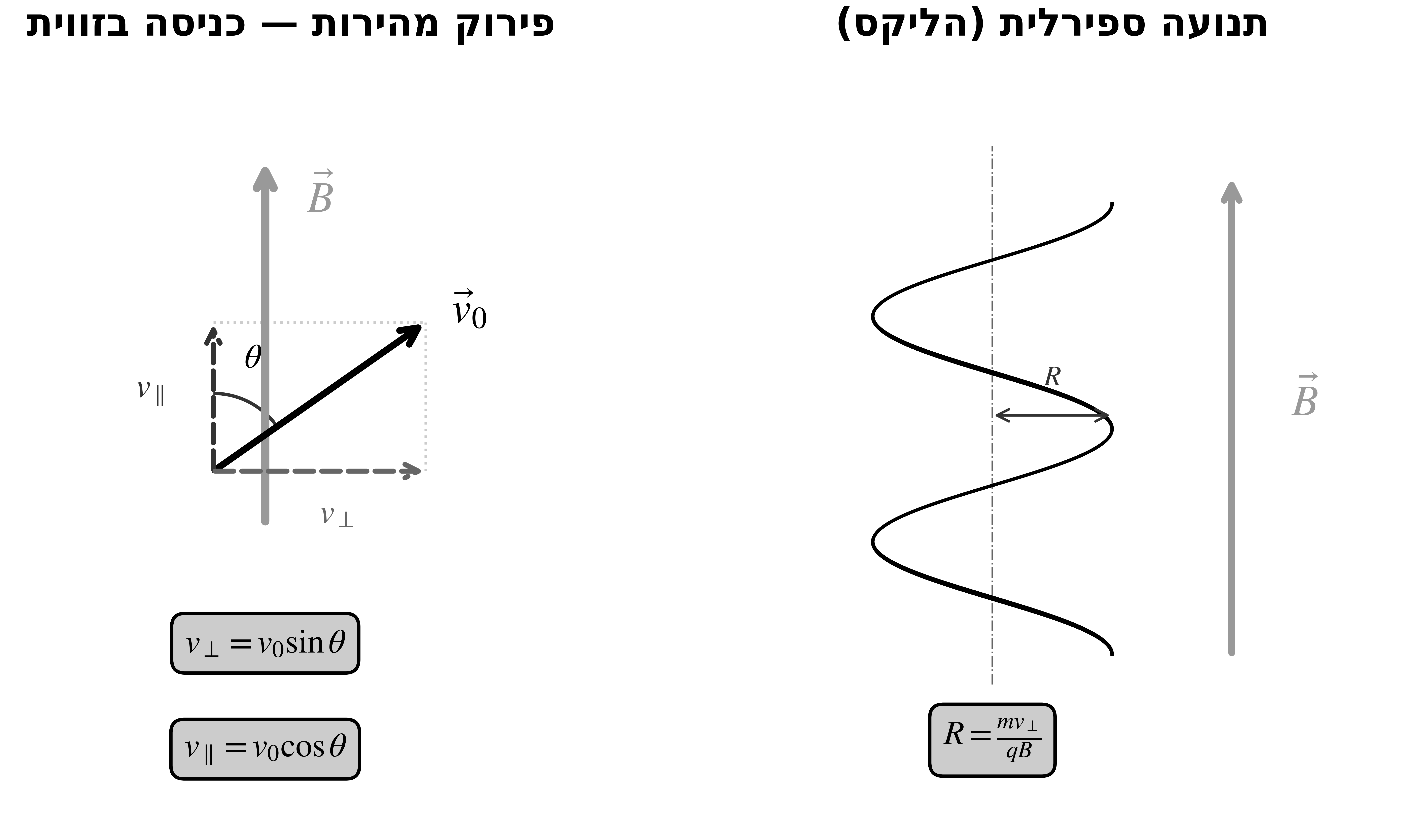
כאשר חלקיק נכנס בזווית $\theta$ ביחס לקווי השדה המגנטי, יש לפרק את המהירות לשני רכיבים:
פירוק המהירות
\[\begin{aligned} v_\perp &= v_0 \sin\theta \quad \text{(NITZAV to the field)} \\[6pt] v_\parallel &= v_0\cos\theta \quad \text{(parallel part)} \end{aligned}\]התנהגות כל רכיב
-
הרכיב הניצב ($v_\perp$): “רואה” את השדה המגנטי ומבצע תנועה מעגלית ברדיוס $R = \frac{mv_\perp}{qB}$
-
הרכיב המקביל ($v_\parallel$): לא רואה את השדה המגנטי כלל! מהחוק הראשון של ניוטון - ממשיך בתנועה קצובה באותה מהירות
התוצאה: תנועה ספירלית (הליקס)
החלקיק מבצע תנועה ספירלית סביב קווי השדה המגנטי:
- מסתובב סביב קו השדה (מהרכיב הניצב)
- מתקדם לאורך קו השדה (מהרכיב המקביל)
החלקיק פשוט “משתחל” על קווי השדה המגנטי.
יישום: השדה המגנטי של כדור הארץ והגנה מקרינה
מקור השדה המגנטי של כדור הארץ
- בליבת כדור הארץ יש ברזל נוזלי שמבצע תנועה סיבובית
- התנועה בקצב שונה מעט מסיבוב כדור הארץ עצמו
- כתוצאה נוצר זרם שמייצר שדה מגנטי
- השדה הוא בצורת דיפול מגנטי (מגנט לא יכול להיות מונופול!)
- קווי השדה יוצאים מהקטבים
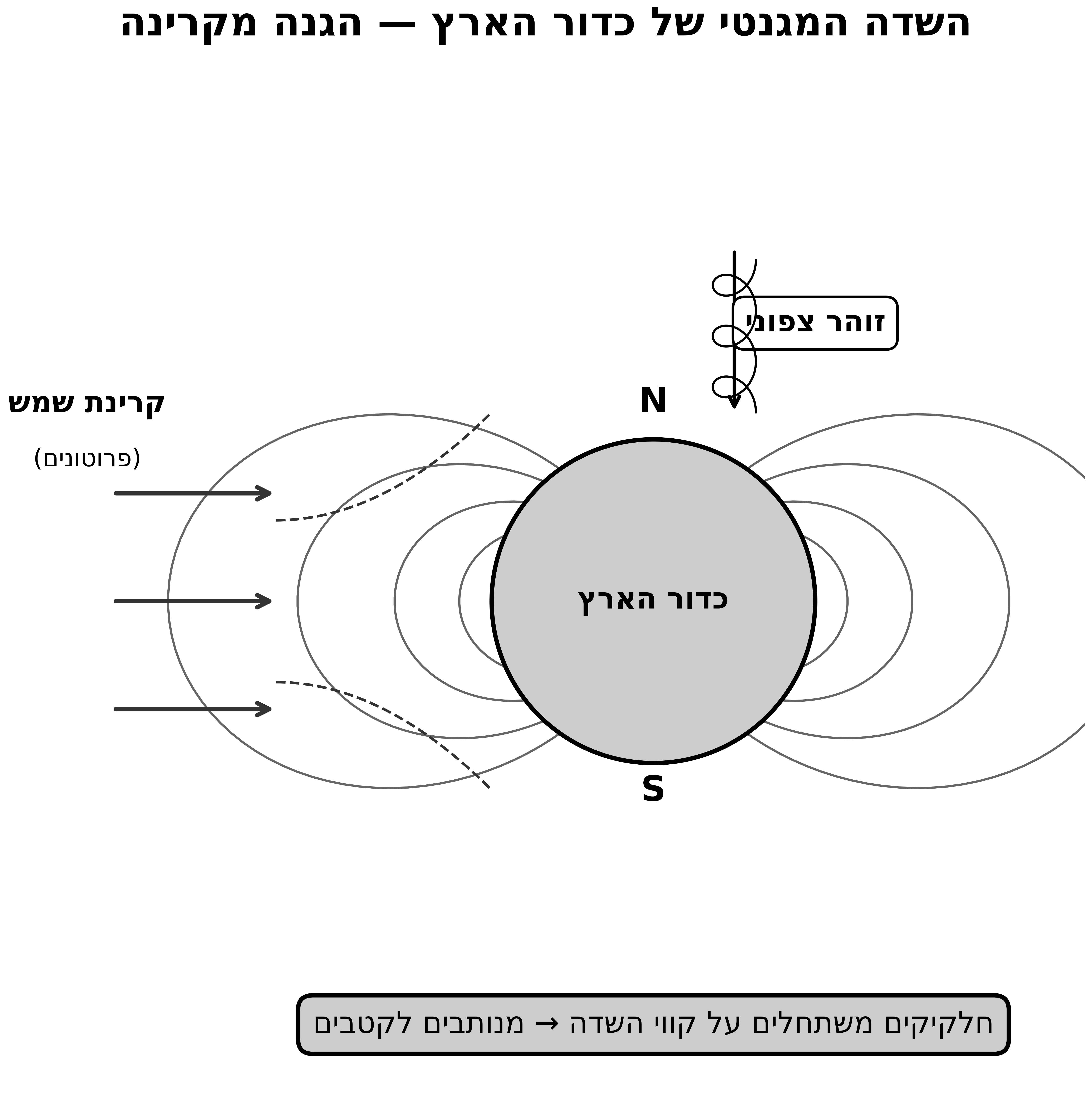
תהליך ההגנה מקרינת השמש
שלב 1: השמש פולטת פרוטונים אנרגטיים (גרעיני מימן) במהירות של 10-20% ממהירות האור. מדוע כל כך מהר? בשמש מתרחשים תהליכים מאוד אנרגטיים שמעניקים לפרוטונים אנרגיה קינטית עצומה.
שלב 2: הפרוטונים מגיעים לקווי השדה המגנטי של כדור הארץ עם שני רכיבי מהירות: ניצב ומקביל לקווי השדה.
שלב 3: הפרוטונים מתחילים להשתחל על קווי השדה (תנועה ספירלית):
- הרכיב הניצב גורם לסיבוב סביב קו השדה
- הרכיב המקביל גורם להתקדמות לאורך קו השדה
שלב 4: קווי השדה מנתבים את הפרוטונים אל הקטבים (בערך בקווי רוחב 68-67 צפון/דרום).
שלב 5: באזור הקטבים, קווי השדה נכנסים לאטמוספירה בזווית חדה מאוד (כמעט אנכית). הפרוטונים פוגעים באטמוספירה בגובה של כ-70-60 ק”מ ומיינים את המולקולות.
שלב 6: התוצאה - זוהר צפוני (Aurora Borealis) וזוהר דרומי (Aurora Australis).
למה זה חשוב?
ללא השדה המגנטי, קרינה זו הייתה פוגעת ישירות באטמוספירה ובפני כדור הארץ, גורמת למוטציות גנטיות במולקולות ה-DNA, ומונעת התפתחות חיים על פני כדור הארץ.
למה בקטבים ולא בקו המשווה?
באזור הקטבים, קווי השדה נכנסים בזווית חדה ביחס לאטמוספירה - הפרוטונים עוברים דרך שכבה עבה של אטמוספירה ומתפזרים (dissipated).
באזור קו המשווה, אם הקרינה הייתה מגיעה ישירות, הייתה עוברת רק שכבה צרה של אטמוספירה והקרינה על פני כדור הארץ הייתה גדולה בהרבה.
הערה על קרינה בגובה
ככל שעולים בגובה, החשיפה לקרינה גדלה. למשל, בטיסה במטוס בגובה 10 ק”מ, הקרינה הקוסמית מהשמש מסוכנת יותר מאשר על פני הקרקע.
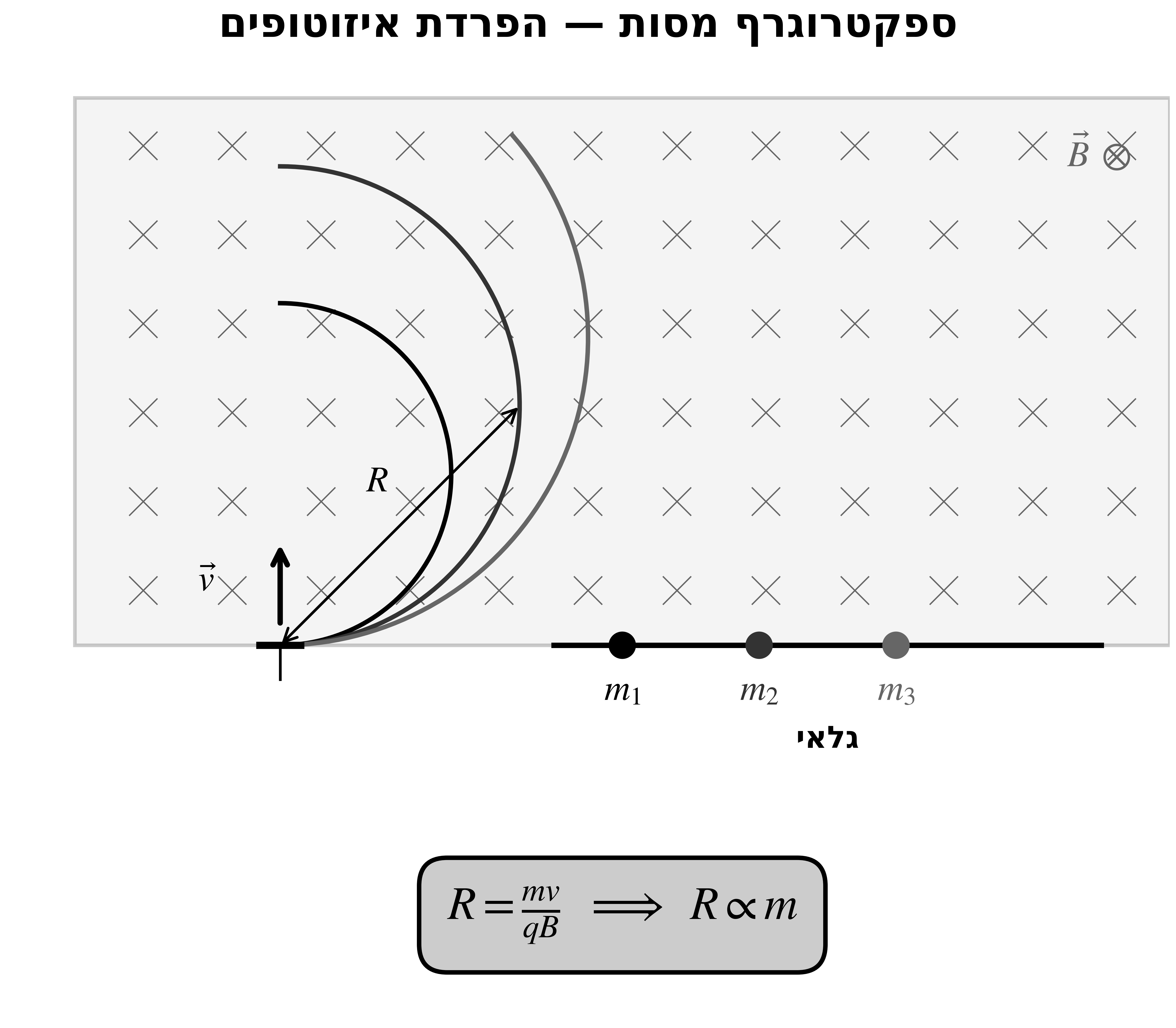
יישום: ספקטרוגרף מסות
עקרון הפעולה
מרדיוס התנועה המעגלית:
\[R = \frac{mv}{qB}\]אם לאיזוטופים שונים יש מסות שונות אך אותו מטען $q$, ואם הם נכנסים באותה מהירות $v$ לאותו שדה מגנטי $B$:
\[R \propto m\]הרדיוס מתכונתי למסה!
שימוש
- איזוטופים שונים נכנסים לשדה מגנטי אחיד
- כל איזוטופ מבצע מעגל ברדיוס שונה
- ניתן להפריד איזוטופים לפי מסה
חוק אוהם
חוק אוהם הדיפרנציאלי (המקומי)
בהרבה מאוד חומרים (בעיקר מתכות וחומרים המשמשים באלקטרוניקה) מתקיים הקשר:
\[\boxed{\vec{j} = \sigma \vec{E}}\]כאשר:
- $\vec{j}$ - צפיפות הזרם
- $\sigma$ - המוליכות הסגולית (קבוע שמאפיין את החומר)
- $\vec{E}$ - השדה החשמלי
זהו חוק אמפירי - לא תמיד מתקיים, אבל מתקיים בתנאים רבים מאוד.
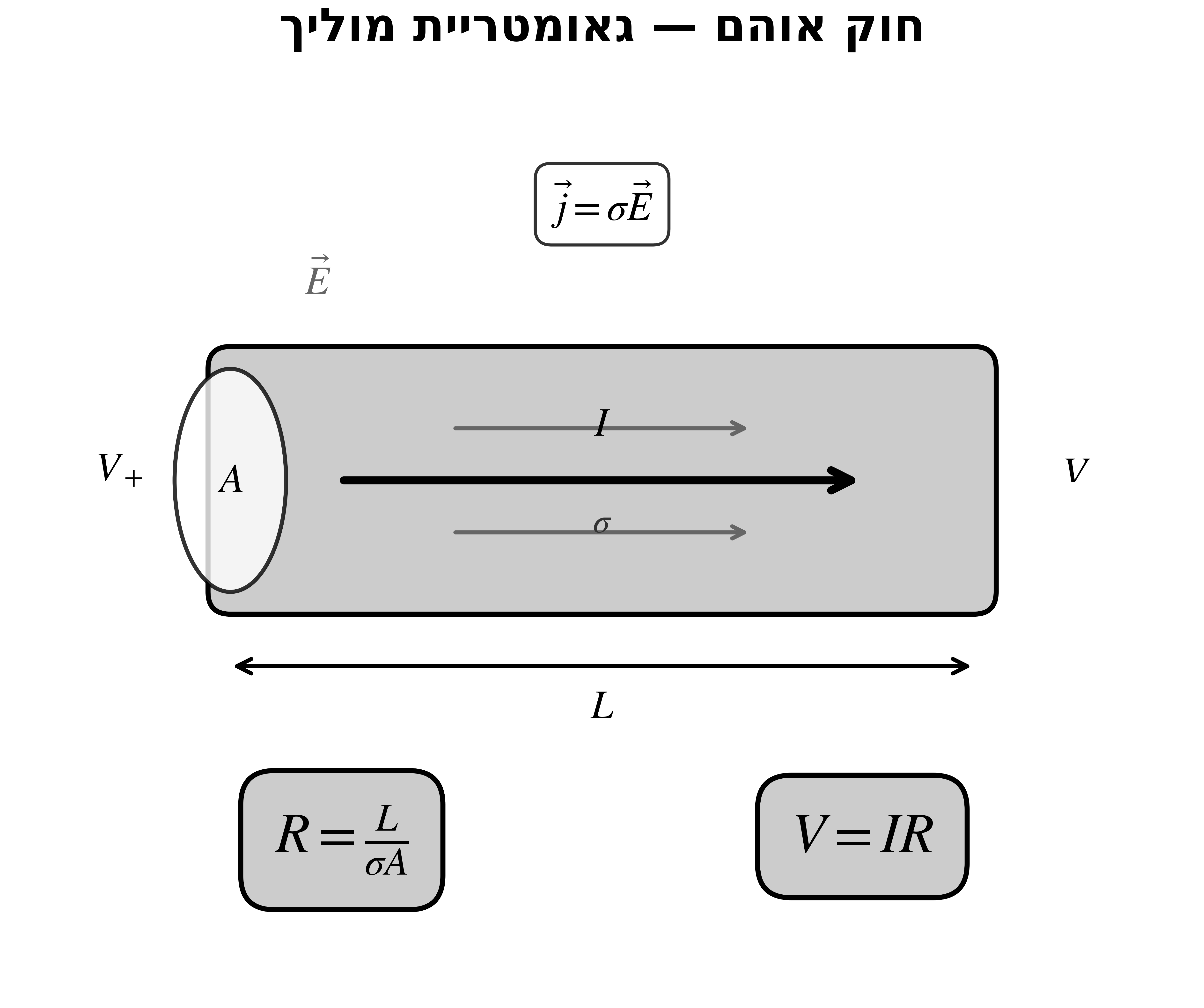
גזירת חוק אוהם למעגלים
שלב 1: השדה החשמלי
השדה החשמלי מורכב משני חלקים - חלק ערבולי (נסמן $\vec{E}_{↺}$) וחלק דיברגנטי
(נסמן $\vec{E}_⊙$):
\[\vec{E} = \vec{E}_{↺} + \vec{E}_{⊙}\]כאשר:
- $\vec{E}_{⊙} = -\nabla\phi$ (גרדיאנט הפוטנציאל)
- $\vec{E}_{↺} = -\dfrac{\partial \vec{A}}{\partial t}$ (נגזרת הפוטנציאל המגנטי)
שלב 2: הכא”מ המושרה
הכא”מ (כוח אלקטרומניע) המושרה בלולאה סגורה:
\[\begin{aligned} \varepsilon &= \oint \vec{E} \cdot d\vec{r} \\[6pt] &= \oint \left(\vec{E}_{↺} + \vec{E}_{⊙}\right) \cdot d\vec{r} \\[6pt] &= \oint \vec{E}_{↺} \cdot d\vec{r} + \oint \vec{E}_{⊙} \cdot d\vec{r} \end{aligned}\]האינטגרל הסגור על הרכיב הדיברגנטי מתאפס (כי $\oint_C \nabla\phi \cdot d\vec{r} = 0$ - זה האינטגרל של כוח משמר על מסלול סגור).
לכן רק הרכיב הערבולי תורם:
\[\varepsilon = \oint \vec{E}_{↺} \cdot d\vec{r} = -\frac{d\Phi_B}{dt}\]שלב 3: עבור שדה אחיד במוליך
אם השדה אחיד לאורך המוליך:
\[\varepsilon = E \cdot L\]כאשר $L$ אורך המוליך.
שלב 4: הצבת חוק אוהם המקומי
מ-$\vec{J} = \sigma\vec{E}$ נקבל $E = \dfrac{J}{\sigma}$:
\[\varepsilon = \frac{j}{\sigma} \cdot L\]שלב 5: מעבר לזרם
נכפיל ונחלק בשטח החתך $A$:
\[\varepsilon = \frac{L}{\sigma A} \cdot (j \cdot A) = \frac{L}{\sigma A} \cdot I\]כאשר $I = j \cdot A$ הוא הזרם הכולל (שטף צפיפות הזרם דרך החתך).
ההתנגדות
\[\boxed{R = \frac{L}{\sigma A}}\]- $L$ - אורך המוליך (ככל שארוך יותר, התנגדות גדולה יותר)
- $A$ - שטח החתך (ככל שרחב יותר, התנגדות קטנה יותר)
- $\sigma$ - מוליכות סגולית
- $\rho = 1/\sigma$ - התנגדות סגולית
חוק אוהם של המעגלים
\[\boxed{V = IR}\]זהו חוק אוהם כפי שהאלקטרונאים והחשמלאים משתמשים בו: המתח (הפרש פוטנציאלים) שווה לזרם כפול ההתנגדות.
הבהרה חשובה: מהירות הזרם לעומת מהירות האות
שני סוגי “מהירות” במעגל חשמלי
| מהירות סחיפת אלקטרונים | מהירות התפשטות המתח | |
|---|---|---|
| ערך | ~מילימטרים לדקה | ~מהירות האור |
| מה נע | אלקטרונים קשורים לשריג | גל אלקטרומגנטי (שדה) |
| הסיבה | התנגדות גבוהה בשריג | שדה חשמלי מתפשט |
הסבר מפורט
מהירות הסחיפה (Drift Velocity): האלקטרונים במוליך קשורים לאטומים בשריג. כשמפעילים שדה חשמלי, הם זזים לאט מאוד - בסדר גודל של מילימטרים לדקה. הם מרגישים התנגדות גדולה כי הם “מחוברים” לשריג האטומי.
מהירות התפשטות המתח: כשסוגרים מעגל (למשל לוחצים על מתג), השדה החשמלי מתפשט לאורך המוליך במהירות האור (או קרוב לה). זה גל אלקטרומגנטי שמתקדם בתוך המוליך.
למה האור נדלק מיד?
כשמדליקים מתג בבית, המתח מגיע מיידית (במהירות האור), ואז הזרם מתחיל לזרום מיד בכל המעגל. האלקטרונים עצמם זזים לאט, אבל הפרש הפוטנציאלים מתפתח מיד על פני כל המעגל.
זה שונה ממצב של מטענים עודפים על מוליך - שם האלקטרונים לא קשורים לאטומים ומאיצים במהירויות קרובות לאור.
קצר חשמלי
הגדרה מתמטית
כאשר $R \to 0$ וקיים הפרש פוטנציאלים $V \neq 0$:
\[I = \frac{V}{R} \to \infty\]המשמעות הפיזיקלית
קצר = חיבור שתי נקודות במוליך אידיאלי (התנגדות אפס).
כשמחברים שתי נקודות במוליך:
- המוליך חייב להיות באותו פוטנציאל בכל נקודותיו
- לכן מתקבלת השוואת פוטנציאלים מיידית
- כדי לבטל את השדה בתוך המוליך, זורם זרם “אינסופי” (מוגבל בפועל ע”י גורמים אחרים)
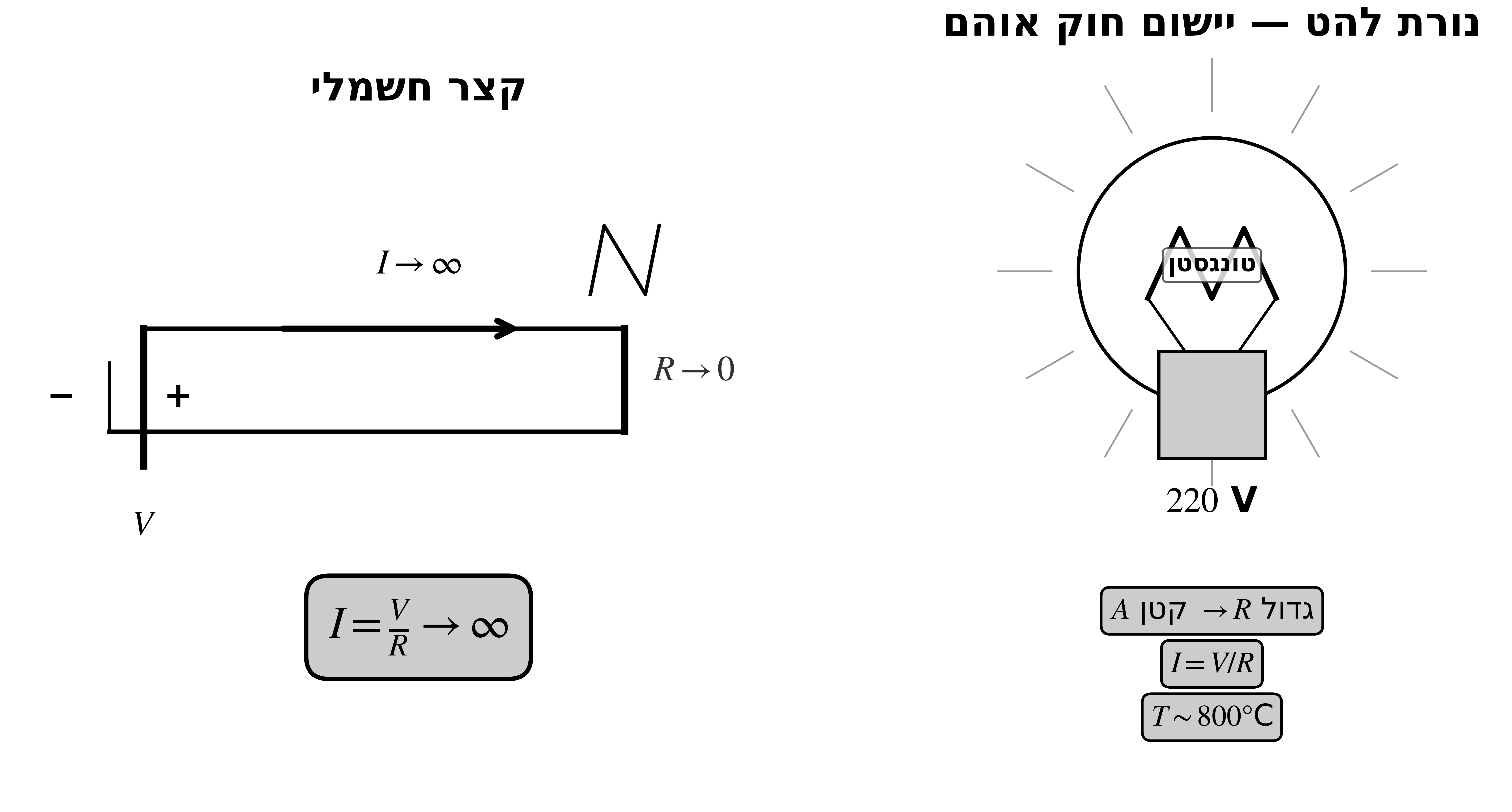
נורת להט - יישום של חוק אוהם
עקרון הפעולה
-
חוט טונגסטן דק - שטח חתך קטן מאוד ($A$ קטן) ← התנגדות גבוהה מאוד
-
הפרש פוטנציאלים 220V - מופעל על החוט
-
זרם זורם - לפי $I = V/R$
-
התחממות - האלקטרונים “מתחככים” בשריג, מייצרים חום, והחוט מתלהט לטמפרטורות של כ-800°C
-
פליטת אור - החוט המתלהט פולט אור (קרינה אלקטרומגנטית)
-
וואקום - שואבים את האוויר מהנורה כדי למנוע שריפה (אינטראקציה של חמצן בטמפרטורה גבוהה = בעירה)
דוגמה נוספת: חימום חשמלי
אותו עיקרון בדיוק עובד בגופי חימום (ספירלות):
- מעבירים זרם דרך מוליך בעל התנגדות גבוהה
- החום שנוצר מחמם את הסביבה