הקדמה: מושגי יסוד בעבודה ואנרגיה
עבודה (Work) היא גודל סקלרי המתאר את האנרגיה המועברת לגוף או ממנו כאשר כוח פועל עליו לאורך מסלול מסוים. מתמטית, העבודה מוגדרת כמכפלה הסקלרית של הכוח וההעתק:
\[W = \mathbf{F} \cdot \Delta\mathbf{r} = F \cdot \Delta r \cdot \cos\alpha\]כאשר $\alpha$ היא הזווית בין כיוון הכוח לכיוון ההעתק. רק הרכיב של הכוח בכיוון התנועה תורם לעבודה - זו הסיבה שאנחנו משתמשים במכפלה סקלרית.
כאשר הכוח משתנה לאורך המסלול, אנחנו צריכים לחשב את העבודה כאינטגרל:
\[W = \int_{\mathbf{r}_1}^{\mathbf{r}_2} \mathbf{F} \cdot d\mathbf{r}\]משפט עבודה-אנרגיה קובע שהעבודה הכוללת שמבצעים כל הכוחות על גוף שווה לשינוי באנרגיה הקינטית שלו:
\[W_{\text{total}} = \Delta E_k = \frac{1}{2}mv_2^2 - \frac{1}{2}mv_1^2\]מאפשר לפתור בעיות מורכבות בלי לדעת את כל פרטי התנועה - מספיק לדעת את המצב ההתחלתי ואת המצב הסופי.
הספק (Power) מתאר את קצב ביצוע העבודה (לפי ההגדרה בכתה: ״השינוי הרגעי בעבודה שמבצע כוח $\mathbf{F}$ על גוף במהלך תנועתו״). הוא מוגדר כנגזרת של העבודה לפי הזמן:
\[P = \frac{dW}{dt} = \mathbf{F} \cdot \mathbf{v}\]שאלה 1: גרירת מזוודה
מזוודה אשר מסתה 20 קילוגרם נגררת על רצפת הטרמינל בכוח של 50 ניוטון ובזווית של 45 מעלות מעל האופק לאורך דרך של מאה מטר.
- מה משקל המזוודה במהלך גרירתה?
- כמה עבודה ביצע הגורר לאורך מסלול הגרירה?
- בהנחה שמהירות המזוודה קבועה לאורך כל הדרך, כמה עבודה ביצע כוח החיכוך על המזוודה לאורך מסלול הגרירה?
- מהו מקדם החיכוך אם ידוע שהוא מתכונתי לגודלו של הכוח הנורמלי?
פתרון מפורט
נתונים:
- מסה: $m = 20 \, \mathrm{kg}$
- כוח גרירה: $F = 50 \, \mathrm{N}$
- זווית: $\alpha = 45°$
- מרחק: $\Delta x = 100 \, \mathrm{m}$
סעיף א: משקל המזוודה
המשקל של גוף הוא הכוח שמפעיל עליו כדור הארץ, והוא תמיד נתון על ידי:
\[\mathbf{W} = m\mathbf{g} \approx 20 \times 10 = 200 \, \mathrm{N}\]שימו לב: המשקל לא תלוי בכוחות אחרים הפועלים על הגוף. גם אם מישהו מרים את המזוודה או גורר אותה - המשקל שלה נשאר קבוע (כל עוד אנחנו באותו מקום על פני כדור הארץ).
הערה נוספת: לא ברור לי לגמרי האם המשקל בקורס הוא וקטור (עם כיוון) או סקאלר. נראה שקבוע הכבידה הוא בדרך כלל סקאלר, ובכל מקרה פועל כלפי מטה.
סעיף ב: העבודה שביצע הגורר
כשמחשבים עבודה, רק הרכיב של הכוח בכיוון התנועה תורם לתוצאה. במקרה שלנו, הכוח פועל בזווית של 45° לאופק, אבל התנועה היא אופקית. לכן נצטרך את ההיטל של הכוח בכיוון התנועה (ציר x).
\[W = F \cos\alpha \cdot \Delta x = 50 \times \cos(45°) \times 100\]נחשב את הקוסינוס:
\[\cos(45°) = \frac{\sqrt{2}}{2} \approx 0.707\]לכן:
\[W = 50 \times 0.707 \times 100 = 3535 \text{ J}\]סעיף ג: עבודת כוח החיכוך
כשגוף נע במהירות קבועה התאוצה שלו היא אפס. לפי החוק השני של ניוטון, זה אומר שסכום הכוחות שפועלים עליו הוא אפס.
בציר האופקי (כיוון x):
\[\sum F_x = 0\] \[F\cos\alpha + f_{\text{friction}} = 0\]כאן $f_{\text{friction}}$ הוא כוח החיכוך (שלילי כי הוא מתנגד לתנועה):
\[f_{\text{friction}} = -F\cos\alpha = -50 \times 0.707 = -35.35 \, \mathrm{N}\]העבודה של כוח החיכוך:
\[W_f = f_{\text{friction}} \cdot \Delta x = -35.35 \times 100 = -3535 \text{ J}\]שימו לב: העבודה של כוח החיכוך שלילית כי הוא פועל בכיוון הפוך לתנועה. זה אומר שכוח החיכוך “גוזל” אנרגיה מהמערכת (הופך אותה לחום).
דרך נוספת להגיע לתוצאה הזאת (שבאופן מעניין הבינה המלאכותית לא הציעה לי אותה), היא בעזרת משפט עבודה אנרגיה:
\[W_{\text{total}} = \Delta E_k\]מכיוון שהמהירות קבועה, אין שינוי באנרגיה הקינטית:
\[\Delta E_k = 0\]לכן:
\[W_{\text{total}} = W + W_f = 0\]מכאן:
\[W = -W_f \implies W_f = -W = -3535 \text{ J}\]סעיף ד: מקדם החיכוך
כדי למצוא את מקדם החיכוך, נמצא קודם את הכוח הנורמלי. נשתמש בשיווי משקל בציר האנכי (כיוון y):
\[\sum F_y = 0\] \[N + F\sin\alpha - mg = 0\]מכאן:
\[\begin{aligned} N &= mg - F\sin\alpha \\[10pt] &\approx 200 - 50 \times 0.707 \\[10pt] &= 200 - 35.35 = 164.65 \, \mathrm{N} \end{aligned}\]עכשיו נוכל לחשב את מקדם החיכוך הקינטי:
\[\mu_k = \frac{|f_{\text{friction}}\vert}{N} \approx \frac{35.35}{160.65} = 0.22 \, \text{ (unitless?)}\]לפי גוגל זה ערך סביר למקדם חיכוך בין מזוודה לרצפת טרמינל.
תזכורת: מקדם החיכוך הוא היחס בין שני כוחות - כוח החיכוך לבין הכוח הנורמלי. מכאן שהוא חסר יחידות להבנתי, אבל אני לא בטוח.
שאלה 2: כוח כבידה על פלנטה
כוח הכבידה בין גוף מאוד מסיבי כמו כוכב לבין גוף הרבה פחות מסיבי כמו פלנטה הסובבת אותו, נתון בביטוי:
\[\mathbf{F}(r) = -\frac{\alpha}{r^3}\mathbf{r}\]באשר $\mathbf{r}$ הוא וקטור המקום של הפלנטה במערכת צירים אשר ראשיתה יושבת במרכז הכוכב, $\alpha$ הוא פרמטר כלשהו שתלוי במסות של שני הגופים.
עוד ידוע שהפלנטה סובבת את הכוכב במסלול אליפטי כך ש-
\[\mathbf{r}(t) = a\cos(\omega t)\mathbf{\hat{x}} + b\sin(\omega t)\mathbf{\hat{y}}\]
- אם $\omega = 2 \times 10^{-7} \text{ sec}^{-1}$ כמה ימים אורכת שנה אחת על פני הפלנטה?
- הסבירו מדוע $d\mathbf{r} = \mathbf{v}dt$
- קבלו ביטוי עבור העבודה כאינטגרל על הזמן
- חשבו כמה עבודה מבצע הכוכב על הפלנטה בארבעה חודשים
- חשבו כמה עבודה מבצע הכוכב על הפלנטה בשנה שלמה
פתרון מפורט
זו שאלה מגניבה לעניות דעתי. הכוח הנתון הוא כוח מרכזי (פועל לכיוון המרכז - ראו פתרון תרגיל 7) והמסלול הוא אליפטי - בדיוק כפי שחזה קפלר וניסח ניוטון.
סעיף א: משך השנה
התדירות הזוויתית $\omega$ קשורה לזמן המחזור $T$ על ידי:
\[T = \frac{2\pi}{\omega}\]נציב את הנתון:
\[T = \frac{2\pi}{2 \times 10^{-7}} = \pi \times 10^7 \text{ seconds}\]כדי להמיר לימים, נחלק במספר השניות ביממה:
\[T = \frac{\pi \times 10^7}{86400} \approx 363.6 \text{ days}\]זה קרוב מאוד לשנה ארצית!
סעיף ב: הקשר $d\mathbf{r} = \mathbf{v}dt$
זאת למעשה ההגדרה הבסיסית של מהירות. המהירות היא קצב השינוי של המיקום:
\[\mathbf{v} = \frac{d\mathbf{r}}{dt}\]כאשר אנחנו מסדרים מחדש:
\[d\mathbf{r} = \mathbf{v}dt\]זה אומר שהשינוי האינפיניטסימלי במיקום שווה למהירות כפול השינוי האינפיניטסימלי בזמן.
סעיף ג: העבודה כאינטגרל על הזמן
נתחיל מההגדרה הבסיסית של עבודה:
\[dW = \mathbf{F} \cdot d\mathbf{r}\]נשתמש בתוצאה מסעיף ב:
\[dW = \mathbf{F} \cdot \mathbf{v}dt\]לכן העבודה הכוללת היא:
\[W = \int_{t_1}^{t_2} \mathbf{F} \cdot \mathbf{v} dt\]זאת נוסחה שימושית כשיודעים את הכוח והמהירות כפונקציות של הזמן.
סעיף ד: עבודה בארבעה חודשים
כדי לחשב את העבודה, נצטרך למצוא קודם את המהירות:
\[\mathbf{v} = \frac{d\mathbf{r}}{dt} = -a\omega\sin(\omega t)\mathbf{\hat{x}} + b\omega\cos(\omega t)\mathbf{\hat{y}}\]עכשיו נחשב את המכפלה הסקלרית $\mathbf{F} \cdot \mathbf{v}$. ראשית, נמצא את $r^3$:
\[r^2 = a^2\cos^2(\omega t) + b^2\sin^2(\omega t)\] \[r^3 = [a^2\cos^2(\omega t) + b^2\sin^2(\omega t)]^{3/2}\]המכפלה הסקלרית:
\[\mathbf{F} \cdot \mathbf{v} = -\frac{\alpha}{r^3}(\mathbf{r} \cdot \mathbf{v})\]נחשב את $\mathbf{r} \cdot \mathbf{v}$:
\[\mathbf{r} \cdot \mathbf{v} = a\cos(\omega t) \cdot (-a\omega\sin(\omega t)) + b\sin(\omega t) \cdot (b\omega\cos(\omega t))\] \[= -a^2\omega\cos(\omega t)\sin(\omega t) + b^2\omega\sin(\omega t)\cos(\omega t)\] \[= \omega\sin(\omega t)\cos(\omega t)(b^2 - a^2)\]תוצאה מעניינת: אם $a = b$ (מסלול מעגלי), אז $\mathbf{r} \cdot \mathbf{v} = 0$, מה שאומר שהכוח תמיד ניצב למהירות והעבודה היא אפס!
סעיף ה: עבודה בשנה שלמה
אם הבנתי נכון: בכל תנועה מחזורית סגורה תחת כוח משמר (כמו כוח הכבידה), העבודה הכוללת במחזור שלם היא תמיד אפס (הגוף חוזר לאותה נקודה עם אותה מהירות, ולכן האנרגיה הקינטית שלו לא השתנתה). לפי משפט עבודה-אנרגיה, העבודה חייבת להיות אפס.
שאלה 3: עבודה לאורך משולש
חשבו את העבודה שמבצע הכוח
\[\mathbf{F}(x,y) = 2\sinh(x+y)\mathbf{\hat{x}} + 2\cosh(x-y)\mathbf{\hat{y}}\]על גוף כלשהו הנגרר לאורך צלעות המשולש ישר-הזווית אשר קודקודיו הם הנקודות:
\[(0,0), (\ln 2, 0), (\ln 2, \ln 2)\]
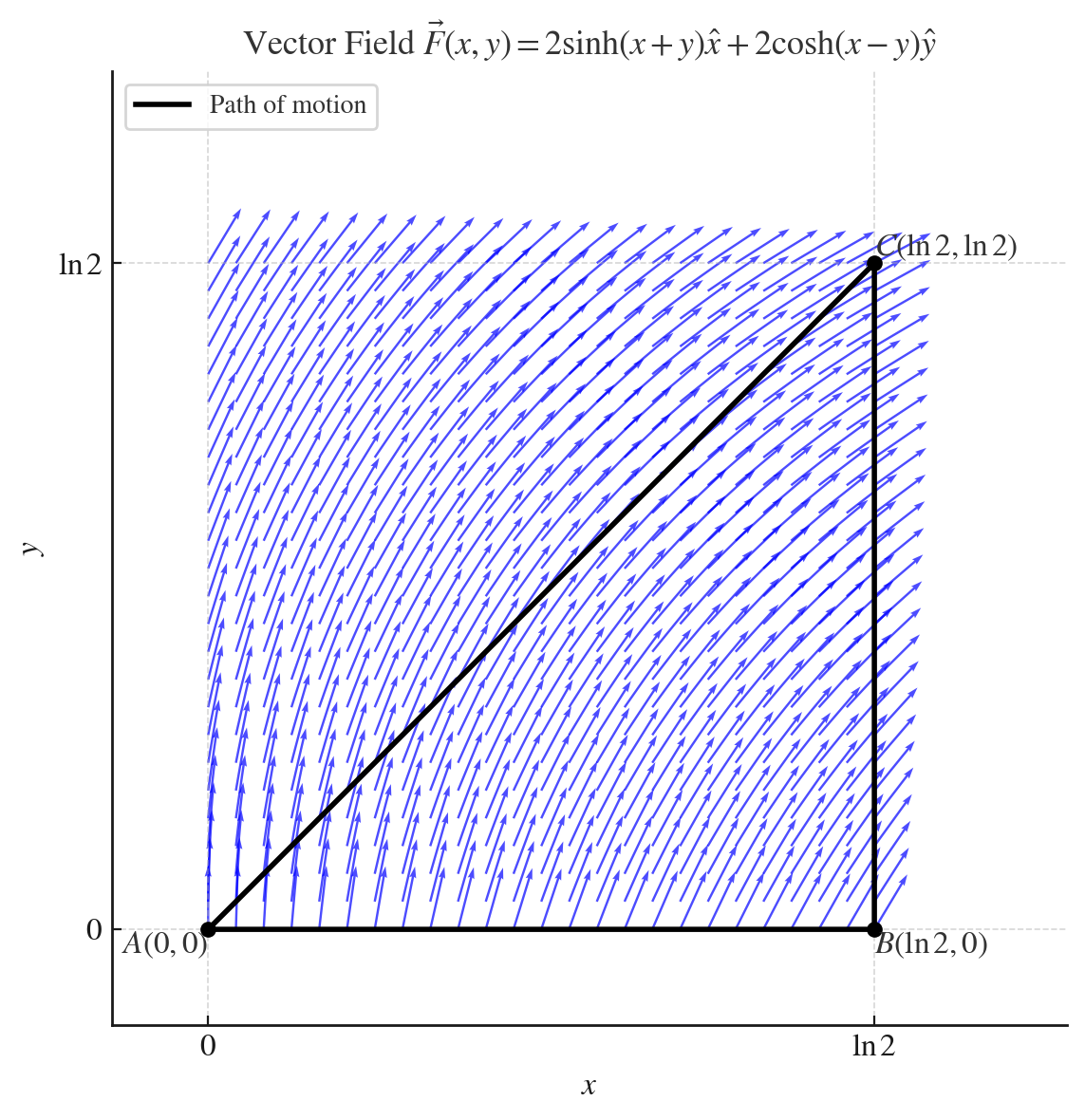 | 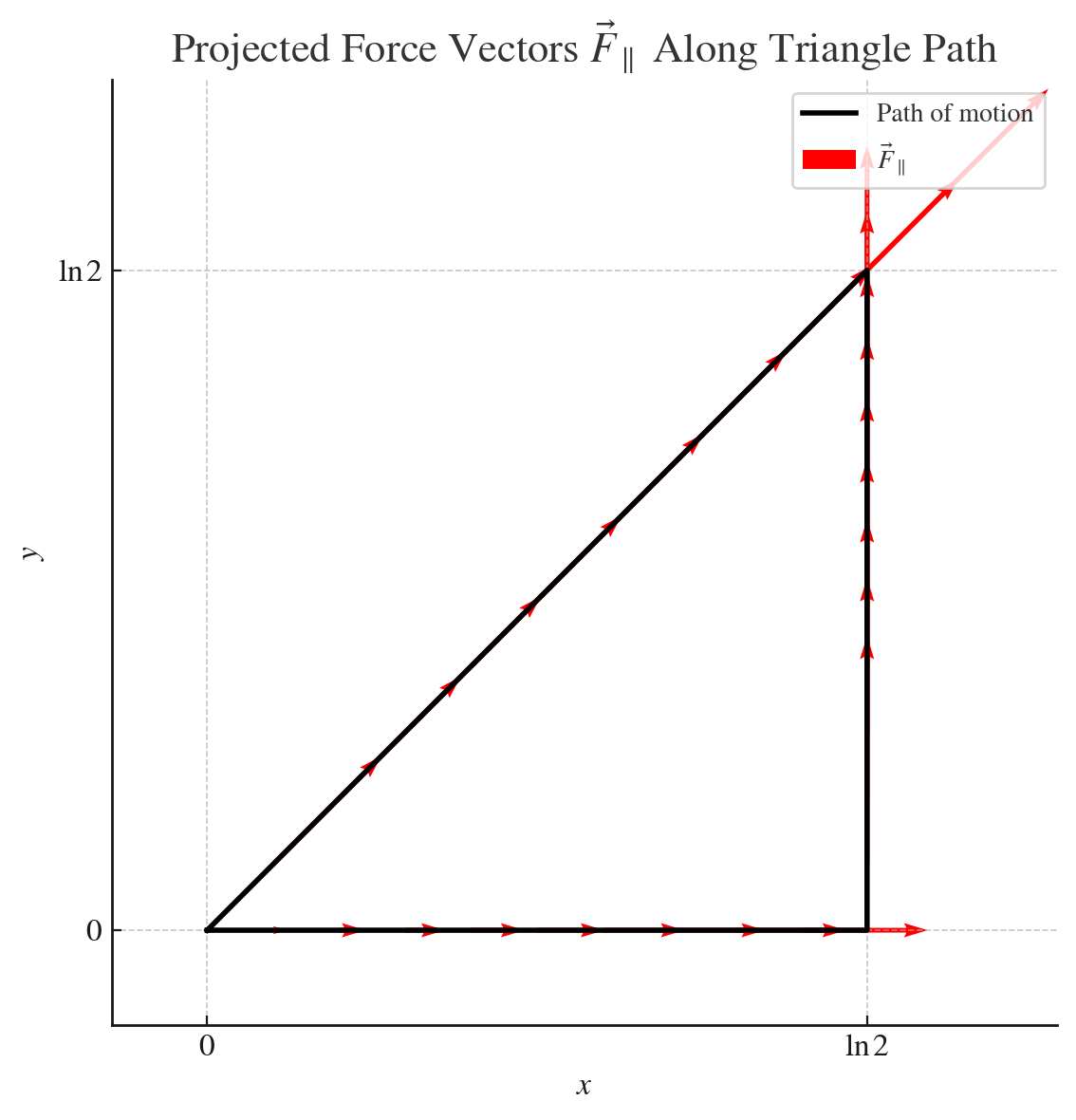 |
|---|---|
| וקטור השדה | היטלי הכוח על צלעות המשולש |
פתרון - חישוב עבודה לאורך משולש
נחלק את החישוב לשלוש צלעות המשולש.
צלע 1: מ-$(0,0)$ ל-$(\ln 2, 0)$
לאורך צלע זו, $y = 0$ ו-$dy = 0$. לכן:
\[W_1 = \int_0^{\ln 2} F_x(x,0)dx = \int_0^{\ln 2} 2\sinh(x)dx\]נחשב את האינטגרל:
\[W_1 = 2[\cosh(x)]_0^{\ln 2} = 2(\cosh(\ln 2) - \cosh(0))\]נשתמש בהגדרה: $\cosh(x) = \frac{e^x + e^{-x}}{2}$
עבור $x = \ln 2$:
\[\cosh(\ln 2) = \frac{e^{\ln 2} + e^{-\ln 2}}{2} = \frac{2 + 1/2}{2} = 1.25\]כמו כן, $\cosh(0) = 1$.
לכן:
\[\boxed{W_1 = 2(1.25 - 1) = 0.5 \text{ J}}\]צלע 2: מ-$(\ln 2, 0)$ ל-$(\ln 2, \ln 2)$
לאורך צלע זו, $x = \ln 2$ ו-$dx = 0$. לכן:
\[W_2 = \int_0^{\ln 2} F_y(\ln 2, y)dy = \int_0^{\ln 2} 2\cosh(\ln 2 - y)dy\]נבצע החלפת משתנים: $u = \ln 2 - y$, אז $du = -dy$:
\[W_2 = -\int_{\ln 2}^0 2\cosh(u)du = \int_0^{\ln 2} 2\cosh(u)du = 2[\sinh(u)]_0^{\ln 2}\]כאשר $\sinh(\ln 2) = \frac{e^{\ln 2} - e^{-\ln 2}}{2} = \frac{2 - 1/2}{2} = 0.75$
לכן:
\[\boxed{W_2 = 2(0.75 - 0) = 1.5 \text{ J}}\]צלע 3: מ-$(\ln 2, \ln 2)$ ל-$(0,0)$ לאורך היתר
על היתר של משולש ישר-זווית שווה-שוקיים מתקיים $x = y$. נוכל להגדיר:
- $x = y = t$
- $t$ משתנה מ-$\ln 2$ ל-$0$
- $dx = dy = dt$
העבודה לאורך צלע זו:
\[\begin{aligned} W_3 &= \int_{\ln 2}^0 [F_x(t,t)dt + F_y(t,t)dt] \\[10pt] &= \int_{\ln 2}^0 [2\sinh(2t) + 2\cosh(0)]dt \\[10pt] &= \int_{\ln 2}^0 [2\sinh(2t) + 2]dt \end{aligned}\]נחשב:
\[\begin{aligned} W_3 &= [2 \cdot \frac{1}{2}\cosh(2t) + 2t]_{\ln 2}^0 \\[10pt] &= [\cosh(2t) + 2t]_{\ln 2}^0 \\[10pt] &= (1 + 0) - (\cosh(2\ln 2) + 2\ln 2) \end{aligned}\]כאשר $\cosh(2\ln 2) = \cosh(\ln 4) = \frac{4 + 1/4}{2} = 2.125$
לכן:
\[\boxed{W_3 = 1 - 2.125 - 2\ln 2 = 1 - 2.125 - 1.386 = -2.511 \text{ J}}\]העבודה הכוללת:
\[\boxed{W_{\text{total}} = W_1 + W_2 + W_3 = 0.5 + 1.5 - 2.511 = -0.511 \text{ J}}\]העובדה שהעבודה לאורך המסלול הסגור אינה אפס מעידה על כך שהכוח אינו משמר.
שאלה 4: הספק
ההספק P (Power) מוגדר כשינוי הרגעי בעבודה שמבצע כוח על גוף במהלך תנועתו.
- הוכיחו: $P = \mathbf{F} \cdot \mathbf{v}$
- קבלו ביטוי עבור ההספק הרגעי של עבודת הכוכב על הפלנטה מהשאלה הקודמת
- טורבינת רוח בחוות עמק הבכא שברמת הגולן עובדת בהספק של 3.2 מגה-ואט. כמה אנרגיה מייצרת החווה כולה בשעת עבודה אחת, אם ידוע שיש בה 36 טורבינות פעילות?
באזור מסוים ע”פ כדור הארץ הספק טורבינת הרוח הוא פונקציה של הזמן כך ש-
\[P(t) = 3.2\sin\left(\frac{2\pi}{\text{day}}t\right)\]כמה אנרגיה מייצרת הטורבינה הנ”ל ביממה אחת?
פתרון מפורט
סעיף א: הוכחת הנוסחה להספק
נתחיל מההגדרה של הספק:
\[P = \frac{dW}{dt}\]נזכור שהעבודה האינפיניטסימלית היא:
\[dW = \mathbf{F} \cdot d\mathbf{r}\]לכן:
\[P = \frac{dW}{dt} = \frac{\mathbf{F} \cdot d\mathbf{r}}{dt} = \mathbf{F} \cdot \frac{d\mathbf{r}}{dt} = \mathbf{F} \cdot \mathbf{v}\]זוהי נוסחה אינטואיטיבית: ההספק גדל כאשר הכוח גדל וכאשר המהירות בכיוון הכוח גדלה.
סעיף ב: הספק רגעי של הכוכב על הפלנטה
משאלה 2, מצאנו ש:
\[\mathbf{F} \cdot \mathbf{v} = -\frac{\alpha\omega\sin(\omega t)\cos(\omega t)(b^2 - a^2)}{r^3}\]זהו ההספק הרגעי. שימו לב שהוא מחליף סימן - לפעמים הכוכב מבצע עבודה חיובית על הפלנטה (מאיץ אותה) ולפעמים שלילית (מאט אותה).
סעיף ג: אנרגיה מחוות טורבינות
ההספק הכולל של החווה:
\[P_{\text{total}} = 36 \times 3.2 = 115.2 \text{ MW}\]האנרגיה המיוצרת בשעה:
\[E = P \times t = 115.2 \text{ MW} \times 1 \text{ hour} = 115.2 \text{ MWh}\]זו כמות אנרגיה משמעותית - מספיקה לכ-100,000 בתים ליום אחד! (מקור מפוקפק)
סעיף ד: אנרגיה עם הספק משתנה
כאשר ההספק משתנה בזמן, האנרגיה הכוללת היא האינטגרל של ההספק:
\[E = \int_0^T P(t)dt = \int_0^{24} 3.2\sin\left(\frac{2\pi}{24}t\right)dt\]נבצע החלפת משתנים: $u = \frac{2\pi}{24}t$, אז $du = \frac{2\pi}{24}dt$:
\[E = 3.2 \times \frac{24}{2\pi}\int_0^{2\pi} \sin(u)du\]האינטגרל של סינוס על מחזור שלם הוא אפס:
\[\int_0^{2\pi} \sin(u)du = [-\cos(u)]_0^{2\pi} = -\cos(2\pi) + \cos(0) = -1 + 1 = 0\]לכן $E = 0$.
תוצאה זו אולי מפתיעה, אבל היא הגיונית: במחצית היממה הטורבינה מייצרת אנרגיה (הספק חיובי) ובמחצית השנייה היא צורכת אנרגיה (הספק שלילי), והסכום הכולל הוא אפס. במציאות, כמובן, טורבינות לא צורכות אנרגיה - זו רק דוגמה מתמטית.
שאלה 5: עבודה ממשפט עבודה-אנרגיה
כתוצאה מעבודתו של כוח כלשהו, מבצע גוף שמסתו $m = 4$ ק”ג תנועה לאורך המסלול
\[\mathbf{r}(t) = (3t^2 - 2t)\mathbf{\hat{x}} + t^3\mathbf{\hat{y}} - t^4\mathbf{\hat{z}}\]חשבו את העבודה שמבצע הכוח על הגוף במהלך השנייה השנייה לתנועתו.
פתרון - חישוב עבודה בעזרת משפט עבודה-אנרגיה
משפט עבודה-אנרגיה מאפשר לחשב את העבודה בלי לדעת את הכוח עצמו! כל שעלינו לעשות הוא למצוא את המהירויות בתחילת פרק הזמן ובסופו.
ראשית, נמצא את וקטור המהירות על ידי גזירה:
\[\mathbf{v}(t) = \frac{d\mathbf{r}}{dt} = (6t - 2)\mathbf{\hat{x}} + 3t^2\mathbf{\hat{y}} - 4t^3\mathbf{\hat{z}}\]עבור השנייה השנייה, אנחנו מסתכלים על הפרק זמן מ-$t = 1$ עד $t = 2$.
ב-$t = 1$:
\[\mathbf{v}_1 = (6 - 2)\mathbf{\hat{x}} + 3\mathbf{\hat{y}} - 4\mathbf{\hat{z}} = 4\mathbf{\hat{x}} + 3\mathbf{\hat{y}} - 4\mathbf{\hat{z}}\]גודל המהירות:
\[v_1 = \sqrt{4^2 + 3^2 + (-4)^2} = \sqrt{16 + 9 + 16} = \sqrt{41} \text{ m/s}\]ב-$t = 2$:
\[\mathbf{v}_2 = (12 - 2)\mathbf{\hat{x}} + 12\mathbf{\hat{y}} - 32\mathbf{\hat{z}} = 10\mathbf{\hat{x}} + 12\mathbf{\hat{y}} - 32\mathbf{\hat{z}}\]גודל המהירות:
\[v_2 = \sqrt{10^2 + 12^2 + (-32)^2} = \sqrt{100 + 144 + 1024} = \sqrt{1268} \text{ m/s}\]נחשב את האנרגיות הקינטיות:
האנרגיה הקינטית ב-$t = 1$:
\[E_{k1} = \frac{1}{2}mv_1^2 = \frac{1}{2} \times 4 \times 41 = 82 \text{ J}\]האנרגיה הקינטית ב-$t = 2$:
\[E_{k2} = \frac{1}{2}mv_2^2 = \frac{1}{2} \times 4 \times 1268 = 2536 \text{ J}\]לפי משפט עבודה-אנרגיה:
\[W = E_{k2} - E_{k1} = 2536 - 82 = \boxed{2454 \text{ J}}\]זוהי עבודה חיובית גדולה מאוד - הכוח האיץ את הגוף באופן משמעותי במהלך השנייה השנייה.
שאלה 6: ניתוח גרף כוח
הערה: השאלה גם הופיעה בדף התרגול הנוסף עם פתרון רשמי של המרצה. הפיתרון כאן הוא לא אותו פיתרון, אבל מגיע לאותן תוצאות.
הגרף המצורף מתאר את הכוח השקול הפועל על גוף שמסתו $m = 2 \, \mathrm{kg}$.
ידוע כי הגוף החל את תנועתו בראשית הצירים במהירות של ארבעה מטרים לשנייה $v(x = 0) = 4 \mathrm{m/s}$.
- איזה גודל פיסיקלי מתואר ע”י השטח הכלוא בין הגרף ובין ציר ה-X?
- חשבו את האנרגיה הקינטית של הגוף בנקודה $x = 3.0 \, \mathrm{m}$.
- מהו שיעור הנקודה $x$ שבה יש לגוף אנרגיה קינטית של $8 \, \mathrm{J}$?
- מהי האנרגיה הקינטית המקסימלית שהגוף מקבל בין הנקודה $x=0$ ל-$x=5$?
- האם שינה הגוף את כיוון תנועתו בין $x=0$ ל-$x=5$?
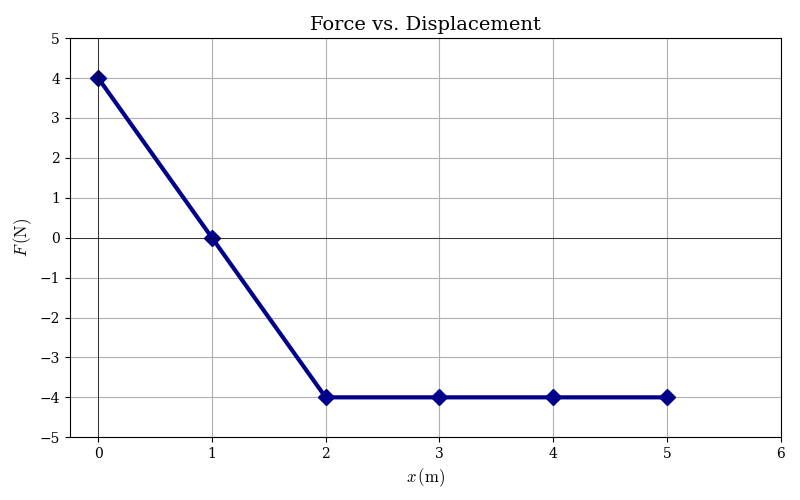
פתרון מפורט
סעיף א: משמעות השטח מתחת לגרף
כאשר יש לנו גרף של כוח כפונקציה של מיקום, השטח מתחת לגרף מייצג את העבודה:
\[W = \int_{x_1}^{x_2} F(x)dx\]זהו עיקרון חשוב: השטח החיובי (מעל ציר ה-x) מייצג עבודה חיובית, והשטח השלילי (מתחת לציר ה-x) מייצג עבודה שלילית.
סעיף ב: אנרגיה קינטית ב-x = 3 מטר
מהגרף, אנחנו רואים שהכוח יורד ליניארית מ-4 ניוטון ב-x=0 ל-0 ב-x=1, ואז ממשיך לרדת ל-(-4) ניוטון ב-$x=2$.
העבודה מ-x=0 עד x=3 היא השטח של משולש חיובי (מ-0 עד 1) ועוד שטח של משולש שלילי (מ-1 עד 2) ועוד שטח מלבן שלילי (מ-2 עד 3):
\[W_{0\to3} = -4 \text{ J}\]האנרגיה הקינטית ההתחלתית:
\[E_{k0} = \frac{1}{2}mv_0^2 = \frac{1}{2} \times 2 \times 16 = 16 \text{ J}\]לכן האנרגיה הקינטית ב-x=3:
\[E_{k3} = E_{k0} + W_{0\to3} = 16 - 4 = 12 \text{ J}\]סעיף ג: נקודה עם אנרגיה קינטית של 8 ג׳אול
נחפש נקודה שבה העבודה המצטברת היא:
\[W = 16 - 8 = 8 \text{ J}\]מהגרף, נצטרך להמשיך מעבר ל-x=3 כדי להגיע לעבודה שלילית של 8 ג׳אול. בין x=3 ל-x=4, הכוח קבוע ושווה ל-($-4$) ניוטון, כך שהעבודה היא:
\[W_{0\to 4} = 16 - 8 = 8 \text{ J}\]סעיף ד: אנרגיה קינטית מקסימלית
האנרגיה הקינטית מקסימלית תהיה בנקודה שבה העבודה המצטברת החיובית היא מקסימלית. מהגרף, זה קורה ב-x=1, שם:
\[W_{0\to1} = \frac{1}{2} \times 1 \times 4 = 2 \text{ J}\]לכן:
\[E_{k,\text{max}} = 16 + 2 = 18 \text{ J}\]סעיף ה: שינוי כיוון
הגוף משנה כיוון כאשר המהירות שלו מתאפסת. זה קורה כאשר כל האנרגיה הקינטית נעלמת, כלומר כאשר $E_k = 0$.
נצטרך עבודה של:
\[W = 0 - 16 = -16 \text{ J}\]כפי שחישבנו, העבודה הכוללת עד x=5 היא $-8$ ג׳אול.
מכיוון שהעבודה הכוללת עד x=5 היא רק $-8$ ג׳אול, ואנחנו צריכים $-16$ ג׳אול כדי לעצור את הגוף, המסקנה היא שהגוף לא הגיע למצב של מהירות אפס בתחום הנתון. לכן, הגוף לא שינה את כיוון תנועתו.
זו דוגמה טובה לכך שכוח שלילי (מתנגד לתנועה) לא בהכרח גורם לגוף לעצור - זה תלוי בגודל האנרגיה הקינטית ההתחלתית ובגודל העבודה השלילית.
דור פסקל