מבחן פיזיקה א׳ - מועד ב תשפ״ד
שאלה 1: קבועי תנועה
בהינתן ההגדרה הבאה:
״קבוע של התנועה הוא גודל כלשהו המאפיין את המערכת הפיזיקלית, אשר אינו משתנה בזמן למרות שמאפיינים אחרים של המערכת – המופיעים בתוך הקבוע - כן עשויים להשתנות בזמן.״
איזה מהטענות הבאות היא מדויקת?
אם האנרגיה המכנית של גוף היא קבוע של התנועה, הרי שגזירתה לפי הזמן מנפקת את משוואות התנועה של הגוף.
אם התנע הזוויתי הוא קבוע של התנועה, הרי ששקול המומנטים במערכת שונה מאפס.
אם האנרגיה הקינטית היא קבוע של התנועה, הרי שבהכרח אין כוחות משמרים במערכת.
אם האנרגיה המכנית היא קבוע של התנועה, הרי שעבודת הכוחות הלא משמרים בהכרח שונה מאפס.
נעבור על כל אחת מהטענות ונבדוק את נכונותה:
טענה א: זו הטענה הנכונה! כאשר האנרגיה המכנית $E$ היא קבוע של התנועה, אז:
\[\frac{dE}{dt} = 0\]אם נרשום את האנרגיה המכנית:
\[E = \frac{1}{2}m\dot{x}^2 + V(x)\]ונגזור לפי הזמן:
\[\frac{dE}{dt} = m\dot{x}\ddot{x} + \frac{dV}{dx}\dot{x} = \dot{x}\left(m\ddot{x} + \frac{dV}{dx}\right) = 0\]מכאן (בהנחה ש-$\dot{x} \neq 0$):
\[m\ddot{x} = -\frac{dV}{dx} = F\]וזו בדיוק משוואת התנועה של ניוטון!
טענה ב: שגויה. אם התנע הזוויתי $\vec{L}$ הוא קבוע של התנועה, אז:
\[\frac{d\vec{L}}{dt} = \vec{\tau} = 0\]כלומר, שקול המומנטים חייב להיות אפס, לא שונה מאפס.
טענה ג: שגויה. אנרגיה קינטית קבועה פירושה שגודל המהירות קבוע, אבל זה יכול לקרות גם עם כוחות משמרים (למשל, תנועה מעגלית קצובה תחת כוח מרכזי).
טענה ד: שגויה. אם האנרגיה המכנית נשמרת, אז דווקא עבודת הכוחות הלא משמרים חייבת להיות אפס.
שאלה 2: מתקף
איזה מהטענות הבאות בנוגע למתקף לחלוטין אינה נכונה?
המתקף שמפעיל כוח חיצוני על גוף הוא הצטברות הכוח הפועל על הגוף לאורך הדרך שעשה הגוף במהלך תנועתו.
המתקף הפועל על גוף מבטא את השינוי בתנע של הגוף.
המתקף שמפעיל גוף A על גוף B בזמן אינטראקציה בניהם, שווה בגודלו והפוך בכיוונו למתקף שגוף B מפעיל על גוף A.
המתקף שמפעיל כוח חיצוני כלשהו על מערכת פיזיקלית מכמת את הצטברות הכוח על המערכת במשך כל זמן האינטראקציה בניהם.
המתקף (Impulse) מוגדר כ:
\[\vec{J} = \int_{t_1}^{t_2} \vec{F} dt\]נבדוק כל טענה:
טענה א: שגויה! זו ההגדרה של עבודה, לא של מתקף. עבודה היא:
\[W = \int \vec{F} \cdot d\vec{r}\]בעוד שמתקף הוא אינטגרל על זמן, לא על דרך.
טענה ב: נכונה. לפי משפט המתקף-תנע:
\[\vec{J} = \Delta\vec{p} = \vec{p}_f - \vec{p}_i\]טענה ג: נכונה. לפי החוק השלישי של ניוטון,
\[\vec{F}_{AB} = -\vec{F}_{BA}\]ולכן:
\[\vec{J}_{AB} = \int \vec{F}_{AB} dt = -\int \vec{F}_{BA} dt = -\vec{J}_{BA}\]טענה ד: נכונה. זו בדיוק ההגדרה של מתקף - הצטברות הכוח לאורך זמן האינטראקציה.
שאלות 4-3: חבל על גג משופע
חבל מסיבי שאורכו הכולל הוא $L$ מחליק מגג בניין משופע כמוראה באיור.
הזניחו את החיכוך של החבל עם הבניין.
|\ \ | \ \ | θ\ \ |---\ \ |↑ | |x | |↓ | |שאלה 3: משוואת התנועה
יהא $x(t)$ החלק המשתלשל מהגג בכל זמן $t$. אזי, המשוואה הדיפרנציאלית המתארת את תנועת החבל היא:
נגדיר את המערכת:
- אורך כולל של החבל: $L$
- חלק משתלשל: $x$
- חלק על הגג המשופע: $L-x$
- זווית השיפוע: $\theta$
- צפיפות ליניארית של החבל: $\lambda = m/L$
כוחות הפועלים על החבל:
- על החלק המשתלשל ($x$): משקל כלפי מטה $\lambda x g$
- על החלק שעל הגג ($L-x$): רכיב המשקל במורד השיפוע $\lambda(L-x)g\sin\theta$
משוואת ניוטון עבור כל החבל:
\[ma = \lambda L \ddot{x} = \lambda x g + \lambda(L-x)g\sin\theta\]נחלק ב-$\lambda L$:
\[\ddot{x} = \frac{g}{L}x(1-\sin\theta) + g\sin\theta\]שאלה 4: ביטוי המהירות
ידוע כי $\theta = \pi/6$ רדיאנים.
ידועים גם תנאי ההתחלה $x(t=0) = b$, $\dot{x}(t=0) = 0$.
בתנאים אלו גזירת הפתרון של משוואת התנועה מובילה אל המהירות כפונקציה של הזמן:
\[v(t) = (b + L)\omega \sinh(\omega t)\]באשר $\omega = \sqrt{g/2L}$.
תהא $a(t)$ תאוצת החבל בכל זמן $t$.
הביטוי $a^2 - \omega^2 v^2$ הוא:
נתון ש-$\theta = \pi/6$, לכן $\sin\theta = 1/2$.
המשוואה הדיפרנציאלית הופכת ל:
\[\ddot{x} = \frac{g}{L}x(1-1/2) + g/2 = \frac{g}{2L}x + \frac{g}{2}\]נבדוק את הביטוי $a^2 - \omega^2 v^2$:
מהמהירות הנתונה:
\[v = (b+L)\omega\sinh(\omega t)\]התאוצה:
\[a = \frac{dv}{dt} = (b+L)\omega^2\cosh(\omega t)\]נחשב את $a^2 - \omega^2 v^2$:
\[a^2 = ((b+L)\omega^2\cosh(\omega t))^2 = (b+L)^2\omega^4\cosh^2(\omega t)\] \[v^2 = ((b+L)\omega\sinh(\omega t))^2 = (b+L)^2\omega^2\sinh^2(\omega t)\] \[a^2 - \omega^2 v^2 = (b+L)^2\omega^4\cosh^2(\omega t) - (b+L)^2\omega^2\sinh^2(\omega t)\] \[= (b+L)^2\omega^2(\omega^2\cosh^2(\omega t) - \sinh^2(\omega t))\]נשתמש בזהות $\cosh^2(x) - \sinh^2(x) = 1$:
\[= (b+L)^2\omega^2\]מכאן שהביטוי $a^2 - \omega^2 v^2$ הוא קבוע בזמן, תלוי רק בפרמטרים של המערכת.
שאלות 7-5: חרוז על קשת מעגלית
חרוז שמסתו $m$ מחליק ע”ג קשת מעגלית נטולת חיכוך כמוראה בתרשים, כך שהקואורדינטה המתארת את מיקומו כפונקציה של הזמן באופן “הכי טבעי” היא $\theta(t)$.
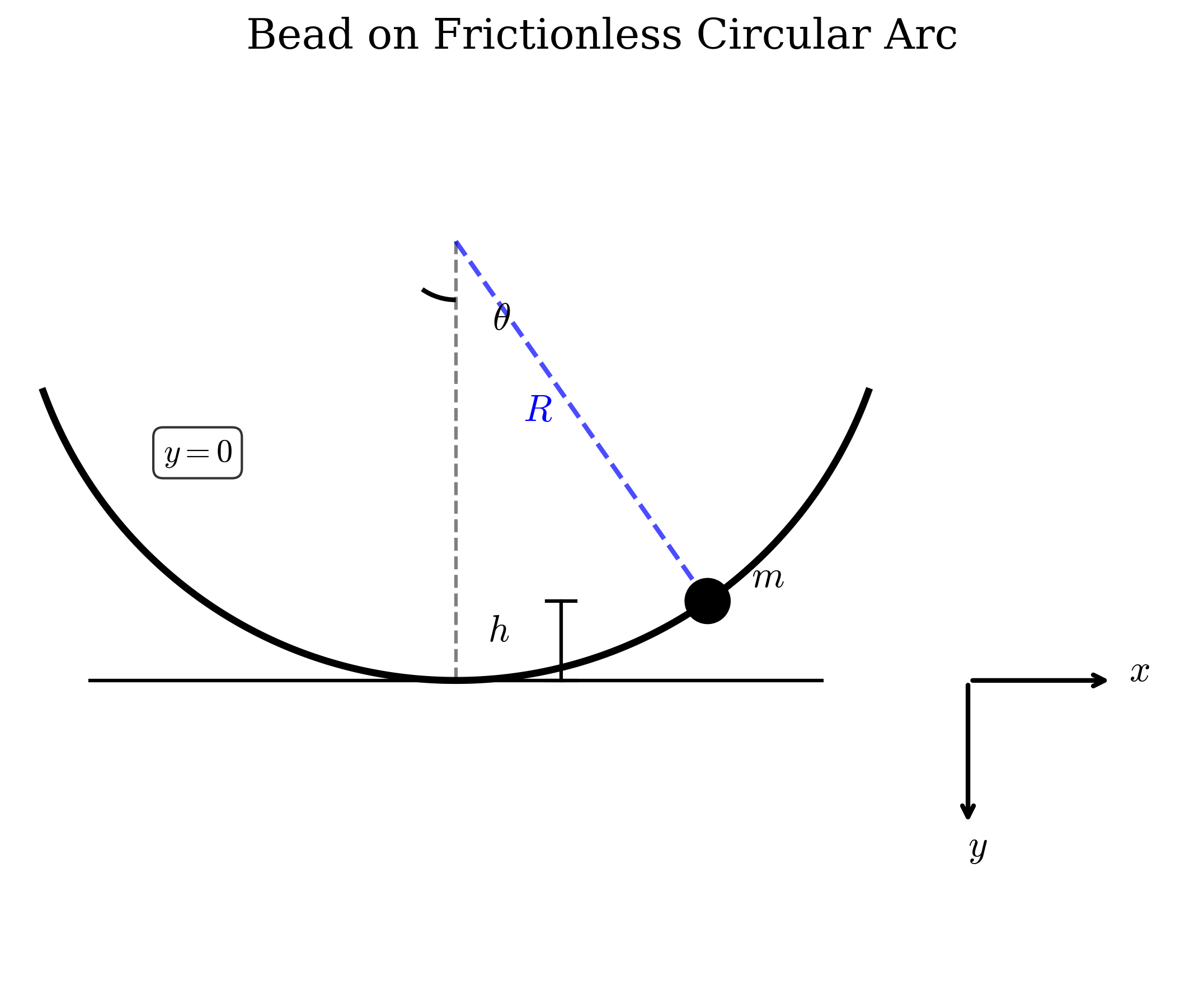
שאלה 5: האנרגיה המכנית
האנרגיה המכנית של החרוז בהתייחס לתחתית הקשת המעגלית ($y=0$) מקיימת:
במערכת קואורדינטות פולריות עבור תנועה על מעגל ברדיוס $R$:
- מיקום: $r = R$ (קבוע), $\theta = \theta(t)$
- מהירות: $v = R\dot{\theta}$
אנרגיה קינטית:
\[E_k = \frac{1}{2}mv^2 = \frac{1}{2}mR^2\dot{\theta}^2\]אנרגיה פוטנציאלית:
הגובה של החרוז מעל נקודת הייחוס (תחתית הקשת):
\[h = R - R\cos\theta = R(1 - \cos\theta)\]לכן:
\[\phi = mgh = mgR(1 - \cos\theta)\]אבל בנתוני השאלה בחרו את מישור הייחוס להיות כלפי $y=0$ חיובי כלפי מטה, לכן:
\[\phi = -mgR(1 - \cos\theta)\]האנרגיה המכנית הכוללת:
\[E = E_k + \phi = \frac{1}{2}mR^2\dot{\theta}^2 - mgR(1 - \cos\theta)\]שאלה 6: מהירות במערכת צופה
צופה נמצא בתנועה בליסטית כך שמשוואות התנועה שלו הן
\[x = v_0t, \quad y(t) = \frac{1}{2}gt^2\]הניחו עתה את ראשית הצירים על מרכז הקשת המעגלית.
וקטור המהירות של החרוז במערכת המנוחה של הצופה הוא:
מהירות החרוז במערכת המעבדה:
- רכיב x: $v_{x,\text{bead}} = -R\sin\theta \cdot \dot{\theta}$
- רכיב y: $v_{y,\text{bead}} = R\cos\theta \cdot \dot{\theta}$
מהירות הצופה:
- $v_{x,\text{man}} = v_0$
- $v_{y,\text{man}} = gt$
מהירות יחסית:
\[\vec{v}_{\text{bead→man}} = \vec{v}_{\text{bead}} - \vec{v}_{\text{man}}\] \[= (-R\dot{\theta}\sin\theta - v_0)\hat{x} + (R\dot{\theta}\cos\theta - gt)\hat{y}\](שאלה 7 כנראה לא בחומר)
שאלות 9-8: כוחות על כדור הארץ המסתובב
שאלה 8: משקל בקו המשווה
משקלו של אדם הנמצא בגובה פני הים בקו המשווה הוא:
בקו המשווה, הכוח הצנטריפוגלי פועל כלפי חוץ (הפוך לכוח הכבידה).
הכוח הצנטריפוגלי:
\[F_{\text{centripetal}} = m\omega^2R_E\]המשקל האפקטיבי (מה שמודד המשקל):
\[W = mg - m\omega^2R_E\]שאלה 9: כוח קוריוליס בנפילה חופשית
אדם נמצא בנפילה חופשית בקו המשווה. כוח קוריוליס הפועל עליו ניתן ע”י:
כוח קוריוליס נתון על ידי:
\[\vec{F}_c = -2m(\vec{\omega} \times \vec{v})\]המהירות של כדור הארץ סביב צירו היא:
\[\vec{\omega} = \omega\hat{z} \quad \text{north pole up}\]המהירות של אדם בנפילה חופשית היא:
\[\vec{v} = v_x\hat{x} + v_y\hat{y}\]מכאן:
\[\vec{F}_c = -2m\omega(v_x\hat{y} - v_y\hat{x}) = 2m(\omega v_y\hat{x} - \omega v_x\hat{y})\]שאלות 11-10: התנגשות כדור ובול עץ
שאלה 10: המתקף על הבול
בול עץ שמסתו היא $M$ מונח על שולחן אופקי חלק. הבול מחובר לקפיץ אשר מקדם הכוח שלו הוא $k$, כמורה באיור.
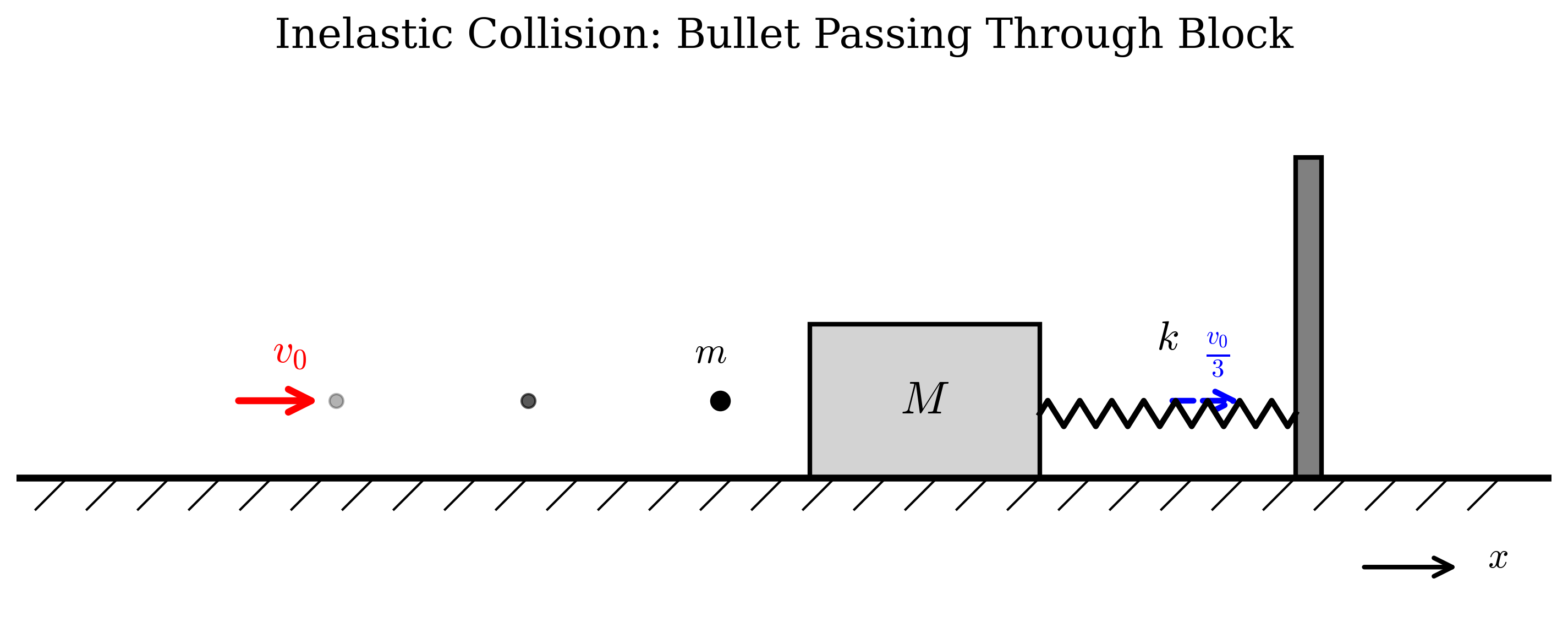
כדור קטן שמסתו היא $m$ נורה אופקית לעבר הבול, ומהירותו לפני הפגיעה בבול היא $v_0$.
הכדור חוזר את הבול ויוצא מצידו השני במהירות $v_0 / 3$ מבלי לפגוע בקפיץ.
נניח שהשינוי במסה הבול כתוצאה ממעבר הכדור דרכו, זניח.
לאחר מעבר הכדור דרכו, הבול המחובר לקפיץ מבצע תנודות הרמוניות.
וקטור המתקף שפעל על הבול במהלך מעבר הכדור דרכו הוא:
שימור תנע לכדור:
- תנע התחלתי: $p_i = mv_0$
- תנע סופי: $p_f = m(v_0/3)$
- שינוי תנע הכדור: $\Delta p_{\text{bullet}} = -2mv_0/3$
מתקף על הבול:
לפי החוק השלישי של ניוטון:
\[\vec{J}_{\text{tree}} = -\vec{J}_{\text{bullet}} = \frac{2mv_0}{3}\hat{x}\]המתקף אינו תלוי בהתכווצות הקפיץ כי זמן ההתנגשות קצר מאוד.
שאלה 11: תנועת הבול אחרי ההתנגשות
פונקציית מקום-זמן של הבול לאחר ההתנגשות:
מהמתקף, מהירות הבול מיד אחרי ההתנגשות:
\[Mv_{\text{tree}} = \frac{2mv_0}{3}\] \[v_{\text{tree}} = \frac{2mv_0}{3M}\]הבול מבצע תנועה הרמונית פשוטה עם:
- תדירות זוויתית: $\omega = \sqrt{k/M}$
- משרעת: $A = v_{\text{tree}}/\omega = \frac{2mv_0}{3\sqrt{Mk}}$
עם תנאי התחלה $x(0) = 0$, $\dot{x}(0) = v_{\text{tree}}$:
\[x(t) = A\sin(\omega t) = \frac{2mv_0}{3\sqrt{Mk}}\sin\left(\sqrt{\frac{k}{M}}t\right)\]שאלות 14-12: תנועה בקואורדינטות פולריות
שאלה 12: הכוח מהפוטנציאל
גוף שמסתו $m$ נע בקואורדינטות פולריות תחת פוטנציאל:
\[\phi(r) = -\frac{\alpha}{r}\]$\alpha$ הוא פרמטר חיובי.
אופרטור הגרדיאנט בקואורדינטות פולריות הוא:
\[\nabla = \hat{r}\frac{\partial}{\partial r} + \hat{\theta}\frac{1}{r}\frac{\partial}{\partial \theta}\](אין במערכת כוחות לא משמרים).
הכוח הנגזר מהאנרגיה הפוטנציאלית $\phi(r) = -\alpha/r$ הוא:
באמצעות הגרדיאנט בקואורדינטות פולריות:
\[\vec{F} = -\nabla\phi = -\hat{r}\frac{\partial\phi}{\partial r} - \hat{\theta}\frac{1}{r}\frac{\partial\phi}{\partial\theta}\]מכיוון ש-$\phi$ תלוי רק ב-$r$:
\[\vec{F} = -\hat{r}\frac{\partial}{\partial r}\left(-\frac{\alpha}{r}\right) = -\hat{r}\frac{\alpha}{r^2}\]לא בטוח מה התשובה הנכונה.
שאלה 13: האנרגיה המכנית
האנרגיה המכנית של הגוף נתונה בביטוי:
בקואורדינטות פולריות, האנרגיה הקינטית:
\[E_k = \frac{1}{2}m(\dot{r}^2 + r^2\dot{\theta}^2)\]האנרגיה המכנית הכוללת:
\[E = E_k + \phi = \frac{1}{2}m(\dot{r}^2 + r^2\dot{\theta}^2) - \frac{\alpha}{r}\]שאלה 14 להבנתי לא בחומר.
דור פסקל