טרנספורמציות גליליי
נושא חשוב הוא טרנספורמציות גליליי. נדון בנושא זה בצורה אנליטית.
מהן טרנספורמציות גליליי? הוגדר כי מערכת התמד היא מערכת שמאופיינת על ידי מהירות קצובה. יש לדייק בהגדרה - מהירות קצובה ביחס למה? מהירות קצובה ביחס לצופה אחד אינה בהכרח מהירות קצובה ביחס לצופה אחר הנע ביחס אליו.
ניתן להניח קיומה של מערכת ייחוס אבסולוטית, שביחס אליה ניתן להגדיר תנועה במהירות קצובה.
לדוגמה, כדור הארץ מסתובב סביב צירו ומשלים סיבוב ב-24 שעות. מערכת שמסתובבת אינה מערכת במהירות קצובה, כי סיבוב הוא תנועה מואצת. תנועה על פני מעגל היא תנועה המואצת לעבר המרכז.
עם זאת, הסיבוב של כדור הארץ הוא איטי מאוד. ניתן לחשב את המהירות הזוויתית, הקשורה לזמן המחזור דרך הקשר:
\[\omega = \frac{2\pi}{T}\]כאשר $T$ הוא זמן המחזור.
בתנועה מעגלית, וקטור המקום מתואר על ידי:
\[\vec{r}(t) = R \cos(\omega t) \hat{x} + R \sin(\omega t) \hat{y}\]הקוסינוס והסינוס הן פונקציות מחזוריות, כאשר המחזור הוא $2\pi$. כלומר, אחרי $\omega t = 2\pi$, הגוף חוזר לאותה פוזיציה. אם $t$ מתאר את הזמן ו-$T$ מתאר את זמן המחזור, אז:
\[\omega T = 2\pi \Rightarrow \omega = \frac{2\pi}{T}\]זמן המחזור $T$ של כדור הארץ הוא 24 שעות. לכן, המהירות הזוויתית $\omega$ של כדור הארץ היא:
\[\omega = \frac{2\pi}{24 \cdot 3600} \approx \frac{2 \cdot 3.14}{86400} \approx 7.27 \times 10^{-5} \text{ rad/s}\]המהירות הזוויתית של כדור הארץ נמוכה מאוד, ובקירוב מצוין כל מה שעל פני כדור הארץ יכול להיחשב כמערכת התמד. כלומר, התאוצה זניחה והמהירות כמעט קבועה.
הדבר דומה לטענה שכדור הארץ שטוח. בקירוב של סביבה מקומית (כיתה, עיר), כדור הארץ נראה שטוח. רק מגובה רב ניתן להבחין בעקמומיות שלו. כדור הארץ גדול והסביבה המיידית שלנו קטנה.
לכן, ניתן להתייחס למרחב הכיתה כאל מרחב קרטזי ולתאוצת הכיתה כאל אפסית ביחס למערכת הייחוס של כדור הארץ.
יש לציין כי המהירות הזוויתית של כדור הארץ בתנועתו סביב השמש נמוכה אף יותר (זמן מחזור של 365 ימים), ומהירות הסיבוב של מערכת השמש סביב מרכז הגלקסיה נמוכה עוד יותר (זמן מחזור של כ-220 מיליון שנה).
בקירוב מצוין, עבור הבעיות הנדונות כאן, ניתן להתייחס לכדור הארץ כמערכת התמד.
הגדרת טרנספורמציות גליליי
נתונות שתי מערכות התמד, $S$ ו-$S’$, הנעות זו ביחס לזו במהירות קצובה.
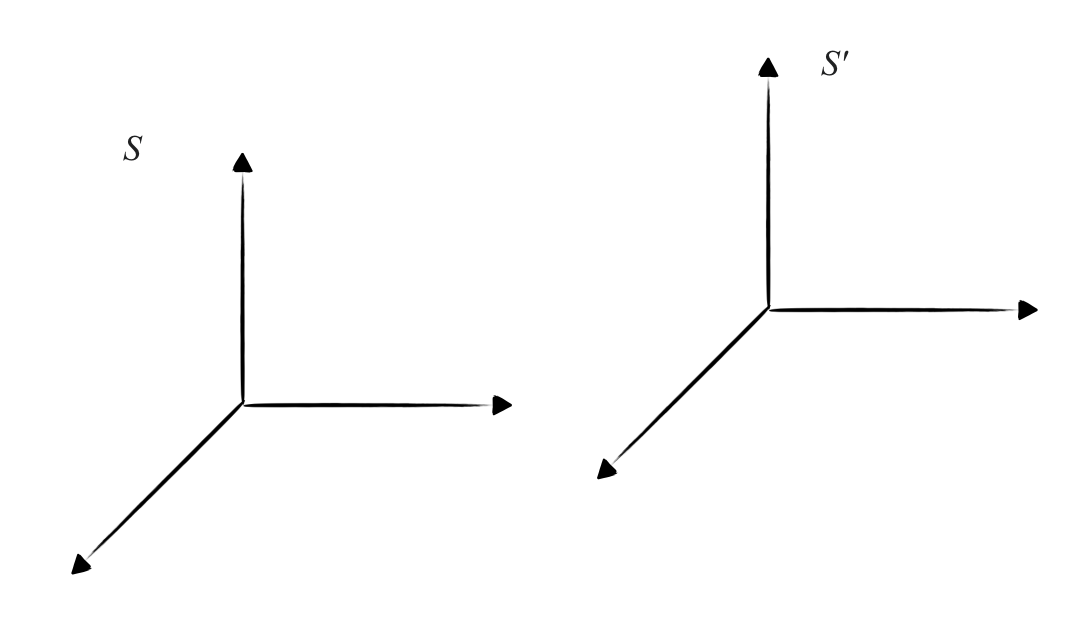
המהירות הקצובה של $S’$ ביחס ל-$S$ היא $\vec{u}$. אם בזמן $t=0$ הראשיות של המערכות התלכדו, אז בזמן $t > 0$ וקטור המרחק בין הראשיות הוא $\vec{u} t$.
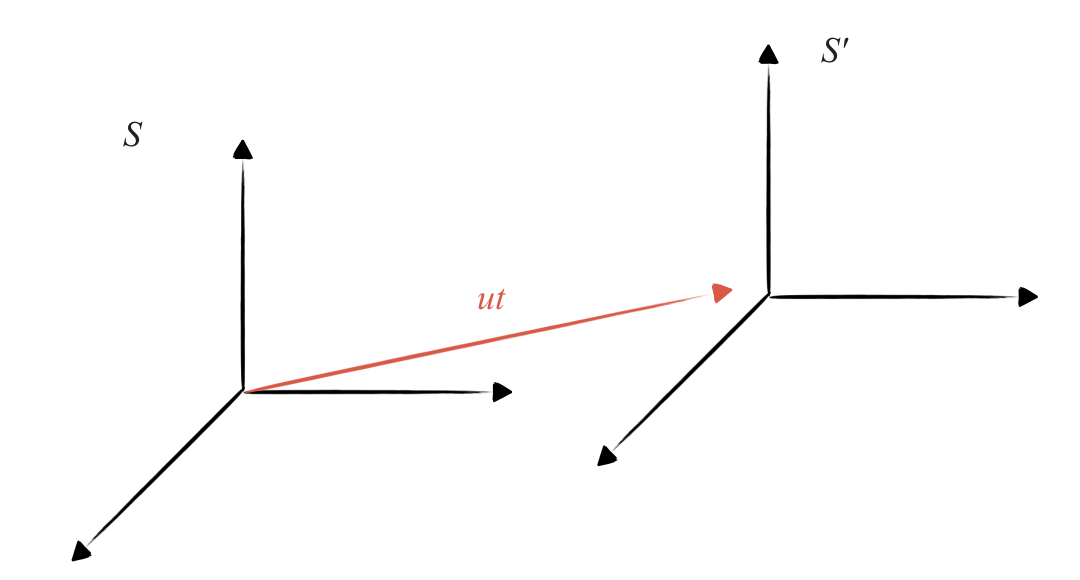
וקטור המקום של ראשית $S’$ ביחס לראשית $S$ בזמן $t$ הוא $\vec{u} t$.
נתבונן בחלקיק הנע במערכת $S$. וקטור המקום שלו הוא $\vec{r}$. וקטור המקום שלו במערכת $S’$ הוא $\vec{r}’$. הקשר בין וקטורי המקום הוא:
\[\vec{r} = \vec{r}' + \vec{u} t\]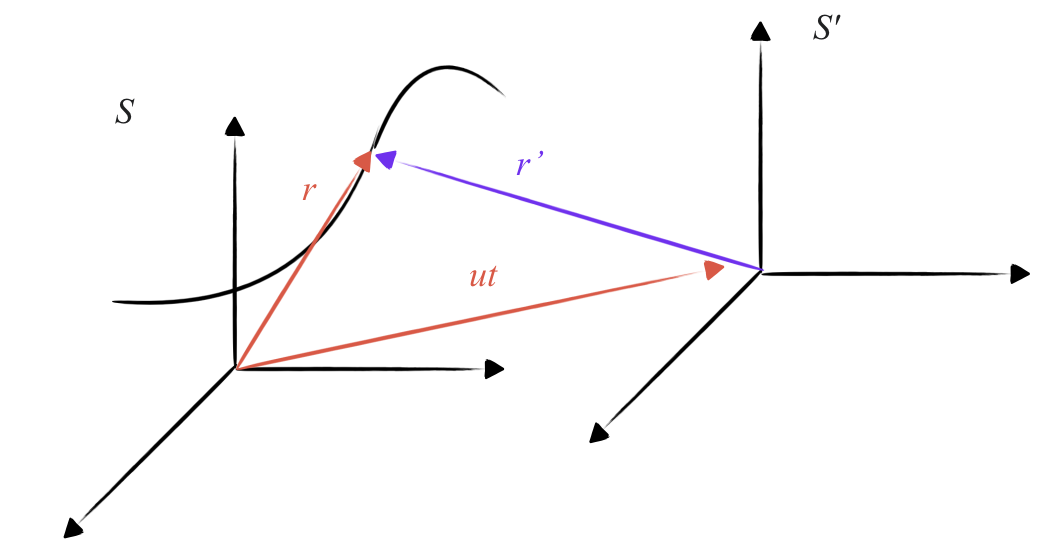
וקטור המקום במערכת $S$ הוא סכום וקטור המקום במערכת $S’$ והווקטור $\vec{u} t$.
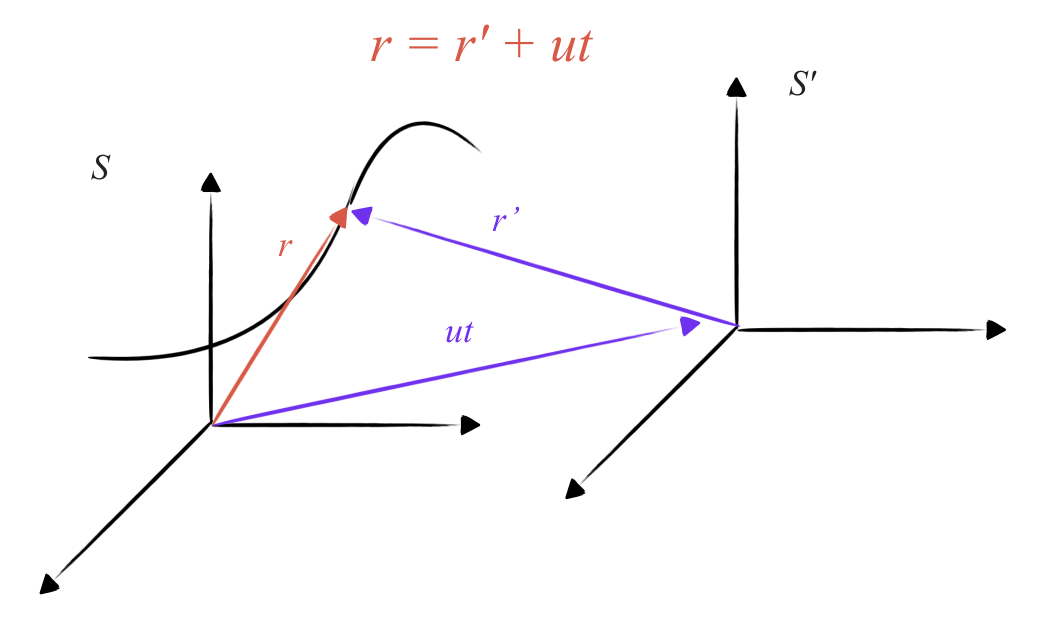
מכאן, חוק הטרנספורמציה של וקטורי המקום הוא:
\[\vec{r}' = \vec{r} - \vec{u} t\]מהירויות הן נגזרות של וקטורי המקום לפי הזמן. מהירות החלקיק $\vec{v}’$ במערכת $S’$ היא:
\[\vec{v}' = \frac{d\vec{r}'}{dt} = \frac{d\vec{r}}{dt} - \frac{d(\vec{u} t)}{dt} = \vec{v} - \vec{u}\]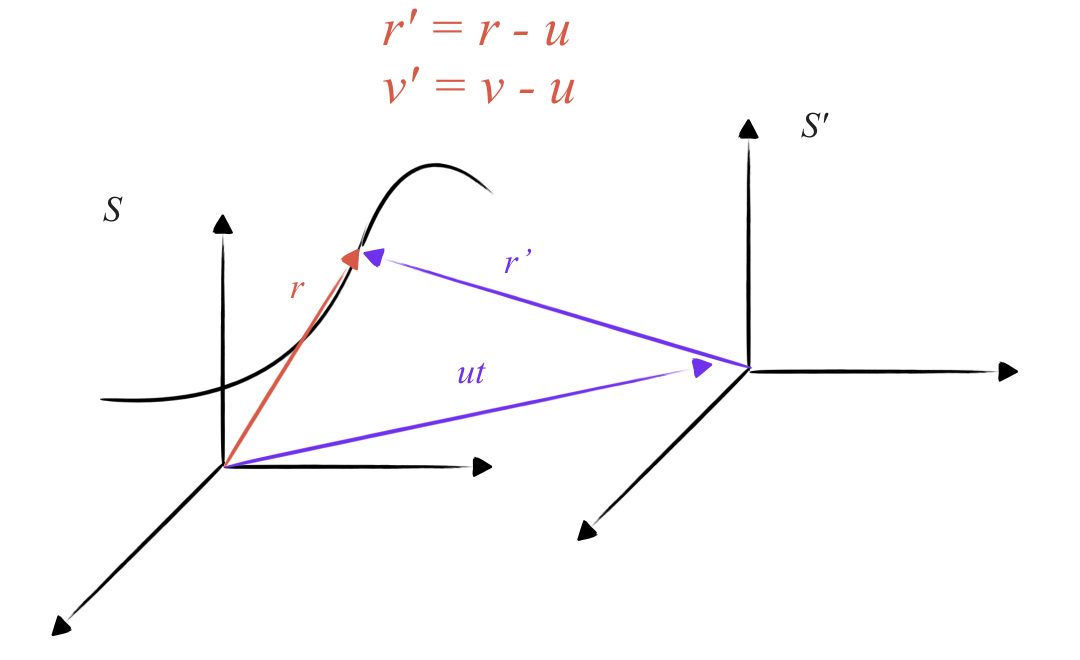
בנוסחה זו נעשה שימוש אינטואיטיבי בחישוב מהירויות יחסיות, עוד לפני ההגדרה הפורמלית של טרנספורמציות גליליי.
אם נגזור פעם נוספת לפי הזמן, ומכיוון שהווקטור $\vec{u}$ קבוע, נקבל:
\[\vec{a}' = \frac{d\vec{v}'}{dt} = \frac{d\vec{v}}{dt} - \frac{d\vec{u}}{dt} = \vec{a} - 0 = \vec{a}\]כלומר, התאוצות בשתי מערכות ההתמד שוות זו לזו. יש הבדל בין וקטורי המקום והמהירות, אך אין הבדל בין וקטורי התאוצה.
מכאן, מתוך החוק השני של ניוטון $\vec{F} = m\vec{a}$, ניתן להסיק שגם אין הבדל בכוחות:
\[\vec{F} = \vec{F}'\]לכן, ניתן להחיל את חוקי ניוטון באופן זהה בכל מערכות ההתמד.
מערכות התמד ומערכות מואצות
הפיתוח המתואר לעיל, שנעשה על ידי מדענים במאות ה-17 וה-18, התבסס על הנחה סמויה: הזמן הוא פרמטר אוניברסלי, זהה בכל המערכות. הנחה זו, שנראית סבירה מנקודת מבט אינטואיטיבית, הופרכה על ידי איינשטיין. תיקון הנחה זו הוביל לפיתוח תורת היחסות, שהיוותה קפיצת מדרגה בהבנת הפיזיקה.
מערכת התמד היא מערכת הנעה במהירות קצובה ביחס למערכת ייחוס אבסולוטית (למשל, היקום הסטטי). בתורה הניוטונית, החוק השני של ניוטון, $\vec{F} = m\vec{a}$ או $\vec{F} = \frac{d\vec{p}}{dt}$, תקף בכל מערכות ההתמד, ללא תלות במהירותן היחסית.
דוגמאות ליישום חוקי ניוטון במערכות שונות
הדיון החל מהקביעה שהכיתה היא מערכת התמד, מכיוון שמהירותה ביחס לכדור הארץ היא אפס (גודל קבוע).
אולם, ניתן לטעון שכדור הארץ עצמו אינו מערכת התמד, שכן הוא מסתובב סביב צירו, ותנועה מעגלית היא תנועה מואצת.
התשובה לכך היא שתאוצת כדור הארץ קטנה מאוד. המהירות הזוויתית $\omega$ זניחה, ולכן התאוצה הצנטריפטלית קטנה מאוד. לכל צורך מעשי בניסויים הנערכים בכיתה (כמו מטוטלת), ניתן להתייחס לכיתה כאל מערכת התמד.
גם אם הכיתה הייתה נעה במהירות של 1000 קמ”ש ביחס לכדור הארץ, כל עוד מהירות זו קבועה, עדיין ניתן היה להחיל את החוק השני של ניוטון.
לעומת זאת, מעלית הנמצאת בתאוצה אינה מערכת התמד. יש להבחין בין תנועה במהירות קבועה (מערכת התמד) לבין תנועה בתאוצה (מערכת לא-אינרציאלית).
גם גוף הנע במהירות של 200,000 ק”מ/שנייה נמצא במערכת התמד, כל עוד מהירותו קבועה. אין הבדל מהותי בין מנוחה לתנועה במהירות קצובה, שכן תמיד ניתן לבצע טרנספורמציית גליליי למערכת שבה הגוף נמצא במנוחה. בתורה הניוטונית, אין הגבלה על גודל המהירות. בתורת היחסות, המצב משתנה ככל שמתקרבים למהירות האור.
תאוצת הנפילה החופשית ודוגמאות נוספות
נחדד את הרעיונות באמצעות דוגמה. נתבונן במערכת של שתי מסות התלויות על חוט הכרוך סביב גלגלת חסרת חיכוך.
ראשית, יש לזכור כי בניסויי מעבדה, תאוצת הנפילה החופשית של גופים בקרבת פני כדור הארץ היא גודל קבוע, המסומן ב-$g$, וערכו כ-9.8 מטר לשנייה בריבוע (ובקירוב 10 לצורך חישובים). המשמעות היא שמהירותו של גוף נופל גדלה בכל שנייה בערך זה.
עבור תאוצה קבועה, מתקיימות משוואות התנועה:
\[v(t) = v_0 + gt\]ו-
\[x(t) = x_0 + v_0t + \frac{1}{2}gt^2\](כאשר ציר $x$ חיובי כלפי מטה).
החוק השני של ניוטון, $\vec{F} = m\vec{a}$, תקף. הכוח הגורם לתאוצת הנפילה החופשית הוא כוח הכובד, $W$. לכן:
\[W = mg\]מעתה ואילך, כוח המשיכה בקרבת פני כדור הארץ יסומן כ-$mg$. קביעה זו נובעת מהידיעה האמפירית שתאוצת הנפילה החופשית קבועה בקרבת פני כדור הארץ.
נחזור למערכת הגלגלת. אם שתי המסות שוות ($m_1=m_2=m$) והמערכת משוחררת ממנוחה, היא תישאר במנוחה. שקול הכוחות הוא אפס, ולכן, לפי החוק הראשון של ניוטון, המערכת תתמיד במצבה. הכוחות הפועלים על כל מסה הם המתיחות בחוט $T$ (כלפי מעלה) וכוח הכובד $mg$ (כלפי מטה). במצב שיווי משקל, $T=mg$.
אם נשים את המערכת הזאת בחללית הנעה במהירות קבועה של 200,000 ק”מ/שנייה ביחס לכדור הארץ, התוצאה תהיה זהה. היות שהחללית היא מערכת התמד, חוקי ניוטון תקפים בה באותו אופן.
כעת, נניח שבכיתה, אנו מעניקים למסה אחת מהירות התחלתית $v$ כלפי מטה. המסה השנייה תעלה במהירות $v$ כלפי מעלה. מכיוון ששקול הכוחות הוא אפס, הגופים יתמידו במהירותם הקבועה.
גם אם נבצע ניסוי זה בחללית הנעה במהירות קבועה, התוצאה תהיה זהה. ההבדל היחיד יהיה במהירות הנמדדת של המסות ביחס לכיתה, שתדרוש חיבור וקטורי של מהירות החללית.
בשלב הבא, נבחן את המקרה שבו המסות שונות ושקול הכוחות אינו אפס.
הערה על הדוגמה הקודמת
לפני שנמשיך, יש להבהיר נקודה לגבי הדוגמה של הגלגלת בחללית. הכוונה הייתה שהחללית, על אף מהירותה הגבוהה, עדיין נמצאת תחת השפעת כוח המשיכה של כדור הארץ. ללא כוח משיכה, הבעיה הייתה שונה. הנקודה החשובה היא שאותם כוחות פועלים הן במערכת הכיתה והן במערכת החללית, מכיוון ששתיהן מערכות התמד.
מערכות לא מאוזנות - מכונת אטווד
כעת נבחן מצב שבו המערכת אינה מאוזנת. יש לנו גלגלת עם מסה $M_1$ מצד אחד ומסה $M_2$ מצד שני, כאשר $M_1 \neq M_2$.
הכוחות הפועלים על $M_2$ הם כוח הכבידה $M_2g$ כלפי מטה והמתיחות $T$ כלפי מעלה. הכוחות הפועלים על $M_1$ הם כוח הכבידה $M_1g$ כלפי מטה והמתיחות $T$ כלפי מעלה. המתיחות בחוט אחידה.
הדרך הנכונה לפתור את הבעיה היא להחיל את החוק השני של ניוטון על כל מסה בנפרד. נניח ש-$M_2 > M_1$, ולכן המערכת מואצת כך ש-$M_2$ יורדת ו-$M_1$ עולה בתאוצה $a$.
עבור המסה $M_2$, החוק השני של ניוטון (בכיוון מטה) הוא:
\[M_2g - T = M_2a\]עבור המסה $M_1$, החוק השני של ניוטון (בכיוון מעלה) הוא:
\[T - M_1g = M_1a\]קיבלנו מערכת של שתי משוואות עם שני נעלמים, $T$ ו-$a$. אם נחבר את שתי המשוואות, המתיחות $T$ תתבטל:
\[M_2g - T + T - M_1g = M_2a + M_1a\] \[(M_2 - M_1)g = (M_2 + M_1)a\]מכאן ניתן לבודד את התאוצה $a$:
\[a = \frac{M_2 - M_1}{M_2 + M_1} \cdot g\]אם $M_2 > M_1$, התאוצה $a$ חיובית, כפי שהנחנו. אם $M_2 = M_1$, אז $a = 0$. אם $M_2 < M_1$, אז $a < 0$, כלומר התאוצה היא בכיוון ההפוך.
טרנספורמציית גליליי מבטיחה שזו תהיה התוצאה גם במערכת התמד אחרת, כמו חללית הנעה במהירות קבועה.
ניתן לפתור את הבעיה גם על ידי החלת החוק השני על המערכת כולה. שקול הכוחות החיצוניים המניעים את המערכת הוא $(M_2 - M_1)g$. המסה הכוללת של המערכת היא $(M_1 + M_2)$. לכן:
\[(M_2 - M_1)g = (M_1 + M_2)a\]ומקבלים את אותה התוצאה עבור $a$.
תנועה במעלית וכוחות מדומים
נבחן כעת מה קורה לאדם במעלית. נניח שבמעלית עומד אדם. כאשר המעלית עולה במהירות קצובה, היא מערכת התמד. שקול הכוחות הפועל על האדם הוא אפס.
הכוחות הפועלים על האדם הם:
- כוח הכבידה $mg$ כלפי מטה.
- הכוח הנורמלי $N$ מהרצפה כלפי מעלה.
מהחוק הראשון של ניוטון:
\[N = mg\]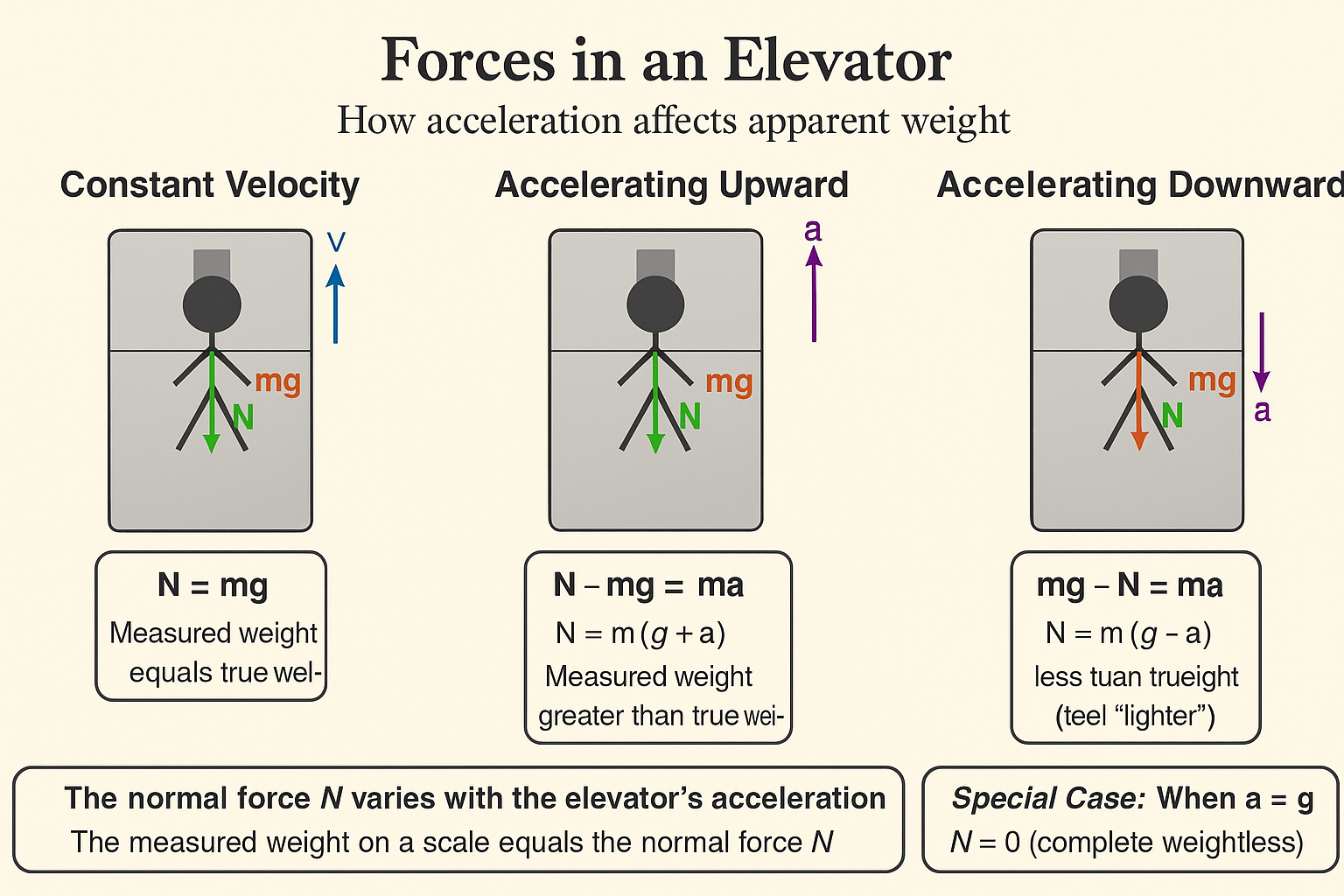
אם מסת האדם היא 80 ק”ג, אז $N = 80 \mathrm{[kg]} \cdot 10 \mathrm{[m/s^2]} = 800 \mathrm{[N]}$.
כעת, נניח שהמעלית מואצת כלפי מעלה בתאוצה $a$. המעלית אינה מערכת התמד. גם האדם שבתוכה מואץ באותה תאוצה. מהחוק השני של ניוטון:
\[N - mg = ma\]מכאן:
\[N = m(g + a)\]אם במעלית הייתה מונחת מאזני משקל, הן היו מודדות את הכוח הנורמלי $N$. לכן, כאשר המעלית מואצת כלפי מעלה, המשקל הנמדד של האדם גדול יותר. למשל, אם $a = 2 \mathrm{ m/s^2}$:
\[\text{observed weight} = 80 \mathrm{ kg} \cdot (10 + 2) \mathrm{ m/s^2} = 960 \mathrm{ N}\]במקרה ההפוך, כאשר המעלית מואצת כלפי מטה בתאוצה $a$, מתקיים:
\[mg - N = ma\]מכאן:
\[N = m(g - a)\]במקרה זה, המשקל הנמדד קטן יותר. אם המעלית נופלת נפילה חופשית ($a=g$), אז $N=0$ והאדם מרחף במצב של חוסר משקל.
כוחות מדומים במערכות מואצות
כיצד ניתן לפתור בעיה במערכת מואצת, למרות שחוקי ניוטון תקפים רק במערכות התמד? בדיון הקודם, פתרנו את הבעיה ממערכת התמד חיצונית (הבניין), וקבענו שהאדם מואץ יחד עם המעלית.
אך ניתן לפתור את הבעיה גם מתוך המערכת המואצת עצמה (המעלית). לשם כך, יש להשתמש במושג של “כוחות מדומים” (fictitious forces).
כדי להמחיש זאת, נתבונן באדם העומד על רצפה חלקה באוטובוס שחלונותיו אטומים. כאשר הנהג מאיץ קדימה, האדם מרגיש שהוא “נדחף” לאחור, למרות שאין כוח ממשי שדוחף אותו.
מנקודת מבט חיצונית, האוטובוס האיץ קדימה, אך האדם, בשל התמדתו, נטה להישאר במקומו. הרצפה החלקה גרמה לאוטובוס “לברוח” מתחת לרגליו.
מנקודת מבטו של האדם בתוך האוטובוס, פעל עליו כוח “מסתורי” אחורה. כוחות אלו, הנובעים מהתבוננות ממערכת מואצת, נקראים “כוחות מדומים”. הם אינם כוחות אמיתיים אלא תוצאה של תאוצת מערכת הייחוס.
גודלו של הכוח המדומה הוא:
\[\vec{F}_{\text{imaginary}} = -m\vec{a}_{\text{system}}\]כאשר $m$ היא מסת הגוף ו-$\vec{a}_{\text{system}}$ היא תאוצת מערכת הייחוס. הסימן השלילי מציין שהכוח המדומה פועל בכיוון ההפוך לתאוצת המערכת.
אם נחזור למעלית המואצת כלפי מעלה בתאוצה $a$, נוכל לנתח את המצב מתוך המעלית. נוסיף למערכת הכוחות כוח מדומה $ma$ הפועל כלפי מטה. כעת, מנקודת המבט של צופה במעלית, האדם נמצא בשיווי משקל, ולכן:
\[N - mg - ma = 0\]מכאן:
\[N = m(g + a)\]זו אותה תוצאה שקיבלנו קודם, אך הפעם היא הושגה על ידי ניתוח בתוך המערכת הלא-אינרציאלית.
דוגמה: גוף על מישור משופע
נתבונן בגוף המונח על מישור משופע חלק. ישנו טריז בזווית $\alpha$ ביחס לאופק, ועליו מונחת מסה $m$ המחליקה מטה ללא חיכוך.
הכוחות הפועלים על המסה הם:
- כוח הכבידה $mg$ כלפי מטה.
- כוח נורמלי $N$ מהמישור, בניצב למישור.
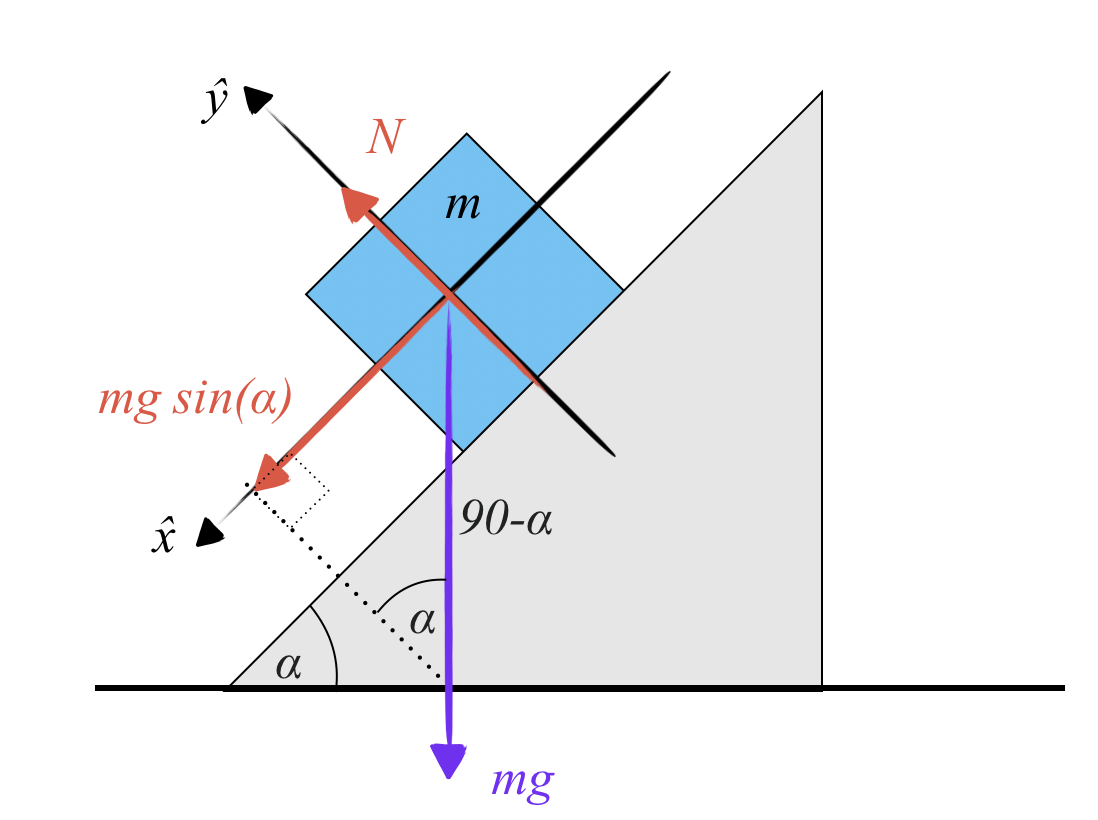
נגדיר מערכת צירים שבה ציר $x$ מקביל למישור (במורד) וציר $y$ ניצב לו. נפרק את וקטור הכבידה $mg$ לרכיביו:
- רכיב $x$: $mg \sin{\alpha}$
- רכיב $y$: $mg \cos{\alpha}$
מהחוק השני של ניוטון בציר $x$:
\[mg \sin{\alpha} = ma\]מכאן, תאוצת הגוף במורד המישור היא:
\[a = g \sin{\alpha}\]בציר $y$ אין תנועה, ולכן שקול הכוחות הוא אפס:
\[N - mg \cos{\alpha} = 0 \implies N = mg \cos{\alpha}\]דוגמה מורכבת: טריז נייד
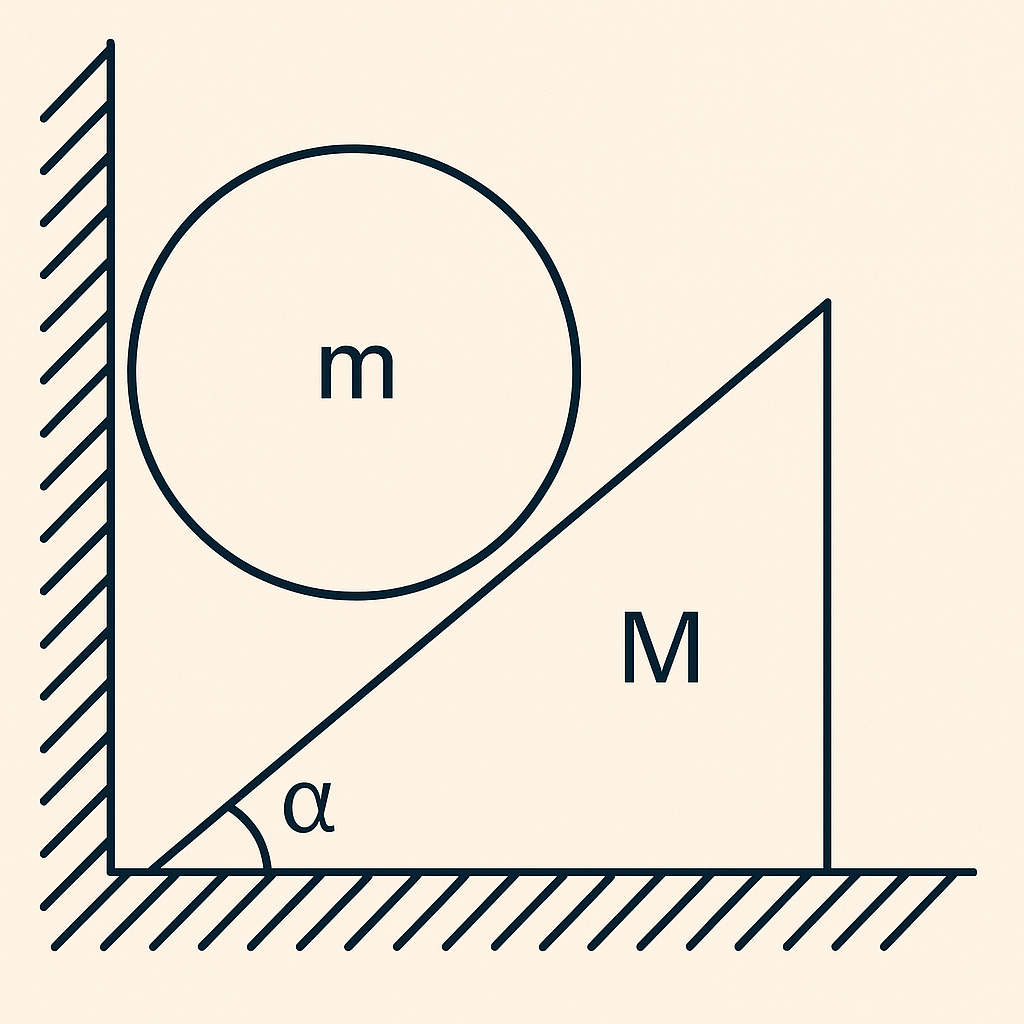
לבסוף, נבחן בעיה מורכבת יותר: טריז שמסתו $M$ נמצא על מישור אופקי חלק, כך שהוא חופשי לנוע. על הטריז מונחת מסה קטנה $m$.
כאשר המסה $m$ מונחת על הטריז, היא מחליקה מטה ודוחפת את הטריז ימינה. הטריז מאיץ ימינה, ולכן המסה $m$ נמצאת במערכת מואצת. כדי לפתור את הבעיה מנקודת מבטה של המסה $m$, יש להתחשב בכוח המדומה.
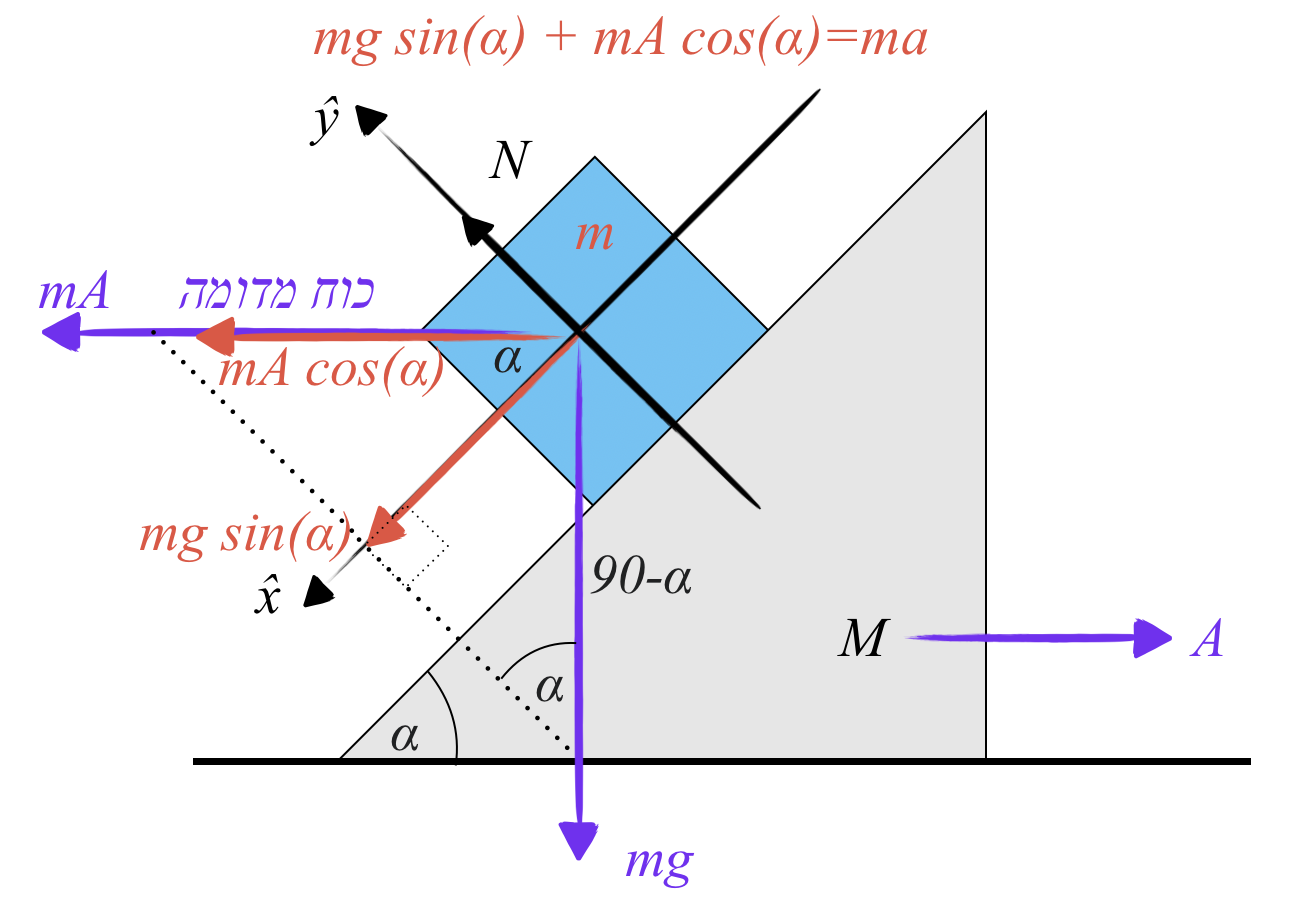
הכוחות הפועלים על המסה $m$ (במערכת הייחוס של הטריז) הם:
- כוח הכבידה $mg$ כלפי מטה.
- כוח נורמלי $N$ מהטריז, בניצב למישור המשופע.
- כוח מדומה $ma_M$ בכיוון אופקי שמאלה, כאשר $a_M$ היא תאוצת הטריז ימינה.
נגדיר מערכת צירים שבה ציר $x$ מקביל למישור המשופע (במורד) וציר $y$ ניצב לו. נפרק את הכוחות לרכיביהם:
משוואת התנועה בציר $x$ (תנועת $m$ ביחס לטריז בתאוצה $a$):
\[mg \sin{\alpha} - ma_M \cos{\alpha} = ma\]משוואת הכוחות בציר $y$ (אין תנועה בניצב למישור):
\[N + ma_M \sin{\alpha} - mg \cos{\alpha} = 0\]בנוסף, נכתוב את משוואת התנועה עבור הטריז עצמו (במערכת המעבדה). הכוח המניע את הטריז ימינה הוא הרכיב האופקי של הכוח הנורמלי שהמסה $m$ מפעילה עליו (מהחוק השלישי של ניוטון):
\[N \sin{\alpha} = Ma_M\]קיבלנו מערכת של שלוש משוואות עם שלושה נעלמים: $a$, $a_M$ ו-$N$, אשר פתרונה יספק את תיאור התנועה המלא.
סיכום
בשיעור זה נלמדו שתי גישות לטיפול במערכות לא-אינרציאליות (מואצות):
- פתרון מחוץ למערכת המואצת, תוך שימוש בחוקי ניוטון ממערכת התמד חיצונית.
- פתרון מתוך המערכת המואצת, תוך הוספת כוחות מדומים למערך הכוחות.
בשיעור הבא נרחיב את הדיון לבעיות עם חיכוך, ונעבור למצבים שבהם החוק השני של ניוטון מוביל למשוואות דיפרנציאליות.
דור פסקל