חלק א׳: קבועים ויחידות
קבועים פיזיקליים
| קבוע | סימון | ערך | יחידות |
|---|---|---|---|
| קבוע קולון | $k$ | $9 \times 10^9$ | $\frac{N \cdot m^2}{C^2}$ |
| פרמיטיביות הריק | $\epsilon_0$ | $8.85 \times 10^{-12}$ | $\frac{C^2}{N \cdot m^2}$ |
| מטען אלקטרון | $e$ | $-1.6 \times 10^{-19}$ | $C$ |
| מטען פרוטון | $e$ | $+1.6 \times 10^{-19}$ | $C$ |
חלק ב׳: צפיפויות מטען
| סוג | סימון | הגדרה | יחידות | דוגמה |
|---|---|---|---|---|
| קווית | $\lambda$ | $\lambda = \frac{dq}{dl}$ | $C/m$ | תיל, טבעת, מוט |
| משטחית | $\sigma$ | $\sigma = \frac{dq}{dA}$ | $C/m^2$ | דיסקה, מישור, קליפה |
| נפחית | $\rho$ | $\rho = \frac{dq}{dV}$ | $C/m^3$ | כדור מלא, גליל מלא |
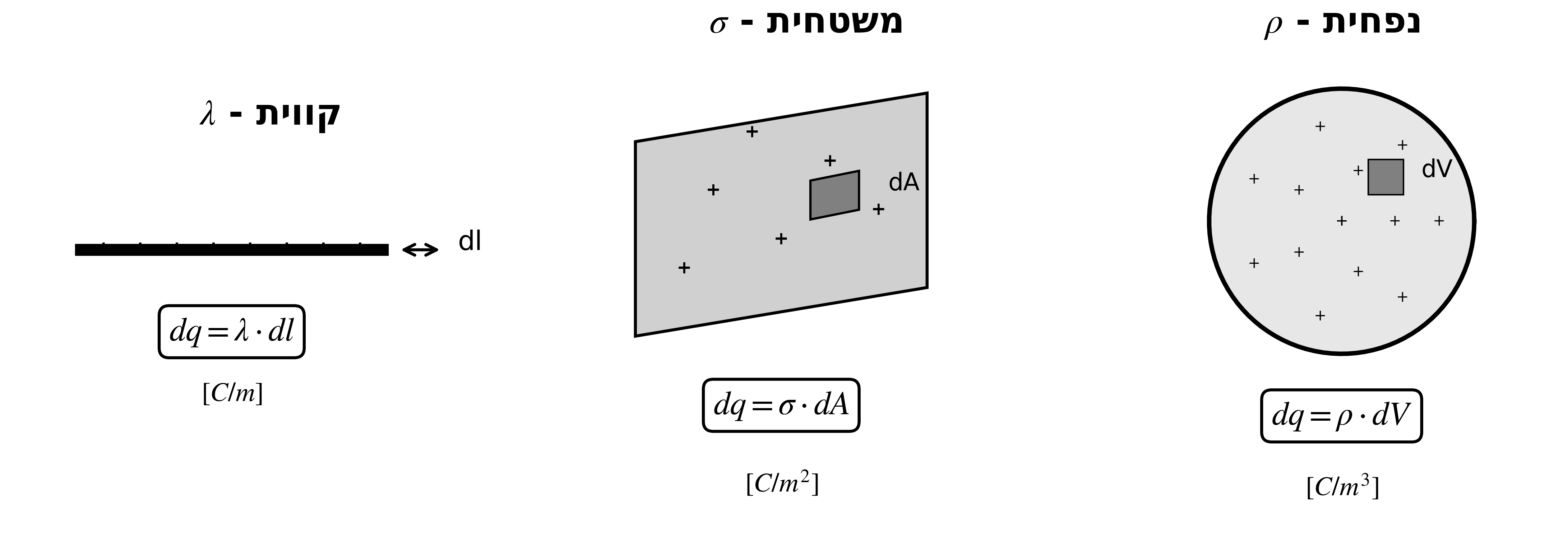
אלמנטי מטען
\[\begin{aligned} dq &= \lambda \cdot dl \quad \text{(linear)} \\[6pt] dq &= \sigma \cdot dA \quad \text{(surface)} \\[6pt] dq &= \rho \cdot dV \quad \text{(volume)} \end{aligned}\]חישוב מטען כולל
\[Q = \int \lambda \, dl = \int \sigma \, dA = \int \rho \, dV\]דוגמה: כדור טעון אחיד
צפיפות נפחית אחידה:
\[\rho = \frac{Q}{\frac{4}{3}\pi R^3} = \frac{3Q}{4\pi R^3}\]דוגמה: טבעת טעונה אחידה
צפיפות קווית אחידה:
\[\lambda = \frac{Q}{2\pi R}\]חלק ג׳: חוק קולון והשדה החשמלי
חוק קולון
\[\boxed{\vec{F} = k\frac{q_1 q_2}{r^2}\hat{r}}\]
- מטענים שווי סימן ← דחייה
- מטענים הפוכי סימן ← משיכה
שדה חשמלי
\[\boxed{\vec{E} = k\frac{q}{r^2}\hat{r}}\] \[\vec{F} = q\vec{E}\]עקרון הסופרפוזיציה
לשדות:
\[\vec{E}_{total} = \sum_i \vec{E}_i\]לכוחות:
\[\vec{F}_{total} = \sum_i \vec{F}_i\]לפוטנציאלים (סקלר!):
\[V_{total} = \sum_i V_i\]
דוגמאות לסופרפוזיציה
דוגמה 1: משושה עם 5 מטענים
בכל אחד מ-5 קודקודי משושה נמצא מטען $+Q$. הקודקוד השישי ריק. מה השדה במרכז?
פתרון:
- משושה מלא ← השדה במרכז = 0 (סימטריה)
- משושה עם מטען חסר = משושה מלא + מטען הפוך
השדה במרכז כאילו יש מטען $-Q$ בקודקוד החסר:
\[E = \frac{kQ}{a^2}\]כיוון: לכיוון הקודקוד הריק (כי המטען ה”חסר” שלילי)
דוגמה 2: משולש שווה צלעות עם 3 מטענים
שלושה מטענים $+q$ בקודקודי משולש שווה צלעות (צלע $a$). מה הפוטנציאל במרכז?
פתרון:
- מרחק מקודקוד למרכז: $r = \frac{a}{\sqrt{3}}$
- כל מטען תורם: $V_i = \frac{kq}{a/\sqrt{3}} = \frac{\sqrt{3}kq}{a}$
דוגמה 3: משולש ישר זווית
משולש ישר זווית שווה שוקיים:
- קודקודים A,C: מטען $+Q$
- קודקוד B (זווית ישרה): מטען $-Q$
- ניצבים: $a\sqrt{2}$, יתר: $2a$
א. כוח על B:
- רכיב $x$: מתאפס מסימטריה
- רכיב $y$:
ב. אנרגיה פוטנציאלית:
\[U = U_{AB} + U_{BC} + U_{AC}\] \[U = \frac{k(+Q)(-Q)}{a\sqrt{2}} + \frac{k(-Q)(+Q)}{a\sqrt{2}} + \frac{k(+Q)(+Q)}{2a}\] \[\boxed{U = \frac{kQ^2}{2a}(1 - 2\sqrt{2})}\]חלק ד׳: חוק גאוס
הצורה האינטגרלית
\[\boxed{\oint_S \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\epsilon_0}}\]הצורה הדיפרנציאלית (משוואת מקסוול 1)
\[\boxed{\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_0}}\]שטף חשמלי
\[\Phi = \int_S \vec{E} \cdot d\vec{A} = \int_S E \cos\theta \, dA\]חשוב: רק הרכיב הניצב למשטח תורם!
בחירת משטח גאוס
| סימטריה | משטח גאוס | שטח |
|---|---|---|
| כדורית | כדור | $4\pi r^2$ |
| גלילית | גליל | $2\pi r L$ |
| מישורית | קופסה/גליל | $2A$ |
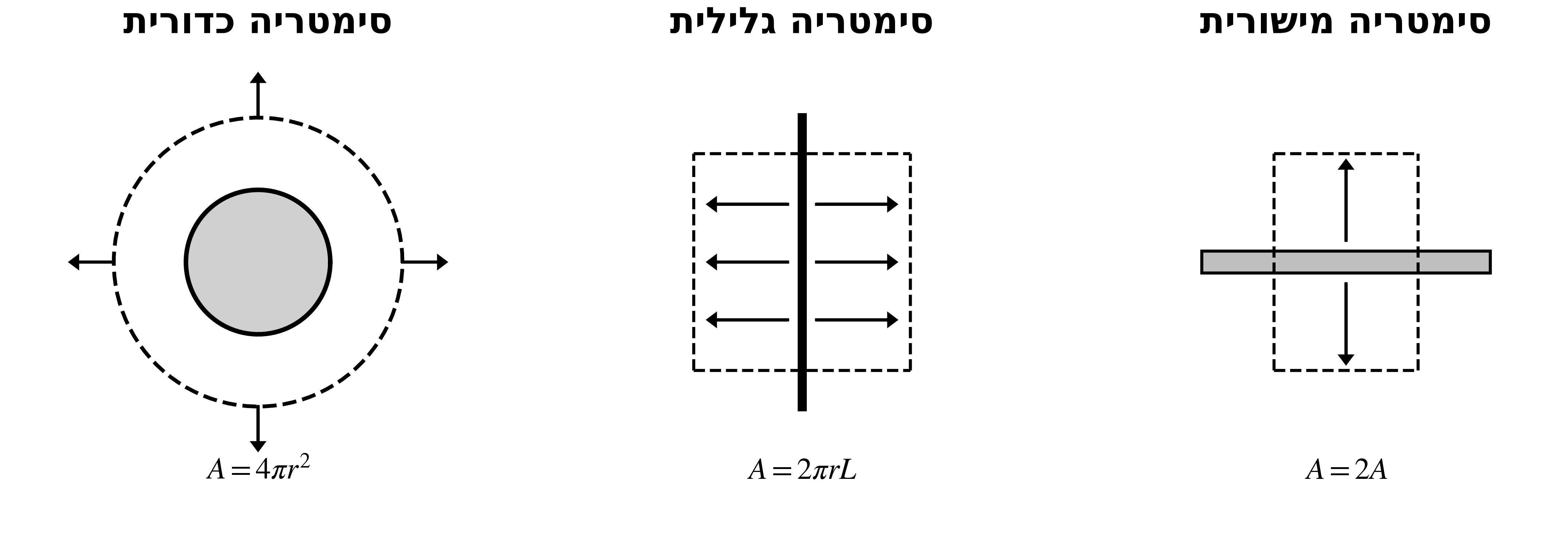
דוגמאות לחוק גאוס
דוגמה 1: כדור מבודד טעון אחיד
כדור ברדיוס $R$ עם צפיפות אחידה $\rho$. מצא את השדה.
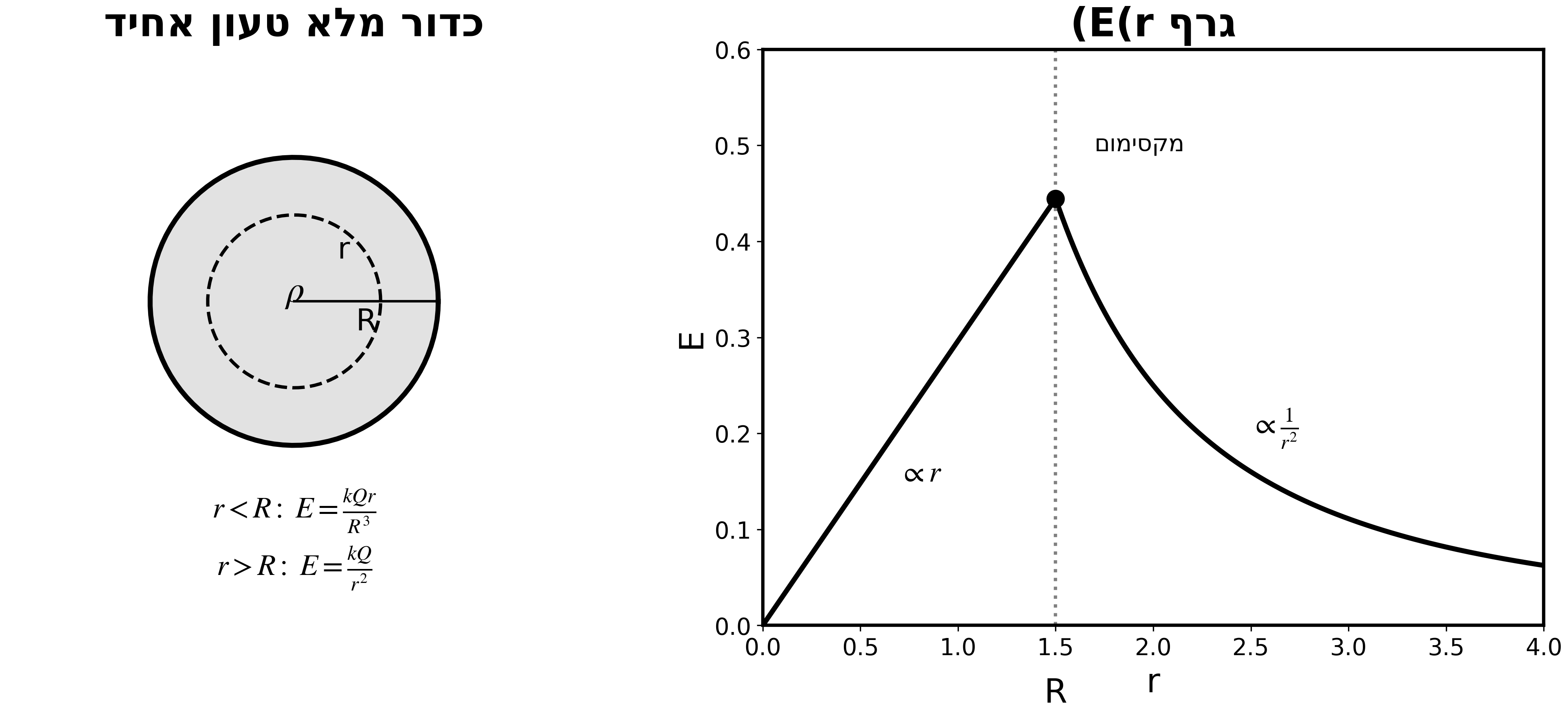
בתוך הכדור ($r < R$):
משטח גאוס כדורי ברדיוס $r$:
\[E \cdot 4\pi r^2 = \frac{Q_{enc}}{\epsilon_0} = \frac{\rho \cdot \frac{4}{3}\pi r^3}{\epsilon_0}\] \[\boxed{E = \frac{\rho r}{3\epsilon_0} = \frac{kQr}{R^3}}\]מחוץ לכדור ($r > R$):
\[E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0}\] \[\boxed{E = \frac{kQ}{r^2}}\]דוגמה 2: גלילים קואקסיאליים
גליל פנימי ברדיוס $a$ עם $+\lambda$, גליל חיצוני ברדיוס $b$ מוארק.
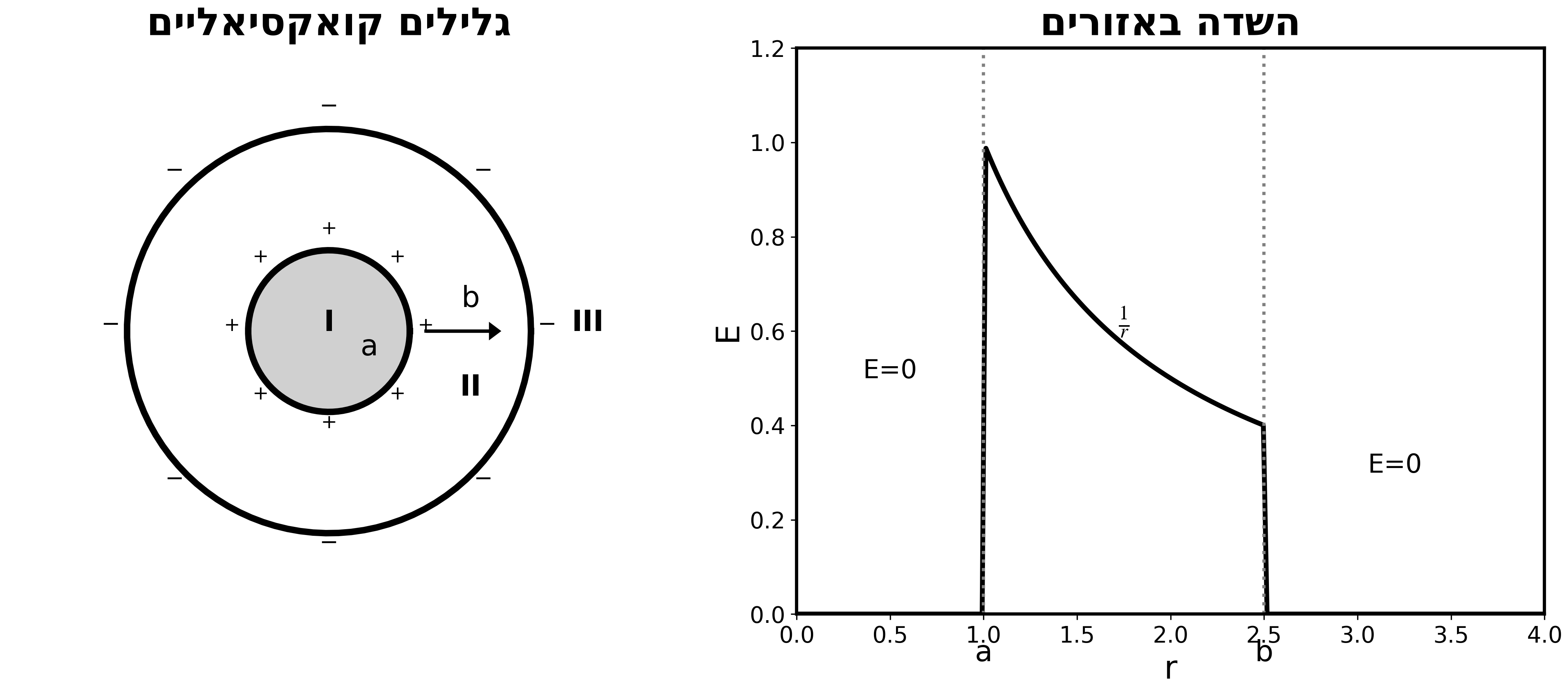
באזור $r < a$ (בתוך מוליך):
\[E = 0\]באזור $a < r < b$:
משטח גאוס גלילי:
\[E \cdot 2\pi r L = \frac{\lambda L}{\epsilon_0}\] \[\boxed{E = \frac{\lambda}{2\pi\epsilon_0 r}}\]באזור $r > b$:
המעטפת מוארקת ← נטענת ב-$-\lambda$ ← סך המטען = 0
\[\boxed{E = 0}\]דוגמה 3: כדור עם חלל (מבודד)
כדור ברדיוס $R_2$ עם חלל פנימי ברדיוס $R_1$. מטען כולל $Q$.
צפיפות המטען:
\[\rho = \frac{Q}{\frac{4}{3}\pi(R_2^3 - R_1^3)} = \frac{3Q}{4\pi(R_2^3 - R_1^3)}\]באזור $r < R_1$:
\[E = 0\]באזור $R_1 < r < R_2$:
\[Q_{enc} = \rho \cdot \frac{4}{3}\pi(r^3 - R_1^3)\] \[\boxed{E = \frac{kQ(r^3 - R_1^3)}{r^2(R_2^3 - R_1^3)}}\]באזור $r > R_2$:
\[\boxed{E = \frac{kQ}{r^2}}\]דוגמה 4: גליל עם חור (סופרפוזיציה)
גליל אינסופי ברדיוס $a$ וצפיפות $\rho_0$. נקדח חור ברדיוס $b$ במרחק $c$ מהמרכז.
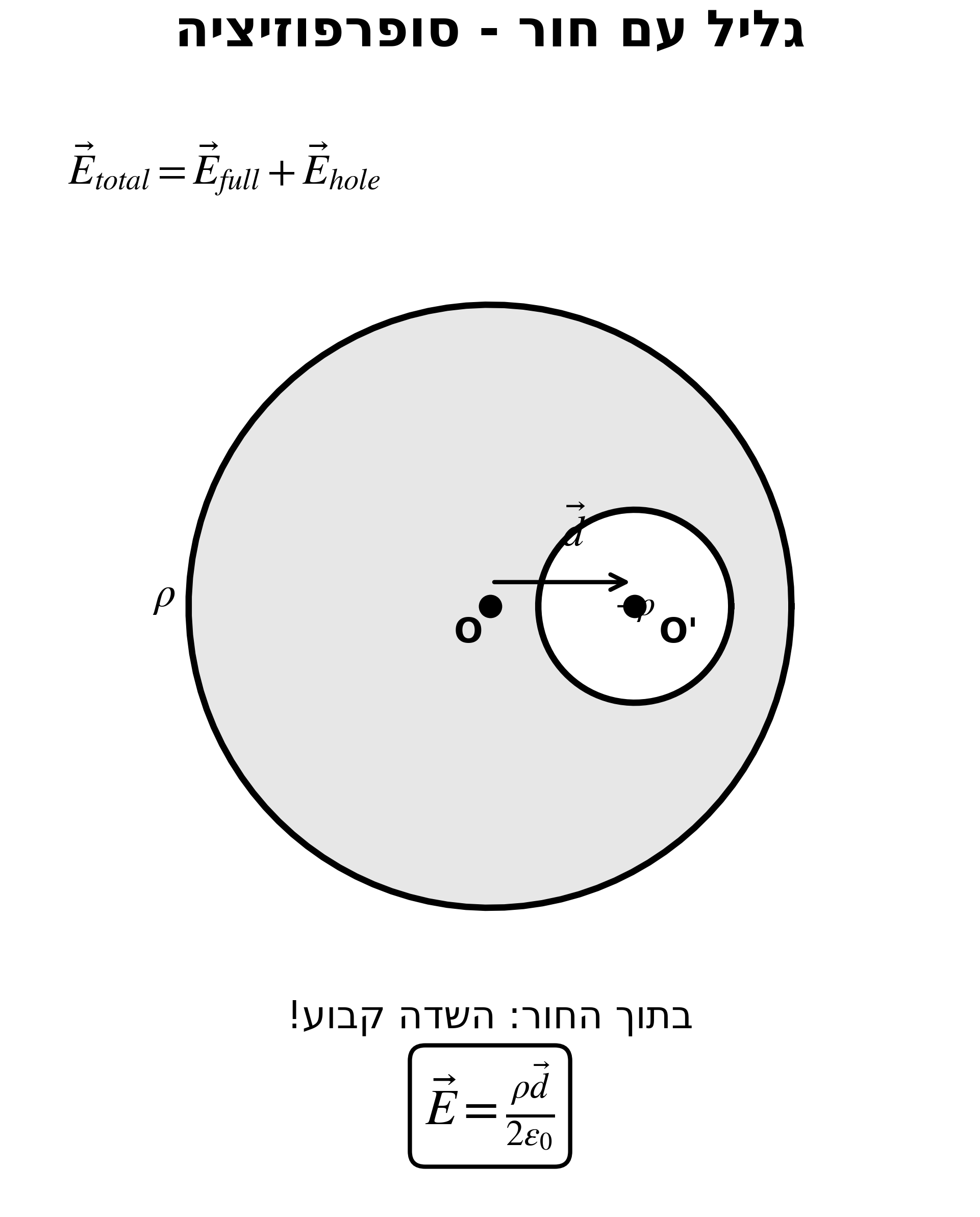
רעיון: גליל עם חור = גליל מלא + גליל “שלילי”
\[\vec{E}_{total} = \vec{E}_{full} + \vec{E}_{hole}\]שדה של גליל מלא (בפנים):
\[\vec{E}_{full} = \frac{\rho_0 \vec{r}}{2\epsilon_0}\]שדה של “גליל שלילי”:
\[\vec{E}_{hole} = -\frac{\rho_0 \vec{r}'}{2\epsilon_0}\]כאשר $\vec{r}’$ הוא וקטור המיקום ביחס למרכז החור.
בתוך החור: השדה קבוע!
\[\boxed{\vec{E} = \frac{\rho_0 \vec{d}}{2\epsilon_0}}\]כאשר $\vec{d}$ הוא הוקטור ממרכז הגליל למרכז החור.
חלק ה׳: טבלת שדות
שדות של קונפיגורציות סימטריות
| קונפיגורציה | שדה | הערות |
|---|---|---|
| מטען נקודתי | $E = \frac{kQ}{r^2}$ | דועך כ-$r^{-2}$ |
| משטח אינסופי | $E = \frac{\sigma}{2\epsilon_0}$ | קבוע! |
| שני משטחים (קבל) | $E = \frac{\sigma}{\epsilon_0}$ | בין המשטחים |
| תיל אינסופי | $E = \frac{\lambda}{2\pi\epsilon_0 r} = \frac{2k\lambda}{r}$ | דועך כ-$r^{-1}$ |
| גליל מלא (בפנים) | $E = \frac{\rho r}{2\epsilon_0}$ | גדל לינארית |
| גליל מלא (בחוץ) | $E = \frac{\lambda}{2\pi\epsilon_0 r}$ | כמו תיל |
| כדור מלא (בפנים) | $E = \frac{kQr}{R^3}$ | גדל לינארית |
| כדור מלא (בחוץ) | $E = \frac{kQ}{r^2}$ | כמו מטען נקודתי |
| קליפה כדורית (בפנים) | $E = 0$ | - |
| קליפה כדורית (בחוץ) | $E = \frac{kQ}{r^2}$ | כמו מטען נקודתי |
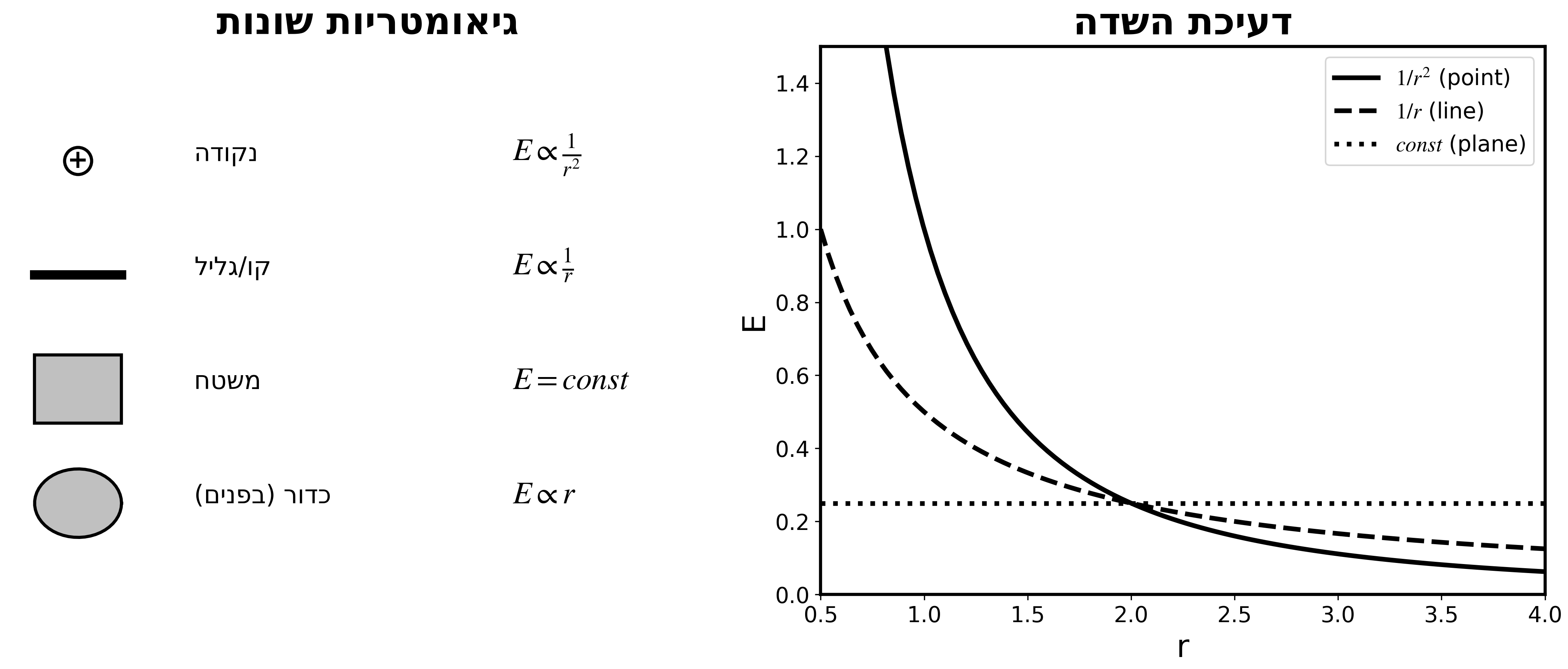
דעיכה לפי ממד טופולוגי
| ממד | קונפיגורציה | התנהגות |
|---|---|---|
| 0D | מטען נקודתי | $E \propto r^{-2}$ |
| 1D | קו/גליל | $E \propto r^{-1}$ |
| 2D | משטח | $E = const$ |
| 3D (בפנים) | כדור מלא | $E \propto r$ |
חלק ו׳: פוטנציאל חשמלי
הגדרות: פוטנציאל ושדה
\[V = \frac{U}{q} = -\int_\infty^r \vec{E} \cdot d\vec{l}\] \[\boxed{\vec{E} = -\nabla V}\] \[\Delta V = V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\]פוטנציאל של מטען נקודתי
\[\boxed{V = \frac{kQ}{r}}\]שים לב: $V \propto r^{-1}$, לא $r^{-2}$ כמו השדה!
סופרפוזיציה של פוטנציאלים
\[V_{total} = \sum_i \frac{kQ_i}{r_i}\]יתרון: פוטנציאל הוא סקלר - חיבור אלגברי פשוט!
טבלת פוטנציאלים
| קונפיגורציה | פוטנציאל |
|---|---|
| מטען נקודתי | $V = \frac{kQ}{r}$ |
| קליפה כדורית (בפנים) | $V = \frac{kQ}{R}$ (קבוע!) |
| קליפה כדורית (בחוץ) | $V = \frac{kQ}{r}$ |
| כדור מוליך (בפנים) | $V = \frac{kQ}{R}$ (קבוע!) |
| טבעת (על הציר) | $V(z) = \frac{kQ}{\sqrt{R^2 + z^2}}$ |
| גליל אינסופי | $V(r) = -\frac{\lambda}{2\pi\epsilon_0}\ln(r) + C$ |
דוגמאות לפוטנציאל
דוגמה 1: פוטנציאל של טבעת על הציר
טבעת ברדיוס $R$ עם מטען $Q$. מצא את הפוטנציאל על ציר $z$.
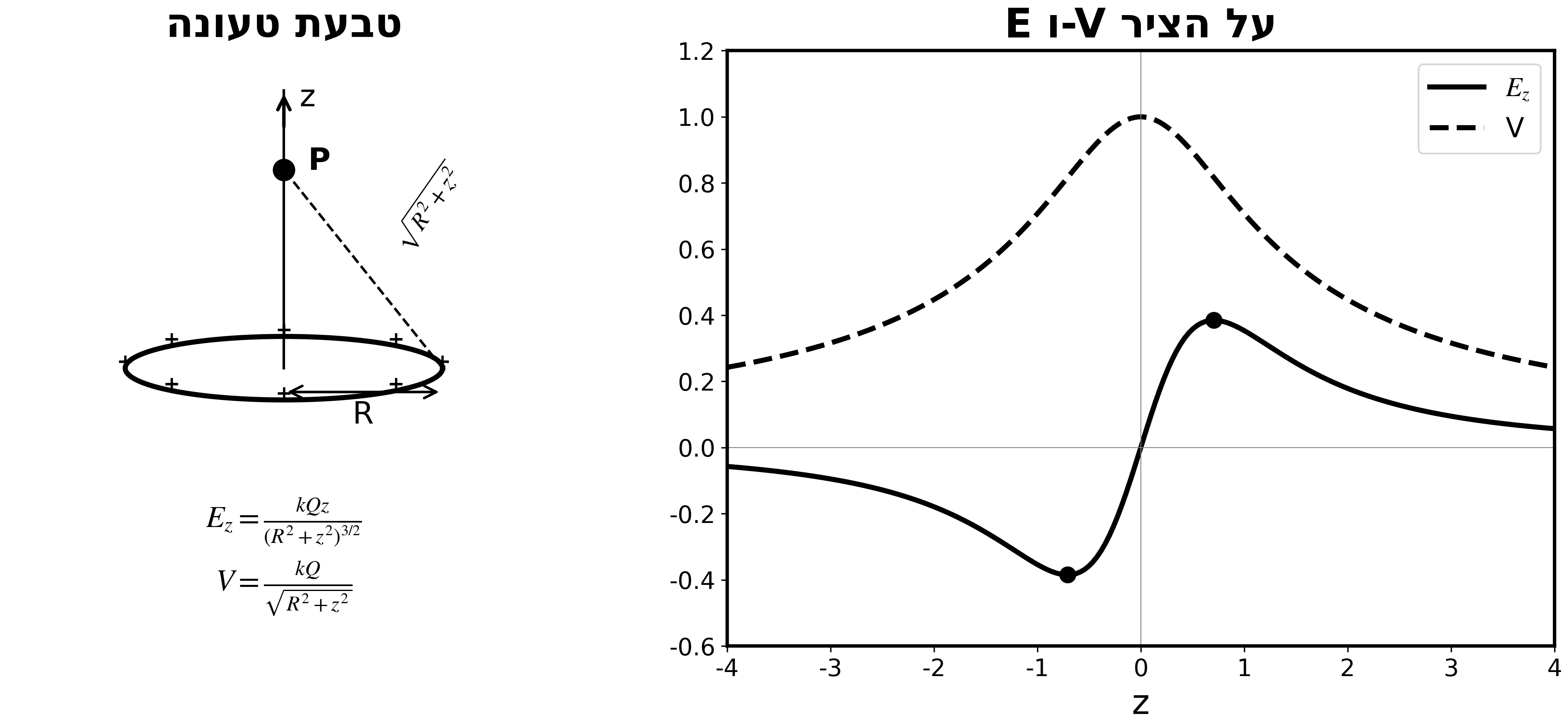
פתרון:
- כל נקודה על הטבעת במרחק $\sqrt{R^2 + z^2}$ מנקודה על הציר
- המרחק קבוע ← יוצא מהאינטגרל
דוגמה 2: טבעת עם צפיפות משתנה
טבעת עם $\lambda(\theta) = \lambda_0 \cos\theta$. מה הפוטנציאל במרכז?
פתרון:
\[V = \int \frac{k \, dq}{R} = \frac{k}{R} \int_0^{2\pi} \lambda_0 \cos\theta \cdot R \, d\theta\] \[= k\lambda_0 \int_0^{2\pi} \cos\theta \, d\theta = k\lambda_0 \cdot 0\] \[\boxed{V = 0}\]הסבר: אינטגרל של $\cos\theta$ על מחזור שלם = 0
דוגמה 3: גלילים קואקסיאליים - פוטנציאל
המשך מדוגמת הגלילים הקואקסיאליים. מצא את הפוטנציאל.
באזור $r > b$:
\(V = 0\) (מוארק)
באזור $a < r < b$:
\[V(r) = -\int_\infty^r \vec{E} \cdot dr = -\int_\infty^b 0 \cdot dr - \int_b^r \frac{\lambda}{2\pi\epsilon_0 r'} dr'\] \[= 0 - \frac{\lambda}{2\pi\epsilon_0}[\ln r']_b^r = -\frac{\lambda}{2\pi\epsilon_0}(\ln r - \ln b)\] \[\boxed{V(r) = \frac{\lambda}{2\pi\epsilon_0}\ln\frac{b}{r}}\]באזור $r < a$: המוליך הפנימי שווה-פוטנציאל
\[\boxed{V = \frac{\lambda}{2\pi\epsilon_0}\ln\frac{b}{a}}\]חלק ז׳: אנרגיה ועבודה
אנרגיה פוטנציאלית
\[\boxed{U = k\frac{q_1 q_2}{r}}\]
- $U > 0$: מטענים דוחים
- $U < 0$: מטענים נמשכים
אנרגיה של מערכת מטענים
\[U_{total} = \sum_{i<j} k\frac{q_i q_j}{r_{ij}}\]חשוב: סכום על כל הזוגות!
עבודה
\[W = q \cdot \Delta V = q(V_f - V_i)\]שימור אנרגיה
\[\boxed{K_i + U_i = K_f + U_f}\] \[\frac{1}{2}mv_i^2 + qV_i = \frac{1}{2}mv_f^2 + qV_f\]
דוגמאות לאנרגיה
דוגמה 1: עבודה להבאת מטען
מטען $q$ מובא מאינסוף למרכז קליפה כדורית ($-Q$, רדיוס $2R$).
פתרון:
\[W = q \cdot \Delta V = q(V_{final} - V_{initial})\] \[V_{initial} = 0 \quad \text{(at infinity)}\] \[V_{final} = \frac{k(-Q)}{2R} = -\frac{kQ}{2R}\] \[\boxed{W = -\frac{kQq}{2R}}\]משמעות: אם $q > 0$, העבודה שלילית ← המטען נמשך מעצמו
דוגמה 2: אנרגיה של משולש
שלושה מטענים $+q$ במשולש שווה צלעות. הוסף מטען $Q$ במרכז כך ש-$U_{total} = 0$.
אנרגיה לפני:
\[U_{initial} = 3 \cdot \frac{kq^2}{a}\]אנרגיה אחרי (3 זוגות חדשים):
\[U_{new} = 3 \cdot \frac{kQq}{a/\sqrt{3}} = \frac{3\sqrt{3}kQq}{a}\]דרישה:
\[U_{initial} + U_{new} = 0\] \[\frac{3kq^2}{a} + \frac{3\sqrt{3}kQq}{a} = 0\] \[q + \sqrt{3}Q = 0\] \[\boxed{Q = -\frac{q}{\sqrt{3}}}\]דוגמה 3: מהירות בשימור אנרגיה
משחררים מטען $-Q$ מנקודה B במשולש ישר זווית. מה מהירותו בנקודה O (מרכז היתר)?
שימור אנרגיה:
\[U_B + 0 = U_O + \frac{1}{2}mv^2\] \[U_B = 2 \cdot \frac{k(+Q)(-Q)}{a\sqrt{2}} = -\frac{\sqrt{2}kQ^2}{a}\] \[U_O = 2 \cdot \frac{k(+Q)(-Q)}{a} = -\frac{2kQ^2}{a}\] \[\frac{1}{2}mv^2 = U_B - U_O = -\frac{\sqrt{2}kQ^2}{a} + \frac{2kQ^2}{a} = \frac{kQ^2(2-\sqrt{2})}{a}\] \[\boxed{v = 2\sqrt{\frac{kQ^2(\sqrt{2}-1)}{ma}}}\]חלק ח׳: מוליכים
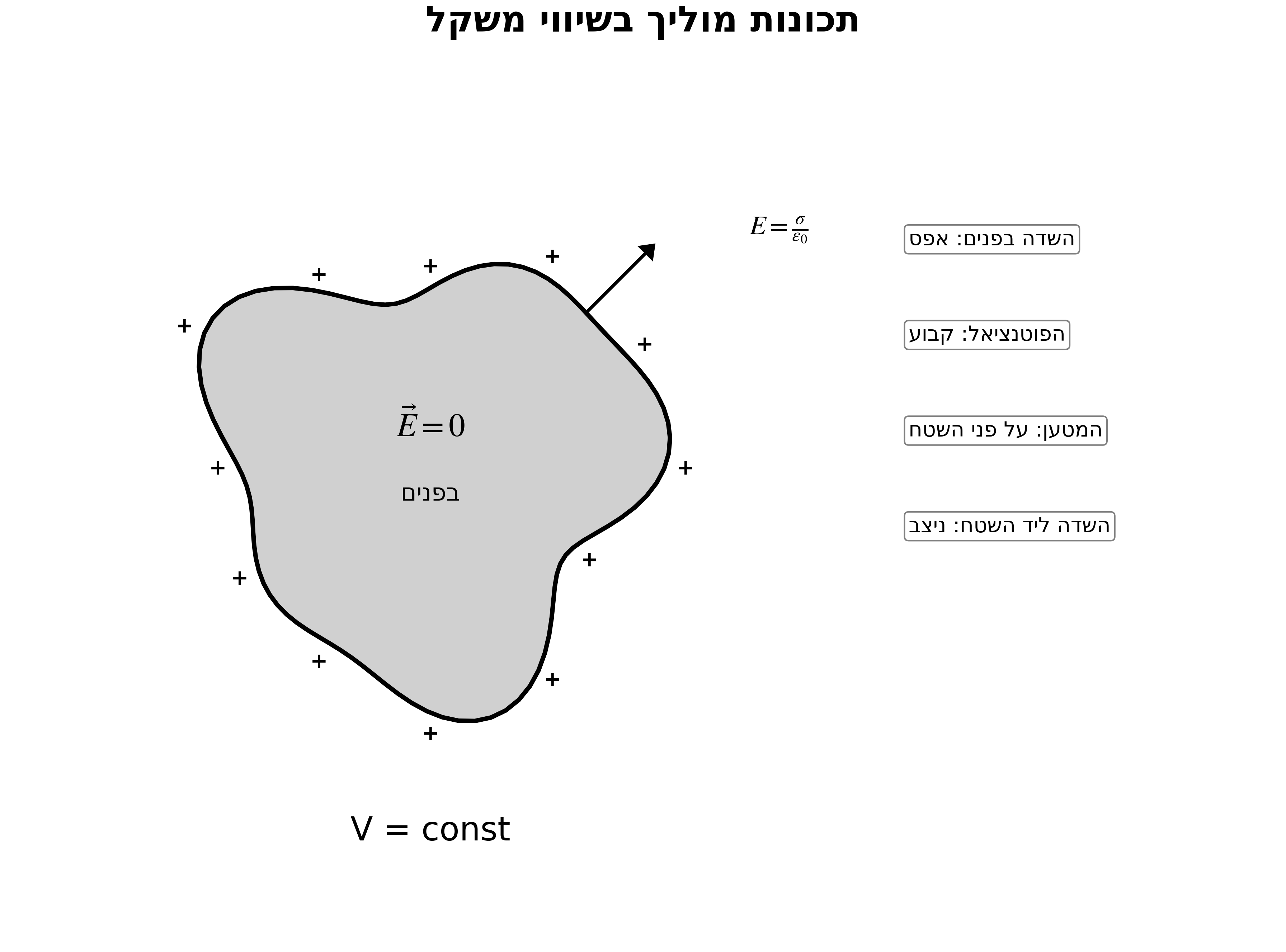
תכונות מוליך בשיווי משקל
- שדה בתוך מוליך: $\vec{E} = 0$
- פוטנציאל: קבוע בכל המוליך
- מטען עודף: על פני השטח בלבד
- שדה ליד פני השטח: $E = \frac{\sigma}{\epsilon_0}$ (ניצב)
הארקה
- מוליך מוארק: $V = 0$
- מטענים זורמים עד שהפוטנציאל מתאפס
דוגמאות למוליכים
דוגמה 1: קליפות קונצנטריות
כדור מוליך A (רדיוס $R$, מטען $+Q$) בתוך קליפה מוליכה B (רדיוס $2R$, נייטרלית).
השראה:
- צד פנימי של B: $-Q$
- צד חיצוני של B: $+Q$
פוטנציאל של A:
\[V_A = \frac{kQ}{R} + \frac{k(-Q)}{2R} + \frac{k(+Q)}{2R} = \frac{kQ}{R}\]דוגמה 2: הארקה
מאריקים את הקליפה B מהדוגמה הקודמת.
לאחר הארקה:
- צד פנימי של B: $-Q$ (נשאר - כדי לאזן את A)
- צד חיצוני של B: $0$ (מטענים נשאבו לאדמה)
- $V_B = 0$
מה הפוטנציאל של A עכשיו?
\[V_A = \frac{kQ}{R} + \frac{k(-Q)}{2R} = \frac{kQ}{2R}\]דוגמה 3: חיבור מוליכים
מחברים שני כדורים מוליכים (רדיוסים $R_1, R_2$) עם מטענים $Q_1, Q_2$.
בשיווי משקל: $V_1 = V_2$
\[\frac{kQ_1'}{R_1} = \frac{kQ_2'}{R_2}\] \[Q_1' + Q_2' = Q_1 + Q_2\]פתרון:
\[Q_1' = \frac{R_1}{R_1 + R_2}(Q_1 + Q_2)\] \[Q_2' = \frac{R_2}{R_1 + R_2}(Q_1 + Q_2)\]חלק ט׳: אינטגרציה וחישובי שדה
שדה מהתפלגות רציפה
\[\vec{E}(\vec{r}) = k \int \frac{dq}{|\vec{r} - \vec{r}'|^2}\hat{R}\]פוטנציאל מהתפלגות רציפה
\[V(\vec{r}) = k \int \frac{dq}{|\vec{r} - \vec{r}'|}\]
דוגמאות לאינטגרציה
דוגמה 1: מוט על ציר y
מוט באורך $L$ על ציר $y$ השלילי (מ-$-L$ עד 0) עם צפיפות $\lambda$. שדה בנקודה $y > 0$.
אלמנט מטען:
\[dq = \lambda \, dy'\]מרחק מאלמנט ב-$y’$ לנקודה ב-$y$:
\[r = y - y'\]שדה:
\[E = \int_{-L}^{0} \frac{k\lambda \, dy'}{(y-y')^2}\]הצבה: $u = y - y’$, $du = -dy’$
\[E = k\lambda \left[\frac{1}{y-y'}\right]_{-L}^{0} = k\lambda\left(\frac{1}{y} - \frac{1}{y+L}\right)\] \[\boxed{E = \frac{k\lambda L}{y(y+L)}}\]דוגמה 2: חצי טבעת
חצי טבעת ברדיוס $R$ עם מטען $Q$. שדה בראשית.
צפיפות:
\[\lambda = \frac{Q}{\pi R}\]שדה מאלמנט:
\[dE = \frac{k \, dq}{R^2} = \frac{k\lambda R \, d\theta}{R^2} = \frac{k\lambda \, d\theta}{R}\]מסימטריה: רק רכיב $x$ שורד
\[E_x = \int_{\pi/2}^{3\pi/2} \frac{k\lambda}{R} \cos\theta \, d\theta = \frac{k\lambda}{R}[\sin\theta]_{\pi/2}^{3\pi/2}\] \[= \frac{k\lambda}{R}(-1 - 1) = -\frac{2k\lambda}{R} = -\frac{2kQ}{\pi R^2}\] \[\boxed{E_x = -\frac{2kQ}{\pi R^2}}\]\[V(y) = k\lambda \int_{-L}^{L} \frac{dx}{\sqrt{x^2 + y^2}}\]דוגמה 3: מוט - פוטנציאל
מוט באורך $2L$ על ציר $x$ (מ-$-L$ עד $+L$). פוטנציאל על ציר $y$.
אינטגרל סטנדרטי:
\[\int \frac{dx}{\sqrt{x^2 + a^2}} = \ln(x + \sqrt{x^2 + a^2}) + C\] \[\boxed{V(y) = k\lambda \ln\left(\frac{L + \sqrt{L^2 + y^2}}{-L + \sqrt{L^2 + y^2}}\right)}\]דוגמה 4: מוט עם צפיפות אי-זוגית
אותו מוט עם $\lambda(x) = \lambda_0 \sin(\pi x/L)$. פוטנציאל על ציר $y$?
פתרון:
\[V = k\lambda_0 \int_{-L}^{L} \frac{\sin(\pi x/L)}{\sqrt{x^2 + y^2}} dx\]- $\sin(\pi x/L)$ היא פונקציה אי-זוגית
- $\frac{1}{\sqrt{x^2 + y^2}}$ היא פונקציה זוגית
- המכפלה: אי-זוגית
כלל: $\int_{-a}^{a} f_{odd}(x) \, dx = 0$
חלק י׳: טריקים ושיטות
1. סופרפוזיציה עם “מטען חסר”
\[\vec{E}_{missing} = \vec{E}_{full} + \vec{E}_{opposite}\]דוגמה: טבעת עם קשת חסרה = טבעת מלאה + קשת הפוכה
2. בדיקת סימטריה
לפני חישוב - בדוק:
- אילו רכיבים מתאפסים?
- האם יש ציר/מישור סימטריה?
3. בדיקת גבולות
- $r \to 0$: התנהגות הגיונית?
- $r \to \infty$: מתנהג כמטען נקודתי?
- $r = R$: רציפות?
פוטנציאל תמיד רציף! שדה לא בהכרח רציף (קפיצה במעבר דרך משטח טעון)
4. מתי להשתמש בכל שיטה?
| מצב | שיטה |
|---|---|
| סימטריה גבוהה | חוק גאוס |
| מטענים בדידים | סופרפוזיציה |
| התפלגות רציפה ללא סימטריה | אינטגרציה |
| חישוב פוטנציאל | עדיף - סקלר! |
5. פונקציות זוגיות ואי-זוגיות
| פונקציה | זוגית/אי-זוגית |
|---|---|
| $\cos\theta$ | זוגית |
| $\sin\theta$ | אי-זוגית |
| $x$, $x^3$ | אי-זוגית |
| $x^2$, $|x|$ | זוגית |
חלק יא׳: נוסחאות גיאומטריות
שטחים
| צורה | שטח |
|---|---|
| עיגול | $\pi R^2$ |
| כדור (מעטפת) | $4\pi R^2$ |
| גליל (מעטפת צדדית) | $2\pi R L$ |
נפחים
| צורה | נפח |
|---|---|
| כדור | $\frac{4}{3}\pi R^3$ |
| גליל | $\pi R^2 L$ |
אלמנטים אינפיניטסימליים
קרטזיות:
\[dV = dx \, dy \, dz\]כדוריות:
\[dV = r^2 \sin\theta \, dr \, d\theta \, d\phi\] \[dA_{sphere} = R^2 \sin\theta \, d\theta \, d\phi\]גליליות:
\[dV = r \, dr \, d\theta \, dz\] \[dA_{cyl} = r \, d\theta \, dz\]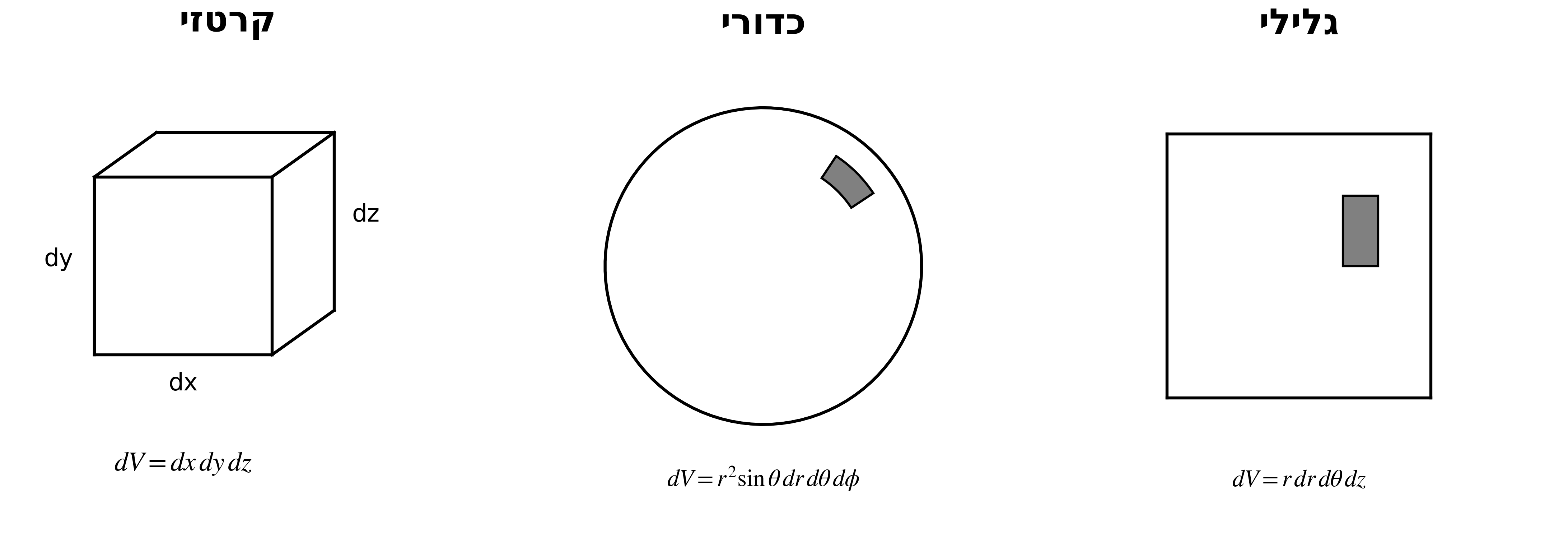
מרחקים מיוחדים
| גיאומטריה | מרחק |
|---|---|
| אלכסון ריבוע | $d\sqrt{2}$ |
| אלכסון קובייה | $d\sqrt{3}$ |
| מרכז משולש שווה צלעות לקודקוד | $\frac{a}{\sqrt{3}}$ |
חלק יב׳: אינטגרלים שימושיים
\[\begin{aligned} &\int \frac{dx}{\sqrt{x^2 + a^2}} = \ln\left(x + \sqrt{x^2 + a^2}\right) + C \\[6pt] &\int \frac{dx}{(x^2 + a^2)^{3/2}} = \frac{x}{a^2\sqrt{x^2 + a^2}} + C \\[6pt] &\int \frac{dx}{x^2} = -\frac{1}{x} + C \\[6pt] &\int \frac{dx}{(a-x)^2} = \frac{1}{a-x} + C \\[6pt] &\int_0^{2\pi} \cos\theta \, d\theta = 0 \\[6pt] &\int_0^{2\pi} \sin\theta \, d\theta = 0 \\[6pt] &\int_0^{\pi} \sin\theta \, d\theta = 2 \end{aligned}\]חלק יג׳: טריגונומטריה
זהויות בסיסיות
\[\sin^2\theta + \cos^2\theta = 1\] \[\tan\theta = \frac{\sin\theta}{\cos\theta}\]ערכים מיוחדים
| $\theta$ | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ |
|---|---|---|---|
| $0°$ | $0$ | $1$ | $0$ |
| $30°$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{3}}$ |
| $45°$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{2}}{2}$ | $1$ |
| $60°$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{2}$ | $\sqrt{3}$ |
| $90°$ | $1$ | $0$ | $\infty$ |
חלק יד׳: אופרטורים וקטוריים
מכפלה סקלרית
\[\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta\]מכפלה וקטורית
\[|\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}|\sin\theta\]- מתאפסת כשהוקטורים מקבילים (זווית $0°$ או $180°$), או אם אחד מהם אפס
- מקסימלית כשהזווית $90°$
גרדיאנט
\[\nabla\phi = \frac{\partial\phi}{\partial x}\hat{x} + \frac{\partial\phi}{\partial y}\hat{y} + \frac{\partial\phi}{\partial z}\hat{z}\]- מצביע לכיוון השיפוע המקסימלי
- ניצב למשטחי שווי-ערך (משטחים של פוטנציאל קבוע, משטחים של שדה חשמלי קבוע, ערך טמפרטורה קבוע וכו׳)
דיברגנס
\[\nabla \cdot \vec{v} = \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z}\]- מודד “מקור” או “בולען”
רוטור
\[\nabla \times \vec{v} = \begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ v_x & v_y & v_z \end{vmatrix}\]זהויות חשובות
\[\boxed{\nabla \times (\nabla\phi) = \vec{0}}\] \[\boxed{\nabla \cdot (\nabla \times \vec{v}) = 0}\]טעויות נפוצות - היזהר
- בלבול בין $V$ ל-$U$:
- $V$ = פוטנציאל (של נקודה)
- $U$ = אנרגיה פוטנציאלית (של מערכת)
- שכחת הדעיכה:
- שדה: $E \propto r^{-2}$
- פוטנציאל: $V \propto r^{-1}$
- גאוס במקום לא מתאים:
- גאוס עובד רק עם סימטריה!
- בלי סימטריה ← אינטגרל ישיר
- שכחת רכיבים באינטגרל:
- תמיד לפרק לרכיבים
- לבדוק מה מתאפס מסימטריה
- שכחת $\epsilon_0$ או $k$:
- $k = \frac{1}{4\pi\epsilon_0}$
- לא לערבב!
- טעות בסימנים:
- $\vec{E} = -\nabla V$ (מינוס!)
- $W = q\Delta V$ (לא $-q\Delta V$)