1. מבוא לתנועה הרמונית
תנועה הרמונית היא תנועה שחוזרת על עצמה - הגוף מבצע תנודה, חוזר לנקודת ההתחלה, ומבצע שוב את אותה תנודה וכן הלאה.
דוגמאות לתנועה הרמונית:
- מטוטלת שמבצעת תנודות
- קפיץ שמבצע תנודות
2. מושגי יסוד בתנועה הרמונית
נקודת שיווי משקל
בתנועה הרמונית, התנודות מתבצעות סביב נקודת שיווי משקל. נקודת שיווי משקל היא הנקודה היציבה - הנקודה שאם הגוף נמצא בה ואינו בתנועה, הוא יישאר במנוחה.
דוגמאות:
- במטוטלת: נקודת שיווי המשקל היא כאשר המטוטלת אנכית לחלוטין (הנקודה הנמוכה ביותר)
- בקפיץ: נקודת שיווי המשקל היא כאשר הקפיץ אינו מתוח ואינו מכווץ
כאשר מזיזים את הגוף מעט מנקודת שיווי המשקל, הוא “ירצה” לחזור לנקודה זו. אולם, בגלל האינרציה, הגוף יעבור את נקודת שיווי המשקל וימשיך לצד השני, ואז שוב ירצה לחזור לנקודת שיווי המשקל. כך נוצרות התנודות ההרמוניות.
מדדים לתנועה הרמונית
כאשר חוקרים תנועה הרמונית, ישנם מספר מדדים חשובים:
-
זמן מחזור $(T)$: הזמן שלוקח לגוף להשלים תנודה שלמה ולחזור לנקודת ההתחלה.
-
אמפליטודה $(A)$: המרחק המקסימלי שהגוף מתרחק מנקודת שיווי המשקל. האמפליטודה תלויה בתנאי ההתחלה (למשל, כמה מתחנו את הקפיץ או כמה הרמנו את המטוטלת).
-
תדירות $(f)$: מספר התנודות שהגוף מבצע בשנייה אחת. זהו הערך ההופכי של זמן המחזור:
3. תיאור מתמטי של תנועה הרמונית
גרף התנועה
התנועה ההרמונית מתוארת על-ידי פונקציות סינוס או קוסינוס. אם מציירים גרף של המיקום $(x)$ כפונקציה של הזמן $(t)$, נקבל עקומת סינוס או קוסינוס.
כוח מחזיר
בתנועה הרמונית פועל כוח מחזיר - כוח שמנסה להחזיר את הגוף לנקודת שיווי המשקל. כוח מחזיר זה פרופורציונלי למרחק מנקודת שיווי המשקל, אך פועל בכיוון הנגדי:
\[F = -kx\]כאשר:
- $F$ הוא הכוח
- $k$ הוא קבוע הפרופורציונליות (קבוע הקפיץ במקרה של קפיץ)
- $x$ הוא המרחק מנקודת שיווי המשקל
- הסימן המינוס מציין שהכוח פועל בכיוון הנגדי למרחק
המשמעות של המינוס:
- אם $x$ חיובי (הגוף נמצא מימין לנקודת שיווי המשקל), הכוח יהיה שלילי (כלומר, כלפי שמאל)
- אם $x$ שלילי (הגוף נמצא משמאל לנקודת שיווי המשקל), הכוח יהיה חיובי (כלומר, כלפי ימין)
משוואת התנועה
לפי החוק השני של ניוטון:
\[F = ma\]כאשר $a$ היא התאוצה, שהיא הנגזרת השנייה של המיקום:
\[a = \frac{d^2x}{dt^2}\]לכן:
\[F = m \frac{d^2x}{dt^2}\]ואם נשלב עם משוואת הכוח המחזיר:
\[-kx = m \frac{d^2x}{dt^2}\]ממנה נקבל:
\[\frac{d^2x}{dt^2} = -\frac{k}{m}x\]זוהי משוואה דיפרנציאלית לינארית הומוגנית מסדר שני. אם נסמן $\omega^2 = \frac{k}{m}$, נקבל:
\[\frac{d^2x}{dt^2} = -\omega^2 x\]פתרון המשוואה הדיפרנציאלית
הפתרון של המשוואה הדיפרנציאלית הזו הוא:
\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]או לחלופין:
\[x(t) = A\cos(\omega t + \phi)\]כאשר:
- $A$ היא האמפליטודה (הערך המקסימלי של $x$)
- $\omega = \sqrt{\frac{k}{m}}$ הוא התדירות הזוויתית
- $\phi$ היא הפאזה ההתחלתית
משמעות הפאזה
הפאזה $\phi$ קובעת את נקודת ההתחלה של התנועה. כלומר, היא מגדירה באיזה מצב של התנודה הגוף נמצא בזמן $t=0$.
- אם $\phi = 0$, אז בזמן $t=0$ המיקום הוא $x = A\cos(0) = A$, כלומר הגוף נמצא באמפליטודה המקסימלית החיובית.
- אם $\phi = \pi$, אז בזמן $t=0$ המיקום הוא $x = A\cos(\pi) = -A$, כלומר הגוף נמצא באמפליטודה המקסימלית השלילית.
- אם $\phi = \frac{\pi}{2}$, אז בזמן $t=0$ המיקום הוא $x = A\cos(\frac{\pi}{2}) = 0$, כלומר הגוף עובר דרך נקודת שיווי המשקל.
4. מקרים מיוחדים
לעתים המשוואה הדיפרנציאלית כוללת איבר נוסף:
\[\frac{d^2x}{dt^2} = -\omega^2 x + C\]במקרה כזה, הפתרון יהיה דומה אך יכלול מרכיב נוסף. זוהי עדיין תנועה הרמונית, אבל סביב נקודת שיווי משקל שונה מהמקור.
משמעות ותפקיד של $\omega$ (אומגה)
ה-$\omega$ (אומגה), שמופיעה במשוואה כ-$\omega^2$, היא התדירות הזוויתית של התנועה ההרמונית. יחידות המידה של $\omega$ הן:
\[[\omega] = \frac{1}{s} \text{ (per second)}\]כאשר $\omega$ גדולה, התנודות מהירות יותר. כאשר $\omega$ קטנה, התנודות איטיות יותר. התדירות הזוויתית $\omega$ קובעת את קצב התנודות.
הקשר בין $\omega$ וזמן המחזור $T$
מכיוון שפונקציית הסינוס והקוסינוס חוזרות על עצמן כל $2\pi$ רדיאנים, זמן המחזור $T$ של התנועה ההרמונית ניתן על ידי:
\[\omega T = 2\pi\]ומכאן:
\[\boxed{T = \frac{2\pi}{\omega}}\]כזכור, $\omega = \sqrt{\frac{k}{m}}$, ולכן:
\[T = 2\pi \sqrt{\frac{m}{k}}\]זמן המחזור תלוי במסה ובקבוע הקפיץ - ככל שהמסה גדולה יותר, זמן המחזור ארוך יותר (תנודות איטיות יותר), וככל שקבוע הקפיץ גדול יותר, זמן המחזור קצר יותר (תנודות מהירות יותר).
מציאת קבועי האינטגרציה $A$ ו-$B$
הקבועים $A$ ו-$B$ במשוואה $x(t) = A\cos(\omega t) + B\sin(\omega t)$ נקבעים על-ידי תנאי ההתחלה של המערכת.
- אם בזמן $t=0$ הגוף נמצא בנקודת המוצא ($x=0$) ואין לו מהירות התחלתית, אז $A=0$ ו-$B=0$ (אין תנועה).
- אם בזמן $t=0$ הגוף נמצא במרחק מקסימלי מנקודת שיווי המשקל ($x=A$) ואין לו מהירות התחלתית, אז $A$ יהיה האמפליטודה ו-$B=0$ (הפתרון יהיה רק קוסינוס).
- אם בזמן $t=0$ הגוף נמצא בנקודת שיווי המשקל ($x=0$) ויש לו מהירות התחלתית, אז $A=0$ והפתרון יכלול רק סינוס.
- במקרים אחרים, כאשר בזמן $t=0$ הגוף נמצא במיקום כלשהו ויש לו מהירות כלשהי, הפתרון יכלול גם קוסינוס וגם סינוס.
5. דוגמה: מערכת של שתי מסות וקפיץ
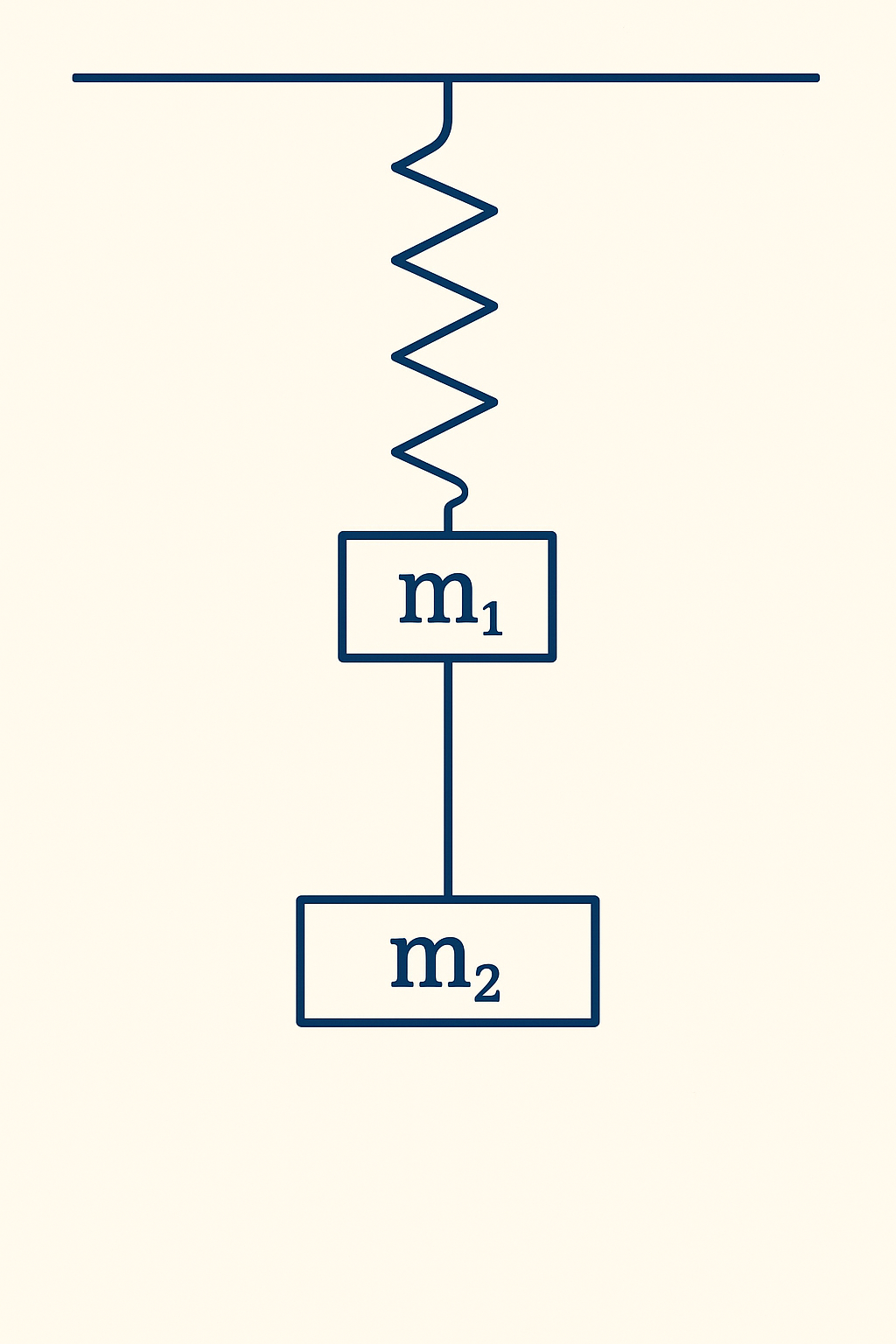
נתונה מערכת שבה מסה $m_2$ קשורה למסה $m_1$ באמצעות חוט דק. המסה $m_1$ קשורה לקפיץ אנכי שקבוע הקפיץ שלו הוא $K$. המערכת נמצאת במנוחה.
אם חותכים את החוט, המסה $m_1$ תתחיל לבצע תנודות הרמוניות.
- מהי האמפליטודה של התנודה ההרמונית?
- מהי התדירות של התנועה?
- איך התשובה הייתה משתנה אם המערכת נמצאת במעלית המאיצה בתאוצה של $A$ כלפי מעלה?
סעיף 1: מציאת האמפליטודה של התנודה ההרמונית
הרעיון: נמצא את נקודת שיווי המשקל של המערכת לפני חיתוך החוט, ואת נקודת שיווי המשקל החדשה אחרי חיתוך החוט. ההפרש בין שתי נקודות שיווי המשקל הוא האמפליטודה של התנודה ההרמונית.
שלב 1: המצב היציב לפני חיתוך החוט
הגדרת מערכת הצירים
ראשית בחרנו את מערכת הצירים כך ש:
- ראשית הצירים היא בנקודה שבה הקפיץ רפוי (אורכו הטבעי)
- הכיוון החיובי של ציר ה-$y$ מוגדר כלפי מטה
- המשתנה $y$ מציין את המרחק של המסה $m_1$ מראשית הצירים
הערה: בתרגילים אחרים, וגם כאן, אולי יהיה נוח יותר לכתוב $x_0$ במקום $y$.
ניתוח הכוחות
נרשום את הכוחות הפועלים על כל מסה:
על המסה $m_1$:
- כוח הכבידה כלפי מטה: $m_1g$ (חיובי)
- כוח הקפיץ כלפי מעלה: $-Ky$ (שלילי)
- מתיחות החוט כלפי מטה: $T$ (חיובי)
על המסה $m_2$:
- כוח הכבידה כלפי מטה: $m_2g$ (חיובי)
- מתיחות החוט כלפי מעלה: $-T$ (שלילי)
משוואות שיווי המשקל
כאשר המערכת נמצאת בשיווי משקל, סכום הכוחות על כל מסה הוא אפס:
עבור $m_1$:
\[m_1g - Ky + T = 0 \tag{1}\]עבור $m_2$:
\[m_2g - T = 0 \tag{2}\]ממשוואה $(2)$ אנחנו מקבלים:
\[T = m_2g\]נציב את הביטוי של $T$ במשוואה $(1)$ כדי לקבל את ערך $y$ בנקודת שיווי המשקל:
\[\begin{aligned} m_1g - Ky + m_2g &= 0 \\[10pt] Ky &= m_1g + m_2g \\[10pt] &= (m_1 + m_2)g \\[10pt] y &= \frac{(m_1 + m_2)g}{K} \end{aligned}\]כלומר, התארכות הקפיץ במצב של שיווי המשקל, או במילים אחרות - נקודת שיווי המשקל לפני שהחוט נקרע, היא במרחק של $y$ מהראשית של מערכת הצירים, כאשר $y$ הוא:
\[\boxed{y = \frac{(m_1 + m_2)g}{K}}\]שלב 2: מה קורה אחרי שהחוט נקרע
אחרי שהחוט נקרע:
- המסה $m_2$ נופלת ויוצאת מהמערכת
- מתיחות החוט $T$ לא פועלת יותר על $m_1$
- נקודת שיווי המשקל של המערכת משתנה
הכוחות החדשים על $m_1$
- כוח הכבידה כלפי מטה: $m_1g$ (חיובי)
- כוח הקפיץ כלפי מעלה: $-Ky$ (שלילי)
נקודת שיווי המשקל החדשה
במצב שיווי המשקל החדש, סכום הכוחות יהיה אפס:
\[\begin{aligned} m_1g - Ky_{new} &= 0 \\[10pt] Ky_{new} &= m_1g \\[10pt] y_{new} &= \frac{m_1g}{K} \end{aligned}\]המעבר בין שתי נקודות שיווי המשקל
המעבר בין שתי נקודות שיווי המשקל גורם לתנועה הרמונית של המסה $m_1$.
לפני חיתוך החוט, המסה נמצאת במיקום $y_{old} = \frac{(m_1 + m_2)g}{K}$. אחרי חיתוך החוט, נקודת שיווי המשקל החדשה היא $y_{new} = \frac{m_1g}{K}$.
ההפרש בין שתי נקודות שיווי המשקל נותן את האמפליטודה $A$ של התנודה ההרמונית:
\[\begin{aligned} \Delta y &= y_{old} - y_{new} \\[10pt] &= \frac{(m_1 + m_2)g}{K} - \frac{m_1g}{K} \\[10pt] &= \frac{m_2g}{K} \end{aligned}\]זה ה”צעד” הראשוני שיגרום לתנועה ההרמונית, כאשר המסה $m_1$ תתחיל לנוע מעלה לכיוון נקודת שיווי המשקל החדשה.
האמפליטודה של התנודה ההרמונית היא:
\[\boxed{A = \frac{m_2g}{K}}\]סעיף 2: מציאת התדירות של התנועה
המשוואה הדיפרנציאלית של התנועה
נסמן ב-$\eta$ את הסטייה של המסה $m_1$ מנקודת שיווי המשקל החדשה:
\[\eta = y - y_{new}\]לפי החוק השני של ניוטון, הכוח הפועל על המסה $m_1$ שווה לשינוי התנועה שלה כפול המסה:
\[m_1 \frac{d^2\eta}{dt^2} = m_1g - K(y_{new} + \eta) \tag{3}\]נציב במשוואה $(3)$ את $y_{new} = \frac{m_1g}{K}$ ונקבל:
\[\begin{aligned} m_1 \frac{d^2\eta}{dt^2} &= m_1g - K\left(\frac{m_1g}{K} + \eta\right) \\[10pt] &= m_1g - m_1g - K\eta \\[10pt] &= -K\eta \end{aligned}\]נבודד את $\frac{d^2\eta}{dt^2}$ על ידי חילוק ב-$m_1$:
\[\frac{d^2\eta}{dt^2} = -\frac{K}{m_1}\eta \tag{4}\]נגדיר $\omega^2 = \frac{K}{m_1}$, ונציב במשוואה $(4)$. נקבל את המשוואה הדיפרנציאלית של התנועה ההרמונית:
\[\boxed{\frac{d^2\eta}{dt^2} = -\omega^2\eta}\]הפתרון של התנועה ההרמונית
הפתרון של המשוואה הדיפרנציאלית הזו הוא:
\[\eta(t) = A\cos(\omega t + \phi)\]כאשר:
- $A$ היא האמפליטודה, שבמקרה זה $A = \frac{m_2g}{K}$ (הסטייה ההתחלתית)
- $\omega = \sqrt{\frac{K}{m_1}}$ היא התדירות הזוויתית
- $\phi$ היא הפאזה ההתחלתית (במקרה זה $\phi = \pi$ כי התנועה מתחילה מהסטייה המקסימלית בכיוון השלילי)
המיקום המלא של המסה $m_1$ כפונקציה של הזמן יהיה:
\[\begin{aligned} y(t) &= y_{new} + \eta(t) \\[10pt] &= \frac{m_1g}{K} + \frac{m_2g}{K}\cos(\omega t + \pi) \end{aligned}\]או בפשטות:
\[y(t) = \frac{m_1g}{K} - \frac{m_2g}{K}\cos(\omega t)\]זמן המחזור של התנודות יהיה:
\[T = \frac{2\pi}{\omega} = 2\pi\sqrt{\frac{m_1}{K}}\]התדירות היא הערך ההופכי של זמן המחזור, מכאן:
\[\boxed{f = \frac{1}{T} = \frac{1}{2\pi}\sqrt{\frac{K}{m_1}}}\]הניתוח המתמטי אחרי חיתוך החוט - הסבר נוסף
כאשר החוט נחתך, המערכת עוברת לנקודת שיווי משקל חדשה. בשלב זה, הכוחות על המסה $m_1$ הם:
- כוח הכבידה כלפי מטה: $m_1g$ (חיובי)
- כוח הקפיץ כלפי מעלה: $-Ky$ (שלילי)
המשוואה הדיפרנציאלית המתארת את התנועה:
\[\frac{d^2y}{dt^2} = \frac{K}{m_1}y + g\]זוהי משוואה דיפרנציאלית מהצורה:
\[\frac{d^2y}{dt^2} = -\omega^2y + C\]כאשר $\omega^2 = \frac{K}{m_1}$ וכאשר יש פה מינוס נוסף (כי הגדרנו את הכיוון החיובי כלפי מטה).
הפתרון של משוואה כזו הוא תנועה הרמונית סביב נקודת שיווי משקל חדשה. האומגה ($\omega$) קובעת את קצב התנודות:
\[\omega = \sqrt{\frac{K}{m_1}}\]אומגה זו קובעת כמה מהר התנודות מתרחשות. ככל שאומגה גדולה יותר, התנודות מהירות יותר, וככל שהיא קטנה יותר, התנודות איטיות יותר.
סעיף 3: השפעת מעלית מואצת על המערכת
השפעת מעלית מואצת על המערכת
כעת נבחן מה קורה כאשר כל המערכת נמצאת בתוך מעלית המאיצה כלפי מעלה בתאוצה $A$.
יש שתי דרכים להסתכל על הבעיה:
1. מנקודת מבט חיצונית
אם מסתכלים מבחוץ, התאוצה של המסה $m_1$ מורכבת משני חלקים:
- התאוצה של התנודות $\frac{d^2y}{dt^2}$
- התאוצה של המעלית $A$
2. מנקודת מבט בתוך המעלית
אם נמצאים בתוך המעלית ולא יודעים שהיא מאיצה, נרגיש “כוח מדומה” הפועל בכיוון ההפוך לתאוצת המעלית. הכוח המדומה שווה ל-$-m_1A$ (כלפי מטה).
המשוואה הדיפרנציאלית תהיה:
\[m_1\frac{d^2y}{dt^2} = m_1g - Ky - m_1A\]שאפשר לכתוב כ:
\[\frac{d^2y}{dt^2} = g - \frac{K}{m_1}y - A\]או:
\[\frac{d^2y}{dt^2} = -\frac{K}{m_1}y + (g-A)\]כאשר משווים למשוואה הסטנדרטית, מקבלים:
- $\omega^2 = \frac{K}{m_1}$ (זהה למקרה ללא מעלית)
- $C = g-A$ (שונה מהמקרה ללא מעלית, שבו $C = g$)
מה משתנה במעלית מואצת?
-
התדירות: לא משתנה! האומגה נשארת זהה: $\omega = \sqrt{\frac{K}{m_1}}$
-
נקודת שיווי המשקל: משתנה. במעלית מואצת, נקודת שיווי המשקל החדשה תהיה במיקום שבו:
\[Ky = m_1(g-A)\] \[y = \frac{m_1(g-A)}{K}\] -
האמפליטודה: תלויה בתנאי ההתחלה ובהפרש בין נקודות שיווי המשקל הישנה והחדשה.
מה שחשוב לזכור זה שתדירות התנודות לא משתנה כאשר המערכת נמצאת במעלית מואצת. זו תכונה חשובה של תנועה הרמונית - התדירות תלויה רק בקבוע הקפיץ ובמסה, ולא בתנאי הסביבה כמו תאוצת המעלית.
דוגמה נוספת: גוף על מישור משופע עם קפיץ
נעבור לשאלה הבאה משיעורי הבית. בסופו של דבר, נרצה להגיע למשוואה מהצורה:
\[\frac{d^2x}{dt^2} + \omega^2 x = 0\]או מהצורה:
\[\frac{d^2y}{dt^2} + \omega^2 y = 0\]ואז נקבל תנודות של קפיץ.
תיאור המערכת הפיזיקלית
נסתכל על התרגיל הזה: קוביה שמונחת על מישור משופע, מחוברת בקפיץ למסה שמחוברת למשולש.
השאלה המקורית:
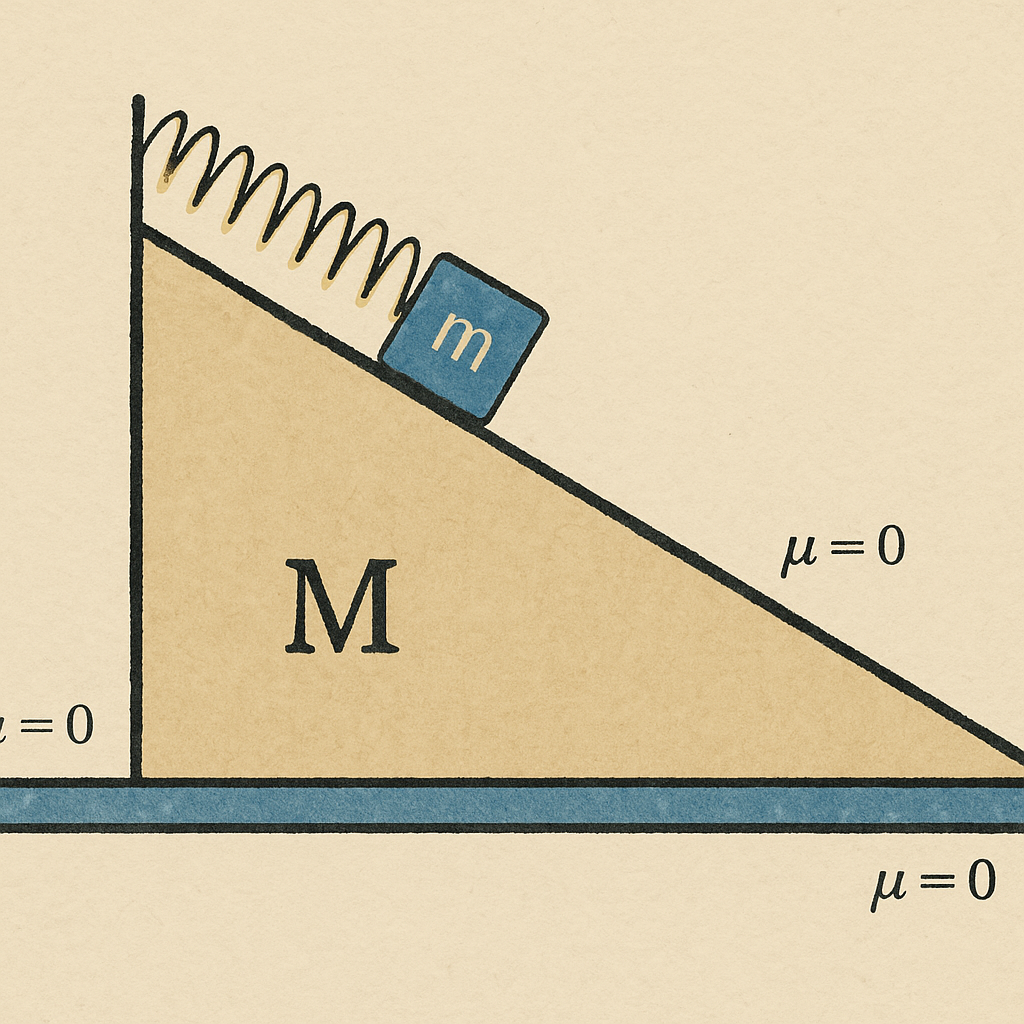
על גבי מישור משופע חסר חיכוך מונחת מסה המחוברת אל ראשו בקפיץ. המישור המשופע יכול להחליק ללא חיכוך על רצפה אופקית.
שיפוע המישור המשופע הוא $\alpha$. קבוע הכוח של הקפיץ הוא $k$ ואורכו הרפוי הוא $\ell$.
נכנה ב-$x(t)$ את המרחק של $m$ מראש המישור המשופע (מהמקום בו הקפיץ מחובר אל המישור המשופע).
מניחים בעדינות את המסה $m$ במקום בו הקפיץ רפוי
\[x(t=0) = \ell\]ומשחררים ממנה.
נציין את תאוצת המישור המשופע $M$ על הרצפה האופקית ב-$A$, ואת תאוצה המסה $m$ על גבי המישור המשופע באות $a$, כך ש:
\[a = \ddot{x}\]במערכת הצמודה ל-$M$, כמה זמן ייקח עד ש-$m$ תיעצר על המישור המשופע לראשונה?
רמז: המסה $m$ מתנדנדת הרמונית.
הגדרת הבעיה
יש לי גוף עם מסה $M$ שמחוברת לקפיץ, והיא מחוברת למשולש. היא מחליקה על המשולש ואין ביניהם חיכוך.
נתונים:
- שיפוע המישור המשופע: $\alpha$
- קבוע הקפיץ: $k$
- אורכו הרפוי של הקפיץ: $\ell$
התנהגות המערכת
כשהקפיץ רפוי, אורכו הוא $\ell$. כשמניחים אותו בשיפוע, הוא ימתח קצת בגלל כוח הכבידה - חלק הרכיב האחד של כוח הכבידה ימתח אותו טיפה.
בעקבות המתיחה הזאת, הקפיץ יתחיל לעשות תנודות סביב נקודת שיווי המשקל החדשה שלו.
מנגנון התנודה:
- כשהמסה עוברת לצד אחד, המשולש (שמתחת) מנסה לזוז לצד השני
- כשהמסה חוזרת, המשולש מנסה לזוז לצד ההפוך
- גם המסה וגם המשולש יבצעו תנודות במקביל
זה כמו שאתם עומדים על קורקינט - אם תלכו לצד אחד, הקורקינט יעוף לצד השני.
 |
|---|
| תיאור לא מדויק - ניסיתי להמחיש את הרעיון של התנודות. שימו לב שמה שה״קיר״ מחובר כולו למאסה הגדולה (בניגוד למה שרואים ב-GIF). |
ניתוח כוחות
שלב 1: זיהוי הכוחות
הדבר הראשון שאני עושה הוא לרשום כוחות על כל אחד מהגופים.
כוחות הפועלים על המסה הקטנה ($m$):
- מתיחות של הקפיץ: $F_{\text{spring}}$
- כוח כבידה: $mg$ כלפי מטה
- כוח נורמלי: $N$ בניצב למשטח
כוחות הפועלים על המשולש ($M$):
- כוח נורמלי מהרצפה
- כוח כבידה: $Mg$ כלפי מטה
- כוח נורמלי מהמסה הקטנה (לפי החוק השלישי של ניוטון)
- כוח הקפיץ
שלב 2: קביעת מערכת הצירים
אני קובע מערכת צירים משופעת עבור הגוף הקטן - זה יותר נוח. עבור המשולש אני קובע מערכת צירים רגילה.
עבור המסה הקטנה:
- כיוון $x$ חיובי: כלפי מטה לאורך השיפוע
- כיוון $y$ חיובי: בניצב למעלה מהמשטח
עבור המשולש:
- כיוון $X$ חיובי: ימינה
- כיוון $Y$ חיובי: כלפי מעלה
שלב 3: פירוק הכוחות לרכיבים
חלק מהכוחות לא יושבים על הצירים, אז צריך לפרק אותם לרכיבים.
עבור המסה הקטנה, צריך לפרק:
- $mg$ ← $mg\cos\alpha$ ו-$mg\sin\alpha$
- $mA$ ← $mA\cos\alpha$ ו-$mA\sin\alpha$
- כוח הקפיץ: $k(x-\ell)$ ← $k(x-\ell)\cos\alpha$ ו-$k(x-\ell)\sin\alpha$
- $N_{21}$ ← $N_{21}\cos\alpha$ ו-$N_{21}\sin\alpha$
הכוחות המדומים
כשהמסה הקטנה יושבת על המשולש, והמשולש נע בתאוצה $A$, המסה הקטנה מרגישה כוח מדומה.
הכוח המדומה:
- כיוון: נגד כיוון התאוצה של המשולש
- גודל: $mA$ (כאשר $A$ היא תאוצת המשולש)
זה כמו במעלית - כשהמעלית עולה למעלה בתאוצה, אתם מרגישים כוח מדומה למטה.
משוואות התנועה
שלב 4: כתיבת משוואות התנועה
לכל ציר ולכל גוף נכתוב משוואת תנועה:
עבור המשולש (כיוון X):
\[MA = k(x-\ell)\cos\alpha - N_{21}\sin\alpha\]עבור המשולש (כיוון Y):
\[0 = N - N_{21}\cos\alpha - Mg - k(x-\ell)\sin\alpha\]עבור המסה הקטנה (כיוון x):
\[m a_x = \sum F_x\]עבור המסה הקטנה (כיוון y):
\[0 = \sum F_y\]ספירת נעלמים ומשוואות
נעלמים:
- $A$ (תאוצת המשולש)
- $a_x$ (תאוצת המסה הקטנה)
- $N_{21}$ (כוח נורמלי)
- $N$ (כוח נורמלי מהרצפה)
מספר משוואות: 4
מספר נעלמים: 4
לכן, המערכת ניתנת לפתרון!
פתרון והגעה לתדירות
אחרי פתרון המערכת (שזה חישוב מורכב), נקבל משוואה מהצורה:
\[\frac{d^2x}{dt^2} + \omega^2 x = C\]המקדם $\omega^2$ הוא התדירות הזוויתית בריבוע של התנודות.
סיכום: תנודות הרמוניות
התנודה ההרמונית מאופיינת על ידי שני פרמטרים עיקריים:
1. התדירות ($\omega$)
התדירות קובעת את קצב התנודות. אני מוצא אותה ברגע שאני מקבל משוואה מהצורה:
\[\frac{d^2x}{dt^2} + \omega^2 x = 0\]אני מסתכל על המקדם של $x$ (עד כדי מינוס), וזה התדירות בריבוע.
2. האמפליטודה
האמפליטודה היא כמה מתחתי את הגוף מעבר לנקודת שיווי המשקל. את האמפליטודה אני מוצא לפי תנאי ההתחלה.
אנלוגיה פיזיקלית
כשאני מסתכל על תנודה הרמונית, אני חושב על קערה עם כדור:
- הכדור נמצא למטה בנקודת שיווי המשקל
- אני מסיט אותו מעבר לנקודת שיווי המשקל
- הכדור מתחיל להתנדד סביב נקודת שיווי המשקל של הקערה
הערות נוספות על כוחות מדומים
בבעיה זו השתמשנו בכוחות מדומים במקום להתעסק עם תאוצות מורכבות. זה עדיף כי:
- יותר קל לזהות כיוונים בכוחות מאשר בתאוצות
- אנחנו רגילים לפרק כוחות לרכיבים ולא תאוצות
- זה מפשט את החישובים
עיקרון כללי: אם גוף נמצא במערכת שנעה בתאוצה, הוא ירגיש כוח מדומה בכיוון הפוך לתאוצה.
דור פסקל