חזרה על מושגי יסוד
שדה חשמלי ממטען נקודתי
\[\vec{E} = \frac{kQ}{r^2}\hat{r}\]- השדה דועך כמו $\frac{1}{r^2}$
- מטען חיובי ← שדה יוצא החוצה
- מטען שלילי ← שדה נכנס פנימה
נוסחאות אנרגיה פוטנציאלית חשמלית
גודל נוסחה וסימון אנרגיה פוטנציאלית חשמלית \(U^{elec}(A) = -\int_\infty^A \vec{F}d\vec{s} \, \mathrm{(J)}\) אנרגיה פוטנציאלית חשמלית
בין שני מטענים נקודתיים
במרחק $r$ אחד מהשני\(U^{elec} = k \frac{q_1 q_2}{r} \, \mathrm{(J)}\)
- מבטאת את העבודה החיצונית שנדרשת בשביל להביא מטען מהאינסוף
- אם המטענים שווי סימן ← עבודה חיובית (דחייה)
- אם המטענים הפוכי סימן ← עבודה שלילית (משיכה)
פוטנציאל חשמלי - הגדרה
פוטנציאל חשמלי הוא אנרגיה פוטנציאלית ליחידת מטען:
\[V = \frac{U^{elec}}{q} = \frac{-W_{\infty}^{elec}}{q}\]יחידות:
\[[V] = \frac{\text{J}}{\text{C}} = \text{Volt}\]- 1 ג’אול לקולון = 1 וולט
- מתח = הפרש פוטנציאלים (למשל 220V בחשמל ביתי)
הקשר בין שדה לפוטנציאל
הכוח הוא מינוס הגרדיאנט של האנרגיה הפוטנציאלית:
\[\vec{F} = -\nabla U\]בחילוק ב-$q$:
\[\vec{E} = -\nabla V\]נוסחאות הפרש פוטנציאל חשמלי
גודל הערות יחידות הפרש פוטנציאל $\Delta V = V_2 - V_1$ העבודה ליחידת מטען הנדרשת להעביר יחידת מטען מנקודה 1 ל-2 וולט (V) חישוב הפרש פוטנציאל בעזרת שדה חשמלי \(\Delta V = -\int_1^2 \vec{E} \cdot d\vec{s}\) וולט (V) והפוך - בהינתן הפוטנציאל השדה הוא \(\vec{E} = -\nabla V\) וולט למטר (V/m) פוטנציאל חשמלי ממטען נקודתי הוא $V=\frac{kq}{r}$ לעומתו השדה הוא $\vec{E}=\frac{kq}{r^2}\hat{r}$ והאנרגיה הפוטנציאלית ממטענים נקודתיים היא $U^{elec} = k \frac{q_1 q_2}{r}$ וולט (V)
חישוב הפרש פוטנציאלים
\[\Delta V = V_B - V_A = -\int_A^B \vec{E} \cdot d\vec{l}\]הערה: הפוטנציאל הוא גודל סקלרי, למרות שהאינטגרל כולל וקטורים.
פוטנציאל ממטען נקודתי
\[V = \frac{kQ}{r}\]- הפוטנציאל דועך כמו $\frac{1}{r}$ (לא $\frac{1}{r^2}$ כמו השדה!)
- נקודת הייחוס: $V(\infty) = 0$
סופרפוזיציה להמונים (?)
הפוטנציאל שמושרה על ידי מספר מטענים:
\[V_{total} = \sum_i V_i = \sum_i \frac{kQ_i}{r_i}\]הפוטנציאל השקול בנקודה שנוצר כתוצאה ממספר מטענים הוא סכום הפוטנציאלים.
אם יש רצף של מטענים אז יש לתרגם הסכום לאינטגרל:
\[V_{total} = \int \frac{k \, dQ}{r} = k \int \frac{\rho(\vec{r'}) dV'}{|\vec{r} - \vec{r'}|}\]
תכונות של מוליכים
שדה בתוך מוליך
בתוך מוליך, השדה החשמלי שווה לאפס:
\[\vec{E}_{\text{inside}} = 0\]
הסיבה הפיזיקלית:
- שדה מפעיל כוח על מטענים
- במוליך, המטענים יכולים לזוז בחופשיות
- המטענים זזים עד שסכום הכוחות עליהם שווה לאפס
- מגיעים לשיווי משקל אלקטרוסטטי
פוטנציאל בתוך מוליך
אם $\vec{E} = 0$ בתוך המוליך, אז:
\[\vec{E} = -\nabla V = 0 \quad \Rightarrow \quad V = \text{const}\]הפוטנציאל בתוך מוליך קבוע (אך לא בהכרח אפס!)
הארקה (Grounding)
מהי הארקה?
הארקה = חיבור פיזי לכדור הארץ.
כאשר מוליך מוארק:
- הפוטנציאל שלו שווה לפוטנציאל כדור הארץ
- כדור הארץ נחשב כמאגר אינסופי עם $V = 0$
- לכן: פוטנציאל על מוליך מוארק = 0
הסבר פיזי
כדור הארץ הוא כדור מוליך ענק. אם יש הפרש פוטנציאלים בין המוליך המוארק לכדור הארץ:
- מטענים יזרמו עד שהפוטנציאלים ישתוו
- בגלל שכדור הארץ ענק, הפוטנציאל שלו נשאר כמעט קבוע (אפס)
חשיבות בטיחותית
בבית, יש שלושה חורים בשקע:
- שניים לפאזה ולאפס (220V)
- השלישי מחובר להארקה
למה זה חשוב?
- אם חוט חשמל נוגע במסגרת מתכתית של מכשיר
- בלי הארקה: הזרם עובר דרך האדם לכדור הארץ
- עם הארקה: הזרם הולך ישר לכדור הארץ דרך חוט ההארקה
תרגיל 1: חשבונות שדה
תרגיל 1א - חצי מעגל
חשבו את השדה החשמלי בראשית הצירים עבור מטען $Q = 4 \mu \, \mathrm{C}$ המפולג באופן אחיד על חצי מעגל ברדיוס $R=0.74 \, \mathrm{m}$.
חצי המעגל על ציר $y$ כך שהחצי רק על החלק השלישי של ציר $x$. להלן תמונה:
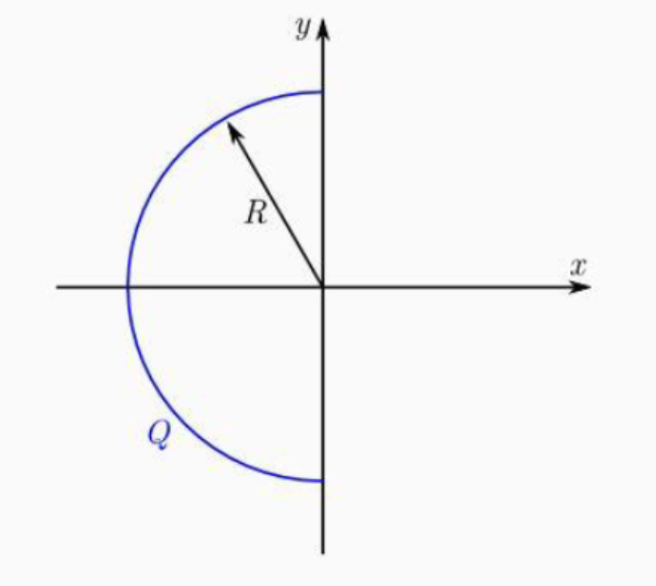
שימו לב: זה חצי מעגל, לא חצי דיסקה (חצי מעגל - משתמשים בהיקף לא בשטח).
להבנתי פחות רלוונטי לסופרפוציפיה. במקרה כזה צריך אינטגרל. כן צריך להבין משיקולי סימטריה מה מתאפס (לא הכל!).
נסתכל על הראשית. נראה שרק בכיוון ציר $x$ יש משהו כי ההשפעות בכיוון ציר $y$ מתאפסות?
ניקח יחידת מטען קטנה (חילקתי את המטען הכולל בהיקף של חצי מעגל):
\[\textcolor{green}{dq} = \frac{Q}{\pi R} d \theta\]נשתמש בגאוס? לא! גאוס לא מתאים כאן כי חסרה סימטריה. צריך לעשות אינטגרל על השדה ישירות! כל אלמנט קטן עושה על הראשית שדה חשמלי קטנטן של:
\[dE = \frac{K \cdot \textcolor{green}{dq}}{R^2}\]צריך לפרק לרכיבים מהסימטריה כדי להשיאר רק עם ההיטל על ציר $x$:
\[dE_x = dE \cdot \cos(\theta) = \frac{K}{R^2} \cdot \frac{Q}{\pi R} \cos(\theta)d\theta\]גבולות האינטגרסיה על $\theta$ הם מ$\frac{\pi}{2}$ אל $\frac{3\pi}{2}$ (ניסיתי לחשוב על מעגל היחידה ועל הציור):
\[\int_{\pi/2}^{3\pi/2} \frac{K}{R^2} \cdot \frac{Q}{\pi R} \cos(\theta)d\theta = \frac{K}{R^2} \cdot \frac{Q}{\pi R} \int_{\pi/2}^{3\pi/2} \cos(\theta)d\theta\] \[= \frac{K}{R^2} \cdot \frac{Q}{\pi R} \sin(\theta)\Big|_{\pi/2}^{3\pi/2} = \boxed{-2 \frac{K}{R^2} \cdot \frac{Q}{\pi R}}\]\[\sin\left(\frac{\pi}{2}\right) = 1\] \[\sin\left(\frac{3\pi}{2}\right) = -1\]
נציב את המספרים כדי לקבל תשובה מספרית:
\[E_x = -\frac{2 \cdot (9 \times 10^9) \cdot (4 \times 10^{-6})}{\pi \cdot (0.74)^2} \approx -4.16 \, \mathrm{N / C}\]דוגמה לטעות:
\[E_x = - \frac{2KQ}{\pi R^2} = - \frac{8K}{\pi \cdot 0.5476} = - \frac{8K}{\sim 1.72} \approx -4.65 K\]שכחתי להציב את ה-$\mu$ (מיקרו) של המטען.
\[Q = 4\mu C = 4 \times 10^{-6} \, \mathrm{C}\]וגם צריך להציב את הערך של $K$:
\[K = 9 \times 10^9 \frac{\mathrm{Nm}^2}{\mathrm{C}^2}\]
תרגיל 1ב - חלל גלילי בתוך גליל מלא
גליל אינסופי מלא טעון בצפיפות מטען נפחית אחידה $\rho_0$. בגליל נקדח חור כמוראה בציור. מהו השדה החשמלי בתוך החור?
רדיוס הגליל הוא $a$, רדיוס החור $b$ החור נקדח בנקודה $(c,0)$.
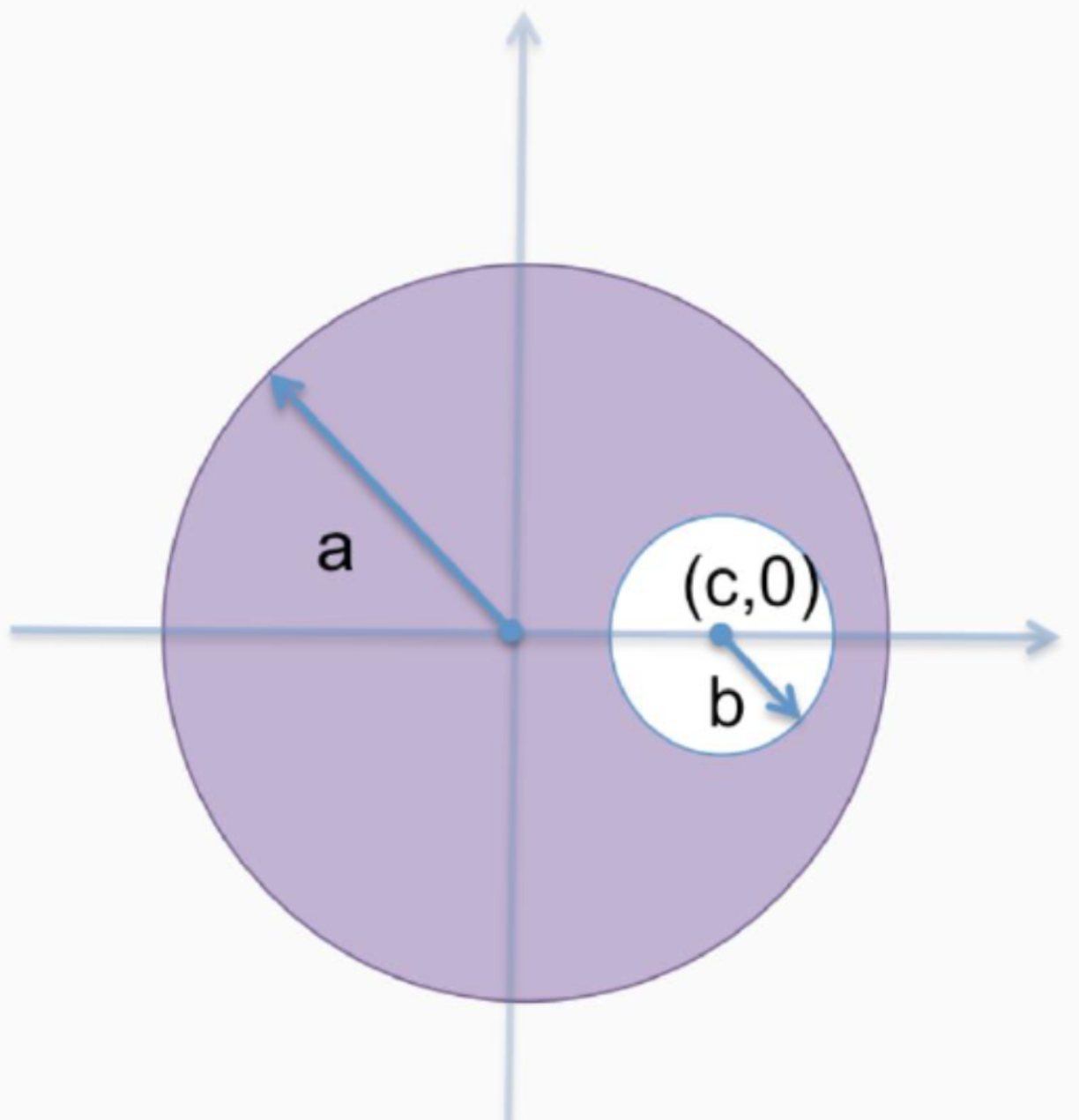
לדעתי צריך להיעזר בסופר פוזיציה ובחוק גאוס: השדה הוא כמו גליל מלא פחות שדה של הגליל הקטן (החור).
החור הוא לא מטען נקודתי!
מה השדה של כל חלק?
גליל מלא ברדיוס $a$ וצפיפות $\rho_0$:
- בתוך הגליל ($r < a$): מה השדה? (נשתמש בגאוס)
המטען בתוך הגליל הוא לא אפס!
להיזהר לא להתבלבל עם מוליך. במוליך אין מטען בפנים.
אבל כאן יש צפיפות מטען נפחית $\rho_0$ - כל הנפח מלא במטען!
חישוב נכון עם גאוס
משטח גאוס גלילי ברדיוס $r$ ואורך $L$:
\[E \cdot 2\pi r L = \frac{Q_{inside}}{\epsilon_0}\]מה המטען בתוך הגליל?
\[Q_{inside} = \rho_0 \cdot V = \rho_0 \cdot \pi r^2 L\]אז:
\[E_1 \cdot 2\pi r L = \frac{\rho_0 \pi r^2 L}{\epsilon_0}\] \[\boxed{\hat{E}_1\left(r\right) = \frac{\rho_0 \hat{r}}{2\epsilon_0}}\]זה השדה בתוך גליל מלא. תובנה חשובה: הוא גדל עם $r$, לא קבוע!
הערה: זה היה המטען בתוך גליל טעון - מחוץ לגליל טעון ככל הנראה:
\[\vec{E} = \frac{\lambda}{2\pi \epsilon_0 r}\hat{r}\]
גליל קטן ברדיוס $b$ וצפיפות $\rho_0$ שמרכזו ב-$(c, 0)$:
- זה גם גליל, לא מטען נקודתי!
- מה השדה שלו בתוכו?
באופן דומה זה לא אפס.
משטח גאוס גלילי ברדיוס מטעים נותן פעם נוספת נוסחה דומה. המטען בגליל הקטן אבל שונה - הוא הפוך בכיוון לצפיפות של הגדול (כי להחסיר זה כמו להוסיף מטען הפוך). וגם הרדיוס כאן להבנתי שונה:
\[\hat{E}_2\left(r\right) = \frac{(-\rho_0) \hat{r'}}{2\epsilon_0}\]הטריק עכשיו זה לזהות ש:
\[\vec{r'} = \vec{r} - \vec{c}\]או ברישום שקול:
\[\vec{r'} = \vec{r} - c \hat{x}\]
סך הכל:
\[\hat{E}_2\left(r\right) = \frac{(-\rho_0) \cdot (\vec{r} - c \hat{x})}{2\epsilon_0}\]השדה הכולל:
\[E = E_1 + E_2 = \frac{\rho_0 \hat{r}}{2\epsilon_0} + \frac{(-\rho_0) \cdot (\vec{r} - c \hat{x})}{2\epsilon_0} = \cancel{\frac{\rho_0 \hat{r}}{2\epsilon_0}} + \cancel{\frac{(-\rho_0) \cdot \vec{r}}{2\epsilon_0}} - \frac{ (-\rho_0) \cdot c \hat{x}}{2\epsilon_0}\] \[= \frac{ \rho_0 \cdot c \hat{x}}{2\epsilon_0}\]תובנה חשובה
שני הגלילים נותנים שדה אחיד בתוכם (לא תלוי ב-$r$, רק בוקטור המיקום מהמרכז). אז כשמחסרים (או מחברים אותם) מקבלים גם כן שדה אחיד, לא משנה איפה בתוך החור.
דילגנו על תרגיל 2 - הוא זמין בפתרון תרגיל 4.
תרגיל 3: מציאת פוטנציאל חשמלי
גליל מוליך ארוך מאוד אשר רדיוסו הוא $a$ טעון בצפיפות מטען אורכית $\lambda$ קולון ליחידת אורך של הגליל. סביב הגליל מונחת מעטפת גלילית דקה ומוארקת ברדיוס $b>a$, כך שציר הגליל וציר המעטפת הגלילית מתלכדים. מהו הפוטנציאל החשמלי בכל המרחב?
הנחייה: מיצאו את השדה והביאו חלקיק מן האינסוף כנגד (או עם) השפעת השדה.
ננסה להיעזר ברמז - נמצא תחילה את השדה. צריך לפצל לשלושה אזורים:
- בתוך המוליך $(r<a)$
- בין הגליל למעטפת $(a < r < b)$
- מחוץ למטעפת $(r>b)$
בתוך מוליך השדה הוא אפס:
\[\vec{E_1} = \vec{0}\]בין הגליל למעטפת - נבנה מעטפת גאוסית גלילית.
בגדול הנוסחה לשדה מחוץ לגליל טעון היא כאמור:
\[\vec{E_2} = \frac{\lambda}{2\pi \epsilon_0 r}\hat{r}\]מחוץ למעטפת - אפשר להיעזר בכך שהמטעפת מוארקת: המעטפת המוארקת “רואה” מטען $+\lambda$ על הגליל הפנימי, אז היא תיטען ב-$-\lambda$ (מטענים נשאבים מהאדמה).
סך המטען הכלוא במשטח גאוס ב-$r > b$:
\[Q_{inside} = (+\lambda L) + (-\lambda L) = 0\]לכן:
\[\vec{E_3}(r > b) = 0\]חישוב הפוטנציאל
יש לנו את השדה בכל מקום. עכשיו צריך לחשב:
\[V(r) = -\int_{\infty}^{r} \vec{E} \cdot d\vec{r}\]נתחיל מ-$r > b$ (שם $V = 0$ כי מוארק), ונתקדם פנימה.
האינטגרל רץ על המסלול מנקודת הייחוס (אינסוף) עד לנקודה שבה רוצים למצוא את הפוטנציאל.
בין המטעפת לגליל - נפרק לאזורים (כי השדה משתנה באזורים שונים)
באזור $a < r < b$:
\[V(r) = -\int_{\infty}^{b} \vec{E_3} \cdot dr - \int_{b}^{r} \vec{E_2} \cdot dr\] \[= -\int_{\infty}^{b} 0 \cdot dr - \int_{b}^{r} \frac{\lambda}{2\pi\epsilon_0 r'} dr'\] \[= 0 - \frac{ \lambda }{2 \pi \epsilon_0} \ln \left(r'\right) \bigg|_b^r\] \[= -\frac{\lambda}{2\pi\epsilon_0} \left[\ln(r) - \ln(b)\right]\] \[= \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{r}\right)\]עכשיו ננסה לחשב את $V(r)$ עבור $r < a$ (בתוך המוליך).
באזור $r < a$:
\[V(r) = -\int_{\infty}^{b} \vec{E_3} \cdot dr - \int_{b}^{a} \vec{E_2} \cdot dr - -\int_{a}^{r} \vec{E_1} \cdot dr\] \[= -\int_{\infty}^{b} 0 \cdot dr - \int_{b}^{a} \frac{\lambda}{2\pi\epsilon_0 r'} dr' -\int_{a}^{r} 0 \cdot dr\] \[= 0 - \frac{ \lambda }{2 \pi \epsilon_0} \ln \left(r'\right) \bigg|_b^a + 0\] \[= \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{a}\right)\]סך הכל:
\[V(r) = \begin{cases} \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{a}\right) \, & \text{for } r<a \\ \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{r}\right) \, & \text{for } a<r<b \\ 0 \, & \text{for } r< b \\ \end{cases}\]פתרון כתה - מציאת הפוטנציאל במרחב
להלן הפתרון לאותה השאלה לפי התרגול בכתה.
פתרון בעזרת חוק גאוס ואינטגרציה
שלב 1: מציאת השדה בין הגלילים ($a < r < b$)
משתמשים בחוק גאוס עם מעטפת גלילית ברדיוס $r$ ואורך $L$:
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{enc}}}{\epsilon_0}\] \[E \cdot 2\pi r L = \frac{\lambda L}{\epsilon_0}\] \[E(a < r < b) = \frac{\lambda}{2\pi\epsilon_0 r}\]שלב 2: מציאת הפוטנציאל
הפוטנציאל על המעטפת המוארקת:
\[V(b) = 0\]הפוטנציאל בנקודה $r$ (בין $a$ ל-$b$):
\[V(r) - V(b) = -\int_b^r E \, dr'\] \[V(r) = -\int_b^r \frac{\lambda}{2\pi\epsilon_0 r'} dr'\] \[V(r) = -\frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{r}{b}\right)\] \[\boxed{V(a < r < b) = \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{r}\right)}\]שלב 3: פוטנציאל בתוך הגליל הפנימי ($r < a$)
השדה בתוך מוליך הוא אפס, לכן הפוטנציאל קבוע:
\[V(r < a) = V(a) = \frac{\lambda}{2\pi\epsilon_0} \ln\left(\frac{b}{a}\right)\]שלב 4: פוטנציאל מחוץ למעטפת ($r > b$)
המעטפת מוארקת ולכן $V(b) = 0$.
מחוץ למעטפת, צריך לחשב את השדה ולבצע אינטגרציה.
תרגיל 4: כדור מוליך עם הארקות
נתון כדור מוליך $A$ שרדיוסו הוא $R$ ומטענו הוא $+Q$.
שרטטו באופן איכותי גרף של הפוטנציאל $V(r)$ כתלות במרחק $r$ ממרכז הכדור, בתחום $0 \le r \le 3R$.
- מקיפים את הכדור $A$ בקליפה מוליכה כדורית דקה $B$ שרדיוסה הוא $2R$, כך שלשני הגופים יש מרכז משותף. הקליפה טעונה במטען חשמלי $-2Q$.
- מהו הפוטנציאל החשמלי בכל המרחב? (רמז: סופרפוזיציה)
- מהי העבודה הנדרשת להביא מטען $q$ כלשהו מהאינסוף אל הקליפה החיצונית? (רמז: אין צורך לחשב אינטגרל)
עתה מאריקים את הקליפה החיצונית. מהו המטען המצטבר על הכדור המוליך ועל הקליפה במצב זה?
- מנתקים את ההארקה ומחברים את שני הגופים במוליך דק. מהו המטען עתה על כל מוליך? (הניחו שלא מצטברים מטענים על המוליך הדק).
סעיף א - כדור מוליך טעון: גרף איכותי של הפוטנציאל החשמלי
נתון כדור מוליך ברדיוס $R$ טעון במטען $Q$.
מהו הפוטנציאל החשמלי בכל המרחב?
מוליך - המטענים יכולים לזוז. צריך להפריד לאזורים.
אזור 1: בתוך הכדור ($r < R$)
השדה בתוך מוליך הוא אפס:
\[E(r < R) = 0\]לכן הפוטנציאל קבוע:
\[V(r < R) = \text{const}\]אזור 2: מחוץ לכדור ($r > R$)
מחוץ לכדור, הוא נראה כמו מטען נקודתי:
\[E(r > R) = \frac{kQ}{r^2}\]הפוטנציאל:
\[V(r > R) = \frac{kQ}{r}\]מציאת הקבוע בתוך הכדור
הפוטנציאל רציף, לכן:
\[V(r < R) = V(R) = \frac{kQ}{R}\]סיכום
\[V(r) = \begin{cases} \frac{kQ}{R} & r \leq R \\ \frac{kQ}{r} & r > R \end{cases}\]גרף איכותי
V
│
│████████████ ← קבוע בתוך הכדור
│ ╲
│ ╲
│ ╲ ← דועך כמו 1/r
│ ╲
│ ╲___
└─────────────────────── r
R
הערה: יש קפיצה בנגזרת (בשדה) על פני המעטפת, אבל הפוטנציאל עצמו רציף.
סעיף ב - חישוב בעזרת סופרפוזיציה
- כדור מוליך ברדיוס $R$ טעון במטען $+Q$
- מקיפים את הכדור בקליפה מוליכה כדורית דקה ברדיוס $2R$
- הקליפה טעונה במטען $-2Q$
- מרכז משותף
מהו הפוטנציאל החשמלי בכל המרחב?
נפתור בנפרד עבור כל גוף ואז נסכום.
תרומת הכדור הפנימי (ירוק) - מטען $+Q$
בתוך הכדור ($r < R$):
\[V_{\text{green}}(r < R) = \frac{kQ}{R} \quad \text{(const)}\]מחוץ לכדור ($r > R$):
\[V_{\text{green}}(r > R) = \frac{kQ}{r}\]תרומת הקליפה החיצונית (אדום) - מטען $-2Q$
בתוך הקליפה ($r < 2R$):
\[V_{\text{red}}(r < 2R) = \frac{k(-2Q)}{2R} = -\frac{kQ}{R} \quad \text{(const)}\]מחוץ לקליפה ($r > 2R$):
\[V_{\text{red}}(r > 2R) = \frac{k(-2Q)}{r} = -\frac{2kQ}{r}\]סופרפוזיציה - סיכום כל האזורים
אזור 1: $r < R$ (בתוך הכדור הפנימי)
\[V = V_{\text{green}} + V_{\text{red}} = \frac{kQ}{R} + \left(-\frac{kQ}{R}\right) = 0\]אזור 2: $R < r < 2R$ (בין הכדור לקליפה)
\[V = \frac{kQ}{r} + \left(-\frac{kQ}{R}\right) = \frac{kQ}{r} - \frac{kQ}{R}\] \[\boxed{V(R < r < 2R) = kQ\left(\frac{1}{r} - \frac{1}{R}\right)}\]אזור 3: $r > 2R$ (מחוץ לקליפה)
\[V = \frac{kQ}{r} + \left(-\frac{2kQ}{r}\right) = -\frac{kQ}{r}\] \[\boxed{V(r > 2R) = -\frac{kQ}{r}}\]הסבר שיטת הסופרפוזיציה
- מחשבים את הפוטנציאל מכל גוף בנפרד
- מתייחסים לכל גוף כאילו האחר לא קיים
- סוכמים את התרומות (חיבור או חיסור לפי הסימן)
יתרון: מפשט בעיות עם מספר גופים טעונים
סעיף ב(2) העבודה הנדרשת להביא מטען $q$ כלשהו מהאינסוף אל הקליפה החיצונית
מצאנו את הפונציאל אז העבודה קשורה להפרש פוטנציאלים. באינסוף הפוטנציאל הוא 0, מכאן שהעבודה להזיז מטען $q$ היא:
\[W = q \cdot \Delta V = q \cdot \left(V_{final \implies r=2R}-V_{initial}\right)\] \[= q ((-\frac{kQ}{r}) - 0) = \boxed{-\frac{qkQ}{2R}}\]להיזהיר לא להתבלבל בסימנים! זאת העבודה הסופית פחות ההתחלתית.
למה העבודה יוצאת שלילית?
הפוטנציאל בקליפה החיצונית הוא שלילי, כלומר מושך מטענים, מכאן שלמעשה השדה עושה עבודה חיובית ואנחנו לא צריכים לעשות מבחוץ עבודה (זה נמשך לבד).
סעיף ג - מטען מצטבר כשמאריקים
נתון שמאריקים את הקליפה החיצונית ושואלים מה המטען המצטבר על הכדור המוליך ועל הקליפה במצב הזה.
כשמאריקים את הקליפה, הפוטנציאל שלה הופך לאפס. אבל זה לא אומר שהמטען נשאר אותו דבר! הקליפה מחוברת לאדמה, אז מטענים יכולים לזרום אליה או ממנה עד שהפוטנציאל שלה יהיה אפס.
שאלות מנחות:
-
הכדור הפנימי - האם הוא מחובר למשהו? האם המטען שלו יכול להשתנות?
המטען שלו לא משתנה!
-
הקליפה - מה צריך להיות המטען עליה כדי שהפוטנציאל ב-$r = 2R$ יהיה אפס?
צריך להשתוות לזה של הכדור? כן!
תובנה מהותית: צריך להשתמש בסופרפוזיציה. הפוטנציאל בקליפה ($r = 2R$) הוא סכום התרומות מהכדור ($+Q$) ומהקליפה עצמה (מטען לא ידוע $Q_{shell}$).
נחשב את הפוטנציאל בקליפה (צריך להיות אפס):
\[V(2R) = \underbrace{\frac{kQ}{2R}}_{\text{inner ball}} + \underbrace{\frac{kQ_{shell}}{2R}}_{\text{shell}} = 0\]נפתור עבור $Q_{shell}$:
\[\frac{kQ}{2R} + \frac{kQ_{shell}}{2R} = 0 \implies \boxed{Q_{shell} = -Q}\]סעיף ד - מטען על כל מוליך לאחר חיבור
לאחר מוליך המטענים מתחלקים עד שנשארים במקום באיזון.
המצב ההתחלתי - אפס
אחרי סעיף ג (הארקה):
- הכדור הפנימי: $+Q$
- הקליפה: $-Q$ (חישבנו בסעיף ג)
סך המטען במערכת: $Q + (-Q) = 0$
כשמחברים מוליך - תנועת מטענים
כשמחברים שני מוליכים, המטענים נעים עד שהפוטנציאל שווה בשניהם.
למה הכל מתאפס?
סך המטען במערכת הוא אפס, והמערכת סימטרית (כדור בתוך קליפה עם מרכז משותף).
אם סך המטען אפס ואין כוחות חיצוניים, המטענים יתפלגו כך שהפוטנציאל אחיד בכל המערכת. הדרך היחידה לעשות זאת היא:
- מטען על הכדור: $0$
- מטען על הקליפה: $0$
(כל חלוקה אחרת תיצור הפרש פוטנציאלים בין המוליכים)
[דילגנו על תרגיל 5]
תרגיל 6: קליפות וכדורים
נתונה קליפה כדורית $B$ דקה ומוליכה, בעלת רדיוס $2R$, ובתוכה כדור מוליך $A$ בעל רדיוס $R$. הקליפה והכדור בעלי מרכז משותף. הכדור $A$ טעון במטען $+Q$ והכדור $B$ נייטרלי (אינו טעון). כדור שלישי $C$, שרדיוסו $R$ ומטענו $+3Q$ נמצא רחוק משני הראשונים. מחברים את הכדורים $B$ ו-$C$ בתיל מוליך.
מה יהיה מטענה של הקליפה הכדורית $B$, אחרי שהמערכת הגיעה למצב של שיווי משקל?
מהו פוטנציאל הכדור $A$ לאחר שהמערכת הגיעה למצב שיווי משקל?
סעיף 1 - מטען הקליפה B בשיווי משקל
נחשב!
הקליפה בהתחלה היא אולי $-Q$ כי היא מאזנת את הכדור הפנימי?
אבל הקליפה $B$ היא בסך הכל נייטרלית, אז בצד החיצוני שלה כנראה נמצא $Q$?
כשמחברים את $B$ ו $C$ הפוטנציאל שלהם צריך להיות שווה, סך המטען שמתחלק ביניהם הוא כנראה $4Q$, אז על כל חלק יש $2Q$? לא! יש כאן הבדלים ברדיוסים.
הפוטנציאל על פני כדור הוא:
\[V = \frac{kQ}{R}\]אז על פני הקליפה הגדולה:
\[V_{big} = \frac{kQ_b}{2R}\]ואילו על הקטנה:
\[V_{small} = \frac{kQ_s}{R}\]הפוטנציאלים אבל שווים, כלומר:
\[V_{small} = V_{big} \implies Q_b = 2Q_s \implies Q_s = \frac{Q_b}{2}\]סך המטען הוא שווה ל-$4Q$, אז:
\[Q_b + Q_s = Q_b + \frac{Q_b}{2} = 4Q\] \[\frac{3Q_b}{2} = 4Q \implies Q_b = \frac{8Q}{3}\]תובנה קריטית: זה לא מספיק! צריך לחבר גם את ההשפעה של הצד הפנימי של הקליפה $B$ בשביל לכל את המטן הכולל!
המטען על הקליפה $B$ כולל:
- צד פנימי: $-Q$
- צד חיצוני: $\frac{8Q}{3}$
סה”כ על $B$:
\[Q_B = -Q + \frac{8Q}{3} = \frac{-3Q + 8Q}{3} = \boxed{\frac{5Q}{3}}\]פתרון כתה - שימור מטען
בפתרון הרשמי הגיעו לתוצאה הזאת בדרך אחרת:
הפוטנציאל על B, בדומה למה שמצאנו, הוא סכום הפוטנציאלים
\[V_B = \frac{kQ_B}{2R} + \underbrace{\frac{kQ}{2R}}_{\text{from inner ball}}\]ועל הכדור החיצוני:
\[V_C=\frac{kQ_C}{R}\]מהשוויון בין הפוטנציאלים נקבל:
\[\frac{\cancel{k}Q_B}{\cancel{2R}} + \frac{\cancel{k}Q}{\cancel{2R}} = \frac{\cancel{k}Q_C}{\cancel{R}}\] \[Q_B = 2Q_C - Q\]ומשימור מטען ניתן לקבל:
\[Q_B + Q_C = 3Q \implies 2Q_c = 6Q - 2Q_B\]נציב ונקבל:
\[Q_B = 6Q - 2Q_B - Q\] \[3Q_B = 5Q \implies \boxed{Q_B = \frac{5Q}{3}}\]סעיף 2 - פוטנציאל הכדור $A$ בשיווי משקל
צריך לחשב כנראה את ההשפעה שלש לקילפה החיצונית, לפי המטען שמצאנו בסעיף הקודם.
הפוטנציאל של כדור $A$ (שנמצא ב-$r \leq R$) מורכב מסופרפוזיציה של:
-
תרומת הכדור $A$ עצמו: $\frac{kQ}{R}$
-
תרומת הקליפה $B$: הפוטנציאל בתוך קליפה הוא קבוע ושווה ל-$\frac{kQ_B}{2R}$
אז:
\[V_A = \frac{kQ}{R} + \frac{kQ_B}{2R} = \frac{kQ}{R} + \frac{k \cdot \frac{5Q}{3}}{2R} = \boxed{\frac{11kQ}{6R}}\]סיכום - נקודות חשובות
פוטנציאל vs שדה
| תכונה | שדה $\vec{E}$ | פוטנציאל $V$ |
|---|---|---|
| סוג | וקטור | סקלר |
| דעיכה ממטען נקודתי | \(\frac{1}{r^2}\) | \(\frac{1}{r}\) |
| בתוך מוליך | אפס | קבוע |
| קשר | \(\vec{E} = -\nabla V\) | \(V = -\int \vec{E} \cdot d\vec{l}\) |
מוליכים
- שדה בתוך מוליך = 0
- פוטנציאל בתוך מוליך = קבוע
- מטענים מתפלגים על פני השטח
הארקה
- מוליך מוארק: $V = 0$
- מטענים יכולים לזרום מ/אל כדור הארץ
סופרפוזיציה
- פוטנציאל כולל = סכום הפוטנציאלים מכל מטען
- עובד כי פוטנציאל הוא גודל סקלרי (פשוט לסכום!)
טיפים לפתרון
- זהה את האזורים - בתוך מוליך, בין מוליכים, מחוץ
- מצא את השדה בכל אזור (חוק גאוס)
- בצע אינטגרציה למציאת הפוטנציאל
- השתמש בתנאי שפה (הארקה, רציפות)
- בדוק סופרפוזיציה כשיש מספר גופים