סקירה על כוחות מדומים
אני רוצה להזכיר לכם שבשיעור שעבר דיברנו על כוחות מדומים - אלו אותם כוחות שמופיעים במערכת שאיננה מערכת התמד (מערכת לא אינרציאלית). כוחות אלה נובעים למעשה מהעובדה שלכל גוף בעל מסה יש התמדה, כלומר כל גוף, בגלל המסה שלו, מתנגד לשינוי מצבו הנוכחי.
למעשה, כל מסה היא מעין “מחסן” של התמדה - היא מבטאת את התמדתו של הגוף. כשהגוף נמצא בתוך מערכת מואצת, ההתמדה הזאת מייצרת כוחות מדומים בתוך המערכת המואצת. אם אנחנו רוצים להפעיל את חוקי ניוטון על מערכת מואצת, עלינו לקחת בחשבון את הכוחות המדומים הללו.
מהם הכוחות המדומים? הכוחות המדומים הם בעצם:
\[\vec{F}_{מדומה} = -m\vec{a}_{מערכת}\]כלומר, מסת הגוף כפול תאוצת המערכת, והם פועלים בכיוון המנוגד לתאוצת המערכת.
לדוגמה, כפי שהסברתי, באוטובוס שבו אדם עומד על רצפה חלקה לגמרי והאוטובוס פתאום מאיץ, מנקודת מבטו של האדם הנמצא בתוך המערכת המואצת, פועל עליו פתאום כוח הדוחף אותו לעבר החלק האחורי של האוטובוס.
הכוח הזה הוא “כוח רפאים” - כוח שכביכול הגיע משום מקום. מנקודת ראותו של האדם במערכת המואצת, זהו כוח שלכאורה אין לו שום מקור. ומהו המקור האמיתי? מנקודת מבט של מערכת התמד (מערכת אינרציאלית), המקור הוא התמדת המסה - התמדת הגוף. המערכת שבה הוא נמצא מואצת ו”בורחת” מתחת לרגליו, ולכן נראה כאילו פועל עליו כוח שדוחף אותו לעבר הקיר האחורי.
הבחנה בין מערכות התמד ומערכות לא-התמד
אני רוצה לחזור לנקודה מאוד חשובה ומרכזית שהשארתי קצת פתוחה: איך נדע להבדיל בין מערכת התמד אמיתית לבין מערכת שאיננה מערכת התמד?
בתחילה הגדרנו מערכת התמד כמערכת הנמצאת במהירות קבועה ביחס לאיזושהי מציאות אבסולוטית. אבל האמת היא שבטבע אין מציאות אבסולוטית כזו.
הראשון שהבין זאת היטב היה גלילאו גליליי, אך הוא ניסח זאת באופן מתמטי לא נכון. כל מי שבא אחריו, עד איינשטיין, הלך בעקבות הטעות של גליליי וניסח באופן לא נכון את העובדה שאין מערכת התמד אבסולוטית. בגלל ניסוח שגוי זה, כולם אימצו את טרנספורמציות גליליי, והדבר הוביל לשגיאה בסיסית מאוד בהבנת המציאות.
איינשטיין היה הראשון שהבין שיש כאן בעיה, וניסח נכון את העובדה שאין מערכת אבסולוטית שביחס אליה אפשר לומר שמערכת נמצאת במהירות קצובה, פשוט מפני שאיננו יכולים להבחין במערכת אבסולוטית כזו.
אם כך, איך בכל זאת נדע מהי מערכת התמד ומהי מערכת שאיננה מערכת התמד?
התשובה פשוטה ביותר: עלינו להניח במערכת שלנו מכשיר המודד כוחות מדומים. אם במערכת שלנו נמדדים כוחות מדומים - המערכת שלנו איננה מערכת התמד. אם במערכת שלנו לא נמדדים כוחות מדומים - המערכת שלנו היא מערכת התמד.
כלומר, הקריטריון להבחנה בין מערכת התמד למערכת שאיננה מערכת התמד הוא קיומם של כוחות מדומים.
מטוטלת כמד תאוצה (אקסלרומטר)
כיצד נוכל להבחין בכוחות מדומים? לדוגמה, כפי שסיפרתי, אדם היושב באוטובוס ופתאום מרגיש שכוח לא מוסבר מצמיד אותו למשענת המושב האחורי - אותו נוסע למעשה “מודד” כוחות מדומים, והוא הופך להיות באותו רגע למעין מד כוחות מדומים.
דוגמה נוספת: נניח שאנחנו נמצאים בקרון של רכבת הנעה במהירות קצובה. אם נתלה מטוטלת מתקרת הרכבת, וכל עוד הרכבת נעה במהירות קצובה (כלומר, היא מערכת התמד), החוט יישאר אנכי והמשקולת תהיה תלויה בדיוק מתחתיו.
אולם אם הרכבת פתאום מאיצה (למשל לכיוון ימין), המשקולת תתפוס זווית מסוימת - החוט המחזיק את המשקולת ייטה בזווית ביחס לאנך. מדוע זה קורה? כי למשקולת יש התמדה. הרכבת מאיצה לכיוון ימין, אך ההתמדה של המשקולת, מנקודת מבט של מערכת התמד, שואפת להשאיר אותה במקום.
כתוצאה מכך, המשקולת כאילו “נשארת מאחור” כשהרכבת מאיצה קדימה, וזה יוצר זווית בין האנך לבין החוט המחזיק את המשקולת.
כלומר, יש לנו פתאום קריטריון או מכשיר שמודד תאוצה - מד תאוצה. המשקולת התלויה על חוט היא סוג של מד תאוצה (אקסלרומטר). כל עוד החוט אנכי, התאוצה היא אפס. ברגע שהחוט נוטה בזווית, התאוצה שונה מאפס.
באמצעות מדידת הזווית נוכל לדעת במדויק מהי תאוצת הרכבת. כאשר החוט יוצר זווית, אנו יודעים שהמערכת איננה מערכת התמד.
ניתוח מתמטי של דוגמת המטוטלת
בואו ננתח את דוגמת המטוטלת ברכבת באופן מתמטי. נניח שהמטוטלת (המשקולת) תלויה בזווית $\theta$ ביחס לאנך.
אני יכול להסתכל על המערכת בשתי דרכים:
מנקודת מבט של מערכת התמד (מחוץ לרכבת)
מחוץ לרכבת, אני רואה שעל המשקולת פועלים שני כוחות:
- כוח הכובד $mg$ כלפי מטה
- מתיחות החוט $T$
אני מפרק את הבעיה לשני צירים:
- ציר $Y$ (אנכי)
- ציר $X$ (אופקי)
בציר $Y$, המשקולת נמצאת במנוחה, לכן:
\[T \cos \theta = mg\]זה מחוק ראשון של ניוטון (תנאי התמדה).
בציר $X$, המשקולת מאיצה יחד עם הרכבת, לכן:
\[T \sin \theta = ma\]זה מחוק שני של ניוטון.
אם נחלק את המשוואה השנייה במשוואה הראשונה, נקבל:
\[\frac{T \sin \theta}{T \cos \theta} = \frac{ma}{mg}\]ומכאן:
\[\tan \theta = \frac{a}{g}\]כלומר:
\[a = g \tan \theta\]זוהי נוסחה המבטאת את תאוצת המערכת כפונקציה של זווית הנטייה של החוט.
מנקודת מבט של מערכת מואצת (בתוך הרכבת)
כאשר אני יושב בתוך הרכבת, אני רואה את המשקולת במצב סטטי - היא תלויה בזווית קבועה. מנקודת מבטי, המשקולת לא זזה, ולכן אני מבין שיש כאן “כוח רפאים” שמחזיק אותה בזווית.
אם מצבה הרגיל של המשקולת היה אמור להיות אנכי, והיא נמצאת כעת בזווית, אני מבין שיש תאוצה במערכת שלי. הכוח הרלוונטי הוא כוח מדומה:
\[F_{מדומה} = -ma_{מערכת}\]שהוא מסת המשקולת כפול תאוצת המערכת (בכיוון ההפוך).
בתנאי שיווי משקל (מצב סטטי בתוך הרכבת):
\[T \sin \theta - ma = 0\]זהו החוק הראשון של ניוטון המתוקן בתוך מערכת מואצת.
שתי נקודות המבט הללו אקוויוולנטיות: האחת מוחלטת יותר (מערכת התמד, שבה חל החוק השני), והשנייה יחסית (מערכת מואצת, שבה אני מיישם את החוק הראשון אך חייב להוסיף את הכוחות המדומים).
כוחות על מישור משופע
אני רוצה להזכיר לכם שכאשר בחנו גוף על מישור משופע בזווית $\alpha$, הראינו שאפשר לפרק את הבעיה לשני צירים קרטזיים:
- ציר אחד בכיוון התנועה (במורד המישור)
- ציר שני ניצב לתנועה
תמיד רצוי לפרק את הבעיה לצירים המכבדים את הסימטריה של הבעיה, כי זה מקל על הפתרון.
במקרה זה, הכוחות הפועלים על המסה הם:
- כוח הכובד $mg$ (כלפי מטה)
- הכוח הנורמלי $N$ מהמישור המשופע
כאשר מפרקים את כוח הכובד לרכיביו, מקבלים:
- במורד המישור: $mg \sin \alpha$
- ניצב למישור: $mg \cos \alpha$
המשוואות הן:
- בציר במורד המישור: $mg \sin \alpha = ma$ (חוק שני של ניוטון)
- בציר הניצב למישור: $N = mg \cos \alpha$ (מצב סטטי)
מכאן מקבלים שהתאוצה היא:
\[a = g \sin \alpha\]ניתן לראות שכאשר $\alpha = 0$ (מישור אופקי), $\sin 0 = 0$ ולכן $a = 0$. כאשר $\alpha = 90°$ (נפילה חופשית), $\sin 90° = 1$ ולכן $a = g$.
חיכוך ותכונותיו
במקרים רבים, במערכת שלנו יש חיכוך. מה שמאפיין את כוח החיכוך, וזוהי עובדה אמפירית, הוא שכוח החיכוך תמיד פרופורציונלי (מתכונתי) לכוח הנורמלי:
\[F = \mu N\]כאשר $\mu$ הוא מקדם החיכוך.
כמובן שכוח החיכוך הוא כוח אפקטיבי, לא כוח יסודי. הכוחות האמיתיים הם הכוחות האלקטרומגנטיים הפועלים בין המולקולות של שני המשטחים, אבל ממרחק זה נראה כמו כוח חיכוך.
חשוב לציין שהמשוואה $F = \mu N$ אינה משוואה וקטורית. כוח החיכוך אמנם פרופורציונלי בגודלו לכוח הנורמלי, אבל בכיוונו הוא תמיד מנוגד לכיוון התנועה או לכיוון שבו הגוף נוטה לנוע. לכן, אם גוף נוטה לנוע במורד מישור משופע, כוח החיכוך יפעל במעלה המישור - בכיוון הפוך לכוח $mg \sin \alpha$ ולא בכיוון הכוח הנורמלי.
יש להבחין בין שני סוגי חיכוך:
- חיכוך קינטי ($F_k$) - כאשר הגוף בתנועה
- חיכוך סטטי ($F_s$) - כאשר הגוף במנוחה
לכל אחד מהם מקדם חיכוך משלו:
- $\mu_k$ - מקדם חיכוך קינטי
- $\mu_s$ - מקדם חיכוך סטטי
ותמיד מתקיים:
\[F_k \leq F_s\] \[\mu_k \leq \mu_s\]כלומר, כוח החיכוך הקינטי תמיד קטן יותר או לכל היותר שווה לכוח החיכוך הסטטי.
נניח שגוף מחליק במורד מישור משופע עם חיכוך. המשוואות הרלוונטיות הן:
בציר במורד המישור: \(mg \sin \alpha - F_k = ma\)
בציר הניצב למישור: \(N = mg \cos \alpha\)
מכיוון ש-$F_k = \mu_k N = \mu_k mg \cos \alpha$, נקבל:
\[mg \sin \alpha - \mu_k mg \cos \alpha = ma\]ולכן:
\[a = g(\sin \alpha - \mu_k \cos \alpha)\]כאשר $\mu_k = 0$ (אין חיכוך), חוזרים לנוסחה $a = g \sin \alpha$.
מקדם החיכוך $\mu$ בדרך כלל נע בין 0 ל-1. כאשר $\mu = 0$, אין חיכוך.
אגב, המשוואה $F = \mu N$ אינה נכונה וקטורית אבל היא כן נכונה טנזורית. אם נתייחס ל-$\mu$ כטנזור (מעין הכללה של מטריצה), אפשר לכתוב:
\[\vec{F} = \overleftrightarrow{\mu} \cdot \vec{N}\]כאשר טנזור כפול וקטור אכן נותן וקטור.
כוחות מדומים וחיכוך יחד
בשיעור שעבר פתרנו בעיה במערכת מואצת ללא חיכוך. באותה צורה אפשר לפתור גם בעיה שבה יש גם תאוצה וגם חיכוך. במקרה כזה, נוסיף לכוחות הפועלים על הגוף גם את כוח החיכוך $F_k$.
בבעיה כזו יופיעו גם כוחות מדומים וגם כוח חיכוך. עליכם להיות מסוגלים להכניס את כוח החיכוך בצורה נכונה ולפתור את הבעיה של המערכת המואצת.
יחסי כוחות במערכת הטריז המואץ
כמובן שהמסה הקטנה יושבת על המסה הגדולה, ולכן מפעילה על המסה הגדולה כוח נורמלי בכיוון ניצב למשטח המגע. כוח נורמלי זה מאיץ את המסה הגדולה ימינה, ומכאן שהמסה הקטנה יושבת למעשה בתוך “קרון רכבת” שמאיץ ימינה. כתוצאה מכך, פועלים על המסה הקטנה כוחות מדומים.
חשוב להבהיר - המסה הגדולה אינה יושבת על המסה הקטנה. המסה הגדולה מונחת על המשטח האופקי. לפי החוק השלישי של ניוטון, אם המסה הקטנה דוחפת את המסה הגדולה בכוח $N$ בכיוון מסוים, אז המסה הגדולה דוחפת את המסה הקטנה בכוח $N$ בכיוון ההפוך.
ניתן לשאול שאלה מעניינת: מה צריכה להיות התאוצה $a_M$ של המסה הגדולה כדי שהמסה הקטנה תתנתק ממנה? כדי לענות על שאלה זו, עלינו למצוא באיזו תאוצה הכוח הנורמלי מתאפס. ברגע שהכוח הנורמלי מתאפס, המסה הקטנה ניתקת מהמסה הגדולה.
החוק השלישי של ניוטון
אני רוצה להדגיש נקודה חשובה לגבי החוק השלישי של ניוטון. כאשר המסה הגדולה $M$ מפעילה על המסה הקטנה $m$ כוח נורמלי בכיוון מסוים, החוק השלישי קובע שהמסה הקטנה מפעילה על המסה הגדולה כוח נורמלי שווה בגודלו ומנוגד בכיוונו:
\[N_{M \to m} = -N_{m \to M}\]חשוב להבחין בין החוק השלישי לחוק הראשון של ניוטון:
- בחוק הראשון מדובר על אוסף כוחות הפועלים על אותו גוף, כאשר שקול הכוחות מתאפס
- בחוק השלישי מדובר על שני כוחות שונים הפועלים על שני גופים שונים, כאשר הכוחות שווים בגודלם ומנוגדים בכיוונם
להמחשה, כשאני עומד על הרצפה, פועלים עליי שני כוחות: כוח הכבידה $mg$ כלפי מטה והכוח הנורמלי $N$ שהרצפה מפעילה עליי כלפי מעלה. לפי החוק הראשון, הכוחות הללו שווים בגודלם: $N = mg$.
לפי החוק השלישי, אם הרצפה מפעילה עליי כוח נורמלי כלפי מעלה, הרי שאני מפעיל על הרצפה כוח נורמלי כלפי מטה באותו גודל.
דוגמה נוספת: כאשר אני נופל בנפילה חופשית, כדור הארץ מושך אותי בכוח $mg$ כלפי מטה. באותה עת, לפי החוק השלישי, אני מושך את כדור הארץ בכוח $mg$ כלפי מעלה. הסיבה שכדור הארץ כמעט לא מואץ כלפי מעלה היא שמסתו אדירה בהשוואה למסה שלי:
\[a_{\text{כדור הארץ}} = \frac{mg}{M_{\text{כדור הארץ}}} \approx 10^{-21} \text{ מ'/שנייה}^2\]כלומר, התאוצה של כדור הארץ כלפיי היא מזערית ביותר - כ-$10^{-21}$ מטר לשנייה בריבוע, שזה פחות ממיליונית של מיליונית של מיליונית של מטר לשנייה בריבוע.
מעבר ממשוואות אלגבריות למשוואות דיפרנציאליות
עד כה, עסקנו בבעיות פיזיקליות פשוטות יחסית, שבהן בנינו תרשים כוחות, זיהינו את הצירים השונים, הפעלנו את החוק הראשון או השני של ניוטון (בהתאם לצורך), והגענו למשוואות אלגבריות פשוטות.
אולם בחיים האמיתיים, הבעיות מורכבות יותר. במערכות פיזיקליות רבות יש משוב (איזונים חוזרים), ובמקרים כאלה החוק השני של ניוטון מתרגם למשוואה דיפרנציאלית ולא למשוואה אלגברית.
משוואות דיפרנציאליות מופיעות בכל תחומי המדע, ובפרט בביולוגיה, משום שכמעט כל התהליכים הביולוגיים כוללים משוב, ולכן ניתן למדל אותם באמצעות משוואות דיפרנציאליות.
דוגמה: בעיית הצנחן וכוחות גרר
הבעיה הראשונה שנבחן, שחורגת מעבר לבעיות אלגבריות פשוטות, היא בעיית הצנחן.
כאשר גוף נופל בנפילה חופשית, הכוח היחיד שפועל עליו הוא כוח הכבידה, והתאוצה היא קבועה ושווה ל-$g$ (בקירוב 10 מטר לשנייה בריבוע). אולם בחיים האמיתיים, יש גם התנגדות אוויר.
כוח הגרר (התנגדות האוויר) גדל ככל שהמהירות גדלה. את כוח הגרר ניתן לייצג בצורות שונות:
-
כוח גרר פרופורציונלי למהירות:
\[F_{\text{גרר}} = \beta v\] -
כוח גרר פרופורציונלי לריבוע המהירות:
\[F_{\text{גרר}} = \beta v^2 \frac{\vec{v}}{|\vec{v}|}\] -
בחלק מהמקרים, כוח הגרר עשוי להיות פרופורציונלי לחזקות גבוהות יותר של המהירות
מהו כוח הגרר? זהו הכוח שבו האוויר (או כל תווך אחר, כגון מים) מתנגד לתנועת הגוף. בשונה מכוח חיכוך, כוח הגרר:
- פועל על כל שטח הפנים של הגוף ולא רק על משטח המגע
- מדובר באינטראקציה בין גוף מוצק לבין גז או נוזל (בשונה מחיכוך בין שני מוצקים)
- התווך (האוויר או המים) יכול להתעוות כתוצאה מהתנועה, בשונה ממשטחים קשיחים
ניתוח בעיית הצנחן
נניח שצנחן נופל ופועלים עליו שני כוחות:
- כוח הכבידה $mg$ כלפי מטה
- כוח הגרר $\beta v$ כלפי מעלה (מנוגד לכיוון התנועה)
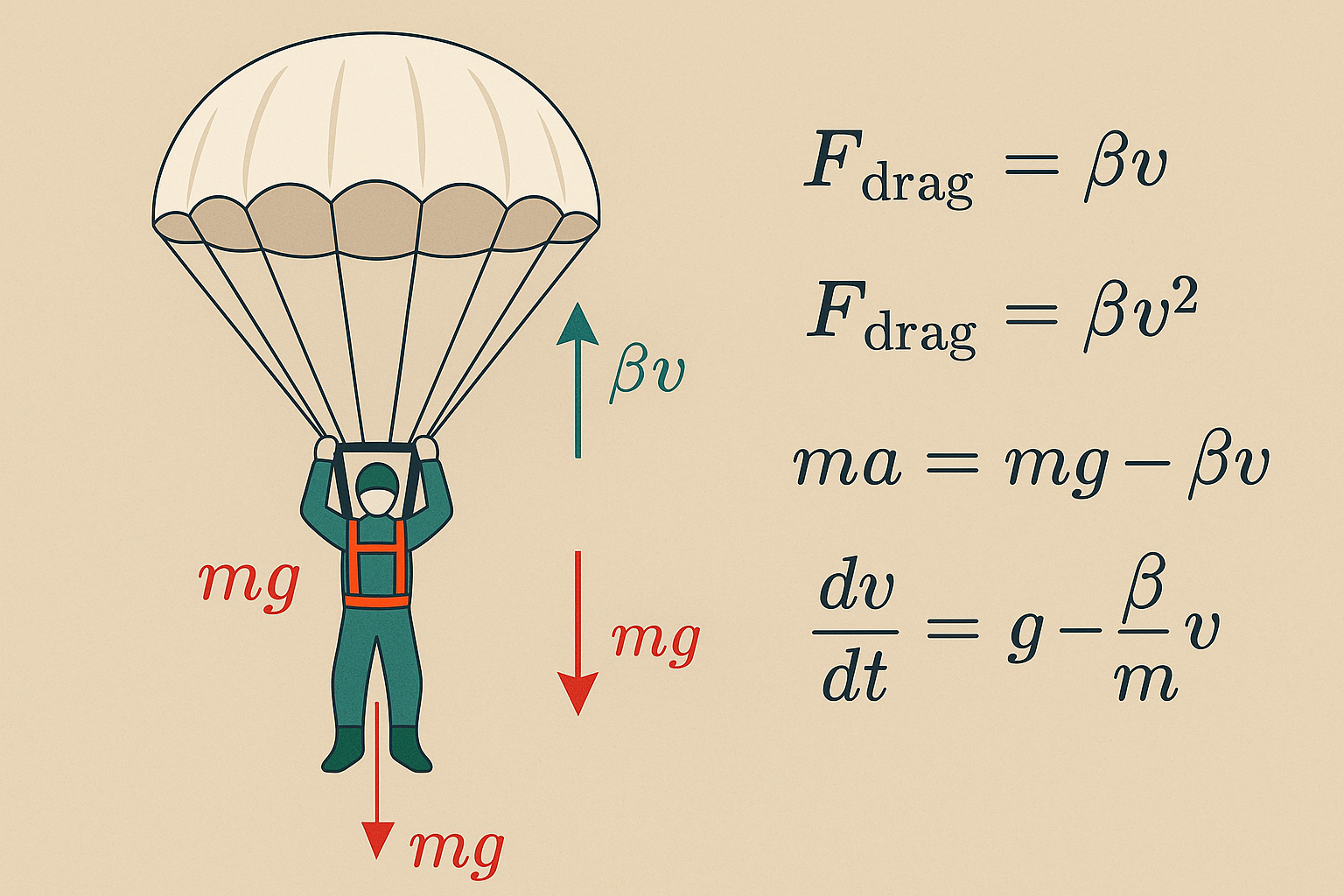
מהחוק השני של ניוטון:
\[ma = mg - \beta v\]כאשר התאוצה היא למעשה הנגזרת של המהירות לפי הזמן:
\[m\frac{dv}{dt} = mg - \beta v\]נחלק את שני האגפים ב-$m$:
\[\frac{dv}{dt} = g - \frac{\beta}{m}v\]זוהי משוואה דיפרנציאלית מסדר ראשון במהירות (ומסדר שני במיקום). נפתור אותה באמצעות הפרדת משתנים.
מהירות טרמינלית
כאשר גוף נופל באוויר, מהירותו גדלה בהדרגה, ובהתאם גדל גם כוח הגרר. בסופו של דבר, כוח הגרר משתווה לכוח הכובד, ובנקודה זו מתאפסת התאוצה והגוף ממשיך ליפול במהירות קבועה. מהירות זו נקראת המהירות הטרמינלית.
המהירות הטרמינלית מקיימת את התנאי:
\[\beta v_{\text{terminal}} = mg\]ומכאן:
\[v_{\text{terminal}} = \frac{mg}{\beta}\]זוהי המהירות המקסימלית שהגוף יכול להגיע אליה. ברגע שמגיעים למהירות זו, שקול הכוחות מתאפס, התאוצה מתאפסת, והגוף ממשיך לנוע במהירות קבועה.
היחידות של $\beta$ הן יחידות של כוח חלקי מהירות, כלומר:
\[[\beta] = \frac{[\text{ניוטון}]}{[\text{מטר/שנייה}]} = \frac{\text{קילוגרם} \cdot \text{מטר}/\text{שנייה}^2}{\text{מטר}/\text{שנייה}} = \frac{\text{קילוגרם}}{\text{שנייה}}\]פתרון המשוואה הדיפרנציאלית
כדי לפתור את המשוואה הדיפרנציאלית:
\[\frac{dv}{dt} = g - \frac{\beta}{m}v\]נשתמש בשיטת הפרדת משתנים. נכפיל את שני האגפים ב-$dt$ ונסדר מחדש:
\[\frac{dv}{g - \frac{\beta}{m}v} = dt\]כעת נוכל להמשיך בפתרון באמצעות אינטגרציה של שני הצדדים.
פתרון משוואה דיפרנציאלית באמצעות הפרדת משתנים
בשיעור הקודם הגענו למשוואה הדיפרנציאלית המתארת את תנועת הצנחן:
\[\frac{dv}{dt} = g - \frac{\beta}{m}v\]כדי לפתור משוואה זו, נשתמש בשיטת הפרדת משתנים. ראשית, נארגן מחדש את המשוואה כך שכל האיברים המכילים $v$ יהיו בצד אחד וכל האיברים המכילים $t$ יהיו בצד השני:
\[\frac{dv}{g - \frac{\beta}{m}v} = dt\]כעת נוכל לאינטגרל את שני צדי המשוואה. באגף ימין, האינטגרל של $dt$ הוא פשוט $t + C$, כאשר $C$ הוא קבוע האינטגרציה.
באגף שמאל, עלינו לחשב:
\[\int \frac{dv}{g - \frac{\beta}{m}v}\]| זהו אינטגרל מהצורה $\int \frac{du}{a - bu}$, שהפתרון שלו הוא $-\frac{1}{b} \ln | a - bu | + C$. |
במקרה שלנו, $a = g$, $b = \frac{\beta}{m}$, ולכן:
\[\int \frac{dv}{g - \frac{\beta}{m}v} = -\frac{m}{\beta} \ln \left|g - \frac{\beta}{m}v \right| + C_1\]נוכל גם להגיע לתוצאה זו באמצעות החלפת משתנים. נגדיר $Y = g - \frac{\beta}{m}v$. כדי לקשר בין $dv$ ל-$dY$, נגזור את $Y$ לפי $v$:
\[\frac{dY}{dv} = -\frac{\beta}{m}\]ולכן:
\[dY = -\frac{\beta}{m}dv\]או:
\[dv = -\frac{m}{\beta}dY\]כעת האינטגרל שלנו הופך ל:
\[\int \frac{dv}{g - \frac{\beta}{m}v} = \int \frac{-\frac{m}{\beta}dY}{Y} = -\frac{m}{\beta}\int \frac{dY}{Y} = -\frac{m}{\beta}\ln|Y| + C_1\]כלומר:
\[-\frac{m}{\beta}\ln \left|g - \frac{\beta}{m}v \right| = t + C\]כאשר $C = C_2 - C_1$ הוא קבוע האינטגרציה המשולב.
פתרון עבור המהירות כפונקציה של הזמן
נארגן את המשוואה כדי לבודד את $v$:
\[\ln \left|g - \frac{\beta}{m}v \right| = -\frac{\beta}{m}t - \frac{\beta C}{m}\]נגדיר $C’ = -\frac{\beta C}{m}$ ונקבל:
\[\ln \left|g - \frac{\beta}{m}v \right| = -\frac{\beta}{m}t + C'\]כעת נעביר לצורה אקספוננציאלית:
\[g - \frac{\beta}{m}v = e^{-\frac{\beta}{m}t + C'} = e^{C'} \cdot e^{-\frac{\beta}{m}t}\]נגדיר $A = e^{C’}$ ונקבל:
\[g - \frac{\beta}{m}v = A \cdot e^{-\frac{\beta}{m}t}\]כעת נבודד את $v$:
\[-\frac{\beta}{m}v = A \cdot e^{-\frac{\beta}{m}t} - g\] \[v = \frac{m}{\beta} \left( g - A \cdot e^{-\frac{\beta}{m}t} \right) = \frac{mg}{\beta} - \frac{m}{\beta} A \cdot e^{-\frac{\beta}{m}t}\]נגדיר $B = \frac{m}{\beta}A$ ונקבל:
\[v(t) = \frac{mg}{\beta} - B \cdot e^{-\frac{\beta}{m}t}\]קביעת קבוע האינטגרציה באמצעות תנאי התחלה
עד כה, $B$ הוא קבוע אינטגרציה שטרם נקבע. כדי לקבוע אותו, נשתמש בתנאי ההתחלה. אם בזמן $t = 0$ המהירות היא $v_0$, אז:
\[v_0 = \frac{mg}{\beta} - B \cdot e^{-\frac{\beta}{m} \cdot 0} = \frac{mg}{\beta} - B\]מכאן נקבל:
\[B = \frac{mg}{\beta} - v_0\]ולכן הפתרון המלא הוא:
\[v(t) = \frac{mg}{\beta} - \left(\frac{mg}{\beta} - v_0 \right) e^{-\frac{\beta}{m}t}\]ניתן לרשום זאת בצורה קומפקטית יותר, במיוחד עבור המקרה שבו $v_0 = 0$ (התחלה ממנוחה):
\[v(t) = \frac{mg}{\beta} \left(1 - e^{-\frac{\beta}{m}t} \right)\]המשמעות הפיזיקלית של הפתרון
הפתרון שקיבלנו מראה כי:
-
המהירות הטרמינלית: כאשר $t \to \infty$, הביטוי $e^{-\frac{\beta}{m}t} \to 0$, ולכן המהירות מתקרבת לערך $\frac{mg}{\beta}$. זוהי המהירות הטרמינלית - המהירות שבה כוח הגרר משתווה לכוח הכובד.
-
התנהגות התחלתית: בזמן $t = 0$, המהירות היא $v_0$ כפי שנדרש מתנאי ההתחלה.
-
קצב ההתקרבות למהירות הטרמינלית: הביטוי $e^{-\frac{\beta}{m}t}$ דועך במהירות, במיוחד כאשר היחס $\frac{\beta}{m}$ גדול. כלומר, גופים קלים עם מקדם גרר גדול יגיעו למהירות הטרמינלית שלהם מהר יותר.
חשוב לציין כי פתרון זה תקף רק עבור מודל שבו כוח הגרר פרופורציונלי למהירות. במציאות, במהירויות גבוהות, כוח הגרר עשוי להיות פרופורציונלי לריבוע המהירות או אף לחזקות גבוהות יותר.
בשיעור הבא, נמשיך לחשב את המיקום $x(t)$ על ידי אינטגרציה של $v(t)$ לפי הזמן:
\[x(t) = \int v(t) dt\]זהו פתרון מלא של בעיית הצנחן, המראה כיצד החוק השני של ניוטון מוביל למשוואה דיפרנציאלית שפתרונה מתאר את התנועה האמיתית בנוכחות התנגדות אוויר.
מערכות התמד
דיברנו על הכוחות המדומים
הכוחות המדוימים הם המסה כפול תאוצה המערכת פועלים בכיוון ההפוך.
לדוגמה אוטובוס שמאיץ - מנקודת מבטו פועל עליו כוח שדוחף אותו לחלק החורי של האוטובוס. זה כוח רפאים מנקודת המבט של מי שנמצא במערכת המאיצה.
מנקודת מבט של מערכת התמד - המקור הוא האצת הגוף.
איך נדע להבדיל בין מערכת התמד אמיתית, לבין מערכת שהיא לא מערכת התמד?
גלילאי אימץ לא נכון, שגיאה בטרנפורמציית גלילאי. איינשטיין היה הראשון שהבין את הטעות - אנחנו לא יכולים להבחין במערכת אבסולוטית
אם במערכת שלנו מאובחנים כוחות מדומים - אז המערכת לא מערכת התמד. אם לא מאובחנים כוחות מדומים - אז המערכת היא מערכת התמד.
כלומר הקריטריון להכריע האם מדובר במערכת התמד היא קיומם של כוחות מדומים. איך מודדים? למשל הנוסע באוטובוס.
למשל רכבת שתלוי בה חוט. הרכבת מאיצה, פתאום תהיה זווית. החוט עם המשקולת הוא למעשה מד תאוצה, כאשר מייצר זווית אנחנו יודעים שהמערכת אינה מערכת התמד.
נניח בדוגמה הרכבת:
יש לי את $mg$ הכוח מטה ויש לי בחוט מהמשקולת לתקרה את הכוח $T$.
נקרא לזווית שבין המצב האנכי לבין המצב המואץ $\theta$.
מהחוק הראשון, כלומר מתנאי ההתמדה, בציר $y$:
\[T \cdot \cos(\theta) - mg = 0\]בציר $x$:
ההיטל של הכוח $T$ על ציר $x$ שווה ל-$ma$. וזה מחוק שני בציר $x$:
\[T \cdot \sin(\theta) = ma\]כלומר בציר $y$ מימשנו את החוק הראשון, ובציר $x$ מימשנו את החוק השני.
הכוח המדומה הוא מסת המשקולת כפול תאוצת המערכת ומקיים את הקשר:
\[T \cdot \sin(\theta) = m \cdot a\]וזה מהחוק הראשון בתוך המערכת המאיצה.
דוגמה עם משולש.
-להשלים-
אפשר לפרק את הבעיה לשני המרכיבים שלה: הרכיב הרכיב הניצב
מהחוק השני ב $\hat{x}$:
\[mg \cdot \sin(\theta) = m \cdot a\]מהחוק השני ב $\hat{y}$:
\[mg \cdot \cos(\theta) = N\]התאוצה היא 0, ב $\theta$…
יש לנו ביטוי עבור הכוח הנורמלי $N$:
\[N = mg \cdot \cos(\theta)\]חיכוך
עובדה אימפירית:
\[f=\mu \cdot N\]…
כשהגוף נמצא בתנועה יש לי מקדם חיכוך אחד, וכשהגוף בתנועה אחר:
\[\begin{cases} \mu_s \text{ - סטטי} \\ \mu_k \text{ - קינטי} \end{cases}\]בכל מקרה מתקיים
\[\mu_k \leq \mu_s\]בציר $x$:
\[f_{friction} = \mu_k \cdot N\]בציר $y$:
\[N = mg \cdot \cos(\theta)\]
החוק השלישי
לעומת החוק הראשון (משהו מתאפס) בחוק השלישי שני כוחות שונים פועלים על מסות שונות.
נניח שנסמן את הכוח כלפי מעלה ב $\vec{N}_{n \to m}$, כלומר הכוח של גוף $n$ על גוף $m$.
נניח שנסמן את הכוח כלפי מטה ב $\vec{N}_{m \to n}$, כלומר הכוח של גוף $m$ על גוף $n$.
לפי החוק הראשון הכוח שהרצפה מפעילה עלי שווה לכוח שאני מפעיל על הרצפה. לפי החוק השלישי הכוח שהרצפה מפעילה עלי שווה בכיוונו ובגודלו לכוח שאני מפעיל על הרצפה.
חוק ראשון - שקול כוחות ומשוואה
חוק שני …
בעיית הצנחן
בחיים האמיתיים התאוצה אינה גודלת קבוע, וגם יש אטמוספירה והתנגדות של אוויר.
המרצה מכנה את כוח ההתנגדות של האוויר ״כוח גרר״.
\[\vec{F}= -\beta \cdot \vec{v}\]אפשר לחשוב על $\beta$ כמקדם חיכוך.
בזה נטל (יש גם גרסה עם החוק השני כאשר $\vec{F} = -\beta v^2 \hat{v}$).
מתכונתי לריבוע המהירות.
נציג את בעיית הצנחן. יש מימד אחד. המהירות הולכת וגדולה. קיימת מהירות שבה כוח הגרר שווה לכוח המשיכה - זו המהירות האסימפטוית שאליה אני מגיע. ברגע שהוכחות משתווים אני מגיע למהירות קבוע שנקראת מהירות טרמינלית שמקיימת את הקשר:
\[\beta \cdot v_t = mg\]או
\[v_t = \frac{mg}{\beta}\]
זו למעשה המהירות המקסימלית. שקול הכוחות שווה אפס (כלומר שאני מפסיק להאיץ) וממשיך במהירות קבועה.
כוח הגדד נשאקר קבוע בנקודה הזאת.
היחידות של בטא יהיו שוות ליחידות של $mg$ שזה כוח כפול תאוצה.
התנאי למהירות טרמינלית הוא כאשר כוח הגרר משתווה ל $mg$.
משוואה דפרנציאלית לפי החוק השני
\[ma = mg - \beta v\]זו משוואה דיפנציאלית מסדר ראשון. נוכל לפתור אותה בעזאת הפרדת משתנים:
\[\frac{dv}{dt} = g - \frac{\beta}{m} v\]המהירות תלויה בזמן. פרמטרים בבעייה:
- $g$ - תאוצת הכובד
- $\beta$ - קבוע גרר
- $m$ - מסה
נחלק את הכל ונפריד:
\[\frac{dv}{g - \frac{\beta}{m} v} = dt\]מצד שמאל $y$ מצד ימין $t+c$
אינטגרל על שני הצדדים:
\[\int \frac{dv}{g - \frac{\beta}{m} v} = \int dt\] \[g-\frac{\beta}{m} v = y\] \[d\left(g-\frac{\beta}{m} v\right) = dy\] \[-\frac{\beta}{m} dv = dy\] \[dv=-\frac{m}{\beta} dy\]…
\[-\frac{m}{\beta} \lim\left(g - \frac{\beta}{m} v\right) = t + c\] \[\lim(g - \frac{\beta}{m} v) = -\frac{\beta t}{m} + c'\] \[g - \frac{\beta}{m} v = e^{\frac{-\beta t}{m}} + c' = e^{c'} e^{\frac{-\beta t}{m}} = c'' e^{\frac{-\beta t}{m}}\] דור פסקלחזרה לעמוד הראשי
חזור לשיעור 5