מדובר בהמשך לדף הנוסחאות הראשון - הפעם עם דגש על חשמל ומגנטיות (אלקטרוסטטיקה, מגנטוסטטיקה, אינדוקציה, חוק אמפר, חוק גאוס, משוואות מקסוול ועוד). דף זה כולל גם טיפים לפתרון מהיר ושגיאות נפוצות.
תוכן עניינים:
- חלק א׳: אלקטרוסטטיקה
- חלק ב׳: מגנטיות
- חלק ג׳: אינדוקציה וכא”מ
- חלק ד׳: חוק אוהם ומעגלים
- חלק ה׳: משוואות מקסוול וגלים
- חלק ו׳: כלים מתמטיים
- חלק ז׳: יחידות וקבועים
- חלק ח׳: טיפים ושגיאות נפוצות
חלק א׳: אלקטרוסטטיקה
1. צפיפויות מטען
| סוג | סימון | יחידות | dq |
|---|---|---|---|
| קווית (חוט/מוט) | $\lambda$ | $\text{C/m}$ | $dq = \lambda\,dl$ |
| משטחית (לוח/קליפה) | $\sigma$ | $\text{C/m}^2$ | $dq = \sigma\,dA$ |
| נפחית (כדור/גליל) | $\rho$ | $\text{C/m}^3$ | $dq = \rho\,dV$ |
מטען כולל מאינטגרציה
\[Q = \int \rho\,dV = \int \sigma\,dA = \int \lambda\,dl\]דוגמה - כדור אחיד
\[Q = \rho \cdot \frac{4}{3}\pi R^3 \implies \rho = \frac{3Q}{4\pi R^3}\]דוגמה - כדור עם חלל פנימי ($R_1 < r < R_2$)
\[\rho = \frac{3Q}{4\pi(R_2^3 - R_1^3)}\]2. חוק קולון
כוח בין שני מטענים
\[\vec{F} = \frac{Kq_1 q_2}{r^2}\hat{r}\]כאשר $K = \frac{1}{4\pi\varepsilon_0} = 8.99 \times 10^9\,\text{N·m}^2/\text{C}^2$
שדה חשמלי ממטען נקודתי
\[\vec{E} = \frac{KQ}{r^2}\hat{r}\]פוטנציאל ממטען נקודתי
\[V = \frac{KQ}{r}\]אנרגיה פוטנציאלית
\[U = \frac{Kq_1 q_2}{r} = q_1 V_2 = q_2 V_1\]3. עקרון הסופרפוזיציה
שדה
\[\vec{E}_{tot} = \sum_i \vec{E}_i = \sum_i \frac{Kq_i}{r_i^2}\hat{r}_i\]פוטנציאל (סקלר - קל יותר!)
\[V_{tot} = \sum_i V_i = \sum_i \frac{Kq_i}{r_i}\]הבדל חשוב: שדה מול פוטנציאל
| מצב | שדה $\vec{E}$ | פוטנציאל $V$ |
|---|---|---|
| שני מטענים שווים $+q,+q$ (באמצע) | $\vec{E} = 0$ (מתקזזים) | $V = \frac{2Kq}{a} \ne 0$ |
| דיפול $+q,-q$ (באמצע) | $\vec{E} \ne 0$ (מתחברים) | $V = 0$ (מתקזזים) |
טריק המשושה
6 מטענים זהים בקודקודי משושה ← שדה אפס במרכז (סימטריה). 5 מטענים (חסר אחד) ← השדה כאילו יש מטען $+Q$ יחיד בקודקוד החסר:
\[E = \frac{KQ}{a^2}\]4. חוק גאוס - חשמלי
הנוסחה
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\varepsilon_0}\]מתי מתאים? רק עם סימטריה מתאימה
| סימטריה | משטח גאוס | $A$ |
|---|---|---|
| כדורית (מטען/כדור) | כדור | $4\pi r^2$ |
| גלילית (תיל/גליל) | גליל | $2\pi r L$ |
| מישורית (לוח) | “קופסה” (pillbox) | $2A$ |
שיטה
- זהה סימטריה
- בחר משטח גאוס שעליו $E$ קבוע (או אפס)
- חשב $Q_{enc}$ - רק המטען בתוך המשטח!
- פתור עבור $E$
5. דעיכת שדה - גיאומטריות שונות
| מקור | $E(r)$ | דעיכה |
|---|---|---|
| מטען נקודתי / כדור (מחוץ) | $\frac{KQ}{r^2}$ | $\propto \frac{1}{r^2}$ |
| קו / גליל (מחוץ) | $\frac{\lambda}{2\pi\varepsilon_0 r}$ | $\propto \frac{1}{r}$ |
| לוח אינסופי | $\frac{\sigma}{2\varepsilon_0}$ | קבוע |
| כדור מלא (בפנים) | $\frac{KQr}{R^3}$ | $\propto r$ |
6. כדור מלא טעון אחיד
שדה חשמלי
\[r < R: \quad E = \frac{KQr}{R^3}\] \[r > R: \quad E = \frac{KQ}{r^2}\]מקסימום: ב-$r = R$
7. קליפה כדורית
שדה
\[r < R: \quad E = 0\] \[r > R: \quad E = \frac{KQ}{r^2}\]פוטנציאל
\[r < R: \quad V = \frac{KQ}{R} \quad \text{(constant!)}\] \[r > R: \quad V = \frac{KQ}{r}\]8. גליל עם חור - סופרפוזיציה
גליל אחיד $\rho$ עם חור בהיסט $\vec{d}$:
\[\vec{E}_{total} = \vec{E}_{full} + \vec{E}_{hole}\]בתוך החור: שדה אחיד!
\[\vec{E} = \frac{\rho\,\vec{d}}{2\varepsilon_0}\]9. לוח אינסופי
\[E = \frac{|\sigma|}{2\varepsilon_0}\]סופרפוזיציה - שלושה לוחות
חבר את התרומה מכל לוח בכל אזור בנפרד. אם $E = 0$ באזור מסוים ← מצא יחס בין $\sigma$-ים.
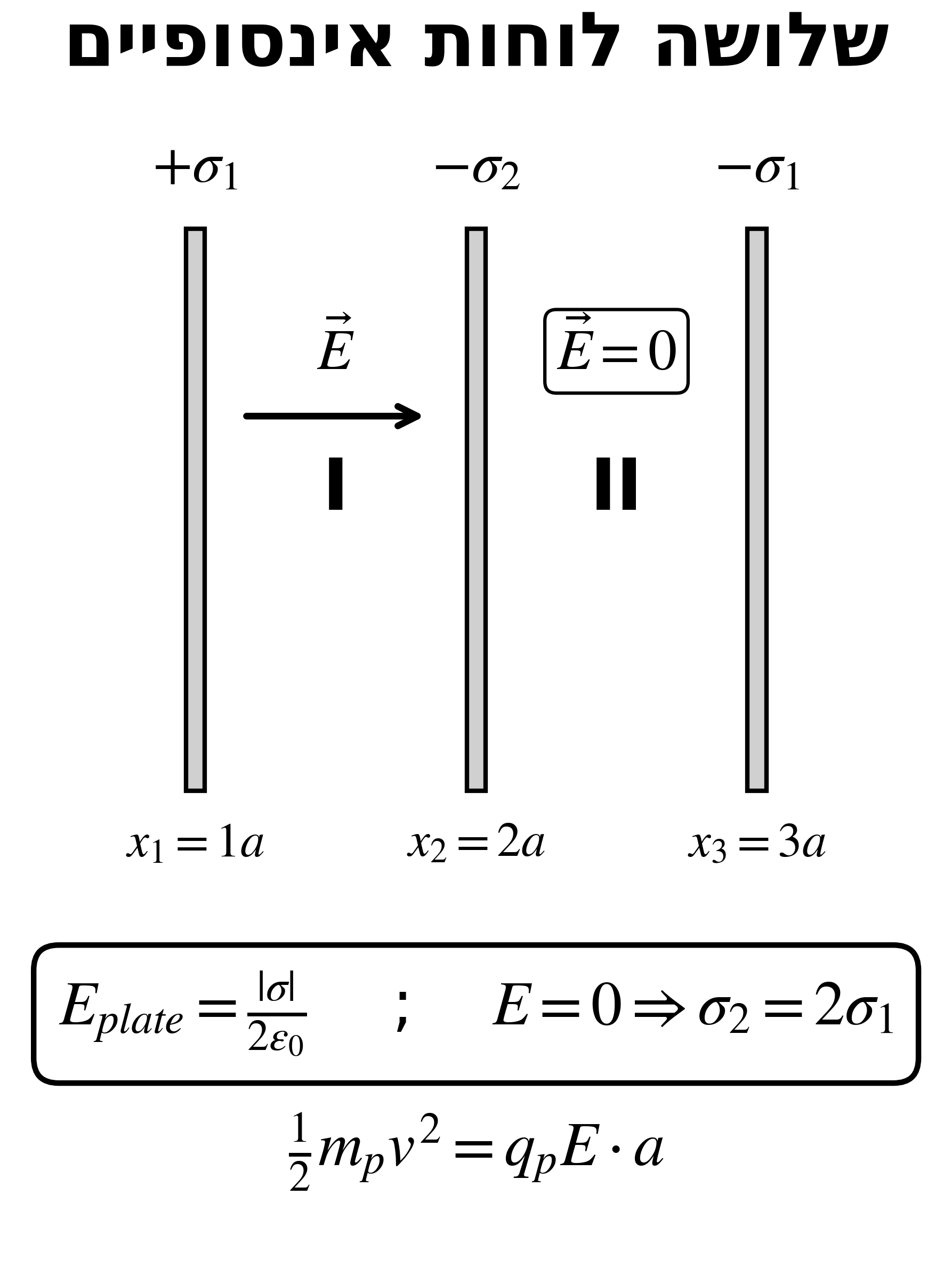
הפרש פוטנציאלים בין לוחות
\[\Delta V = E \cdot d\]10. טבעת טעונה - שדה ופוטנציאל על הציר
שדה
\[E_z = \frac{KQz}{(R^2 + z^2)^{3/2}}\]פוטנציאל
\[V = \frac{KQ}{\sqrt{R^2 + z^2}}\]מקסימום שדה ב-$z = \frac{R}{\sqrt{2}}$
טבעת עם $\lambda(\theta) = \lambda_0\cos\theta$
\[V = \frac{K}{R}\int_0^{2\pi} \lambda_0\cos\theta \cdot R\,d\theta = 0\]כי $\int_0^{2\pi}\cos\theta\,d\theta = 0$ (מחזור שלם).
11. חצי טבעת - שדה בראשית
צפיפות: $\lambda = \frac{Q}{\pi R}$
מסימטריה: רכיב אחד שורד (ניצב למישור הסימטריה).
\[E_x = \int \frac{K\,dq}{R^2}\cos\theta = \frac{K\lambda}{R}\int_{\pi/2}^{3\pi/2}\cos\theta\,d\theta\] \[= \frac{K\lambda}{R}\cdot(-2) = -\frac{2KQ}{\pi R^2}\]12. מוט ישר - שדה על צירו
מוט באורך $L$, צפיפות $\lambda$, קצה עליון בראשית. שדה בנקודה $y > 0$:
מרחק מאלמנט ב-$y’$ (שלילי) לנקודה ב-$y$: $r = y - y’$
\[E = K\lambda\int_{-L}^{0}\frac{dy'}{(y - y')^2} = K\lambda\left[\frac{1}{y} - \frac{1}{y + L}\right]\]13. מוליכים בשיווי משקל
תכונות
- שדה בפנים: $\vec{E} = 0$
- פוטנציאל: קבוע בכל המוליך
- מטען: על פני השטח בלבד
- שדה ליד השטח: $E = \frac{\sigma}{\varepsilon_0}$ (ניצב למשטח)
14. קליפות קונצנטריות
פוטנציאל על קליפה - סופרפוזיציה
כל מטען בתוך הקליפה תורם $\frac{Kq}{R_{shell}}$
כל מטען מחוץ לקליפה תורם $\frac{Kq}{r_{charge}}$
דוגמה - שלוש קליפות ($R_1 < R_2 < R_3$)
פוטנציאל על הפנימית:
\[V(R_1) = \frac{KQ_1}{R_1} + \frac{KQ_2}{R_2} + \frac{KQ_3}{R_3}\]הארקה
כשמאריקים מוליך ← $V = 0$. מטען זורם מ/אל האדמה עד שזה קורה.
חשוב: מטען מושרה על צד פנימי של קליפה לא נשפע מהארקה!
דוגמה - קליפה עם מטען $Q$ וּמטען $q$ בחלל פנימי
פני שטח פנימיים: $-q$ (מושרה), חיצוניים: $Q + q$
אחרי הארקה: האדמה מוציאה $Q + q$ מהחיצוני, נשאר $-q$ בפנים ו-$0$ בחוץ.
15. שימור אנרגיה
\[K_A + U_A = K_B + U_B\] \[\frac{1}{2}mv_A^2 + qV_A = \frac{1}{2}mv_B^2 + qV_B\]עבודה
\[W = q\Delta V = q(V_f - V_i)\]16. גלילים קואקסיאליים
שלושה אזורים
| אזור | $E$ |
|---|---|
| $r < a$ (בתוך פנימי) | $0$ |
| $a < r < b$ (ביניהם) | $\dfrac{\lambda}{2\pi\varepsilon_0 r}$ |
| $r > b$ (בחוץ) | $0$ (אם סך מטען = 0) |
פוטנציאל - לפרק לקטעים
\[V(a < r < b) = -\int_b^r \vec{E}\cdot dr = \frac{\lambda}{2\pi\varepsilon_0}\ln\frac{b}{r}\]חשוב: לא לאינטגר ישר מאינסוף! פרק לאזורים.
17. כדור חלול ($R_1 < r < R_2$, $\rho$ אחיד)
מטען כלוא ב-$r$ ($R_1 < r < R_2$)
\[Q_{enc}(r) = \rho \cdot \frac{4}{3}\pi(r^3 - R_1^3) = Q\cdot\frac{r^3 - R_1^3}{R_2^3 - R_1^3}\]שדה
\[E(R_1 < r < R_2) = \frac{KQ(r^3 - R_1^3)}{r^2(R_2^3 - R_1^3)}\] \[E(r > R_2) = \frac{KQ}{r^2}\] \[E(r < R_1) = 0\]חלק ב׳: מגנטיות
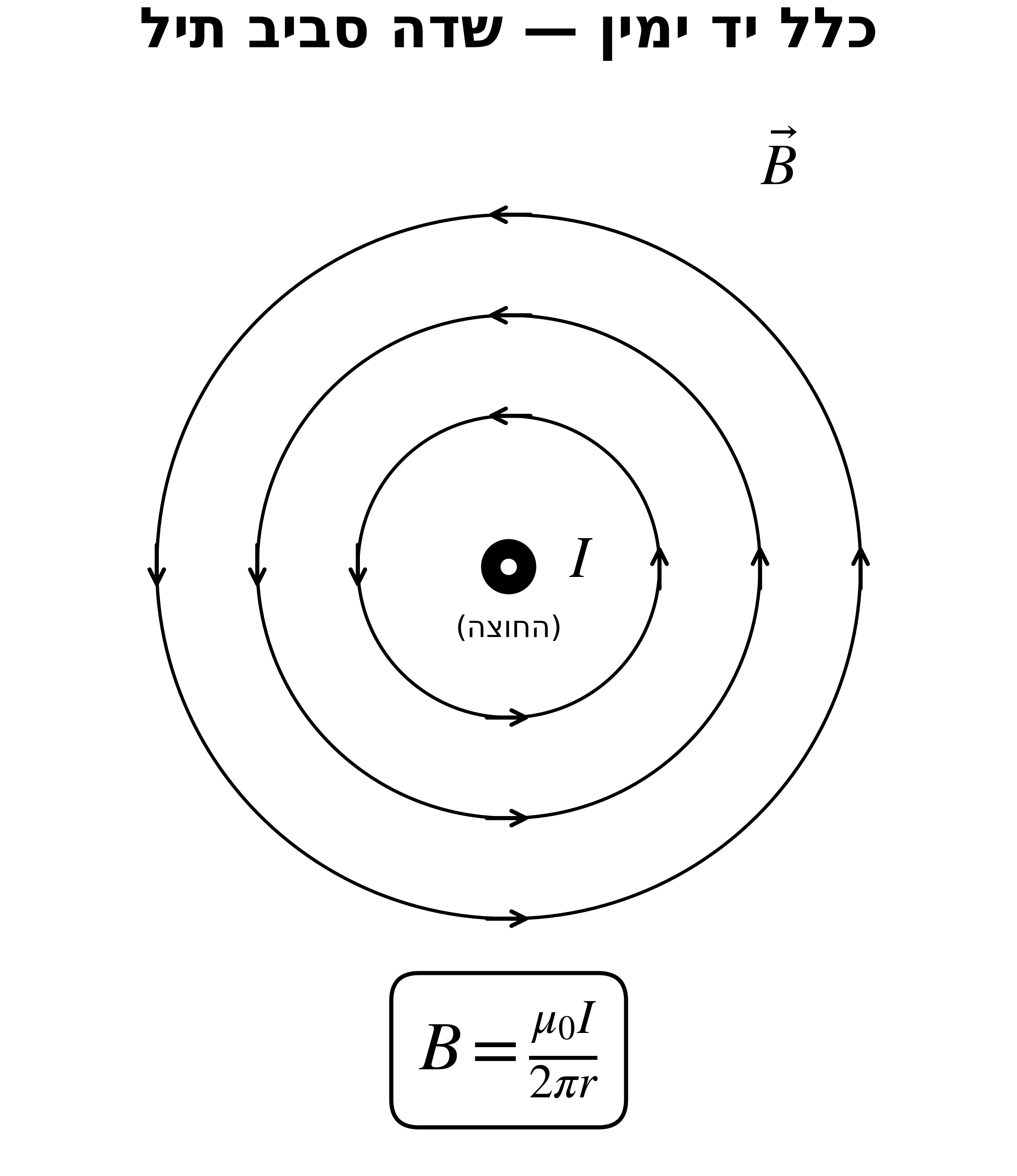
18. שדה מגנטי מתיל ישר ארוך
\[B(r) = \frac{\mu_0 I}{2\pi r}\]כלל יד ימין
אגודל בכיוון הזרם ← האצבעות מצביעות בכיוון קווי השדה (מעגליים סביב התיל).
19. כוחות בין תיילים מקבילים
\[\frac{F}{L} = \frac{\mu_0 I_1 I_2}{2\pi d}\]- אותו כיוון ← משיכה
- כיוון הפוך ← דחייה
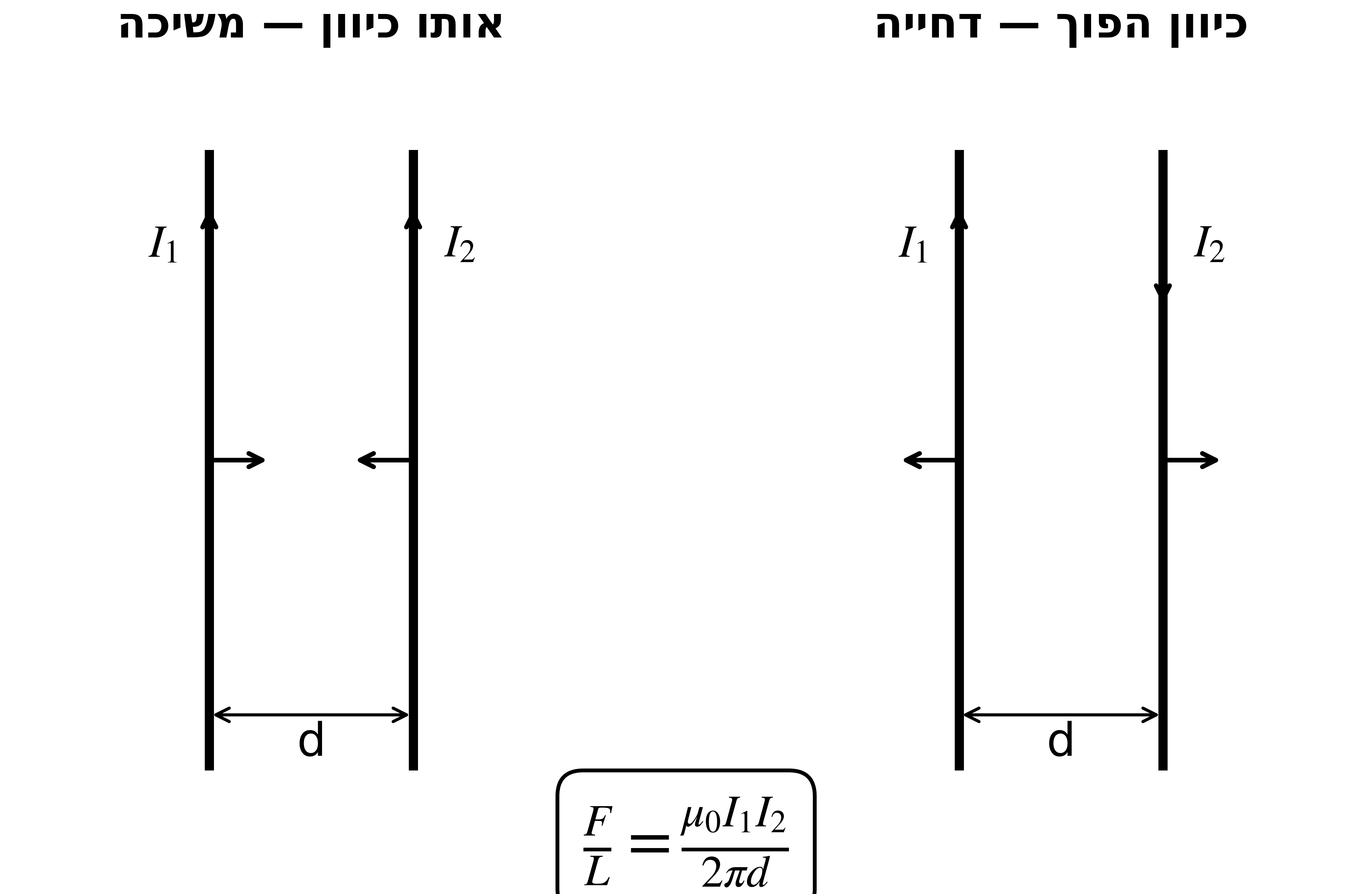
שלושה תיילים - שיווי משקל
$I_B$ מצטמצם! מיקום שיווי משקל:
\[\frac{I_A}{x} = \frac{I_C}{d - x}\]20. סופרפוזיציה של שדות - שני תיילים
בין התיילים (זרמים באותו כיוון, $-a < x < a$)
\[B(x) = \frac{\mu_0 I}{\pi}\cdot\frac{x}{a^2 - x^2}\]שיטה
- מרחק מכל תייל
- כיוון שדה מכל תייל (יד ימין)
- חבר/חסר וקטורית
- מכנה משותף: $(a+x)(a-x) = a^2 - x^2$
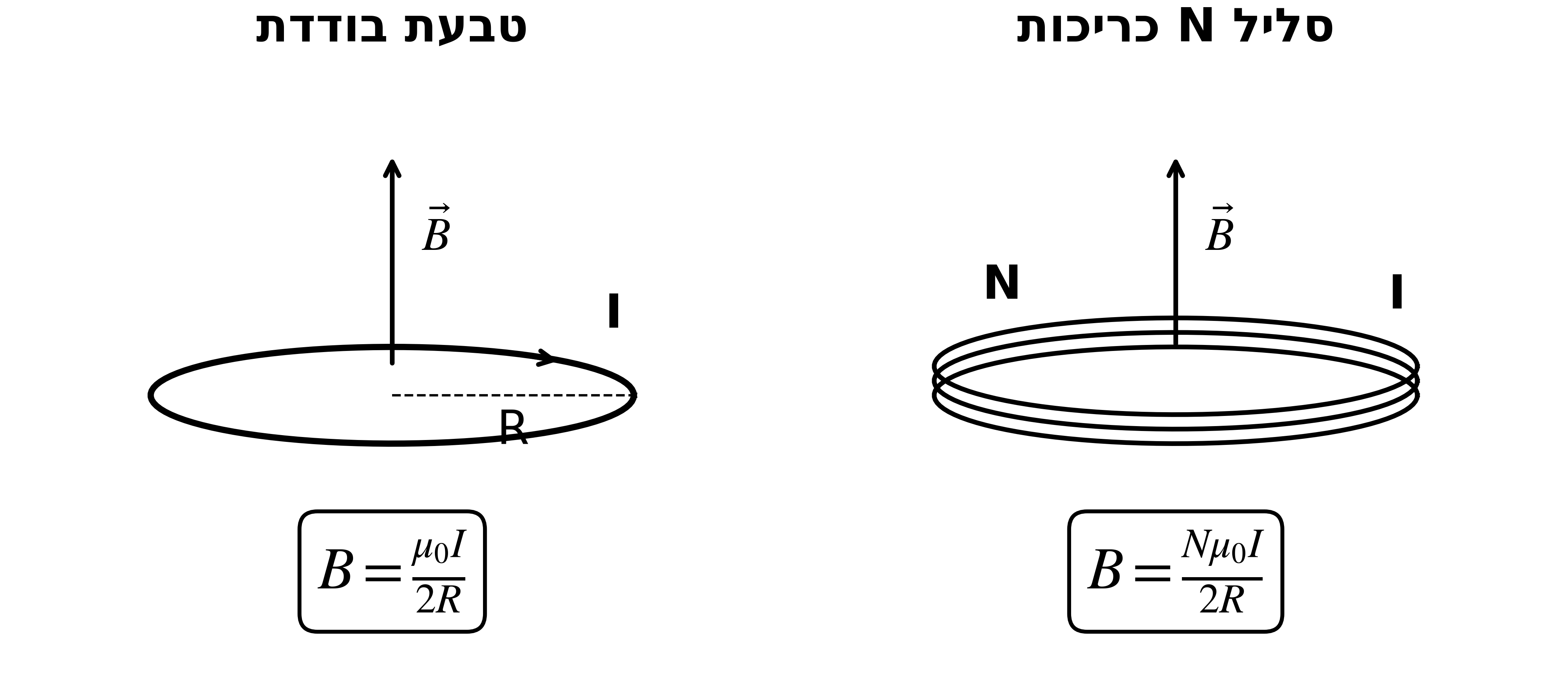
21. שדה במרכז טבעת / סליל
| מקור | $B$ במרכז |
|---|---|
| טבעת בודדת | $\dfrac{\mu_0 I}{2R}$ |
| סליל $N$ כריכות | $\dfrac{N\mu_0 I}{2R}$ |
22. כוח על מוליך נושא זרם
\[\vec{F} = I\vec{L} \times \vec{B}\]מכפלה וקטורית - כלל מעגלי
\[\hat{x} \to \hat{y} \to \hat{z} \to \hat{x}\]| מכפלה | תוצאה |
|---|---|
| $\hat{x} \times \hat{y}$ | $+\hat{z}$ |
| $\hat{y} \times \hat{z}$ | $+\hat{x}$ |
| $\hat{z} \times \hat{x}$ | $+\hat{y}$ |
| $\hat{y} \times \hat{x}$ | $-\hat{z}$ |
| $\hat{a} \times \hat{a}$ | $0$ |
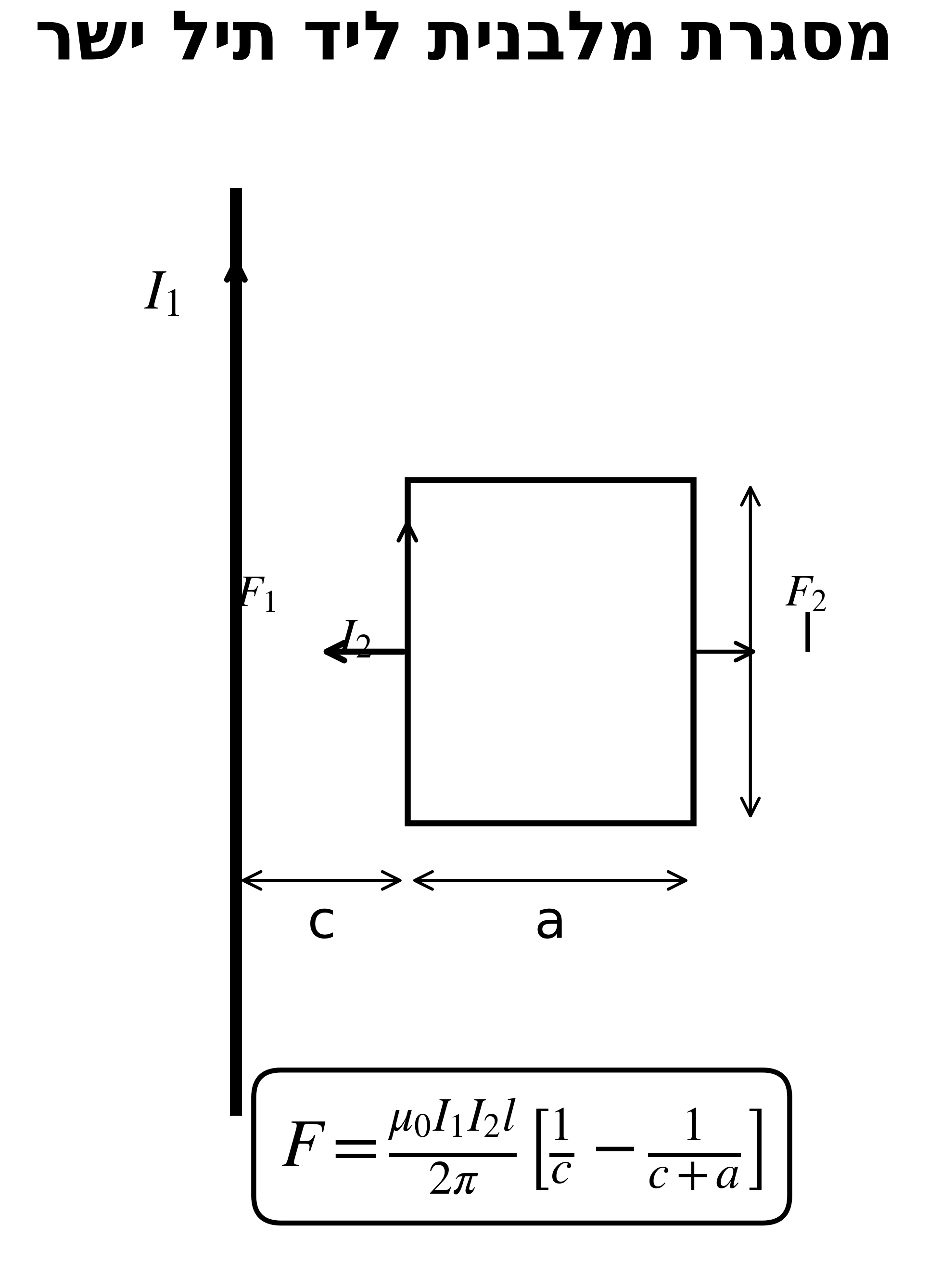
23. מסגרת מלבנית ליד תיל ישר
\[F_{net} = \frac{\mu_0 I_1 I_2 l}{2\pi}\left[\frac{1}{c} - \frac{1}{c + a}\right]\]צלעות מקבילות לתיל: כוחות לא שווים (מרחקים שונים).
צלעות מאונכות: מתקזזים (סימטריה).
24. חוק אמפר
\[\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}\]שדה בתוך תיל ($r < R$, צפיפות אחידה)
\[B(r) = \frac{\mu_0 I r}{2\pi R^2} \quad (\propto r)\]שדה מחוץ לתיל ($r > R$)
\[B(r) = \frac{\mu_0 I}{2\pi r} \quad (\propto 1/r)\]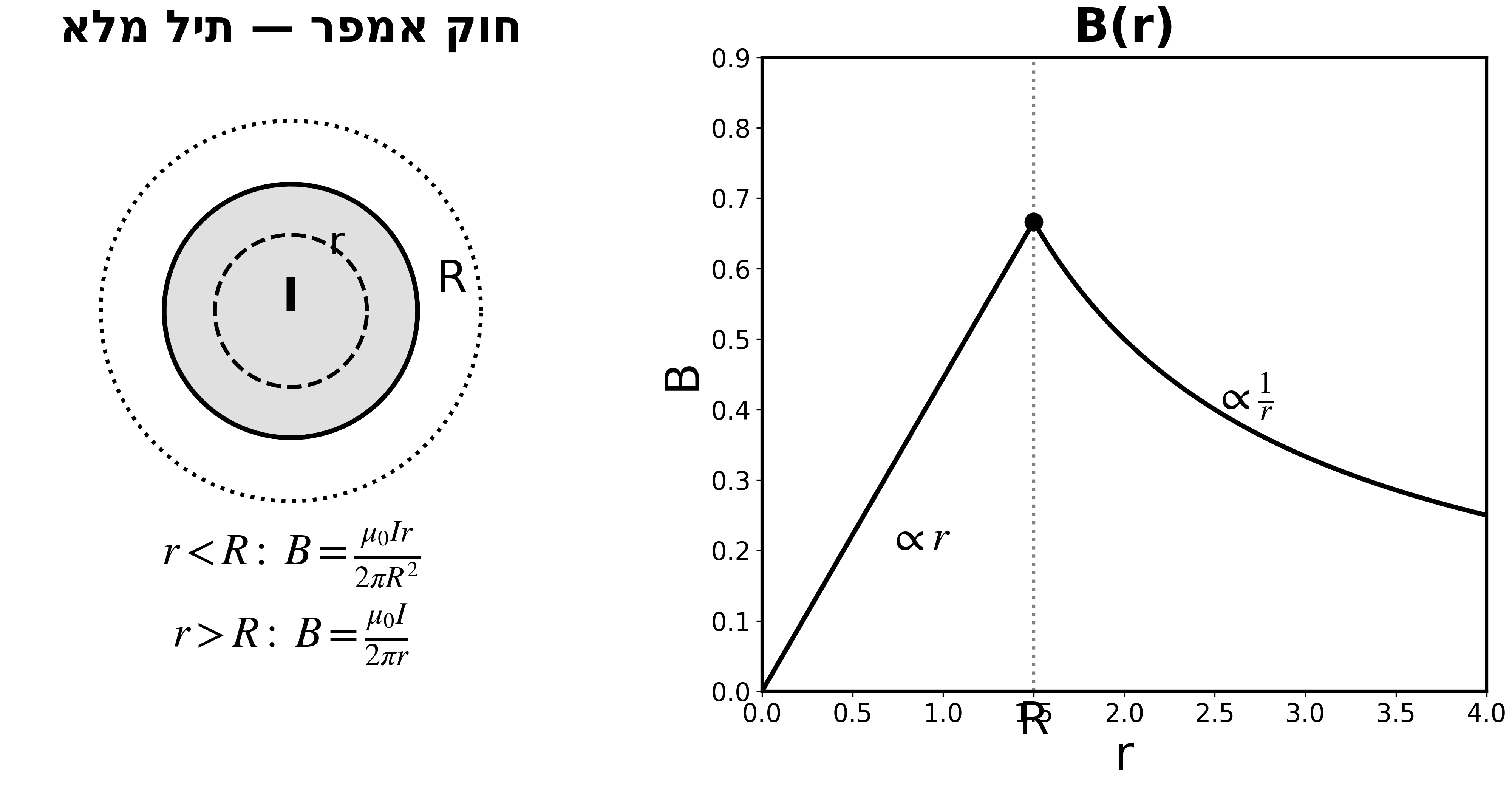
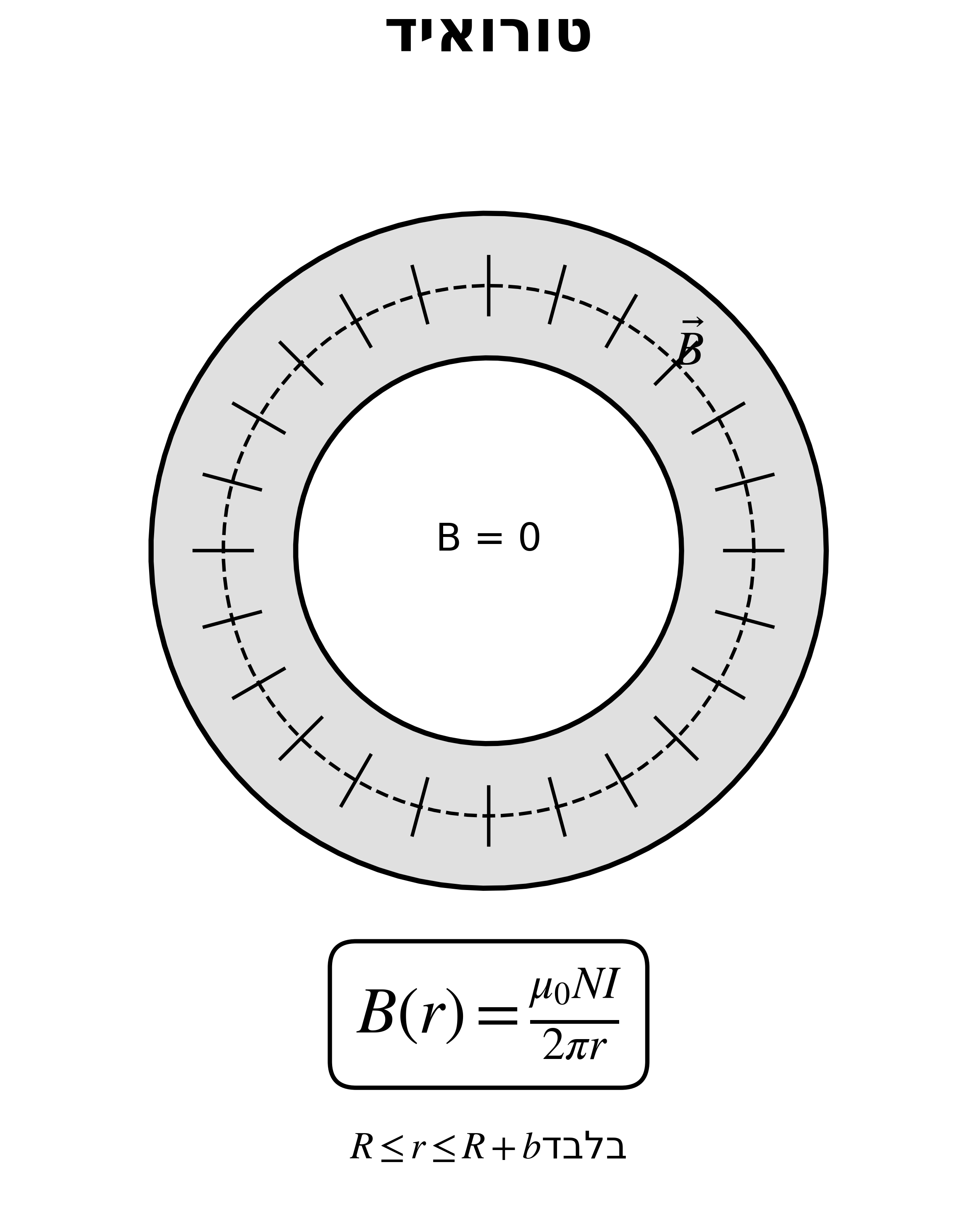
25. טורואיד
\[B(r) = \frac{\mu_0 NI}{2\pi r}\]רק בתוך הטורואיד ($R \le r \le R + b$). מחוצה לו: $B = 0$.
26. צפיפות זרם מגליל מסתובב
\[\vec{J} = \rho(r)\cdot\vec{v}(r) = \rho(r)\cdot\omega r\,\hat{\theta}\]ה-$r$ מצטמצם כשמציבים $\rho \propto 1/r$!
27. כוח לורנץ
כוח
\[\vec{F} = q\vec{v} \times \vec{B}\]תנועה מעגלית
\[r = \frac{mv}{qB}, \qquad T = \frac{2\pi m}{qB}, \qquad f = \frac{qB}{2\pi m}\]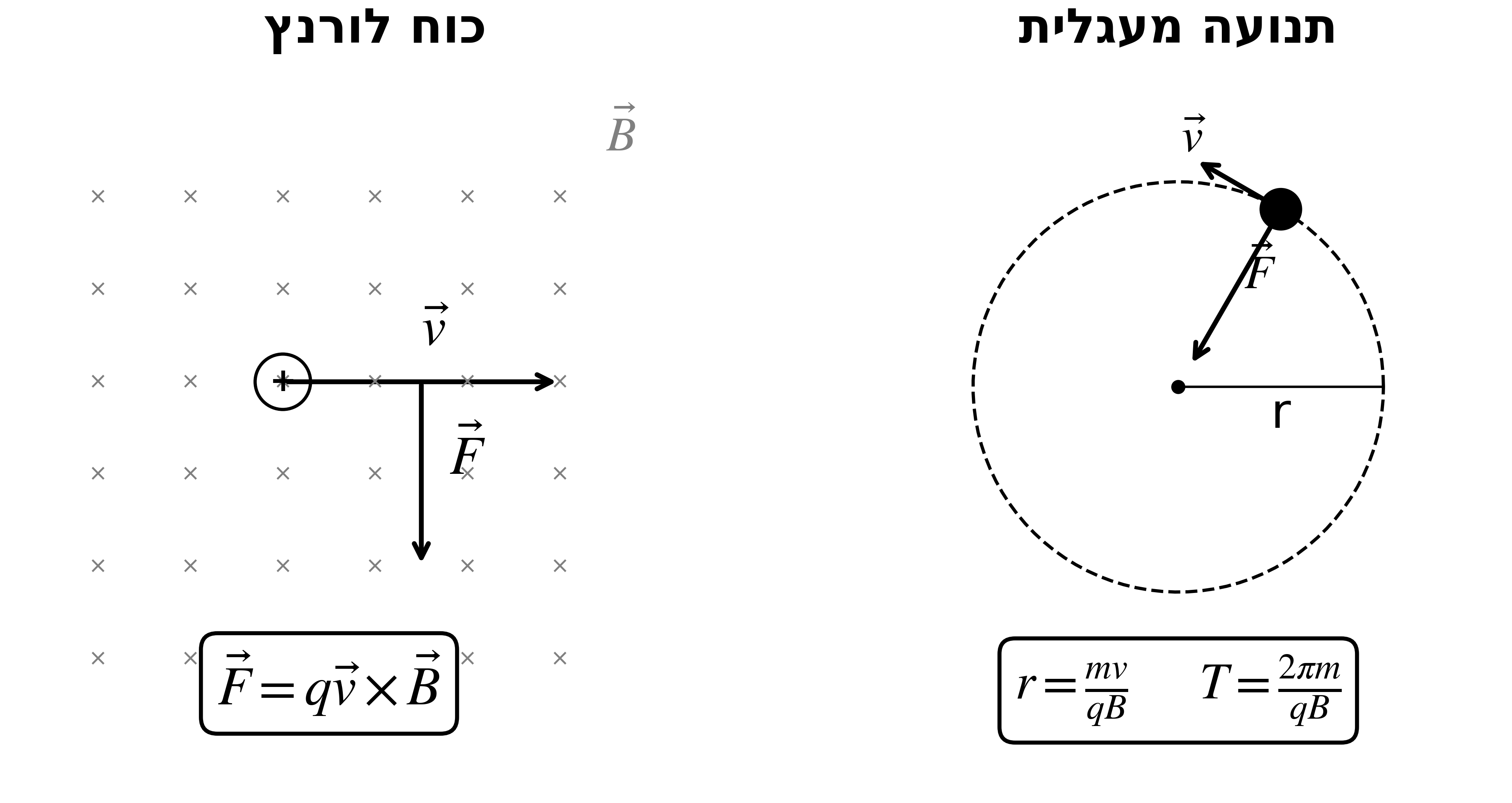
תכונות חשובות
- שדה מגנטי לא עושה עבודה ($\vec{F} \perp \vec{v}$)
- אנרגיה קינטית לא משתנה, רק הכיוון
- $T$ לא תלוי במהירות!
28. תנועה הליקלית
\[v_\parallel = v\cos\theta, \qquad v_\perp = v\sin\theta\]מרווח פסיעה (Pitch)
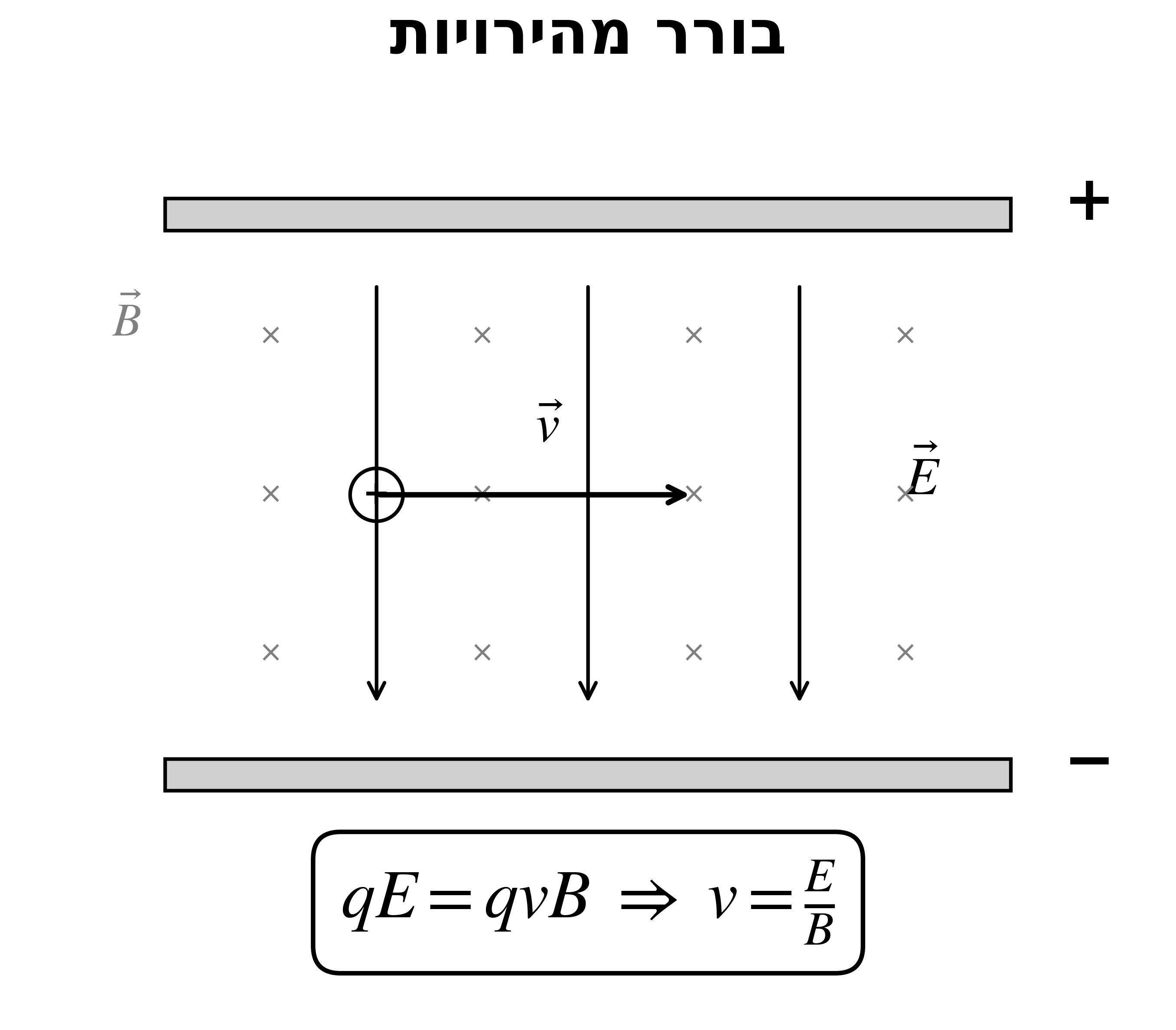
\[p = v_\parallel \cdot T = \frac{2\pi mv\cos\theta}{qB}\]29. בורר מהירויות
\[qE = qvB \implies v = \frac{E}{B}\]לא תלוי במסה או במטען!
הפרדת איזוטופים (אחרי בורר מהירויות)
\[\Delta r = \frac{v}{qB}(m_1 - m_2)\]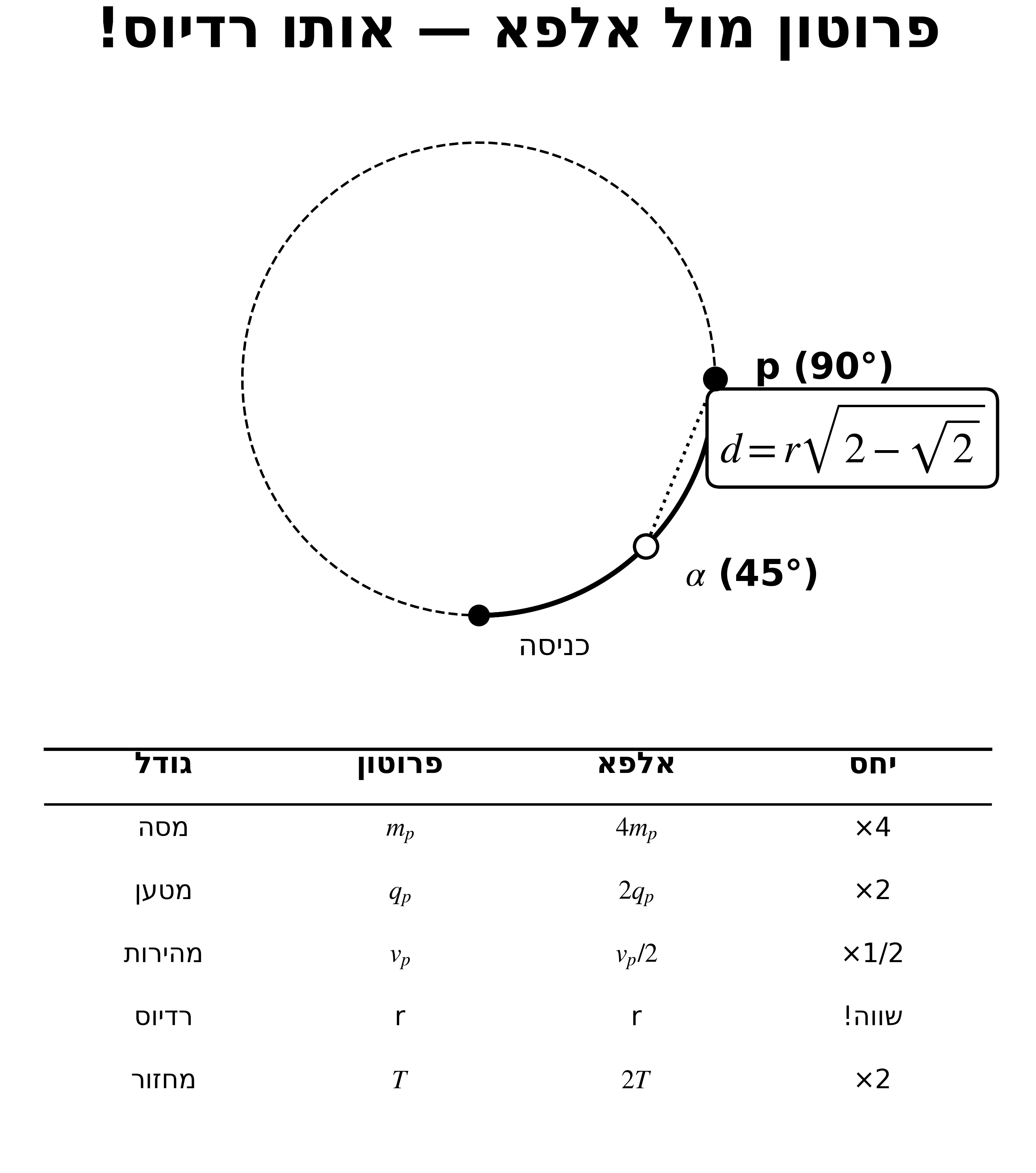
30. פרוטון מול אלפא - השוואה
| גודל | פרוטון | אלפא | יחס |
|---|---|---|---|
| מסה | $m_p$ | $4m_p$ | ×4 |
| מטען | $q_p$ | $2q_p$ | ×2 |
| מהירות (אותו $E_k$) | $v_p$ | $v_p/2$ | ×1/2 |
| רדיוס | $r$ | $r$ | שווים! |
| מחזור | $T$ | $2T$ | ×2 |
מיקום על המעגל
כניסה ב-$(0,0)$ בכיוון $+\hat{x}$, מרכז ב-$(0,r)$:
\[x(\theta) = r\sin\theta, \qquad z(\theta) = r(1 - \cos\theta)\]מרחק אחרי זוויות שונות
\[d = r\sqrt{2 - \sqrt{2}} \quad \text{(proton 90° and alpha 45°)}\]חלק ג׳: אינדוקציה וכא”מ
31. חוק פאראדיי - כא”מ מושרה
\[\mathcal{E} = -\frac{d\Phi_B}{dt}\]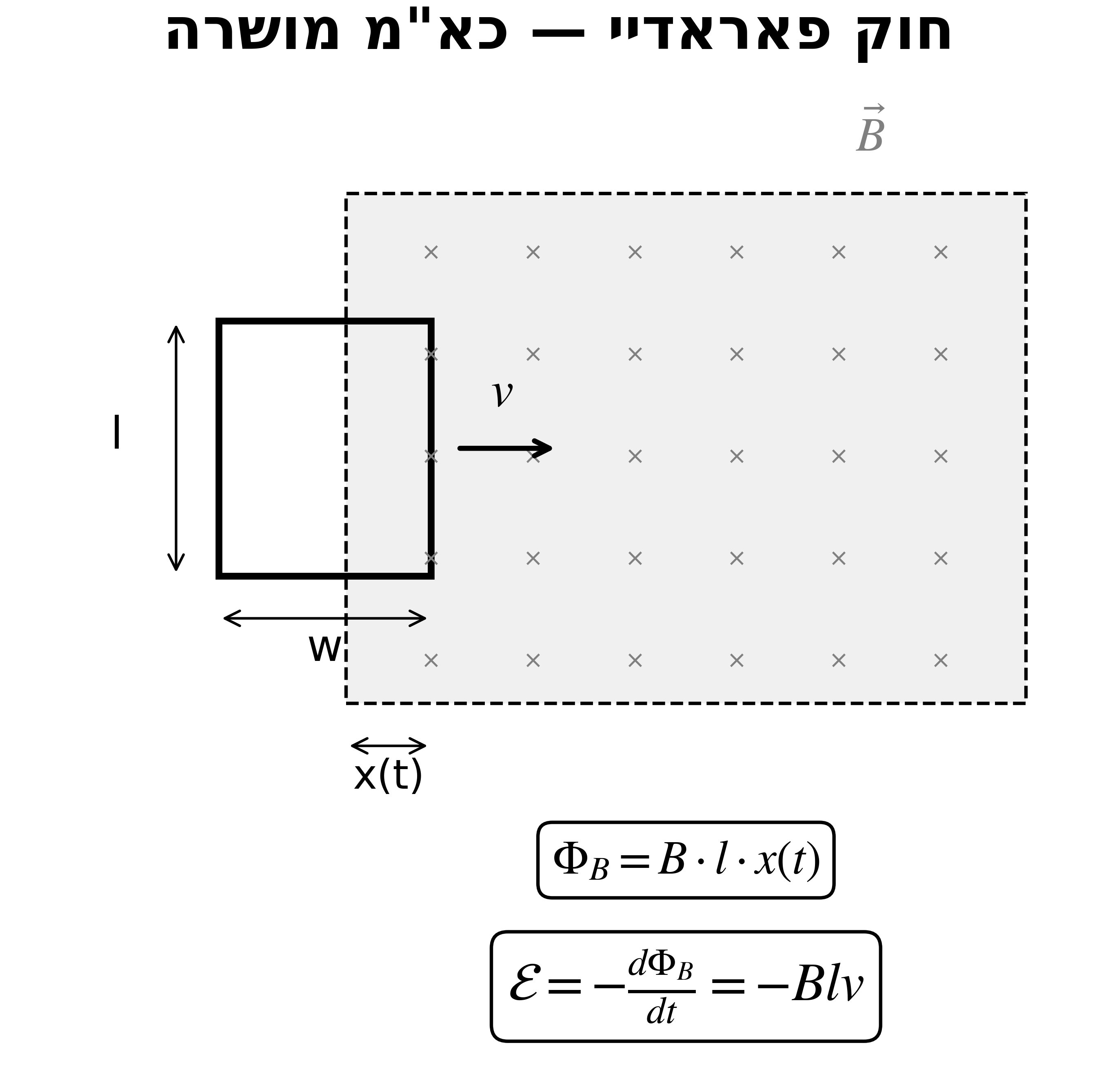
שטף מגנטי
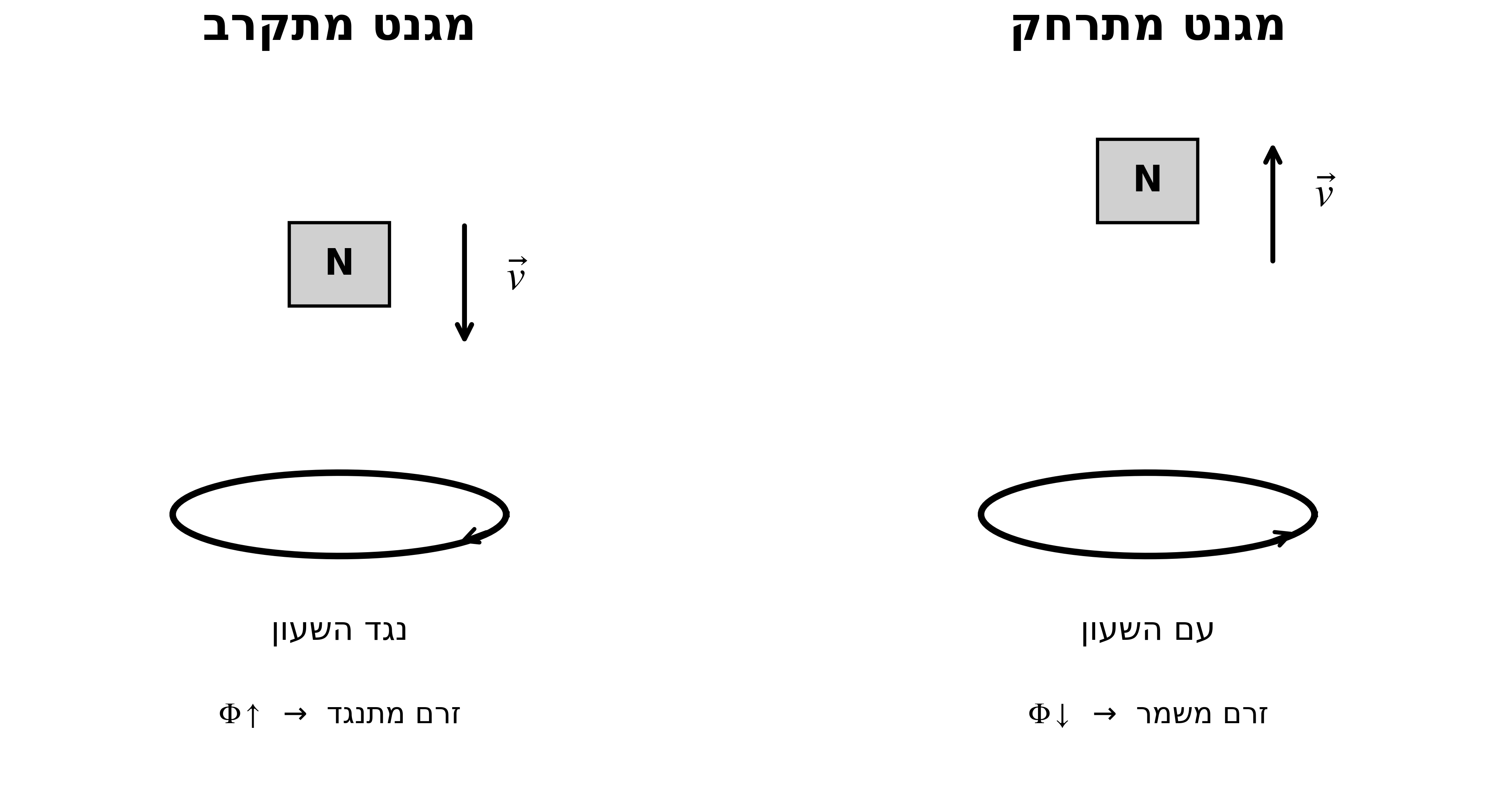
\[\Phi_B = \int \vec{B}\cdot d\vec{A} = BA\cos\theta\]חוק לנץ
הזרם המושרה מתנגד לשינוי בשטף:
- שטף גדל ← זרם יוצר שדה נגדי
- שטף קטן ← זרם יוצר שדה באותו כיוון
32. כא”מ - מקרים שכיחים
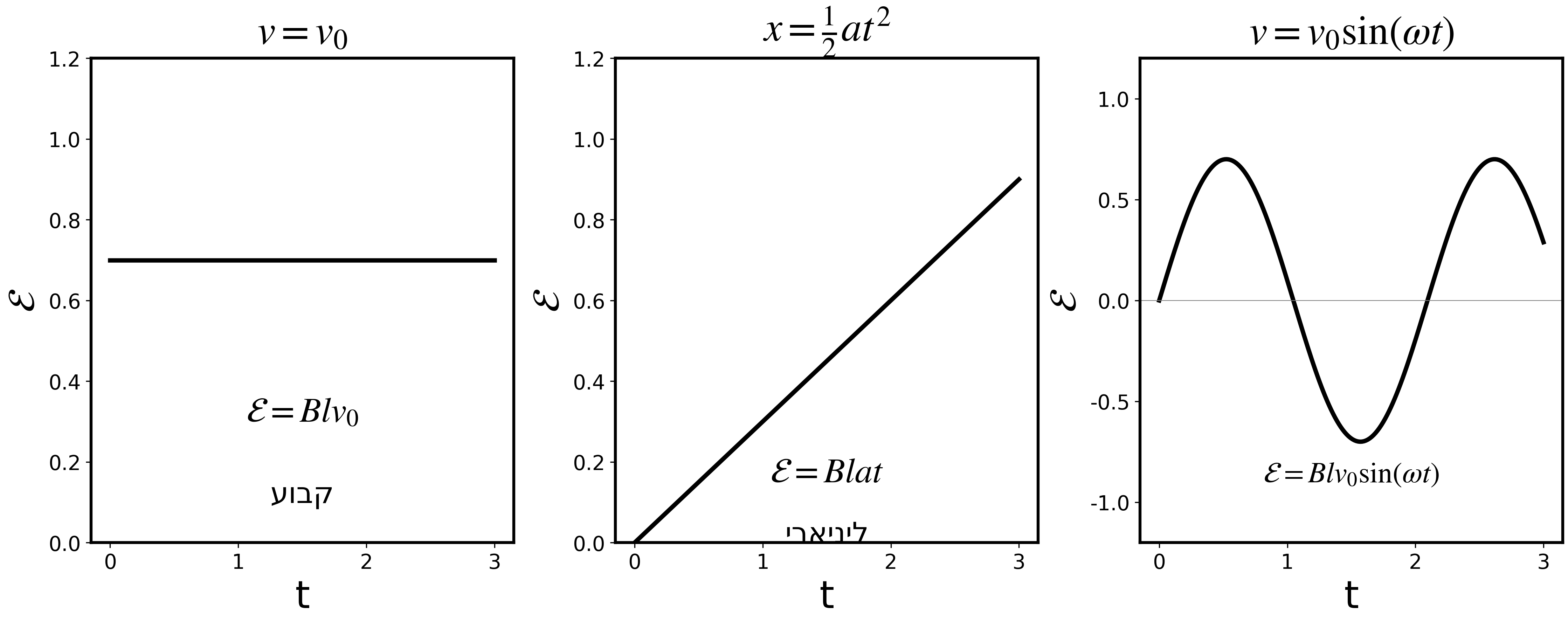
מסגרת נכנסת במהירות קבועה $v_0$
\[\mathcal{E} = Blv_0 \quad \text{(constant)}\]מסגרת נכנסת בתאוצה $a$
\[\mathcal{E}(t) = Blat \quad \text{(linear in time)}\]מוט על מסילה עם $v(t) = v_0\sin(\omega t)$
\[\mathcal{E} = Blv_0\sin(\omega t)\]קיצור: $\frac{d\Phi}{dt} = Bl\frac{dx}{dt} = Blv(t)$ - אם נתון $v(t)$, אין צורך ב-$x(t)$!
מסגרת נכנסת + סיבוב
\[\Phi = B \cdot \frac{1}{2}lat^2\cos(\omega t)\]גזירה בלייבניץ:
\[\mathcal{E} = Blat\cos(\omega t) - \frac{1}{2}Bla\omega t^2\sin(\omega t)\]33. מסגרת מסתובבת בשדה משתנה
\[\vec{B}(t) = B_0\sin(\omega t), \qquad \theta(t) = \omega t\] \[\Phi = a^2 B_0\sin(\omega t)\cos(\omega t) = \frac{a^2 B_0}{2}\sin(2\omega t)\] \[\mathcal{E} = -\omega a^2 B_0\cos(2\omega t)\]זהות טריגונומטרית חיונית
\[\sin\alpha\cos\alpha = \frac{1}{2}\sin(2\alpha)\]34. מסגרת נופלת בשדה מגנטי
\[\mathcal{E} = Bwv, \qquad i = \frac{Bwv}{R}, \qquad F_{mag} = \frac{B^2w^2v}{R}\]משוואת תנועה (ניוטון)
\[mg - \frac{B^2w^2}{R}v = m\dot{v}\]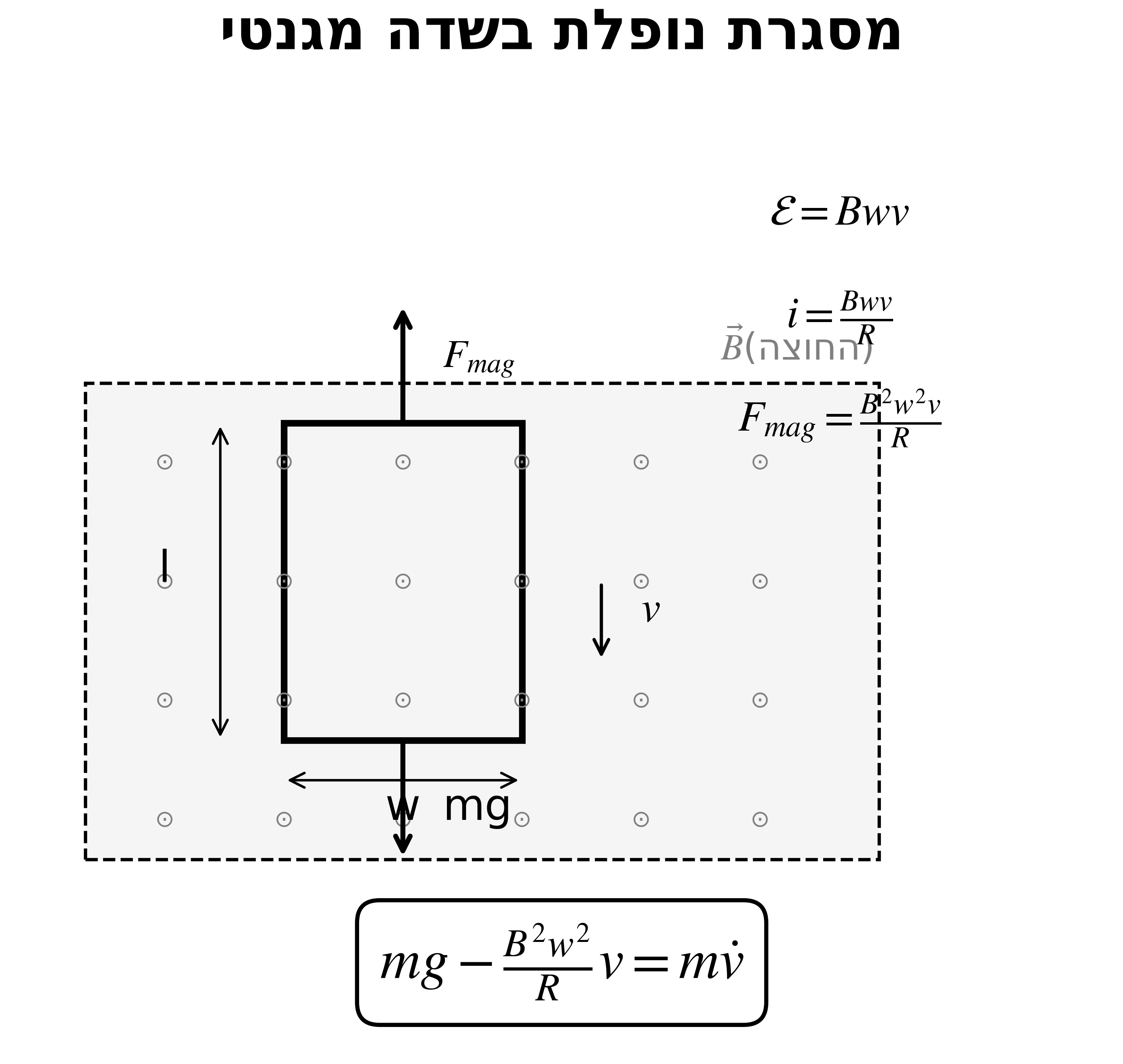
35. שטף דרך טורואיד (חתך מלבני)
\[\Phi_B = \frac{a\mu_0 NI}{2\pi}\ln\left(\frac{R + b}{R}\right)\]כא”מ מושרה (עם $N_2$ כריכות ו-$I = I_0\sin\omega t$)
\[\mathcal{E} = -\frac{N_2 a\mu_0 N\omega I_0}{2\pi}\ln\left(\frac{R + b}{R}\right)\cos(\omega t)\]36. מסגרת על ציר - איזון מומנטים
כוח על צלע קצרה: $F = idB$
צלעות ארוכות ($\vec{L} \parallel \vec{B}$): $F = 0$
\[\tau_{mg} = \tau_{mag} \implies m^*g\cdot l = 2F\cdot l\]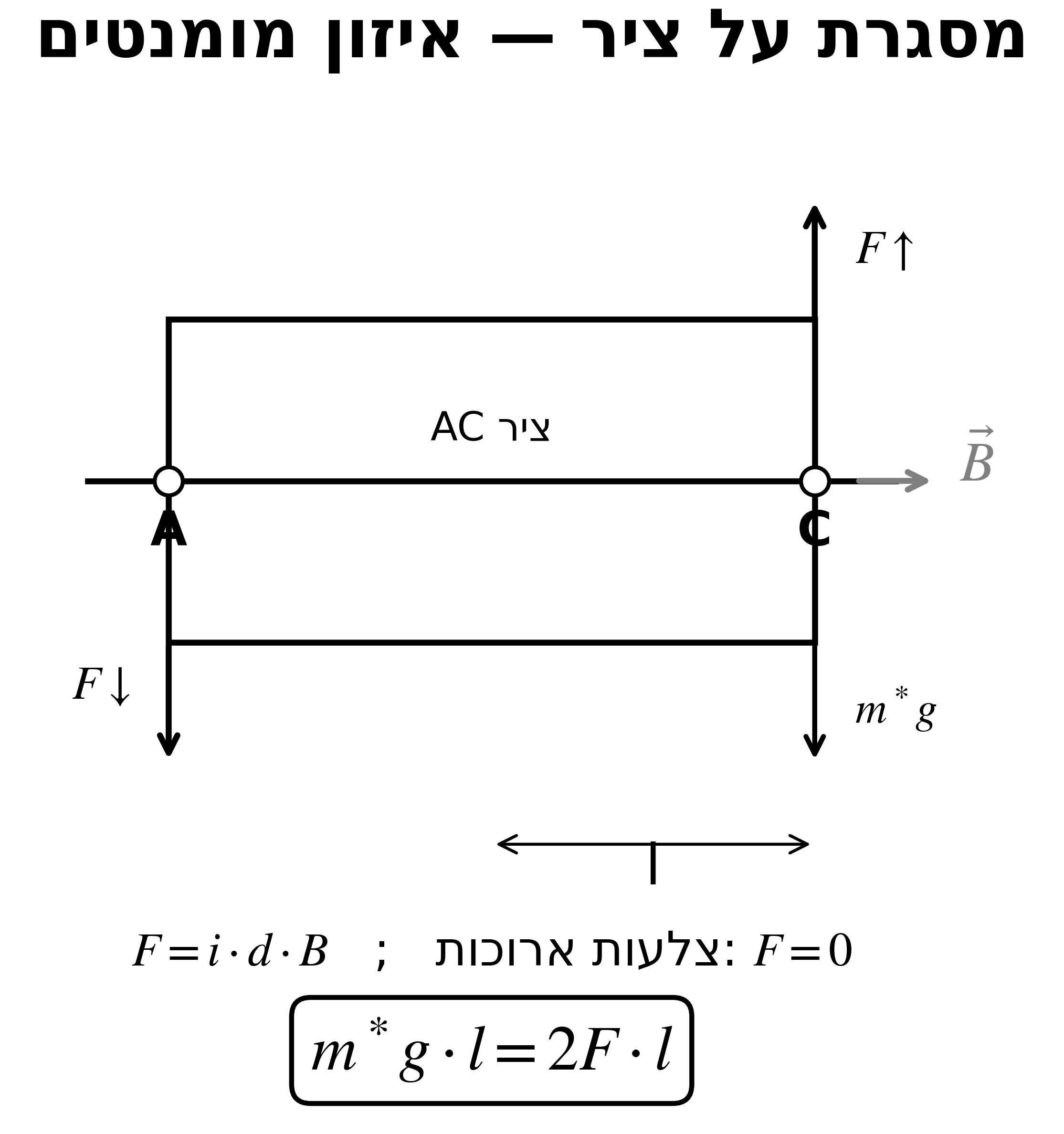
חלק ד׳: חוק אוהם ומעגלים
37. חוק אוהם
צורה מיקרוסקופית
\[\vec{j} = \sigma\vec{E}\]כאשר $\sigma$ = מוליכות סגולית.
צורה מקרוסקופית
\[\mathcal{E} = IR\]התנגדות
\[R = \frac{\ell}{\sigma A}\]כאשר $\ell$ = אורך, $A$ = שטח חתך.
צפיפות זרם וזרם
\[I = \int_S \vec{j}\cdot d\vec{A} = ja\]חלק ה׳: משוואות מקסוול וגלים
38. משוואות מקסוול
צורה דיפרנציאלית
| משוואה | נוסחה | שם |
|---|---|---|
| 1 | $\vec{\nabla}\cdot\vec{D} = \rho$ | חוק גאוס |
| 2 | $\vec{\nabla}\times\vec{H} = \vec{j} + \frac{\partial\vec{D}}{\partial t}$ | חוק אמפר (מוכלל) |
| 3 | $\vec{\nabla}\cdot\vec{B} = 0$ | אין מונופולים |
| 4 | $\vec{\nabla}\times\vec{E} = -\frac{\partial\vec{B}}{\partial t}$ | חוק פאראדיי |
צורה אינטגרלית
\[\oint \vec{D}\cdot d\vec{A} = Q_{enc}\] \[\oint \vec{H}\cdot d\vec{l} = I_{enc} + \frac{d}{dt}\int\vec{D}\cdot d\vec{A}\] \[\oint \vec{B}\cdot d\vec{A} = 0\] \[\oint \vec{E}\cdot d\vec{l} = -\frac{d}{dt}\int\vec{B}\cdot d\vec{A}\]יחסי חומר (בוואקום)
\[\vec{D} = \varepsilon_0\vec{E}, \qquad \vec{B} = \mu_0\vec{H}\]39. משוואת הגלים
\[\nabla^2\vec{E} = \mu_0\varepsilon_0\frac{\partial^2\vec{E}}{\partial t^2}\] \[\nabla^2\vec{B} = \mu_0\varepsilon_0\frac{\partial^2\vec{B}}{\partial t^2}\]מהירות האור
\[c = \frac{1}{\sqrt{\mu_0\varepsilon_0}} = 3\times 10^8\,\text{m/s}\]פתרון גלי
\[\vec{E} = \vec{E}_0\cos(\vec{k}\cdot\vec{r} - \omega t + \phi_0)\] \[\vec{B} = \frac{1}{\omega}\vec{k}\times\vec{E}\] \[v = \frac{\omega}{k}, \qquad k^2 = \frac{\omega^2}{c^2}\]40. פוטנציאלים
פוטנציאל מגנטי
\[\vec{B} = \vec{\nabla}\times\vec{A}\]שדה חשמלי כללי
\[\vec{E} = -\vec{\nabla}V - \frac{\partial\vec{A}}{\partial t}\]זהויות ווקטוריות חשובות
\[\vec{\nabla}\cdot(\vec{\nabla}\times\vec{A}) = 0\] \[\vec{\nabla}\times(\vec{\nabla}\phi) = 0\] \[\vec{\nabla}\times(\vec{\nabla}\times\vec{B}) = \vec{\nabla}(\vec{\nabla}\cdot\vec{B}) - \nabla^2\vec{B}\]חלק ו׳: כלים מתמטיים
41. אינטגרלים שימושיים
\[\int e^{-z/a}\,dz = -ae^{-z/a}\] \[\int_0^\infty e^{-z/a}\,dz = a\] \[\int_0^\infty ze^{-z/a}\,dz = a^2\] \[\int \frac{1}{r}\,dr = \ln|r|\] \[\int r^n\,dr = \frac{r^{n+1}}{n+1} \quad (n \ne -1)\] \[\int \sin(kx)\,dx = -\frac{1}{k}\cos(kx)\] \[\int \cos(kx)\,dx = \frac{1}{k}\sin(kx)\] \[\int_0^{2\pi}\cos\theta\,d\theta = 0\] \[\int_0^{2\pi}\sin\theta\,d\theta = 0\] \[\int_0^{\pi}\sin\theta\,d\theta = 2\] \[\int_{\pi/2}^{3\pi/2}\cos\theta\,d\theta = -2\] \[\int \frac{dr}{r^2} = -\frac{1}{r}\] \[\int x\,dx = \frac{x^2}{2}\]42. נגזרות שימושיות
\[\frac{d}{dt}\sin(\omega t) = \omega\cos(\omega t)\] \[\frac{d}{dt}\cos(\omega t) = -\omega\sin(\omega t)\] \[\frac{d}{dt}e^{-\alpha t} = -\alpha e^{-\alpha t}\] \[\frac{d}{dt}\ln(t) = \frac{1}{t}\] \[\frac{d}{dt}t^n = nt^{n-1}\]כלל המכפלה (לייבניץ)
\[\frac{d}{dt}[f(t)\cdot g(t)] = f'(t)g(t) + f(t)g'(t)\]כלל השרשרת
\[\frac{d}{dx}f(g(x)) = f'(g(x))\cdot g'(x)\]כלל המנה
\[\frac{d}{dx}\frac{f}{g} = \frac{f'g - fg'}{g^2}\]43. זהויות טריגונומטריות
\[\sin\alpha\cos\alpha = \frac{1}{2}\sin(2\alpha)\] \[\sin^2\alpha + \cos^2\alpha = 1\] \[\cos(2\alpha) = \cos^2\alpha - \sin^2\alpha = 1 - 2\sin^2\alpha\] \[\sin(\alpha \pm \beta) = \sin\alpha\cos\beta \pm \cos\alpha\sin\beta\] \[\cos(\alpha \pm \beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta\]44. אלמנטי נפח ושטח
קרטזי
\[dV = dx\,dy\,dz\]כדורי
\[dV = r^2\sin\theta\,dr\,d\theta\,d\phi\] \[dA = R^2\sin\theta\,d\theta\,d\phi \quad \text{(on a sphere)}\]גלילי
\[dV = r\,dr\,d\theta\,dz\] \[dA = r\,d\theta\,dz \quad \text{(side of a cylinder)}\]45. קואורדינטות
גליליות ← קרטזיות
\[x = r\cos\theta, \qquad y = r\sin\theta\] \[r = \sqrt{x^2 + y^2}\]כדוריות ← קרטזיות
\[x = r\sin\theta\cos\phi, \qquad y = r\sin\theta\sin\phi, \qquad z = r\cos\theta\]חלק ז׳: יחידות וקבועים
46. יחידות SI
| גודל | סימון | יחידה |
|---|---|---|
| מטען | $q, Q$ | קולון (C) |
| זרם | $I$ | אמפר (A = C/s) |
| שדה חשמלי | $\vec{E}$ | V/m = N/C |
| שדה מגנטי | $\vec{B}$ | טסלה (T = kg/(A·s²)) |
| פוטנציאל | $V$ | וולט (V = J/C) |
| שטף מגנטי | $\Phi_B$ | וובר (Wb = T·m²) |
| כא”מ | $\mathcal{E}$ | וולט (V) |
| התנגדות | $R$ | אוהם ($\Omega$ = V/A) |
| קיבול | $C$ | פאראד (F = C/V) |
| כוח | $\vec{F}$ | ניוטון (N = kg·m/s²) |
| אנרגיה | $U, W$ | ג’אול (J = N·m) |
47. קבועים חשובים
| קבוע | סימון | ערך | יחידות |
|---|---|---|---|
| חדירות הוואקום | $\mu_0$ | $4\pi\times 10^{-7}$ | T·m/A |
| חלחלות הוואקום | $\varepsilon_0$ | $8.85\times 10^{-12}$ | C²/(N·m²) |
| קבוע קולון | $K$ | $8.99\times 10^9$ | N·m²/C² |
| מטען אלמנטרי | $e$ | $1.6\times 10^{-19}$ | C |
| מסת פרוטון | $m_p$ | $1.67\times 10^{-27}$ | kg |
| מסת אלקטרון | $m_e$ | $9.1\times 10^{-31}$ | kg |
| מהירות האור | $c$ | $3\times 10^8$ | m/s |
קשרים בין קבועים
\[K = \frac{1}{4\pi\varepsilon_0}, \qquad c = \frac{1}{\sqrt{\mu_0\varepsilon_0}}, \qquad \varepsilon_0\mu_0 = \frac{1}{c^2}\]48. המרות נפוצות
| מ- | ל- | כפול |
|---|---|---|
| cm | m | $\times 10^{-2}$ |
| mm | m | $\times 10^{-3}$ |
| $\mu$C | C | $\times 10^{-6}$ |
| nC | C | $\times 10^{-9}$ |
| mA | A | $\times 10^{-3}$ |
| eV | J | $\times 1.6\times 10^{-19}$ |
חלק ח׳: טיפים ושגיאות נפוצות
49. טיפים כלליים לפתרון
- ציירו תרשים - תמיד! סמנו כיוונים, מרחקים, זוויות.
- כלל יד ימין - לכל מקור שדה בנפרד.
- סופרפוזיציה - קבעו כיוון לכל שדה, חברו וקטורית.
- סימטריה - נצלו אותה (כוחות מתקזזים, שדה מתאפס).
- יחידות - $\text{cm} \to \text{m}$ לפני הצבה!
- בדקו מקרי קצה - $r \to 0$, $r \to \infty$, $x = 0$.
- $r$ מצטמצם - חפשו $\rho \propto 1/r$ עם $dV \propto r$.
- שדה מגנטי לא עושה עבודה - $E_k$ לא משתנה.
- מספרים רק בסוף - איברים מצטמצמים.
- גאוס/אמפר - רק עם סימטריה! אחרת אינטגרל ישיר.
50. שגיאות נפוצות - היזהר
| טעות | תיקון |
|---|---|
| בלבול $E \propto 1/r^2$ עם $V \propto 1/r$ | שדה דועך מהר יותר! |
| בלבול $V$ (פוטנציאל) עם $U$ (אנרגיה) | $U = qV$ |
| שכחת מינוס ב-$\vec{E} = -\nabla V$ | המינוס חיוני! |
| גאוס ללא סימטריה | אם אין סימטריה ← אינטגרל |
| $Q_{enc}$ של כל המטען (במקום רק מה שבפנים) | רק המטען בתוך המשטח! |
| נפח כדור $4\pi R^2$ במקום $\frac{4}{3}\pi R^3$ | $4\pi R^2$ = שטח פנים |
| שכחת $\varepsilon_0$ במכנה | $\Delta V = \frac{Q}{\varepsilon_0}\cdot d$ לא $Q\cdot d$ |
| אינטגרל מ-$\infty$ דרך כמה אזורים | פרקו לקטעים! |
| הארקה = מטען אפס | הארקה = פוטנציאל אפס |
| $\int_0^{2\pi}\cos\theta\,d\theta = 1$ | $= 0$ (מחזור שלם) |