שאלה 1
נתונה הפונקציה:
\[f(x) = \left( \frac{1}{x} \right)^{\left( \frac{1}{(1/x) - 1} \right)}, \quad x \neq 0,1\]חשב את הגבול:
\[\lim_{x \to 1^-} f(x)\]בכל דרך שתראה לך.
פתרתי בעזרת כלל לופיטל.
שאלה 2
מצא את ערך הנגזרת של הפונקציה בנקודה $x_0 = 2$.
שאלה הרבה יותר קשה לדעתי. לוקחים לוג לפישוט (שורה ראשונה) ואז גוזרים את שני הצדדים לפי $x$ (שורה שנייה).
\[\begin{aligned} \ln(f(x)) &= \frac{1}{\frac{1}{x}-1} \cdot \ln\left(\frac{1}{x}\right) = \frac{\ln 1 - \ln x}{\frac{1-x}{x}} = \frac{-\ln x \cdot x}{1-x} \\ \frac{f'(x)}{f(x)} &= \frac{\left(\frac{-1}{x} \cdot x - (-\ln x)\cdot 1\right) \cdot (1-x) - (-\ln x \cdot x) \cdot (-1)}{(1-x)^2} \\ &= \frac{(-1 + \ln x)(1-x) + x\ln x}{(1-x)^2} = \frac{-1 + \ln x}{1-x} + \frac{x\ln x}{(1-x)^2} \end{aligned}\]הנגזרת של אגף ימין נעשתה לפי כלל המנה:
\[\frac{d}{dx} \left( \frac{g(x)}{h(x)} \right) = \frac{g'(x)h(x) - g(x)h'(x)}{h(x)^2}\]
מכאן מתקבל הביטוי הבא עבור $f’(x)$:
\[f'(x) = f(x) \left( \frac{-1 + \ln x}{1-x} + \frac{x\ln x}{(1-x)^2} \right)\]נציב את $x_0 = 2$:
\[f(2)=\left(\frac{1}{2}\right)^{\left(\frac{1}{(1/2)-1}\right)} = \left(\frac{1}{2}\right)^{-2} = 4\]מכאן נקבל:
\[\begin{aligned} f'(2) &= 4 \left( \frac{-1 + \ln 2}{1-2} + \frac{2\ln 2}{(1-2)^2} \right) \\ & = 4 \left( -1 + \ln 2 - 2\ln 2 \right)\\ & = \boxed{4 \left( -1 - \ln 2 \right)} \end{aligned}\]שאלה 3
נתונה הפונקציה:
\[g(x) = (\tan^{-1} x)^{\tan^{-1} x}, \quad x > 0\]האם מתקיים:
\[\ln(g(\tan(\ln x))) = \ln^2 x\]אמת או לא אמת?
נציב את $g(x)$:
\[\begin{aligned} \ln(g(\tan(\ln x))) &= \ln((\tan^{-1}(\tan(\ln x)))^{\tan^{-1}(\tan(\ln x))}) \\ &= \ln(\ln x)^{\ln x} = (\ln x) \cdot \ln(\ln x) \ne \ln^2 x \end{aligned}\]צריך להיזהר ולשים לב שהביטוי בתוך הוא $\ln x$ ולא $x$ כפי שנראה בתחילת הפתרון.
לא אמת.
שאלה 4
האם מתקיים:
\[\tan^{-1} (\tan (g^{-1}(g(x)))) = x\]אמת או לא אמת?
אמת. אפשר להציב ולראות שהביטוי מתקיים או פשוט להשתמש בתכונה של הפונקציות ההפוכות: $f^{-1}(f(x)) = x$.
שאלה 5
נגדיר פונקציה חדשה:
\[h(x) = g(\tan x)\]האם קיימת נקודת מינימום עבור $h(x)$? אם כן, מהי הנקודה?
נציב ונכתוב במפורש את $h(x)$:
\[h(x) = g(\tan x) = (\tan^{-1}(\tan x))^{\tan^{-1}(\tan x)} = x^x\]נגזור את $x^x$ בעזרת טכניקה דומה לזאת שהשתמשנו בה בשאלה 2 (גזירה לוגריתמית):
\[\begin{aligned} \ln(h(x)) &= x \ln x \\ \frac{h'(x)}{h(x)} &= \ln x \cdot 1 + x \cdot \frac{1}{x} = 1 + \ln x \end{aligned}\]בצד ימין השתמשנו בנגזרת לפי כלל המכפלה:
אם $f(x) = g(x) \cdot h(x)$ אז:
\[f'(x) = g'(x) \cdot h(x) + g(x) \cdot h'(x)\]
נקבל כי הנגזרת היא:
\[h'(x) = h(x) \cdot (1 + \ln x) = x^x \cdot (1 + \ln x)\]הערה: אפשרה גם להיעזר באקספוננט ולגזור לפי הנוסחה לפונקציה מורכבת.
נבדוק מתי $h’(x) = 0$:
\[x^x \cdot (1 + \ln x) = 0 \Leftrightarrow \ln x = -1 \Leftrightarrow x = \frac{1}{e}\]שימו לב לא להיזהר - $x$ חייב להיות חיובי כי הפונקציה מוגדרת רק עבור $x > 0$. בכל מקרה $0^0$ לא מוגדר.
כדי לוודא שמדובר בנקודת מינימום אפשר לגזור שוב את הנגזרת ולבדוק את הסימן שלה:
\[\begin{aligned} h''(x) &= h'(x) \cdot (1 + \ln x) + h(x) \cdot \frac{1}{x} = x^x \cdot (1 + \ln x) \cdot (1 + \ln x) + x^x \cdot \frac{1}{x} \\ &= x^x \cdot (1 + \ln x)^2 + \frac{1}{x} \cdot x^x \end{aligned}\]נציב את $x = \frac{1}{e}$ ונקבל שהנגזרת השנייה חיובית.
דרך לעצלנים כמותי - אפשר להחליט שזה מינימום בעזרת הערכה של התנהגות הפונקציה. הנה גרף שלה באזור הזה להשלמת התמונה (היא עולה בקצב עצום במספרים גדולים ובמספרים קטנים, אל תטעו מקנה המידה המקורב).
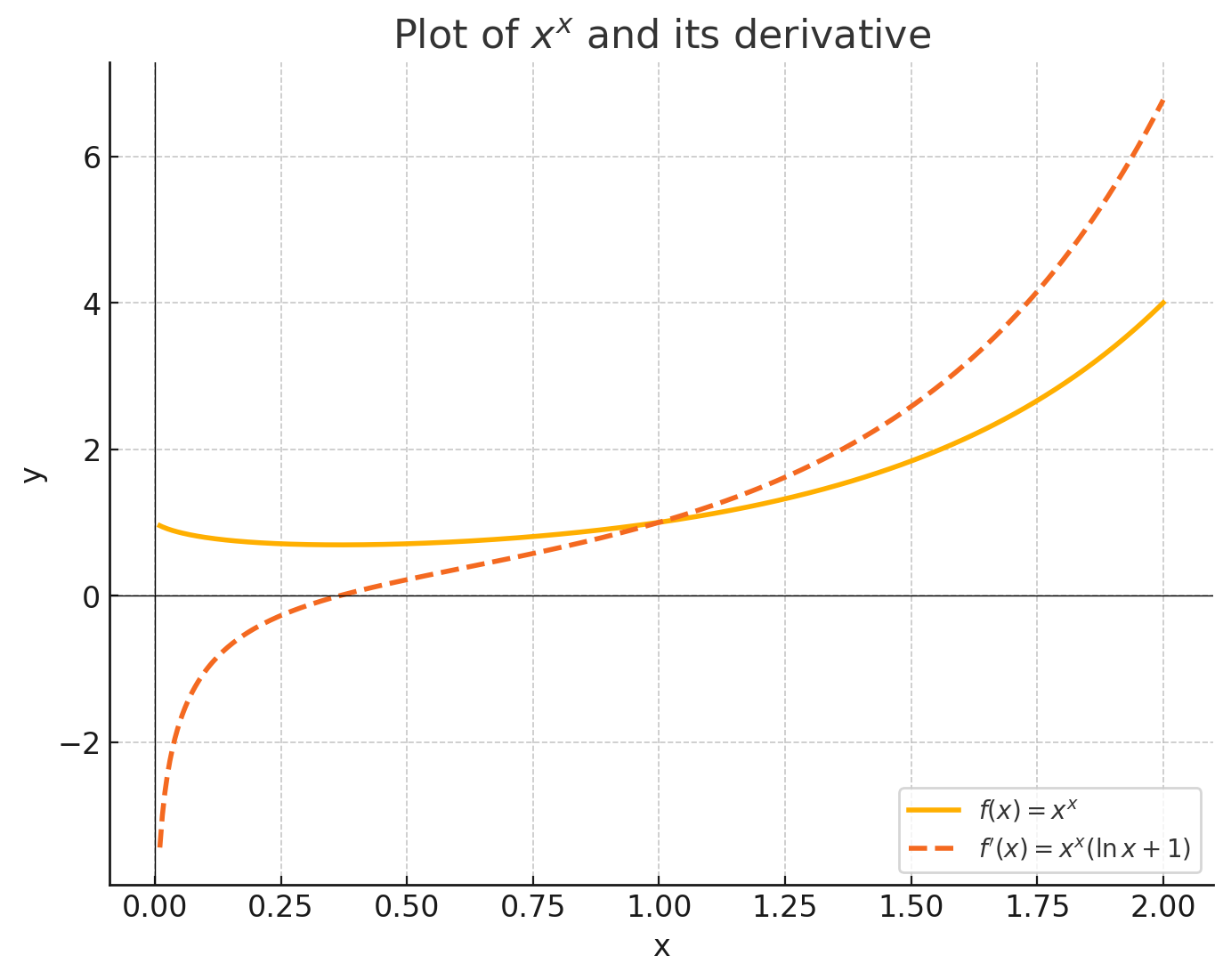
שאלה 6
נתון הפולינום:
\[P(x) = (x+1)^3 + (x+1)^2 + (x+1) + 1\]מה נכון מבין האפשרויות הבאות לגבי הפונקציה $y = P(x)$?
- יש שתי נקודות פיתול משופעות, אחת עם שיפוע חיובי והשנייה עם שלילי.
- אין נקודות פיתול משופעות ואין נקודות פיתול אופקיות.
- קיימות נקודת מקסימום אחת, נקודת מינימום אחת ונקודת פיתול ביניהן.
- קיימת נקודת פיתול משופעת אחת עם שיפוע חיובי.
מוצאים את הנגזרת הראשונה ומנסים לאפס אותה. אין שורשים ממשיים אז מסיקים שאין נקודות קיצון וגם לא נקודות פיתול אופקית.
הנגזרת השנייה למיטב זכרוני התאפסה לי בנקודה אחת. התשובה הנכונה היא 4.
שאלה 7
חשב את הגבול:
\[\lim_{x \to 0} y\left(\frac{\sin(-2x)}{x}\right)\]הגבול שבתוך $y$ הוא $-2$ ולכן הגבול הוא $y(-2) = 0$.
שאלה 8
רשום את הפונקציה $y(x)$ בטור חזקות סביב $x = 1$.
צריך לשים לב לעצרת.
שאלה 9
נתונה פונקציה פרמטרית:
\[x(t) = \tanh^{-1} t, \quad y(t) = \tan^{-1} t\]חשב את הגבול:
\[\lim_{t \to \infty} \frac{dy}{dx}\]שאלה 10
מצא את הפונקציה ההפוכה $y^{-1}(x)$.
שאלות 14-11
שאלה 11
האם הפונקציה:
\[f(x) = \begin{cases} x \sin\left(\frac{1}{x}\right), & x < 0 \\ 0, & x = 0 \\ x^2 \sin\left(\frac{1}{x}\right), & x > 0 \end{cases}\]רציפה בנקודה $x_0 = 0$ ? אמת או לא אמת.
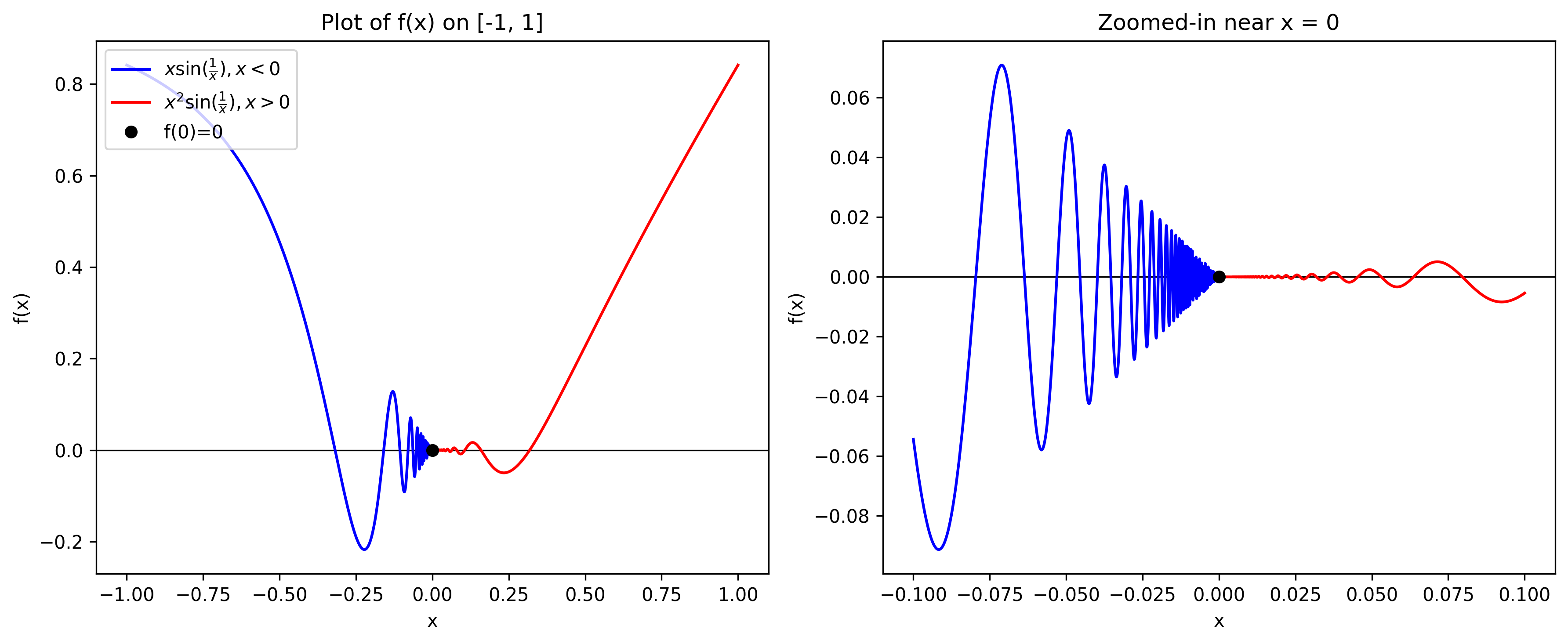 |
|---|
| $f(x)$ |
$f(x)$ רציפה, אפשר לבדוק את הגבול מימין ומשמאל ולראות שהוא שווה לאפס.
שאלה 12
האם הפונקציה $f(x)$ גזירה בנקודה $x_0 = 0$ ? אמת או לא אמת.
היא לא גזירה. אפשר להשתמש בנוסחה של הנגזרת כדי לראות שהגבול בצד שמאל לא קיים:
\[f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \quad \Rightarrow \quad f'(0) = \lim_{h \to 0} \frac{f(h) - f(0)}{h}\]
נציב $x = 0$:
\[f'(0) = \lim_{h \to 0} \frac{h \sin\left(\frac{1}{h}\right) - 0}{h} = \lim_{h \to 0} \sin\left(\frac{1}{h}\right)\]שאלה 13
האם הנגזרת $f’(x)$ רציפה בנקודה $x_0 = 0$ ? אמת או לא אמת.
אין נגזרת אז בטח שלא רציפה.
שאלה 14
האם גרף הפונקציה מתנדנד בין שתי פרבולות בקטע $0 < x < \infty$ ? אמת או לא אמת.
אמת. אפשר לראות בגרף - הפונקציה $\sin\left(\frac{1}{x}\right)$ מתנדנדת בין $-1$ ל-$1$ והפונקציה $x^2$ מתנדנדת בין הפרבולות.
שאלה 15
חשב את הגבול:
\[\lim_{x \to \infty} \left( x + e^x + e^{2x} \right)^{\frac{1}{x}}\]
נעשה על הביטוי $\ln$:
\[\begin{aligned} \lim_{x \to \infty} \left( x + e^x + e^{2x} \right)^{\frac{1}{x}} &= \lim_{x \to \infty} e^{\ln \left(\left( x + e^x + e^{2x} \right)^{\frac{1}{x}}\right)} \\ &= \lim_{x \to \infty} e^{\frac{1}{x} \ln \left( x + e^x + e^{2x} \right)} \\ &= e^{\lim_{x \to \infty} \frac{1}{x} \ln \left( x + e^x + e^{2x} \right)} \end{aligned}\]נפתח את הביטוי שבחזקה בעזרת כלל לופיטל:
\[\begin{aligned} \lim_{x \to \infty} \frac{1}{x} \ln \left( x + e^x + e^{2x} \right) &= \lim_{x \to \infty} \cdot \frac{1 + e^x + 2e^{2x}}{x + e^x + e^{2x}} \end{aligned}\]נשתמש בלופיטל פעם נוספת:
\[\begin{aligned} \lim_{x \to \infty} \frac{1 + e^x + 2e^{2x}}{x + e^x + e^{2x}} &= \lim_{x \to \infty} \frac{e^x + 4e^{2x}}{1 + e^x + 2e^{2x}} \end{aligned}\]נחלק את המונה ואת המכנה ב-$e^{2x}$:
\[\begin{aligned} \lim_{x \to \infty} \frac{e^{-x} + 4}{e^{-2x} + e^{-x} + 2} &= \frac{0 + 4}{0 + 0 + 2} = 2 \end{aligned}\]שאלה 16
חשב את הגבול:
\[\lim_{x \to \infty} x \ln \left( \frac{x+3}{x-3} \right)\]
ננסה לשים הכל על $e$:
\[\begin{aligned} \lim_{x \to \infty} x \ln \left( \frac{x+3}{x-3} \right) &= \lim_{x \to \infty} x \ln \left( 1 + \frac{6}{x-3} \right) \\ &= \lim_{x \to \infty} x \ln \left( 1 + \frac{6}{x} \cdot \frac{1}{1 - \frac{3}{x}} \right) \\ &= \lim_{x \to \infty} x \ln \left( 1 + \frac{6}{x} \right) \\ &= \lim_{x \to \infty} x \cdot \frac{6}{x} = 6 \end{aligned}\]המעבר $\ln(1+\frac{6}{x}) = \frac{6}{x}$ נובע מפיתוח טיילור של $\ln(1+x)$ סביב $x=0$.
באופן כללי, כאשר $y\rightarrow 0$ אז $\ln(1+y) \approx y$.
שאלות 18-17
שאלה 17
נתונה הפונקציה:
\[y(x) = \sinh(a x) + \cosh(b x)\]עבור אלו ערכים של הפרמטרים $a, b$ הפונקציה מקיימת את המשוואה:
\[y'' + 2y' - 3y = 0\]לכל $x$.
נגזור את $y$:
\[\begin{aligned} y' &= a \cosh(a x) + b \sinh(b x) \\ y'' &= a^2 \sinh(a x) + b^2 \cosh(b x) \end{aligned}\]נכניס את הנגזרות למשוואה:
\[\begin{aligned} a^2 \sinh(a x) + b^2 \cosh(b x) + 2(a \cosh(a x) + b \sinh(b x)) - 3(\sinh(a x) + \cosh(b x)) &= 0 \\ (a^2 - 3) \sinh(a x) + (b^2 - 3) \cosh(b x) + 2(a - 3) \cosh(a x) + 2(b - 3) \sinh(b x) &= 0 \end{aligned}\]כלומר, נצטרך למצוא ערכים שיקיימו:
\[\begin{aligned} a^2 - 3 &= 0 \\ b^2 - 3 &= 0 \\ a - 3 &= 0 \\ b - 3 &= 0 \end{aligned}\]ככל הנראה אין פתרון שיקיים את כל המשוואות.
שאלה 18
מהו שיפוע המשיק לפונקציה הנתונה באופן הסתום:
\[x^y = y^x\]בנקודה $(x_0, y_0) = (1,1)$ ?
ניעזר בלוגריתם הטבעי ונמצא ביטוי ל $\frac{dy}{dx}$:
\[\begin{aligned} x^y &= y^x \\ y \ln x &= x \ln y \\ \frac{dy}{dx} \ln x + y \cdot \frac{1}{x} &= \ln y + x \cdot \frac{1}{y} \cdot \frac{dy}{dx} \\ \frac{dy}{dx} \ln x - \frac{x}{y} \cdot \frac{dy}{dx} &= \ln y - y \cdot \frac{1}{x} \\ \frac{dy}{dx} \left( \ln x - \frac{x}{y} \right) &= \ln y - \frac{y}{x} \\ \frac{dy}{dx} &= \frac{\ln y - \frac{y}{x}}{\ln x - \frac{x}{y}} \end{aligned}\]הבהרה לגבי הגזירה: $\ln y$ שנגזרת לפי $x$ היא $\frac{1}{y} \cdot \frac{dy}{dx}$ ולא $\frac{1}{y}$. כך גם עם $\ln x$.
נציב את $(x_0, y_0) = (1,1)$:
\[\begin{aligned} \frac{dy}{dx} &= \frac{\ln 1 - \frac{1}{1}}{\ln 1 - \frac{1}{1}} = \frac{0 - 1}{0 - 1} = 1 \end{aligned}\] דור פסקל