מבוא ותזכורת
בשיעורים הקודמים, כולל בשיעור התגבור, ראינו שבסיטואציות מסוימות החוק השני של ניוטון מוביל למשוואה דיפרנציאלית המתארת תנועה הרמונית.
המשוואה הדיפרנציאלית של תנועה הרמונית
החוק השני של ניוטון הוא:
\[m \cdot a = F \tag{1}\]כאשר $F$ זה שקול הכוחות.
החוק הזה, במקרים מסוימים, מוביל אותנו אל המשוואה הדיפרנציאלית של תנועה הרמונית פשוטה:
\[\ddot{x} = -\omega^2 \cdot x\]הסיטואציה הזאת מתרחשת כאשר מדובר במימד אחד והכוח הוא כוח מחזיר שמתכונתי להעתק. הסיטואציה הטריוויאלית והמובהקת ביותר היא כאשר:
\[F = -k \cdot x \tag{2}\]משוואה $(2)$ מתארת את הכוח של קפיץ, כאשר $k$ הוא הקבוע של הקפיץ. הכוח הזה הוא כוח מחזיר, כלומר הוא פועל בכיוון ההפוך להעתק $x$.
ממשוואות $(1)$ ו-$(2)$ נוכל לפתח את משוואת התנועה ההרמונית הפשוטה:
\[\begin{align} m \cdot a &= \underbrace{-k \cdot x}_{F} \\[10pt] m \cdot \ddot{x} &= -k \cdot x \tag{$a=\ddot{x}$} \\[10pt] \ddot{x} &= -\frac{k}{m} \cdot x \tag{$\div m$} \\[10pt] \ddot{x} &= -\omega^2 \cdot x \tag{$\omega^2 = \frac{k}{m}$} \end{align}\]סך הכל:
\[\boxed{\ddot{x} = -\omega^2 \cdot x} \tag{Simple Harmonic Motion}\]כוח מחזיר ונקודת שיווי משקל
בסיטואציות רבות נגיע אל המשוואה הזאת לא באמצעות הכוח הפשוט שמתואר במשוואה $(1)$. המשוואה הזאת יכולה להתקבל בסיטואציות רבות נוספות. זה מקרה מאוד אלמנטרי שבו יש לנו קפיץ, ואנחנו יודעים שקפיצים מתנדנדים. קל לדמיין שהכוח המחזיר של הקפיץ מתכונתי למתיחה שלו מהאורך הרפוי.
שימו לב, פה רשמנו $F = -kx$, כלומר הכוח מתאפס כש-$x = 0$, אבל בחיים האמיתיים הוא יותר דומה ל:
\[F = -k \cdot \Delta x\]כאשר $\Delta x = x - x_0$, ו-$x_0$ הוא האורך הרפוי. כאשר $x = x_0$, $F = 0$.
שימו לב שהתנאי $F = 0$ מייצר את נקודת שיווי המשקל: זאת אותה נקודה שבה הכוח הוא אפס. אם הכוח הוא אפס, התאוצה היא אפס. ברגע שנרחיק את המסה מנקודת שיווי המשקל, נוצר כוח מחזיר, ואז שקול הכוחות שונה מאפס, ואז יש לנו תאוצה.
דוגמה: מסה תלויה על קפיץ
לדוגמה, נניח שתולים מסה על קפיץ שהאורך הרפוי שלו הוא 0 ($x_0 = 0$), כלומר, שהאורך הרפוי של הקפיץ נמצא למעלה. אפשר לראות שבמצב של שיווי משקל מתקיים:
\[mg = k\overset{*}{x}\]כאשר \(k\overset{*}{x}\) הוא הכוח שקשור בעובדה שהקפיץ נמתח ומושך כלפי מעלה. \(\overset{*}{x}\) הוא ה-$x$ של שיווי המשקל. במצב הזה $F_{total} = 0$ (שקול הכוחות שווה לאפס).
מכאן נקבל:
\[\overset{*}{x} = \frac{mg}{k}\]זו נקודת שיווי המשקל, ואנחנו נצפה שהמסה תתנדנד סביבה ברגע שנשחרר אותה. מה שמכתיב את נקודת שיווי המשקל זה ששקול הכוחות שווה לאפס. זאת אותה נקודה בודדת בתוך התנועה שעבורה שקול הכוחות שווה לאפס.
פתרון המשוואה הדיפרנציאלית
אם נמתח את הקפיץ ואז נשחרר, המסה תתנדנד. במקרה הזה, לפי החוק השני של ניוטון ($F = ma$), משוואת התנועה תהיה:
\[\begin{aligned} ma &= \underbrace{mg -kx}_{F} \\[10pt] m\ddot{x} &= mg - kx \end{aligned}\]זה החוק השני של ניוטון, כאשר $(-kx)$ הוא הכוח המחזיר ו-$mg$ הוא כוח הכבידה. אם נבודד את התאוצה $\ddot{x}$, נקבל:
\[\begin{align} m\ddot{x} &= mg - kx \tag{/m} \\[10pt] \ddot{x} &= g - \frac{k}{m}x \\[10pt] \ddot{x} &= -\frac{k}{m}\left(\underbrace{x - \frac{mg}{k}}_{y}\right) \tag{3} \end{align}\]נסמן:
\[y = x - \frac{mg}{k}\]ואז אם נציב את $y$ במשוואה $(3)$, נקבל את המשוואה הדיפרנציאלית של התנועה ההרמונית:
\[\ddot{y} = -\omega^2 y\]כאשר $\omega^2 = \frac{k}{m}$
הפתרון למשוואה הזאת הוא:
\[y(t) = A\cos(\omega t) + B\sin(\omega t)\]לכן, אם נציב $y=x - \frac{mg}{k}$, כדי להחזיר את $x$ למשוואה, נקבל:
\[\begin{align} x(t) - \frac{mg}{k} &= A\cos(\omega t) + B\sin(\omega t) \\[10pt] x(t) &= A\cos(\omega t) + B\sin(\omega t) + \frac{mg}{k} \tag{4} \end{align}\]תנאי התחלה
עכשיו צריך להכניס את תנאי ההתחלה. אם:
\[\begin{aligned} x(t=0) &= x_0 \\[10pt] v(t=0) &= v_0 \end{aligned}\]ניקח לדוגמה את המקרה של $x_0 = 0$ ו-$v_0 \neq 0$.
נציב את התנאי $x(0) = 0$ במשוואה $(4)$:
\[\begin{aligned} x(t=0) &= A\cos(0) + B\sin(0) + \frac{mg}{k} \\[10pt] 0 &= A \cdot 1 + B \cdot 0 + \frac{mg}{k} \end{aligned}\]מכאן:
\[\boxed{A = -\frac{mg}{k}}\]ביחס לתנאי על התאוצה ההתחלתית, אנחנו למעשה צריכים לגזור את משוואה $(4)$, כי התאוצה ($\ddot{x}$) היא נגזרת שנייה של $x$:
\[\begin{aligned} v(t)=\dot{x}(t) &= -A\omega\sin(\omega t) + B\omega\cos(\omega t) \\[10pt] &= -\frac{mg}{k}\omega\sin(\omega t) + B\omega\cos(\omega t) \end{aligned}\]עכשיו נציב את התנאי $v(0) = v_0$ במשוואה $(4)$:
\[\begin{aligned} v(t=0) = v_0 &= -\frac{mg}{k}\omega\sin(0) + B\omega\cos(0) \\[10pt] &= B\omega \end{aligned}\]מכאן:
\[\boxed{B = \frac{v_0}{\omega}}\]ולכן הפתרון לפי תנאי ההתחלה שנתנו הוא:
\[\boxed{x(t) = \frac{mg}{k}\left(1 - \cos(\omega t)\right) + \frac{v_0}{\omega}\sin(\omega t)}\]דוגמה מורכבת: תנועה הרמונית של שתי מסות מחוברות בקפיץ
תיאור המערכת
יש לנו מערכת הכוללת:
- רצפה חלקה (ללא חיכוך)
- מסה גדולה $M$ הנמצאת על הרצפה החלקה
- מסה קטנה $m$ הנמצאת על גבי המסה הגדולה
- קפיץ המחבר בין שתי המסות
- אין חיכוך בין המסות: $\mu = 0$
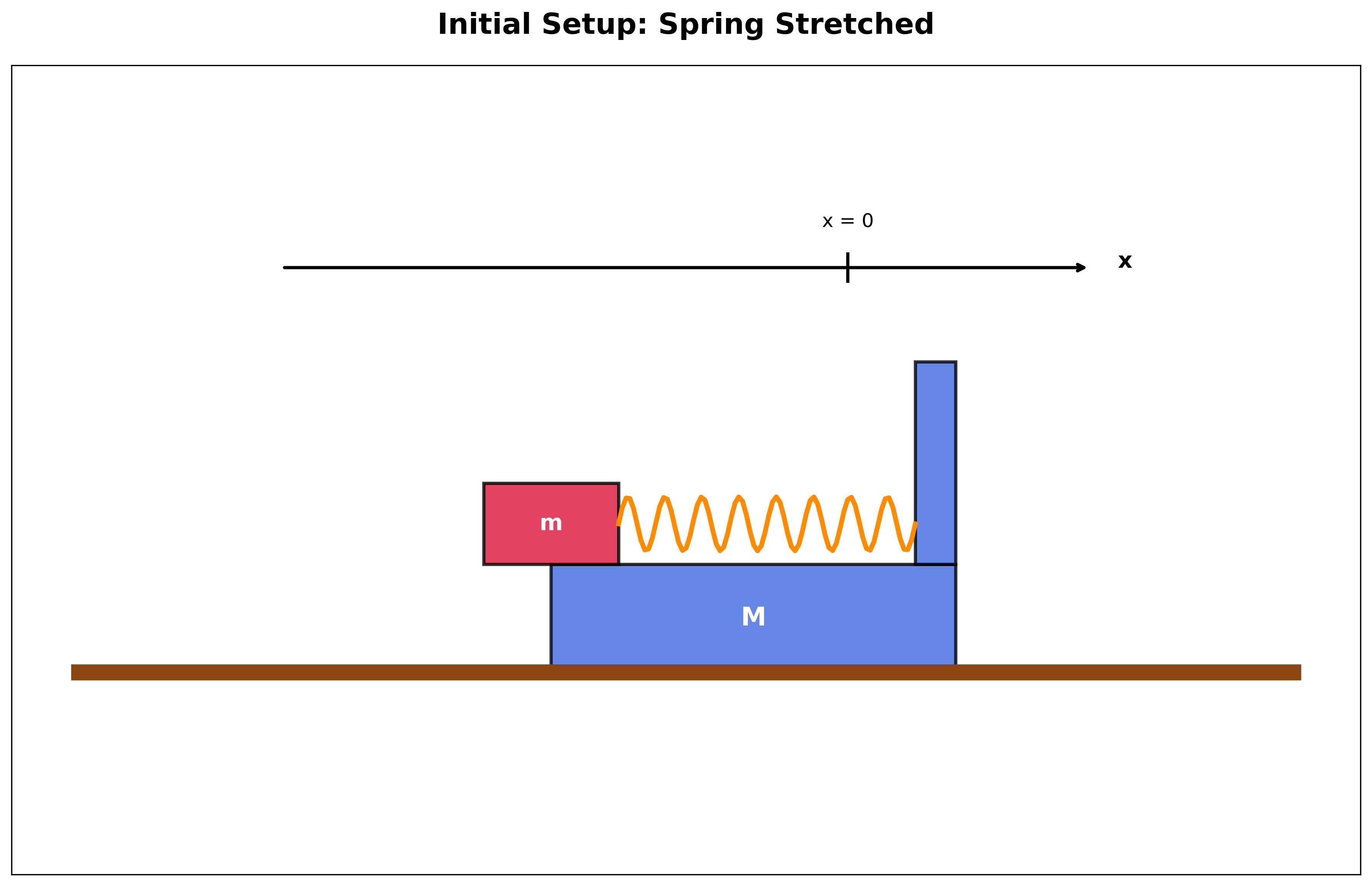
הגדרת קואורדינטות
נגדיר כי האורך הטבעי של הקפיץ הוא $x = 0$.
בזמן $t = 0$:
- אנו מותחים את הקפיץ (מסה קטנה נמצאת במיקום שלילי)
- משחררים את שתי המסות בו-זמנית
ניתוח הכוחות והתנועה
מה קורה לאחר השחרור?
כאשר אנו משחררים את המערכת:
- הקפיץ רוצה להתכווץ (כי הוא מתוח)
- הקפיץ מושך את המסה הקטנה ימינה (לכיוון $x = 0$)
- אותו קפיץ דוחף את המסה הגדולה שמאלה (כוח תגובה)
מערכות ייחוס
חשוב להבין: המסה הקטנה נמצאת במערכת ייחוס מואצת (של המסה הגדולה), ולכן פועלים עליה כוחות מדומים.
בניית משוואות התנועה
הגדרת משתנים
- $A$ = תאוצת המסה הגדולה (שמאלה, חיובית)
- $a$ = תאוצת המסה הקטנה יחסית למסה הגדולה (ימינה, חיובית)
- $x$ = מיקום המסה הקטנה במערכת ייחוס של המסה הגדולה
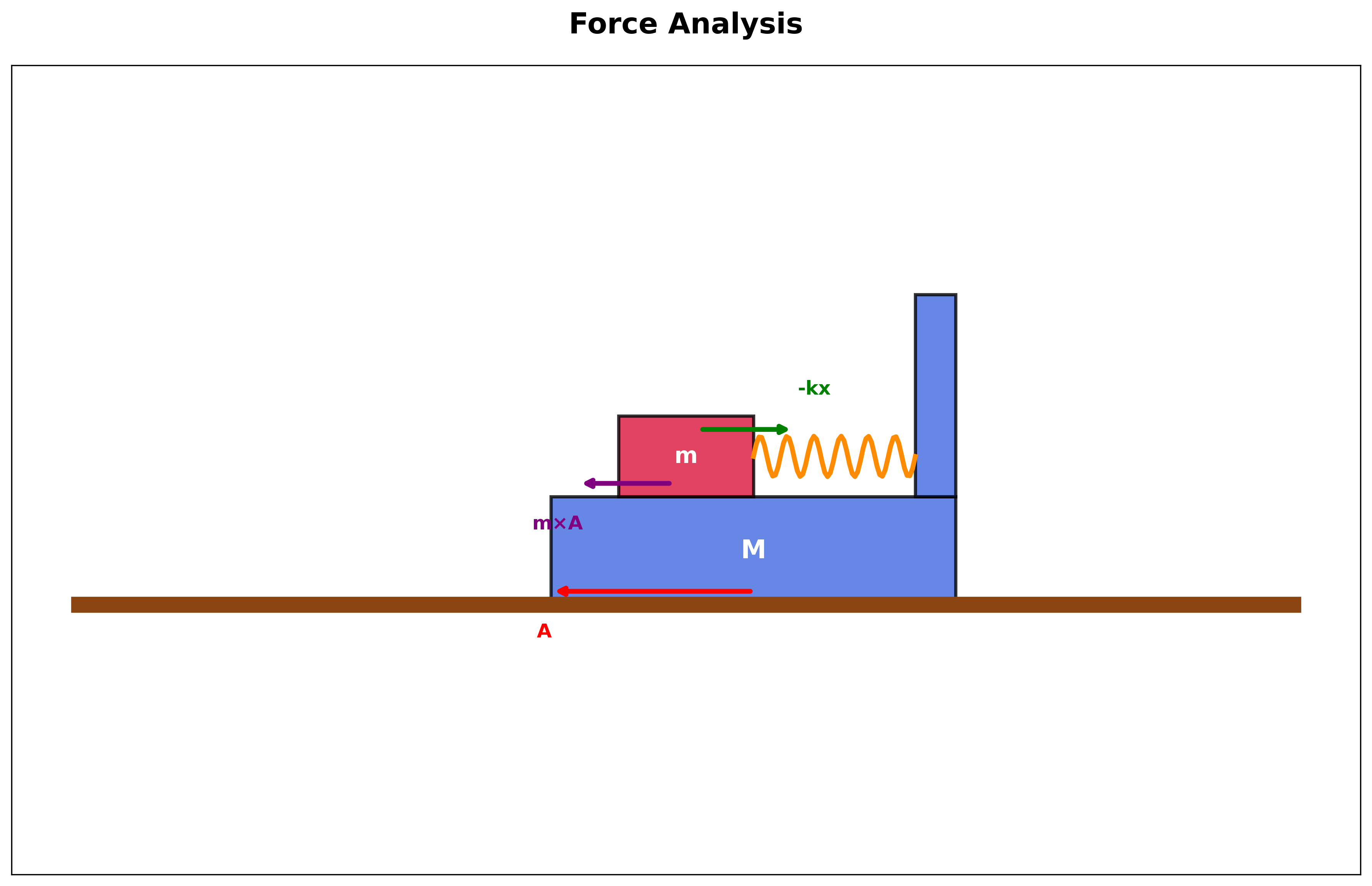
משוואה עבור המסה הקטנה
המסה הקטנה מרגישה:
- כוח הקפיץ: $-kx$ (מחזיר לעמדת שיווי משקל)
- כוח מדומה: $mA$ (בכיוון הפוך לתאוצת המערכת)
מהחוק השני של ניוטון ($\sum F = ma$):
\[m \cdot a = -kx + m \cdot A \tag{1}\]משוואה עבור המסה הגדולה
על המסה הגדולה פועל רק כוח הקפיץ. שוב לפי החוק השני של ניוטון:
\[M \cdot A = -kx\]מכאן:
\[\boxed{A = -\frac{k}{M}x}\]חיבור המשוואות
נציב את הביטוי עבור $A$ במשוואה $(1)$:
\[\begin{align} m \cdot a &= -kx + m \cdot \left(-\frac{k}{M}x\right) \\[10pt] m \cdot a &= -kx - \frac{mk}{M}x \\[10pt] m \cdot a &= -k\left(1 + \frac{m}{M}\right)x \\[10pt] a &= -\frac{k}{m}\left(1 + \frac{m}{M}\right)x \end{align}\]עיבוד לצורה סטנדרטית
\[\begin{align} a &= -\frac{k}{m} \cdot \frac{M + m}{M} \cdot x \\[10pt] a &= -\frac{k(M + m)}{mM} \cdot x \tag{2} \end{align}\]המסה המצומצמת
נגדיר את המסה המצומצמת:
\[\mu = \frac{mM}{m + M}\]אז המשוואה $(2)$ הופכת ל:
\[a = -\frac{k}{\mu}x\]או במונחים של נגזרות:
\[\frac{d^2x}{dt^2} = -\frac{k}{\mu}x\]הערה: ההצבה של $\mu$ מאפשרת לראות את התנועה ההרמונית של שתי המסות כבעיה של מסה יחידה $\mu$ המחוברת לקפיץ עם קבוע $k$. לדעתי היא לא טריוויאלית, ואני בספק אם הייתי מגיע אליה לבד.
פתרון המשוואה - תנועה הרמונית
המשוואה שקיבלנו היא משוואת תנועה הרמונית פשוטה:
\[\ddot{x} = -\omega^2 x\]כאשר:
\[\begin{align} \omega^2 &= \frac{k}{\mu} \\[10pt] &= \frac{k(m + M)}{mM} \\[10pt] \omega &= \sqrt{\frac{k(m + M)}{mM}} \end{align}\]הפתרון הכללי
\[x(t) = A\cos(\omega t) + B\sin(\omega t)\]כאשר $A$ ו-$B$ נקבעים מתנאי ההתחלה.

תכונות התנועה
תדירות ומחזור
המהירות הזוויתית: $\omega = \sqrt{\frac{k(m + M)}{mM}}$
זמן מחזור: $T = \frac{2\pi}{\omega}$
תדירות: $f = \frac{1}{T} = \frac{\omega}{2\pi}$
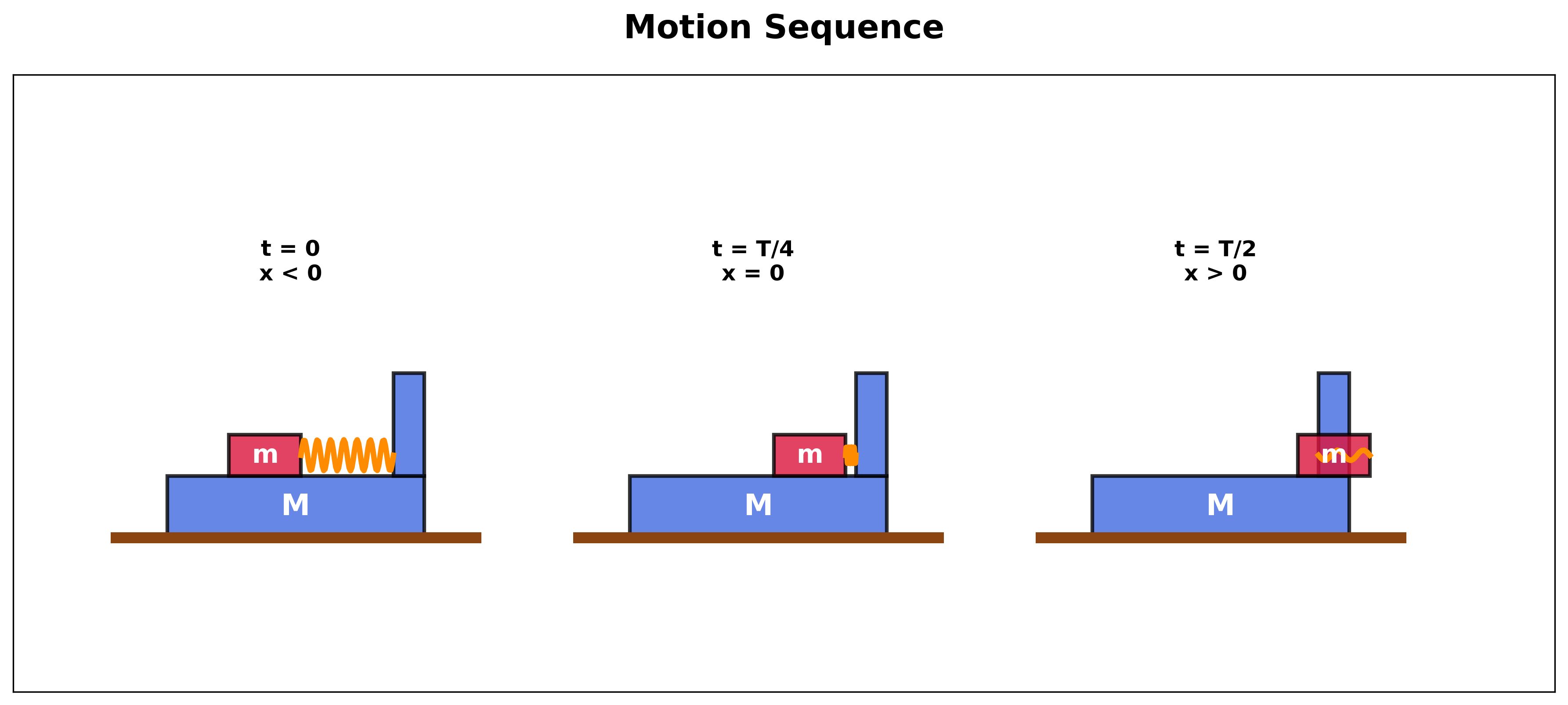
זמן התנגשות
הזמן עד להתנגשות בין המסות (כאשר $x = 0$) הוא רבע מחזור:
\[t_{collision} = \frac{T}{4} = \frac{\pi}{2\omega}\]סיכום
60% מהבעיה - הבנת הסיטואציה הפיזיקלית:
- זיהוי הכוחות הפועלים
- הבנת מערכות הייחוס המואצות
- זיהוי הכוחות המדומים
30% מהבעיה - בניית משוואות התנועה:
- יישום חוק ניוטון השני
- חיבור המשוואות
10% מהבעיה - הפתרון המתמטי:
- פתרון משוואה דיפרנציאלית רגילה
- יישום תנאי התחלה
תובנה פיזיקלית
המערכת מתנהגת כמו מסה יחידה $\mu$ (המסה המצומצמת) המחוברת לקפיץ בעל קבוע $k$. זוהי תובנה חשובה שמאפשרת לנו לפתור בעיות מורכבות של שתי מסות כבעיה פשוטה יותר של מסה יחידה.
הערה: כדי לפתור באופן מלא את מיקומי שתי המסות בזמן, יש צורך לפתור גם את המשוואה עבור המסה הגדולה, מה שמצריך אינטגרציה כפולה של הפתרון שמצאנו.
מעבר לנושא חדש: קואורדינטות פולאריות
התעסקנו בבעיות וקטוריות שנוח לטפל בהן באמצעות קואורדינטות קרטזיות. היה נוח לחלק את הכוחות לציר $x$, ציר $y$, ולפרק את הבעיה התלת-ממדית לשתיים או שלוש בעיות חד-ממדיות.
אבל לא מעט פעמים נתקלים במצב שבו לבעיה יש סימטריה גלילית או כדורית. בעיה פיזיקלית עם סימטריה רדיאלית היא בעיה שבה הכל תלוי אך ורק במרחק מהראשית. כלומר, תלוי בגודל של וקטור המקום $\vec{r}$.
סימטריה רדיאלית
אם יש לנו בעיה שתלויה אך ורק במרחק מהראשית, אז הכוח במקומות שבמרחק זהה מהראשית הוא זהה. במעגל, למשל, אין נקודה שמיוחדת ביחס לנקודות האחרות שנמצאות עליו - בכל נקודה הכוח תלוי רק בווקטור שיוצא אליה מהראשית.
בסיטואציות כאלה נוח לעבוד בקואורדינטות שמכבדות סימטריה רדיאלית, ולא בקואורדינטות קרטזיות שאינן מכבדות סימטריה רדיאלית.
מערכת צירים פולרית
במערכת צירים פולרית, יש לנו:
- רדיוסים בכיוונים שונים (קרניים)
- מעגלים ברדיוסים שונים
הקואורדינטות שמתארות את המערכת הזאת הן $r$ ו-$\theta$, כאשר:
- $r$ - המרחק מהראשית
- $\theta$ - הזווית שהרדיוס יוצר ביחס לציר $x$
וקטורי יחידה במערכת פולרית
נגדיר במערכת הפולארית שני וקטורי יחידה:
-
וקטור יחידה רדיאלי ($\hat{r}$):
\[\hat{r} = \cos\theta \cdot \hat{x} + \sin\theta \cdot \hat{y}\] -
וקטור יחידה אזימוטלי ($\hat{\theta}$):
\[\hat{\theta} = -\sin\theta \cdot \hat{x} + \cos\theta \cdot \hat{y}\]
שימו לב ש-$\hat{r}$ ו-$\hat{\theta}$ ניצבים זה לזה (המכפלה הסקלרית שלהם היא אפס) ושניהם וקטורי יחידה (אורכם 1).
וקטור המקום יינתן תמיד על ידי:
\[\vec{r} = r \cdot \hat{r}\]כאשר $r$ ו-$\hat{r}$ תלויים בזמן אם הגוף נע.
מהירות במערכת פולרית
מהירות היא הנגזרת של וקטור המקום לפי הזמן:
\[\vec{v} = \frac{d\vec{r}}{dt} = \dot{r}\hat{r} + r\dot{\hat{r}} \tag{1}\]מכיוון ש-$\hat{r}$ תלוי בזמן דרך $\theta(t)$, נמצא תחילה את $\dot{\hat{r}}$, כלומר, את הנגזרת של $\hat{r}$ לפי הזמן:
\[\begin{aligned} \dot{\hat{r}} &= \frac{d}{dt}(\cos\theta \cdot \hat{x} + \sin\theta \cdot \hat{y}) \\[10pt] &= (-\sin\theta \cdot \dot{\theta}) \cdot \hat{x} + (\cos\theta \cdot \dot{\theta}) \cdot \hat{y} \\[10pt] &= \dot{\theta} \cdot \hat{\theta} \end{aligned}\]נציב את $\dot{\hat{r}}$ במשוואה $(1)$ ונקבל שהמהירות היא:
\[\boxed{\vec{v} = \dot{r}\hat{r} + r\underbrace{\dot{\theta}\hat{\theta}}_{\dot{\hat{r}}}} \tag{2}\]יש לנו כאן שני רכיבים של המהירות:
- מהירות רדיאלית - $\dot{r}\hat{r}$ - המהירות בכיוון הרדיאלי
- מהירות משיקית - $r\dot{\theta}\hat{\theta}$ - המהירות בכיוון המשיק למעגל
זה מזכיר את מה שחלק אולי למדו בשיעורי פיזיקה בתיכון: $v = r\omega$ (כאשר $\omega = \dot{\theta}$ היא המהירות הזוויתית).
תאוצה במערכת פולרית
התאוצה היא הנגזרת של המהירות לפי הזמן:
\[\vec{a} = \frac{d\vec{v}}{dt} = \frac{d}{dt}(\dot{r}\hat{r} + r\dot{\theta}\hat{\theta})\]פתיחת הנגזרת לפי כלל המכפלה:
\[\vec{a} = \ddot{r}\hat{r} + \dot{r}\dot{\hat{r}} + \dot{r}\dot{\theta}\hat{\theta} + r\ddot{\theta}\hat{\theta} + r\dot{\theta}\dot{\hat{\theta}}\]מצאנו כבר ש-$\dot{\hat{r}} = \dot{\theta}\hat{\theta}$. נחשב גם את $\dot{\hat{\theta}}$:
\[\begin{aligned} \dot{\hat{\theta}} &= \frac{d}{dt}(-\sin\theta \cdot \hat{x} + \cos\theta \cdot \hat{y}) \\[10pt] &= (-\cos\theta \cdot \dot{\theta}) \cdot \hat{x} + (-\sin\theta \cdot \dot{\theta}) \cdot \hat{y} \\[10pt] &= -\dot{\theta} \cdot \hat{r} \end{aligned}\]לכן, התאוצה היא:
\[\boxed{\vec{a} = \underbrace{(\ddot{r} - r\dot{\theta}^2)\hat{r}}_{a_r} + \underbrace{(r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta}}_{a_{\theta}}} \tag{3}\]משוואה $(3)$ היא ביטוי כללי לתאוצה במערכת קואורדינטות פולאריות. היא מורכבת משני רכיבים:
- תאוצה רדיאלית - התאוצה בכיוון הרדיאלי: $a_r = (\ddot{r} - r\dot{\theta}^2)\hat{r}$
- תאוצה משיקית - התאוצה בכיוון המשיקי (האזימוטלי): $a_\theta = (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta}$
התאוצה בכיוון הרדיאלי משלבת בתוכה גם את הנגזרת של $\theta$ לפי הזמן וגם את הנגזרת של $r$ לפי הזמן.
נסכם את הביטויים שפיתחנו:
- וקטור המקום: $\vec{r} = r\hat{r}$
- וקטור המהירות: $\vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta} = v_r\hat{r} + v_{\theta}\hat{\theta}$
- וקטור התאוצה: $\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta} = a_r\hat{r} + a_{\theta}\hat{\theta}$
יישום למקרה של תנועה מעגלית
כזכור, שכשלמדנו תנועה מעגלית (שיעור 3), ראינו שווקטור המקום היה שווה ל:
\[\vec{r} = R\cos(\omega t)\hat{x} + R\sin(\omega t)\hat{y}\]אבל $\cos(\omega t)\hat{x} + \sin(\omega t)\hat{y}$ זה פשוט $\hat{r}$. כלומר, בתנועה מעגלית וקטור המקום תמיד מצביע לעבר נקודה על המעגל. גודלו $R$ לא משתנה עם הזמן, וכיוונו $\hat{r}$:
\[\boxed{\vec{r} = R\hat{r}}\]כזכור, וקטור המהירות בתנועה מעגלית קצובה היה שווה ל:
\[\vec{v} = -\omega R\sin(\omega t)\hat{x} + \omega R\cos(\omega t)\hat{y}\]וזה שווה ל:
\[\vec{v} = \omega R\hat{\theta}\]משום ש-$-\sin(\omega t)\hat{x} + \cos(\omega t)\hat{y}$ זה $\hat{\theta}$. זהו וקטור המהירות בתנועה מעגלית.
וקטור התאוצה בתנועה מעגלית היה שווה ל:
\[\vec{a} = -\omega^2 R\hat{r}\]שימו לב, כשהרדיוס $R$ קבוע, $\dot{r}$ מתאפס, $\ddot{r}$ מתאפס, ואם גם $\dot{\theta}$ קבוע (כלומר $\ddot{\theta}=0$), מקבלים:
\[\boxed{\vec{a} = -R\omega^2\hat{r}}\]סיכום: תיאור אלגנטי של תנועה מעגלית בקואורדינטות פולאריות
בתיאור הכי יפה, אלגנטי וכללי שמכבד את העובדה שאנחנו נעים על פני מעגל:
- וקטור המקום הוא $\vec{r} = R\hat{r}$ (פונקציה של $t$)
- וקטור המהירות הוא $\vec{v} = R\omega\hat{\theta}$ - זאת המהירות המשיקית
- וקטור התאוצה שווה ל-$\vec{a} = -\omega^2 R\hat{r}$ - זאת התאוצה הצנטריפטלית
והכוח שווה למסה כפול התאוצה, כלומר, הכוח הוא רדיאלי (מופנה לכיוון מרכז המעגל).
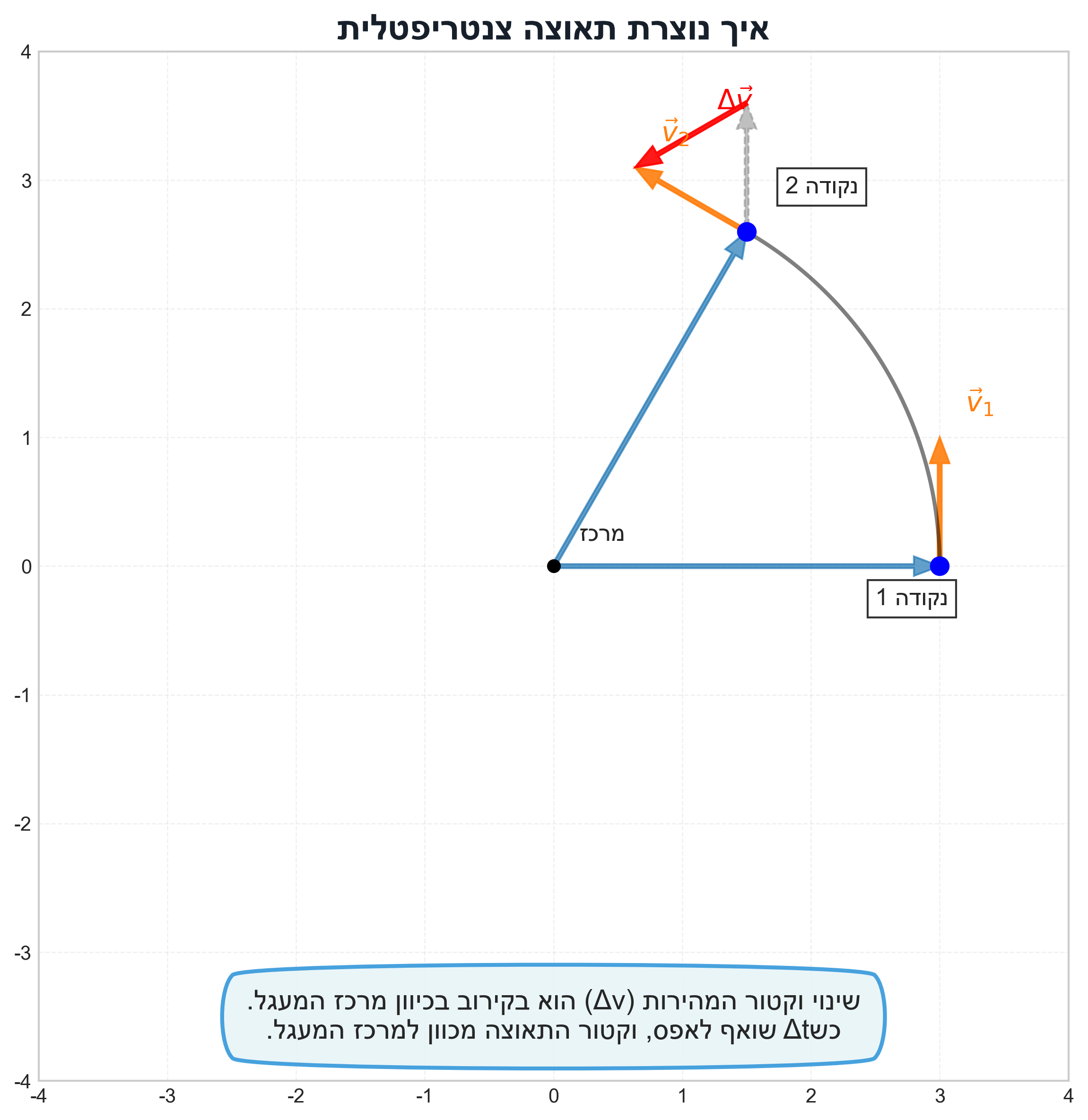
נראה שתיארנו את הבעיה מכל היבט שאפשר להעלות על הדעת:
- מיהו וקטור המקום כפונקציה של הזמן
- מיהו וקטור המהירות כפונקציה של הזמן, כגודל וככיוון
- מיהו וקטור התאוצה כפונקציה של הזמן, בייחס לוקטור המקום
- התאוצה בכיוון מינוס וקטור המקום - תאוצה צנטריפטלית
- שקול הכוחות שווה למסה כפול תאוצה
הכל נמצא בתיאור הזה. תיאור בפיזיקה סובב סביב תיאור המציאות כפי שהיא מתפתחת בזמן. כל הגדלים תלויים ב-$t$ - זהו תיאור מושלם (לשימושים שלנו).
דור פסקל