המשך: דיאגנוסטיקה רפואית וכלל בייז

בשיעור הקודם עסקנו בבעיה הבייזיאנית בתחום הדיאגנוסטיקה, בבעיית הסרטן. הפואנטה הייתה שהסיכוי לאדם להיות חולה, בהינתן שתוצאת הבדיקה היא חיובית, הוא 9$\%$.

זה אולי לא מרשים, בעיקר בהתחשב בכך שהבדיקה הצודקת היא לכאורה טובה ב-$99\%$. אנחנו רואים כאן את השקלול שכלל בייז עושה בין ההסתברות האפריורית להיות חולה לבין הסיכוי שהבדיקה תצא נכונה.

במקרה הזה ההסתברות האפריורית להיות חולה - השכיחות של המחלה - היא מאוד נמוכה, בפרט נמוכה ביחס לרזולוציה, ליכולת ההפרדה, ליכולת הבדיקה של אותה בדיקה.

זה מה שנותן לנו את האחוזים הדי עצובים האלה, את ה-positive predictive value הלא מספיק טוב הזה.

המלצות לפיתוח בדיקות דיאגנוסטיות

אם רוצים לבדוק או לפתח בדיקה לסרטן, לצורך העניין, שמופיע בשכיחות של $\frac{1}{1000}$, כדאי שהרזולוציה של הבדיקה תהיה הרבה יותר טובה מ-$\frac{1}{1000}$.

סרטן שמופיע בסיכוי של $\frac{1}{1000}$ - תרצו לבדוק עם בדיקה שצודקת, שטועה לצורך העניין ב-$\frac{1}{10,000}$ מקרים.

העיקרון: הסרטן מופיע בסיכויים מאוד קטנים, ובהתאמה הבדיקה, בשביל לזהות אותו, ובשביל שהבדיקה - תוצאה חיובית - תהיה אינפורמטיבית, היא צריכה להיות מאוד מדויקת, יותר מדויקת משכיחות הופעת המחלה.

זה מה שאנחנו רוצים שתשאירו בראש.

קיצור דרך לחישוב בייזיאני

קיצור דרך שיעשה את החיים קלים, לדעת המרצה, ושהוא שקול למה שאנחנו עשינו לחישובים ההסתברותיים, הוא לספור חולים ובריאים מתוך אוכלוסייה גדולה.

למשל, מתוך 100,000 נבדקים:

  • על פי השכיחות, 100 יהיו חולים
  • מתוכם 99 יזוהו על ידי הבדיקה
  • השאר, 99,900 יהיו בריאים
  • אבל מתוכם 999 יזוהו על ידי הבדיקה כחולים

לכן הסיכוי של נבדק חיובי להיות חולה הוא ההסתברות המותנת:

\[\begin{aligned} P(\text{Sick} \mid \text{Positive}) &= \frac{\text{Number of sick positives}}{\text{Total number of positives}} \\ &= \frac{99}{99 + 999} \end{aligned}\]

ככה יכולים לראות שבקירוב זה:

\[\frac{100}{100 + 1000} = \frac{100}{1100} \approx \frac{100}{1000} = 0.1 = 10\%\]

אבל ככה אפשר לעשות חישוב מהיר ופשוט, בשביל לקבל הערכה כמה הבדיקה באמת טובה. אם רוצים בדיוק, אז נחשב: $\frac{99}{99 + 999}$.

alt text

סיכום: החשיבות של כלל בייז בדיאגנוסטיקה

החשיבות של כלל בייז בדיאגנוסטיקה היא עצומה.

האינטואיציה: אם מחלה היא נדירה, הרוב המכריע של הנבדקים יהיו בריאים, וגם עם שגיאה חיובית קטנה, יהיו הרבה נבדקים בריאים עם תוצאה חיובית - מה שימסך או ישטוף את כל החיוביים שבאמת לוקים במחלה.

אפילו אם אנחנו מניחים שכל החולים חיוביים, עדיין מספר החולים החיוביים יכול להיות מאוד קטן ביחס למספר הבריאים החיוביים - שוב, אם הבדיקה מזהה בטעות חלק או אחוז קטן אפילו מהבריאים כחיוביים.

הבעיה הקוגניטיבית

אם כל הנושא הזה מבלבל, אז זה בסדר. דניאל כהנמן, שהלך לעולמו לפני כמה חודשים, ועמוס טברסקי, זיהו את הבעיות האלה בהערכה שלנו כבר בשנות ה-70. כהנמן קיבל אחרי מותו של טברסקי פרס נובל לכלכלה על העבודה הזו.

הפואנטה: בני אדם אינם מכונות בייזיאניות, ולכן האינטואיציה שלנו גרועה.

לכן אתם הרבה פעמים צריכים לשבת, לעשות חישוב קצר, כלשהו אפילו אינטואיטיבי, לספור מספר חולים או לדמיין אוכלוסייה גדולה. בגלל שבתנאים של אי-ודאות אנחנו נוטים לא לעשות חישובים על כלל בייז, ומתעלמים מההסתברות הפריורית.

בדוגמה של הסרטן, ההסתברות הפריורית מכתיבה שיש מעט מאוד חולים באוכלוסייה, והרבה מהחיוביים בבדיקה בעצם אינם חולים.

משתנים מקריים

עכשיו הנושא האחרון בעולם התיאורטי של ההסתברות - הנושא של משתנים מקריים. נרוץ על משתנים מקריים בדידים עד וכולל משתנה מקרי בינומי.

מבוא למשתנים מקריים

ראינו הסתברויות של מאורעות שמתקבלים כתוצאה מניסוי: סטודנט יאחר לשיעור, אדם יהיה חולה, בחרנו קלפים, קיבלנו בלק ג’ק, דברים כאלה.

הרבה פעמים נוח לבטא תוצאות של ניסוי במספרים גם אם התוצאה לא מספרית. ולשם כך מתמטיקאים וסטטיסטיקאים המציאו את הרעיון של משתנה מקרי.

הגדרה: משתנה מקרי הוא פונקציה שמתאימה לכל תוצאה במרחב המדגם ערך מספרי. זאת אומרת, משתנה מקרי הוא פונקציה על מרחב המדגם.

בדרך כלל מסמנים משתנים מקריים ב-$X$, $Y$, לפעמים $Z$, ובקיצור כותבים Random Variable (RV).

דוגמאות למשתנים מקריים

  1. מצב של מחלה: נגדיר משתנה מקרי $X$ שמקבל את הערך 1 אם האדם שנבדק חולה במחלה ו-0 אם הוא בריא.

  2. הימור ב-100 שקל על הטלת מטבע: אנחנו מגדירים משתנה מקרי $X$ שמקבל את תוצאת ההימור - פלוס 100 אם יצא עץ (הרווחתי 100 שקל), ומינוס 100 אם יצא פלי.

  3. הטלת קובייה, מדידת גובה: אנחנו יכולים להגדיר משתנה מקרי שהוא הגובה הנמדד, ובמקרה כזה הערכים שהמשתנה המקרי מקבל הם הגובה בסנטימטר של אותו אדם שמדדנו את גובהו.

דוגמה פשוטה: הטלת מטבע שלוש פעמים

נסתכל על דוגמה פשוטה - הטלת מטבע שלוש פעמים:

  • אנחנו מגדירים משתנה מקרי $X$ בתור מספר הפעמים שיצא עץ בשלוש ההטלות
  • משתנה מקרי $Y$ - ההפרש בין מספר הפעמים שיצא עץ למספר הפעמים שיצא פלי

מרחב המדגם הוא תוצאות הניסוי:

  • (פלי, פלי, פלי), (פלי, פלי, עץ), (פלי, עץ, פלי), (עץ, פלי, פלי)
  • (פלי, עץ, עץ), (עץ, פלי, עץ), (עץ, עץ, פלי), (עץ, עץ, עץ)

לכל תוצאה כזו יש ערך למשתנה מקרי $X$ וערך למשתנה מקרי $Y$:

  • הערך של המשתנה המקרי $X$ ב-(עץ, עץ, פלי) הוא מספר הפעמים שיצא עץ: שתיים
  • הערך של $Y$ ב-(עץ, פלי, עץ) הוא מספר הפעמים שיצא עץ (שתיים) פחות מספר הפעמים שיצא פלי (אחד) = אחד

חשיבות המשתנים המקריים בסטטיסטיקה

משתנים מקריים חשובים מאוד בעבודה סטטיסטית, כי הם ממדלים את העולם ההסתברותי.

אנחנו מתעניינים בתכונות באוכלוסייה, למשל קולסטרול בדם. התכונה באוכלוסייה היא משתנה מקרי - היא תוצאה מספרית של ניסוי שבו אנחנו מודדים את התכונה על פרט אקראי.

יותר מכך, ממוצע המדגם שאנחנו מכירים מסטטיסטיקה תיאורית גם הוא משתנה מקרי, כי הוא תוצאה מספרית של ניסוי שבו אנחנו מודדים תכונה על מספר פרטים.

אנחנו נשתמש בחוקים של ההסתברות, במה שלמדנו, בשביל ללמוד מתוך תוצאות המדגם על תכונות האוכלוסייה. זו העבודה של הסטטיסטיקאי.

הסטטיסטיקאי מסתכל על מדגם, רוצה ללמוד על האוכלוסייה, ועכשיו אנחנו לומדים על אוכלוסייה היפותטית שממנה אנחנו מוציאים משתנה מקרי, ובאמצעותם נוכל לייצר מדגם.

אז הסטטיסטיקה היא הבעיה ההפוכה להסתברות. ובשביל להבין את הסטטיסטיקה, אנחנו צריכים להבין הסתברות.

סוגי משתנים מקריים

בגדול, בקורס שלנו, אנחנו נגדיר שני סוגים של משתנה מקרי:

  1. משתנה מקרי רציף: מקבל כל ערך בטווח ערכים
    • זמן עד שמכונית מתקלקלת
    • רמת קולסטרול, גובה, משקל, טמפרטורה
  2. משתנה מקרי בדיד: מקבל ערכים בדידיים
    • מספר הילדים במשפחה
    • מספר לקוחות שנכנסו לחנות
    • מספר חולים שהבריאו מניתוח

משתנה מקרי בדיד מקבל ערכים בדידיים (1, 2, 3…), ומשתנה מקרי רציף מקבל כל ערך בטווח.

אנחנו נתחיל עם משתנים בדידים, ואז נמשיך לרציפים, בגלל שמשתנים בדידים יותר פשוטים להבנה, וגם יש להם מאפיינים שונים ממשתנים מקריים רציפים.

התפלגות של משתנה מקרי

הרעיון הראשון, או ההגדרה הראשונה, או המושג הראשון של משתנה מקרי, הוא התפלגות.

הגדרה: התפלגות מתארת את הערכים האפשריים שמשתנה מקרי יכול לקבל, ואת ההסתברויות שלהם.

דוגמאות להתפלגויות

דוגמה 1: אנחנו מטילים קובייה, אנחנו מגדירים משתנה מקרי $X$ שמקבל 1 אם הערך זוגי, ו-$-1$ אם הערך אי-זוגי:

  • ההסתברות לערך 1: $P(X = 1) = \frac{3}{6} = \frac{1}{2}$
  • ההסתברות לערך $-1$: $P(X = -1) = \frac{3}{6} = \frac{1}{2}$

דוגמה 2: אנחנו יכולים להגדיר משתנה מקרי $Y$ שמקבל:

  • 10 אם יצא 1 או 2 (הסתברות $\frac{2}{6} = \frac{1}{3}$)
  • 20 אם יצא 3, 4, 5 (הסתברות $\frac{3}{6} = \frac{1}{2}$)
  • 30 אם יצא 6 (הסתברות $\frac{1}{6}$)

דוגמה מפורטת: מספר העצים בשלוש הטלות מטבע

נסמן ב-$X$ את מספר העצים, או מספר ההצלחות, בשלוש הטלות מטבע. אנחנו רוצים לדעת מהם הערכים האפשריים ומה ההסתברויות המתאימות.

בואו נהיה קצת נאיביים ופשוט נרשום את כל התוצאות האפשריות של הניסוי:

תוצאה מספר עצים ($X$)
(פלי, פלי, פלי) 0
(פלי, פלי, עץ) 1
(פלי, עץ, פלי) 1
(עץ, פלי, פלי) 1
(פלי, עץ, עץ) 2
(עץ, פלי, עץ) 2
(עץ, עץ, פלי) 2
(עץ, עץ, עץ) 3

אנחנו יכולים לאגד את כל התוצאות האפשריות האלה בטבלת התפלגות:

ערך ($x$) הסתברות $P(X = x)$
0 $\frac{1}{8}$
1 $\frac{3}{8}$
2 $\frac{3}{8}$
3 $\frac{1}{8}$

עכשיו שכחנו לחלוטין מהניסוי שנמצא מאחורינו. יש לנו משתנה מקרי ויש לו התפלגות.

הגדרה פורמלית של התפלגות

באופן פורמלי, התפלגות של משתנה מקרי בדיד היא רשימה של:

  • הערכים שהמשתנה מקבל: $x_1, x_2, \ldots, x_k$
  • ההסתברות המתאימה לכל אחד מהערכים: $p_1, p_2, \ldots, p_k$

אנחנו מסמנים $p_i = P(X = x_i)$ - ההסתברות ל-$X$ להיות שווה ל-$x_i$.

בדרך כלל:

  • הערכים מסומנים בעותיות קטנות
  • המשתנה המקרי מסומן באותיות גדולות

תכונות של התפלגות

  1. הסתברות חיובית: ההסתברות לקבל כל ערך היא תמיד בין 0 ל-1: $0 \leq p_i \leq 1$

  2. הסתברות אפס לערכים לא רלוונטיים: ההסתברות לקבל ערך שהוא לא אחד מתוך הערכים שברשימה היא 0

  3. חיבור הסתברויות: ההסתברות לקבל ערך מתוך קבוצה של ערכים היא סכום ההסתברויות

    למשל:

    \[\begin{aligned} P(X = x_2 \text{ or } X = x_3) &= P(X = x_2) + P(X = x_3) \\ &= p_2 + p_3 \end{aligned}\]

    זה מתקיים כי המאורעות האלה זרים - אי אפשר לקבל גם $x_2$ וגם $x_3$ באותו זמן.

  4. נורמליזציה: סכום כל ההסתברויות חייב להיות שווה ל-1:

    \[\sum_{i=1}^{k} p_i = 1\]

    התכונה הזו נקראת נורמול.

בדיקת התכונות בדוגמה שלנו

אם נחזור לדוגמה של מספר העצים בשלוש הטלות מטבע, אנחנו רואים:

  1. כל ההסתברויות נמצאות בתחום $[0,1]$: $\frac{1}{8}, \frac{3}{8}, \frac{3}{8}, \frac{1}{8}$

  2. ההסתברות של $X$ לקבל כל ערך מלבד 0, 1, 2, 3 היא 0 (למשל $P(X = 4) = 0$ או $P(X = 1.5) = 0$)

  3. ההסתברות לקבל עץ אחד או שני עצים:

    \[\begin{aligned} P(X = 1 \text{ or } X = 2) &= P(X = 1) + P(X = 2) \\ &= \frac{3}{8} + \frac{3}{8} = \frac{6}{8} = \frac{3}{4} \end{aligned}\]

  4. סכום ההסתברויות:

    \[\frac{1}{8} + \frac{3}{8} + \frac{3}{8} + \frac{1}{8} = \frac{8}{8} = 1\]

ייצוג ויזואלי של התפלגות

דרך ויזואלית, גרפית, להציג התפלגות של משתנה מקרי בדיד היא באמצעות דיאגרמת עמודות.

  • בציר ה-$X$ יש לנו תוצאה אפשרית
  • בציר ה-$Y$ יש לנו את ההסתברות של אותה תוצאה

למשל, עבור דוגמה של מספר העצים מתוך 3 הטלות מטבע:

  • הסיכוי לקבל 0 הוא $0.125 = \frac{1}{8}$
  • הסיכוי לקבל 2 הוא $0.375 = \frac{3}{8}$

תוחלת (Expected Value)

נושא מאוד חשוב.

תוחלת היא הממוצע של משתנה מקרי בדיד.

הרעיון הבסיסי

למשל, אם יש לנו משתנה מקרי $X$ שמתאר תוצאה של ניסוי:

  • בהסתברות $\frac{1}{2}$ הוא מקבל 3
  • בהסתברות $\frac{1}{2}$ הוא מקבל 7

$X$ מקבל רק שני ערכים אפשריים בהסתברות שווה, והגיוני להגדיר את הממוצע שלהם בתור:

\[\frac{3 + 7}{2} = 5\]

המקרה הכללי יותר

נסתכל על דוגמה דומה: $X$ מקבל שוב שני ערכים אפשריים, אבל בהסתברויות שונות:

  • הוא מקבל ערך 3 בהסתברות 0.25
  • ערך 7 בהסתברות 0.75

ממוצע פשוט לא מייצג את הסיכוי הגבוה יותר לקבל 7. באופן אינטואיטיבי, אנחנו נצפה שהממוצע יסחב לכיוון 7.

אם הסיכוי לקבל 3 הוא, נגיד, מיליונית, והסיכוי לקבל 7 הוא מה שנשאר $1 - \frac{1}{1000000}$, אנחנו נצפה שהממוצע יהיה מאוד מאוד קרוב ל-7.

איך אנחנו עושים את זה מתמטית? אנחנו משתמשים בממוצע משוקלל.

אנחנו מגדירים את הממוצע של $X$ בתור:

\[\text{Expected value: } \quad \sum (\text{Value} \times \text{Probability})\] \[3 \times 0.25 + 7 \times 0.75 = 0.75 + 5.25 = 6\]

זה המשקל של 7. ואומנם, הממוצע הזה הוא 6, יותר קרוב ל-7.

הגדרה פורמלית של תוחלת

באופן כללי, התוחלת של משתנה מקרי בדיד שמקבל ערכים $x_1, x_2, \ldots, x_k$ בהסתברויות מתאימות $p_1, p_2, \ldots, p_k$:

מסמנים כ-$\mu$, כותבים $\mathbb{E}$ (expected value) של משתנה מקרי $X$, ומגדירים כ:

\[\mathbb{E}[X] = \sum_{i=1}^{k} x_i \cdot p_i\]

לוקחים כל ערך, כופלים במשקל שלו וסוכמים.

מי שיש לו אולי אינטואיציה פיזיקלית - זה בעצם מרכז הכובד של ההתפלגות. זה המרכז המשוקלל של ההתפלגות.

דוגמה: הטלת קובייה

אנחנו מטילים קובייה. מהי תוחלת של תוצאת ההטלה?

נסמן ב-$X$ את תוצאת ההטלה. התוחלת היא לפי הגדרה $x_i$ כפול המשקל של $x_i$:

\[\mathbb{E}[X] = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6}\] \[= \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = \frac{21}{6} = 3.5\]

אחרי החישוב הלא כל כך מסובך הזה, התוחלת היא $3.5$.

כל העבודה הקשה הייתה להבין איך אנחנו מפרמלים את ההתפלגות הזו. מהרגע שפרמלנו, אנחנו עובדים כמו מכונה:

  • הערך הראשון כפול ההסתברות
  • הערך השני כפול ההסתברות שלו
  • הערך השלישי כפול ההסתברות שלו
  • וכן הלאה

alt text

דוגמה נוספת: משתנה מקרי מותאם אישית

נגדיר משתנה מקרי חדש שבו:

  • $X = 10$ אם יצא 1 או 2
  • אחרת, הוא שווה ל-25

אם יצא 1 או 2, ההסתברות למאורע הזה היא $\frac{2}{6} = \frac{1}{3}$, ואנחנו מקבלים ערך 10.

אם יצא כל ערך אחר, ההסתברות לכל ערך אחר היא $\frac{4}{6} = \frac{2}{3}$, והערך הרלוונטי הוא 25.

שימו לב: כאן אנחנו כבר לא צריכים לדעת שום דבר על הקובייה. זאת אומרת, יש לנו משתנה מקרי שמקבל את הערך הזה בהסתברות הזו ואת הערך הזה בהסתברות הזו. כבר שכחנו ממרחב המדגם שלנו.

זו התועלת העצומה - אנחנו לא צריכים לספור או לחשוב על מרחב מדגם או שום דבר כזה. יש לנו משתנה מקרי, הוא מקבל ערכים, יש לו תכונות מסוימות, הסתברויות מסוימות, ואנחנו משתמשים בהסתברויות האלה.

אחרי שיש לנו את הטבלה הזו, מרחב המדגם כבר אינו רלוונטי.

נחשב את התוחלת של $X$:

\[\mathbb{E}[X] = 10 \cdot \frac{1}{3} + 25 \cdot \frac{2}{3} = \frac{10}{3} + \frac{50}{3} = \frac{60}{3} = 20\]

הבדלה בין משתנה מקרי לעומת מדגם

מדדי מדגם

ממוצע מדגם או שונות מדגם הם מדדים שמחושבים על סמך אוסף של תצפיות. הם מאפיינים סטטיסטיים של המדגם, ויכולה להיות, או חייבת להיות, חוקיות מסוימת בתצפיות.

משתנה מקרי

להבדיל, משתנה מקרי מקבל ערכים מסוימים בהסתברויות ידועות. למשתנה מקרי תמיד יש הסתברויות ידועות - הכל בו ידוע, או ידוע ברמה שאנחנו מסמנים את זה מתמטית במספר כלשהו.

בשימושים מסוימים הוא מייצג מודל למערכת שיש בה אי-ודאות. בשימושים אחרים הוא מייצג תכונה של כלל האוכלוסייה - אוכלוסייה שאולי רלוונטית לנו.

השוואה מפורטת

משתנה מקרי מדגם
אין גודל מדגם (או $n = \infty$) יש גודל מדגם $n$
אין תצפיות, יש $k$ ערכים אפשריים יש $n$ תצפיות: $x_1, x_2, \ldots, x_n$
לכל ערך יש הסתברות התפלגות = כמה פעמים מתקבל כל ערך
ההסתברות נתונה בטבלה צריכים לספור כדי לקבל התפלגות

הגדרת ממוצע

ממוצע של מדגם: רעיון יחסית פשוט שאנחנו מכירים מסטטיסטיקה תיאורית - לוקחים את כל הערכים, סוכמים אותם, ומחלקים בגודל המדגם:

\[\bar{x} = \frac{x_1 + x_2 + \cdots + x_n}{n}\]

תוחלת: אנחנו ממשקלים כל ערך על פי ההסתברות הרלוונטית שלו:

\[\mathbb{E}[X] = \sum_{i=1}^{k} x_i \cdot p_i\]

יש אנלוגיה - אם כאן הערך שלוש מופיע עשר פעמים מתוך חמישים, אז המשקל של הערך שלוש יהיה $\frac{10}{50} = \frac{1}{5}$.

יש דמיון, אבל כאן אנחנו לא צריכים לספור - המשקלים או המשקולות כבר נתונים לנו.

אינטואיציה לתוחלת

כמו שאמרנו, התוחלת של משתנה מקרי היא ממוצע משוקלל.

אנחנו יכולים לחשוב על התוחלת בתור מצב שבו אנחנו חוזרים על הניסוי מספר רב של פעמים - מספר קרוב לאינסוף של פעמים, מספר אינסופי של פעמים. בסוף אנחנו מחשבים את הממוצע על כל הערכים של $X$, והממוצע הזה יהיה שווה לתוחלת.

יחידות: היחידות של התוחלת הן אותן יחידות של $X$.

לדעת מה היחידות זה תמיד כזה “sanity check” - זה דרך לוודא שאתם עושים דברים נכון. אם אתם פתאום מקבלים משהו ומקבלים שהגובה נמדד בקילוגרמים, או התוחלת של הגובה היא עשרה קילוגרמים, אתם יודעים שעשיתם משהו לא נכון.

תמיד טוב לדעת מה הן היחידות ולסחוב אותן איתכם.

בעיית התכנון המשפחתי

אוקיי, אז בעיה שאנחנו נפתור כבר בסרטון הבא שכבר עלה בתכלס:

זוג החליט להביא ילדים לעולם והם ממש רוצים בת. הם החליטו להביא בנים לעולם עד שתיוולד להם בת, וכשתיוולד להם הבת הראשונה הם יפסיקו.

השאלות:

  • מה תהיה תוחלת מספר הבנות של הזוג הזה?
  • מה תהיה תוחלת מספר הבנים?
  • בממוצע לזוג כזה תהיינה יותר בנות או יותר בנים?

אנחנו יודעים שבממוצע לזוג כזה תמיד תהיה בת אחת - יעשו ילדים עד שתהיה להם בת. אבל בנים אולי יהיו להם אפס בנים, אולי יהיה להם בן אחד, אולי יהיה להם מאה בנים.

בשביל להבין בממוצע מה יקרה לזוג הזה וכמה ילדים יהיו לו וכמה בנות וכמה בנים, אנחנו נצטרך להשתמש במשתנים מקריים.

דוגמאות נוספות לתוחלת

דוגמה: רולטה

בואו נראה כמה כסף אפשר להרוויח בפעם הבאה שאתם מגיעים ללס וגאס.

ברולטה התוצאות האפשריות הן המספרים מ-0 עד 36, וכל אחד מתקבל בסיכוי שווה. אנחנו משקיעים שקל בהימור שיצא מספר זוגי:

  • אם יצא מספר זוגי: אנחנו מרווחים שקל (זאת אומרת מקבלים שני שקלים פחות סכום ההימור שזה שקל)
  • אם יצא מספר אי-זוגי או 0: אנחנו מפסידים שקל (זאת אומרת לא מקבלים שום דבר)

מהי תוחלת הרווח שלי?

אנחנו ממדלים את הרולטה כמשתנה מקרי:

  • בסיכוי $\frac{18}{37}$ (18 זוגיים מתוך 37 מקומות ברולטה) אנחנו מרווחים שקל
  • בסיכוי $\frac{19}{37}$ (מספר האי-זוגיים ואפס) אנחנו מפסידים שקל (מרווחים $-1$)

תוחלת הרווח:

\[\begin{aligned} \mathbb{E}[\text{profit}] &= 1 \cdot \frac{18}{37} + (-1) \cdot \frac{19}{37} \\ &= \frac{18-19}{37} = -\frac{1}{37} \approx -0.027 \end{aligned}\]

זאת אומרת שאם אנחנו הולכים לרולטה, בתוחלת אנחנו מפסידים משהו כמו שלוש אגורות בסיבוב (2.7 אגורות בסיבוב).

מסקנה: לא כדאי ללכת לרולטה.

דוגמה: הטלת מטבע שלוש פעמים (חזרה)

נסתכל על דוגמה של משתנה מקרי שנשתמש בו בהמשך. אנחנו מטילים מטבע שלוש פעמים ומסמנים ב-$X$ את מספר הפעמים שיצא עץ.

אנחנו רוצים לדעת מה התוחלת של $X$.

מההתפלגות שחישבנו קודם:

  • בהסתברות $\frac{1}{8}$ אנחנו מקבלים 0
  • בהסתברות $\frac{3}{8}$ מקבלים 1
  • בהסתברות $\frac{3}{8}$ מקבלים 2
  • בהסתברות $\frac{1}{8}$ מקבלים 3

חישוב התוחלת:

\[\mathbb{E}[X] = 0 \cdot \frac{1}{8} + 1 \cdot \frac{3}{8} + 2 \cdot \frac{3}{8} + 3 \cdot \frac{1}{8} = \frac{0 + 3 + 6 + 3}{8} = \frac{12}{8} = 1.5\]

התוחלת של מספר הפעמים שיצא עץ היא 1.5. זאת אומרת בממוצע, בסט של ניסויים כאלה, אנחנו מקבלים 1.5 עצים על כל ניסוי (או על כל שלוש הטלות).

זה הגיוני - בממוצע מצפים לקבל מחצית מההטלות כעצים.

alt text

דוגמה: זמן הישרדות

עוד דוגמה - בבדיקה/סקר התגלה גידול סרטני:

  • בהסתברות $0.5$: הגידול יהיה מסוג א’ וזמן ההישרדות יהיה 10 חודשים
  • בהסתברות $0.4$: הגידול יהיה מסוג ב’ וזמן ההישרדות יהיה 5 חודשים
  • בהסתברות $0.1$: הגידול יהיה מסוג ג’ וזמן ההישרדות יהיה 15 חודשים

מהי תוחלת זמן ההישרדות בחודשים?

נסמן ב-$X$ את זמן ההישרדות ונכתוב בטבלה (זה החלק של הפרמול - אנחנו לוקחים את השאלה ומעבירים אותה לעולם המתמטי):

זמן הישרדות (חודשים) הסתברות
10 0.5
5 0.4
15 0.1

התוחלת תהיה:

\[\begin{aligned} \mathbb{E}[X] &= 10 \cdot 0.5 + 5 \cdot 0.4 + 15 \cdot 0.1 \\ &= 5 + 2 + 1.5 = 8.5 \end{aligned}\]

זאת אומרת בממוצע אני אשרוד 8.5 חודשים.

שאלה מעניינת: תרופה מסוימת מבטיחה לחולה בדיוק 8 חודשי חיים. האם כדאי לו לקחת אותה? או האם אתם, בתור רופאים, תיתנו את התרופה הזו לפציינטים שלכם?

כנראה שלא, כי בממוצע התרופה הזו מגלחת חצי חודש (שבועיים) מהחיים של האדם שאתם נותנים לו אותה.

יש עוד שיקולים - בן אדם יודע בדיוק מתי הוא ימות, זה לאבד אי-ודאות. זה משהו שהרבה אנשים אולי כן ירצו, יש אנשים שכן ירצו. אבל בממוצע התרופה הזו חותכת שבועיים מהחיים - כנראה שלא כדאי לקחת אותה.

דוגמה: ביטוח רכב

דוגמה אולי יותר קונקרטית או יותר ארצית:

נאמר רכב מסוים שווה 50 אלף שקל, וביטוח רכב עולה 3 אלפים שקל לשנה. הסיכוי שהרכב יגנב או יאבד או יקרה לו משהו בשנה הוא 1%.

האם שווה לעשות ביטוח?

אם עשינו ביטוח - שילמנו 3 אלפים שקל ולא תהיינה הוצאות נוספות.

ואם לא עשינו ביטוח, נסמן ב-$X$ את תוחלת ההוצאות שלנו:

  • בסיכוי של $0.01$ הוצאנו 50 אלף שקל
  • בסיכוי של $0.99$ הוצאנו 0 שקל

האם שווה לעשות ביטוח?

בתוחלת, כאשר אנחנו לא עושים ביטוח, אנחנו מוציאים:

\[\mathbb{E}[X] = 50000 \cdot 0.01 + 0 \cdot 0.99 = 500 \text{ money per year}\]

הביטוח עולה 3,000 שקל לשנה. זאת אומרת שבממוצע הביטוח עולה 2,500 שקל יותר מאשר המצב שבו לא עשינו ביטוח.

אבל יש אנשים שמעדיפים לשלם את הכסף הזה בשביל שיהיה להם ראש שקט ולא יצטרכו לדאוג. לשקוע את כל הכסף הזה יכול להוציא אתכם - להכניס אתכם לקושי כלכלי.

תוחלת של סכום משתנים מקריים

כלל מאוד חשוב:

נגיד שנתונים שני משתנים מקריים $X_1$ ו-$X_2$ בעלי תוחלות ידועות, ו-$Y$ הוא הסכום שלהם. אנחנו מגדירים משתנה מקרי $Y$ להיות הסכום שלהם:

\[Y = X_1 + X_2\]

התוחלת של $Y$ שווה לסכום התוחלות - תמיד, תמיד, תמיד:

\[\mathbb{E}[Y] = \mathbb{E}[X_1 + X_2] = \mathbb{E}[X_1] + \mathbb{E}[X_2]\]

תוחלת של סכום היא סכום התוחלות - תמיד!

לא צריך תלות או אי-תלות, לא צריך לחשוב שום דבר. תוחלת של סכום היא סכום התוחלות תמיד.

אם רוצים, אפשר לחשב את זה (אולי זה חישוב קצת מסובך).

דוגמה: הטלת שתי קוביות

למשל:

  • משתנה מקרי $X_1$ הוא תוצאת הטלת קובייה 1
  • משתנה מקרי $X_2$ הוא תוצאת הטלת קובייה 2
  • $Y$ הוא הסכום של שתי ההטלות

התוחלת של $Y$ תהיה:

\[\mathbb{E}[Y] = \mathbb{E}[X_1] + \mathbb{E}[X_2] = 3.5 + 3.5 = 7\]

גם אם שתי הקוביות זהות (זהות זה אומר שאם אחת נופלת על 3, גם השנייה נופלת על 3; אם אחת נופלת על 5, גם השנייה נופלת על 5) - התוחלת תהיה 7.

גם אם הן זהות וגם אם הן בלתי תלויות - תוחלת של סכום היא סכום התוחלות תמיד.

הילוך אקראי (Random Walk)

דוגמה שמאוד תועיל לנו בהמשך היא הילוך אקראי או הילוך שיכור.

אנחנו נמצאים בבית בראשית הצירים. סיימנו ערב בפאב של ראש פינה ואנחנו הולכים צעד אחד ימינה או צעד אחד שמאלה בהסתברות $\frac{1}{2}$ כל אחד.

אנחנו מסמנים ב-$X$ את המיקום שלנו אחרי $k$ צעדים או אחרי $k$ זמן. נגיד עשינו 8 צעדים:

  • הסיכוי שלנו להיות ב-$(-8)$ הוא קטן מאוד
  • הסיכוי שלנו להיות ב-$(-2)$ הוא בערך 0.2 וקצת
  • סיכוי שלנו להיות ב-0 הוא כך וכך

אז $X$ הוא משתנה מקרי בעל התפלגות מסובכת. אנחנו רוצים לדעת אם אנחנו יכולים למצוא את התוחלת שלו בלי להתאמץ.

בואו נסתכל על הצעד ה-$i$. אנחנו מגדירים משתנה מקרי $X_i$ שמקבל:

  • $+1$ אם הלכנו ימינה בצעד ה-$i$
  • $-1$ אם הלכנו שמאלה בצעד ה-$i$

אז $X_i$ הוא השינוי במיקום שלנו, או במיקום של החלקיק, בצעד ה-$i$.

$X_i$ מקבל $-1$ בהסתברות $\frac{1}{2}$ ומקבל $+1$ בהסתברות $\frac{1}{2}$.

אפשר לראות שהמיקום שלנו הוא סכום הצעדים על פני כל הצעדים שעשינו:

\[X = X_1 + X_2 + X_3 + \cdots + X_k\]

זה הגיוני - מיקום שלנו הוא צעד הראשון ועוד הצעד השני ועוד הצעד השלישי ועוד הצעד ה-$k$.

אנחנו יודעים שהתוחלת של $X_i$ היא:

\[\mathbb{E}[X_i] = (-1) \cdot \frac{1}{2} + 1 \cdot \frac{1}{2} = 0\]

ולכן, תוחלת של סכום היא סכום התוחלות תמיד, תמיד, תמיד:

\[\mathbb{E}[X] = \mathbb{E}[X_1] + \mathbb{E}[X_2] + \cdots + \mathbb{E}[X_k] = 0 + 0 + \cdots + 0 = 0\]

תוחלת של המיקום שלנו היא 0. זאת אומרת שבממוצע אנחנו נשאר בפתח של הפאב החביב בראש פינה.

alt text

שונות (Variance)

נושא חשוב מאוד במשתנים מקריים אחרי התוחלת הוא השונות.

השונות היא מדד למידת הפיזור של הערכים שהמשתנה המקרי יכול לקבל. במובן מסוים השונות היא מדד לאי-ודאות.

הגדרת השונות

השונות מוגדרת באופן דומה לשונות של מדגם:

שונות של מדגם: לקחנו סטיות מממוצע המדגם $\bar{x}$, העלינו אותן בריבוע, סכמנו את הסטיות הריבועיות וחילקנו ב-$(n-1)$ או $n$ (זה גודל המדגם). למה מינוס 1? אנחנו לא ניכנס לזה, אנחנו נגיע לזה בהמשך.

השונות של משתנה מקרי מוגדרת בצורה אנלוגית לחלוטין:

אם $X$ מקבל ערכים $x_1, x_2, \ldots, x_k$ בהסתברויות מתאימות $p_1, p_2, \ldots, p_k$, אנחנו מסמנים את השונות ב-$\sigma^2$ או $\text{Var}(X)$.

השונות היא התוחלת של הסטיות מהתוחלת של המשתנה המקרי בריבוע:

\[\text{Var}(X) = \mathbb{E}[(X - \mu)^2] = \sum_{i=1}^{k} (x_i - \mu)^2 \cdot p_i\]

כאשר $\mu = \mathbb{E}[X]$ היא התוחלת.

התוחלת (אולי לא הודגש מספיק) היא העוגן שלנו, היא נקודת הייחוס. אז עכשיו אנחנו מודדים סטיות סביב העוגן שלנו.

נתנו את הדוגמה של הנסיעות שלנו לצפת - הנסיעה שלנו לצפת היא בממוצע 70 ק”מ נגיד. אז נמדוד כל נסיעה אחרת ביחס לעוגן שלנו של ה-70 ק”מ. נגיד היום נסעתי 70.5 ק”מ, אז הסטייה שלי מהעוגן תהיה 0.5 ק”מ.

וזה בדיוק מה שנכנס כאן.

בשביל לקבל, למיליון סיבות מתמטיות ובשביל לקבל ערכים חיוביים, אנחנו מעלים את הסטיות בריבוע ומגדירים את השונות בתור התוחלת של הסטייה הריבועית מהתוחלת.

או אם זה הסטייה מהעוגן - התוחלת של המשתנה המקרי - אנחנו מחשבים את הסטייה הריבועית מהעוגן ומחשבים את התוחלת של הסטייה הריבועית הזו מהעוגן.

אולי בצורה אחרת: אנחנו מחשבים סטייה ריבועית מהעוגן ומשקללים אותה על פי המשקל שלה. סטייה $(x_i - \mu)^2$ יש לה הסתברות של $p_i$ (כמובן, בגלל שהסיכוי של $x_i$ הוא $p_i$), מעלים את הסטייה בריבוע ונותנים לה את המשקל שלה.

דוגמה: שונות של הילוך אקראי

עבור הילוך אקראי, למשל, אנחנו רוצים לגלות מה השונות. אנחנו מסתכלים על צעד יחיד ואנחנו רוצים לחשב את השונות.

אז אנחנו יודעים שהעוגן שלנו הוא התוחלת, והעוגן הזה הוא אפס. חישבנו את זה כבר - התוחלת של המשתנה המקרי הזה היא אפס.

השונות היא סטייה ריבועית מהעוגן כפול ההסתברות לסטייה הזו, ועוד סטייה ריבועית אחרת מהעוגן כפול ההסתברות לסטייה הזו:

\[\begin{aligned} \text{Var}(X_i) &= (-1 - 0)^2 \cdot \frac{1}{2} + (1 - 0)^2 \cdot \frac{1}{2} \\ &= 1 \cdot \frac{1}{2} + 1 \cdot \frac{1}{2} = 1 \end{aligned}\]

השונות הזו של צעד אחד היא 1.

סטיית התקן (Standard Deviation)

סטיית התקן של משתנה מקרי בדיד מוגדרת באופן דומה למה שעשינו במדגם. סטיית התקן היא שורש השונות:

\[\sigma = \sqrt{\text{Var}(X)}\]

נחשב את השונות, ומתוכה נוציא שורש ונקבל את סטיית התקן.

יחידות:

  • לשונות יש יחידות של $X$ בריבוע
  • לסטיית התקן יחידות של $X$
  • שתיהן תמיד חיוביות

הסטייה האופיינית מ-$\mu$ היא בסדר גודל של סטיית התקן $\sigma$.

אם $\mu$ הוא העוגן, אז $\sigma$ (סטיית התקן) - וזה נורא נורא חשוב - היא הסרגל, היא אמת המידה, היא היחידה על פיה אנחנו מודדים סטיות.

או היא היחידה הנכונה במובנים מסוימים (אנחנו נראה בהמשך) למדוד סטיות. אז אתם יכולים להגיד שאנחנו במרחק של 500 מטר מהתוחלת - וזה בסדר. אתם יכולים גם להגיד אולי שאנחנו במרחק של חצי סטיית תקן מהתוחלת - וזה כבר אומר לכם… זה ייתן פירוש הסתברותי מועיל מאוד בהמשך.

אז תזכרו תמיד, בעיקר כשאנחנו דנים במשתנה מקרי נורמלי (אבל לא רק): סטיית התקן היא הסרגל, היא אמת המידה, היא מודדת מרחק, היא יחידת המידה למדידת מרחק מהעוגן.

העוגן הוא התוחלת, וסטיית התקן היא הסרגל.

דוגמה: חישוב שונות של הטלת מטבע שלוש פעמים

בואו נחשב שונות של משתנה מקרי בדיד פשוט - הטלת המטבעות.

אנחנו מטילים מטבע שלוש פעמים, כמו שראינו, מסמנים ב-$X$ כמה פעמים יצא עץ. יש לנו כבר את ההתפלגות, חישבנו אותה, וברגע שיש את ההתפלגות אנחנו לא צריכים את המשתנה המקרי - אנחנו יודעים מה הסיכוי ל-0, יודעים מה הסיכוי ל-1, סיכוי ל-2 וכו’.

מה השונות וסטיית התקן של $X$?

חישבנו מקודם שהתוחלת של $X$ היא 1.5, ועכשיו אנחנו רוצים למדוד סטיות מהעוגן הזה של ה-1.5.

\[\text{Var}(X) = \sum_{i} (x_i - 1.5)^2 \cdot p_i\]
  • בהסתברות $\frac{1}{8}$ הסטייה שלנו תהיה $(0 - 1.5)^2 = (-1.5)^2 = 2.25$
  • בהסתברות של $\frac{3}{8}$ הסטייה תהיה $(1 - 1.5)^2 = (-0.5)^2 = 0.25$
  • בהסתברות של $\frac{3}{8}$ הסטייה תהיה $(2 - 1.5)^2 = (0.5)^2 = 0.25$
  • בהסתברות של $\frac{1}{8}$ הסטייה תהיה $(3 - 1.5)^2 = (1.5)^2 = 2.25$
\[\begin{aligned} \text{Var}(X) &= 2.25 \cdot \frac{1}{8} + 0.25 \cdot \frac{3}{8} + 0.25 \cdot \frac{3}{8} + 2.25 \cdot \frac{1}{8} \\ &= \frac{2.25 + 0.75 + 0.75 + 2.25}{8} = \frac{6}{8} = 0.75 \end{aligned}\]

השונות היא 0.75.

סטיית התקן: $\sigma = \sqrt{0.75} \approx 0.87$

סטיית התקן היא אמת המידה לשינוי. אז במשתנה מקרי בדיד זה אומר לכם בערך כמה אתם קרובים לתוחלת. כמובן שאתם לא תהיו במקרה הזה בדיוק על התוחלת (התוחלת היא 1.5 ואתם יכולים לקבל רק ערכים שלמים), אבל זה נותן לכם אמת מידה.

במשתנה המקרי הזה אתם כנראה לא תהיו במרחק של 200 אלף מהתוחלת, ואתם גם לא תהיו במרחק של 0.0003 מהתוחלת. זה נותן לכם תחושה לפיזור של אותו משתנה מקרי, וזה יהיה יותר ויותר אינטואיטיבי כשנגיע למשתנה המקרי הנורמלי - זה המשתנה המקרי הכי חשוב שנלמד.

alt text

השוואה: מדגם לעומת משתנה מקרי

עכשיו אנחנו יכולים להוסיף לטבלה של ההשוואה בין מדגם למשתנה מקרי את השונות:

מדגם משתנה מקרי
שונות המדגם היא סטיות ריבועיות מממוצע המדגם מחולק במספר עדכניים שונות היא סטיות ריבועיות מהעוגן (מהתוחלת), כל אחת משוקללת על פי המשקל שלה (על פי ההסתברות שלה)
חישוב דורש ספירת תצפיות כל ההסתברויות נתונות

ההסתברות לסטייה הזו הוא $p_i$, ההסתברות לסטייה אחרת יהיה אחר.

תכונות של שונות

שונות של סכום משתנים מקריים

אם נתונים שני משתנים מקריים $X_1$ ו-$X_2$ עם שוניות ידועות, ואנחנו מגדירים משתנה מקרי בתור הסכום, ואנחנו מניחים ש-$X_1$ ו-$X_2$ אינם תלויים (זאת אומרת הערך של $X_1$ לא נותן מידע על הערך של $X_2$ וההפך), אז:

השונות של הסכום שווה לסכום השוניות:

\[\text{Var}(X_1 + X_2) = \text{Var}(X_1) + \text{Var}(X_2)\]

להבדיל מתוחלת:

  • תוחלת של סכום שווה לסכום התוחלות תמיד
  • השונות של סכום שווה לסכום השוניות אם המשתנים המקריים הם בלתי תלויים

אם הם תלויים אז השונות של הסכום תהיה יותר קטנה. אנחנו נגיע לזה במדגמים מזווגים.

דוגמה: שונות של הטלת שתי קוביות

זה כנראה פשוט - אתם יכולים לעשות את החישוב. זה לא באמת מסובך. חישוב של שונות של משתנה מקרי של הטלת קובייה כמו מקודם, והשונות של שתי ההטלות היא סכום השוניות.

דוגמה מעניינת: הילוך אקראי

דוגמה יותר מעניינת שמלמדת אותנו משהו על העולם היא עבור הילוך אקראי.

אז אנחנו יודעים שהילוך אקראי מורכב מ-$T$ צעדים ($T$ זה הזמן שאנחנו נותנים לעצמנו לצעוד). בכל צעד אנחנו הולכים ימינה בהסתברות $\frac{1}{2}$ או שמאלה בהסתברות $\frac{1}{2}$ - לוקחים צעד $-1$ בהסתברות $\frac{1}{2}$ וצעד $+1$ בהסתברות $\frac{1}{2}$.

התוחלת היא אפס. השונות היא אחד.

והשונות של כל ההילוך המקרי היא סכום השוניות של ההילוכים הפרטיים, בגלל שהצעדים אינם תלויים:

\[\begin{aligned} \operatorname{Var}(\text{Total position}) &= \operatorname{Var}(X_1) + \operatorname{Var}(X_2) + \cdots + \operatorname{Var}(X_T) \\ &= 1 + 1 + \cdots + 1 \\ &= T \end{aligned}\]

השונות של הסכום היא סכום השוניות, והשונות הזו היא $T$ (בגלל שזה $T$ פעמים 1).

סטיית התקן היא שורש של $T$:

\[\sigma = \sqrt{T}\]

מה זה אומר?

בממוצע, אמנם כשאנחנו יוצאים מהבר, בממוצע אנחנו נשאר במרכז הבר, אבל הסטייה האופיינית שלנו ממרכז הבר תהיה סימטרית לכל כיוון, והיא תהיה בסדר גודל של $\sqrt{T}$.

זאת אומרת:

  • אחרי עשרה צעדים, אנחנו נגיע אולי לרחוב של הירידה (סטיית תקן בסדר גודל של $\sqrt{10} \approx 3$)
  • אחרי מאה צעדים, אנחנו נגיע אולי כבר לצומת אליפלת אם התחלנו בבר הקבת ברוש פינה (סטיית תקן בסדר גודל של $\sqrt{100} = 10$)
  • אחרי אלף צעדים, אנחנו יכולים להגיע אולי באותה הסתברות או לצפת או לכנרת (סטיית תקן בסדר גודל של $\sqrt{1000} \approx 32$)

אמנם בממוצע אנחנו עדיין נשאר באמצע, אבל הפיזור של כל המקומות שאנחנו יכולים להגיע אליהם יגדל מאוד.

זאת אומרת בממוצע אתם באמצע, אבל פרקטית אתם רחוקים מהאמצע - אתם פשוט לא יודעים לאיזה כיוון. שני הכיוונים סימטריים, ולכן אתם בממוצע באמצע, אבל כנראה שהלכתם לאיבוד.

טרנספורמציות של משתנים מקריים בדידים

אם יש לנו משתנה מקרי $X$ שעבורו אנחנו יודעים את התוחלת והשונות, ואנחנו מעוניינים במשתנה מקרי חדש:

\[Y = aX + b\]

($X$ הוא משתנה מקרי, אבל עבורו אנחנו יודעים הכל)

למשל, אנחנו רוצים לעבור מטמפרטורה בצלזיוס לטמפרטורה בפרנהייט:

  • הטמפרטורה בצלזיוס היא $X$
  • טמפרטורה בפרנהייט תהיה בערך $Y = 2X + 30$ (זה קירוב של $\frac{9}{5}X + 32$)

או אם יש לנו זמן בשניות ופתאום אנחנו רוצים לעבור לזמן בדקות.

אנחנו רוצים לדעת מה התוחלת והשונות של המשתנה המקרי החדש.

תוחלת של טרנספורמציה לינארית

אנחנו יכולים להוכיח שהתוחלת מתנהגת כמו שאנחנו רוצים שהיא תתנהג - כמו שתוחלת של סכום היא סכום התוחלות.

טרנספורמציה לינארית של תוחלת היא תוחלת של אותה טרנספורמציה לינארית:

\[\mathbb{E}[aX + b] = a\mathbb{E}[X] + b\]

פה זה תוחלת של הטרנספורמציה הלינארית, ופה אנחנו לוקחים טרנספורמציה לינארית רק על התוחלת.

התוחלת תמיד (או לא רוצים להגיד תמיד - בקונטקסט שלנו בכל אופן) מתנהגת כמו שאנחנו רוצים.

שונות של טרנספורמציה לינארית

השונות היא זו שמסבכת אותנו.

אם אנחנו כופלים את המשתנה המקרי $X$ ב-$a$, השונות תגדל פי $a$ בריבוע:

\[\text{Var}(aX + b) = a^2 \text{Var}(X)\]

זה הגיוני בגלל שאם $a$ נגיד מייצג שינוי יחידות, אנחנו יודעים שהיחידות של השונות הן ריבוע יחידות של המשתנה המקרי. אז זה הגיוני שאם $a$ משנה יחידות, גם השונות תגדל בריבוע.

הוספת קבוע ($b$) לא משנה את הפיזור ולכן השונות לא תלויה בכלל ב-$b$.

סטיית התקן של טרנספורמציה לינארית

סטיית התקן היא שורש השונות, וכמובן שהיא תמיד חיובית. אז גם אם $a$ שלילי, אנחנו לוקחים ערך מוחלט של $a$:

\[\sigma_{aX+b} = |a| \sigma_X\]

האינטואיציה

הוספת קבוע פשוט לוקחת את כל ההתפלגות שלנו וסוחבת אותה ימינה. נגיד לקחנו טרנספורמציה שמוסיפה 5 - לקחנו את כל ההתפלגות ובצורה קשיחה הזזנו אותה ימינה.

אם אתם חושבים על מרכז כובד, אז מרכז הכובד שלנו נמצא עכשיו על הכיסא כי אנחנו בבית. ואם אנחנו מזיזים את כל ההתפלגות של המסה שלנו 5 צעדים ימינה, גם מרכז הכובד - גם התוחלת שלנו - תזוז 5 צעדים ימין.

מכפלה בקבוע זה כבר קצת יותר מבלבל. אם אנחנו לוקחים משתנה מקרי $X$ שיש לו התפלגות סביב 5, ומכפילים את כל התוצאות האפשריות פי 2, אז ההתפלגות גם נסחבת ימינה (כי אנחנו מכפילים את התוחלת) וגם מתנפחת.

התוחלת (שאתם רואים אינטואיטיבית - פשוט להסתכל על הגרפים) מוכפלת בקבוע פי 2:

  • מינוס 5 עבר לחמש
  • 8 עבר ל-16
  • 2 עבר ל-4

והמרכז באמת גדל פי 2. ההתפלגות הופכת להיות רחבה פי 2, מה שאומר שהשונות גדלה פי 4 ($2^2$), וסטיית התקן גדלה פי 2.

דוגמה: זמן נסיעה

דוגמה פשוטה - זמן נסיעה:

נסיעה ברכבת לוקחת 3 דקות, אבל יש זמן המתנה. זמן המתנה יכול להיות 1, 2, 3, 4, 5 או 6 דקות בהסתברות של שישית לכל זמן המתנה.

אנחנו רוצים לדעת מה צריך להיות זמן ההליכה כדי שיהיה עדיף ללכת.

תוחלת זמן המתנה:

\[\mathbb{E}[\text{waiting time}] = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6}\] \[= \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = \frac{21}{6} = 3.5\]

זמן הנסיעה הטוטלי הוא זמן ההמתנה פלוס זמן הנסיעה שהוא תמיד 3 ברכבת:

\[\text{total time} = \text{waiting time} + 3\]

תוחלת זמן הנסיעה הכולל ברכבת:

\[\mathbb{E}[\text{total time}] = \mathbb{E}[\text{waiting time}] + 3 = 3.5 + 3 = 6.5 \text{ minutes}\]

כלומר, אם זמן ההליכה קטן מ-6.5 דקות, עדיף ללכת מאשר לנסוע ברכבת.

זה מסיים את החלק שעוסק בתוחלת ובשונות של משתנים מקריים בדידים. בהרצאות הבאות נמשיך למשתנים מקריים ספציפיים כמו הבינומי והגיאומטרי.

משתנה מקרי ברנולי (Bernoulli Random Variable)

מבוא למשתנה מקרי בינומי

משתנה מקרי מאוד חשוב, למרות שהוא לא הכי חשוב, הוא משתנה מקרי בינומי.

בשביל להבין משתנה מקרי בינומי, אנחנו צריכים להציג משתנה מקרי יותר פשוט שמרכיב את המשתנה המקרי הבינומי, והוא משתנה מקרי ברנולי.

הגדרה: ניסוי ברנולי

ניסוי ברנולי הוא ניסוי מקרי עם שתי תוצאות אפשריות:

  • הצלחה או כישלון

אנחנו נותנים לסיכוי ההצלחה - מסמנים סיכוי ההצלחה ב-$p$, וסיכוי הכישלון ב-$(1-p)$.

דוגמאות:

  • הטלת מטבע: סיכוי ההצלחה אם, נגיד, אנחנו קוראים להצלחה עץ - והסיכוי להצלחה הוא $\frac{1}{2}$
  • זריקת קובייה: הצלחה אם יצא לנו 6, הסיכוי להצלחה הוא $\frac{1}{6}$

הגדרה: משתנה מקרי ברנולי

משתנה מקרי ברנולי מקבל:

  • 0 במקרה של כישלון, בהסתברות $(1-p)$
  • 1 במקרה של הצלחה, בהסתברות $p$

alt text

תכונות בסיסיות של משתנה מקרי ברנולי

תוחלת

התוחלת של משתנה מקרי ברנולי מחושבת בצורה פשוטה:

\[\mathbb{E}[X] = 0 \cdot (1-p) + 1 \cdot p = 0 + p = p\]

התוחלת היא $p$.

שונות

שונות של משתנה מקרי ברנולי:

\[\text{Var}(X) = (0-p)^2 \cdot (1-p) + (1-p)^2 \cdot p\]

כאשר $p$ זו התוחלת עכשיו:

  • $0-p = -p$ זו הסטייה של 0 מהתוחלת
  • $1-p$ זו הסטייה של 1 מהתוחלת

אנחנו יכולים לעשות אלגברה - זה כבר די פשוט:

\[\text{Var}(X) = p^2(1-p) + (1-p)^2 p = p[1-p](p + (1-p)) = p(1-p) \cdot 1 = p(1-p)\]

השונות היא $p(1-p)$.

דוגמאות:

  • אם $p = \frac{1}{2}$, אז השונות תהיה $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$
  • אם $p = \frac{1}{4}$, אז השונות תהיה $\frac{1}{4} \cdot \frac{3}{4} = 0.1875$

משתנה מקרי בינומי (Binomial Random Variable)

הגדרה

משתנה מקרי בינומי מונה מספר ההצלחות (ראינו את זה כבר) בסדרה של $n$ ניסויי ברנולי, המקיימת את הדרישות הבאות:

alt text

1. מספר ניסויים קבוע מראש

מספר ניסויים לא תלוי בתוצאות. אנחנו לא עושים ילדים עד שיוצאת לנו ילדה, אלא החלטנו מראש שאנחנו עושים חמישה ילדים. אנחנו לא משחקים ברולטה עד שאנחנו מנצחים, אלא החלטנו מראש שאנחנו משחקים ברולטה פעמיים.

2. ההסתברות להצלחה קבועה ושווה ל-$p$ בכל הניסויים

הסיכוי שלנו לילד זכר הוא זהה בכל לידה. הסיכוי שלנו לזכות ברולטה הוא זהה בכל משחק. זה סיכוי קבוע.

3. הניסויים בלתי תלויים

זה שנולד לנו ילד - זה שנולדו לנו למשל שני בנים רצופים - לא אומר שום דבר על הסיכוי שלנו ללדת בת בלידה הבאה. זה שהפסדנו עכשיו ברולטה שבע פעמים לא אומר שעכשיו, עכשיו, עכשיו אנחנו אמורים לזכות. זה לא נכון. הניסויים הם בלתי תלויים.

תכונות של משתנה מקרי בינומי

משתנה מקרי בינומי מקבל ערכים שלמים מ-0 עד מספר ההצלחות המקסימלי, $n$:

  • 0 הצלחות, או הצלחה אחת, או שתי הצלחות, או לכל היותר $n$ הצלחות

ההתפלגות תלויה בשני פרמטרים בלבד:

  • $n$ - מספר הניסויים
  • $p$ - ההסתברות להצלחה

סימון: אנחנו מסמנים $X \sim \text{Binomial}(n,p)$ - $X$ מתפלג בינומית עם $n$ ניסויים ו-$p$ סיכוי להצלחה.

alt text

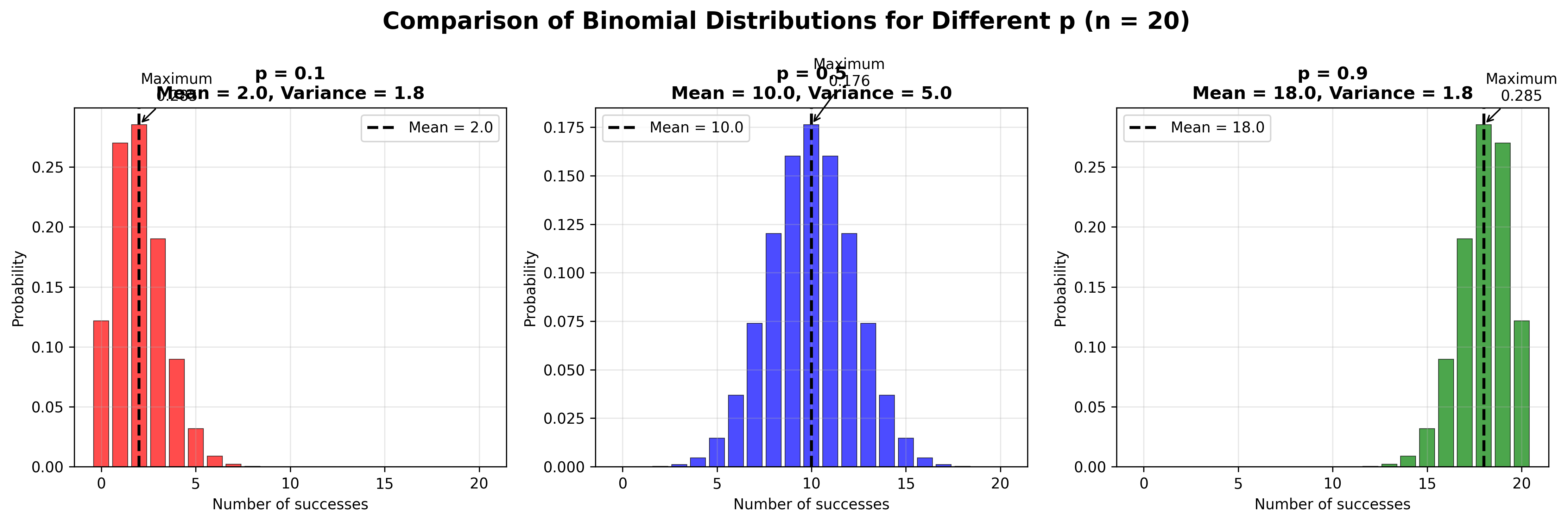
דוגמאות למשתנה מקרי בינומי

דוגמה בסיסית: הטלת מטבע

מטילים מטבע שלוש פעמים וסופרים את מספר ההצלחות. כמו שראינו מקודם, אנחנו קוראים לעץ הצלחה. ולכן $X \sim \text{Binomial}(3, \frac{1}{2})$.

דוגמה: לוטו

אנחנו יכולים למלא אלף תפסי לוטו. סיכוי ההצלחה הוא מיליונית. אנחנו סופרים את מספר הזכיות - זה משתנה מקרי בינומי עם אלף תפסי לוטו וסיכוי של מיליונית להצלחה: $X \sim \text{Binomial}(1000, 10^{-6})$.

דוגמה: הדבקה במחלה

100 אנשים באו במגע עם אדם חולה במחלה מסוימת. סיכוי ההידבקות 0.7, ואנחנו סופרים את מספר הנדבקים. “הצלחה” היא לא בהכרח אירוע חיובי - הצלחה היא מה שאנחנו סופרים.

אז 100 אנשים הגיעו במגע, ולכל אחד יש סיכוי בלתי תלוי להידבק - סיכוי של 0.7 להידבק. מספר הנדבקים מתפלג בינומית: $X \sim \text{Binomial}(100, 0.7)$.

בחינה: בינומי לעומת לא בינומי

דוגמאות לניסויים בינומיים:

  1. זריקה לסל: אנחנו זורקים לסל 20 פעמים, סופרים את מספר הקליעות - בינומי עם ההסתברות לקליעה קבועה.

  2. הוצאת כדורים עם החזרה: אנחנו מוציאים שני כדורים מתוך קערה עם שלושה כדורים אדומים ושני ירוקים, סופרים את מספר הכדורים האדומים. אם אנחנו מוציאים עם החזרה, אז כל פעם יש לנו את אותו סיכוי להוציא כדור אדום.

  3. קניית כרטיסי הגרלה: קונים כרטיסי הגרלה עם מספר כרטיסים קבוע מראש ואנחנו סופרים מספר הזכיות - זה משתנה מקרי בינומי.

דוגמאות לניסויים שאינם בינומיים:

  1. שיפור במהלך הזריקות: אנחנו זורקים לסל 20 פעמים, אבל תוך כדי הזריקות אנחנו משתפרים - זה לא בינומי.

  2. הוצאת כדורים ללא החזרה: אם ההוצאה נעשית ללא החזרה, אז ההסתברות להצלחה אינה קבועה - היא תלויה בהצלחות קודמות ולכן זה לא בינומי.

  3. קניית כרטיסים עד זכייה: אם כל זמן שאנחנו מפסידים אנחנו קונים כרטיסים, וכשאנחנו מרווחים אנחנו מפסיקים - מספר הניסויים אינו קבוע והניסויים תלויים, ולכן זה לא משתנה מקרי בינומי.

התפלגות של משתנה מקרי בינומי

התפלגות של משתנה מקרי בינומי קצת מסובכת, אבל בואו נבנה את זה מלמטה למעלה.

בניית ההתפלגות הבינומית

מקרה פשוט: ניסוי אחד ($n=1$)

נסתכל על המקרה הכי פשוט - שיש לנו ניסוי אחד. מה ההסתברות? מה ההתפלגות?

זה פשוט משתנה מקרי ברנולי:

  • הסיכוי לכישלון (אפס הצלחות) הוא $(1-p)$
  • סיכוי להצלחה אחת הוא $p$

שני ניסויים ($n=2$)

הסיכוי לקבל אפס הצלחות הוא סיכוי לכישלון כפול סיכוי לכישלון: $(1-p)^2$

הסיכוי לקבל הצלחה אחת הוא הסיכוי להצלחה כפול סיכוי לכישלון, פלוס הסיכוי לכישלון כפול הסיכוי להצלחה (הצלחה-כישלון או כישלון-הצלחה): $2p(1-p)$

הסיכוי לשתי הצלחות הוא $p^2$ - סיכוי להצלחה כפול סיכוי להצלחה. אנחנו רק משתמשים פה בכלל הכפל.

שלושה ניסויים ($n=3$)

התפלגות בינומית עם שלושה ניסויים וסיכוי הצלחה $p$, או $\text{Binomial}(3,p)$:

  • הסיכוי לקבל אפס הצלחות: $(1-p)^3$ (כישלון, כישלון, כישלון)

  • הסיכוי לקבל הצלחה אחת:

\[p(1-p)^2 + (1-p)p(1-p) + (1-p)^2p = 3p(1-p)^2\]

(הצלחה-כישלון-כישלון + כישלון-הצלחה-כישלון + כישלון-כישלון-הצלחה)

בצורה דומה אנחנו מחשבים את הסיכוי לשתי הצלחות ולשלוש הצלחות. כמובן שסכום ההסתברויות שווה לאחד.

הנוסחה הכללית

אם $X$ משתנה מקרי בינומי כללי עם פרמטרים $n$ ו-$p$ (כלומר $n$ ניסויים ו-$p$ סיכוי להצלחה), אז ההסתברות ש-$X$ יקבל ערך מסוים $k$ מחושבת על פי:

ההסתברות לסדרה מסוימת שבה $k$ הצלחות ו-$(n-k)$ כישלונות: $p^k(1-p)^{n-k}$

הסיכוי הזה שווה לכל אחת מהסדרות שבהן יש $k$ הצלחות ו-$(n-k)$ כישלונות, כמו שראינו מקודם.

עבור $n=5$, ההסתברות לסדרה (כישלון, כישלון, הצלחה, כישלון, הצלחה) - כלומר שתי הצלחות - הוא:

\[(1-p)(1-p)(p)(1-p)(p) = p^2(1-p)^3\]

וכל תמורה אחרת - כל צירוף אחר של כישלונות והצלחות, כל עוד יש לנו שתי הצלחות ושלושה כישלונות - אז ההסתברות לסדרה מסוימת עם $k$ הצלחות ו-$(n-k)$ כישלונות היא $p^k(1-p)^{n-k}$.

אבל יש יותר מסדרה אחת של הצלחות וכישלונות שיובילו ל-$k$ הצלחות בסך הכל. אז אנחנו צריכים לספור כמה סדרות כאלה יש.

למשל, יש עשר סדרות של חמישה ניסויים עם שתי הצלחות. בואו נספור:

אנחנו יכולים לקודד את הסדרות האלה על פי מיקום ההצלחות:

  • אנחנו מקודדים את הסדרה (הצלחה, הצלחה, כישלון, כישלון, כישלון) באמצעות (1,2) - הצלחה במקום 1 והצלחה במקום 2
  • מקודדים את הסדרה (כישלון, הצלחה, כישלון, הצלחה, כישלון) באמצעות (2,4) - הצלחה במקום 2 והצלחה במקום 4

הקידוד הוא מיקום ההצלחות - זאת אומרת ההסתברות לשתי הצלחות היא:

עשר אפשרויות לבחור סדרה עם שתי הצלחות ושלושה כישלונות, ולכל אחת מהסדרות האלה סיכוי של $p^2(1-p)^3$

מספר הסדרות - המקדם הבינומי

אז כמה סדרות יש סך הכל? אנחנו מחפשים את מספר הסדרות באורך $n$ שמכילות $k$ הצלחות.

אבל אנחנו יכולים פשוט לספור את מספר הסדרות הזה בתור מספר אפשרויות לבחור את המיקום של ההצלחות. כאן פשוט בחרנו את המיקום של ההצלחות - אנחנו מתעלמים מהתוכן הפנימי ובוחרים:

  • הצלחה במקום הראשון, הצלחה במקום השני
  • הצלחה במקום הראשון, הצלחה במקום השלישי

עכשיו אנחנו רק סופרים - אנחנו לא מחשבים הסתברויות, אנחנו רק סופרים כמה אפשרויות יש לנו לבחור שתי הצלחות - לבחור מיקומים לשתי הצלחות בתוך סדרה של חמישה ניסויים עם שתי הצלחות בדיוק.

זה מספר אפשרויות לבחור $k$ עצמים מתוך קבוצה של $n$ עצמים. אנחנו בוחרים את המקום הראשון ואת המקום השני, או את המקום הראשון והמקום השלישי, או את המקום השני והמקום הרביעי, המקום השני והמקום החמישי, אנחנו בוחרים את המקום השלישי והמקום החמישי, או שאנחנו בוחרים את המקום הרביעי והמקום החמישי.

סך הכל, מספר האפשרויות הזה הוא מספר האפשרויות לבחור $k$ עצמים מתוך קבוצה של $n$ עצמים.

אבל כבר חישבנו את המספר הזה! מספר האפשרויות לבחור $k$ עצמים מתוך $n$, או $k$ מקומות להצלחה בסדרה של $n$ ניסויים, הוא המקדם הבינומי $\binom{n}{k}$.

זה דבר שחישבנו. כרגע אנחנו יודעים שהוא קיים - אנחנו לא צריכים עכשיו לחזור ולהיזכר איך חישבנו את זה. אנחנו זוכרים, אבל אנחנו לא חייבים. פשוט צריכים לזכור שאיפשהו חישבנו את זה - רצוי שאנחנו נדע לחשב את זה שוב, אבל זה שחישבנו את זה פעם אחת ואנחנו כבר יודעים את צורת החישוב - זה מספיק.

אז יש לנו:

  • $n$ אפשרויות לבחור את ההצלחה הראשונה
  • כפול $(n-1)$ אפשרויות לבחור את ההצלחה השנייה
  • כפול $(n-2)$ אפשרויות לבחור את ההצלחה השלישית
  • …

יש לנו סך הכל $n \cdot (n-1) \cdot (n-2) \cdots (n-k+1)$ אפשרויות לבחור $k$ מקומות מתוך $n$.

אבל בגלל שאין לנו חשיבות לסדר, הפרוצדורה הזו בשורה העליונה ספרה כל סדרה מסוימת של $k$ מקומות $k!$ פעמים. כבר עשינו את זה.

לכן מספר הסדרות עם $k$ הצלחות מתוך $n$ הוא המנה של השורה העליונה עם השורה התחתונה:

\[\binom{n}{k} = \frac{n!}{k!(n-k)!}\]

אפשר לכתוב את זה בצורה קצת יותר קומפקטית עם פקטוריאל, ואנחנו מסמנים את זה בתור “$n$ choose $k$” - המקדם הבינומי $\binom{n}{k}$.

הנוסחה הסופית להתפלגות בינומית

מספר הסדרות של $n$ ניסויים שיש להם בדיוק $k$ הצלחות הוא המקדם הבינומי $\binom{n}{k}$.

וההסתברות לקבל כל סדרה מסוימת היא $p^k(1-p)^{n-k}$.

ולכן הסיכוי לקבל $k$ הצלחות עבור סדרה כלשהי - הסיכוי לקבל $k$ הצלחות מתוך ניסוי כלשהו - הסיכוי שמשתנה מקרי בינומי יהיה שווה ל-$k$ הוא:

\[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\]

מה יש לנו כאן?

  • כאן יש לנו סיכוי לקבל $k$ הצלחות בצורה ספציפית - סדרה מסוימת עם $k$ הצלחות
  • וכאן אנחנו סוכמים על ידי כך שאנחנו סופרים כמה סדרות כאלה יש

כל עוד הבנתם את שתי החתיכות האלה, הבנתם את הנוסחה הבינומית.

מה שנותר לכם, אם תרצו, זה להבין מאיפה מגיעה הנוסחה הזו $\binom{n}{k}$. אתם צריכים לשכנע את עצמכם (ועשינו את זה כבר) שזה מספר אפשרויות לבחור $k$ עצמים מתוך $n$ ללא חשיבות לסדר.

כאן $n$ הוא מספר העצמים - הוא מספר המיקומים של ההצלחות או הכישלונות, אלה הניסויים. ו-$k$ אלו המיקומים של ההצלחות.

סיכום: נוסחת ההתפלגות הבינומית

עבור משתנה מקרי בינומי:

אם $X$ משתנה מקרי בינומי עם פרמטרים של $n$ ניסויים ו-$p$ הצלחות, ההסתברות ש-$X$ יקבל את הערך $k$ (זאת אומרת ההסתברות ל-$k$ הצלחות מתוך $n$ ניסויים) היא:

\[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\]

alt text

איך אנחנו מקבלים את זה? שוב:

  • סיכוי לסדרה ספציפית עם $k$ הצלחות ו-$(n-k)$ כישלונות: $p^k(1-p)^{n-k}$
  • ו-$\binom{n}{k}$ הוא מספר הסדרות האלו - אז אנחנו בעצם סוכמים את כל האפשרויות הללו.

דוגמאות לחישובי התפלגות בינומית

דוגמה 1: הטלת קובייה

אנחנו מטילים קובייה שלוש פעמים ומגדירים הצלחה בתור שש. נסמן ב-$X$ את מספר ההצלחות.

פרמול: $X$ הוא משתנה מקרי בינומי עם $n=3$ ניסויים ו-$p=\frac{1}{6}$ סיכוי להצלחה.

עכשיו אנחנו בעולם המתמטי - אנחנו לא צריכים את העולם האמיתי בשביל לעשות את החישובים. אנחנו עושים את החישובים בעולם המתמטי.

חישוב ההתפלגות של $X$:

על פי הנוסחה, הסיכוי ל-$X$ להיות שווה ל-$k$ הוא:

\[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} = \binom{3}{k} \left(\frac{1}{6}\right)^k \left(\frac{5}{6}\right)^{3-k}\]

הסיכוי ל-0 הצלחות

\[P(X = 0) = \binom{3}{0} \left(\frac{1}{6}\right)^0 \left(\frac{5}{6}\right)^3\]

$\binom{3}{0} = 1$ (מספר הדרכים לבחור 0 עצמים מתוך 3)

למה $0! = 1$?

\[P(X = 0) = 1 \cdot 1 \cdot \left(\frac{5}{6}\right)^3 = \frac{125}{216}\]

הסיכוי ל-1 הצלחה

\[P(X = 1) = \binom{3}{1} \left(\frac{1}{6}\right)^1 \left(\frac{5}{6}\right)^2\] \[\binom{3}{1} = \frac{3!}{1! \cdot 2!} = \frac{6}{1 \cdot 2} = 3\] \[P(X = 1) = 3 \cdot \frac{1}{6} \cdot \left(\frac{5}{6}\right)^2 = 3 \cdot \frac{1}{6} \cdot \frac{25}{36} = \frac{75}{216}\]

וכן הלאה לשאר הערכים…

בקלות אפשר לבדוק שסכום ההסתברויות שווה ל-1.

מקרים פרטיים

מקרה פרטי:

  • $P(X = 0) = (1-p)^n$ - הסיכוי ל-$X$ להיות שווה 0
  • $P(X = n) = p^n$ - הסיכוי ל-$X$ להיות שווה ל-$n$

אומנם יש רק אפשרות אחת לבחירת הסדר - זה המקרה הבינומי שקצת התבלבלנו בהסבר שלו מקודם.

לא צריכים להסביר למה $0! = 1$, אלא למה $\binom{n}{n} = \binom{n}{0} = 1$.

אם זה בילבל אתכם, אז אולי נפסיק להיכנס לזה. בכל אופן, המקדם הבינומי שווה ל-1 - יש רק אפשרות אחת לבחירת הסדר, ואנחנו מקבלים את המקרים הפרטיים האלה.

כאשר $p = \frac{1}{2}$ (מקרה פרטי אחר):

ההסתברות של $X$ להיות שווה ל-$k$ היא:

\[P(X = k) = \binom{n}{k} \left(\frac{1}{2}\right)^n\]

כמספר הדרכים לבחור את ההצלחות והכישלונות כפול $\left(\frac{1}{2}\right)^n$, כי $p = 1-p = \frac{1}{2}$ ואנחנו מקבלים הכל ביחד.

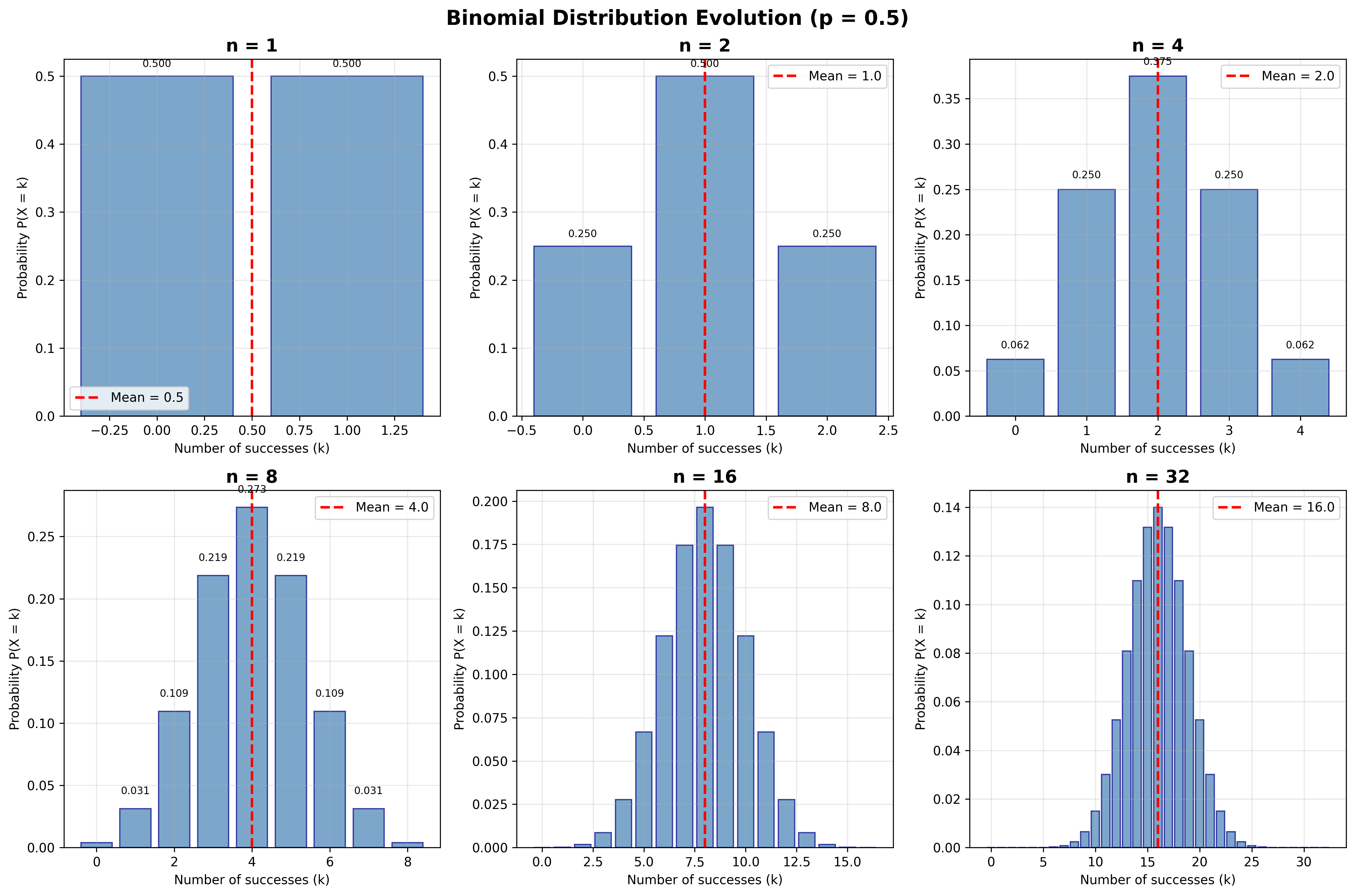
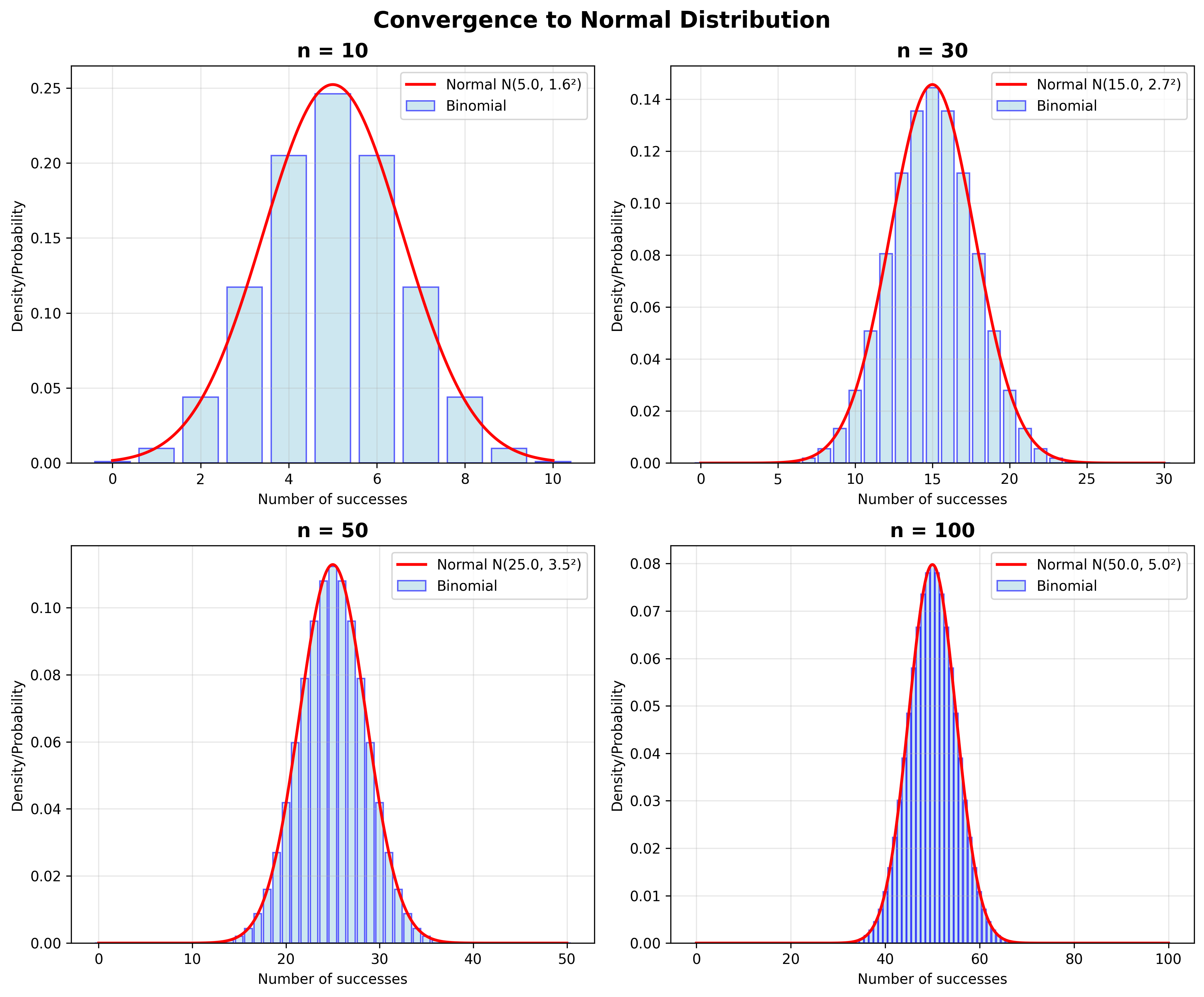
ייצוג גרפי של ההתפלגות הבינומית

דרך נחמדה להבין התפלגות בינומית היא גרפית.

אנחנו רואים שהגרפים - ההיסטוגרמות עבור:

  • $n = 1$
  • $n = 2$
  • כש-$n$ גדל

מתכנסים למשהו כזה יפה וסימטרי.

שימו לב שהתוחלת גדלה:

  • כאן התוחלת היא $\frac{1}{2}$
  • תוחלת היא 1
  • תוחלת היא 2
  • תוחלת היא 4
  • תוחלת היא 8
  • תוחלת היא 32

זה $\frac{n \cdot p}{2}$ - מספר הניסויים כפול הסיכוי להצלחה.

אבל אנחנו נהיים גם סימטריים ומסודרים סביב התוחלת.

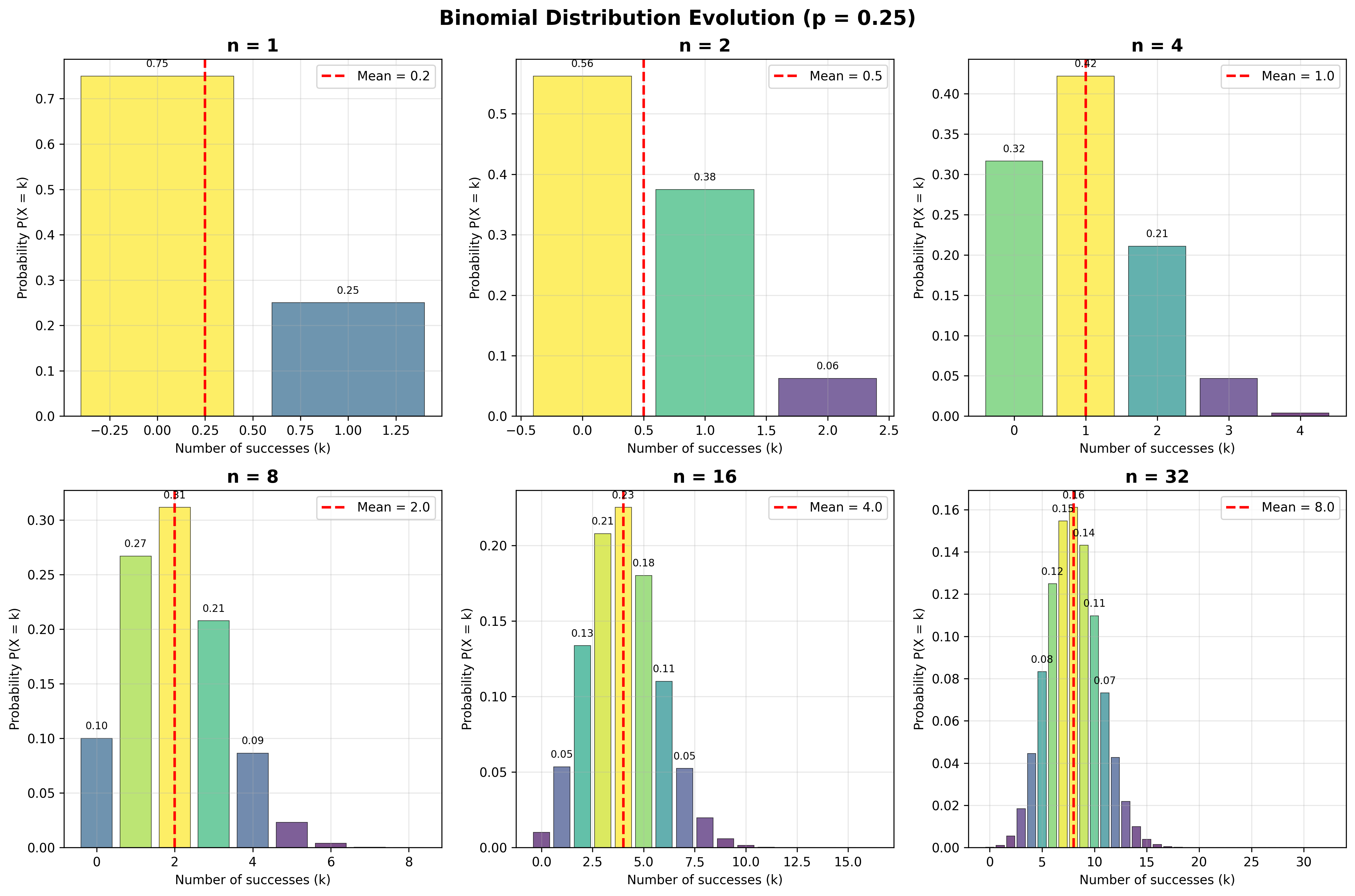
זה עובד גם אם הסיכוי להצלחה הוא 0.25. אנחנו מתחילים ממשהו שנראה עקום, לא סימטרי, אבל לאט לאט כשאנחנו מוסיפים עוד ועוד דגימות, אנחנו מתכנסים לאותה צורה סימטרית.

זה מזכיר לכם, ובצדק, את ההתפלגות הנורמלית שנכיר בהמשך עם משפט הגבול המרכזי.

alt text

alt text

alt text

מקרה מיוחד: מספר הכישלונות

אם אנחנו מגדירים את $Y$ כמספר הכישלונות, אז $Y = n - X$ ($X$ הוא מספר ההצלחות).

ההתפלגות של $Y$ - הגיוני שהיא תהיה בינומית. עכשיו עדיין יש לנו $n$ ניסויים, ופשוט הסיכוי להצלחה הוא $(1-p)$, כי עכשיו אנחנו מגדירים הצלחה ככישלון וכישלון כהצלחה.

גרפית: אם אנחנו מציירים את ההיסטוגרמות של ההצלחות והופכים אותן סביב התוחלת, אז אנחנו מקבלים את ההיסטוגרמות של הכישלונות. יש ביניהם קשר הדוק.

דוגמאות מעשיות

דוגמה: סוג דם AB

אוכלוסייה מסוימת - 5% הם בעלי סוג דם מסוג AB. עשרה אנשים נבדקים באקראי. אנחנו רוצים לדעת מה ההסתברות שביניהם בדיוק אדם אחד עם סוג דם AB.

פרמול: $X$ משתנה מקרי בינומי עם עשרה ניסויים וסיכוי להצלחה (ההצלחה זה סוג דם AB) סיכוי להצלחה 0.05.

יש לנו את הנוסחה. אנחנו רוצים לדעת מהו הסיכוי שדגמנו בדיוק אחד עם סוג דם AB:

\[P(X = 1) = \binom{10}{1} (0.05)^1 (0.95)^9\]

$\binom{10}{1} = 10$ - מספר האפשרויות לבחור אדם אחד מתוך קבוצה של 10.

\[P(X = 1) = 10 \cdot 0.05 \cdot (0.95)^9 \approx 0.315\]

דוגמה: מחלה תורשתית רצסיבית

שני בני זוג הם נושאים הטרוזיגוטיים של מוטציה למחלה תורשתית רצסיבית. אנחנו רוצים לדעת מה הסיכוי שאם יש להם שלושה ילדים, לפחות ילד אחד יהיה חולה.

עבור כל ילד, המוטציה מתקבלת בסיכוי $\frac{1}{2}$. הילד יהיה חולה אם הוא מקבל משני ההורים את המוטציה. זו מחלה רצסיבית -

הסבר: הטרוזיגוטים זה אומר שיש להם כרומוזום אחד תקין וכרומוזום אחד מוטנטי. המחלה רצסיבית אומר שבשביל להיות חולה (ולא רק נושא) אנחנו צריכים לקבל שני כרומוזומים מוטנטיים או פגומים.

אז הילד יהיה חולה אם הוא יקבל משני ההורים את המוטציה, וזה בסיכוי של $\frac{1}{4}$.

אנחנו מסמנים ב-$X$ את מספר הילדים החולים. יש לנו שלושה ניסויים של ילדים, אז $n=3$. סיכוי להצלחה (במקרה הזה הצלחה זה מחלה או ילד שחולה במחלה) הוא $p = \frac{1}{4}$.

ואנחנו רוצים לדעת מה הסיכוי שלפחות ילד אחד יהיה חולה. הזוג מחליט להביא שלושה ילדים בלי קשר למחלה ובלי קשר לשום דבר אחר.

אנחנו רוצים לדעת $P(X \geq 1)$. יותר קל לחשב את הסיכוי למאורע המשלים - שאף ילד איננו חולה.

בואו נחשב הסיכוי שאף ילד לא יהיה חולה - זה הסיכוי ש-$X = 0$:

\[P(X = 0) = \binom{3}{0} \left(\frac{1}{4}\right)^0 \left(\frac{3}{4}\right)^3\]

$\binom{3}{0} = 1$ - מספר הדרכים לבחור 0 אנשים מאוכלוסייה של שלושה (שזה כמו מספר הדרכים לבחור שלושה אנשים מאוכלוסייה של שלושה בלי חשיבות לסדר - יש לנו בדיוק דרך אחת לעשות את זה).

\[P(X = 0) = 1 \cdot 1 \cdot \left(\frac{3}{4}\right)^3 = \frac{27}{64} \approx 0.42\]

כשאתם מחשבים הסתברויות, אנחנו מבטיחים לכם שבמבחן אנחנו נשים לכם פח שהתשובה הנכונה - אחת התשובות תהיה המשלים. ואנחנו צריכים להיות קפדניים ולא לשכוח לחשב את ההסתברות הרצויה בתור 1 פחות ההסתברות שחישבנו:

\[P(X \geq 1) = 1 - P(X = 0) = 1 - 0.42 = 0.58\]

ההסתברות הרצויה היא 0.58.

תוחלת של משתנה מקרי בינומי

חישוב ישיר (דוגמה פשוטה)

עבור $n = 1$, המשתנה מקרי בינומי הוא משתנה מקרי ברנולי והתוחלת כבר חישבנו - היא $p$.

עבור משתנה מקרי בינומי עם $n = 2$, התוחלת היא:

\[\mathbb{E}[X] = 0 \cdot P(X = 0) + 1 \cdot P(X = 1) + 2 \cdot P(X = 2)\]

בסך הכל זה יוצא $2p$.

גישה יעילה יותר: פירוק לסכום של ברנוליים

בצורה יותר ישירה, אנחנו מגדירים משתנה מקרי בינומי $X \sim \text{Binomial}(n,p)$ בתור סכום של משתנים מקריים ברנוליים.

מותר לנו לעשות זאת כי כל ניסוי הוא בלתי תלוי, אז $X$ הוא סכום ההצלחות:

\[X = X_1 + X_2 + \cdots + X_n\]

כאשר $X_i$ הם משתנים מקריים ברנוליים בלתי תלויים.

אנחנו זוכרים שבמשתנה מקרי ברנולי, הסיכוי להצלחה הוא $p$ והתוחלת היא $p$.

לכן, בקלות בלי חישובים מסובכים: תוחלת הסכום היא סכום התוחלות:

\[\begin{aligned} \mathbb{E}[X] &= \mathbb{E}[X_1] + \mathbb{E}[X_2] + \cdots + \mathbb{E}[X_n] \\ &= p + p + \cdots + p = np \end{aligned}\]

ולכן התוחלת של משתנה מקרי בינומי כללי היא:

\[\mathbb{E}[X] = np\]

אינטואיציה לתוחלת

זה הגיוני למה? כי אם יש לנו 100 ניסויים למשל, וסיכוי ההצלחה של כל אחד מהם הוא 0.2, בממוצע יהיו לנו $0.2 \times 100 = 20$ הצלחות.

אז כאן $n = 100$ ו-$p = 0.2$, והתוחלת באמת $n \times p = 20$.

שונות של משתנה מקרי בינומי

שימוש בפירוק לברנוליים

שוב, הפירוק הזה של משתנה מקרי בינומי בתור סכום של משתנים מקריים ברנוליים זה פירוק מאוד מאוד מועיל - מאוד מועיל לכם, מאוד מועיל לחשיבה שלנו.

אנחנו מפרקים את המשתנה מקרי הבינומי בתור סכום של $n$ משתנים מקריים ברנוליים, כל אחד עם הסתברות הצלחה $p$:

\[X = X_1 + X_2 + \cdots + X_n\]

כאשר $X_i$ הוא תוצאת הניסוי הברנולי ה-$i$.

אנחנו מזכירים ששונות של כל אחד מאלה היא $p(1-p)$.

הניסויים בלתי תלויים, ועבור שונות: שונות של סכום היא סכום השוניות (כי הניסויים בלתי תלויים), לכן אנחנו יכולים להשתמש בנוסחה:

\[\text{Var}(X) = \text{Var}(X_1) + \text{Var}(X_2) + \cdots + \text{Var}(X_n)\] \[= p(1-p) + p(1-p) + \cdots + p(1-p) = np(1-p)\]

והשונות היא:

\[\text{Var}(X) = np(1-p)\]

מצוין!

אינטואיציה לשונות

קצת אינטואיציה לשונות הזו: השונות היא $np(1-p)$.

השונות מאוד קטנה כש-$p$ קרוב ל-0 ומאוד קטנה כש-$p$ קרוב ל-1.

השונות ממוקסמת כש-$p$ קרוב ל-$\frac{1}{2}$ - אז היא $\frac{n}{4}$.

וזה יועיל לנו נורא בהמשך בבדיקת השערות. כשאנחנו נדע שיש $p$ כלשהו, אנחנו לא נדע מהו, אז נגיד: “אוקיי, בואו ניקח לצורך בדיקת השערות את השונות המקסימלית כדי שלא נטעה, כדי להיות ודאים שאנחנו מאוד קונסרבטיביים, מאוד שמרניים.”

אנחנו נראה את זה בהמשך - ואנחנו לא יודעים מה השונות. אוקיי, בסדר, אז קחו את השונות המקסימלית. יותר גרוע מזה זה לא יכול להיות - יותר גרוע מ-$\frac{n}{4}$ זה לא יכול להיות.

דוגמה לאינטואיציה

למשל, אם אנחנו לוקחים דוגמה של 10 אנשים שממלאים לוטו - סיכוי הזכייה קרוב ל-0, מספר הזוכים כמעט תמיד יהיה 0, ואומנם השונות היא נמוכה.

דוגמאות לחישוב תוחלת ושונות

דוגמה: משפחה עם שישה ילדים

תוחלת ושונות במשפחה עם שישה ילדים (שישה ניסיונות ברנולי). בן לצורך העניין או בת - מה שבא לכם זו הצלחה.

תוחלת מספר הבנים:

\[\mathbb{E}[X] = np = 6 \times \frac{1}{2} = 3\]

השונות:

\[\text{Var}(X) = np(1-p) = 6 \times \frac{1}{2} \times \frac{1}{2} = 1.5\]

לא צריך לחזור לנוסחאות סטייה ריבועית וזה, זה בלאגן - השונות היא 1.5.

דוגמה: סוכרת

דוגמה שקולה לחלוטין עם סוכרת

דוגמה: סופגניות בחנוכה

בכל יום של חנוכה, סטודנט אוכל:

  • בהסתברות 0.2 סופגניה עם ריבה
  • ובאופן בלתי תלוי, בהסתברות 0.1 סופגניה עם שוקולד

אנחנו רוצים לדעת מה תוחלת מספר הסופגניות שהסטודנט אוכל בחנוכה.

פתרון:

נסמן מספר הסופגניות הכולל ב-$X$:

\[X = X_1 + X_2\]

כאשר:

  • $X_1$ = מספר הסופגניות ריבה
  • $X_2$ = מספר הסופגניות השוקולד

$X_1$ מתפלג בינומי: $X_1 \sim \text{Binomial}(8, 0.2)$ (8 ימי חנוכה, 0.2 סיכוי להצלחה)

תוחלת שלו היא: $\mathbb{E}[X_1] = 8 \times 0.2 = 1.6$

בצורה אדומה, תוחלת של $X_2$ היא: $\mathbb{E}[X_2] = 8 \times 0.1 = 0.8$

תוחלת של סכום היא תמיד סכום התוחלות, לכן מותר לנו לחבר את התוחלות:

\[\mathbb{E}[X] = \mathbb{E}[X_1] + \mathbb{E}[X_2] = 1.6 + 0.8 = 2.4\]

הערה חשובה: התנהגות עם $n$ גדל

הערה קטנה שתיתן לכם אולי קונטקסט:

עבור $p = \frac{1}{2}$ למשל, השונות היא $\frac{n}{4}$ וסטיית התקן היא $\frac{\sqrt{n}}{2}$.

כמו שראינו בדוגמה של הדיפוזיה, סטיית התקן גדלה עם $n$ אבל היא גדלה כשורש. עזבו את הפקטור הזה של חצי - סטיית התקן גדלה כשורש של $n$.

משמעות: ודאות יחסית גדלה

אז היא גדלה, אבל הערך היחסי שלה לעומת מספר הדגימות קטן. זאת אומרת:

\[\begin{aligned} \frac{\text{Standard deviation}}{n} &= \frac{\sqrt{n}/2}{n} \\ &= \frac{1}{2\sqrt{n}} \end{aligned}\]

זה אומר שאומנם סטיית התקן גדלה, אבל ביחס למספר הדגימות - ביחס לתוחלת למשל - היא קטנה.

למה? כי התוחלת גדלה כמו $np$, וסטיית התקן גדלה כמו $\sqrt{n}$.

ואם אתם זוכרים מגבולות:

  • $n$ גדל יותר מהר מ-$\sqrt{n}$
  • הגבול של $\frac{n}{\sqrt{n}} = \sqrt{n}$ הוא אינסוף
  • והגבול של $\frac{\sqrt{n}}{n} = \frac{1}{\sqrt{n}}$ הוא 0

אז $\sqrt{n}$ גדל הרבה יותר לאט, סטיית התקן גדלה הרבה יותר לאט.

משמעות פרקטית

זה אומר שכביכול מידת הוודאות שיש לנו קטנה (כי סטיית התקן גדלה), אבל מידת הוודאות היחסית שלנו גדלה.

סיכום

זה הסוף של משתנה מקרי בינומי.

מה למדנו:

  • תוחלת: $\mathbb{E}[X] = np$
  • שונות: $\text{Var}(X) = np(1-p)$
  • סטיית תקן: $\sigma = \sqrt{np(1-p)}$

כלים חשובים:

  • פירוק משתנה בינומי לסכום של ברנוליים
  • שימוש בתכונות של תוחלת ושונות של סכומים
  • הבנת ההתנהגות עם $n$ גדל

בשיעור הבא: ההמשך של משתנים מקריים בדידים נוספים - משתנה מקרי גיאומטרי, ומשתנה מקרי נורמלי.

דור פסקל
לשיעור הבא