קינמטיקה ופונקציות וקטוריות
הגדרות בסיסיות
כדי לתאר את תנועת גוף במרחב או במישור, נדרש אובייקט מתמטי הנקרא “פונקציה וקטורית”. פונקציה וקטורית היא וקטור שהרכיבים שלו הם פונקציות התלויות בזמן.
 |
|---|
| וקטורים |
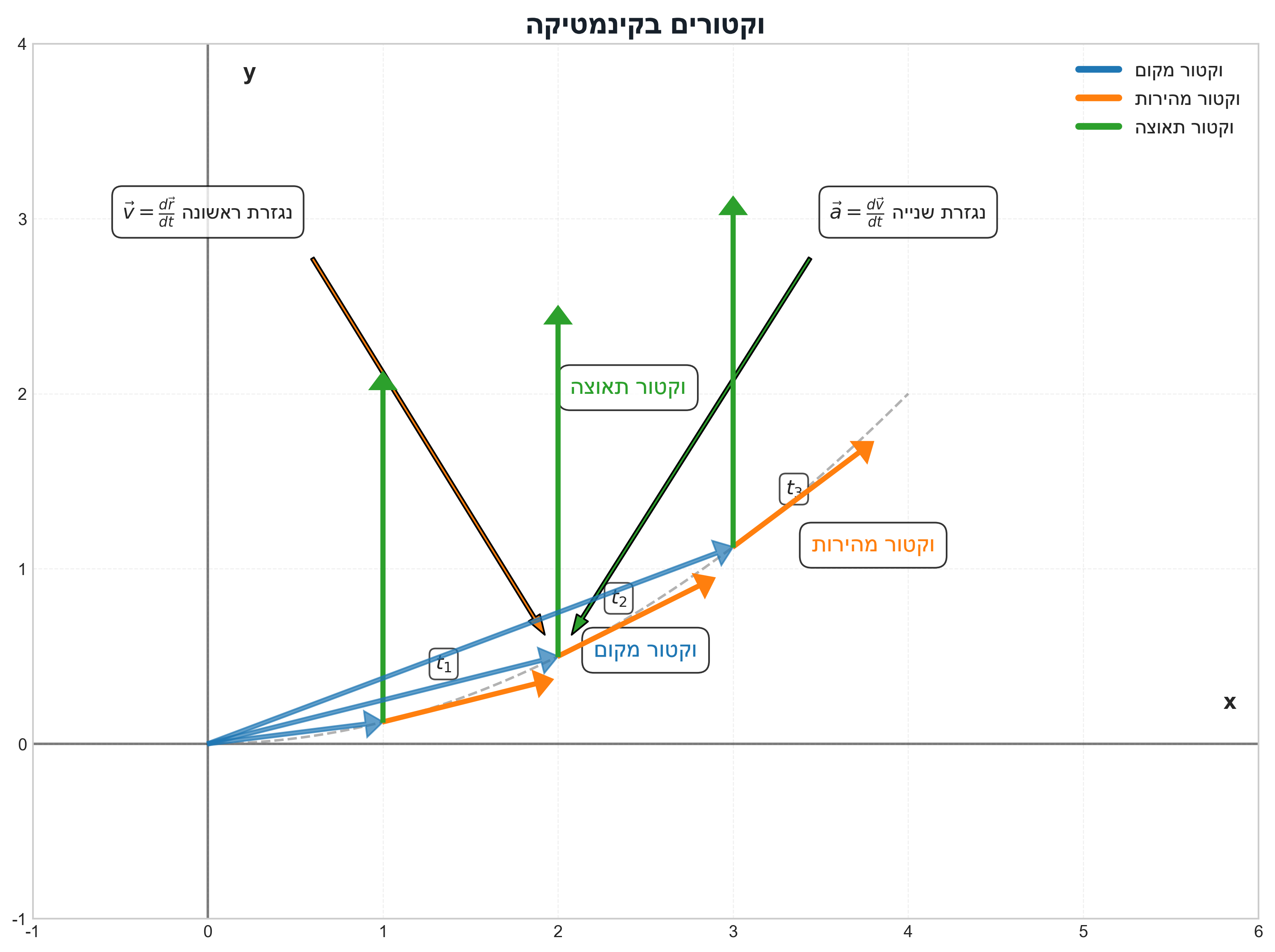
וקטור המקום
- וקטור המקום מתאר את מיקום הגוף בכל רגע $t$.
- מסומן כ-$\vec{r}(t)$.
- הביטוי המתמטי בקואורדינטות קרטזיות: $\vec{r}(t) = x(t)\hat{x} + y(t)\hat{y} + z(t)\hat{z}$.
- שלוש הפונקציות $x(t)$, $y(t)$, ו-$z(t)$ הן הקואורדינטות של הגוף בכל רגע $t$.
- ניתן לרשום גם כשלשה סדורה: $\vec{r}(t) = (x(t), y(t), z(t))$.
וקטור העתק
הגדרה
- בזמן $t$ הגוף נמצא במיקום המתואר על ידי $\vec{r}(t)$.
- בזמן $t + \Delta t$ הגוף נמצא במיקום המתואר על ידי $\vec{r}(t + \Delta t)$.
- וקטור ההעתק $\Delta\vec{r}$ מוגדר כהפרש בין שני וקטורי המיקום: \(\Delta\vec{r} = \vec{r}(t + \Delta t) - \vec{r}(t)\)
- וקטור ההעתק מתאר את השינוי במיקום הגוף בפרק הזמן $\Delta t$.
דוגמה: נסו לצייר מערכת צירים תלת-ממדית ולייצג מיקום של גוף בזמן $t$ ובזמן $t + \Delta t$, ולהגדיר את וקטור ההעתק כהפרש ביניהם (מופיע בתמונות בעמודים באתר).
וקטור מהירות
הגדרת וקטור המהירות
- המהירות היא קצב שינוי המקום לפי הזמן.
-
מהירות ממוצעת (וקטור) בפרק זמן $\Delta t$:
\[\mathbf{v}_{\text{avg}} = \frac{\Delta\mathbf{r}}{\Delta t}\]
כאשר $\Delta\mathbf{r}$ הוא וקטור ההעתק ו-$\Delta t$ הוא סקלר הזמן.
דוגמה: “אם בשעה 7 בבוקר הייתי בתל אביב ובשעה 8 בבוקר הייתי בירושלים, וקטור ההעתק $\Delta\mathbf{r}$ בין תל אביב לירושלים חלקי פרק הזמן $\Delta t = 1$ שעה נותן את וקטור המהירות הממוצעת.”
מהירות רגעית
-
וקטור המהירות הרגעית הוא הגבול של וקטור המהירות הממוצעת כאשר $\Delta t$ שואף לאפס:
\[\mathbf{v}(t) = \lim_{\Delta t \to 0} \frac{\Delta\mathbf{r}}{\Delta t} = \frac{d\mathbf{r}}{dt} = \dot{\mathbf{r}}\] -
הביטוי בקואורדינטות קרטזיות:
\[\mathbf{v}(t) = \frac{dx}{dt}\hat{\mathbf{x}} + \frac{dy}{dt}\hat{\mathbf{y}} + \frac{dz}{dt}\hat{\mathbf{z}} = v_x(t)\hat{\mathbf{x}} + v_y(t)\hat{\mathbf{y}} + v_z(t)\hat{\mathbf{z}}\]
כאשר:
- $v_x(t)$, $v_y(t)$, $v_z(t)$ הם רכיבי המהירות (סקלרים)
- $\hat{\mathbf{x}}$, $\hat{\mathbf{y}}$, $\hat{\mathbf{z}}$ הם וקטורי יחידה
הבחנה בין וקטור לסקלר
- וקטור המהירות $\mathbf{v}$: כמות וקטורית עם גודל וכיוון
-
גודל המהירות (speed) $\vert\mathbf{v}\vert$ או $v$: כמות סקלרית חיובית
\[|\mathbf{v} \vert = \sqrt{\mathbf{v} \cdot \mathbf{v}} = \sqrt{v_x^2 + v_y^2 + v_z^2}\]
הערה: כשמדברים על מהירות, לא מספיק להגיד מהו ה-speed. Speed זה הגודל הסקלרי $\vert\mathbf{v}\vert$ של וקטור המהירות. צריך להגיד גם מהו הכיוון, והכיוון נקבע על ידי שלושת הרכיבים הסקלריים $v_x, v_y, v_z$.
תכונות וקטור המהירות
- וקטור המהירות $\mathbf{v}(t)$ תמיד משיק למסלול התנועה (מצביע בכיוון התנועה).
-
וקטור יחידה בכיוון המהירות:
\[\hat{\mathbf{v}} = \frac{\mathbf{v}}{|\mathbf{v}\vert}\]כאשר $\hat{\mathbf{v}}$ הוא וקטור יחידה ו-$\vert\mathbf{v}\vert$ הוא הגודל הסקלרי.
- וקטור היחידה $\hat{\mathbf{v}}$ מתאר את כיוון התנועה בכל רגע $t$.
סיכום: וקטורים לעומת סקלרים במהירות
| כמות | סוג | סימון | יחידות |
|---|---|---|---|
| וקטור המהירות | וקטור | $\mathbf{v}$ | $\mathrm{m/s}$ בכיוון מסוים |
| גודל המהירות (speed) | סקלר | $\vert\mathbf{v}\vert$ או $v$ | $\mathrm{m/s}$ |
| רכיבי המהירות | סקלרים | $v_x, v_y, v_z$ | $\mathrm{m/s}$ |
| וקטור יחידה של המהירות | וקטור | $\hat{\mathbf{v}}$ | ללא יחידות |
וקטור תאוצה
הגדרת וקטור התאוצה
- התאוצה היא קצב שינוי המהירות לפי הזמן.
-
תאוצה ממוצעת בפרק זמן $\Delta t$:
\[\vec{a}_{\text{avg}} = \frac{\Delta\vec{v}}{\Delta t} = \frac{\vec{v}(t+\Delta t) - \vec{v}(t)}{\Delta t}\] -
התאוצה הרגעית היא הגבול של התאוצה הממוצעת כאשר $\Delta t$ שואף לאפס:
\[\vec{a}(t) = \lim_{\Delta t \to 0} \frac{\Delta\vec{v}}{\Delta t} = \frac{d\vec{v}}{dt} = \dot{\vec{v}} = \frac{d^2\vec{r}}{dt^2} = \ddot{\vec{r}}\]
שאלה: מהו בדיוק $\Delta\vec{v}$?
תשובה: $\Delta\vec{v}$ זה וקטור המהירות בזמן $t + \Delta t$ פחות וקטור המהירות בזמן $t$. כלומר, זה הפרש וקטורי של מהירויות.
דוגמה להמחשה
- “אם בשעה 7 בבוקר נעתי במהירות של 40 קמ״ש ובשעה 8 בבוקר נעתי במהירות של 80 קמ״ש, אז התאוצה הממוצעת במשך השעה הזאת היא 80 קמ״ש פחות 40 קמ״ש, חלקי שעה אחת, שזה 40 קמ״ש לשעה בריבוע.”
שאלה: האם זו תאוצה ממוצעת או רגעית?
תשובה: זאת תאוצה ממוצעת. התאוצה הרגעית תתקבל כאשר $\Delta t$ שואף לאפס.
שאלה: מה כיוון התאוצה?
תשובה: התאוצה היא הפרש וקטורי של המהירויות חלקי הזמן. אין שום התחייבות שכיוון וקטור התאוצה יהיה בכיוון המהירות או בכיוון המקום. התאוצה תהיה בכיוון של $\Delta\vec{v}$.
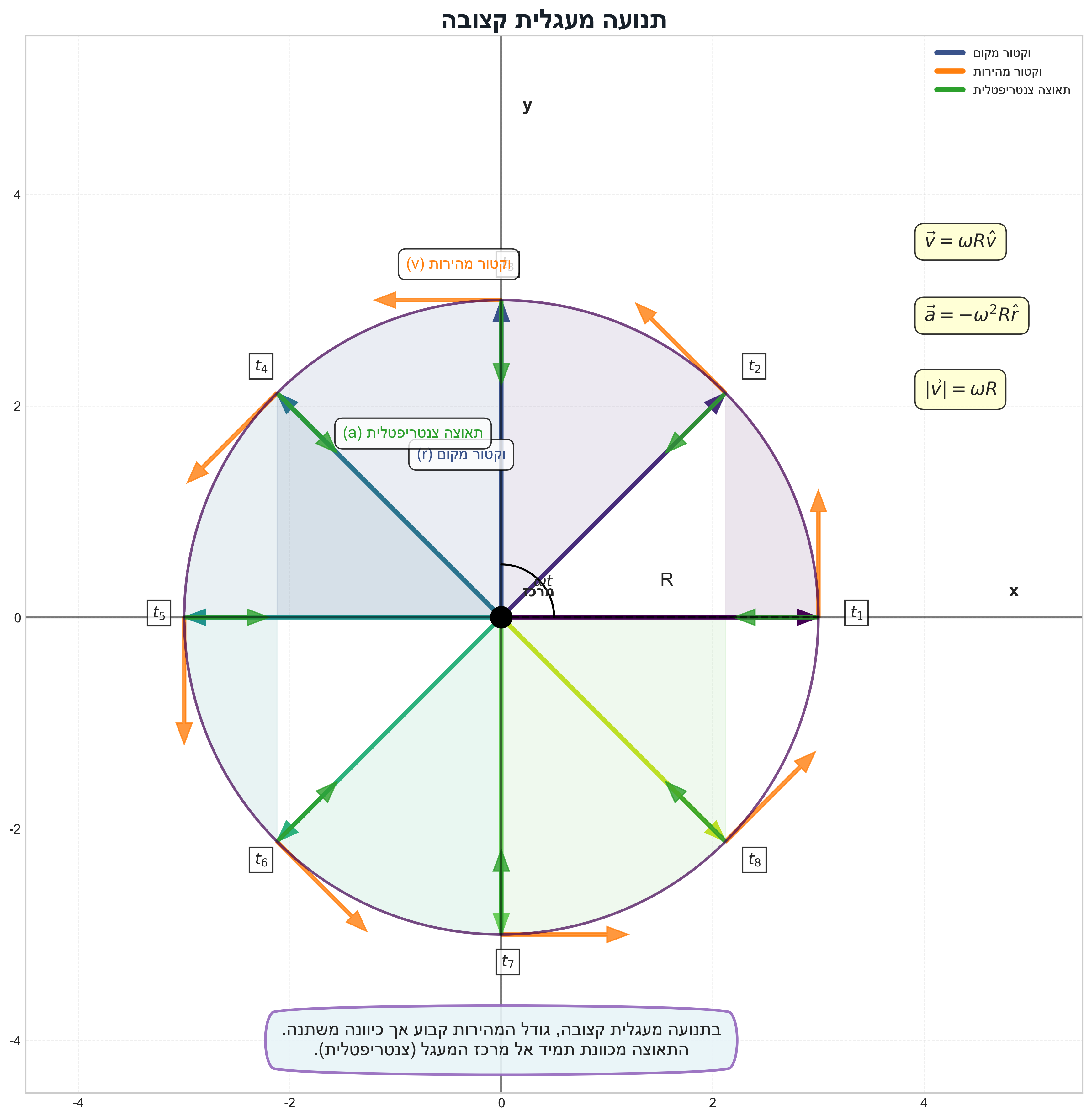
תנועה מעגלית קצובה
 |
|---|
| תנועה מעגלית קצובה |
הגדרת התנועה המעגלית הקצובה
- תנועה על מסלול מעגלי בגודל מהירות קבוע.
-
המסלול מתואר על ידי וקטור המקום $\vec{r}(t)$, בהצגה קרטזית:
\[\vec{r}(t) = R\cos(\omega t)\hat{x} + R\sin(\omega t)\hat{y}\] - $R$ הוא רדיוס המעגל (קבוע).
- $\omega$ היא המהירות הזוויתית (נמדדת ברדיאנים לשנייה).
- $\theta(t) = \omega t$ היא הזווית, המשתנה לינארית עם הזמן.
כשנדבר על תנועה קצובה, הכוונה לכיסוי קשתות שוות במרווחי זמן שווים.
הערה (דור): אני חושב שיעזור להבין את ההבדל בין קואורדינטות קרטזיות לפולריות. זה מופיע בשיעורים הבאים. בקצרה, ההצגה שלמעלה היא בקואורדינטות קרטזיות $(x, y)$. לעומת זאת, קואורדינטות פולריות מתארות מיקום באמצעות רדיוס וזווית $(R, \theta)$.
הערה נוספת: שימו לב שהנוסחה תלויה בבחירת מערכת הצירים. אם למשל הזווית $\theta$ נמדדת מציר ה-$y$ ולא מציר ה-$x$, הנוסחה תשתנה:
\[\vec{r}(t) = R\sin(\omega t)\hat{x} + R\cos(\omega t)\hat{y}\]אפשר לעבור בין הנוסחאות בעזרת זהויות טריגונומטריות.
וקטור המהירות בתנועה מעגלית
-
נגזור את וקטור המקום לפי הזמן:
\[\vec{v}(t) = \frac{d\vec{r}}{dt} = -\omega R\sin(\omega t)\hat{x} + \omega R\cos(\omega t)\hat{y}\] -
גודל המהירות:
\[\vert\vec{v}\vert = \sqrt{(-\omega R\sin(\omega t))^2 + (\omega R\cos(\omega t))^2} = \sqrt{\omega^2 R^2(\sin^2(\omega t) + \cos^2(\omega t))} = \omega R\] -
גודל המהירות המשיקית קבוע ושווה ל-$v = \omega R$.
הערה: “המהירות המשיקית היא $\omega R$. $\omega$ במקרה שלנו הוא קבוע. היחידות של $\omega$ הן רדיאנים לשנייה. כאשר $\omega$ (רדיאן/שנייה) כפול $R$ (מטר) נותן מהירות במטר/שנייה.”
תכונות מיוחדות
- המהירות ניצבת תמיד לוקטור המקום: $\vec{v} \cdot \vec{r} = 0$.
- המהירות משיקה למעגל.
-
וקטור יחידה בכיוון המהירות:
\[\hat{v} = \frac{\vec{v}}{\vert\vec{v}\vert} = -\sin(\omega t)\hat{x} + \cos(\omega t)\hat{y}.\]
הערת המרצה: “אם וקטור המקום הוא בכיוון הרדיוס, ווקטור המהירות ניצב לו, הרי שווקטור המהירות משיק למעגל. הוא בזווית של 90 מעלות מהרדיוס.”
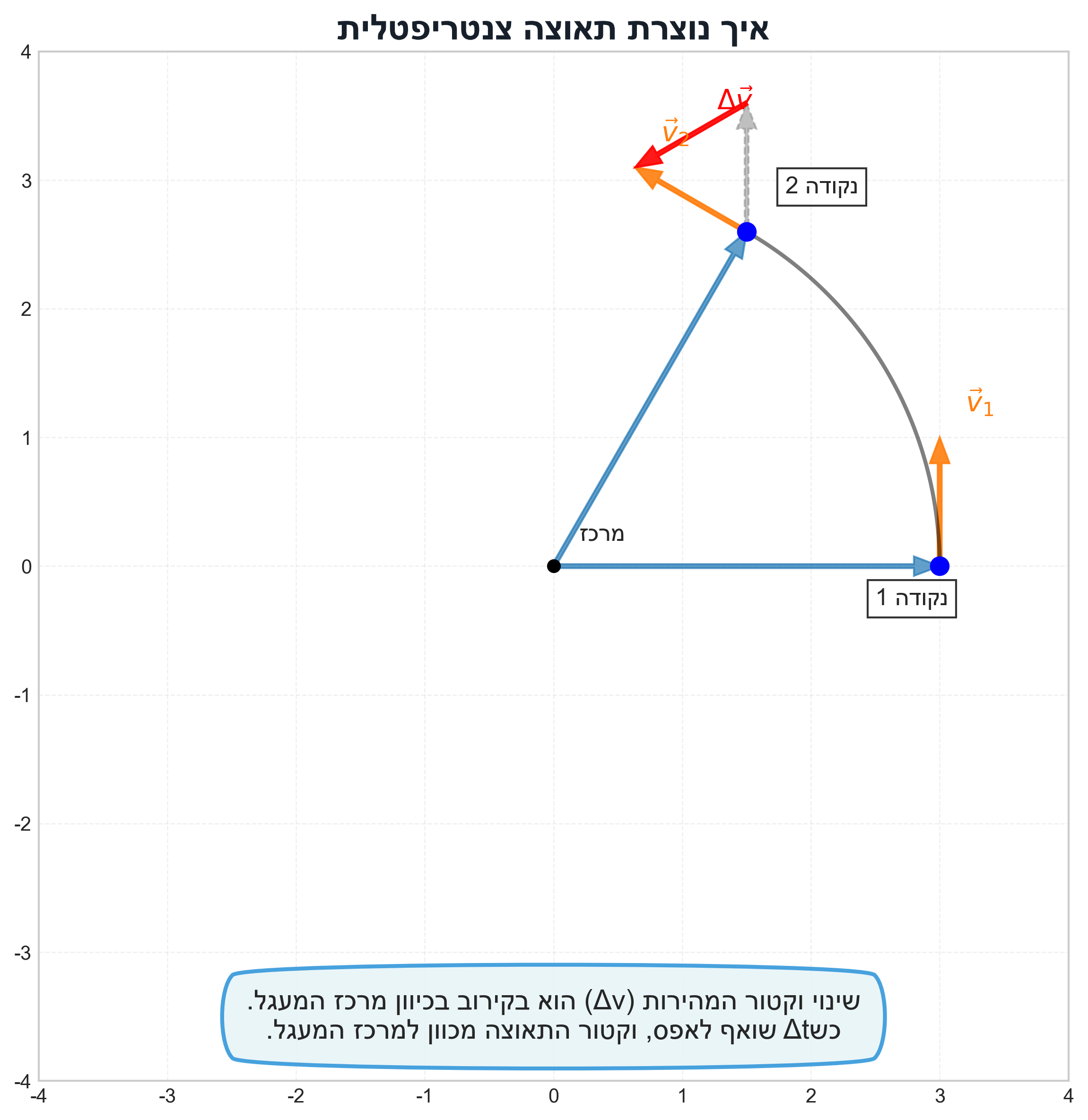
תאוצה צנטריפטלית
 |
|---|
| תאוצה צנטריפטלית |
וקטור התאוצה בתנועה מעגלית
-
נגזור את וקטור המהירות לפי הזמן:
\[\vec{a}(t) = \frac{d\vec{v}}{dt} = -\omega^2 R\cos(\omega t)\hat{x} - \omega^2 R\sin(\omega t)\hat{y}\] -
ניתן לראות שזהו פשוט $-\omega^2$ כפול וקטור המקום המקורי:
\[\vec{a}(t) = -\omega^2 \vec{r}(t)\]
תוצאה חשובה: בתנועה מעגלית קצובה, התאוצה מכוונת תמיד בכיוון הפוך לוקטור המקום, כלומר לעבר מרכז המעגל.
הערה: שימו לב שהתוצאה ($\vec{a}=-\omega^2 \vec{r}$) נכונה בתנועה מעגלית קצובה, כלומר כאשר המהירות הזוויתית $\omega$ קבועה. אם גודל המהירות היה משתנה, הייתה קיימת גם תאוצה משיקית.
תשובת המרצה: “אני מזכיר לכם שאנחנו עוסקים כאן בוקטורים. וקטור המהירות לא מאופיין רק על ידי גודל אלא גם על ידי כיוון. כשאני נע על פני המעגל, אומנם גודל וקטור המהירות קבוע, אבל כיוון המהירות משתנה כל הזמן. אם כיוון המהירות משתנה, יש לי תאוצה, משום שיש שינוי בוקטור המהירות.”
תכונות התאוצה בתנועה מעגלית
- התאוצה מכוונת תמיד לעבר מרכז המעגל.
- גודל התאוצה: $\vert\vec{a}\vert = \omega^2 R$. מאחר ו-$v = \omega R$, ניתן לכתוב גם $\vert\vec{a}\vert = \frac{v^2}{R}$.
- תאוצה זו נקראת “תאוצה צנטריפטלית” (centripetal acceleration).
המחשה גרפית: המרצה צייר על הלוח שני וקטורי מהירות $\vec{v}(t)$ ו-$\vec{v}(t+\Delta t)$ בתנועה מעגלית, והראה שוקטור ההפרש ביניהם $\Delta\vec{v}$ תמיד יצביע לכיוון מרכז המעגל.
סיכום סימונים חשובים
- $\vec{v} = \dot{\vec{r}}$ (נגזרת ראשונה של המקום לפי הזמן)
- $\vec{a} = \dot{\vec{v}} = \ddot{\vec{r}}$ (נגזרת שנייה של המקום לפי הזמן)
- נגזרת שלישית מסומנת בשלוש נקודות ($\dddot{\vec{r}}$) ונקראת “Jerk”, אך השימוש בה במכניקה קלאסית נדיר.
תנועה בתאוצה קבועה
הגדרת המצב
- נניח שהתאוצה קבועה: $\vec{a}(t) = \vec{a}_0 = \text{const}$.
- דוגמה נפוצה היא נפילה חופשית בקרבת פני כדור הארץ, שם $\vec{a} = -g\hat{z}$ (כאשר ציר $z$ מצביע כלפי מעלה).
- $g$ הוא קבוע תאוצת הכובד (בקירוב $g \approx 9.8 \mathrm{ m/s^2}$).
הערת המרצה: “אתם בטח שמעתם שבהיעדר התנגדות אוויר ובקרבת פני כדור הארץ, גופים נופלים בתאוצה קבועה $g$. זה קירוב, ונתקן אותו בהמשך, אבל כרגע נניח שזה נכון.”
מציאת וקטור המהירות באמצעות אינטגרציה
\[\vec{v}(t) = \int \vec{a}(t) dt = \int \vec{a}_0 dt = \vec{a}_0 t + \vec{C}\]הקבוע הווקטורי $\vec{C}$ נקבע על פי תנאי התחלה. אם נתונה המהירות $\vec{v}_0$ בזמן $t=0$:
\[\vec{v}(0) = \vec{a}_0 \cdot 0 + \vec{C} = \vec{v}_0 \implies \vec{C} = \vec{v}_0\]ולכן, משוואת המהירות היא:
\[\vec{v}(t) = \vec{v}_0 + \vec{a}_0 t\]מציאת וקטור המקום באמצעות אינטגרציה
\[\vec{r}(t) = \int \vec{v}(t) dt = \int (\vec{v}_0 + \vec{a}_0 t) dt = \vec{v}_0 t + \frac{1}{2}\vec{a}_0 t^2 + \vec{D}\]הקבוע הווקטורי $\vec{D}$ הוא וקטור המקום בזמן $t=0$, כלומר $\vec{r}_0$. לכן, משוואת המיקום היא:
\[\vec{r}(t) = \vec{r}_0 + \vec{v}_0 t + \frac{1}{2}\vec{a}_0 t^2\]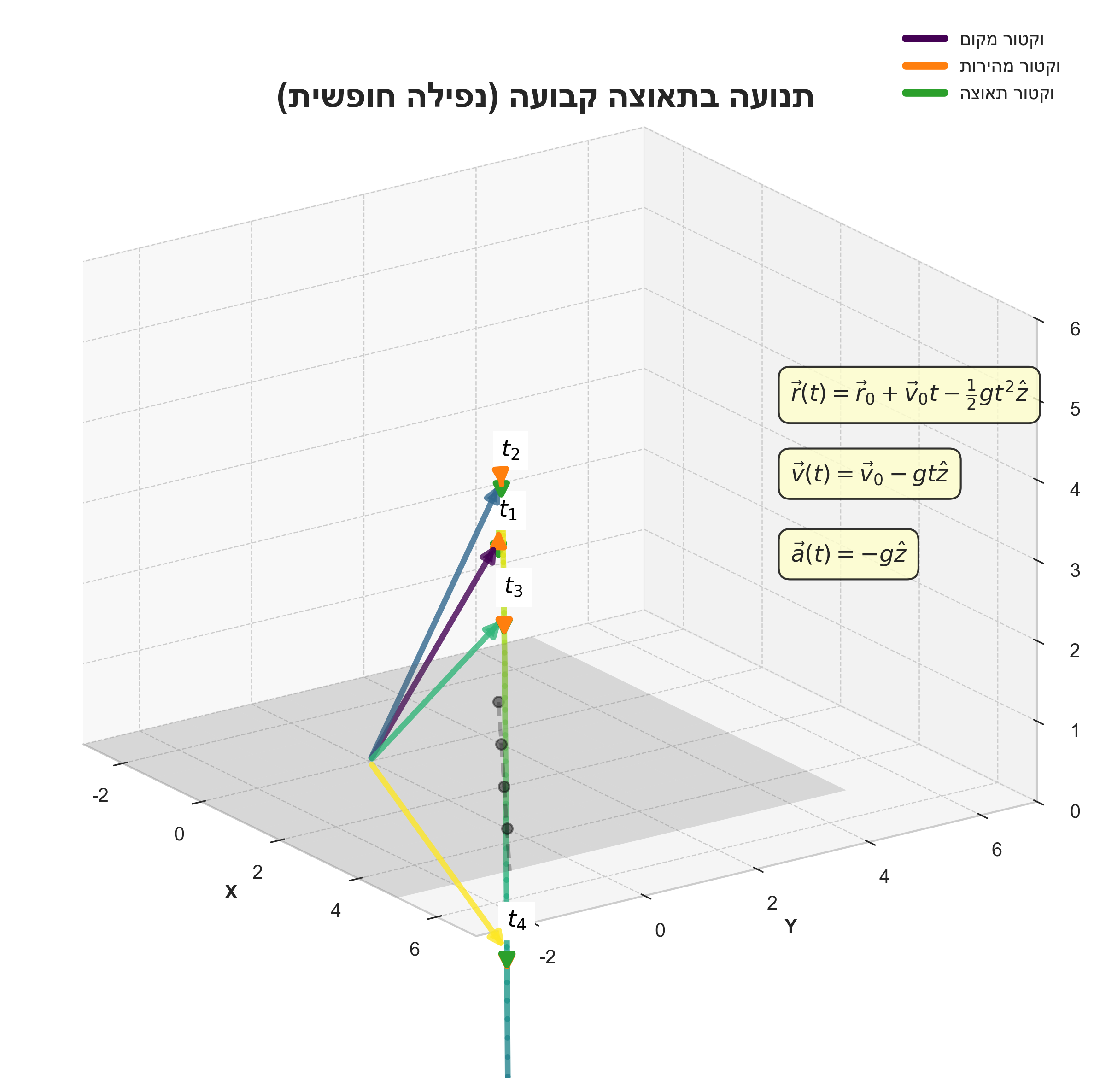 |
|---|
| תנועת קליע (Projectile Motion) |
דוגמה מפורטת
- נתון:
- מיקום התחלתי: $\vec{r}_0 = -\hat{x} + 3\hat{y} + 2\hat{z}$
- מהירות התחלתית: $\vec{v}_0 = 3\hat{x} - 2\hat{y}$
- תאוצה קבועה: $\vec{a}_0 = -g\hat{z}$
-
נציב במשוואת המיקום:
\[\vec{r}(t) = (-\hat{x} + 3\hat{y} + 2\hat{z}) + (3\hat{x} - 2\hat{y})t + \frac{1}{2}(-g\hat{z})t^2\] -
נקבץ איברים לפי רכיבים:
\[\vec{r}(t) = (3t-1)\hat{x} + (-2t+3)\hat{y} + (-\frac{1}{2}gt^2+2)\hat{z}\] - זהו וקטור המיקום בכל רגע $t$.
הערת המרצה: “תנו לי איזה $t$ שאתם רוצים, ואני אגיד לכם בדיוק איפה יהיה הגוף. זו עוצמה גדולה מאוד, יש לי פה יכולת חיזוי פנטסטית.”
תנועה יחסית
מיקום יחסי
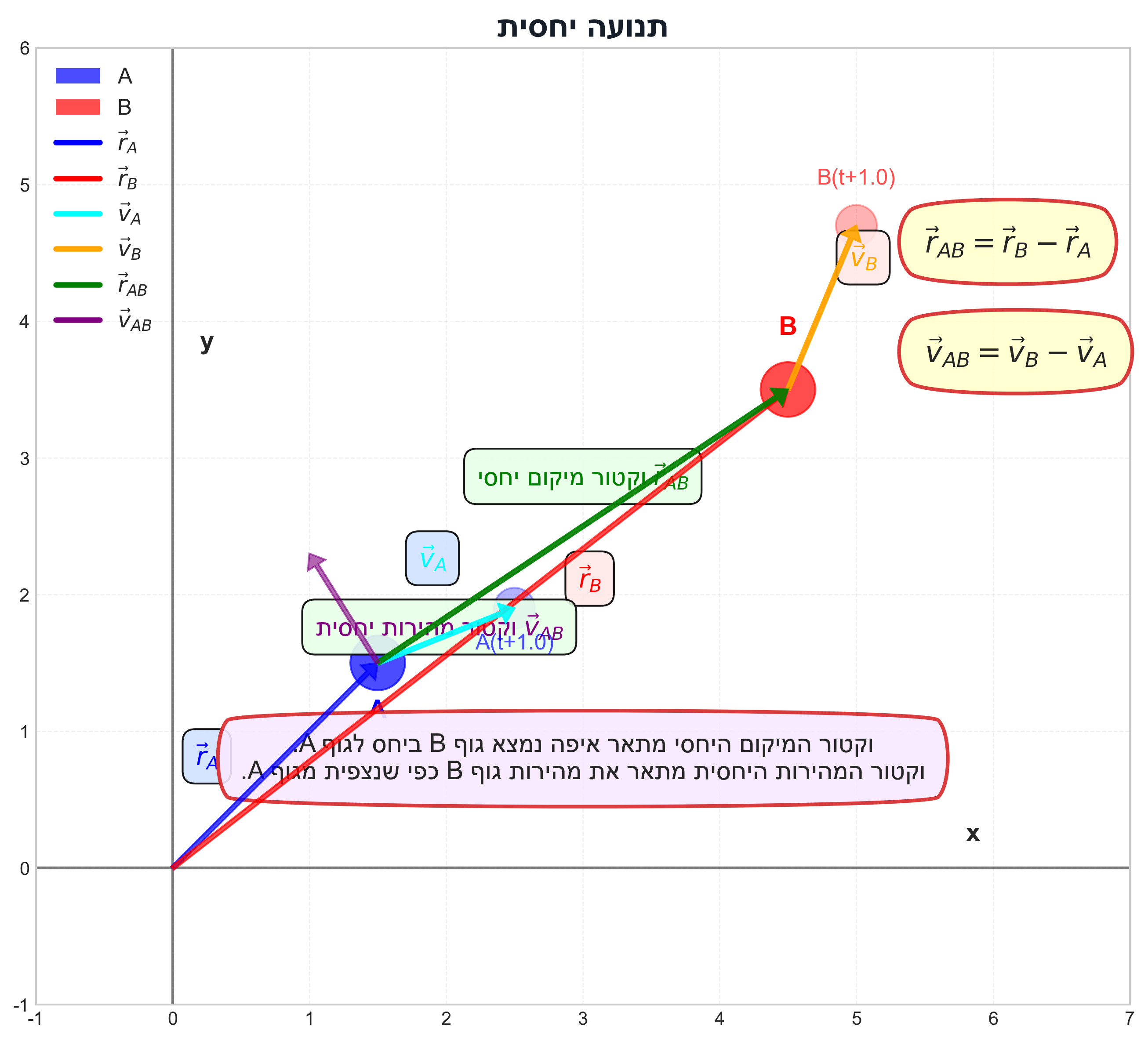
- נניח שיש שני גופים $A$ ו-$B$ עם וקטורי מקום $\vec{r}_A$ ו-$\vec{r}_B$ ביחס לאותה ראשית צירים.
-
וקטור המקום של $B$ ביחס ל-$A$ הוא:
\[\vec{r}_{B/A} = \vec{r}_B - \vec{r}_A\] - המיקום היחסי מתאר איפה נמצא גוף $B$ מנקודת המבט של גוף $A$.
הבחירה של ראשית הצירים היא שרירותית, אבל מרגע שבחרנו אותה, אנחנו צריכים להיות עקביים.
מהירות יחסית
-
על ידי גזירת המיקום היחסי לפי הזמן, נקבל את המהירות היחסית:
\[\vec{v}_{B/A} = \frac{d\vec{r}_{B/A}}{dt} = \frac{d\vec{r}_B}{dt} - \frac{d\vec{r}_A}{dt} = \vec{v}_B - \vec{v}_A\]
 |
|---|
| תנועה יחסית |
דוגמה 1: מהירות יחסית בתנועה בקו ישר
- “אני נע במהירות של 50 קמ״ש צפונה ($\vec{v}_A = 50\hat{x}$) ויותם נע במהירות של 100 קמ״ש צפונה ($\vec{v}_B = 100\hat{x}$).”
- “מה המהירות שלי יחסית ליותם? $\vec{v}_{A/B} = \vec{v}_A - \vec{v}_B = 50\hat{x} - 100\hat{x} = -50\hat{x}$.”
- “מנקודת מבטו של יותם, אני נע דרומה (בכיוון השלילי) במהירות של 50 קמ״ש.”
דוגמה 2: תנועה מורכבת
- “אם אני נע במסלול מסובך על פני כדור הארץ, וחייזר על הירח רוצה לדעת מה המהירות שלי ביחס אליו…”
- “כל מה שהוא צריך לעשות הוא למדוד את המהירות שלו (\(\vec{v}_B\)) ואת המהירות שלי (\(\vec{v}_A\)) ביחס לאותה ראשית צירים (למשל, השמש), ואז לחשב את ההפרש \(\vec{v}_{A/B} = \vec{v}_A - \vec{v}_B\).”
הערת המרצה על יישומים: “כך פועל למשל טיל ‘חץ’. אם יש לי מכ”ם טוב, אני יכול לשחזר את מסלול המטרה, לדעת את $\vec{v}(t)$ שלה, לחשב את המהירות היחסית, ובהתאם לכך לכוון את טיל היירוט.”
נוסחאות מרכזיות:
- וקטור מקום: $\vec{r}(t) = x(t)\hat{x} + y(t)\hat{y} + z(t)\hat{z}$
- וקטור מהירות: $\vec{v}(t) = \frac{d\vec{r}}{dt} = \dot{\vec{r}}$
- וקטור תאוצה: $\vec{a}(t) = \frac{d\vec{v}}{dt} = \ddot{\vec{r}}$
- תנועה מעגלית קצובה (רדיוס $R$, מהירות זוויתית $\omega$):
- מקום: $\vec{r}(t) = R\cos(\omega t)\hat{x} + R\sin(\omega t)\hat{y}$
- מהירות: $\vec{v}(t) = -\omega R\sin(\omega t)\hat{x} + \omega R\cos(\omega t)\hat{y}$
- גודל מהירות: $\vert\vec{v}\vert = \omega R$
- תאוצה: $\vec{a}(t) = -\omega^2 \vec{r}(t)$
- גודל תאוצה: $\vert\vec{a}\vert = \omega^2 R = \frac{\vert\vec{v}\vert^2}{R}$
- תנועה בתאוצה קבועה $\vec{a}_0$:
- מהירות: $\vec{v}(t) = \vec{v}_0 + \vec{a}_0 t$
- מקום: $\vec{r}(t) = \vec{r}_0 + \vec{v}_0 t + \frac{1}{2}\vec{a}_0 t^2$
- תנועה יחסית (של B יחסית ל-A):
- מיקום: $\vec{r}_{B/A} = \vec{r}_B - \vec{r}_A$
- מהירות: $\vec{v}_{B/A} = \vec{v}_B - \vec{v}_A$
- תאוצה: $\vec{a}_{B/A} = \vec{a}_B - \vec{a}_A$
הערות חשובות:
- התאוצה הצנטריפטלית קיימת גם כאשר גודל המהירות קבוע, כי כיוון המהירות משתנה.
- תאוצה מתארת שינוי בוקטור המהירות - שינוי בגודל, בכיוון, או בשניהם.
- בתנועה עם תאוצה קבועה, ניתן לחזות את המיקום והמהירות בכל זמן עתידי בהינתן תנאי התחלה.
- אינטגרציה של תאוצה נותנת מהירות (עד כדי קבוע אינטגרציה), ואינטגרציה של מהירות נותנת מיקום (עד כדי קבוע). הקבועים נקבעים מתנאי ההתחלה.
- חשוב להבחין בין speed (גודל המהירות) לבין וקטור המהירות (velocity).
- הבחירה של ראשית הצירים היא שרירותית, אך יש להיות עקביים בשימוש בה.