סיכום חומר קודם
חוק קולון
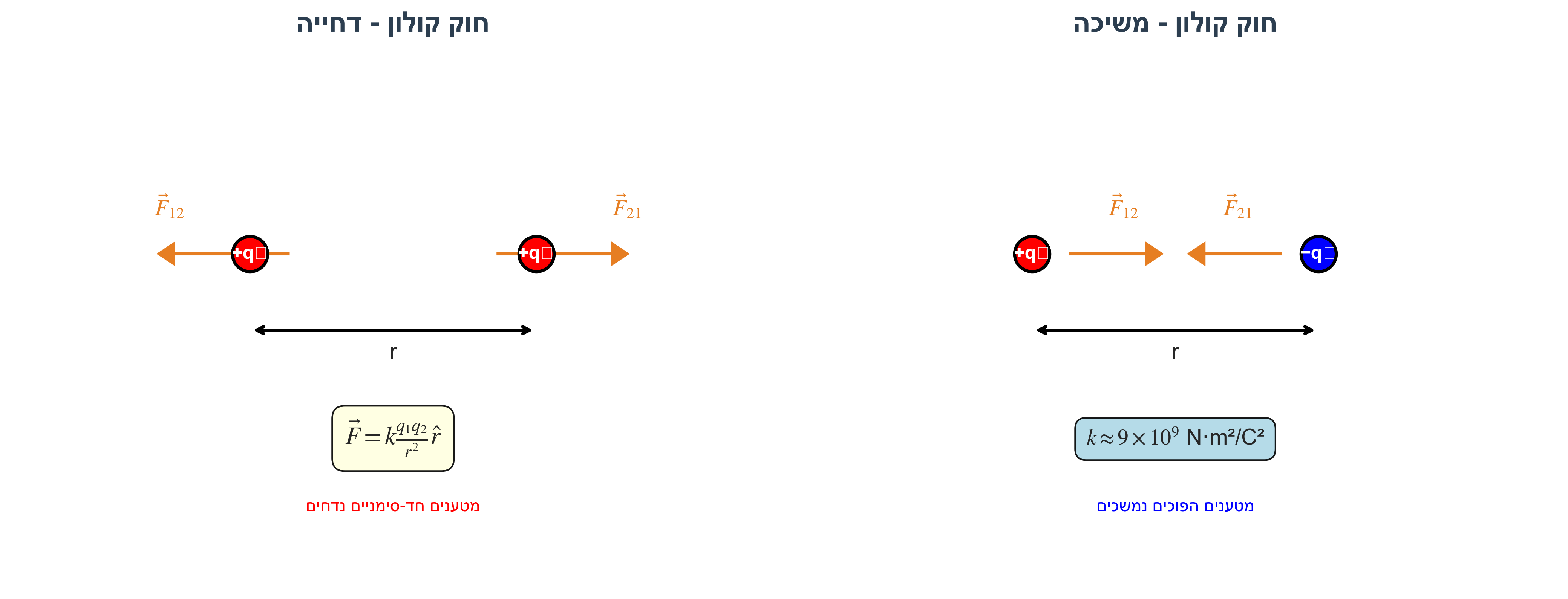
הכוח בין שני מטענים נקודתיים:
\[\vec{F} = k \frac{q_1 q_2}{r^2} \hat{r}\]- $k \approx 9 \times 10^9 \, \text{N·m}^2/\text{C}^2$ - קבוע קולון
- מטענים שווי סימן נדחים, מטענים בעלי סימנים הפוכים נמשכים
שדה חשמלי
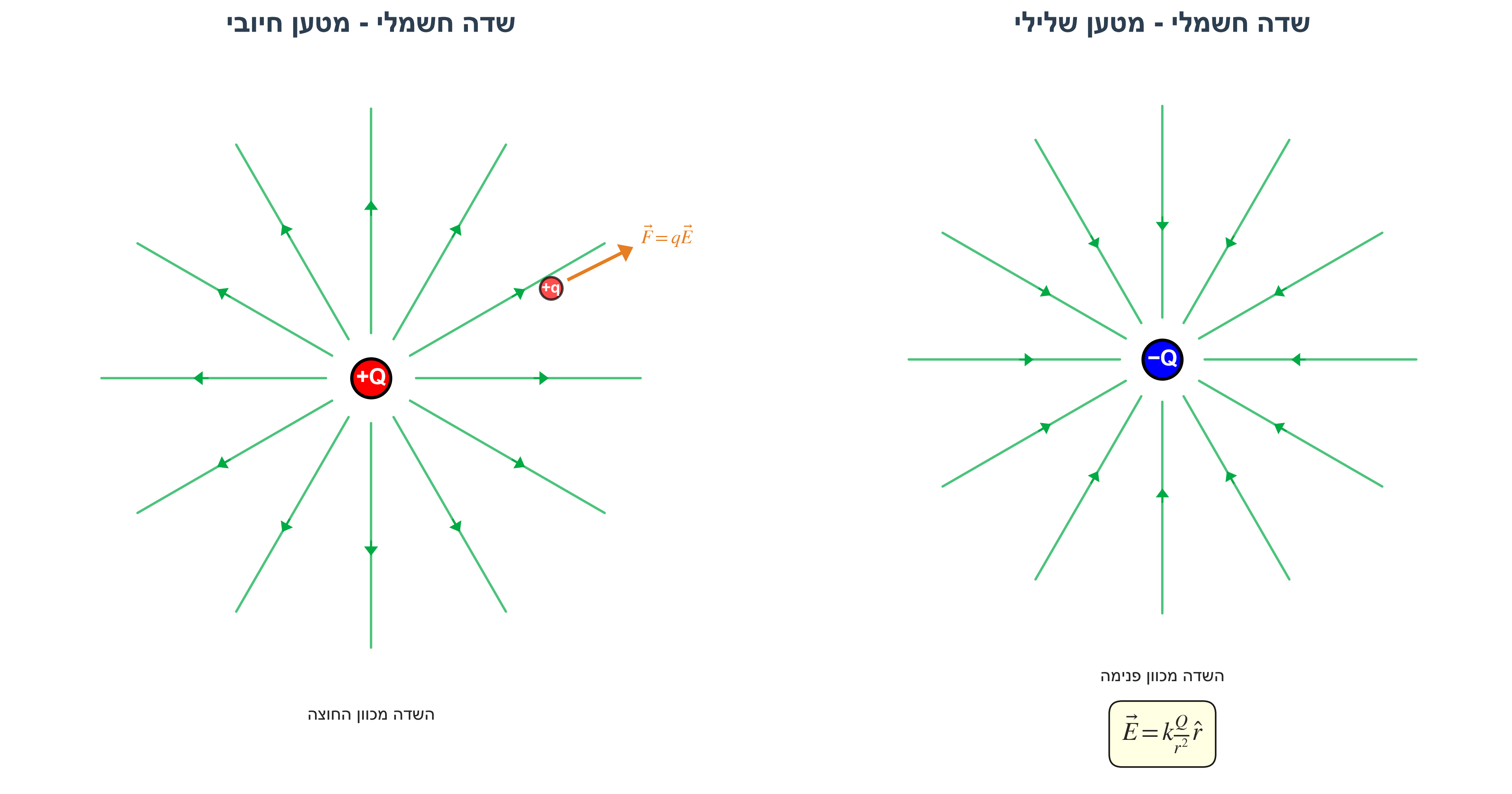
שדה חשמלי נוצר על ידי מטענים קבועים במרחב:
\[\vec{E} = \frac{\vec{F}}{q} = k\frac{Q}{r^2}\hat{r}\]הכוח על מטען $q$ בשדה חשמלי:
\[\vec{F} = q\vec{E}\]- מטען חיובי ← כוח בכיוון השדה
- מטען שלילי ← כוח נגד כיוון השדה
עקרון הסופרפוזיציה
השדה הכולל הוא סכום וקטורי של השדות מכל המטענים:
\[\vec{E}_{\text{total}} = \sum_i \vec{E}_i\]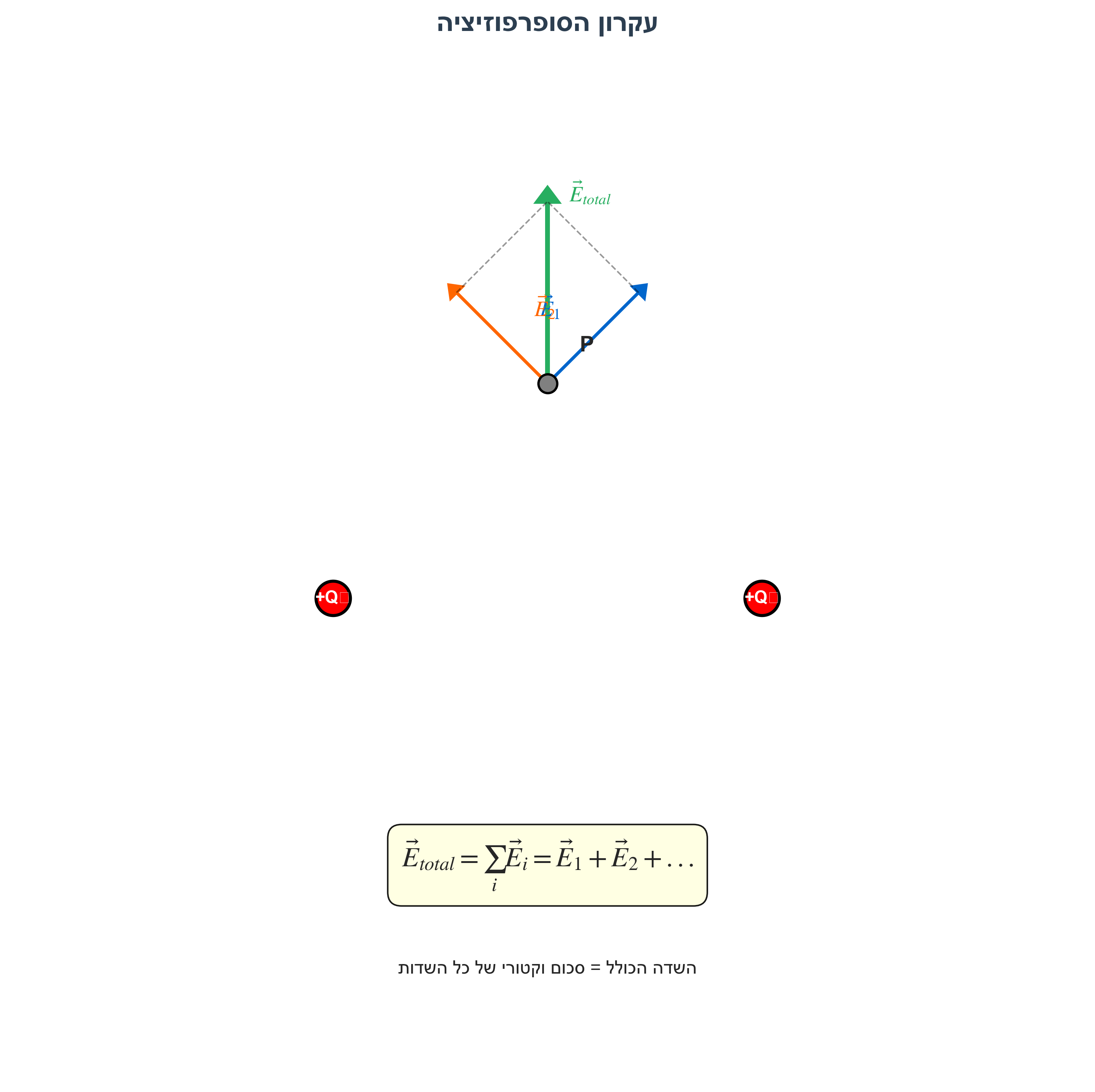
שדה משמר
שדה חשמלי הוא שדה משמר:
- העבודה במעגל סגור שווה לאפס
- העבודה בין שתי נקודות אינה תלויה במסלול
אנרגיה פוטנציאלית חשמלית
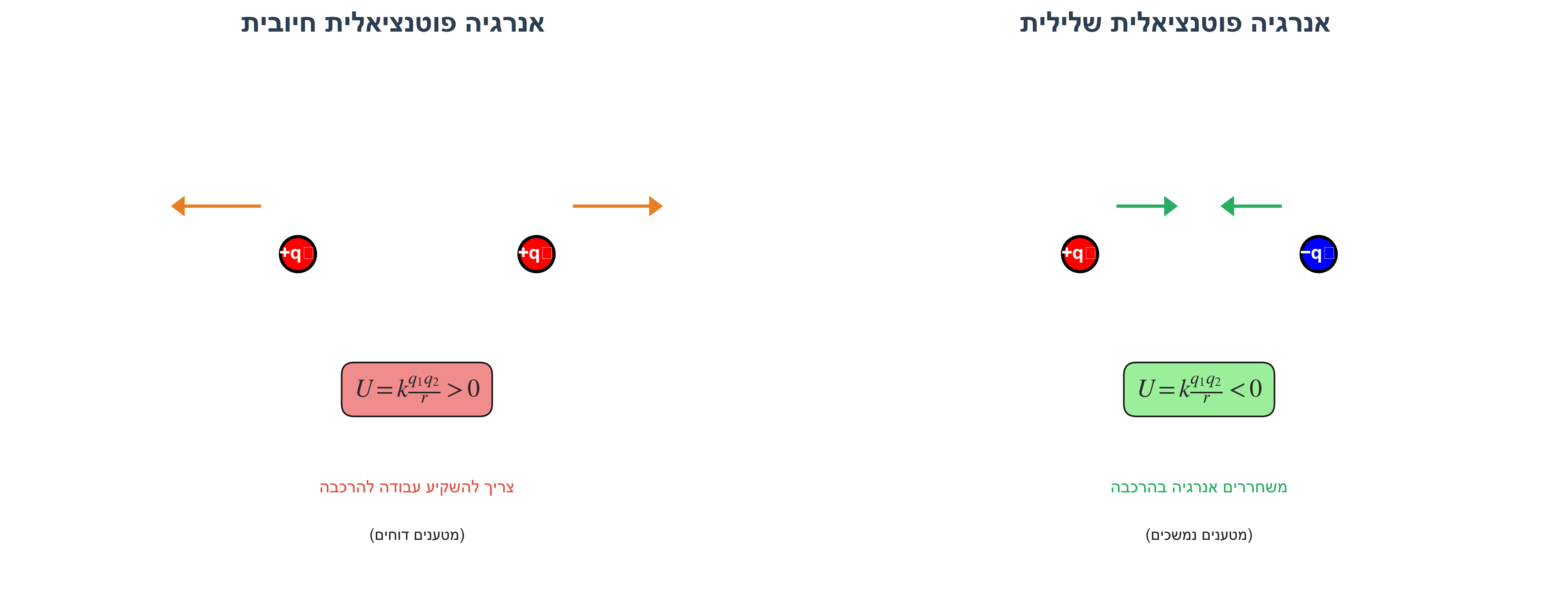
\[U = k\frac{q_1 q_2}{r}\]- $U > 0$ (חיובית) ← המטענים דוחים זה את זה, נדרשה עבודה להרכבת המערכת
- $U < 0$ (שלילית) ← המטענים נמשכים זה לזה, התקבלה אנרגיה בהרכבת המערכת
תרגיל 1: משושה עם מטענים
נתון משושה משוכלל עם אורך צלע $a$. בחמישה מתוך שישה קודקודים (A, B, C, D, E) נמצא מטען נקודתי חיובי $+Q$. בקודקוד F אין מטען.
- חשב את השדה החשמלי בנקודה O (מרכז המשושה).
- מהי העבודה שנדרשת להבאת מטען נוסף $+Q$ ממרחק אינסופי לנקודה O?
- אם נוסיף מטען $+Q$ גם בקודקוד F, מהו השדה החשמלי בנקודה O? ומהי העבודה להבאת מטען $+Q$ מאינסוף לנקודה O?
- אם נשנה את סימני המטענים בקודקודים A, C, E ל-$-Q$, האם תשתנה העבודה להבאת מטען $+Q$ לנקודה O?
סעיף א’: השדה החשמלי במרכז המשושה
שאלה: מהו וקטור השדה החשמלי השקול בנקודה O (מרכז המשושה)?
פתרון:
משיקולי סימטריה, מטענים הנמצאים בקודקודים מנוגדים יוצרים שדות שמבטלים זה את זה:
- השדה מ-A מבטל את השדה מ-D
- השדה מ-B מבטל את השדה מ-E
נשאר רק התרומה של המטען ב-C:
\[\vec{E}_O = \vec{E}_C = \frac{kQ}{a^2}\hat{x}\]סעיף ב’: עבודה להבאת מטען נוסף למרכז
שאלה: מעבירים מטען נוסף $Q$ ממרחק אינסופי לנקודה O. מהי העבודה שנעשתה?
פתרון:
העבודה שווה לאנרגיה הפוטנציאלית של המערכת (סכום התרומות מכל הזוגות):
\[W = U = \sum_{i} k\frac{Q \cdot Q}{r_i}\]המרחק מכל קודקוד למרכז הוא $a$, ויש 5 מטענים:
\[W = 5 \cdot \frac{kQ^2}{a}\]הערה: בחישוב זה התעלמנו מהאנרגיה שנדרשה לבניית המערכת המקורית (5 המטענים).
סעיף ג’: הוספת מטען לקודקוד F
שאלה:
- (א) מהו השדה החשמלי במרכז כעת?
- (ב) מהי העבודה להבאת מטען $Q$ מאינסוף למרכז?
פתרון:
(א) השדה במרכז:
כעת יש סימטריה מלאה - כל המטענים מבטלים זה את זה:
\[\vec{E}_O = 0\](ב) העבודה:
\[W = 6 \cdot \frac{kQ^2}{a}\]סעיף ד’: החלפת סימני מטענים
שאלה: בקודקודים A, C, E מחליפים את המטען החיובי במטען שלילי $-Q$. האם תשתנה העבודה להבאת מטען למרכז?
פתרון:
כעת יש שלושה מטענים $+Q$ ושלושה מטענים $-Q$:
\[W = 3 \cdot \frac{kQ \cdot Q}{a} + 3 \cdot \frac{kQ \cdot (-Q)}{a} = 0\]התשובה: אפס - התרומות מתבטלות בסופרפוזיציה.
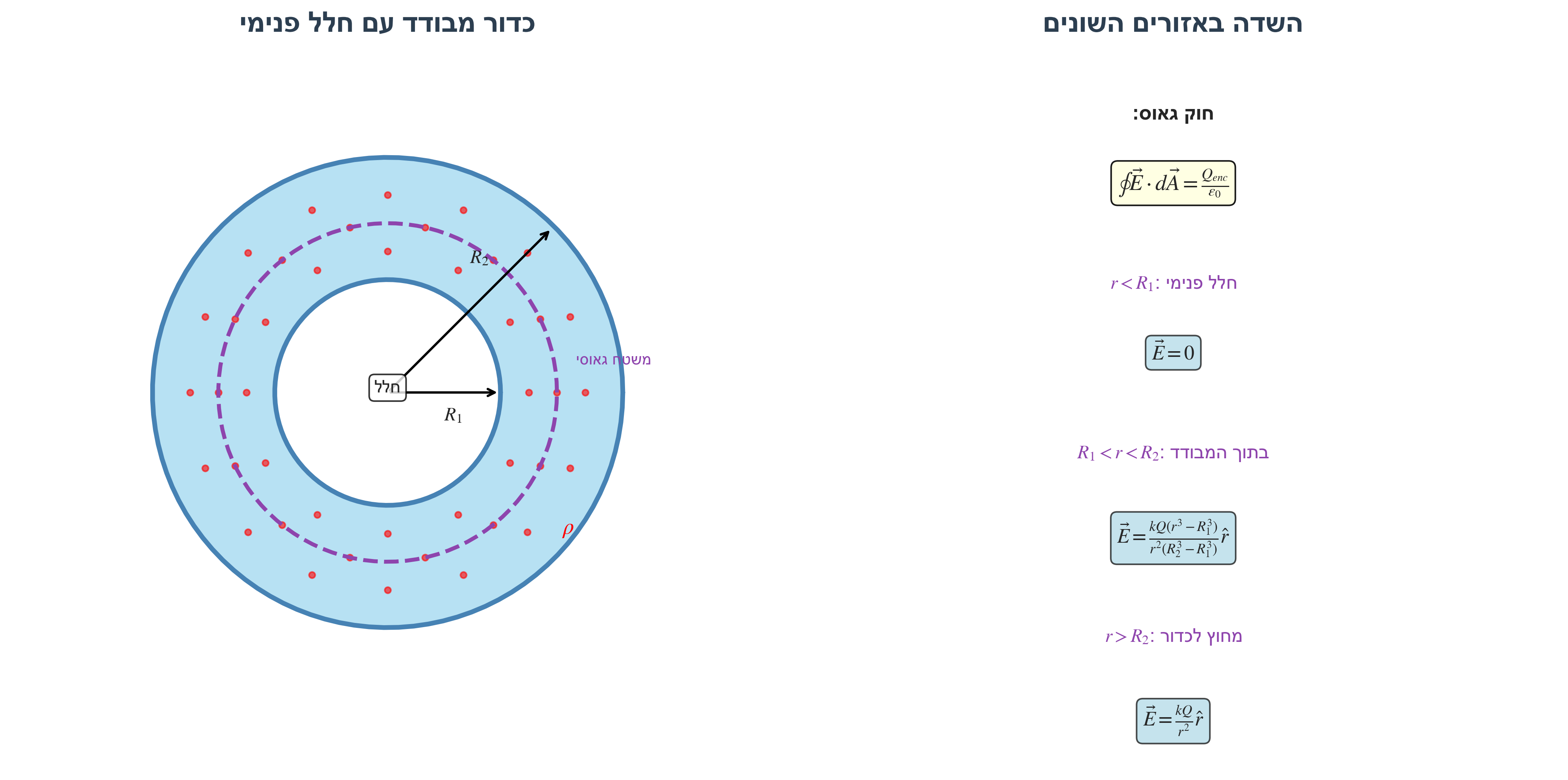
תרגיל 2: חוק גאוס - כדור מבודד עם חלל פנימי
כדור מבודד עם חלל פנימי כדורי (קונצנטרי):
- רדיוס החלל הפנימי: $R_1$
- רדיוס הכדור החיצוני: $R_2$
- צפיפות מטען אחידה $\rho$ בחומר המבודד
- סך המטען: $Q$
חשב את השדה החשמלי באזורים השונים:
- בתוך החלל הפנימי ($r < R_1$)
- בתוך החומר המבודד ($R_1 < r < R_2$)
- מחוץ לכדור ($r > R_2$)
חוק גאוס
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{enclosed}}}{\epsilon_0}\]כאשר $\frac{1}{4\pi\epsilon_0} = k$
סעיף א’: השדה באזור $r < R_1$ (בתוך החלל)
פתרון:
נבחר מעטפת גאוסית כדורית ברדיוס $r < R_1$.
המטען הכלוא בתוך המעטפת: $Q_{\text{enclosed}} = 0$ (אין מטען בחלל הפנימי)
לפי חוק גאוס:
\[E \cdot 4\pi r^2 = \frac{0}{\epsilon_0}\] \[\boxed{\vec{E}(r < R_1) = 0}\]סעיף ב’: השדה באזור $R_1 < r < R_2$ (בתוך החומר המבודד)
פתרון:
נבחר מעטפת גאוסית כדורית ברדיוס $r$.
המטען הכלוא הוא חלק יחסי מהמטען הכולל:
\[Q_{\text{enclosed}} = Q \cdot \frac{V(R_1 \to r)}{V(R_1 \to R_2)} = Q \cdot \frac{\frac{4}{3}\pi r^3 - \frac{4}{3}\pi R_1^3}{\frac{4}{3}\pi R_2^3 - \frac{4}{3}\pi R_1^3}\] \[Q_{\text{enclosed}} = Q \cdot \frac{r^3 - R_1^3}{R_2^3 - R_1^3}\]לפי חוק גאוס:
\[E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0} \cdot \frac{r^3 - R_1^3}{R_2^3 - R_1^3}\] \[\boxed{\vec{E}(R_1 < r < R_2) = \frac{kQ(r^3 - R_1^3)}{r^2(R_2^3 - R_1^3)}\hat{r}}\]פתרון אחר, משיעור תגבור:
השימוש בחוק גאוס כאן הוא הכדור הגדול, פחות הכדור הקטן (למעשה סופר פוזיציה).
\[Q_{in} = \underbrace{\frac{4\pi r^3}{3}\rho}_{\text{full ball}} - \underbrace{\frac{4\pi R_1^3}{3}\rho}_{\text{full negative ball with R radius}}=\frac{4\pi \rho}{3\epsilon_0}\left(r^3-R_1^3\right)\]מצד אחד
כאשר לפי שיעור 4:
\[Q = \rho \cdot \frac{4\pi R^3}{3} \implies \rho = \frac{3Q}{4\pi R^3}\]כלומר:
\[\rho = \frac{3Q}{4\pi (R_2^3 - R_1^3)}\]נציב חזרה:
\[Q_{in} = \frac{4\pi }{3\epsilon_0}\left(r^3-R_1^3\right) \cdot \frac{3Q}{4\pi (R_2^3 - R_1^3)} = \frac{Q(r^3 - R_1^3)}{(R_2^3 - R_1^3)}\]וכל זה לחלק לאפסילון 0 שווה לאינטגרל של השדה על המעטפת:
\[E \cdot 4\pi r^2 = \frac{Q(r^3 - R_1^3)}{\epsilon_0 (R_2^3 - R_1^3)} \implies E = \frac{kQ(r^3 - R_1^3)}{r^2(R_2^3 - R_1^3)} \hat{r}\]
סעיף ג’: השדה באזור $r > R_2$ (מחוץ לכדור)
פתרון:
המטען הכלוא הוא כל המטען: $Q_{\text{enclosed}} = Q$
\[E \cdot 4\pi r^2 = \frac{Q}{\epsilon_0}\] \[\boxed{\vec{E}(r > R_2) = \frac{kQ}{r^2}\hat{r}}\]מסקנה: מחוץ לכדור, השדה זהה לשדה של מטען נקודתי $Q$ במרכז.
תרגיל 3: משולש ישר-זווית עם מטענים
נתון משולש ישר-זווית שווה-שוקיים עם:
- קודקודים A ו-C: מטען $+q$
- קודקוד B (בזווית הישרה): מטען $-q$
- אורך הניצבים: $a$
- אורך היתר: $a\sqrt{2}$
B(-q) /|\ a√2 / | \ a√2 / |a \ / a | a \ -------|-------- C(+q) O A(+q)
סעיף א’: הכוח על המטען ב-B
פתרון:
הכוח על $-q$ ב-B הוא סכום הכוחות מ-A ומ-C.
כיוון x (לאורך הניצב): הרכיבים מתאפסים. פורמאלית:
הכוח מ-A בכיוון x:
\[F_{A,x} = -\frac{kq^2}{2a^2} \cos(45°) = -\frac{kq^2}{2a^2} \cdot \frac{1}{\sqrt{2}}\]הכוח מ-C בכיוון x:
\[F_{C,x} = \frac{kq^2}{2a^2} \cos(45°) = \frac{kq^2}{2a^2} \cdot \frac{1}{\sqrt{2}}\]סך הכל אפס:
\[F_x = F_{A,x} + F_{C,x} = 0\]כיוון y:
שני הכוחות פועלים באותו כיוון:
\[F_y = 2 \cdot \frac{kq^2}{2a^2} \sin(45°) = \frac{kq^2}{\sqrt{2}a^2}\]הכוח הכולל:
\[\boxed{\vec{F}_B = \frac{kq^2}{\sqrt{2}a^2}\hat{y}}\]סעיף ב’: האנרגיה הפוטנציאלית של המערכת
פתרון:
נסכום את האנרגיה של כל זוגות המטענים:
\[U = U_{AB} + U_{BC} + U_{AC}\] \[U_{AB} = k\frac{(+q)(-q)}{\sqrt{2}a} = -\frac{kq^2}{a\sqrt{2}} = U_{BC}\] \[U_{AC} = k\frac{(+q)(+q)}{2a} = \frac{kq^2}{2a}\]סך הכל:
\[U = -\frac{kq^2}{a\sqrt{2}} - \frac{kq^2}{a\sqrt{2}} + \frac{kq^2}{2a} = -\frac{2kq^2}{a\sqrt{2}} + \frac{kq^2}{2a}\] \[\boxed{U = k\frac{q^2}{2a}\left(1 - 2\sqrt{2}\right)}\]סעיף ג’: מהירות המטען B בנקודה O
שאלה: משחררים את המסה B (בעלת מסה $m$) ומחזיקים את שני המטענים האחרים במקומם. מהי מהירות B כשעוברת דרך נקודה O (מרכז היתר)?
גילוי נאות - לא הבנתי עד הסוף את הפתרון לסעיף הזה.
פתרון:
משימור אנרגיה:
\[U_{\text{initial}} + K_{\text{initial}} = U_{\text{final}} + K_{\text{final}}\] \[U_1 + 0 = U_0 + \frac{1}{2}mv^2\]ממה שקיבלנו בסעיף הקודם:
\[U_0 = k\frac{q^2}{2a}\left(1 - 2\sqrt{2}\right)\]כמו כן:
\[U_1 = U_{AO} + U_{CO} + U_{AC} = \frac{-2kq^2}{a} + \frac{kq^2}{2a} = k\frac{q^2}{2a}\left(1 - 4\right) = -\frac{3kq^2}{2a}\]נעבור לחישוב האנרגיה:
\[\underbrace{E_{k_0}}_{=0} + E_{p_0} = E_{kf} + E_{pf}\] \[E_{kf} = E_{p_0} - E_{pf} = U_0 - U_1\] \[= k\frac{q^2}{2a}\left(1 - 2\sqrt{2}\right) - \left(-\frac{3kq^2}{2a}\right) = k\frac{q^2}{2a}\left(4 - 2\sqrt{2}\right)\]כמו כן:
\[E_{kf} = \frac{1}{2}mv^2 \implies v = \sqrt{\frac{2E_{kf}}{m}} = \sqrt{\frac{kq^2}{am}\left(4 - 2\sqrt{2}\right)}\] \[\boxed{v = \sqrt{\frac{kq^2}{am}\left(4 - 2\sqrt{2}\right)}}\]או בגרסה שבתשובות:
\[\boxed{v = \sqrt{\frac{4kq^2}{am}\left(1 - \frac{\sqrt{2}}{2}\right)} = \sqrt{\frac{4kq^2}{am}\left(1 - \frac{1}{\sqrt{2}}\right)}}\]נקודות שחשוב לזכור
- סופרפוזיציה - תקפה רק במערכות לינאריות
- אנרגיה פוטנציאלית - גודל סקלרי (לא וקטור), יש לו סימן
- חוק גאוס - שימושי כשיש סימטריה (כדורית, גלילית, מישורית)
- שדה בתוך חלל במבודד - תלוי רק במטען הכלוא בתוך המעטפת הגאוסית
- שימור אנרגיה - $K_i + U_i = K_f + U_f$ (בכוח משמר)
- מחוץ להתפלגות כדורית - השדה זהה לשדה של מטען נקודתי במרכז