בעיית החבל המשתלשל

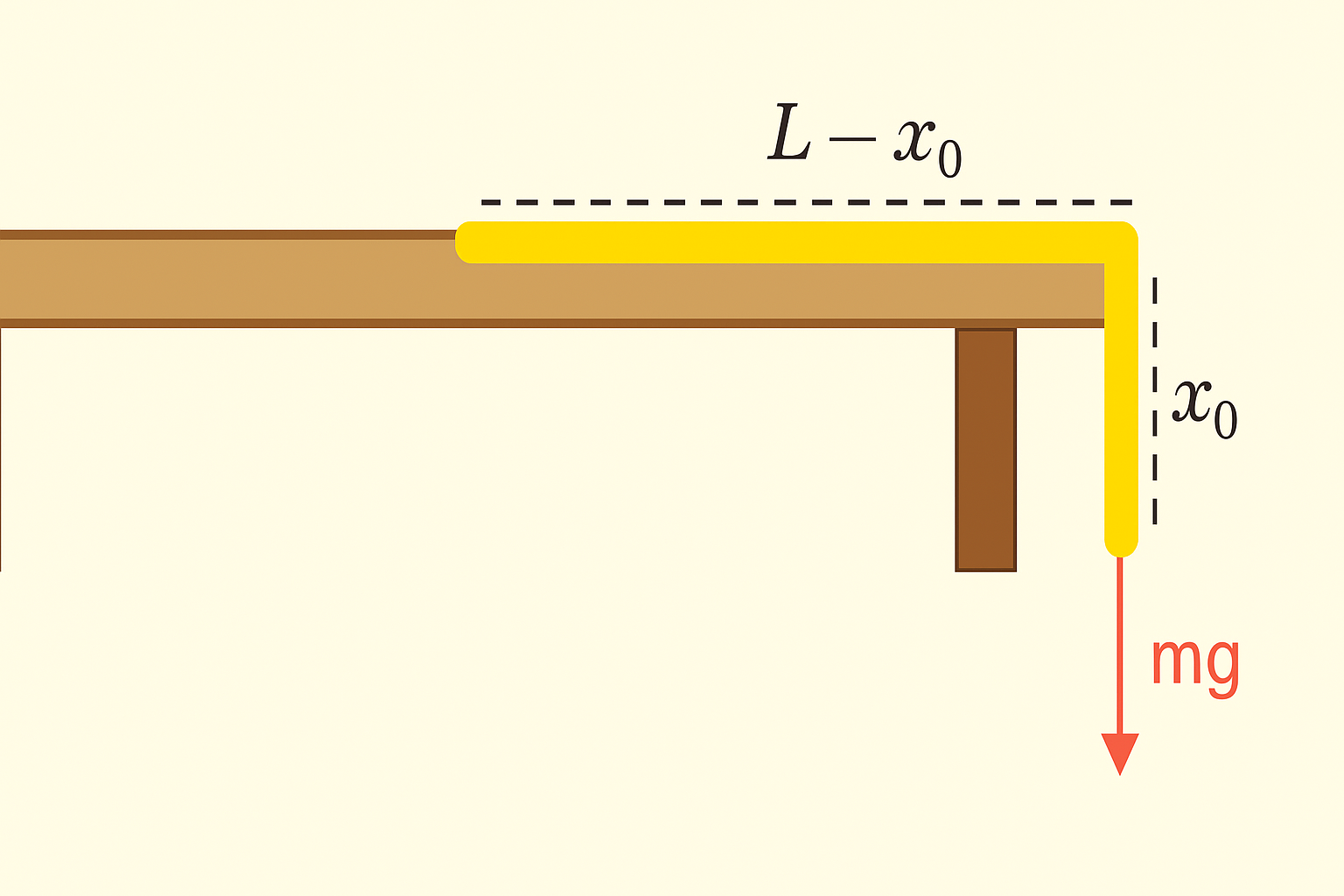
נניח שחבל משתלשל מקצה של שולחן. הפרמטרים והיחידות שלהם:

  • $L\ \text{m}$ - אורך החבל הכולל
  • $g\ \text{m/s}^2$ - תאוצת הכבידה
  • $x(t)$ - אורך החבל המשתלשל (מחוץ לשולחן) בזמן $t$
  • $\rho\ \text{kg/m}$ - צפיפות החבל
  • $t\ \text{s}$ - זמן
  • $v(t)\ \text{m/s}$ - מהירות החבל

תנאי התחלה ($t=0$)

\[\begin{cases} x(0) = x_0\ \text{m} \\ \dot{x}(0) = v(0) = 0\ \text{m/s} \end{cases}\]

אנחנו מניחים שהחבל מתחיל ממנוחה, כלומר המהירות ההתחלתית היא אפס, וצריכים למצוא:

  • $v(t)\ \text{m/s}$ - מהירות החבל בזמן $t$
  • $x(t)\ \text{m}$ - אורך החבל המשתלשל בזמן $t$
  • $T\ \text{s}$ - זמן ההחלקה המלאה של החבל מהשולחן (כאשר $x(T) = L$)

alt text

תחילה נניח שאין חיכוך. נסמן:

  • $m = \rho L$ - המסה הכוללת של החבל [ק”ג]
  • $m^* = \rho x$ - המסה של החלק המשתלשל [ק”ג]

נתבונן בכוחות הפועלים על המערכת:

  1. כוח הכבידה על החלק המשתלשל: $F_g = m^* g = \rho x g \left[\text{N}\right]$
  2. אין חיכוך בין החבל לשולחן

לפי החוק השני של ניוטון, הכוח השקול מייצר תאוצה בכל המסה של החבל. בצורה הכללית של החוק השני של ניוטון:

\[\underbrace{F}_{\text{force}} = \underbrace{m}_{\text{mass}} \cdot \underbrace{a}_{\text{velocity}} \tag{1}\]

נציב את הערכים המתאימים במשאוואה $(1)$:

\[\underbrace{\rho x(t) g}_{\text{forces on the rope}} = \underbrace{\rho L}_{\text{rope mass}} \cdot \underbrace{\ddot{x}(t)}_{\text{rope velociry}} \tag{2}\]

נסביר את משוואה $(2)$:

  • הכוח הפועל: $\underbrace{\rho x g}_{\text{weight of the falling part}}$

    • $\rho$ = צפיפות החבל [ק”ג/מטר]
    • $x(t)$ = אורך החלק המשתלשל בזמן $t$ [מטר]
    • $g$ = תאוצת הכבידה [מטר/שנייה²]

  • המסה המואצת: $\underbrace{\rho L}_{\text{rope velocity}}$

    • $\rho$ = צפיפות החבל [ק”ג/מטר]
    • $L$ = האורך הכולל של החבל [מטר]

  • התאוצה: $\underbrace{\ddot{x}}_{\text{2nd derivient of }x\text{ in time t}}$

נפשט את משוואה $(2)$:

\[\begin{aligned} \rho x g &= \rho L \ddot{x} \\ \ddot{x} &= \underbrace{\frac{g}{L}}_{\text{constant}} \cdot \underbrace{x}_{\text{falling part length}} \end{aligned}\]

זוהי המשוואה הדיפרנציאלית המתארת את תנועת החבל. אם נסמן $\omega^2 = \frac{g}{L}$, נקבל:

\[\ddot{x} = \underbrace{\omega^2}_{\text{constant}} \cdot x \tag{3}\]

היחידות של $\omega^2$ הן [1/שנייה²], מכיוון ש-$g$ הוא תאוצת הכבידה [מטר/שנייה²] ו-$L$ הוא אורך החבל [מטר].

alt text

פתרון המשוואה הדיפרנציאלית

alt text

משוואה $(3)$ היא משוואה דיפרנציאלית לינארית הומוגנית מסדר שני. הפתרון הכללי הוא:

\[x(t) = A\cosh(\omega t) + B\sinh(\omega t) \,\text{m} \tag{4}\]

כאשר:

  • $\cosh(y) = \frac{e^y + e^{-y}}{2}$ (פונקציית הקוסינוס ההיפרבולי)
  • $\sinh(y) = \frac{e^y - e^{-y}}{2}$ (פונקציית הסינוס ההיפרבולי)
  • $A$ ו-$B$ הם קבועים שנקבעים לפי תנאי ההתחלה [M]

מציאת הקבועים A ו-B

נשתמש בתנאי ההתחלה כדי למצוא את הקבועים $A$ ו-$B$:

  1. תנאי ראשון: $x(0) = x_0$

    נציב $t = 0$ בפתרון הכללי (משוואה $(4)$):

    \[x(0) = A\cosh(0) + B\sinh(0)\]

    מכיוון ש-$\cosh(0) = 1$ ו-$\sinh(0) = 0$, מתקבל:

    \[x_0 = A \cdot 1 + B \cdot 0 = A\]

    לכן $\boxed{A = x_0 \ \text{m}}$.

  2. תנאי שני: $\dot{x}(0) = 0$

    נחשב את הנגזרת של $x(t)$:

    \[\dot{x}(t) = A\omega\sinh(\omega t) + B\omega\cosh(\omega t) \,\text{m/s}\]

    נציב $t = 0$:

    \[\dot{x}(0) = A\omega\sinh(0) + B\omega\cosh(0)\]

    מכיוון ש-$\sinh(0) = 0$ ו-$\cosh(0) = 1$, מתקבל:

    \[\begin{aligned} 0 &= 0 + B\omega \cdot 1 \\ B \omega &= 0 \end{aligned}\]

    לכן $\boxed{B = 0 \ \text{m}}$.

הפתרון המלא

כעת, כאשר $A = x_0$ ו-$B = 0$, הפתרון המלא הוא:

\[\begin{aligned} x(t) &= \underbrace{A}_{x_0}\cosh(\omega t) + \underbrace{B}_{0}\sinh(\omega t) \\ &= x_0 \cosh(\omega t) + 0 \\ &= x_0 \cosh(\omega t) \,\text{m} \end{aligned}\]

והמהירות:

\[v(t) = \dot{x}(t) = x_0 \omega \sinh(\omega t) \,\text{m/s}\]

חישוב זמן ההחלקה המלאה

alt text

זמן ההחלקה המלאה $T$ הוא הזמן שבו $x(T) = L$, כלומר כל החבל נמצא מחוץ לשולחן:

\[x_0 \cosh(\omega T) = L\] \[\cosh(\omega T) = \frac{L}{x_0}\] \[\omega T = \cosh^{-1}\left(\frac{L}{x_0}\right)\] \[T = \frac{1}{\omega}\cosh^{-1}\left(\frac{L}{x_0}\right) = \sqrt{\frac{L}{g}}\cosh^{-1}\left(\frac{L}{x_0}\right) \,\text{s}\]

הסבר פיזיקלי

פתרון זה מראה שתנועת החבל היא לא בתאוצה קבועה אלא בתאוצה שגדלה עם הזמן. ככל שיותר חבל משתלשל, כך גדל הכוח המושך, וכתוצאה מכך גדלה התאוצה. זהו מקרה של “משוב חיובי” - תהליך שמגביר את עצמו.

ככל שהחלק המשתלשל ההתחלתי ($x_0$) גדול יותר, כך זמן ההחלקה ($T$) קטן יותר. זה הגיוני פיזיקלית כי חלק משתלשל גדול יותר מייצר כוח משיכה חזק יותר מההתחלה.

גרסה עם חיכוך

הסבר על חיכוך

החיכוך הוא כוח המתנגד לתנועה היחסית בין שני משטחים במגע. ישנם שני סוגי חיכוך:

  1. חיכוך סטטי ($f_s$) - פועל כאשר הגוף במנוחה ומונע ממנו להתחיל לנוע
  2. חיכוך קינטי ($f_k$) - פועל כאשר הגוף בתנועה ומאט אותו

עוצמת כוח החיכוך הקינטי מתוארת על ידי:

\[f_k = \mu_k N \left[\text{N}\right]\]

כאשר $\mu_k$ הוא מקדם החיכוך הקינטי ו-$N$ הוא הכוח הנורמלי.

ניתוח הכוחות עם חיכוך

הכוח הנורמלי שווה למשקל החלק של החבל שעל השולחן:

\[\begin{align} N &= (m-m^*)g \\ &= (\rho L - \rho x)g \\ &= \rho(L-x)g \left[\text{N}\right] \end{align}\]

לכן, כוח החיכוך הקינטי יהיה:

\[f_k = \mu_k N = \mu_k \rho (L - x) g \left[\text{N}\right]\]

החוק השני של ניוטון קובע כי הכוח השקול הפועל על גוף שווה למכפלת מסת הגוף בתאוצתו: $F = m \cdot a$. בבעיית החבל המשתלשל, נפעל בשלבים מסודרים:

שלב 1: זיהוי הכוחות הפועלים על המערכת

הכוחות העיקריים הפועלים על החבל:

  1. כוח הכובד על החלק המשתלשל ($m^* g$):

    • פועל כלפי מטה
    • $m^* = \rho x$ היא מסת החלק המשתלשל
    • $m^* g = \rho x g \ \text{N}$

  2. כוח החיכוך הקינטי ($f_k$):

    • פועל בכיוון המתנגד לתנועה (מושך את החבל חזרה)
    • $f_k = \mu_k N$ כאשר $N$ הוא הכוח הנורמלי
    • $N = \rho (L-x) g$ היא משקל החלק הנמצא על השולחן
    • $f_k = \mu_k \rho (L-x) g \ \text{N}$

שלב 2: חישוב הכוח השקול (סכום הכוחות)

הכוח השקול הוא ההפרש בין כוח הכובד המושך את החבל מטה לבין כוח החיכוך המעכב את התנועה:

\[\sum F = m^* g - f_k\]

נציב את הביטויים המפורטים:

\[\sum F = \rho x g - \mu_k \rho (L-x) g\]

שלב 3: יישום החוק השני של ניוטון

לפי החוק השני של ניוטון, הכוח השקול שווה למכפלת המסה בתאוצה. המסה של כל החבל היא $m = \rho L$, והתאוצה היא $\ddot{x}$:

\[\sum F = m \cdot a\] \[\rho x g - \mu_k \rho (L-x) g = \rho L \cdot \ddot{x}\]

שלב 4: פיתוח מתמטי לקבלת המשוואה הדיפרנציאלית

נפתח את המשוואה שלב אחר שלב:

\[\rho L \cdot \ddot{x} = \rho x g - \mu_k \rho (L-x) g\]

נחלק את שני האגפים ב-$\rho L$ כדי לבודד את התאוצה $\ddot{x}$:

\[\ddot{x} = \frac{\rho x g - \mu_k \rho (L-x) g}{\rho L}\]

נצמצם את $\rho$ בכל האגפים:

\[\ddot{x} = \frac{x g - \mu_k (L-x) g}{L}\]

נוציא גורם משותף $g$:

\[\ddot{x} = \frac{g}{L} [x - \mu_k (L-x)]\]

נפתח את הסוגריים:

\[\ddot{x} = \frac{g}{L} [x - \mu_k L + \mu_k x]\]

נאסוף איברים:

\[\ddot{x} = \frac{g}{L} [(1 + \mu_k)x - \mu_k L]\]

נפתח את הסוגריים שוב:

\[\ddot{x} = \frac{g}{L} (1 + \mu_k) x - \frac{g}{L} \mu_k L\]

נפשט:

\[\ddot{x} = \frac{g}{L} (1 + \mu_k) x - \mu_k g \left[\frac{\text{M}}{\text{S}^2}\right]\]

סיכום והסבר פיזיקלי

המשוואה הסופית שקיבלנו:

\[\ddot{x} = \frac{g}{L} (1 + \mu_k) x - \mu_k g\]

משמעות פיזיקלית:

  • האיבר הראשון $\frac{g}{L} (1 + \mu_k) x$ מייצג את ההאצה בגלל כוח הכובד וההשפעה של החיכוך על החלק המשתלשל. ככל שהחלק המשתלשל גדל, כך גדלה ההאצה.
  • האיבר השני $\mu_k g$ הוא קבוע שלילי המייצג את ההשפעה המעכבת של החיכוך.

כשמגדירים $\omega^2 = \frac{g}{L} (1 + \mu_k)$, מקבלים משוואה דיפרנציאלית בצורה קומפקטית:

\[\ddot{x} = \omega^2 x - \mu_k g\]

זוהי משוואה דיפרנציאלית לינארית לא הומוגנית מסדר שני, שהפתרון שלה יהיה סכום של פתרון המשוואה ההומוגנית ופתרון פרטי.

נגדיר $\omega^2 = \frac{g}{L} (1 + \mu_k) \ \text{[1/s²]}$, כך שהמשוואה הסופית היא:

\[\ddot{x} = \omega^2 x - \mu_k g\]

זוהי משוואה דיפרנציאלית לא הומוגנית מסדר שני.

פתרון המשוואה הדיפרנציאלית עם חיכוך

הפתרון הכללי למשוואה מסוג זה מורכב מהפתרון של המשוואה ההומוגנית (ללא האיבר הקבוע) ומפתרון פרטי:

\[x(t) = A\cosh(\omega t) + B\sinh(\omega t) + C \,\text{m}\]

נציב את הפתרון הפרטי $C$ במשוואה המקורית:

\[\ddot{C} = \omega^2 C - \mu_k g\]

מכיוון ש-$C$ הוא קבוע, אז $\ddot{C} = 0$:

\[0 = \omega^2 C - \mu_k g\] \[C = \frac{\mu_k g}{\omega^2} = \frac{\mu_k g}{\frac{g}{L} (1 + \mu_k)} = \frac{\mu_k L}{1 + \mu_k} \,\text{m}\]

לכן, הפתרון הכללי:

\[x(t) = A\cosh(\omega t) + B\sinh(\omega t) + \frac{\mu_k L}{1 + \mu_k}\]

נשתמש בתנאי ההתחלה כדי למצוא את הקבועים $A$ ו-$B$:

  1. תנאי ראשון: $x(0) = x_0$

    \[x(0) = A\cosh(0) + B\sinh(0) + \frac{\mu_k L}{1 + \mu_k}\] \[x_0 = A \cdot 1 + 0 + \frac{\mu_k L}{1 + \mu_k}\] \[A = x_0 - \frac{\mu_k L}{1 + \mu_k} \,\text{m}\]

  2. תנאי שני: $\dot{x}(0) = 0$

    \[\dot{x}(t) = A\omega\sinh(\omega t) + B\omega\cosh(\omega t) + 0\] \[\dot{x}(0) = A\omega\sinh(0) + B\omega\cosh(0)\] \[0 = 0 + B\omega \cdot 1\] \[B = 0 \,\text{m}\]

לכן, הפתרון המלא:

\[x(t) = \left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\cosh(\omega t) + \frac{\mu_k L}{1 + \mu_k} \,\text{m}\]

והמהירות:

\[v(t) = \left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\omega\sinh(\omega t) \,\text{m/s}\]

תנאי הסף להחלקה

טרם תחילת התנועה, חיכוך סטטי מונע את תנועת החבל. החבל יחל להחליק רק כאשר כוח המשיכה של החלק המשתלשל יהיה גדול מכוח החיכוך הסטטי המקסימלי:

\[F_{\text{drag}} > F_{\text{max static friction}}\] \[\rho g x_0 > \mu_s \rho g (L - x_0)\]

פישוט:

\[x_0 > \frac{\mu_s L}{1 + \mu_s} \,\text{m}\]

זהו תנאי הסף להחלקה. אם החלק המשתלשל ההתחלתי קטן מדי, החבל כלל לא יחל להחליק!

זמן ההחלקה המלאה עם חיכוך

לחישוב זמן ההחלקה המלאה, נציב $x(T) = L$:

\[\left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\cosh(\omega T) + \frac{\mu_k L}{1 + \mu_k} = L\]

פישוט:

\[\left(x_0 - \frac{\mu_k L}{1 + \mu_k}\right)\cosh(\omega T) = L - \frac{\mu_k L}{1 + \mu_k} = \frac{L}{1 + \mu_k}\] \[\cosh(\omega T) = \frac{\frac{L}{1 + \mu_k}}{x_0 - \frac{\mu_k L}{1 + \mu_k}} = \frac{L}{(1 + \mu_k)(x_0 - \frac{\mu_k L}{1 + \mu_k})}\]

ומכאן:

\[T = \frac{1}{\omega}\cosh^{-1}\left(\frac{L}{(1 + \mu_k)(x_0 - \frac{\mu_k L}{1 + \mu_k})}\right) \,\text{s}\] \[T = \sqrt{\frac{L}{g(1+\mu_k)}}\cosh^{-1}\left(\frac{L(1+\mu_k)}{(1+\mu_k)x_0 - \mu_k L}\right) \,\text{s}\]

הסבר פיזיקלי להשפעת החיכוך

החיכוך מתנגד לתנועת החבל ומאט את קצב ההחלקה. כתוצאה מכך:

  1. נדרש ערך מינימלי של $x_0$ כדי שהחבל יתחיל בכלל להחליק. אם $x_0 \leq \frac{\mu_s L}{1 + \mu_s}$, החבל יישאר במנוחה.
  2. זמן ההחלקה המלאה $T$ גדול יותר בהשוואה למקרה ללא חיכוך, שכן החיכוך מאט את תנועת החבל.
  3. הפתרון כולל איבר קבוע $\frac{\mu_k L}{1 + \mu_k}$ שמייצג את ההשפעה של החיכוך על דינמיקת המערכת.
  4. החיכוך גם משנה את ערך $\omega$ (מ-$\sqrt{\frac{g}{L}}$ ל-$\sqrt{\frac{g}{L}(1+\mu_k)}$), מה שמשפיע על קצב הגידול של המהירות וההאצה.

במקרה הגבולי שבו $\mu_k = 0$ (אין חיכוך), נקבל $\omega^2 = \frac{g}{L}$ ו-$C = 0$, והפתרון יהיה זהה לפתרון שמצאנו במקרה הראשון:

\[x(t) = x_0 \cosh(\omega t)\]

זה מאשר את נכונות הפתרון הכללי שלנו.

אוסצילטור הרמוני

הקדמה

אני אגדיר לכם מה זה אוסילטור הרמוני ואשלח אתכם לפתרון אנליטי של בעיית האוסילטור בבלוג שלי, שם יש פוסט קטן על האוסילטור ההרמוני הקלאסי. תוכלו לראות שם איך אני פותר את הבעיה האנליטית, אבל פה אני אנחש פתרון משום שקל מאוד לנחש את הפתרון.

הגדרת האוסילטור ההרמוני

אתן דוגמה לאוסילטור הרמוני ואז אסביר אותו. נניח שיש לנו קיר ורצפה נטולת חיכוך, כאשר על הרצפה מונחת מסה $M$ שמחוברת בקפיץ לקיר.

הקפיץ - פיזיקה

צריך להבין מה זה קפיץ מבחינה פיזיקלית. קפיץ מפעיל כוח מחזיר כאשר מותחים אותו. הכוח מתכונתי (פרופורציונלי, ליניארי) לאורך המתיחה.

באופן וקטורי (בתלת-ממד):

\[\vec{F} = -k \cdot \vec{r}\]

זהו כוח מחזיר המתכונתי לבקטור המקום, כאשר $k$ נקרא קבוע הכוח של הקפיץ.

היחידות של $k$ הן ניוטון למטר. ככל ש-$k$ גדול יותר, הכוח המחזיר חזק יותר. ככל ש-$k$ קטן יותר, הכוח המחזיר חלש יותר.

בממד אחד, כמו במקרה שלנו, זה:

\[F = -k \cdot x\]

שימו לב שכאשר $x = 0$, הכוח הוא אפס. עכשיו תשאלו בצדק: איזה קפיץ בעולם יש לו אורך אפס, שרק אז הוא לא מפעיל כוח? הרי לכל הקפיצים יש אורך שונה מאפס כשהם רפויים.

התשובה היא שהמודל הזה של קפיץ הוא מודל פשוט. בחיים האמיתיים ישנם קפיצים “כביכול” שהאורך הרפוי שלהם הוא אפס, כלומר שרק ב-$x = 0$ הם לא מפעילים כוח.

מי הם הקפיצים האלו? אלו הם הסריגים האטומיים. כשאני מכניס אטום לסריג אטומי, האטום יושב במקום שבו, אם אני מכניס את הסריג לטמפרטורה של אפס קלווין (האפס המוחלט), האטומים לא רוטטים. האטום יושב בדיוק במקום של שיווי המשקל, כלומר כל האטומים מסביב מפעילים עליו כוחות בכיוונים מנוגדים והוא יושב בנקודת שיווי משקל.

אם אני מסיט את האטום משיווי המשקל, אז הכוחות של האטומים האחרים ירצו להחזיר אותו לנקודת שיווי המשקל. רק בנקודת שיווי המשקל הוא ירגיש כוח אפס שפועל עליו. כך שבעצם, כל הסריגים האטומיים והמולקולריים שאנחנו מכירים הם סוג של אוסף של מספר רב של קפיצים שמשפיעים זה על זה, והאורך הרפוי שלהם הוא אפס.

אם בכל זאת רוצים לדבר על קפיץ מהחיים האמיתיים, אז הכוח יוחלף ב:

\[F = -k \cdot (x - x_0)\]

כאשר $x_0$ הוא האורך הרפוי. כאשר $x = x_0$, הכוח מתאפס. זה מה שמחליף את $F = -kx$ במקרים מעשיים.

המשוואה הדיפרנציאלית של האוסילטור ההרמוני

מה תהיה המשוואה הדיפרנציאלית עבור הבעיה הזאת עם אורך רפוי אפס?

מהחוק השני של ניוטון:

\[F = ma\]

הכוח הוא:

\[F = -kx\]

ולכן:

\[-kx = m \ddot{x}\]

או:

\[\ddot{x} = -\frac{k}{m} \cdot x\]

זוהי המשוואה הדיפרנציאלית המתקבלת מהחוק השני עבור קפיץ עם אורך רפוי אפס, או אוסצילטור (מתנד).

אם נסמן:

\[\omega^2 = \frac{k}{m}\]

אז המשוואה מקבלת את הצורה:

\[\ddot{x} = -\omega^2 x\]

זוהי משוואת האוסצילטור ההרמוני.

אוסצילטור זה מתנד, משהו שמתנדנד (כמו מטרונום במוזיקה). בעברית אוסצילטור הוא “מתנד”. תנודות הרמוניות הן תנודות המתוארות באמצעות פונקציות סינוס וקוסינוס.

לאוסצילטור ההרמוני יש חשיבות רבה מאוד, כיוון שכל האטומים בחומרים מוצקים הם בעצם אוסצילטורים הרמוניים. כמעט כל התכונות הפיזיקליות של החומרים מקורן באופן שבו האטומים מתנדדים.

האוסצילטור ההרמוני הוא אבן יסוד של המצבים הפיזיקליים. כמעט כל המצבים הפיזיקליים ניתנים לתיאור על ידי קומבינציות ליניאריות של אוסצילטורים הרמוניים.

בנוסף, במכניקה הקוונטית, יש רק שתי בעיות שניתנות לפתרון אנליטי סופי: האוסצילטור ההרמוני ואטום המימן. כל הבעיות האחרות דורשות טכניקות של קירוב.

פתרון המשוואה הדיפרנציאלית של האוסילטור ההרמוני

המשוואה שאנו רוצים לפתור היא:

\[\ddot{x} = -\omega^2 x\]

כאשר $\omega^2 = \frac{k}{m}$, כאשר $k$ הוא קבוע הכוח של הקפיץ ו-$m$ היא מסת הגוף המתנדד.

פתרון באמצעות ניחוש

מהי הפונקציה שאם נגזור אותה פעמיים, נקבל מינוס הפונקציה עצמה? התשובה היא סינוס וקוסינוס.

הפתרון המלא הוא:

\[x(t) = A \cos(\omega t) + B \sin(\omega t)\]

כאשר $A$ ו-$B$ הם קבועים שייקבעו על פי תנאי ההתחלה.

למה זה עובד? כאשר נגזור את הקוסינוס פעמיים, נקבל מינוס קוסינוס:

\[\frac{d^2}{dt^2}[\cos(\omega t)] = -\omega^2 \cos(\omega t)\]

וכן לגבי הסינוס:

\[\frac{d^2}{dt^2}[\sin(\omega t)] = -\omega^2 \sin(\omega t)\]

אלו שני פתרונות בלתי תלויים, והפתרון הכללי הוא הקומבינציה הליניארית שלהם.

קביעת הקבועים באמצעות תנאי התחלה

נניח שהמערכת התחילה ממיקום $x_0$ ובמהירות $v_0$. נציב את תנאי ההתחלה כדי לקבוע את $A$ ו-$B$.

בזמן $t = 0$:

\[x(0) = x_0 = A\cos(0) + B\sin(0) = A\]

מאחר ש-$\cos(0) = 1$ ו-$\sin(0) = 0$, מיד נקבל:

\[A = x_0\]

כדי לדעת מהו $B$, נגזור פעם אחת ונקבל את המהירות:

\[v(t) = \frac{dx}{dt} = -A\omega\sin(\omega t) + B\omega\cos(\omega t)\]

אם $v(0) = v_0$, אז:

\[v_0 = -A\omega\sin(0) + B\omega\cos(0) = B\omega\]

ולכן:

\[B = \frac{v_0}{\omega}\]

הפתרון המלא יהיה, אם כן:

\[x(t) = x_0\cos(\omega t) + \frac{v_0}{\omega}\sin(\omega t)\]

זהו הפתרון בתנאי ההתחלה הנתונים, כאשר $\omega^2 = \frac{k}{m}$.

צורה אלטרנטיבית של הפתרון

את הפתרון הנ”ל ניתן לרשום גם באופן הבא:

\[x(t) = C\cos(\omega t + \phi)\]

כאשר $C$ ו-$\phi$ הם קבועים חדשים שתלויים ב-$A$ ו-$B$.

אם נפתח את הקוסינוס של סכום זוויות:

\[x(t) = C\cos(\omega t)\cos(\phi) - C\sin(\omega t)\sin(\phi)\]

כאשר משווים את שתי הצורות של הפתרון, נקבל:

\[A = C\cos(\phi)\] \[B = -C\sin(\phi)\]

מחלוקת המשוואות זו בזו:

\[\frac{B}{A} = -\frac{\sin(\phi)}{\cos(\phi)} = -\tan(\phi)\]

ולכן:

\[\phi = \arctan\left(-\frac{B}{A}\right)\]

בנוסף:

\[A^2 + B^2 = C^2\cos^2(\phi) + C^2\sin^2(\phi) = C^2\]

ולכן:

\[C = \sqrt{A^2 + B^2}\]

ובהצבת הערכים של $A$ ו-$B$ בתנאי ההתחלה:

\[C = \sqrt{x_0^2 + \frac{v_0^2}{\omega^2}}\]

משמעות פיזיקלית של הפתרון

מדוע הצורה השנייה של הפתרון לפעמים יותר שימושית? כיוון שמהצורה הזו קל לראות את המגבלות על התנועה.

הקוסינוס נע בין $+1$ ל-$-1$, ולכן $x(t) = C\cos(\omega t + \phi)$ נע בין $+C$ ל-$-C$. לערך $C$ קוראים המשרד של התנודה או אמפליטודה (מהמילה האנגלית amplitude).

המשרד של התנודה הוא:

\[C = \sqrt{x_0^2 + \frac{v_0^2}{\omega^2}}\]

כלומר, בהינתן תנאי התחלה, אנו יודעים מהי האמפליטודה של התנודה. המסה מתנדדת בין מרחק מקסימלי שהוא $+C$ לבין מרחק מקסימלי שהוא $-C$.

זמן המחזור של התנודה

המחזור של פונקציות הסינוס והקוסינוס הוא $2\pi$. תנודה מלאה תסתיים כאשר הארגומנט בתוך הקוסינוס והסינוס משלים $2\pi$, כלומר כאשר $\omega T = 2\pi$.

לכן, זמן המחזור של התנודה הוא:

\[T = \frac{2\pi}{\omega} = \frac{2\pi}{\sqrt{\frac{k}{m}}} = 2\pi\sqrt{\frac{m}{k}}\]

זהו זמן המחזור של התנודה - הזמן שלוקח למסה להתחיל בנקודה מסוימת, להגיע לצד השני המקסימלי, ואז לחזור לנקודת ההתחלה.

סיכום

המתנד נקרא “מתנד הרמוני” כיוון שהתנודה שלו היא תנודה הרמונית, כלומר תנודה שמתוארת באמצעות פונקציות סינוס וקוסינוס. יש גם תנודות שאינן הרמוניות, כפי שנראה בהמשך.

התנודה ההרמונית היא הפשוטה ביותר, כיוון שהיא מתוארת על ידי סינוס וקוסינוס. היא מאוד אלגנטית, זמן המחזור שלה ברור, והאמפליטודה (המשרד) שלה מוגדרת היטב.

בשיעור הבא, נפתור אנליטית את בעיית האוסילטור ההרמוני, נראה דוגמאות של תנודות הרמוניות, ונעבור לקואורדינטות גליליות. שם נתקל בתופעה מעניינת שבה וקטורי היחידה תלויים בזמן ומשתנים בזמן, מה שהופך את הבעיות למעניינות יותר.

שאלות ותשובות מהתלמידים

שאלה: למה $\omega$ בריבוע שווה ל-$\frac{k}{m}$?

תשובה: $\omega$ בריבוע זה שורש של $\frac{k}{m}$. $k$ זה קבוע הכוח של הקפיץ, ו-$m$ זו מסת הגוף המתנדד. האומגה מופיעה בנוסחה בצורה זו כי בכל גזירה של פונקציית הסינוס או הקוסינוס, ה-$\omega$ נשלף החוצה, וכשגוזרים פעמיים מקבלים $\omega^2$.

שאלה: למה צריך את שני הפתרונות (סינוס וקוסינוס) ולא מספיק אחד מהם?

תשובה: אם היינו לוקחים רק את הקוסינוס, היינו מפספסים את החלק עם הסינוס בפתרון. אם היינו לוקחים רק את הסינוס, היינו מפספסים את החלק עם הקוסינוס. תנאי ההתחלה מכתיבים את האופן שבו הפתרון מתנהג. בסיטואציות מסוימות, תנאי ההתחלה ידרשו רק פתרון אחד, אך בסיטואציות אחרות הם ידרשו את שני הפתרונות.

שאלה: מה היחידות של $\omega$?

תשובה: היחידות של $\omega$ הן $\frac{1}{\text{s}}$ או הרץ (Hz), שהיא יחידת תדירות. זה נובע מכך ש-$\omega^2 = \frac{k}{m}$, כאשר $k$ ביחידות של ניוטון למטר ו-$m$ ביחידות של ק”ג, כך ש-$\omega^2$ ביחידות של $\frac{1}{\text{s}^2}$.

שאלה: המסה $m$ היא של הקפיץ או של הגוף?

תשובה: המסה $m$ היא של הגוף המתנדד (במקרה שלנו, המסה $M$ שמחוברת לקפיץ). בדרך כלל מניחים שלקפיץ עצמו אין מסה במודל הפשוט הזה.

דור פסקל
חזרה לשיעור 5
חזור לשיעור 6