הערה חשובה: תשובות מפורטות יותר לרוב התרגילים כאן נמצאות בסיכומי השיעורים והתרגולים, כולל סיכומי שיעורי התגבור. התשובות שלהלן לקוחות מתוך טיוטה ישנה שמצאתי ושאלי תסייע למישהו, אך מומלץ לעבור על התשובות בסיכומי השיעורים, התרגולים והתגבורים.
שאלה 1: מסה על מישור משופע עם קפיץ
נתון: על גבי מישור משופע חסר חיכוך מונחת מסה $m$ המחוברת אל ראשו של המישור בקפיץ. המישור המשופע יכול להחליק ללא חיכוך על גבי רצפה אופקית. שיפוע המישור המשופע הוא $\alpha$, קבוע הכוח של הקפיץ הוא $k$, אורכו הרפוי של הקפיץ הוא $\ell$. מסת המישור המשופע היא $M$.
נכנה ב-$x(t)$ את מרחקה של $m$ מראש המישור המשופע. תנאי התחלה: $x(t=0) = \ell$ (הקפיץ רפוי), ומשחררים ממנוחה.
מושגים חשובים
- מערכת ייחוס לא אינרציאלית: מערכת המישור המשופע מאיצה, לכן נצטרך להתחשב בכוחות מדומים
- כוח מדומה (פסאודו-כוח): \(\vec{F}_{pseudo} = -m\vec{a}_{frame}\) כאשר \(\vec{a}_{frame}\) היא תאוצת מערכת הייחוס
סעיף א: דיאגרמת כוחות
על המסה $m$ (במערכת המישור המשופע):
- כוח הכבידה: $mg$ (כלפי מטה)
- כוח הקפיץ: $F_s = k(\ell-x)$ (לאורך המישור)
- כוח נורמלי: $N_1$ (ניצב למישור)
- כוח מדומה: $F_{pseudo} = mA$ (כאשר $A$ היא תאוצת המישור)
על המישור המשופע $M$:
- כוח הכבידה: $Mg$ (כלפי מטה)
- כוח נורמלי מהרצפה: $N_2$ (כלפי מעלה)
- כוח תגובה מהמסה: $-N_1$ (בכיוון הפוך לנורמל על $m$)
- כוח תגובה מהקפיץ: $k(\ell-x)$ (בכיוון הפוך לכוח על $m$)
סעיף ב: משוואות תנועה
עבור המישור המשופע $M$ (בכיוון אופקי):
\[MA = N_1\sin\alpha + k(\ell-x)\cos\alpha\]עבור המסה $m$ במערכת המישור המשופע:
לאורך המישור (ציר x):
\[ma = mg\sin\alpha - k(\ell-x) + mA\cos\alpha\]ניצב למישור:
\[0 = N_1 - mg\cos\alpha - mA\sin\alpha\]מהמשוואה האחרונה:
\[N_1 = mg\cos\alpha + mA\sin\alpha\]סעיף ג: משוואה דיפרנציאלית עבור $x$
נציב את $N_1$ במשוואת התנועה של $M$:
\[MA = (mg\cos\alpha + mA\sin\alpha)\sin\alpha + k(\ell-x)\cos\alpha\]נפתור עבור $A$:
\[MA = mg\cos\alpha\sin\alpha + mA\sin^2\alpha + k(\ell-x)\cos\alpha\] \[A(M - m\sin^2\alpha) = mg\cos\alpha\sin\alpha + k(\ell-x)\cos\alpha\] \[A = \frac{mg\cos\alpha\sin\alpha + k(\ell-x)\cos\alpha}{M + m\cos^2\alpha}\]נציב במשוואת התנועה של $m$ לאורך המישור:
\[m\ddot{x} = mg\sin\alpha - k(\ell-x) + m\cos\alpha \cdot \frac{mg\cos\alpha\sin\alpha + k(\ell-x)\cos\alpha}{M + m\cos^2\alpha}\]לאחר פישוט:
\[\ddot{x} = -\frac{k(M + m)}{m(M + m\cos^2\alpha)}x + \frac{k(M + m)\ell + Mmg\sin\alpha}{m(M + m\cos^2\alpha)}\]זאת משוואה מהצורה:
\[\ddot{x} = -\omega^2 x + x_0\]כאשר:
\[\omega^2 = \frac{k(M + m)}{m(M + m\cos^2\alpha)}\] \[x_0 = \frac{k(M + m)\ell + Mmg\sin\alpha}{k(M + m)}\]סעיף ד: זמן עד עצירה ראשונה
בתנועה הרמונית, הזמן עד עצירה ראשונה הוא רבע מחזור:
\[t^* = \frac{T}{4} = \frac{\pi}{2\omega} = \frac{\pi}{2}\sqrt{\frac{m(M + m\cos^2\alpha)}{k(M + m)}}\]סעיף ה: פתרון עבור $x(t)$
הפתרון הכללי למשוואה הדיפרנציאלית:
\[x(t) = x_{eq} + A\cos(\omega t) + B\sin(\omega t)\]כאשר $x_{eq} = x_0/\omega^2$ היא נקודת שיווי המשקל.
מתנאי ההתחלה:
- $x(0) = \ell$: נותן $x_{eq} + A = \ell$
- $\dot{x}(0) = 0$: נותן $B = 0$
לכן:
\[x(t) = x_{eq} + (\ell - x_{eq})\cos(\omega t)\]סעיף ו: תיאור תנועת המישור המשופע
המישור המשופע מבצע תנועה מחזורית:
- בהתחלה הוא מאיץ ימינה (כשהקפיץ דחוס)
- מהירותו גדלה עד שהמסה $m$ מגיעה לנקודת שיווי המשקל
- אז הוא ממשיך בתנועה אך מאט
- בנקודה שבה $m$ נעצרת לראשונה, גם המישור נעצר רגעית
- התנועה מתהפכת והמחזור חוזר
סעיף ז: משוואה דיפרנציאלית עבור המישור המשופע
מיקום המישור המשופע: $X(t)$
ממשוואת התנועה של $M$:
\[M\ddot{X} = N_1\sin\alpha + k(\ell-x)\cos\alpha\]כאשר $x$ הוא המיקום היחסי של $m$ ביחס למישור.
סעיף ח: מהירות המישור המשופע
אינטגרציה של התאוצה:
\[V(t) = \int_0^t A(\tau)d\tau\]עם הפתרון שמצאנו עבור $x(t)$, ניתן לחשב את $A(t)$ ולאנטגר.
שאלה 2: מטוטלת בקרון מאיץ
נתון: מתקרתו של קרון המאיץ ימינה תלויה מטוטלת. החוט באורך $\ell$, המסה $m$.
סעיף א: תאוצת הקרון בשיווי משקל
בשיווי משקל בזווית $\theta_0$:
כוחות על המסה:
- כוח הכבידה: $mg$ (כלפי מטה)
- מתיחות החוט: $T$ (לאורך החוט)
- כוח מדומה: $ma$ (שמאלה, כאשר $a$ היא תאוצת הקרון)
תנאי שיווי משקל:
\[T\sin\theta_0 = ma\] \[T\cos\theta_0 = mg\]מחלוקת המשוואות:
\[\tan\theta_0 = \frac{a}{g}\]לכן:
\[a = g\tan\theta_0\]סעיף ב: תדירות תנודות קטנות
עבור תנודות קטנות סביב $\theta_0$, נסמן $\theta = \theta_0 + \phi$ כאשר $\phi$ קטנה.
משוואת התנועה:
\[m\ell\ddot{\phi} = -mg\sin(\theta_0 + \phi) + ma\cos(\theta_0 + \phi)\]לזוויות קטנות ועם $a = g\tan\theta_0$:
\[\ddot{\phi} = -\frac{g}{\ell\cos\theta_0}\phi\]תדירות זוויתית:
\[\omega = \sqrt{\frac{g}{\ell\cos\theta_0}}\]משרעת: אם מסיטים למצב אנכי ($\theta = 0$), המשרעת היא $\theta_0$.
סעיף ג: חרק על דופן הקרון
החרק נצמד לדופן הימנית ומחליק מטה בתאוצה $g/2$.
כוחות על החרק:
- כוח כבידה: $mg$ (מטה)
- כוח נורמלי מהדופן: $N$ (שמאלה)
- כוח חיכוך: $f = \mu N$ (מעלה)
- כוח מדומה: $ma$ (שמאלה)
משוואות תנועה:
- אופקי: $N = ma$
- אנכי: $mg - \mu N = m(g/2)$
נציב:
\[mg - \mu ma = mg/2\] \[1 - \mu\tan\theta_0 = 1/2\] \[\tan\theta_0 = \frac{1}{2\mu}\]סעיף ד: מסלול נפילה במערכת העגלה
כשהחוט נקרע בזווית $\theta = 0°$, המסה נופלת בתאוצה יחסית:
- אופקית: $-a$ (שמאלה ביחס לעגלה)
- אנכית: $g$ (מטה)
המסלול הוא פרבולה עם ציר סימטריה בזווית $\arctan(a/g) = \theta_0$ ביחס לאנך.
שאלה 3: שאלת הזבוב - מערכת גלגלת
נתון: שתי מסות זהות $m_1 = m_2 = 99$ גרם קשורות בחוט על גלגלת. זבוב במסה $m = 2$ גרם נוחת על $m_1$ ב-$t=0$, מתעופף ב-$t=2s$, ונוחת על $m_2$ ב-$t=4s$.
| מצב התחלתי | הזבוב מגיע ל-$m_2$ |
סעיף א: סקיצת המערכת ב-$t=0$
בזמן נחיתת הזבוב:
- שתי המסות במנוחה באותו גובה
- הזבוב נוחת על $m_1$ (הימנית)
- $m_1$ מתחילה לרדת עם תאוצה $a$ כלפי מטה
- $m_2$ עולה עם אותה תאוצה
סעיף ב: תיאור התנועה
$0 \leq t < 2s$: $m_2$ מאיצה מעלה בתאוצה קבועה ממהירות התחלתית אפס
$2s \leq t < 4s$: הזבוב מעופף, המערכת בהתמדה, $m_2$ ממשיכה במהירות קבועה מעלה
$t \geq 4s$: הזבוב על $m_2$, התאוצה מתהפכת, $m_2$ מאטה ואז יורדת
סעיף ג: חישוב התאוצות
שלב א ($0 \leq t < 2s$):
\[(m_1 + m)g - T = (m_1 + m)a\] \[T - m_2g = m_2a\]פתרון:
\[a = \frac{mg}{2M + m} = \frac{2 \times 10}{2 \times 99 + 2} = 0.1 \text{ m/s}^2\]שלב ב: $a = 0$ (התמדה)
שלב ג: $a = -0.1$ m/s² (סימטרי לשלב א)
סעיף ד: מהירות כפונקציה של הזמן
\[v(t) = \begin{cases} 0.1t & 0 \leq t < 2s \\ 0.2 & 2s \leq t < 4s \\ 0.2 - 0.1(t-4) & t \geq 4s \end{cases}\]סעיף ה: גרף מהירות-זמן
גרף ליניארי למקוטעין:
- עולה מ-0 ל-0.2 m/s בין $t=0$ ל-$t=2s$
- קבוע ב-0.2 m/s בין $t=2s$ ל-$t=4s$
- יורד מ-0.2 ל-(-0.4) m/s בין $t=4s$ ל-$t=10s$
סעיף ו: העתק כולל
ההעתק הוא השטח מתחת לגרף מהירות-זמן:
- משולש: $\frac{1}{2} \times 2 \times 0.2 = 0.2$ m
- מלבן: $2 \times 0.2 = 0.4$ m
- טרפז: $\frac{1}{2} \times 6 \times (0.2 - 0.4) = -0.6$ m
סה”כ: $0.2 + 0.4 - 0.6 = 0$ m
המערכת חוזרת למצבה ההתחלתי!
שאלה 4: טס על מישור משופע
נתון: על מישור משופע מחליק טס ועליו תורן. בראש התורן קשור חוט ובקצהו משקולת במסה $m$.
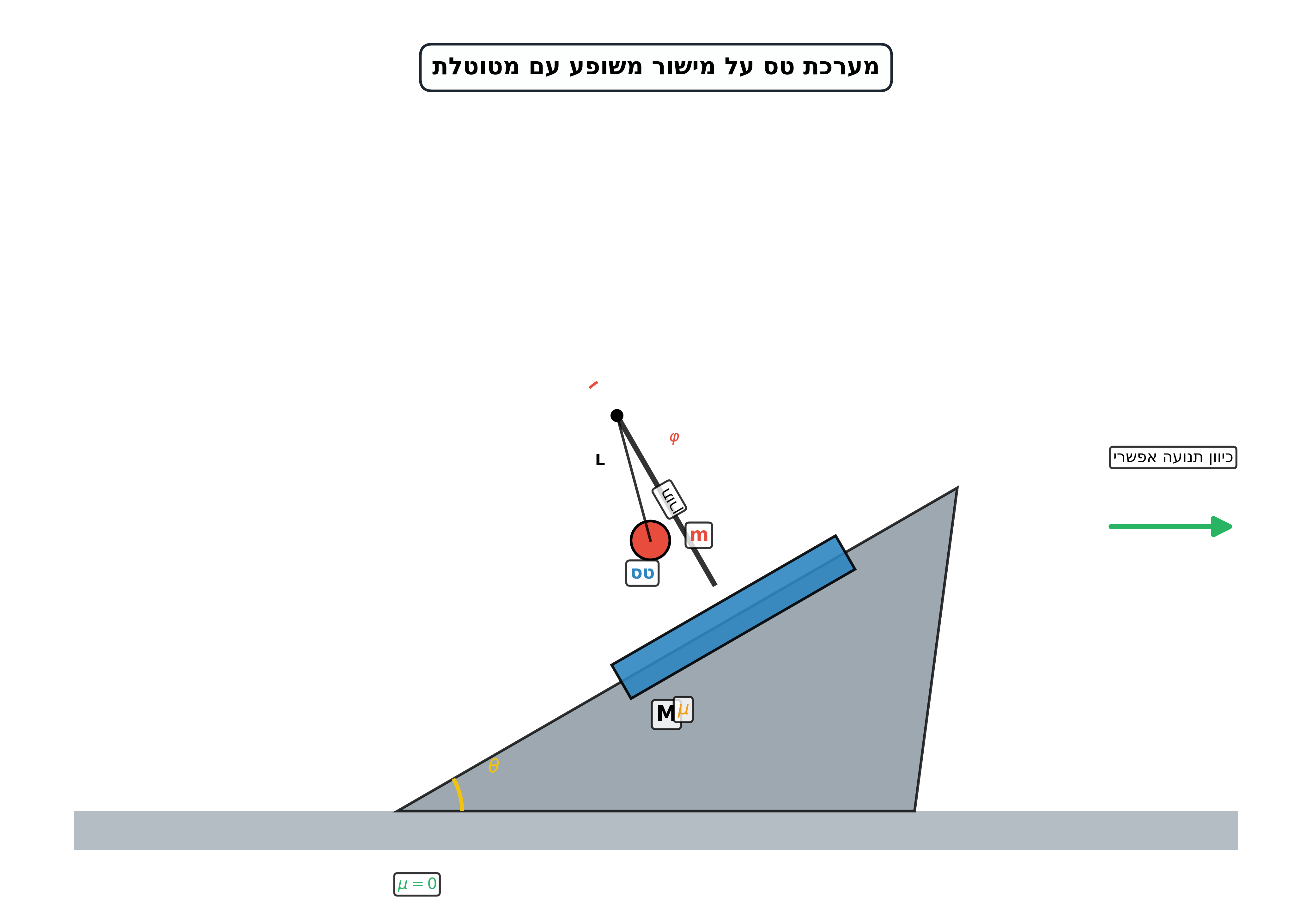
סעיף א: הגדרת מערכת התמד
מערכת התמד (אינרציאלית): מערכת ייחוס שבה לא מורגשים כוחות מדומים. זאת מערכת שאינה מאיצה ביחס למערכת אינרציאלית אחרת.
סעיף ב: זווית פרישה כאשר $\mu = \tan\theta$
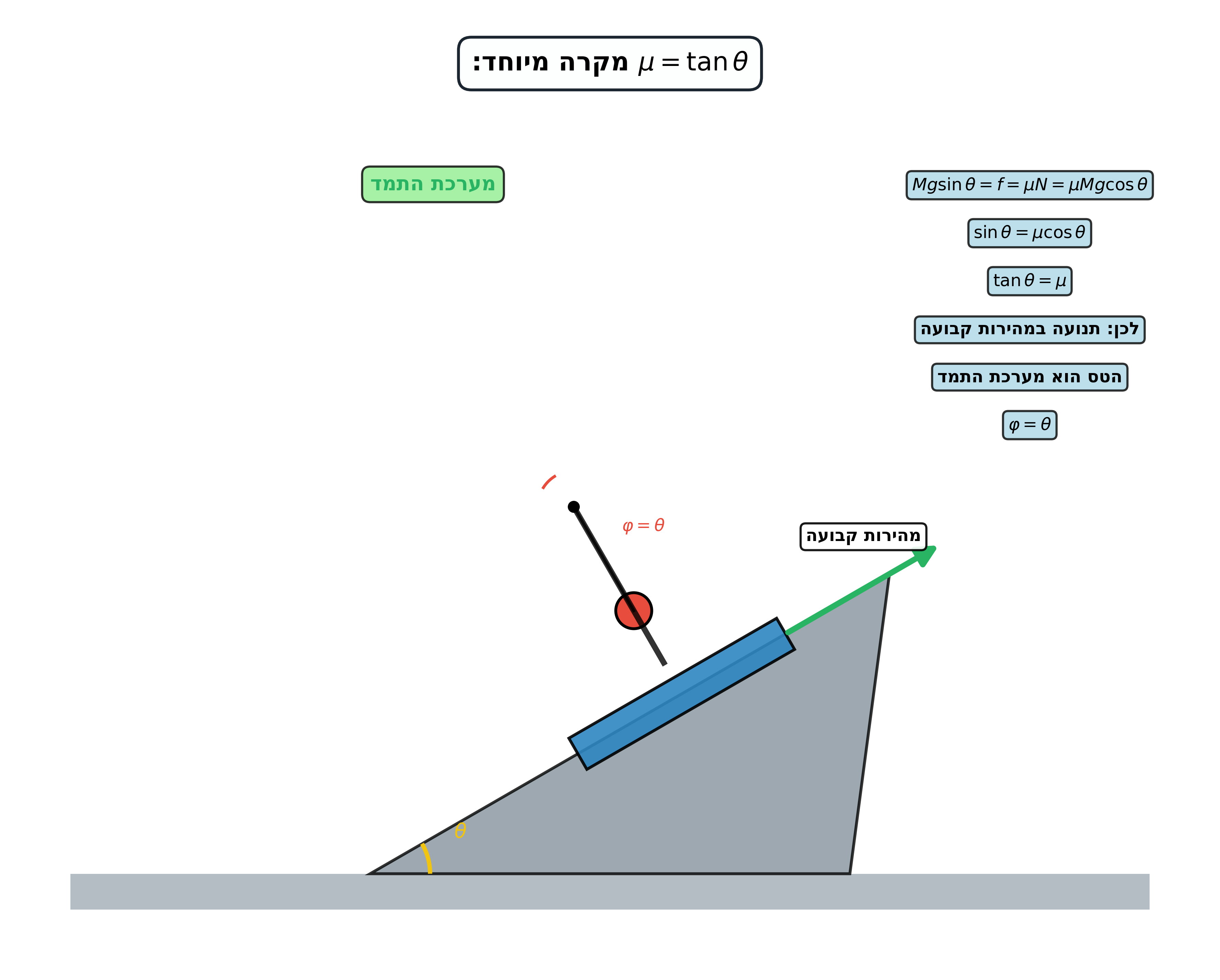
כאשר $\mu = \tan\theta$, הטס גולש במהירות קבועה (ללא תאוצה).
במערכת הטס (שהיא מערכת התמד במקרה הזה):
- כוח הכבידה: $mg$ (אנכית מטה)
- מתיחות החוט: $T$ (לאורך החוט)
בשיווי משקל, החוט אנכי: $\varphi = 0$
סעיף ג: תנועה ללא חיכוך
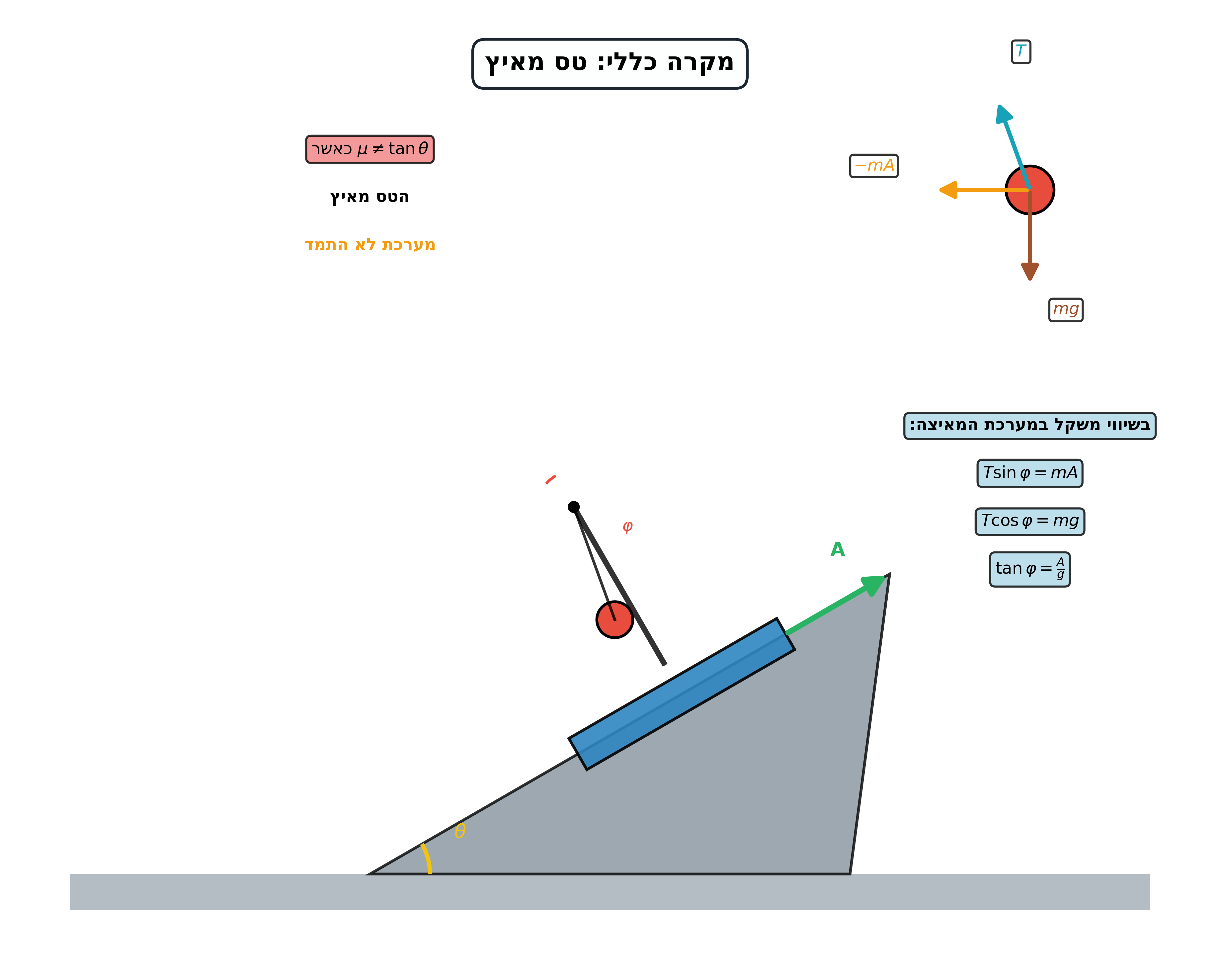
ללא חיכוך, הטס מאיץ עם $a = g\sin\theta$.
במערכת הטס:
- כוח כבידה: $mg$
- כוח מדומה: $ma = mg\sin\theta$ (במעלה המישור)
זווית הפרישה:
\[\tan\varphi = \frac{a}{g\cos\theta} = \tan\theta\]לכן: $\varphi = \theta$
לפי הדרישה $\Delta x_2 = \frac{1}{2}\Delta x_1$:
\[\frac{mg\cos\varphi}{k} = \frac{mg}{2k}\] \[\cos\varphi = \frac{1}{2}\] \[\varphi = 60°\]סעיף ד: מסלול נפילה
כשהחוט נקרע ב-$\theta = 0°$, במערכת העגלה:
- תאוצה אופקית: $-a$ (שמאלה)
- תאוצה אנכית: $g$ (מטה)
המסלול הוא פרבולה עם ציר סימטריה בזווית $\theta$ ביחס לאנך.
שאלה 5: שתי מסות מחוברות בקפיץ
נתון: מסה $m_1$ על מסה $m_2$, מחוברות בקפיץ עם קבוע $k$. אורך רפוי אפס. מושכים את $m_1$ שמאלה מרחק $\ell$ ומשחררים.
נוסחאות חשובות
- מסה מצומצמת: $\mu = \frac{m_1m_2}{m_1 + m_2}$
- תדירות זוויתית: $\omega = \sqrt{\frac{k}{\mu}}$
סעיף א: בדיקת יחידות
\[t^* = \frac{\pi}{2}\sqrt{\frac{\mu}{k}} = \frac{\pi}{2}\sqrt{\frac{[kg]}{[N/m]}} = \frac{\pi}{2}\sqrt{\frac{[kg]}{[kg \cdot m/s^2]/[m]}} = [s]\]סעיף ב: פונקציית מקום-זמן
מתנאי ההתחלה $x(0) = -\ell$, $\dot{x}(0) = 0$:
\[x(t) = -\ell\cos(\omega t)\]סעיף ג: הפרש מהירויות
\[v_1(t) = \dot{x}(t) = \ell\omega\sin(\omega t)\] \[v_2(t) = -\frac{m_1}{m_2}v_1(t)\] \[\Delta v = v_1 - v_2 = v_1\left(1 + \frac{m_1}{m_2}\right) = v_1\frac{m_1 + m_2}{m_2}\]סעיף ד: העתק של $m_2$
משימור תנע:
\[X(t) = \frac{m_1}{m_1 + m_2}\ell[1 - \cos(\omega t)]\]סעיף ה: תנועת זבוב ללא חיכוך
הזבוב נע בקו ישר במערכת התמד. מיקומו משתנה בין שתי המסות באופן מחזורי.
סעיף ו: זמן התנתקות זבוב עם חיכוך
הזבוב מתנתק כאשר:
\[|ma_{rel}| > \mu mg\]כאשר $a_{rel} = \omega^2 \ell\cos(\omega t)$ היא התאוצה היחסית.
זמן התנתקות:
\[t_{detach} = \frac{1}{\omega}\arccos\left(\frac{\mu g}{\omega^2 \ell}\right)\]סעיף ז: משוואות עם חיכוך בין המסות
עם חיכוך $\mu$ בין המסות:
\[m_1\ddot{x} = -kx - \mu m_1 g \cdot \text{sgn}(\dot{x})\] \[m_2\ddot{X} = -kx + \mu m_1 g \cdot \text{sgn}(\dot{x})\]כאשר $\text{sgn}$ היא פונקציית הסימן.
דור פסקל