יחידות וצפיפויות מטען
יחידות מטען חשמלי
יחידת המטען החשמלי: קולון (C)
סוגי צפיפות מטען
| סוג | סימון | הגדרה | יחידות |
|---|---|---|---|
| צפיפות קווית | $\lambda$ | מטען ליחידת אורך | C/m |
| צפיפות משטחית | $\sigma$ | מטען ליחידת שטח | C/m² |
| צפיפות נפחית | $\rho$ | מטען ליחידת נפח | C/m³ |

צפיפות אחידה לעומת לא אחידה
צפיפות אחידה:
\[\lambda = \frac{Q}{L}, \quad \sigma = \frac{Q}{A}, \quad \rho = \frac{Q}{V}\]צפיפות לא אחידה: הצפיפות היא פונקציה של המיקום במרחב, למשל $\lambda(x)$, $\sigma(\theta, \phi)$, $\rho(r)$.
אלמנטי מטען
\[dq = \lambda \cdot dl \quad \text{(linear)}\] \[dq = \sigma \cdot dA \quad \text{(surface)}\] \[dq = \rho \cdot dV \quad \text{(volume)}\]אלמנטים בקואורדינטות שונות
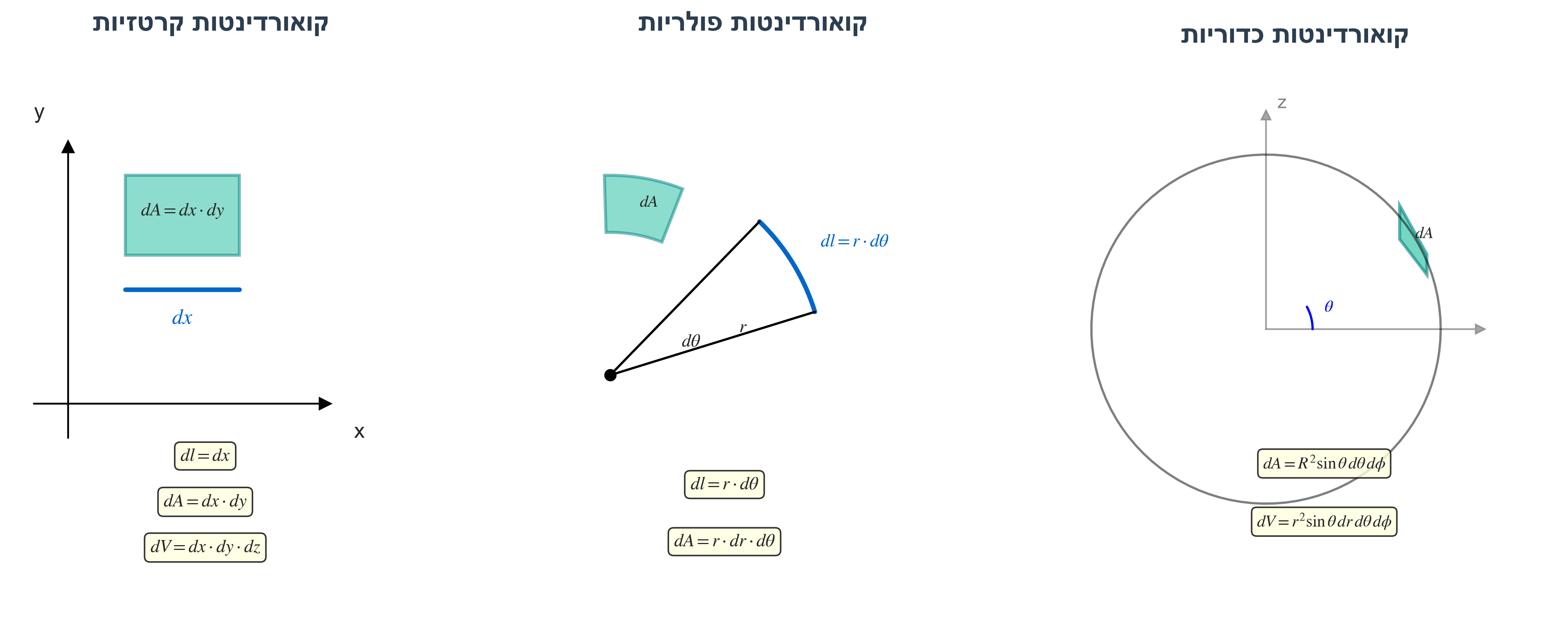
קואורדינטות קרטזיות
| אלמנט | ביטוי |
|---|---|
| אורך | $dl = dx$ |
| שטח | $dA = dx \cdot dy$ |
| נפח | $dV = dx \cdot dy \cdot dz$ |
קואורדינטות פולריות (דו-ממד)
| אלמנט | ביטוי |
|---|---|
| אורך קשת | $dl = r \cdot d\theta$ |
| שטח | $dA = r \cdot dr \cdot d\theta$ |
קואורדינטות כדוריות (תלת-ממד)
| אלמנט | ביטוי |
|---|---|
| שטח מעטפת כדור | $dA = R^2 \sin\theta \, d\theta \, d\phi$ |
| נפח | $dV = r^2 \sin\theta \, dr \, d\theta \, d\phi$ |
תחומי האינטגרציה:
- $\theta$: מ-$0$ עד $\pi$ (מקוטב לקוטב)
- $\phi$: מ-$0$ עד $2\pi$ (סיבוב מלא)
- $r$: מ-$0$ עד $R$ (מהמרכז לשפה)
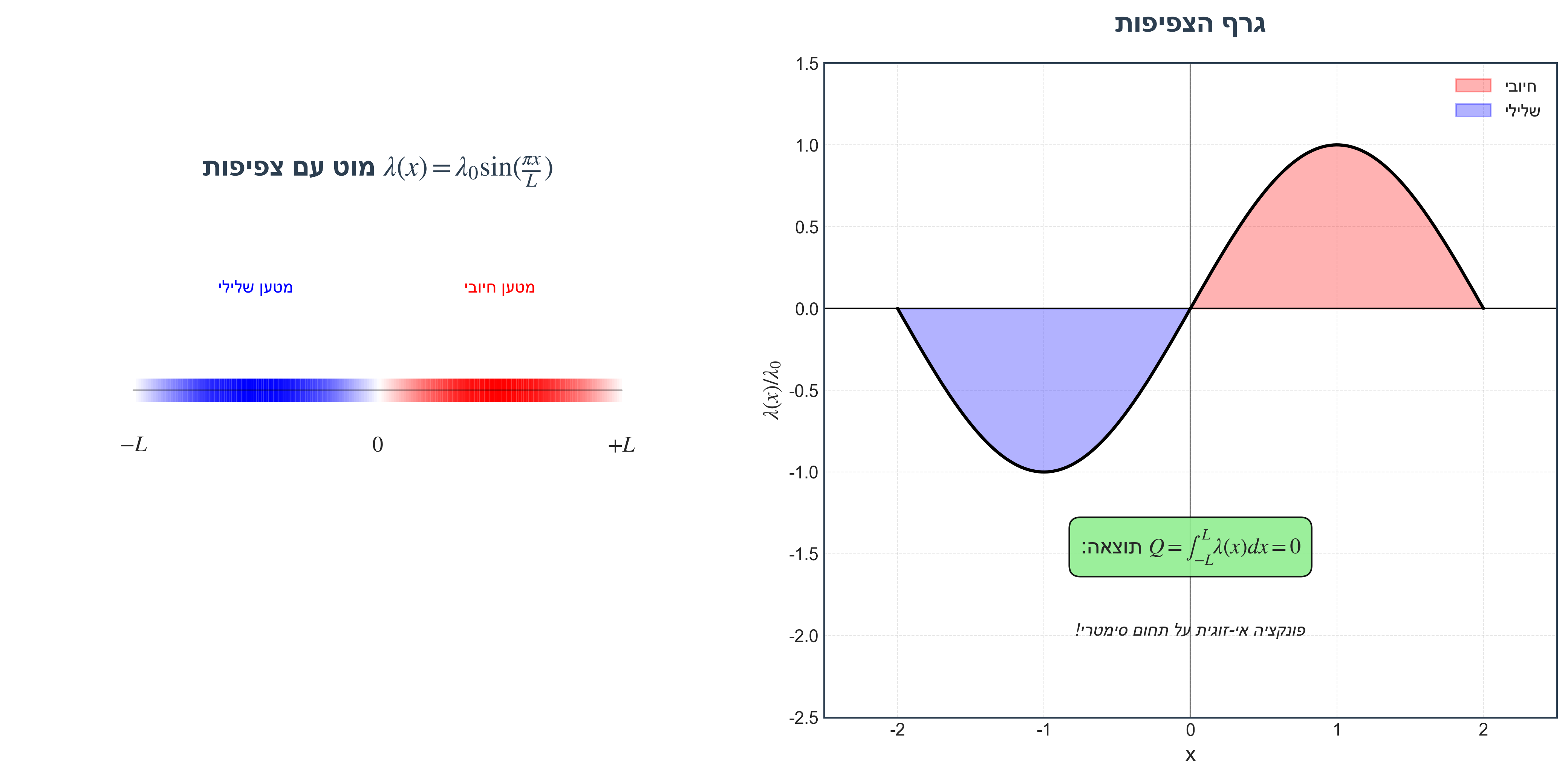
תרגיל 1: מטען כולל על מוט עם צפיפות לא אחידה
מוט באורך $2L$ (מ-$(-L)$ עד $(+L)$) עם צפיפות מטען:
\[\lambda(x) = \lambda_0 \sin\left(\frac{\pi x}{L}\right)\]מהו המטען הכולל?
פתרון בעזרת אינטגרל על אורך המוט
\[Q = \int dq = \int_{-L}^{L} \lambda(x) \, dx = \int_{-L}^{L} \lambda_0 \sin\left(\frac{\pi x}{L}\right) dx\] \[Q = \lambda_0 \left[-\frac{L}{\pi} \cos\left(\frac{\pi x}{L}\right)\right]_{-L}^{L}\] \[Q = -\frac{\lambda_0 L}{\pi} \left[\cos(\pi) - \cos(-\pi)\right] = -\frac{\lambda_0 L}{\pi} \left[-1 - (-1)\right] = 0\]תוצאה: $Q = 0$
הסבר: הפונקציה $\sin\left(\frac{\pi x}{L}\right)$ היא פונקציה אי-זוגית - חיובית בצד אחד ושלילית בצד השני. לכן האינטגרל על תחום סימטרי מתאפס.
תרגיל 2: מטען כולל על מעטפת כדור
מעטפת כדור ברדיוס $R$ עם צפיפות מטען משטחית:
\[\sigma(\phi) = \sigma_0 \cos\phi\]מהו המטען הכולל?

פתרון בעזרת אינטגרל על שטח כדור
\[Q = \int dq = \iint \sigma \, dA = \int_0^{\pi} \int_0^{2\pi} \sigma_0 \cos\phi \cdot R^2 \sin\theta \, d\phi \, d\theta\] \[Q = \sigma_0 R^2 \int_0^{\pi} \sin\theta \, d\theta \int_0^{2\pi} \cos\phi \, d\phi\]האינטגרל על $\phi$:
\[\int_0^{2\pi} \cos\phi \, d\phi = [\sin\phi]_0^{2\pi} = 0\]תוצאה: $Q = 0$
הסבר: כאשר $\phi = 0$ הצפיפות חיובית (צד אחד של הכדור), וכאשר $\phi = \pi$ הצפיפות שלילית (הצד הנגדי). המטענים מתקזזים.
תרגיל 3: מטען כולל על קשת (חצי מעגל)
קשת (חצי מעגל) ברדיוס $r$ עם צפיפות מטען:
\[\lambda(\theta) = \lambda_0 \theta^2\]כאשר $\theta$ רץ מ-$0$ עד $\pi$.
מהו המטען הכולל?
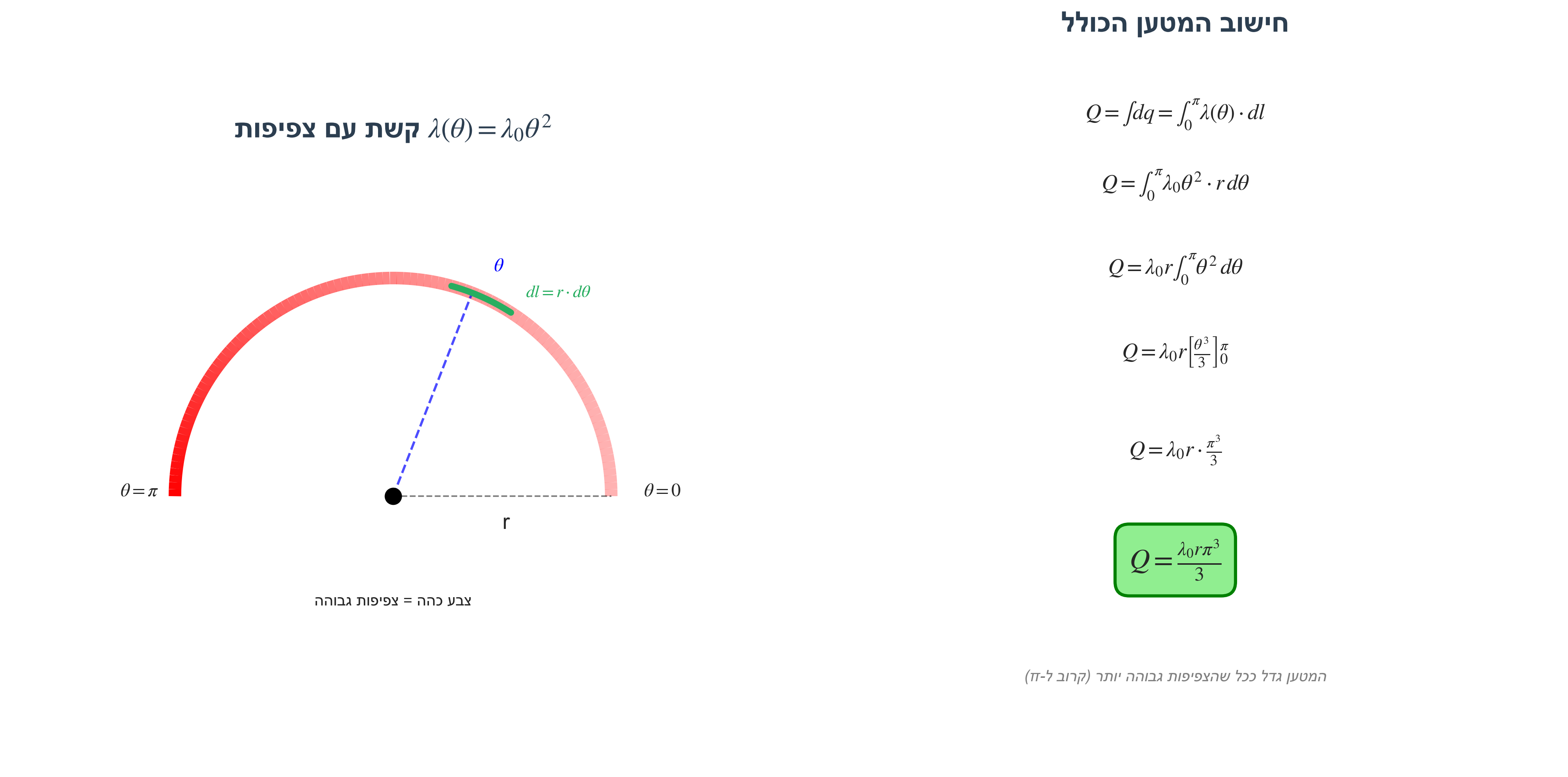
פתרון בעזרת אינטגרל על אורך הקשת
\[Q = \int dq = \int_0^{\pi} \lambda(\theta) \cdot dl = \int_0^{\pi} \lambda_0 \theta^2 \cdot r \, d\theta\] \[Q = \lambda_0 r \int_0^{\pi} \theta^2 \, d\theta = \lambda_0 r \left[\frac{\theta^3}{3}\right]_0^{\pi}\] \[\boxed{Q = \frac{\lambda_0 r \pi^3}{3}}\]שדה חשמלי - שיטת החישוב
העיקרון
- בחר אלמנט מטען קטן $dq$
- חשב את השדה $d\vec{E}$ שהוא יוצר בנקודה הרצויה
- פרק לרכיבים ($x$, $y$, $z$)
- בדוק סימטריות - אילו רכיבים מתאפסים?
- בצע אינטגרציה על הרכיבים שנותרו
נוסחת השדה מאלמנט מטען
\[d\vec{E} = \frac{k \cdot dq}{r^2} \hat{r}\]תרגיל 4: שדה חשמלי של דיפול (מוט עם צפיפות משתנה)
מוט באורך $L$ (מ-$-L/2$ עד $+L/2$) עם צפיפות מטען:
\[\lambda(x) = \lambda_0 \frac{x}{L}\]נקודת התצפית בגובה $H$ מעל מרכז המוט.
מהו השדה החשמלי בנקודה זו?
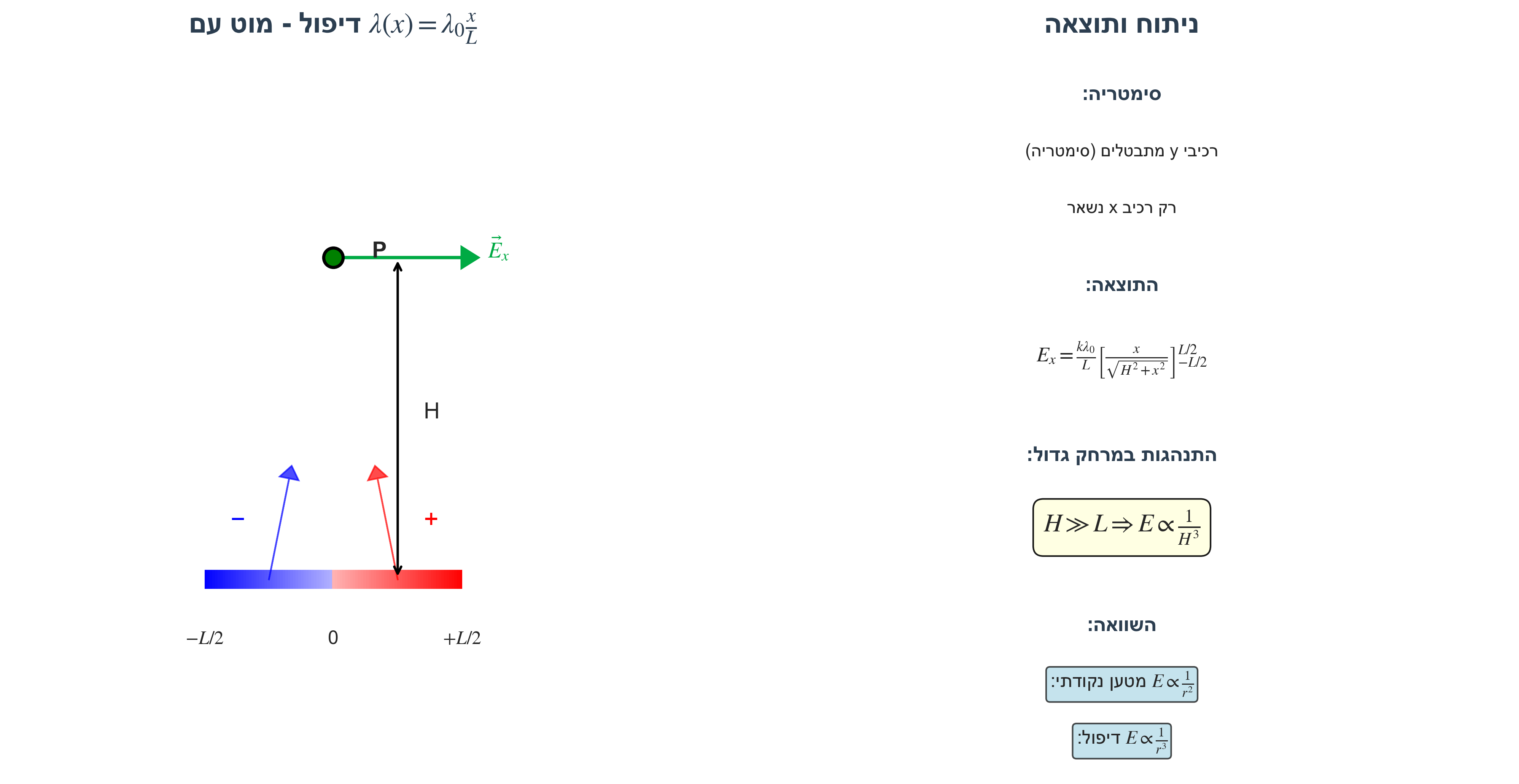
ניתוח הבעיה
התנהגות הצפיפות:
- ב-$x > 0$: צפיפות חיובית (מטען חיובי)
- ב-$x < 0$: צפיפות שלילית (מטען שלילי)
- המטען הכולל: $Q = 0$
זהו דיפול - מערכת עם מטען כולל אפס אך פיזור לא אחיד.
סימטריה
מניתוח סימטריה: השדה הכולל יהיה בכיוון $x$ בלבד.
הסבר: לכל מטען חיובי בצד ימין יש מטען שלילי מקביל בצד שמאל. רכיבי ה-$y$ מתבטלים, ורכיבי ה-$x$ מתחברים.
פתרון
\[E_x = \int dE_x = \int dE \cos\theta\]כאשר:
\[dE = \frac{k \cdot dq}{r^2} = \frac{k \lambda(x) dx}{r^2}\] \[\cos\theta = \frac{x}{r}, \quad r = \sqrt{H^2 + x^2}\] \[E_x = \int_{-L/2}^{L/2} \frac{k \lambda_0 \frac{x}{L} \cdot x}{(H^2 + x^2)^{3/2}} dx\] \[E_x = \frac{k \lambda_0}{L} \int_{-L/2}^{L/2} \frac{x^2}{(H^2 + x^2)^{3/2}} dx\]תוצאה
\[\boxed{E_x = \frac{k \lambda_0}{L} \left[\frac{x}{\sqrt{H^2 + x^2}}\right]_{-L/2}^{L/2}}\]התנהגות במרחק גדול
כאשר $H \gg L$ (רחוק מהמוט):
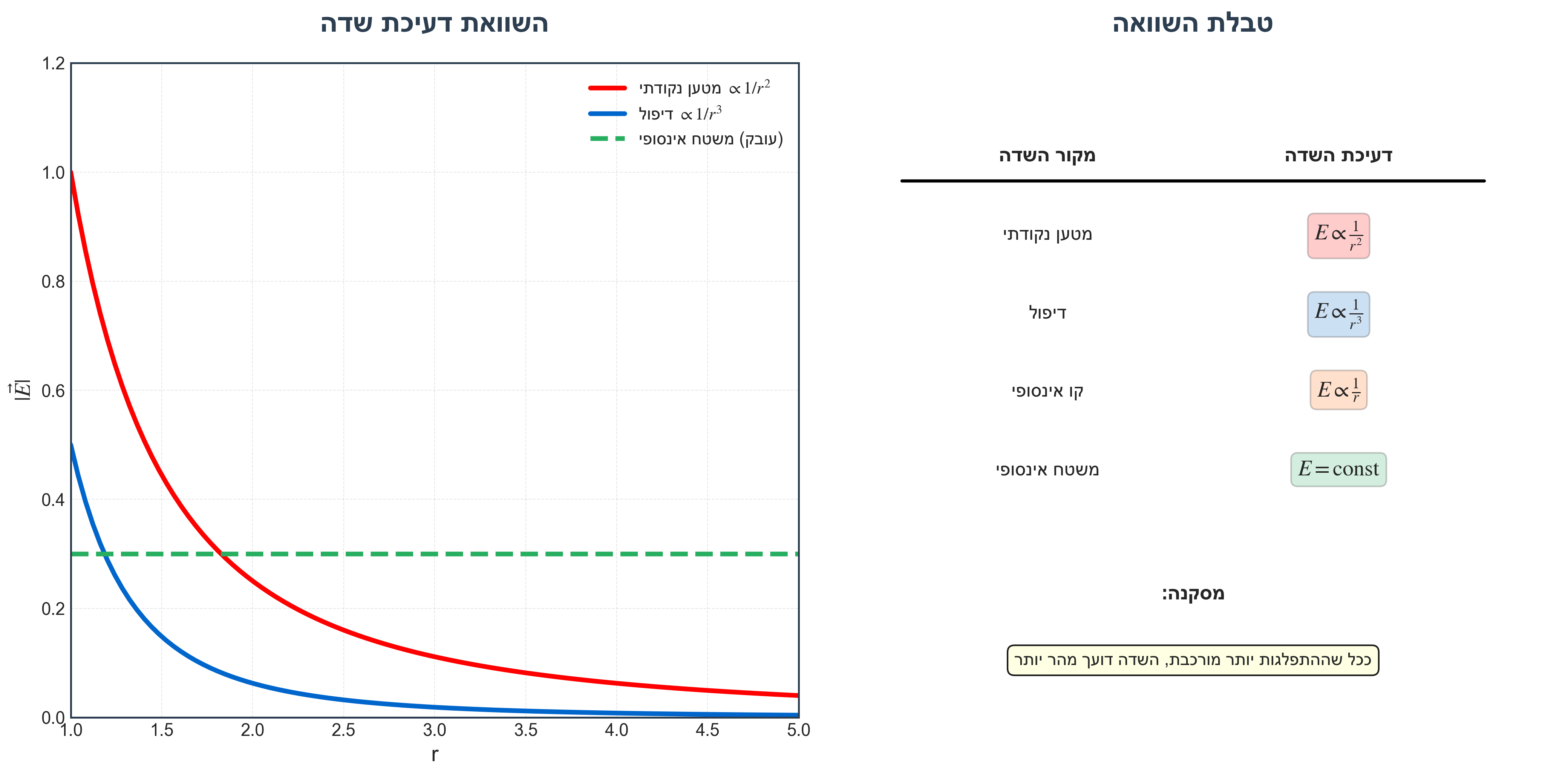
\[E \propto \frac{1}{H^3}\]מסקנה חשובה: שדה של דיפול דועך כמו $\frac{1}{r^3}$, לעומת שדה של מטען נקודתי שדועך כמו $\frac{1}{r^2}$.
תרגיל 5: שדה חשמלי של מלבן טעון
מלבן בממדים $a \times b$ עם צפיפות מטען משטחית אחידה $\sigma$.
נקודת התצפית בגובה $H$ מעל מרכז המלבן.
מהו השדה החשמלי בנקודה זו?

ניתוח סימטריה
מסימטריית הבעיה: השדה הכולל יהיה בכיוון $z$ בלבד (ניצב למשטח).
הסבר: הנקודה נמצאת במרכז המלבן, ולכל אלמנט מטען יש אלמנט מקביל בצד הנגדי שמבטל את רכיבי $x$ ו-$y$.
פתרון:
\[E_z = \int dE_z = \int dE \cos\alpha\]כאשר:
\[dE = \frac{k \cdot dq}{R^2} = \frac{k \sigma \, dx \, dy}{R^2}\] \[\cos\alpha = \frac{H}{R}, \quad R = \sqrt{H^2 + x^2 + y^2}\] \[E_z = \int_{-a/2}^{a/2} \int_{-b/2}^{b/2} \frac{k \sigma H}{(H^2 + x^2 + y^2)^{3/2}} dx \, dy\]תוצאה סופית:
\[\boxed{E_z = 4k\sigma \arctan\left(\frac{ab}{4H\sqrt{H^2 + \frac{a^2}{4} + \frac{b^2}{4}}}\right)}\]בדיקת גבולות
1. מרחק גדול ($H \gg a, b$):
\[E_z \approx \frac{kQ}{H^2}\]כמו מטען נקודתי! (כאשר $Q = \sigma \cdot a \cdot b$)
2. מרחק קטן ($H \to 0$):
כאשר $H$ קטן מאוד (קרוב למשטח), המלבן נראה כמו משטח אינסופי:
\[E_z \to \frac{\sigma}{2\epsilon_0}\]זהו השדה של משטח אינסופי (ניתן לחשב בעזרת חוק גאוס).
סיכום - שיטת חישוב שדה חשמלי מהתפלגות מטען
שלבי הפתרון
-
זיהוי סוג הצפיפות - קווית ($\lambda$), משטחית ($\sigma$), או נפחית ($\rho$)
-
בחירת אלמנט מטען - $dq = \lambda \, dl$ או $dq = \sigma \, dA$ או $dq = \rho \, dV$
-
בחירת מערכת קואורדינטות מתאימה - קרטזית, פולרית, כדורית
-
ניתוח סימטריה - אילו רכיבים מתאפסים מראש?
-
רישום השדה מאלמנט מטען: \(d\vec{E} = \frac{k \cdot dq}{r^2} \hat{r}\)
-
פירוק לרכיבים - שימוש בטריגונומטריה
-
ביטוי הכל במשתנה אינטגרציה אחד - כל המשתנים צריכים להיות מבוטאים במשתנה האינטגרציה
-
ביצוע האינטגרל - במבחן יינתנו נוסחאות לאינטגרלים מורכבים
דור פסקלטבלת השוואה - התנהגות שדה במרחק גדול
מקור השדה דעיכת השדה מטען נקודתי $E \propto \frac{1}{r^2}$ דיפול $E \propto \frac{1}{r^3}$ משטח אינסופי $E = \text{const}$