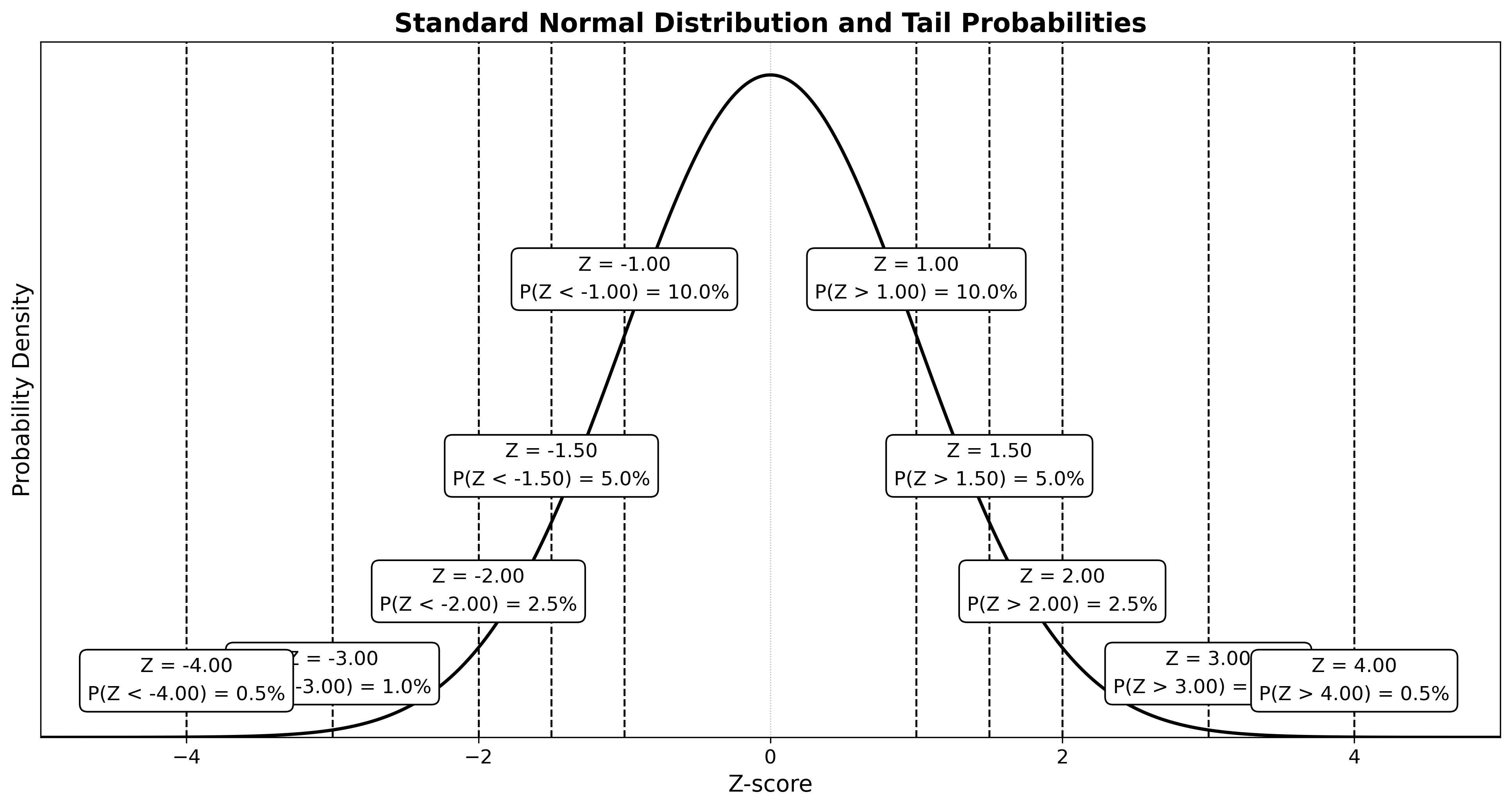
קירובים (Z לפי iSF)
רמת מובהקות חד-צדדית
($\alpha$) | $\textbf{iSF}(\alpha)$ | $\text{P}(Z > Z_{\alpha})$
$=\text{P}(Z < -Z_{\alpha})$ | רמת סמך דו-צדדית
(1−2α) |
| 0.10 | 1 | 10% | 80% |
| 0.05 | 1.5 | 5% | 90% |
| 0.025 | 2 | 2.5% | 95% |
| 0.01 | 3 | 1% | 98% |
| 0.005 | 4 | 0.5% | 99% |
מדדי מרכז ופיזור
ממוצע: $\bar{X} = \frac{1}{n}\sum_{i=1}^{n}X_i$
שונות מדגם: $s^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i - \bar{X})^2$
(במקרה של אוכלוסייה $\sigma^2$ חלוקה ב-$n$ במקום $n-1$)
סטיית תקן: $s = \sqrt{s^2}$
$\text{IQR} = Q_3 - Q_1$
חריגים: $x < Q_1 - 1.5 \cdot \text{IQR}$ או $x > Q_3 + 1.5 \cdot \text{IQR}$
טרנספורמציות לינאריות
אם $\mathbf{X} \sim \mathcal{N}(\mu, \sigma^2)$ אז $\mathbf{Y} = a\mathbf{X} + b \sim \mathcal{N}(a\mu + b, a^2\sigma^2)$
$\mathbf{E}[Y] = a\mathbf{E}[X] + b$
$\text{Var}(Y) = a^2\text{Var}(X)$
$\text{SD}(Y) = |a| \cdot \text{SD}(X)$
כלל בייס וקומבינטוריקה
$P(A|B) = \frac{P(B|A)P(A)}{P(B|A)P(A) + P(B|\neg A)P(\neg A)}$ קירוב שימוש למקרה של יעילות בדיקה: $P(\text{sick}| \text{positive}) = \frac{\text{sick individuals}}{\text{sick individuals + false positives}}$
$P(B) = P(B|A)P(A) + P(B|\neg A)P(\neg A)$
$P(B) = \sum_{i} P(B|A_i)P(A_i)$ נוסחת ההסתברות השלמה
מאוראות בלתי תלויים אם״ם $P(A \cap B) = P(A)P(B)$, $P(A|B) = P(A)$
בחירה: $\binom{n}{k} = \frac{n!}{k!(n-k)!}$
סידור: $P(n,k) = \frac{n!}{(n-k)!}$
רגרסיה לינארית
$r = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2}\sqrt{\sum(y_i-\bar{y})^2}}$
שיפוע: $a = r \cdot \frac{s_y}{s_x}$
חותך: $b = \bar{y} - a\bar{x}$
$\hat{y} = ax + b$
רגרסיה מרובה
$Y = \beta_0 + \beta_1X_1 + ... + \beta_kX_k + \epsilon$
פירוש $\beta_i$: שינוי ב-$Y$ עבור שינוי יחידה ב-$X_i$ כשהשאר קבועים
$\textbf{Prob (F-statistic)}$: הסתברות לקבלת סטטיסטיקת F כזו או יותר קיצונית אם כל המקדם $\beta_i = 0$
$\textbf{R-squared}$: אחוז השונות ב-$Y$ המוסברת על ידי המשתנים הבלתי תלויים
התפלגויות דיסקרטיות
בינומית $X \sim \text{Bin}(n,p)$
$P(X=k) = \binom{n}{k}p^k(1-p)^{n-k}$
$\mathbf{E}[X] = np$, $\text{Var}(X) = np(1-p)$
גיאומטרית $X \sim \text{Geom}(p)$
$P(X=k) = (1-p)^{k-1}p$
$\mathbf{E}[X] = \frac{1}{p}$, $\text{Var}(X) = \frac{1-p}{p^2}$
התפלגויות רציפות
אקספוננציאלית $X \sim \text{Exp}(\lambda)$
$f(x) = \lambda e^{-\lambda x}$, $x \geq 0$
$\text{SF}(x) = e^{-\lambda x}$
$\mathbf{E}[X] = \frac{1}{\lambda}$, $\text{Var}(X) = \frac{1}{\lambda^2}$
חוסר זיכרון: $P(X>s+t|X>s) = P(X>t)$
נורמלית $X \sim \mathcal{N}(\mu, \sigma^2)$
תקנון: $Z = \frac{X-\mu}{\sigma} \sim \mathcal{N}(0,1)$
כלל $3\sigma$: 68%, 95%, 99.7% בקירובים במבחן:
$\text{80% in} \pm 1 \sigma$
$\text{95% in} \pm 2 \sigma$
$\text{98% in} \pm 3 \sigma$
קירוב בינומי: אם $np \geq 5$, $n(1-p) \geq 5$
שגיאות תקן
ממוצע: $\text{SE}_{\bar{X}} = \frac{\sigma}{\sqrt{n}}$ (או $\frac{s}{\sqrt{n}}$)
פרופורציה: $\text{SE}_{\bar{p}} = \sqrt{\frac{p(1-p)}{n}}$
הפרש ממוצעים: $\text{SE} = \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}$
רווחי סמך
| מצב | רווח סמך |
|---|
| ממוצע, $\sigma$ ידוע או $n>30$ | $\bar{X} \pm Z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}$ |
| ממוצע, $\sigma$ לא ידוע, $n \leq 30$ | $\bar{X} \pm t_{\alpha/2,n-1} \cdot \frac{s}{\sqrt{n}}$ |
| פרופורציה | $\bar{p} \pm Z_{\alpha/2} \cdot \sqrt{\frac{\bar{p}(1-\bar{p})}{n}}$ |
| יחס צולב (OR) | $\ln(\text{OR}) \pm Z_{\alpha/2} \cdot \sqrt{\frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}}$ |
גודל מדגם נדרש: $n \geq \left(\frac{2 \cdot Z_{\alpha/2} \cdot \sigma}{W}\right)^2$
רוחב רווח סמך: $W = 2 \cdot Z_{\alpha/2} \cdot \text{SE}$
בדיקת השערות - מדגם אחד
| מבחן | תנאים | סטטיסטי (observed) | התפלגות |
|---|
| Z | $n>30$ או נורמלי+$\sigma$ ידוע | $Z_{\text{obs}} = \frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}$ | $\mathcal{N}(0,1)$ |
| t | $n \leq 30$, נורמלי, $\sigma$ לא ידוע | $t_{\text{obs}} = \frac{\bar{X}-\mu_0}{s/\sqrt{n}}$ | $t_{n-1}$ |
| Z לפרופורציה | $np_0 > 5$, $n(1-p_0) > 5$ | $Z_{\text{obs}} = \frac{\bar{p}-p_0}{\sqrt{p_0(1-p_0)/n}}$ | $\mathcal{N}(0,1)$ |
בדיקת השערות - שני מדגמים
מדגמים בלתי תלויים
$t = \frac{\bar{X}_1-\bar{X}_2}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$, df = $n_1+n_2-2$
$s_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2}$ (שונות משותפת)
מדגמים מזווגים
$D_i = X_i^{(1)} - X_i^{(2)}$
$t = \frac{\bar{D}}{s_D/\sqrt{n}}, \, \text{df} = n-1$ מבחן t למדגמים מזווגים
יתרון: $\text{Var}(D) < \text{Var}(X_1) + \text{Var}(X_2)$ אם יש מתאם חיובי
חישוב P-value
| מבחן | דו-צדדי | חד-צדדי ימני |
|---|
| Z | $2 \cdot P(Z > |z_{\text{obs}}|)$ | $P(Z > z_{\text{obs}})$ |
| t | $2 \cdot P(T > |t|)$ | $P(T > t)$ |
| $\chi^2$ | $P(\chi^2 > \chi^2_{\text{obs}})$ | - |
כללי החלטה (אם $\text{P-value} < \alpha$ דוחים את $H_0$)
דו-צדדי ($H_1: \mu \neq \mu_0$): דחה $H_0$ אם $|Z| > Z_{\alpha/2}$
חד-צדדי ($H_1: \mu > \mu_0$): דחה $H_0$ אם $Z > Z_\alpha$
תנאי תקפות למבחנים
מבחן Z: $n \geq 30$ או נורמלי + $\sigma$ ידוע
מבחן t: נורמליות או $n$ גדול
מבחן פרופורציה: $np \geq 5$, $n(1-p) \geq 5$
מבחן $\chi^2$: תצפיות בלתי תלויות, $E_{ij} \geq 5$
מבחן $\chi^2$ לאי-תלות
$\chi^2 = \sum\frac{(O-E)^2}{E}$
$E_{ij} = \frac{\text{total row} \times \text{total column}}{\text{total}}$
$\text{df} = (r-1)(c-1)$
תנאי: $E_{ij} \geq 5$ בכל תא
מדדי סיכון
| חולה | בריא |
|---|
| חשוף | A | B |
| לא חשוף | C | D |
סיכון יחסי (RR)
$\text{RR} = \frac{P(\text{הלוח}|\text{ףושח})}{P(\text{הלוח}|\text{ףושח אל})} = \frac{A/(A+B)}{C/(C+D)}$
$\text{Var}(\ln(\text{RR})) = \frac{1}{A} - \frac{1}{A+B} + \frac{1}{C} - \frac{1}{C+D}$
יחס סיכויים (OR)
$\text{OR} = \frac{AD}{BC}$
$\text{Var}(\ln(\text{OR})) = \frac{1}{A} + \frac{1}{B} + \frac{1}{C} + \frac{1}{D}$
CI ל-OR: $e^{\ln(\text{OR}) \pm 1.96\sqrt{\text{Var}(\ln(\text{OR}))}}$
ניתוח הישרדות
פונקציית הישרדות
$\text{SF(t) = P(T > t)}, \quad \text{SF}(0) = 1, \, \text{SF}(\infty) = 0$
בכל $t$, $\text{SF}(t)$ הוא מספר השורדים לחלק למספר המשתתפים.
קפלן-מאייר
הסתברות מצטברת לחיות: $S(t) = \prod_{t_i \leq t} \left(1 - \frac{d_i}{n_i}\right)$
$d_i$ = מקרי מוות בזמן $t_i$
$n_i$ = מס׳ אנשים שהיו בסיכון בזמן $t_i$
טעויות בבדיקת השערות
| המציאות | דחיית $H_0$ | אי-דחיית $H_0$ |
|---|
| $H_0$ נכונה | טעות I ($\alpha$) | ✓ ($1-\alpha$) |
| $H_1$ נכונה | ✓ (עוצמה $1-\beta$) | טעות II ($\beta$) |
