הסתברויות חשובות בהתפלגות נורמלית
נושא ההסתברות מתקרב לסיום כנושא השני בקורס. בשיעור זה ממשיכים ללמוד על משתנה מקרי נורמלי ונתחיל בנושא של ערכים קריטיים.
הסתברויות בסיסיות חשובות
עבור משתנה מקרי נורמלי מתוקנן $Z$:
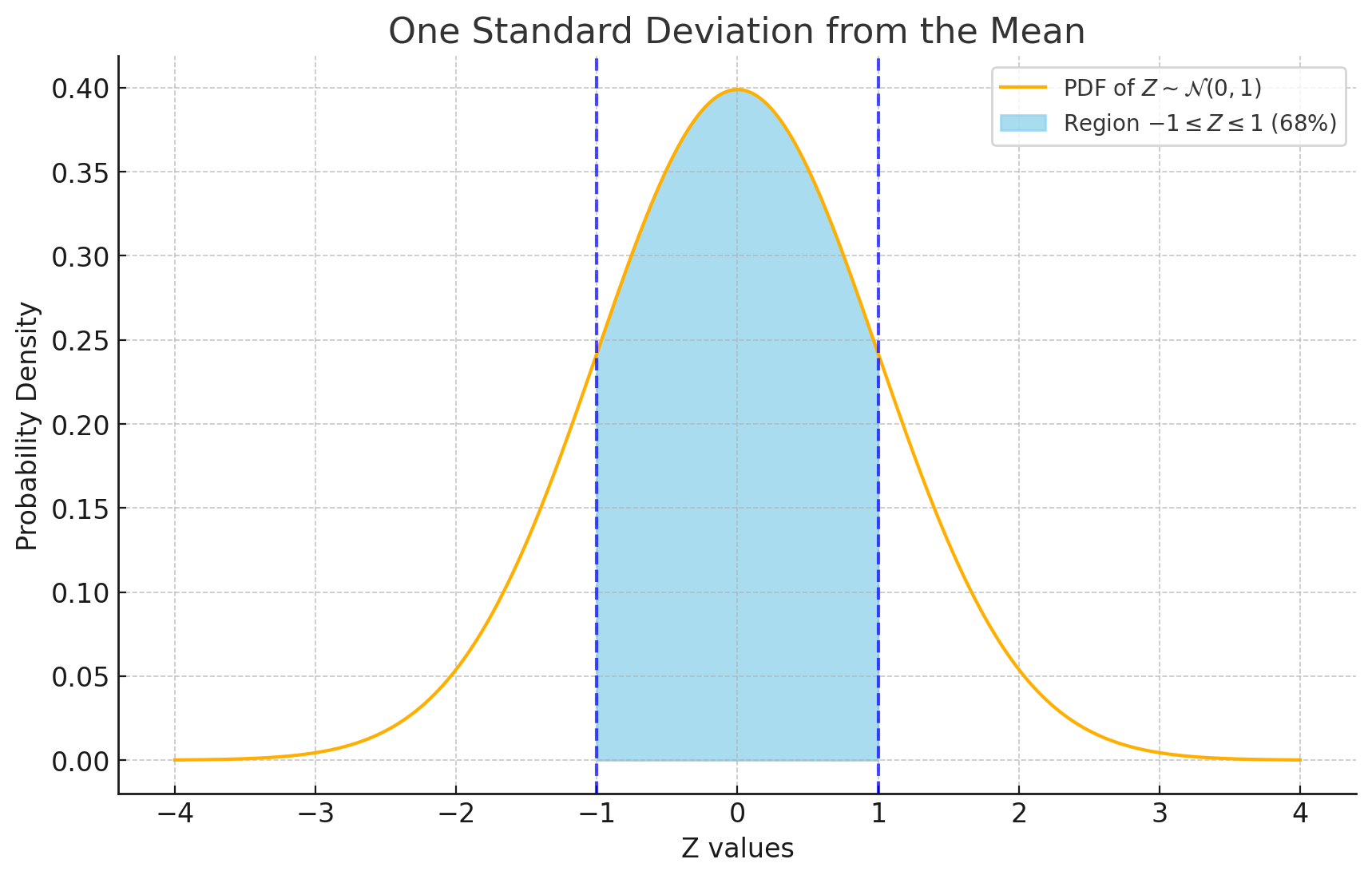
סטיית תקן אחת ($68\%$)
\[P(-1 \leq Z \leq 1) = 0.68\]זאת אומרת שהסיכוי של משתנה מקרי נורמלי מתוקנן להיות בין -1 ל-1 הוא השטח המסומן בתכלת - $68\%$.
עבור משתנה מקרי נורמלי כלשהו: הסיכוי להיות במרחק של מינוס סטיית תקן אחת עד סטיית תקן אחת מהתוחלת הוא אותו דבר - $68\%$.
שתי סטיות תקן ($95\%$)
\[P(-2 \leq Z \leq 2) = 0.95\]במדעים ביולוגיים, רפואיים וגם בפסיכולוגיה - מדעים ניסויים “מלוכלכים” (לעומת מדעים ניסויים יותר מדויקים כמו פיזיקה) - $95\%$ זה סטנדרט להגדרת “הרוב החשוב של התופעות האפשריות”.
שלוש סטיות תקן ($99.7\%$)
\[P(-3 \leq Z \leq 3) = 0.997\]הסיכוי של משתנה מקרי נורמלי מתוקנן להיות בין -3 ל-3 הוא $99.7\%$, וזה מכסה כמעט את כל העולם ההסתברותי הצפוי.
סימונים עבור משתנה מקרי נורמלי כללי
עבור משתנה מקרי נורמלי $X \sim \mathcal{N}(\mu, \sigma^2)$:
- $68\%$ מהערכים יהיו בין $\mu - \sigma$ ל-$\mu + \sigma$
- $95\%$ מהערכים יהיו בין $\mu - 2\sigma$ ל-$\mu + 2\sigma$
- $99.7\%$ מהערכים יהיו בין $\mu - 3\sigma$ ל-$\mu + 3\sigma$
דוגמה: משקל תינוקות
נניח שמשקל לידה מתפלג נורמלית עם:
- תוחלת: $\mu = 3000$ גרם
- סטיית תקן: $\sigma = 500$ גרם
באנגלית פורמאלית יותר:
\[\begin{aligned} &\textbf{Example: Birth Weights} \\ &\text{Assume birth weight is normally distributed with:} \\ &\quad \mu = 3000 \text{ grams} \quad \text{(mean)} \\ &\quad \sigma = 500 \text{ grams} \quad \text{(standard deviation)} \end{aligned}\]חישובים מיידיים
\[\begin{aligned} \textbf{1 SD:} \quad & \text{68\% of babies: } 3000 - 500 = 2500 \text{ to } 3000 + 500 = 3500 \text{ grams} \\ \textbf{2 SD:} \quad & \text{95\% of babies: } 3000 - 2 \cdot 500 = 2000 \text{ to } 3000 + 2 \cdot 500 = 4000 \text{ grams} \\ \textbf{3 SD:} \quad & \text{99.7\% of babies: } 3000 - 3 \cdot 500 = 1500 \text{ to } 3000 + 3 \cdot 500 = 4500 \text{ grams} \end{aligned}\]כלומר:
\[\begin{aligned} \text{68\%:} \quad & [2500,\; 3500] \\ \text{95\%:} \quad & [2000,\; 4000] \\ \text{99.7\%:} \quad & [1500,\; 4500] \end{aligned}\]הסתברויות נוספות מהגרף
מתוך הגרף ניתן לראות:
-
הסיכוי להיות גדול מסטיית תקן אחת: בערך $16\%$
\[P(Z > 1) \approx 0.16\] -
הסיכוי להיות קטן משתי סטיות תקן מהתוחלת: בערך $2.5\%$
\[P(Z < -2) \approx 0.025\]
בדוגמה שלנו: $2.3\%$ מהתינוקות יהיו במשקל של מעל 4000 גרם.
ערכים קריטיים (Critical Values)
עד כה נבחנו הסתברויות שמחושבות על ידי פונקציית ההישרדות:
\[P(Z > z_0) = \text{some value}\]לעתים נשאלת שאלה הפוכה: עבור איזה $z_0$ ההסתברות לקבל ערך יותר גדול ממנו היא $5\%$?
הגדרה פורמלית
ערך קריטי $z_0$ הוא הערך שמקיים:
\[P(Z > z_0) = \alpha\]עבור $\alpha$ נתון (למשל 0.05).
דוגמאות לערכים קריטיים נפוצים
ערך קריטי של $5\%$
\[P(Z > z_0) = 0.05\] \[z_0 = 1.64\]ערך קריטי סימטרי של $95\%$
כאשר רצוי שההסתברות להיות בין $-z_0$ ל-$z_0$ תהיה 0.95:
\[P(-z_0 \leq Z \leq z_0) = 0.95\]נדרש להשאיר מימין ומשמאל 0.05. כלומר, מכל צד נדרש להשאיר 0.025:
\[P(Z > z_0) = 0.025\] \[z_0 = 1.96 \approx 2\]זו בדיוק הסיבה לאמירה הקודמת - שתי סטיות תקן מכסות $95\%$ מהתוצאות.
חישוב ערכים קריטיים
הערכים הקריטים מחושבים באמצעות הפונקציה ההופכית לפונקציית ההישרדות, המסומנת כ-iSF - Inverse Survival Function.
דוגמה: ציון סף לפסיכומטרי
הבעיה: אורלי מעוניינת שציוני הפסיכומטרי של הסטודנטים לרפואה יהיו בעשירון העליון. נניח שציוני הפסיכומטרי מתפלגים נורמלית עם:
- תוחלת: $\mu = 550$
- סטיית תקן: $\sigma = 100$
השאלה: מה צריך להיות ערך הסף שמעליו סטודנט יתקבל לפקולטה?
פתרון
שלב 1: פורמליזציה
$X$ הוא משתנה מקרי של ציון פסיכומטרי:
\[X \sim \mathcal{N}(550, 100^2)\]יש לחשב את הערך הקריטי הרלוונטי: ערך $C$ שמעליו הסיכוי להיות הוא רק $10\%$ (עשירון עליון):
\[P(X > C) = 0.1\]שלב 2: תקנון
\[P\left(\underbrace{\frac{X - 550}{100}}_{Z} > \frac{C - 550}{100}\right) = 0.1\]משמאל מתקבל משתנה מקרי נורמלי מתוקנן:
\[P\left(Z > \frac{C - 550}{100}\right) = 0.1\]שלב 3: מציאת הערך הקריטי
עבור משתנה מקרי נורמלי מתוקנן, הערך של iSF(1) מתקבל מפייתון כך:
from scipy.stats import norm
critical_value = norm.isf(0.1) # Inverse Survival Function for 0.1
print("Critical value:", critical_value) # 1.2815515655446004
שלב 4: פתרון עבור C
הצבת הערך הקריטי שנמצא:
\[\begin{aligned} P\left(Z > \frac{C - 550}{100}\right) &= 0.1 \iff \frac{C - 550}{100} = 1.28 \end{aligned}\]פתרון המשוואה:
\[\begin{aligned} C - 550 &= 100 \cdot 1.28 \\ C &= 550 + 100 \cdot 1.28 \\ C &= 550 + 128 \\ C &= \boxed{678} \end{aligned}\]תשובה: ציון הסף צריך להיות 678 כדי שרק העשירון העליון יתקבל לפקולטה.
חשיבות הערכים הקריטיים
במדעים ביולוגיים/רפואיים, כאשר בודקים האם מאורע הוא סביר, נבדק האם ההסתברות שלו היא $95\%$ - וזה הקטע הסטנדרטי.
לעתים מוגדר ש”סביר” זה:
- 90% (פחות מחמיר)
- 99% (יותר מחמיר)
אך בדרך כלל סביר זה מאורע שנמצא בטווח של $95\%$.
הלוגיקה
- מגדירים תחום כלשהו על פי מה שמחוץ לתחום הוא לא סביר
- דואגים שמה שמחוץ לתחום יהיה בעל הסתברות נמוכה (למשל 0.05)
- אז טוענים שמה שבתוך התחום סביר מבחינתנו
זה לא אומר שהסיכוי למאורע הזה הוא $95\%$, אלא שהמאורע נופל בטווח שהוגדר אפריורית והטווח הזה מכסה $95\%$ מהתוצאות האפשריות.
קירוב נורמלי להתפלגות בינומית
למשתנה המקרי הנורמלי יש שימוש שיעזור להבנת נושאים בהמשך - קירוב למשתנה הבינומי.
תזכורת: ההתפלגות הבינומית
$X$ מתפלג בינומית עם מספר ניסיונות $n$ וסיכוי הצלחה $p$, מסומן ב-$X \sim B(n,p)$.
תנאים חשובים:
- הניסויים חייבים להיות בלתי תלויים
- בעלי סיכוי הצלחה קבוע
הסיכוי לקבל $k$ הצלחות ב-$n$ ניסיונות:
\[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\]כאשר $\binom{n}{k}$ הוא מספר הדרכים לבחור $k$ איברים מתוך $n$ איברים.
למה צריכים קירוב נורמלי?
במחקרים קיים צורך תכוף לחשב הסתברויות מהסוג:
- מה ההסתברות שמשתנה מקרי בינומי יהיה גדול מ-$k$?
- מספר החולים שמחלימים אחרי טיפול (שסיכוי הצלחה שלו הוא $p$) - מה ההסתברות שיחלימו יותר ממספר מסוים של חולים?
הדגמה ויזואלית: לוח גלטון
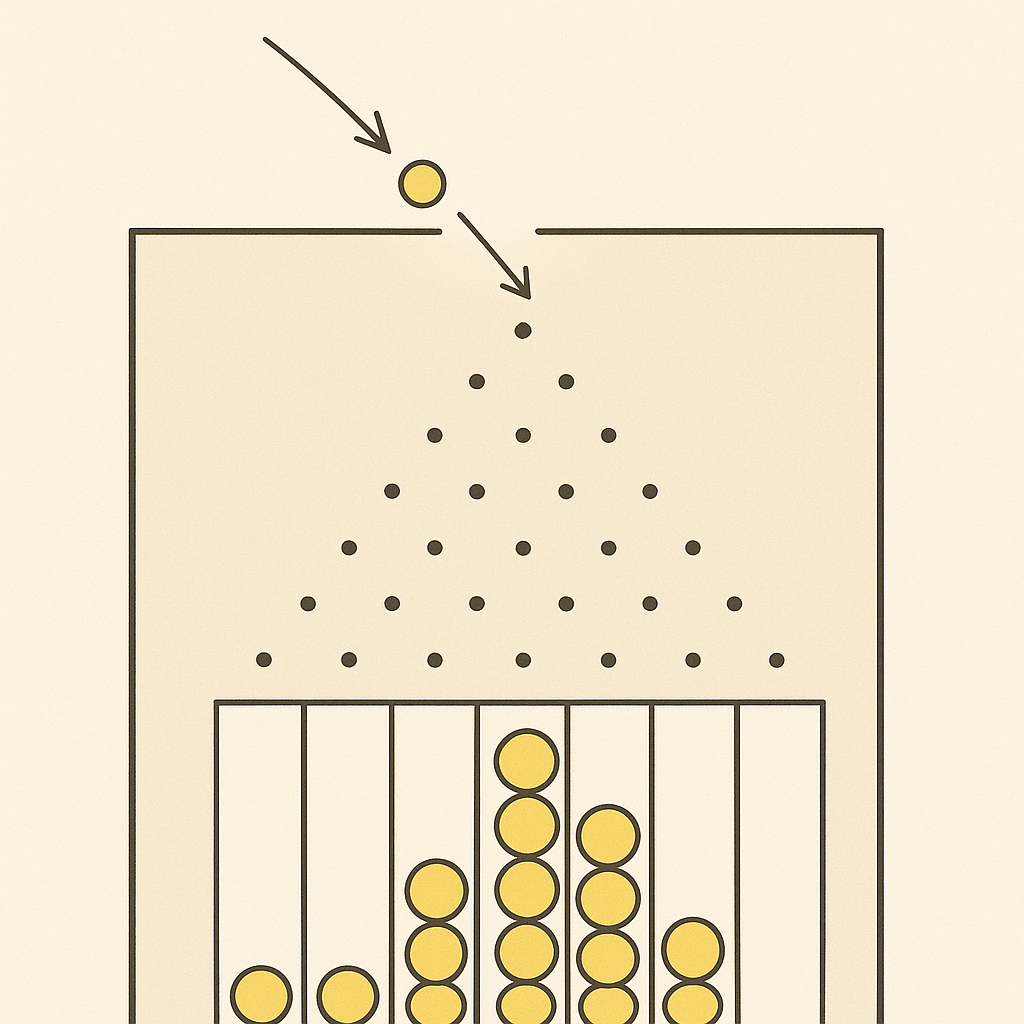
איך זה עובד:
- כל כדור מתנגש במסמרים והולך ימינה או שמאלה בהסתברות $\frac{1}{2}$
- התא הימני ביותר פירושו שהכדור הלך שמאלה, שמאלה, שמאלה… (אפס “הצלחות”)
- התא השמאלי ביותר פירושו שהכדור הלך ימינה בכל פעם
- ההתפלגות של מספר הכדורים בכל תא נראית דומה להתפלגות נורמלית
מעבר מבינומי לנורמלי: גרפים
כשמספר הניסיונות גדל, ההתפלגות הבינומית הופכת דומה יותר ויותר להתפלגות נורמלית:
עם $p = 0.5$ (סימטרי):
- $n = 1$: התפלגות דיסקרטית פשוטה
- $n = 2, 4, 8, 16, 64$: הגרף הופך יותר ויותר דומה לעקומת הפעמון
עם $p = 0.25$ (לא סימטרי):
- בתחילה ההתפלגות מוטה
- ככל ש-$n$ גדל, היא הופכת סימטרית יותר ודומה לנורמלית
עם $p = 0.05$ (מוטה מאוד):
- צריך $n$ גדול הרבה יותר כדי להשיג קירוב נורמלי טוב
מסקנות מהגרפים
- ככל ש-$p$ קטן (קרוב יותר ל-0), הקירוב הנורמלי נהיה יותר גרוע
- אם $p$ לא קרוב ל-0, ו-$n$ יותר ויותר גדול, הקירוב הנורמלי משתפר
- הקירוב הנורמלי עובד בערך כאשר מספר ההצלחות הממוצע $np$ מספיק גדול
תנאי תקפות הקירוב הנורמלי
סימטריה - מספר ההצלחות הממוצע וגם מספר הכישלונות הממוצע צריכים להיות גדולים מספיק.
יוריסטיקה (כלל אצבע): הקירוב הנורמלי תקף כאשר:
- $np > 5$ (תוחלת מספר ההצלחות גדולה מ-5)
- $\mathcal{N}(1-p) > 5$ (תוחלת מספר הכישלונות גדולה מ-5)
איך מבצעים את הקירוב הנורמלי?
אם $X \sim B(n,p)$, אז בקירוב נורמלי:
\[X \sim \mathcal{N}(\mu, \sigma^2)\]כאשר:
- התוחלת: $\mu = np$
- השונות: $\sigma^2 = np(1-p)$
התהליך:
- בדיקה שהתנאים מתקיימים: $np > 5$ ו-$\mathcal{N}(1-p) > 5$
- חישוב $\mu = np$ ו-$\sigma^2 = np(1-p)$
- הגדרת משתנה מקרי נורמלי $Y \sim \mathcal{N}(\mu, \sigma^2)$
- $P(X > k) \approx P(Y > k)$
- חישוב באמצעות תקנון ופונקציית הישרדות
דוגמה: ניסוי קליני
300 חולים משתתפים בניסוי קליני. סיכוי ההחלמה בעזרת הטיפול הוא 0.4.
שאלה: מה ההסתברות שמספר המחלימים יהיה בין 110 ל-145?
פתרון
שלב 1: הגדרת המשתנה
$X \sim B(300, 0.4)$ - מספר המחלימים
שלב 2: בדיקת תנאי הקירוב
- $np = 300 \times 0.4 = 120 > 5$ ✓
- $\mathcal{N}(1-p) = 300 \times 0.6 = 180 > 5$ ✓
הקירוב הנורמלי תקף!
שלב 3: חישוב פרמטרי ההתפלגות הנורמלית
- תוחלת: $\mu = np = 120$
- שונות: $\sigma^2 = np(1-p) = 300 \times 0.4 \times 0.6 = 72$
- סטיית תקן: $\sigma = \sqrt{72} \approx 8.485$
שלב 4: מעבר לעולם הנורמלי
החישוב הנדרש: $P(110 \leq X \leq 145)$
תקנון:
\[Z_1 = \frac{110 - 120}{8.485} = \frac{-10}{8.485} \approx -1.178\] \[Z_2 = \frac{145 - 120}{8.485} = \frac{25}{8.485} \approx 2.946\]שלב 5: חישוב ההסתברות
\[\begin{aligned} P(110 \leq X \leq 145) &\approx P(-1.178 \leq Z \leq 2.946) \\[10pt] &= P(Z \leq 2.946) - P(Z \leq -1.178) \\[10pt] &= \Phi(2.946) - \Phi(-1.178) \end{aligned}\]from scipy.stats import norm
p1 = norm.cdf(2.946) # P(Z <= 2.946)
p2 = norm.cdf(-1.178) # P(Z <= -1.178)
probability = p1 - p2
print("Probability:", probability) # 0.878
הערה: לא נתבקש לעבוד עם טבלאות במבחן. המרצה יכול לכתוב או להגיד שהתשובה היא $P(-1.178 < Z < 2.946)$ או לתת את הערכים.
הדגמה: השוואת קבוצות
המשחק: שתי קבוצות של חמישה סטודנטים
- קבוצה א׳ וקבוצה ב׳ - דגימות הממוקמות על ציר אבסטרקטי (לחץ דם, למשל)
- השאלה: האם הלחץ דם הממוצע של קבוצה א׳ שונה מקבוצה ב׳?
תרחיש 1: קבוצות קרובות וצפופות
כשהקבוצות עומדות יחסית קרוב זו לזו, והפיזור בתוך כל קבוצה קטן:
- המסקנה: קשה להגיד שיש הבדל משמעותי
- ההבדל בין הממוצעים קטן יחסית לפיזור בתוך הקבוצות
תרחיש 2: קבוצות רחוקות וצפופות
כשהקבוצות עומדות רחוק זו מזו, והפיזור בתוך כל קבוצה קטן:
- ההבדל: כמה צעדים של סטיית תקן? ← 5-6 צעדים
- הידע מהעולם הנורמלי: 5-6 סטיות תקן זה המון! לא סביר במקרה
- המסקנה: יש הבדל משמעותי בין הקבוצות
תרחיש 3: קבוצות קרובות ומפוזרות
כשהקבוצות קרובות זו לזו, והפיזור בתוך הקבוצות גדול:
- ההבדל בממוצעים: פחות מסטיית תקן אחת (בערך חצי)
- יש המון שונות בתוך האוכלוסיות ביחס להבדל ביניהן
- המסקנה: לא ניתן להבדיל ביניהם - השונות בתוך האוכלוסייה מסבירה היטב את ההבדל
העיקרון המרכזי בבדיקת השערות
הנושאים המרכזיים מכאן ועד סוף הנושא של אומדן ובדיקת השערות יתמקדו בשאלות הבאות:
- כמה הממוצע רחוק מנקודת ייחוס מסוימת?
- כמה יחידות של סטיית תקן יש מסביב לממוצע?
- האם ההבדל משמעותי או שהוא יכול להיות במקרה?
המושגים המרכזיים
- השוואת ממוצעים - האם יש הבדל אמיתי בין קבוצות?
- יחידות של סטיית תקן - מדידת המרחק ביחידות סטנדרטיות
- פיזור בתוך הקבוצות לעומת הבדל בין הקבוצות - יחס signal-to-noise
- משמעותיות סטטיסטית - האם התוצאה יכולה להיות במקרה?
סיכום השיעור
השיעור הציג שני נושאים מרכזיים:
קירוב נורמלי לבינומי
- תנאי תקפות: $np > 5$ ו-$\mathcal{N}(1-p) > 5$
- פרמטרים: $\mu = np$, $\sigma^2 = np(1-p)$
- יישום מעשי בניסויים קליניים
מבוא לבדיקת השערות
- השוואת קבוצות במונחים של ממוצעים וסטיות תקן
- חשיבות היחס בין הבדל בין קבוצות לפיזור בתוך קבוצות
- הבסיס הקונספטואלי לכל הנושאים הבאים בקורס