תוכן עניינים:
- רקע תיאורטי
- שאלה 1: שדה מגנטי של גליל מוליך
- שאלה 2: חישוב שדה מגנטי עם שכבה אינסופית
- שאלה 3: מציאת שדה מגנטי של גליל מסתובב
- שאלה 4: שדה מגנטי, כא״מ מושרה וחוק לנץ
- שאלה 5: טורואיד עם כריכה
רקע תיאורטי
הנחת יסוד
בתרגול זה מניחים שאין שדה חשמלי משתנה בזמן, ולכן מתקיימת הגרסה הסטטית של חוק אמפר.
חוק אמפר - צורה אינטגרלית
\[\oint_C \vec{B} \cdot d\vec{l} = \mu_0 I_{\text{enc}}\]או באמצעות צפיפות הזרם:
\[\oint_C \vec{B} \cdot d\vec{l} = \mu_0 \iint_S \vec{J} \cdot d\vec{A}\]המשמעות הפיזיקלית: האינטגרל הקווי של השדה המגנטי לאורך מסילה סגורה שווה ל-$\mu_0$ כפול הזרם הכלוא בתוך המסילה.
הבחנה בין $\vec{B}$ ו-$\vec{H}$
| גודל | משמעות | קשר |
|---|---|---|
| $\vec{B}$ | שדה מגנטי בתוך החומר (כולל השפעת החומר) | |
| $\vec{H}$ | עוצמת השדה המגנטי (“השדה החיצוני”) | $\vec{B} = \mu \vec{H}$ |
בוואקום או באוויר: $\mu \approx \mu_0$, ולכן $\vec{B} = \mu_0 \vec{H}$.
תזכורת: כוח לורנץ
\[\vec{F} = q\vec{E} + q(\vec{v} \times \vec{B})\]כוח זה פועל על מטען $q$ הנע במהירות $\vec{v}$ בנוכחות שדה חשמלי $\vec{E}$ ושדה מגנטי $\vec{B}$.
שאלה 1: שדה מגנטי של גליל מוליך
נתון גליל אינסופי מוליך עם רדיוס פנימי: $R_1$, רדיוס חיצוני: $R_2$, וצפיפות זרם:
\[\vec{J}(r) = j_0 \left(\frac{r}{r_0}\right)^2 \hat{z}\]נדרש: למצוא את השדה המגנטי $\vec{B}$ בכל המרחב.
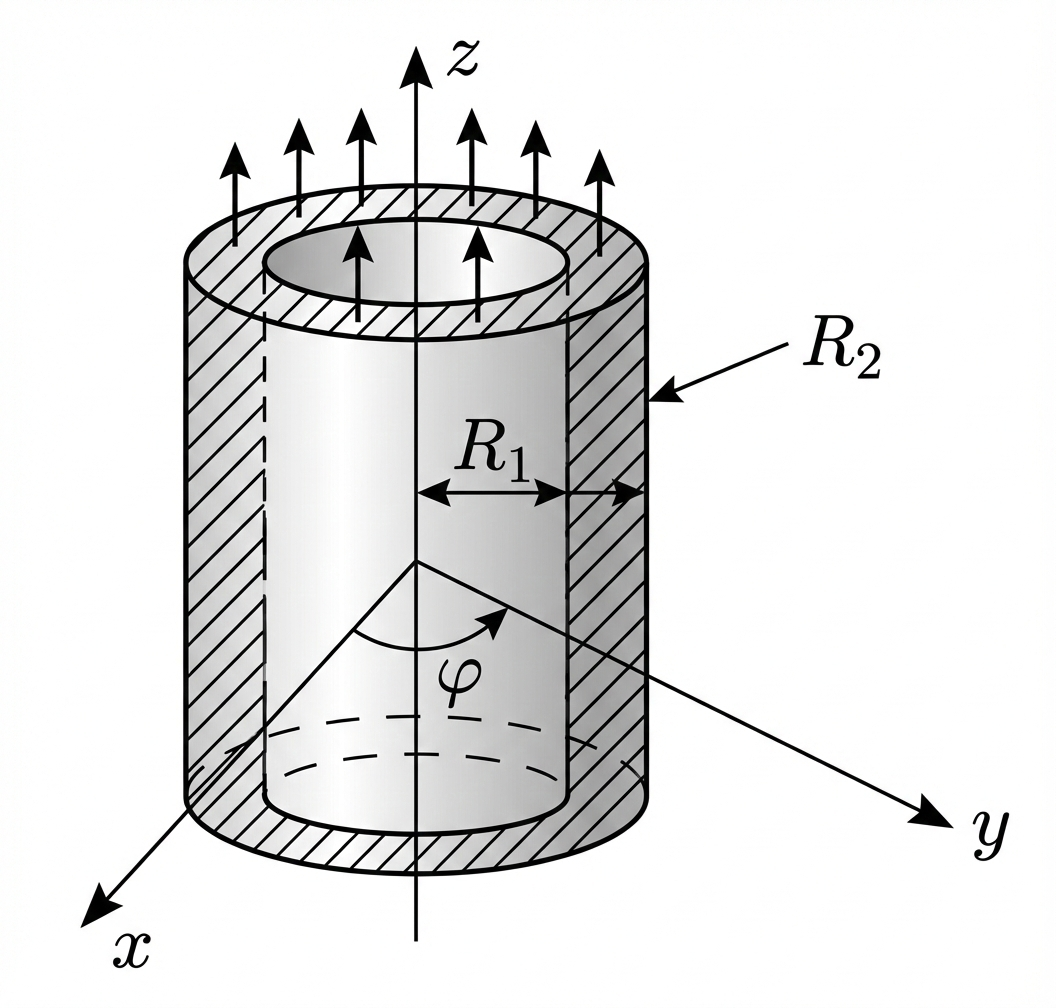
שלב 1: זיהוי הסימטריה
הבעיה בעלת סימטריה גלילית:
- אין תלות בזווית $\varphi$ (סימטריה סיבובית)
- אין תלות ב-$z$ (גליל אינסופי)
לכן:
\[\left| \vec{B} \right| = B(r)\]שלב 2: קביעת כיוון השדה
לפי כלל יד ימין: כאשר הזרם זורם בכיוון $+\hat{z}$, השדה המגנטי מקיף את הזרם בכיוון $+\hat{\varphi}$ (נגד כיוון השעון במבט מלמעלה).
\[\vec{B} = B(r)\,\hat{\varphi}\]שלב 3: בחירת מסילת אמפר
נבחר מעגל ברדיוס $r$ במישור ה-$xy$, כך שהמסילה מקבילה לכיוון השדה.
יתרון הבחירה: $\vec{B} \parallel d\vec{l}$ לאורך כל המסילה, ולכן קבוע לכל נקודה וניתן להוציא אותו מהאינטגרל. סך הכל נקבל שבצד שמאל של חוק אמפר מתקיים:
\[\oint \vec{B} \cdot d\vec{l} = B(r) \underbrace{\oint dl}_{=2\pi r} = B(r) \cdot 2\pi r\]שלב 4: הגדרת התחומים
צפיפות הזרם בכל תחום:
\[\vec{J}(r) = \begin{cases} 0 & r < R_1 \\[6pt] j_0 \left(\dfrac{r}{r_0}\right)^2 \hat{z} & R_1 < r < R_2 \\[6pt] 0 & r > R_2 \end{cases}\]פתרון לפי תחומים
תחום I: $r < R_1$ (בתוך החלל הפנימי)
צד שמאל (אינטגרל קווי): (כבר מצאנו)
\[\oint \vec{B} \cdot d\vec{l} = 2\pi r \cdot B(r)\]צד ימין (זרם כלוא):
\[\mu_0 I_{\text{enc}} = \mu_0 \iint_S \vec{J} \cdot d\vec{A} = 0\]אין זרם בתחום זה.
תוצאה:
\[\boxed{\vec{B} = 0 \quad (r < R_1)}\]תחום II: $R_1 < r < R_2$ (בתוך המוליך)
צד שמאל:
\[\oint \vec{B} \cdot d\vec{l} = 2\pi r \cdot B(r)\]צד ימין:
\[\begin{aligned} \mu_0 I_{\text{enc}} &= \mu_0 \int_{R_1}^{r} \vec{J} \cdot d\vec{A} \\[5pt] &= \mu_0 \int_{R_1}^{r} j_0 \left(\frac{r'}{r_0}\right)^2 \cdot 2\pi r' \, dr' \end{aligned}\]חישוב האינטגרל:
\[= \frac{2\pi \mu_0 j_0}{r_0^2} \int_{R_1}^{r} r'^3 \, dr' = \frac{2\pi \mu_0 j_0}{r_0^2} \cdot \frac{r^4 - R_1^4}{4}\]איחוד שני הצדדים:
\[2\pi r \cdot B(r) = \frac{\pi \mu_0 j_0}{2 r_0^2} \left(r^4 - R_1^4\right)\]תוצאה:
\[\boxed{\vec{B} = \frac{\mu_0 j_0}{4 r_0^2} \cdot \frac{r^4 - R_1^4}{r} \, \hat{\phi} \quad (R_1 < r < R_2)}\]תחום III: $r > R_2$ (מחוץ לגליל)
צד שמאל:
\[\oint \vec{B} \cdot d\vec{l} = 2\pi r \cdot B(r)\]צד ימין:
האינטגרציה על כל הזרם במוליך (מ-$R_1$ עד $R_2$ בלבד):
\[\mu_0 I_{\text{enc}} = \frac{2\pi \mu_0 j_0}{r_0^2} \int_{R_1}^{R_2} r'^3 \, dr' = \frac{\pi \mu_0 j_0}{2 r_0^2} \left(R_2^4 - R_1^4\right)\]תוצאה:
\[\boxed{\vec{B} = \frac{\mu_0 j_0}{4 r_0^2} \cdot \frac{R_2^4 - R_1^4}{r} \, \hat{\phi} \quad (r > R_2)}\]סיכום: השדה המגנטי בכל המרחב
\[\boxed{\vec{B}(r) = \begin{cases} 0 & r < R_1 \\[10pt] \dfrac{\mu_0 j_0}{4 r_0^2} \cdot \dfrac{r^4 - R_1^4}{r} \, \hat{\phi} & R_1 < r < R_2 \\[10pt] \dfrac{\mu_0 j_0}{4 r_0^2} \cdot \dfrac{R_2^4 - R_1^4}{r} \, \hat{\phi} & r > R_2 \end{cases}}\]תובנות
- בתוך החלל הפנימי ($r < R_1$): השדה מתאפס כי אין זרם כלוא.
- בתוך המוליך ($R_1 < r < R_2$): השדה גדל עם $r$ (תלות מורכבת).
- מחוץ לגליל ($r > R_2$): השדה דועך כ-$1/r$, בדומה לחוט אינסופי.
שאלה 2: חישוב שדה מגנטי עם שכבה אינסופית
נתונה שכבה אינסופית עבה שמצאת בין $z=+h$ ל $z=-h$. בשכבה זורם זרם בעל צפיפות אחידה:
\[\vec{j} = J\hat{x}\]חשבו את השדה המגנטי בתוך השכבה ומחוצה לה.
z
↑
│
──────────┼───────── (h)
--------│-----→ j
----------┼────────→ x
--------│-----→ j
──────────┼───────── (-h)
│
הסימטריה של השאלה היא סימטריה של מישור אינסופי, ולכן השדה המגנטי ($\vec{B}$) יהיה קווי ויהיה תלוי רק ב-$z$.
קיוון השדה המגנטי יהיה בכיוון $\pm y$ (לפי כלל יד ימין).
נשים לב ש $B(z=0)=0$ משיקולי סימטריה.
מצד שני, $B(z>0)=-\alpha^2 \hat{y}$ כלומר, השדה המגנטי יהיה בכיוון $-\hat{y}$ .
כמו כן, $B(z<0)=\alpha^2 \hat{y}$. כלומר, השדה המגנטי יהיה בכיוון $+\hat{y}$.
אנו מסיקים שהבעייה היא אנטיסימטרית סביב ציר $z$.
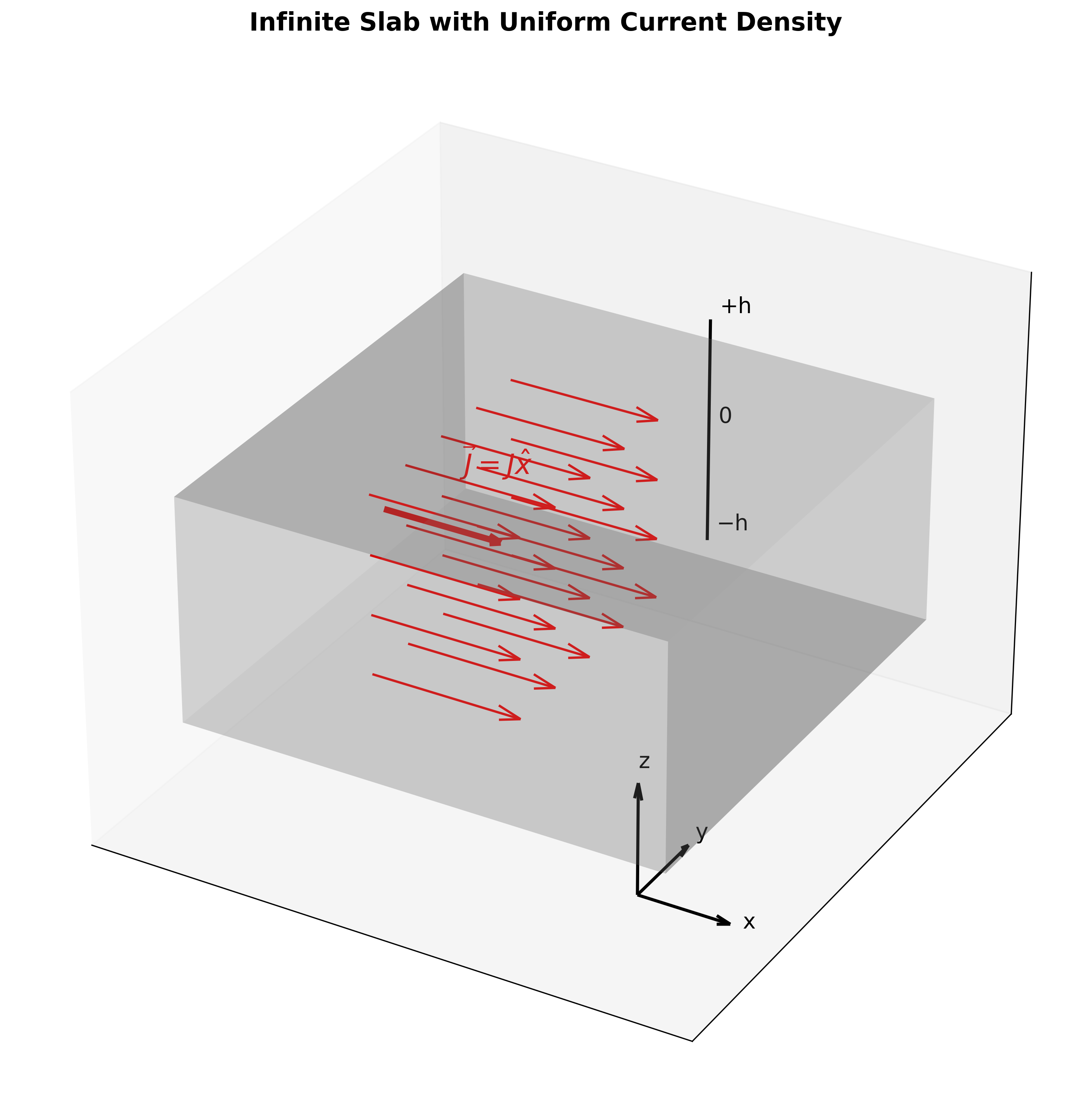 | 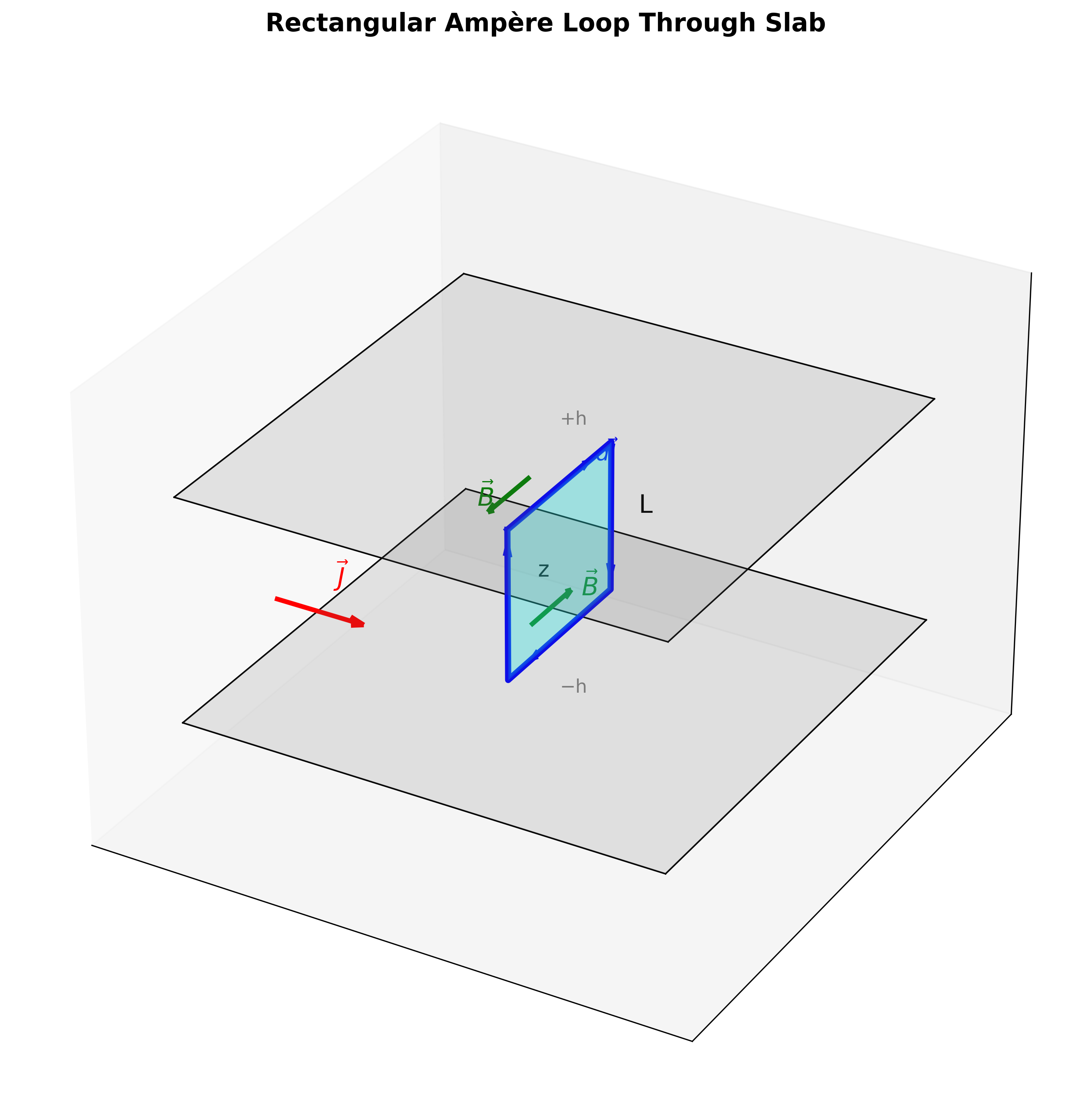 |
בונים לולאת אמפר סימטרית מעל ומתחת לציר $z=0$, והיא חייבת להכיל רכיבים בכיוון ציר $y$ (שיתאפסו?)
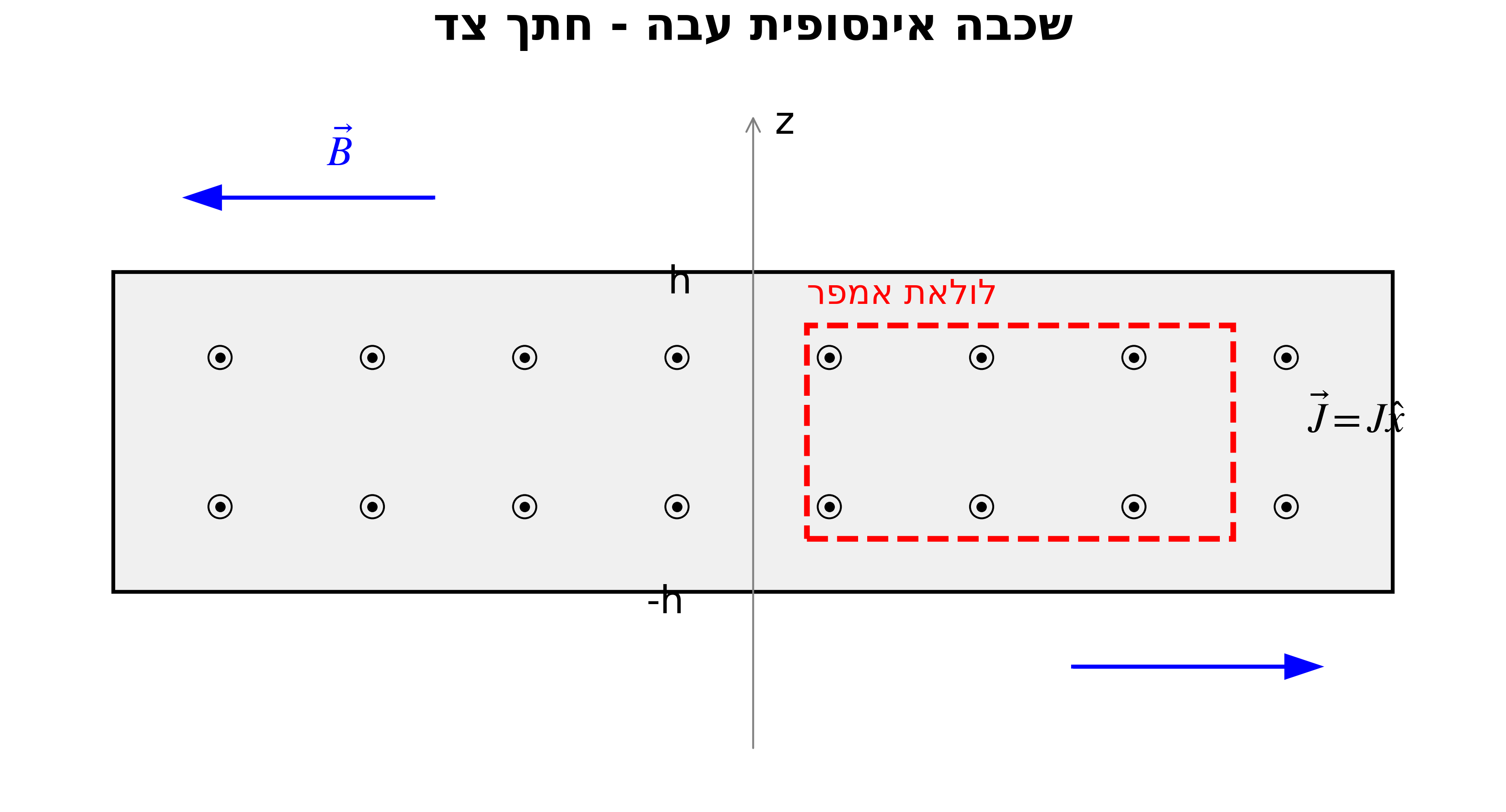
חישוב השטף כאשר הלולאה בתוך המשטח ($z<h$)
הצלעות הצידיות (אלמנט האורך) ניצב לכיוון השדה $B$ ולכן $\vec{B}\cdot \vec{l} = 0$.
לעומת זאת, הבסיסים העליון והתחתון - הרכיבים של הלולאה בכיוון $y$, מקיימים
\[\int \vec{B}\cdot \vec{l} = B(z) \cdot L\]יש שניים כאלו ולכן כל הלולאה היא:
\[\oint Bdl = 2B(z)L\]מצד שני של חוק אמפר (צד ימין של המשוואה):
\[\int \vec{j} \cdot d \vec{s} = J \cdot A\]כאשר $A$ הוא השטח הכלוא בתוך הלולאה, כלומר:
\[\int \vec{j} \cdot d \vec{s} = J \cdot A = \mu_0 J \cdot 2z \cdot L\]נשוואה בין שני הצדדים של חוק אמפר:
\[2B(z)\cancel{L}= \mu_0 J \cdot 2z\] \[\implies B(z) = \mu_0 J \cdot z\]כיוון מינו $\hat{y}$ אם זי חיובי ולהפך, כלומר:
\[B(|z|<h)=-\mu_0 Jz \hat{y}\]חישוב השטף כשהלולאה בחוץ
במקרה כזה ומשיקולים דומים מגיאים לכך ש $h$ מחליף את $z$ כלומר:
\[B(|z|>h)=-\mu_0 J h \hat{y}\]שאלה 3: מציאת שדה מגנטי של גליל מסתובב
נתון גליל אינסופי בעל רדיוס $a$, שבתוכו צפיפות מטען (נפחית!):
\[\rho(r) = \rho_0 \frac{a}{r}\]מסובבים את הגליל במהירות זוויתית קבועה $\omega$ סביב ציר הגליל.
מהו השדה המגנטי בכל המרחב?
הטריק כאן זה לזהות שמדובר במהירות זוויתית בכיוון אזימוטלי.
יש כאן זרם מעגלי ואילו השדה $B$ קוי (לפי GPT זה לא מדויק אבל ככה לפי התרגול).
\[\vec{v} = \omega \, r \, \vec{\varphi}\]צפיפות הזרם היא מכפלת צפיפות המטען הנפחית עם המהירות:
\[\begin{aligned} J &= \vec{v} \rho \\[5pt] &= \omega \cancel{r} \vec{\varphi} \cdot \rho_0 \frac{a}{\cancel{r}} \\[5pt] &= a \, \omega \, \rho_0 \, \varphi \\[5pt] \end{aligned}\]קבוע - $r$ הצמטצמם!
השדה המגנטי בסימטרייה של השאלה:
\[\vec{B} = B_z (r) \hat{Z}\]בניית לולאת אמפר
בשלב הבא אנחנו צריכים לולאה אמפרית כדי לשתמש בחוק אמפר בצורה האינטגרלית:
\[\oint \vec{B} \cdot dl = \mu_0 I_{\text{enc}}\]צריך לבחור לולאה לא סמטרית (אחרת הכל מתאפס משיקולי סימטריות).
לולאה מלבנית מחוץ לאיזור הזרם
במקרה של $r>a$, כלומר גדול מרדיוס הגליל, אפשר לבנות לולאה מלבנית שלא נכנסת לאיזור הזרם - אין תלות ואז:
\[\oint \vec{B}\underbrace{d\vec{l}}_{L} = \left[B(r)-B(r_2)\right]L=0\]מכאן
\[B(r)=B(r_2)\]משהו שלא הבנתי - לפי התרגול בגלל ש $r_2$ אקראי ניתן לבחור אותו גדול כרצוננו - מספיק גדול במקום שהשדה מתאפס בו - ואז $B(r_2)=0$ ולכן גם $B(r>a)=0$.
לולאה מלבנית שחלק ממנה באיזור הזרם
נניח ש $r<a$ שאחת מצלעותיו עם $r_2>a$, כלומר חלק בפנים וחלק בחוץ.
←------------------| <-- z
----┌──<────────┐-- r
│ │ }(a-r)
------------------- a
↓ ↑
│ │
←---└──────→────┘-- r2
L
צד שמאל:
\[\oint \vec{B}d\vec{l}=B(r)L\]צד ימין:
\[\begin{aligned} \mu_0 I &= \mu_0 \int \underbrace{\vec{J}\cdot \hat{n}}_{\vec{J} \perp \hat{n} \, \text{in } \hat{y}}da \\[5pt] &= \mu_0 \underbrace{(a-r)\cdot L}_{Size} \cdot \rho_0 \omega a \end{aligned}\]נאחד את הצדדים:
\[B(r) \cancel{L}= \mu_0 (a-r)\cdot \cancel{L} \cdot \rho_0 \omega a\]הגיוני להבנתי, הצלעות המקבילות מתאפסות גם משיקולי סימטריות ולא אמורות להשפיע? בעצם משהו פה לא מסתדר לי.
\[\boxed{B(r)=a\cdot(a-r)\mu_0 \rho_0 \omega \hat{z}}\]סיכום - השדה המגנטי בכל המרחב
\[\vec{B}(r) = \begin{cases} a\cdot (a-r)\mu_0 \rho_0 \omega \hat{z} & r < a \\[5pt] 0 & r \ge a \end{cases}\]פתרון לא נכון:
אנחנו יודעים שהצפיפות היא:
\[J = v \rho = v \rho_0 \frac{a}{r}\]המהירות היא:
\[v = \omega \times r = \omega r\]נציב:
\[J = \omega r \rho_0 \frac{a}{r}\]נוסחה של שדה מגנטי של גליל אינסופי - כמו תייל:
\[B(r)=\frac{\mu_0 I}{2\pi r}\]נקבל את הזרם הכולל מצפיפות הזרם ואינטגרל:
\[\begin{aligned} I &= \iint J Ad \\[5pt] &= \iint \omega r \rho_0 \frac{a}{r} Ad \\[5pt] &= \iint \omega r \rho_0 \frac{a}{r} Ad \\[5pt] \end{aligned}\]שאלה 4: שדה מגנטי, כא״מ מושרה וחוק לנץ
מוליך ישר ואינסופי מונח אופקית ומעביר זרם קבוע $I$ (כמתואר באיור). המוליך יוצר שדה מגנטי במרחב.
בסמוך למוליך נמצאת לולאה מלבנית מוליכה, הנמצאת במישור הדף. הלולאה נעה במהירות קבועה $\vec{v}$ אופקית, כך שהשטף המגנטי דרכה משתנה בזמן.
- חשבו את השדה המגנטי $\vec{B}$ הנוצר על־ידי המוליך בכל המרחב.
- חשבו את הכא״מ המושרה בלולאה.
- קבעו את כיוון הזרם המושרה בלולאה.
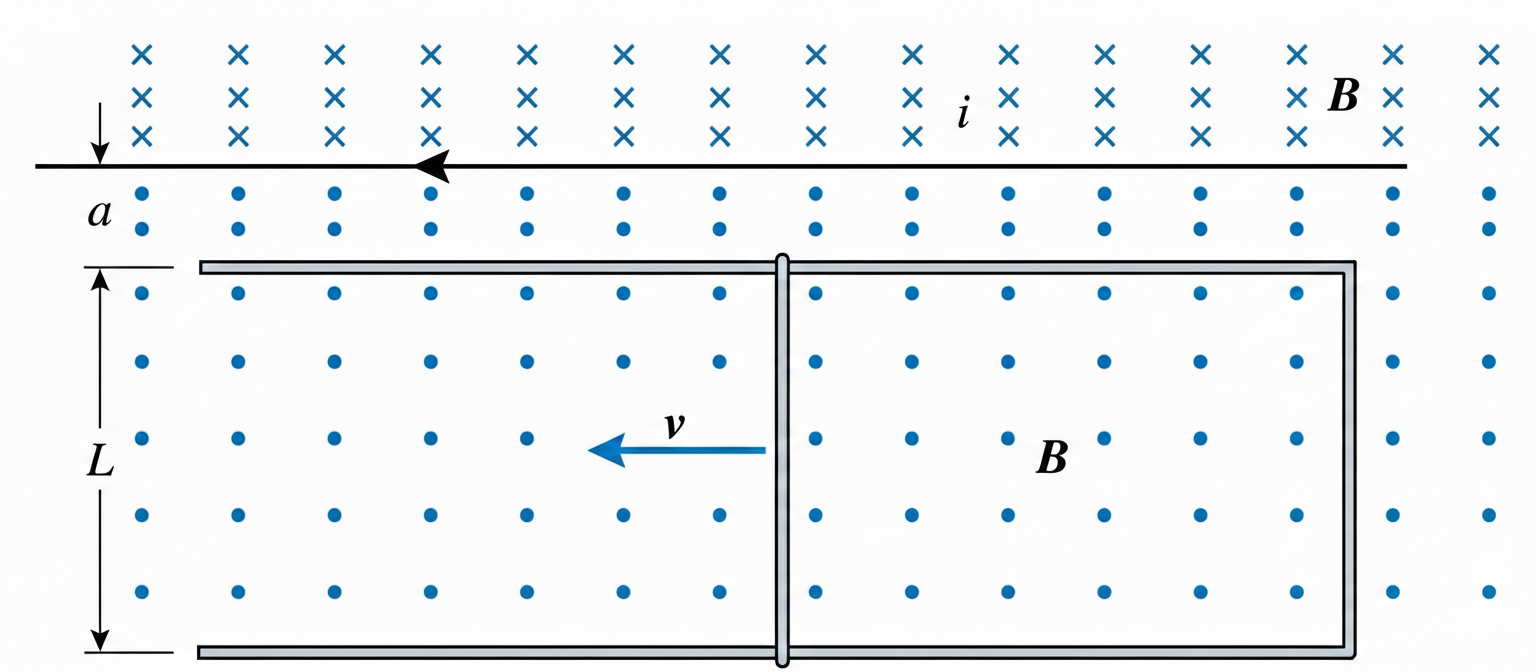
איור 1: לולאה מלבנית נעה ליד מוליך ישר נושא זרם $I$.
להלן פתרון של קלוד. התרגיל גם קיים בבלוג המעולה (ברצינות) של המרצה. לעניות דעתי הפתרון שם פחות ברור - למשל, המיקום חולץ מהמירות למרות שעושים לה אחר כך אינטגרל כך שמראש היה ניתן לכתוב את המהירות.
הבנת הבעיה
מהתרשים עולה שמדובר בבעיית מסילות (rails): שני פסים אופקיים מוליכים במרחקים $a$ ו-$a+L$ מהמוליך, ומוט מוליך מחליק עליהם שמאלה במהירות $v$, כך ששטח הלולאה גדל והשטף המגנטי משתנה.
סעיף 1: השדה המגנטי $\vec{B}$
ממוליך ישר ואינסופי הנושא זרם $I$, השדה המגנטי במרחק $r$ מהמוליך הוא:
\[\boxed{B = \frac{\mu_0 I}{2\pi r}}\]כיוון: לפי כלל יד ימין, עבור זרם הזורם שמאלה:
- מעל המוליך - השדה נכנס לדף (×)
- מתחת למוליך - השדה יוצא מהדף (•)
סעיף 2: כא”מ מושרה בלולאה
המוט הנע חותך את קווי השדה המגנטי הלא-אחיד. כא”מ התנועתי (motional EMF) נובע מהאינטגרציה לאורך המוט:
\[\mathcal{E} = \int_{a}^{a+L} v \cdot B(r)\, dr = \int_{a}^{a+L} v \cdot \frac{\mu_0 I}{2\pi r}\, dr\] \[\mathcal{E} = \frac{\mu_0 I v}{2\pi} \int_{a}^{a+L} \frac{dr}{r} = \frac{\mu_0 I v}{2\pi} \Big[\ln r\Big]_{a}^{a+L}\] \[\boxed{\mathcal{E} = \frac{\mu_0 I v}{2\pi} \ln\!\left(\frac{a+L}{a}\right)}\]סעיף 3: כיוון הזרם המושרה (חוק לנץ)
ניתוח השטף:
- הלולאה נמצאת מתחת למוליך ← השדה דרכה יוצא מהדף (•)
- המוט נע שמאלה ← שטח הלולאה גדל ← השטף היוצא מהדף גדל
לפי חוק לנץ: הזרם המושרה מתנגד לשינוי בשטף, ולכן ייצור שדה נכנס לדף בתוך הלולאה.
לפי כלל יד ימין, שדה נכנס לדף בתוך הלולאה מתקבל מזרם הזורם בכיוון השעון.
שאלה 5: טורואיד עם כריכה
טורואיד בעל חתך מלבני $(a=2\,\mathrm{cm},\, b=4\,\mathrm{cm})$ ורדיוס פנימי $R=4\,\mathrm{cm}$ מורכב מ־$500$ כריכות של תיל בעל זרם
\[I = I_0 \sin(\omega t)\]כאשר תדירות החלפת הזרם נתונה על ידי:
\[f=\frac{\omega}{2\pi}=60\,\mathrm{s^{-1}}=60\,\mathrm{Hz}\]ו־$I_0 = 50\,\mathrm{A}$.
כריכה בעלת $20$ ליפופים של תיל מוליך מקיפה את הטורואיד. מה הכא”מ המושרה בכריכה על ידי הזרם המשתנה?
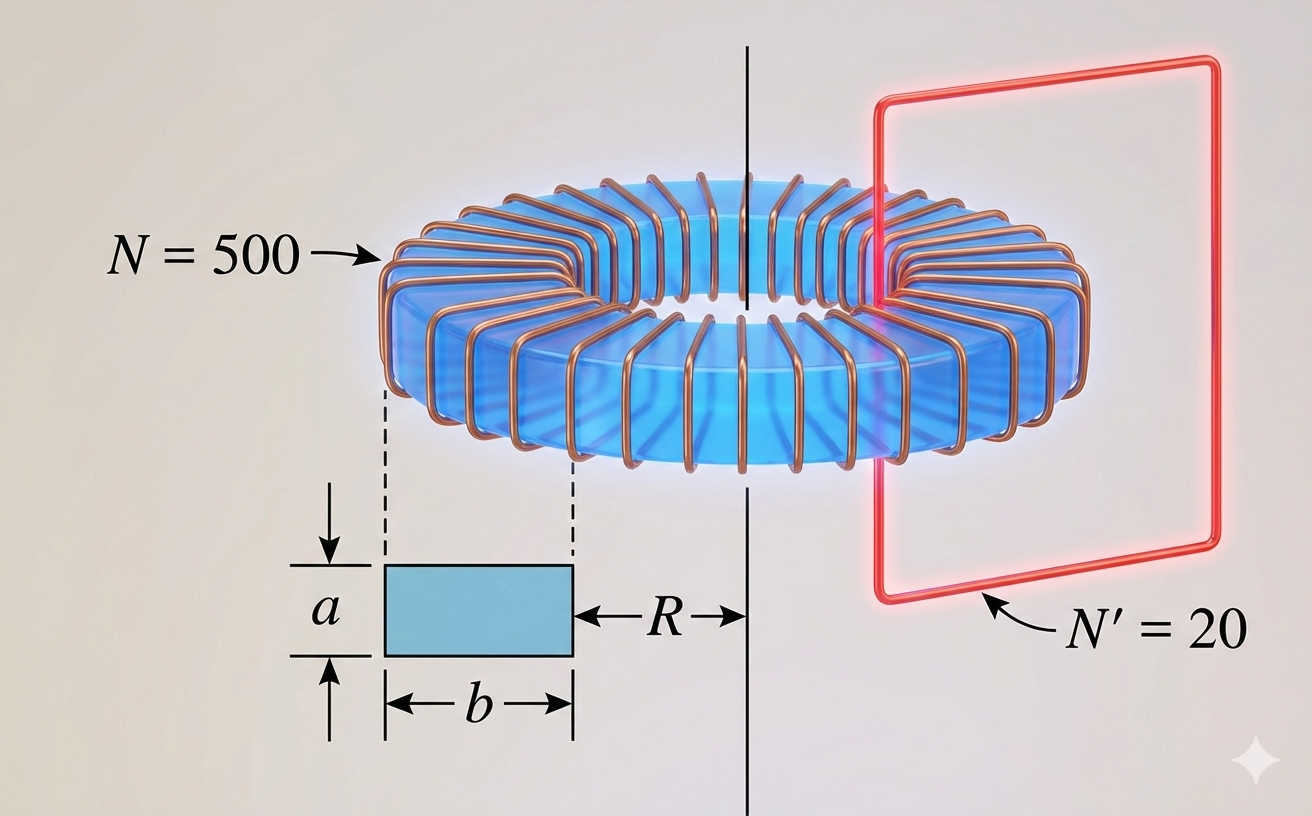
לקחתי את השאלה מהתרגול העוקב (11).
מבקשים כא״מ מושרה - נרצה להשתמש בחוק פאראדיי כדי לקבל:
\[\mathcal{E} = -\frac{d\Phi_B}{dt}\]צריך למצוא את B ואז לגזור.
מציאת השטף
הטורואיד הוא למעשה סלילונית באורך $2\pi r$, השדה המגנטי שלה מתקבל מהנוסחה הבאה:
\[B(r) = \frac{\mu_0 N I}{2\pi r}\]נציב את הנתונים:
\[\begin{aligned} B(r) &= \frac{\mu_0 N I_0 \sin(\omega t)}{2\pi r} \\[5pt] &= \frac{\mu_0 500 \cdot 50\,\mathrm{A} \sin(\omega t)}{2\pi r} \\[5pt] &= \frac{\mu_0 12,500 \,\mathrm{A} \sin(\omega t)}{\pi r} \\[5pt] \end{aligned}\]זה נכון לכל $R \le r \ge R+b$, לרדיוס גדול יותר השדה המגנטי החיצוני של סלילונית מתאפס.
עכשיו נקבל את השטף המגנטי דרך כל חתך מלבני שנמצא במישור הכריכה הדקה:
\[\begin{aligned} \Phi_B &= \int_R^{R+b} B \cdot d A \\[5pt] &= \int_R^{R+b} B(r) \cdot \underbrace{a}_{\text{Gova HaMalben}} dr \\[5pt] &= \int_R^{R+b} \frac{\mu_0 12,500 \,\mathrm{A} \sin(\omega t)}{\pi r} \cdot a dr \\[5pt] &= \frac{a \cdot \mu_0 12,500 \,\mathrm{A} \sin(\omega t)}{\pi } \int_R^{R+b} \frac{1}{r} \cdot dr \\[5pt] &= \frac{a \cdot \mu_0 12,500 \,\mathrm{A} \sin(\omega t)}{\pi } \left[\ln{r}\right]_R^{R+b} \\[5pt] &= \frac{a \cdot \mu_0 12,500 \,\mathrm{A} \sin(\omega t)}{\pi } \ln{\left(\frac{R+b}{R}\right)} \\[5pt] \end{aligned}\]אפשר גם להציב את המהירות הזוויתית שנתונה לנו:
\[\begin{aligned} \Phi_B &= \frac{a \cdot \mu_0 12,500 \,\mathrm{A} \sin(120\pi t )}{\pi } \ln{\left(\frac{R+b}{R}\right)} \\[5pt] \end{aligned}\]תובנה חשובה (שפספסתי): בגלל שיש 20 כריכות, השטף הכולל דרכן יהיה $20\Phi_B$.
שימוש בחוק פאראדיי
\[\begin{aligned} \mathcal{E} &= -\frac{\partial 20 \,\Phi_B}{\partial t} \\[5pt] &= -\frac{d}{dt}\left( \frac{a \cdot \mu_0 250,000 \,\mathrm{A} \sin(120\pi t )}{\pi } \ln{\left(\frac{R+b}{R}\right)}\right) \\[5pt] &= -\ln{\left(\frac{R+b}{R}\right)} \frac{a \cdot \mu_0 250,000 \,\mathrm{A} }{\pi }\frac{d}{dt}\left(\sin(120\pi t ) \right) \\[5pt] &= -\ln{\left(\frac{R+b}{R}\right)} \frac{a \cdot \mu_0 250,000 \,\mathrm{A} }{\cancel{\pi} }\frac{d}{dt} \cdot 120 \cancel{\pi} \cos(120\pi t) \\[5pt] &= -\ln{\left(\frac{R+b}{R}\right)} a \cdot \mu_0 30,000,000 \,\mathrm{A} \cos(120\pi t) \\[5pt] \end{aligned}\]סך הכל:
\[\boxed{\mathcal{E} = -\ln\left(\frac{R+b}{R}\right) \cdot a \cdot \mu_0 \cdot 30{,}000{,}000 \cdot \cos(120\pi t)}\]נציב את הנתונים: $a = 0.02\,\text{m}$, $R = 0.04$, $b = 0.04$, $\mu_0 = 4\pi \times 10^{-7}$:
\[\mathcal{E} = -\ln\left(2\right) \cdot 0.02\,\text{m} \cdot 4\pi \times 10^{-7} \cdot 30{,}000{,}000 \cdot \cos(120\pi t)\]תרגיל מייגע לעניות דעתי.
\[0.02 \times 4\pi \times 10^{-7} \times 3 \times 10^{7} = 0.02 \times 12\pi = 0.24\pi\] \[\mathcal{E} = -0.24\pi \cdot \ln(2) \cdot \cos(120\pi t) \approx -0.52\cos(120\pi t) \,\text{V}\] דור פסקל