משתנה מקרי גיאומטרי
בשיעור הקודם סיימנו את הנושא של משתנים מקריים בינומיים. נמשיך לעסוק במשתנים מקריים בדידים, ובפרט במשתנה מקרי גיאומטרי, ולאחר מכן נעבור למשתנה מקרי נורמלי.
הגדרה
משתנה מקרי גיאומטרי מתאר מצב של ניסוי עם סיכוי הצלחה קבוע $p$, כאשר תוצאות הניסויים החוזרים בלתי תלויות זו בזו. המשתנה סופר את מספר הפעמים שמבצעים את הניסוי עד להצלחה הראשונה.
אם נסמן ב-$X$ את מספר הניסויים עד להצלחה הראשונה (כולל), אז $X$ הוא משתנה מקרי גיאומטרי עם פרמטר $p$.
הערכים האפשריים של $X$ הם: $1, 2, 3, \ldots$ (עד אינסוף).
דוגמאות
- מספר הילדים שנולדים למשפחה עד לידת בת
- מספר הפעמים שצריך להטיל קובייה עד שיוצא 6
- מספר כרטיסי חן שצריך לגרד עד זכייה בפרס
- מספר חשיפות לחיידק עד הידבקות במחלה
- מספר תאונות עבודה עד למקרה מוות
- מספר הזריקות לסל עד קליעה (בהנחה שאין שיפור בין זריקה לזריקה)
- מספר חודשים עד כניסה להריון
התפלגות גיאומטרית
ההסתברות שהניסוי יצליח בפעם הראשונה בניסיון ה-$k$ מחייבת כישלון בכל $k-1$ הניסיונות הראשונים, ואז הצלחה בניסיון ה-$k$.
לדוגמה, כדי להצליח בפעם הראשונה בניסיון העשירי ($X = 10$), נדרשת הסדרה: כישלון, כישלון, …, כישלון ($k-1$ פעמים), הצלחה.
- ההסתברות ל-$k-1$ כישלונות: $(1-p)^{k-1}$
- ההסתברות להצלחה בניסוי ה-$k$: $p$
לכן ההסתברות למשתנה מקרי גיאומטרי להיות שווה ל-$k$ היא:
\[\boxed{P(X = k) = p \cdot (1-p)^{k-1}}\]הדמיה גרפית
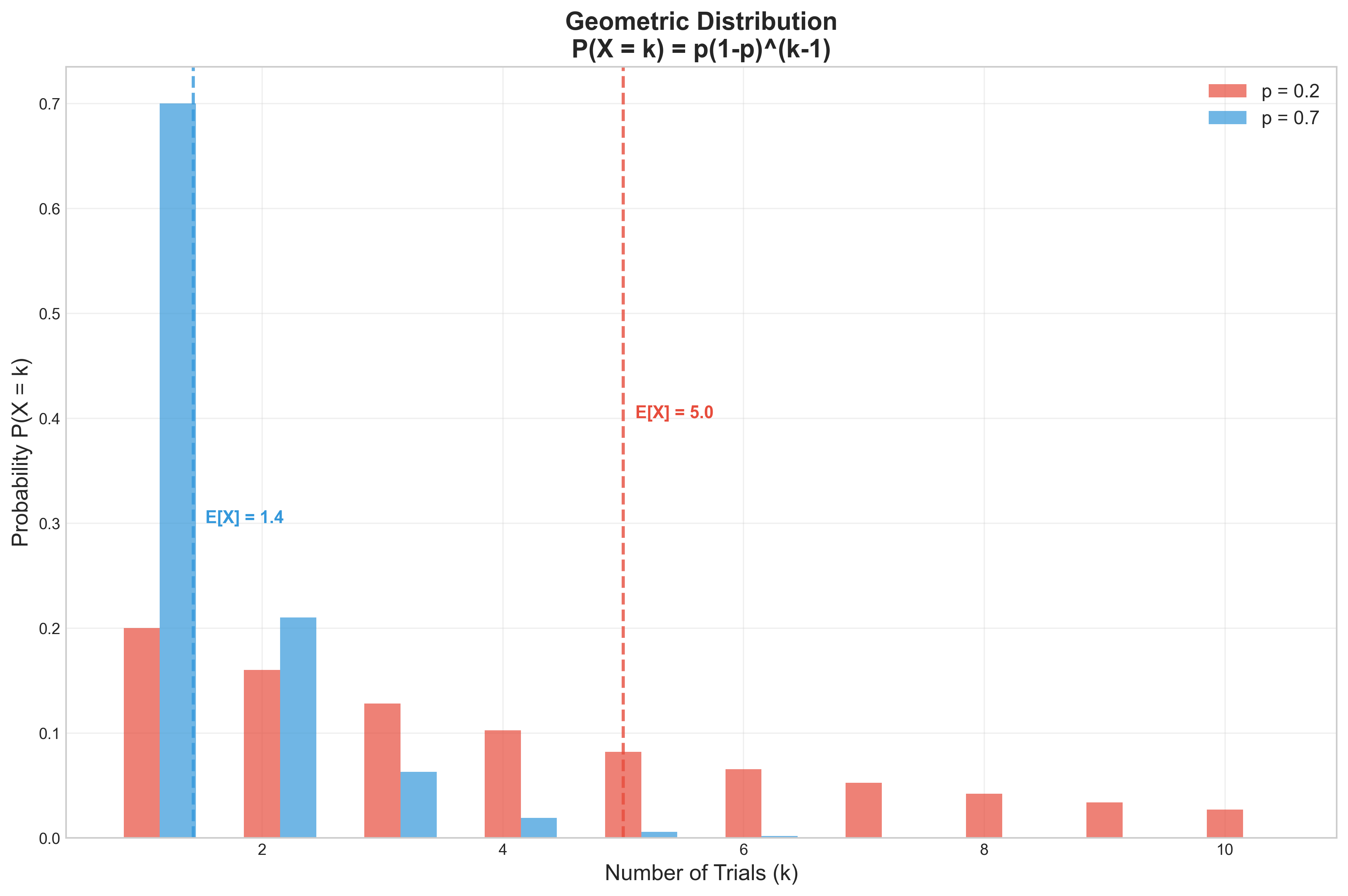
בגרף מוצגת פונקציית ההתפלגות של משתנים מקריים גיאומטריים עם פרמטרים שונים:
- ציר X: מספר הניסיונות
-
ציר Y: ערך ההסתברות עבור מספר הניסיונות
- בצבע אדום: משתנה מקרי גיאומטרי עם פרמטר $p = 0.2$
- בצבע כחול: משתנה מקרי גיאומטרי עם פרמטר $p = 0.8$
ההסתברות דועכת לכיוון 0. זה הגיוני - הסיכוי לקבל את ההצלחה הראשונה דווקא בניסוי המאוחר (העשירי, המאה או המאתיים) הולך וקטן. ההתפלגות שואפת ל-0 כאשר $X$ גדל.
שימו לב: הסיכוי לקבל הצלחה מיד בניסוי הראשון, לפי הנוסחה, הוא $p$ - בדיוק ההסתברות להצלחה בכל ניסוי.
דוגמה ספציפית
עבור $p = \frac{1}{2}$, ההסתברות לקבל הצלחה בניסוי ה-$k$ היא:
\[P(X = k) = \frac{1}{2} \cdot \left(\frac{1}{2}\right)^{k-1} = \left(\frac{1}{2}\right)^k\]מתקבלת הסדרה: $\frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, \ldots$ - סדרה גיאומטרית מוכרת.
דוגמאות יישום
דוגמה 1: לידת בן
שאלה: מה ההסתברות שיוולד בן בפעם הראשונה רק בלידה החמישית?
בכל לידה מתבצע ניסוי ברנולי - ניסוי הסתברותי בלתי תלוי עם הסתברות קבועה. הסיכוי בכל לידה ללידת בן הוא $\frac{1}{2}$, לכן $p = \frac{1}{2}$.
$X$ (מספר הילדים שנולדו עד לידת בן, כולל) הוא משתנה מקרי גיאומטרי עם פרמטר $\frac{1}{2}$.
הסיכוי ש-$X = 5$:
\[\begin{aligned} P(X = 5) &= \frac{1}{2} \cdot \left(\frac{1}{2}\right)^4 \\ &= \left(\frac{1}{2}\right)^5 \\ &= \boxed{\frac{1}{32} \approx 0.03} \end{aligned}\]דוגמה 2: התקף לב
נתון: בהתקף לב יש סיכוי של 70% למות.
שאלה: מה ההסתברות למות בהתקף הלב השלישי?
כדי למות בהתקף הלב השלישי, החולה צריך לשרוד שני התקפי לב ראשונים ולמות בשלישי.
$X$ מתפלג כמשתנה מקרי גיאומטרי עם פרמטר $p = 0.7$.
הסיכוי למוות בהתקף השלישי:
\[P(X = 3) = 0.7 \cdot (0.3)^2 = 0.7 \cdot 0.09 = \boxed{0.063}\]תכונת חוסר הזיכרון
תכונה חשובה של משתנה מקרי גיאומטרי היא חוסר זיכרון.
הניסוח המילולי
העתיד אינו תלוי בעבר, בהינתן ההווה.
הסבר אינטואיטיבי
בדוגמת הרולטה: אם מחכים שיצא מספר מסוים (למשל 32), העובדה שעד כה לא יצא המספר הזה לא משפיעה על הסיכוי להוציאו בהטלות הבאות.
ההתפלגות של המשתנה המקרי תלויה רק במצב הנוכחי, לא בהיסטוריה.
הניסוח המתמטי
הסיכוי לחכות $m$ הטלות נוספות, בהינתן שכבר חיכינו $n$ הטלות, שווה לסיכוי לחכות $m$ הטלות מההתחלה.
ההתפלגות “לא זוכרת” את העבר.
דוגמאות רפואיות
הידבקות בחיידק במחלקה: אם בכל יום אשפוז יש סיכוי קבוע להידבק בחיידק עמיד לאנטיביוטיקה, והחולה לא נדבק עד היום (גם אם מאושפז חודש), התפלגות מספר הימים עד להידבקות נשארת זהה. ההתפלגות עדיין גיאומטרית עם אותו פרמטר.
וידוא נרמול
הערכים האפשריים של ההתפלגות הם $1, 2, 3, \ldots$ עד אינסוף. למרות שהסיכוי להגיע לערכים גבוהים מאוד הוא קלוש, הוא אינו אפסי.
בדיקת הנרמול - סכום ההסתברויות שווה אחד:
\[\sum_{k=1}^{\infty} P(X = k) = \sum_{k=1}^{\infty} p \cdot (1-p)^{k-1}\]מוציאים $p$ מחוץ לסכום:
\[= p \sum_{k=1}^{\infty} (1-p)^{k-1}\]שינוי אינדקס הסכימה מ-$k=1$ ל-$k=0$:
\[= p \sum_{k=0}^{\infty} (1-p)^k\]שימוש בנוסחת טור גיאומטרי כאשר $(1-p) < 1$:
\[= p \cdot \frac{1}{1 - (1-p)} = p \cdot \frac{1}{p} = 1\]תוחלת
התוחלת של משתנה מקרי גיאומטרי היא:
\[\mathbb{E}[X] = \frac{1}{p}\]האינטואיציה
אם הסיכוי להצליח הוא רבע, נדרשים בממוצע 4 ניסיונות להצלחה. באופן כללי, אם הסיכוי להצליח הוא $\frac{1}{m}$, נדרשים בממוצע $m$ ניסיונות.
ממוצע מספר הניסיונות הוא ההופכי של סיכוי ההצלחה.
דוגמאות לתוחלת
דוגמה 1: לידת בן תוחלת מספר הלידות עד לידת בן:
משתנה מקרי גיאומטרי עם $p = \frac{1}{2}$.
התוחלת: $\mathbb{E}[X] = \frac{1}{\frac{1}{2}} = 2$.
דוגמה 2: התקפי לב בהתקף לב יש סיכוי של 70% למות.
תוחלת מספר התקפי הלב עד למוות: $\frac{1}{0.7} = 1.43$ התקפי לב.
הערה חשובה: התוחלת אינה חייבת להיות ערך שההתפלגות יכולה לקבל. במקרה זה, אין משמעות מעשית ל-1.43 התקפי לב.
בעיית ההורים
זוג מחליט להביא ילדים עד שתיוולד להם בת, ואז יפסיקו.
תוחלת מספר הילדים: שניים. לזוג תמיד תהיה בת אחת בדיוק (כי הם עוצרים ברגע לידת הבת).
מכאן שתוחלת מספר הבנים היא אחת, שווה למספר הבנות.
תוצאה מפתיעה: למרות שהזוג יכול ללדת מספר רב של בנים, בממוצע מספר הבנים שווה למספר הבנות.
מעבר למשתנים מקריים רציפים
הערה: נדלג על משתנה מקרי פואסון מפאת קוצר הזמן.
תזכורת
- משתנה מקרי: פונקציה שמתאימה ערך מספרי לכל תוצאה במרחב המדגם
- התפלגות של משתנה מקרי בדיד: רשימת הערכים וההסתברויות שלהם
- כל ההסתברויות בין 0 ל-1
- ההסתברות לערך שאינו ברשימה היא 0
- ההסתברות לקבוצת ערכים היא סכום ההסתברויות שלהם
משתנה מקרי רציף
משתנה מקרי רציף יכול לקבל כל ערך בתחום מסוים:
- כל ערך במקטע $[0, 1]$
- כל ערך במקטע $[-2, 2]$
- כל הישר הממשי
- כל ערך ממשי בין $0$ לאינסוף
דוגמאות לערכים: $1$, $7.5$, $7.234$, $\pi$, $e$, $-\frac{1}{\pi}$, $-320.4547 + \pi$
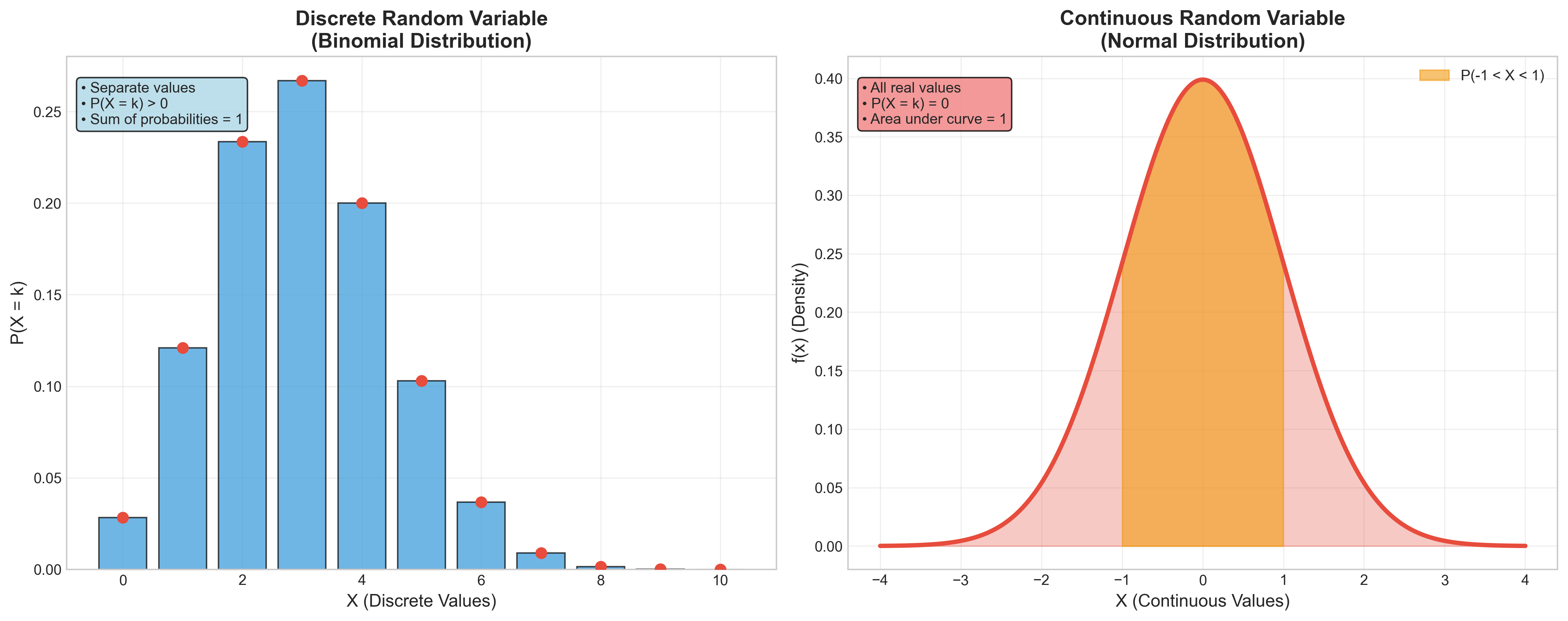
דוגמאות למשתנים מקריים רציפים
- גובה: למרות שנמדד במטרים או סנטימטרים, עקרונית יכול לקבל כל ערך בטווח
- משקל: נמדד בקילוגרמים, אך עקרונית יכול להיות כל ערך רציף
- זמן עד לתקלה: נמדד בימים או ביחידות זמן רציפות
- שכיחות של מחלה
- טמפרטורה
פונקציית צפיפות
התפלגות של משתנה מקרי רציף מתוארת על ידי פונקציית צפיפות $f(x)$.
פונקציית הצפיפות דומה אך שונה מהותית מפונקציית ההתפלגות של משתנה בדיד.
מה מבטאת פונקציית הצפיפות?
פונקציית הצפיפות מבטאת כמות הסתברות ליחידת אורך, לא הסתברות בנקודה.
הבדל חשוב: ערכי פונקציית הצפיפות אינם מוגבלים להיות קטנים מאחת.
כיצד להשתמש בפונקציית הצפיפות?
אם הצפיפות בנקודה מסוימת היא 0.05, וטווח קטן באורך $\Delta x$, אז ההסתברות להיות בטווח:
\[P(X \in \text{interval}) = \text{interval width} \times \text{density} = \Delta x \times 0.05\]או בניסוח פורמלי:
\[P(a \leq X \leq b) = \text{range width} \times \text{density} = \Delta x \times 0.05\]חישוב הסתברויות
לחישוב ההסתברות להיות בין $A$ ל-$B$:
- חלוקת הטווח לחתיכות קטנות
- בכל חתיכה: כפל אורך הטווח בצפיפות
- סכימת כל ההסתברויות
בגבול של מקטעים אינפיניטסימליים, מתקבל אינטגרל:
\[P(A \leq X \leq B) = \int_A^B f(x) \, dx\]הבדלים בין משתנה מקרי בדיד למשתנה מקרי רציף
| תכונה | משתנה מקרי בדיד | משתנה מקרי רציף |
|---|---|---|
| הגבלות על הסתברויות / צפיפות | כל הסתברות בין 0 ל-1 | הצפיפות אי-שלילית (יכולה להיות > 1) |
| חישוב הסתברות | \(\begin{aligned}P(X = x_1 \lor X = x_2)= \\ P(X = x_1) + P(X = x_2)\end{aligned}\) | $P(A \leq X \leq B) = \int_A^B f(x) , dx$ |
| נרמול | סכום ההסתברויות = 1 | $\int_{-\infty}^{\infty} f(x) , dx = 1$ |
| הסתברות ערך בודד | $P(X = x_i) = p_i$ | $P(X = c) = 0$ |
נקודה חשובה: הסתברות ערך בודד
במשתנה מקרי בדיד:
\[P(X = 2) = 0.375, \quad P(X = 0) = 0.125\]במשתנה מקרי רציף: ההסתברות של ערך בודד היא תמיד 0.
זה נובע מההגדרה המתמטית של הסתברות במשתנים רציפים.
הסתברות של ערך בודד במשתנה מקרי רציף
כאשר $B$ מתקרב ל-$A$, השטח מתחת לעקומה בין $A$ ל-$B$ קטן.
בגבול כאשר $B = A$:
\[P(X = A) = \int_A^A f(x) \, dx = 0\]המסקנה החשובה
במשתנים מקריים רציפים תמיד מדברים על טווחים, לא על ערכים בודדים. הסיכוי לכל ערך ספציפי הוא 0.
תוחלת של משתנה מקרי רציף
ההגדרה מחליפה סכומים באינטגרלים.
השוואה בין בדיד לרציף
משתנה מקרי בדיד
התוחלת היא ממוצע משוקלל של הערכים:
\[\mathbb{E}[X] = \sum_i x_i \cdot P(X = x_i)\]משתנה מקרי רציף
התוחלת מחושבת באמצעות אינטגרל משוקלל:
\[\mathbb{E}[X] = \int_{-\infty}^{\infty} x \cdot f(x) \, dx\]התוצאה היא מרכז הכובד של ההתפלגות.
שונות של משתנה מקרי רציף
משתנה מקרי בדיד
\[\text{Var}(X) = \sum_i (x_i - \mathbb{E}[X])^2 \cdot P(X = x_i)\]משתנה מקרי רציף
\[\text{Var}(X) = \int_{-\infty}^{\infty} (x - \mathbb{E}[X])^2 \cdot f(x) \, dx\]סיכום המושגים הסטטיסטיים
- התוחלת: ממוצע משוקלל של הערכים
- השונות: ממוצע של ריבוע הסטיות, יחידות: $(x)^2$
- סטיית התקן: $\sigma = \sqrt{\text{Var}(X)}$, יחידות: $x$
האינטואיציה החשובה
התוחלת היא העוגן - המרכז שסביבו מסתובב המשתנה המקרי.
דוגמה: נסיעות לצפת
המרחק הממוצע לצפת: כ-70 ק”מ (העוגן). כל נסיעה תהיה סביב ערך זה, עם סטיות קטנות.
סטיית התקן מודדת את גודל הסטיות מהעוגן.
יחידת המידה הסטטיסטית היא סטיית התקן.
פונקציית הישרדות (SF)
הגדרה
פונקציית ההישרדות (Survival Function) מוגדרת כהסתברות שמשתנה מקרי רציף $X$ יהיה גדול מערך מסוים $x$:
\[\text{SF}(x) = P(X > x) = \int_x^{\infty} f(s) \, ds\]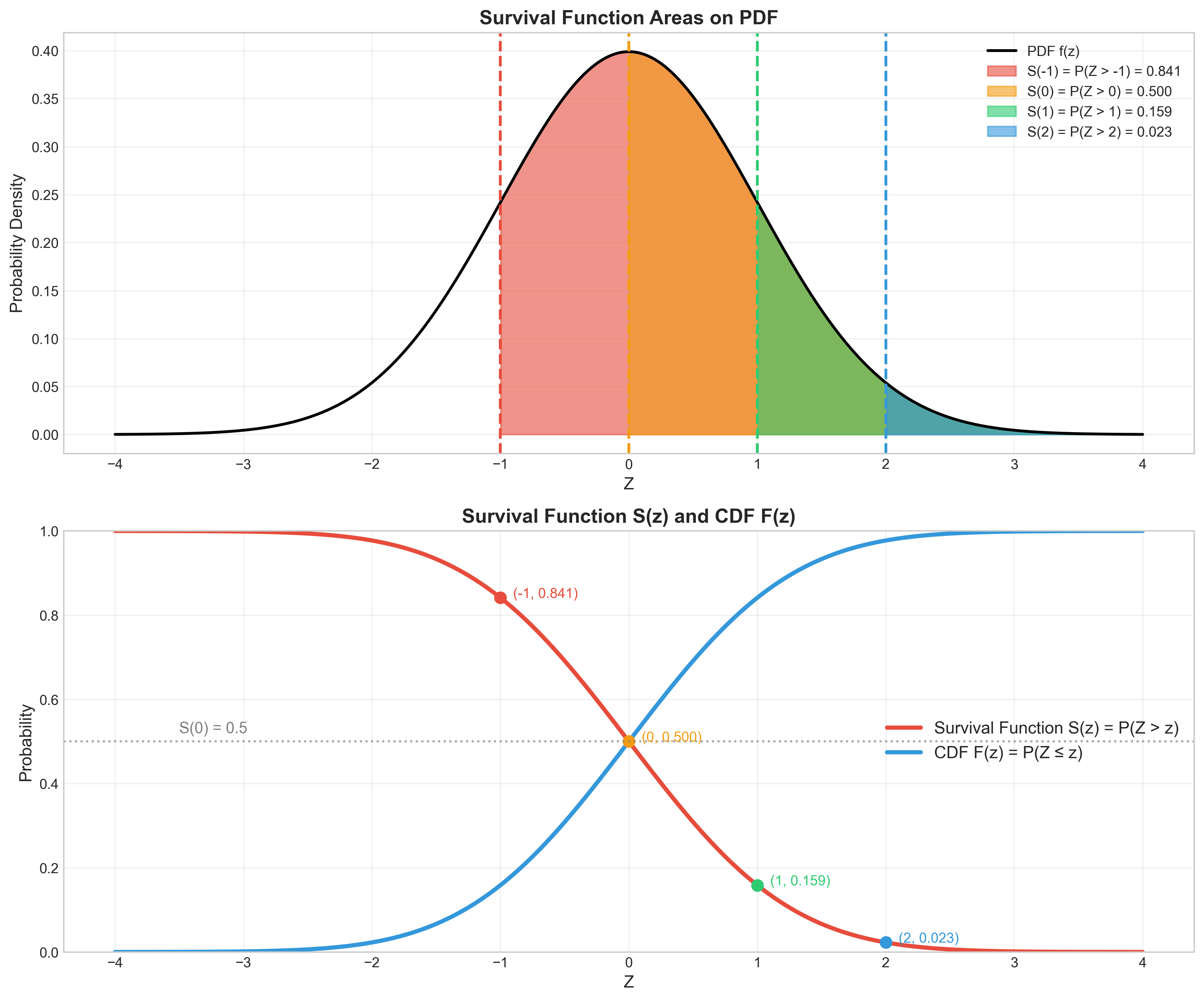
זה למעשה ערך הגבול הימני של התפלגות רציפה.
תכונות
- מקבלת ערכים ממשיים ומחזירה הסתברויות
- רלוונטית במיוחד בניתוח הישרדות ברפואה
יישומים רפואיים
בניתוח הישרדות: מה הסיכוי לחולה לשרוד יותר משנתיים?
מה ההבדל בין SF ל-CDF?
תשובה:
CDF (פונקציית התפלגות מצטברת) מחשבת את ההסתברות שהמשתנה יהיה קטן או שווה לערך מסוים: $P(X ≤ x)$
SF (פונקציית הישרדות) מחשבת את ההסתברות שהמשתנה יהיה גדול מערך מסוים: $P(X > x)$
הקשר המתמטי: השתיים הן פונקציות משלימות (לא הופכיות):
- SF(x) = 1 - CDF(x)
- CDF(x) = 1 - SF(x)
זה הגיוני - ההסתברות להיות מעל ערך מסוים פלוס ההסתברות להיות במקום מסוים או מתחתיו חייבות להסתכם ל-1.
דוגמה: אם
\[\text{CDF}(5) = 0.7\](70% מהערכים ≤ 5), אז:
\[\text{SF}(5) = 0.3\](30% מהערכים > 5).
פונקציית ההישרדות ההופכית (iSF)
עונה לשאלה: מהו הזמן שהסיכוי לשרוד מעבר לו הוא $x$?
בהמשך נראה שכאשר $Z$ מתפלג נורמלית סטנדרטית:
\[\text{iSF}(\alpha) = Z_\alpha\]למשל:
\[\text{iSF}(0.05) = Z_{0.05} \approx 1.5 (1.645)\]ושאם אנחנו מחשבים רווח סמך דו צדדי ברמת סמך של 95%:
\[\text{iSF}(0.025) = Z_{\alpha/2 = 0.025} \approx (1.96)\]
לדוגמה: מה הזמן שמעבר לו חצי מהחולים ישרדו?
שאלות הפוכות
- פונקציית ההישרדות: מה הסיכוי לשרוד יותר מזמן נתון?
- ההופכית: מהו הזמן שמעבר לו אחוז נתון ישרוד?
הבהרה לגבי פרשנות
שאלה: ההופכית מתייחסת לחולים או לחולה אחד?
תשובה: שתי הפרשנויות שקולות:
- אחוז מהאוכלוסייה שישרוד
- הסתברות הישרדות של חולה יחיד
סימונים
ההופכית מסומנת ב-iSF - מקבלת הסתברויות ומחזירה ערכי זמן.
משתנה מקרי אחיד
משתנה מקרי אחיד סטנדרטי
הדוגמה הפשוטה ביותר למשתנה מקרי רציף - מקבל בסיכוי שווה כל ערך בין 0 ל-1.
מאפיינים
- סימון: $X \sim U(0,1)$ (Uniform)
- פונקציית הצפיפות:
- התוחלת: $\mathbb{E}[X] = \frac{1}{2}$ - באמצע ההתפלגות
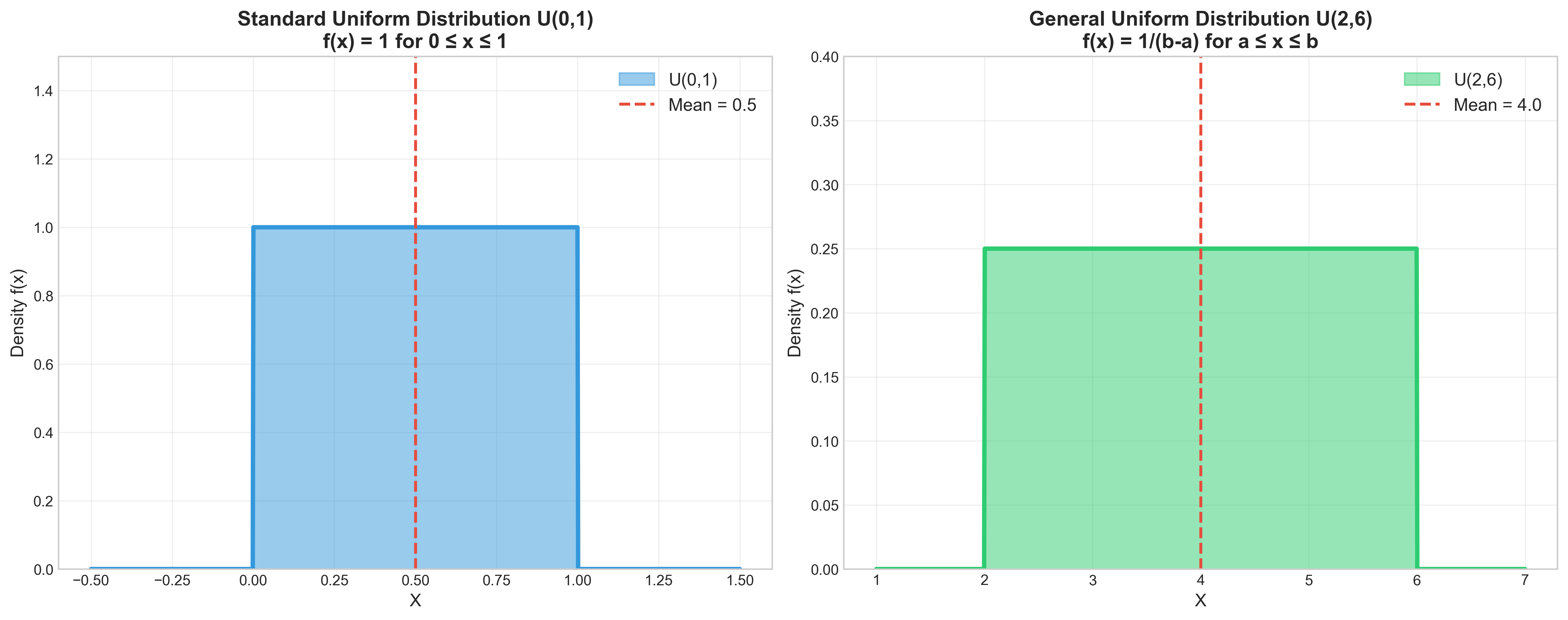
פונקציית הישרדות
- $S(0) = 1$ (הסיכוי להיות > 0)
- $S(1) = 0$ (הסיכוי להיות > 1)
- ירידה לינארית בין הערכים
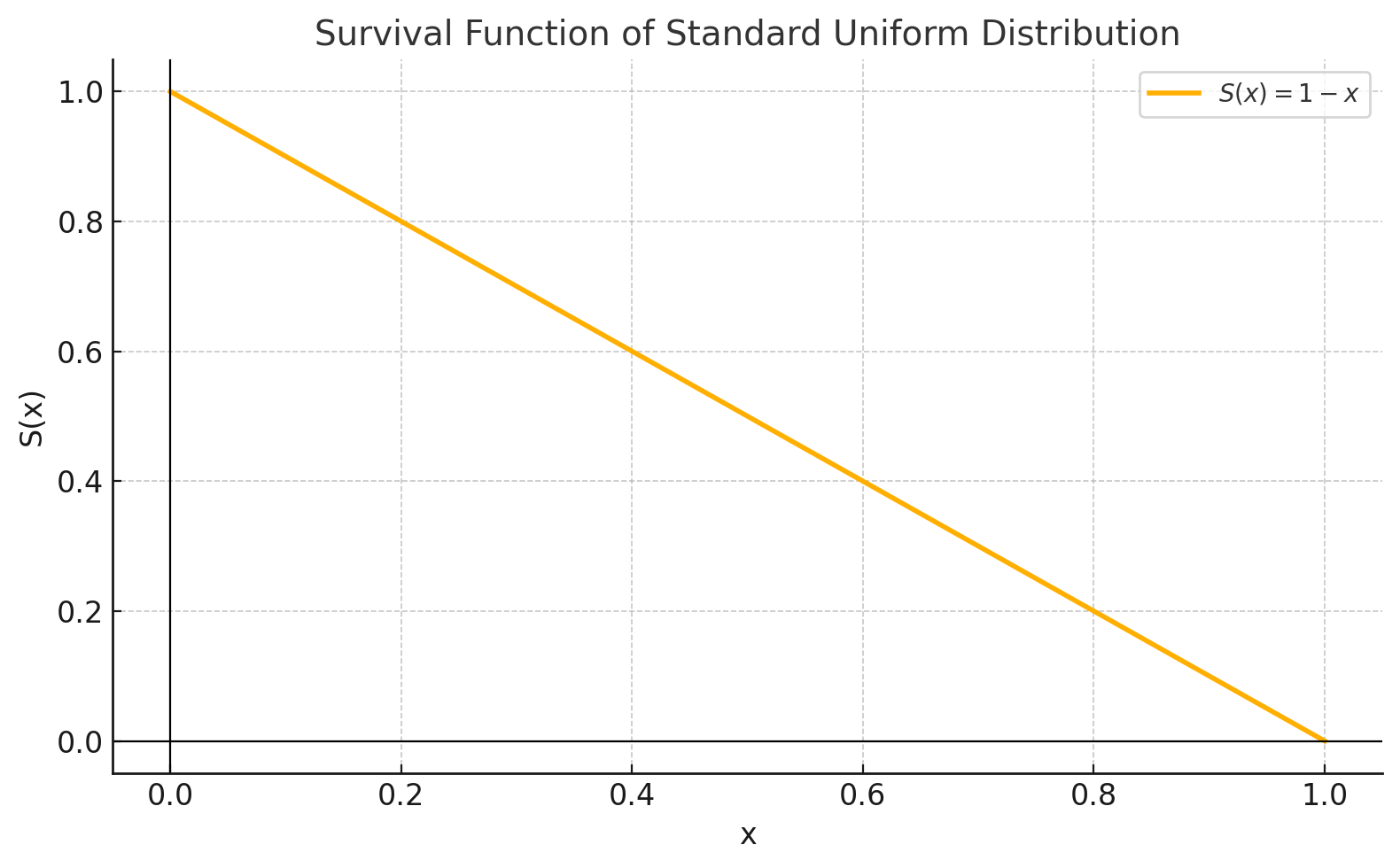 | 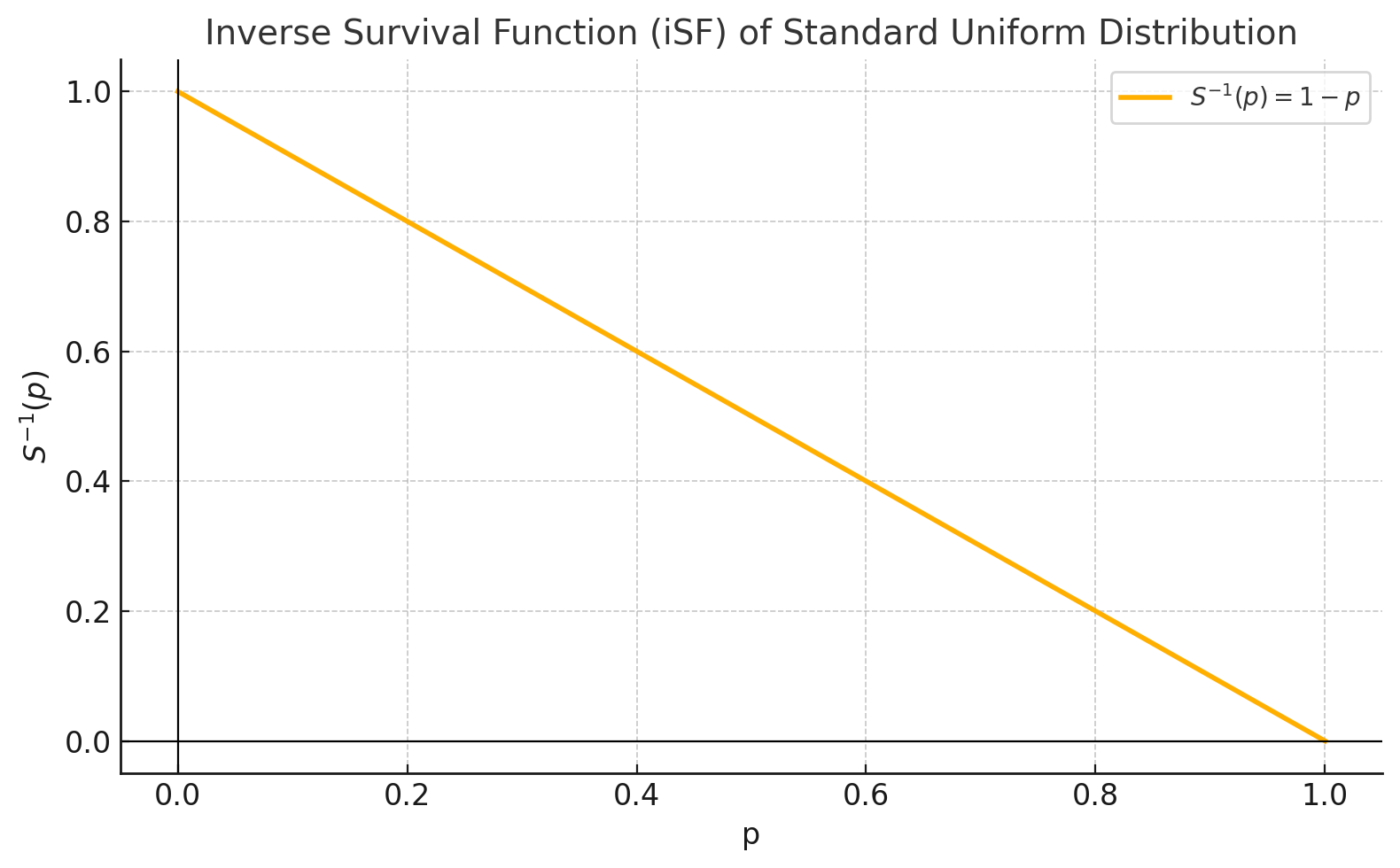 |
|---|---|
| פונקציית הישרדות | פונקציית הישרדות ההופכית |
משתנה מקרי אחיד כללי
משתנה מקרי שמקבל בסיכוי זהה כל ערך בין $A$ ל-$B$.
מאפיינים
- סימון: $X \sim U(A,B)$
- פונקציית הצפיפות:
וידוא נרמול
השטח הכולל: $(B-A) \times \frac{1}{B-A} = 1$ ✓
דוגמה: צפיפות גדולה מ-1
אם $B-A = 0.5$, אז הצפיפות היא $\frac{1}{0.5} = 2$.
זה מדגים שהצפיפות יכולה להיות גדולה מ-1, כי היא מבטאת הסתברות ליחידת אורך.
דוגמאות למשתנה מקרי אחיד כללי:
- זמן המתנה לאוטובוס (מגיע כל 10 דקות):
- הגעה אקראית לתחנה
- זמן ההמתנה: $U(0,10)$
- סיכוי לפיק בדופק (דופק מנוחה 60):
- מדידה בזמן אקראי במהלך שנייה
- התפלגות: $U(0,1)$
- מיקום רקומבינציה על כרומוזום:
- אורך כרומוזום: $L$
- מיקום רקומבינציה: $U(0,L)$
משתנה מקרי מעריכי (אקספוננציאלי)
האנלוג הרציף של המשתנה המקרי הגיאומטרי.
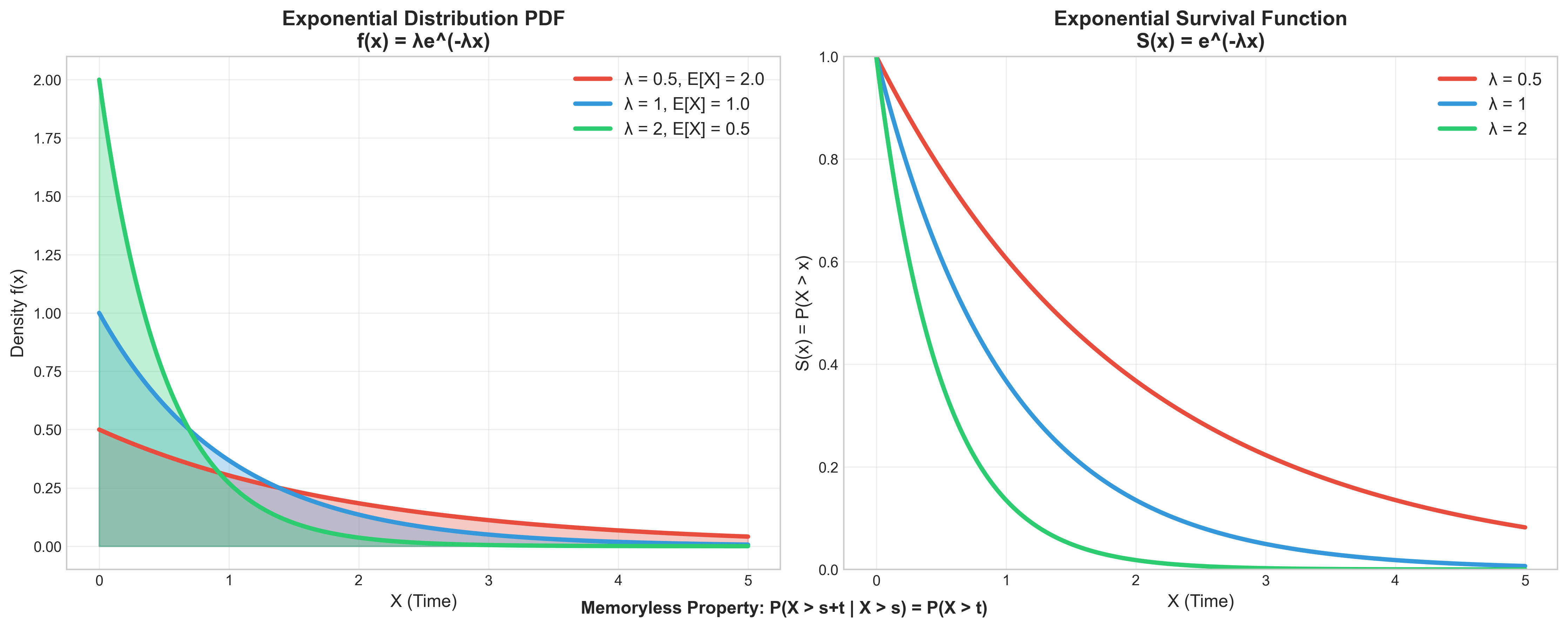
הקשר לגיאומטרי
מודד זמן רציף עד להתרחשות של אירוע, כאשר לאירוע יש סיכוי קבוע להתרחש בכל נקודת זמן.
מאפייני המשתנה המקרי האקספוננציאלי
- פרמטר: קצב $\lambda$ (חיובי)
- סימון: $X \sim \text{Exp}(\lambda)$
- פונקציית הצפיפות: $f(x) = \lambda e^{-\lambda x}$ עבור $x \geq 0$
- התוחלת: $\mathbb{E}[X] = \frac{1}{\lambda}$ = לסטיית תקן
- השונות: $\text{Var}(X) = \frac{1}{\lambda^2}$
תכונת חוסר הזיכרון
כמו במשתנה גיאומטרי: העתיד אינו תלוי בעבר בהינתן ההווה.
דוגמה: התפרקות רדיואקטיבית
אטום רדיואקטיבי:
- סיכוי שווה להתפרק בכל פרק זמן
- זמן ההמתנה שחלף לא משפיע על זמן ההמתנה הנותר
השוואה לגיאומטרי
| גיאומטרי | מעריכי | |
|---|---|---|
| פרמטר | סיכוי הצלחה $p$ | קצב $\lambda$ |
| תוחלת | $\frac{1}{p}$ | $\frac{1}{\lambda}$ |
| מאפיין | זמן בדיד | זמן רציף |
פונקציית הישרדות של משתנה אקספוננציאלי
\[S(x) = P(X > x) = e^{-\lambda x}\]דעיכה מעריכית של הסיכוי לשרוד.
דוגמה: קוהורט חולים
מתוך מיליון חולים עם זמן הישרדות אקספוננציאלי, אחרי זמן $x$:
- $e^{-\lambda x}$ ישרדו
- השאר לא שרדו
רלוונטיות רפואית
חשוב בניתוח הישרדות - זמן הישרדות אחרי מתן תרופה. המודל הפשוט ביותר לפונקציית הישרדות.
המשתנה המקרי הנורמלי
המשתנה המקרי החשוב ביותר בסטטיסטיקה.
חשיבות המשתנה הנורמלי
- ממדל תופעות רבות בטבע
- בסיס להבנת:
- מבחנים סטטיסטיים
- בדיקת השערות
- רווחי סמך
- פותח דלת להבנת סטטיסטיקה מתקדמת
הגדרות ודוגמאות
השם והמאפיינים
נקרא גם גאוסיאן (Gaussian). התפלגות בצורת פעמון.
תופעות שמתפלגות נורמלית
מדדים פיזיולוגיים
- גובה, משקל
- לחץ דם, קולסטרול
מבחנים
- בגרות, פסיכומטרי
תופעות מדעיות
- טעויות מדידה
- ממוצע מדגם
משפט הגבול המרכזי - הסבר ראשוני
סכום של הרבה השפעות קטנות ובלתי תלויות מתנהג כמשתנה נורמלי.
דוגמה: גובה האדם
גובה נקבע על ידי גורמים רבים:
- פיזיולוגיים
- גנטיים
- תזונתיים
- סביבתיים
כל גורם תורם תרומה קטנה, והסכום מתפלג נורמלית.
הכלל: סכום של הרבה גורמים קטנים → התפלגות נורמלית.
נוסחת הצפיפות
\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \cdot e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]פירוק הנוסחה
גורם הנרמול
\[\frac{1}{\sqrt{2\pi\sigma^2}}\]גורם זה מבטיח שהאינטגרל של הצפיפות שווה 1.
האקספוננט - הלב של הנוסחה
\[e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]האינטואיציה
הצפיפות נקבעת על ידי:
\[\frac{(x - \mu)^2}{2\sigma^2} = \left(\frac{x - \mu}{\sigma}\right)^2\]זוהי סטייה מהתוחלת, מנורמלת בסטיית התקן, בריבוע.
המשמעות
- מרכז ההתפלגות: $\mu$
- סימטריה: סביב $\mu$
- רוחב אופייני: $\sigma$
התנהגות הצפיפות
- ככל ש-$\vert x - \mu \vert$ גדל, האקספוננט שלילי יותר
- $e^{-\text{large value}}$ קטן
- הסתברות קטנה להיות רחוק מהמרכז
ככל ש-$\sigma$ גדל, ההתפלגות רחבה יותר.
סימונים ופרמטרים למשתנה מקרי נורמלי
\[X \sim \mathcal{N}(\mu, \sigma^2)\]הערה: כותבים $\sigma^2$ (השונות), לא סטיית התקן.
פרמטרים
- תוחלת: $\mu$
- שונות: $\sigma^2$
- סטיית תקן: $\sigma$
המשתנה הנורמלי הסטנדרטי
הגדרה
משתנה נורמלי עם:
| תוחלת | שונות |
|---|---|
| $\mu = 0$ | $\sigma^2 = 1$ |
סימון
\[Z \sim \mathcal{N}(0, 1)\]
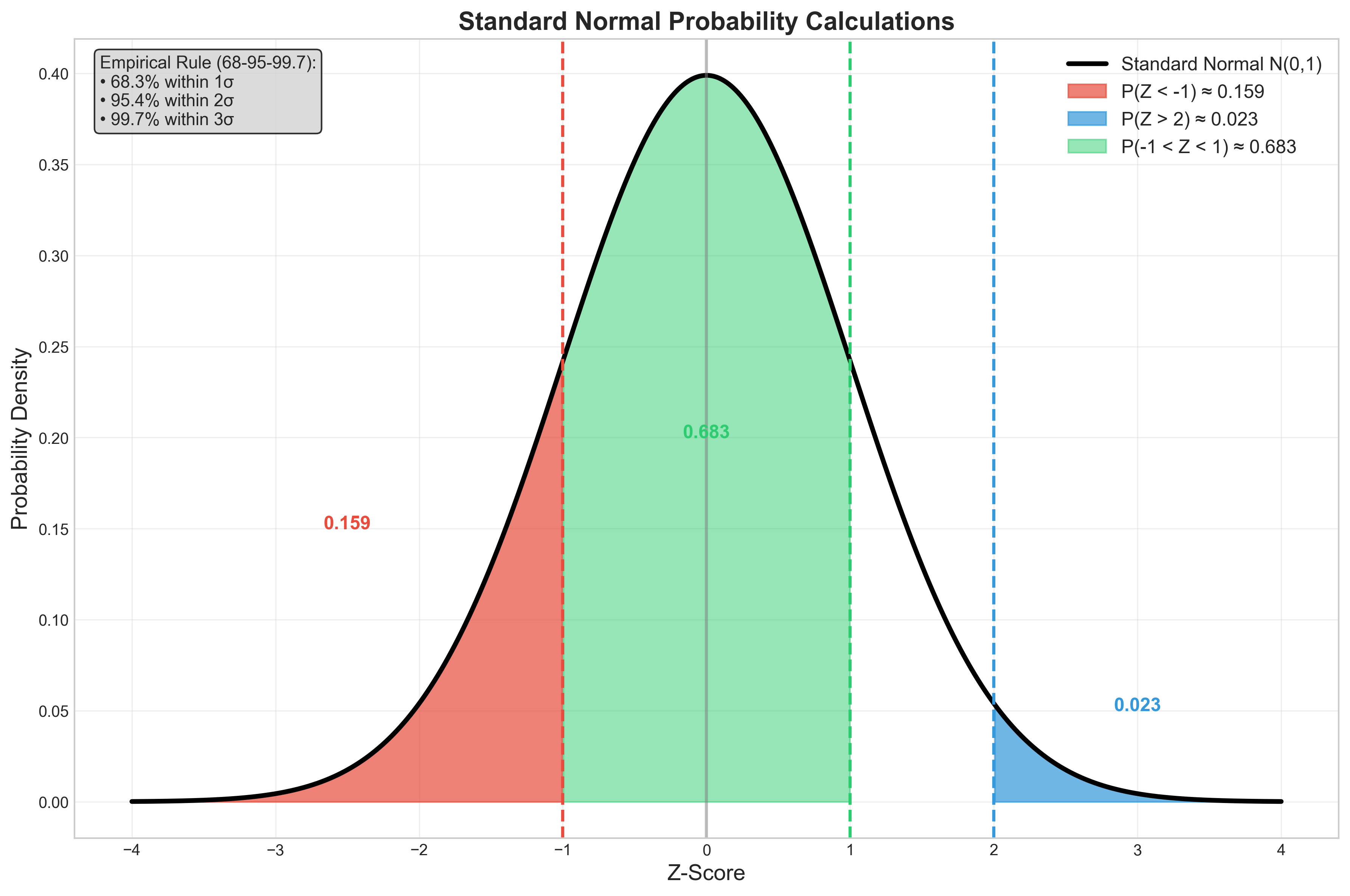
תכונות חשובות
- סימטריה סביב 0
- שטח כולל: 1
- שטח מימין ל-0: $\frac{1}{2}$
- שטח משמאל ל-0: $\frac{1}{2}$
מיקום הערכים
- הצפיפות מקסימלית בתוחלת
- השכיח = התוחלת = 0
התנהגות בקצוות
ההתפלגות שואפת ל-0 בקצוות.
כלל אצבע: במרחק 4 סטיות תקן מהמרכז, ההסתברות כמעט אפס.
סטיית התקן כקנה מידה
סטיית התקן היא קנה המידה לסטיות אופייניות מהתוחלת.
רוב הערכים נמצאים בטווח של כמה סטיות תקן מהתוחלת.
השוואה בין התפלגויות נורמליות שונות
השפעת השונות על הרוחב
- שונות קטנה (0.2): עקומה צרה, ערכים מרוכזים סביב התוחלת
- שונות גדולה (25): עקומה רחבה, פיזור גדול
השפעת התוחלת על המיקום
שינוי התוחלת מזיז את כל ההתפלגות ימינה או שמאלה.
הבנה מעמיקה של הנוסחה
האקספוננט
\[e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]ככל ש-$\vert x - \mu \vert $ גדל:
- $(x - \mu)^2$ גדל
- האקספוננט שלילי יותר
- הצפיפות קטנה
השפעת סטיית התקן
ככל ש-$\sigma$ גדל:
- צריך להתרחק יותר מ-$\mu$ כדי לקבל אותה ירידה בצפיפות
- ההתפלגות רחבה יותר
דוגמאות של משתנה מקרי נורמלי
דופק במנוחה
התפלגות דופק באוכלוסייה - קרובה לנורמלית סביב 80.
משקל לידה
- תוחלת: 3.4 ק”ג
- סטיית תקן: 0.55 ק”ג
- שונות: $(0.55)^2$ ק”ג²
ההתפלגות הנורמלית מופיעה בתופעות רבות בטבע וברפואה.
טרנספורמציות לינאריות של משתנה נורמלי
המשפט החשוב
אם
\[X \sim \mathcal{N}(\mu, \sigma^2)\]ו-
\[Y = AX + B\]אז $Y$ גם מתפלג נורמלית:
\[Y \sim \mathcal{N}(A\mu + B, A^2\sigma^2)\]התוחלת של הטרנספורמציה
\[\mathbb{E}[Y] = \mathbb{E}[AX + B] = A\mu + B\]השונות של הטרנספורמציה
השונות מושפעת רק מהכפל:
\[\text{Var}(Y) = A^2\sigma^2\]סטיית התקן של הטרנספורמציה
\[\sigma_Y = |A| \cdot \sigma\]הדמיה גרפית
- הוספת קבוע $B$: הזזת ההתפלגות ימינה/שמאלה
- כפל בקבוע $A$:
- הזזת התוחלת ל-$A\mu$
- שינוי הרוחב פי $\vert A \vert$
תקנון - הפעולה החשובה ביותר
כלל הזהב
בכל בעיה עם משתנה מקרי נורמלי - להתחיל בתקנון!
מה זה תקנון?
אם $X \sim \mathcal{N}(\mu, \sigma^2)$:
\[\boxed{Z = \frac{X - \mu}{\sigma}}\]מתקבל משתנה נורמלי סטנדרטי $Z \sim \mathcal{N}(0, 1)$.
נוכיח לעצמו ש-$Z$ מתפלג נורמלית סטנדרטית.
התוחלת של Z:
\[\mathbb{E}[Z] = \mathbb{E}\left[\frac{X - \mu}{\sigma}\right] = \frac{\mathbb{E}[X] - \mu}{\sigma} = \frac{\mu - \mu}{\sigma} = 0\]השונות של Z:
\[\text{Var}(Z) = \text{Var}\left(\frac{X - \mu}{\sigma}\right) \overset{\star}{=} \frac{1}{\sigma^2} \cdot \text{Var}(X) = \frac{\sigma^2}{\sigma^2} = 1\]השוויון $\overset{\star}{=}$ נובע מהתכונה של שונות: $\text{Var}(aX) = a^2 \cdot \text{Var}(X)$.
בנוסף, השתמשנו בתכונה של שונות: $\text{Var}(X - \mu) = \text{Var}(X)$, כי חיסור קבוע לא משפיע על השונות.
המסקנה
התקנון יוצר משתנה נורמלי סטנדרטי.
מה התקנון עושה?
- שלב 1 - מירכוז: חיסור התוחלת ממרכז סביב 0.
- שלב 2 - נרמול: חלוקה בסטיית התקן מנרמלת את יחידת המידה.
יחידת המידה הסטטיסטית
יחידת המידה הסטטיסטית היא סטיית התקן ($\sigma$).
דוגמה
בנסיעות לצפת:
- סטייה ממוצעת: 200 מטר
- סטייה בפועל: 100 מטר
- ציון תקן: $\frac{100}{200} = 0.5$ סטיות תקן
דוגמה: משקל לידה
תינוק נולד במשקל 3.95 ק”ג. עם תוחלת 3.4 וסטיית תקן 0.55: סטייה של סטיית תקן אחת בדיוק מהממוצע.
Z-Score (ציון תקן)
הגדרה
ציון תקן מודד סטייה מהתוחלת ביחידות של סטיית תקן.
היתרון של Z-Score
מאפשר השוואה בין משתנים שונים באותו סולם.
האסטרטגיה הכללית
- תקנון המשתנה המקרי
- עבודה בעולם הסטנדרטי
- החזרת התוצאות לעולם המקורי
דוגמה: גובה בלידה
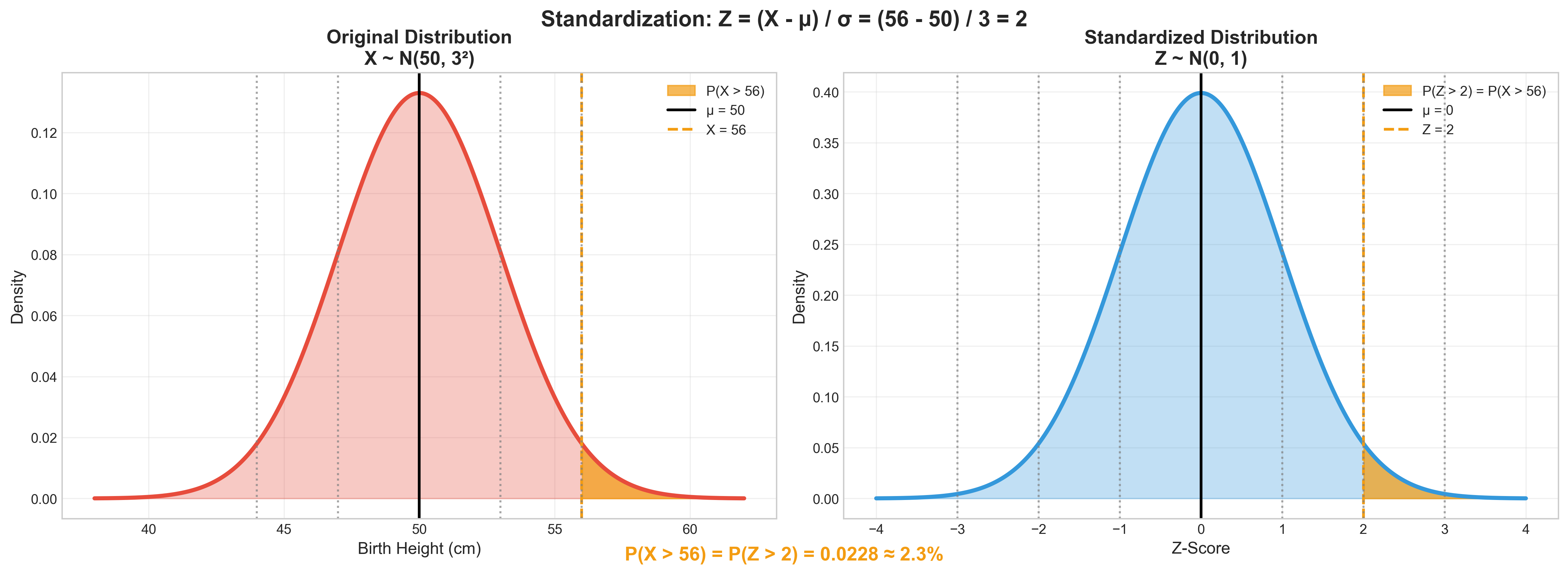
נתון: גובה בלידה $X \sim \mathcal{N}(50, 3^2)$
שאלה: מה ההסתברות שגובה הלידה יהיה גבוה מ-56 ס”מ?
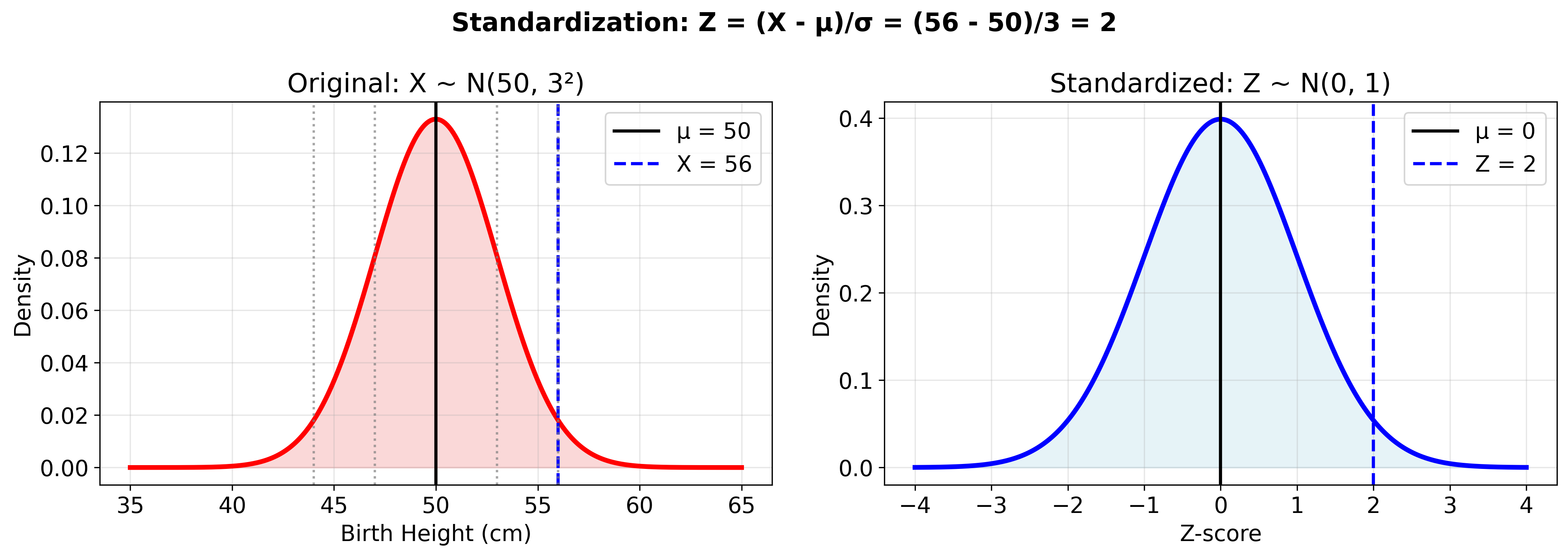
שלב 0: פורמליזציה
\[P(X > 56) = ?\]שלב 1: תקנון
\[P(X > 56) = P\left(\frac{X - 50}{3} > \frac{56 - 50}{3}\right) = P(Z > 2)\]הפרשנות
השאלה המקורית שקולה ל: מה הסיכוי להיות שתי סטיות תקן מעל התוחלת?
שלב 2: חישוב
באמצעות פייתון:
from scipy.stats import norm
sf_value = norm.sf(2)
print("P(Z > 2) =", sf_value)
לחלופין, אפשר להיעזר בפונקציית ההתפלגות המצטברת (CDF):
from scipy.stats import norm
p = 1 - norm.cdf(2)
print(p) # 0.02275013194817921
התוצאה: 0.023 (כ-2.3%)
אם היו שואלים מה הגובה שרק 2.3% מהתינוקות יהיו גבוהים ממנו, היינו משתמשים ב-iSF (ההופכית של פונקציית ההישרדות):
from scipy.stats import norm p = norm.isf(0.02275013194817921) # P(Z > p) = 0.02275013194817921 print(p) # 2.0000000000000004
חישוב הסתברויות - בניית אינטואיציה
דוגמה 1: P(X > 50)
הסיכוי להיות גבוה מ-50 כאשר התוחלת היא 50 וסטיית התקן 3.
ציון תקן: $\frac{50 - 50}{3} = 0$
\[P(X > 50) = P(Z > 0) = 0.5\]דוגמה 2: P(X > 53)
הסיכוי להיות גבוה מ-53 כאשר התוחלת היא 50 וסטיית התקן 3.
זה בעצם כמו לשאול מה הסיכוי להיות מעל סטיית תקן אחת מהתוחלת.
ציון תקן: $\frac{53 - 50}{3} = 1$
\[P(X > 53) = P(Z > 1) < 0.5\]דוגמה 3: P(X > 51.5)
ציון תקן: $\frac{51.5 - 50}{3} = 0.5$
\[P(X > 51.5) = P(Z > 0.5) < 0.5\]דוגמה 4: P(X > 59)
ציון תקן: $\frac{59 - 50}{3} = 3$
$P(X > 59) = P(Z > 3)$ - הסתברות קטנה מאוד
דוגמה 5: P(X > 47)
ציון תקן: $\frac{47 - 50}{3} = -1$
\[P(X > 47) = P(Z > -1) > 0.5\]תכונות של פונקציית ההישרדות
ככל ש-$c$ גדל, $P(X > c)$ קטן.
חישוב הסתברויות במשתנה מתוקנן
כלל 1: המשלים
\[P(Z < z_0) = 1 - P(Z > z_0)\]כלל 2: סימטריה
\[P(Z > -z_0) = P(Z < z_0)\]כלל 3: הסתברות בטווח
\[P(z_1 < Z < z_2) = P(Z > z_1) - P(Z > z_2)\]תכונות נוספות חשובות
- $P(Z > 0) = \frac{1}{2}$
- $P(Z = c) = 0$ לכל $c$
דוגמה: ציוני פסיכומטרי
ציונים מתפלגים $X \sim \mathcal{N}(550, 100^2)$
מה ההסתברות לקבל מעל 650?
ציון תקן: $z=\frac{650 - 550}{100} = 1$
\[P(X > 650) = P(Z > 1) \approx 0.16 \implies 16\%\]החישוב מתקבל מפייתון:
from scipy.stats import norm
p = norm.sf(1) # P(Z > 1)
print("P(X > 650) =", p) # 0.15865525393145707
סיכום
הנקודות החשובות:
- תמיד להתחיל בתקנון במשתנה נורמלי
- תקנון = מדידת מרחק מהתוחלת ביחידות של סטיית תקן
- Z-Score מאפשר השוואה בין משתנים שונים
- פונקציית ההישרדות לחישוב הסתברויות
- סימטריה של ההתפלגות הנורמלית מפשטת חישובים