פתרון שאלה 3 משיעורי הבית
שתי מסות זהות:
\[m_1 = m_2 = 99_{grams} = 0.099_{kg}\]קשורות בחוט הכרוך על גלגלת שצירה מקובע בגובה רב מעל הרצפה.
בתחילה המסות נמצאות במנוחה בגובה זהה מעל הרצפה.
זבוב שמסתו \(m = 2_{grams} = 0.002_{kg}\) נוחת בעדינות על מסה \(m_1\) (נניח, זו הימנית).
לאחר שתי שניות מתעופף לו הזבוב, ולאחר שתי שניות נוספות הוא נוחת בעדינות על מסה $m_2$ השמאלית.
הנחות: מסת החוט, מסת הגלגלת, והחיכוך ביניהם ניתנים להזנחה.
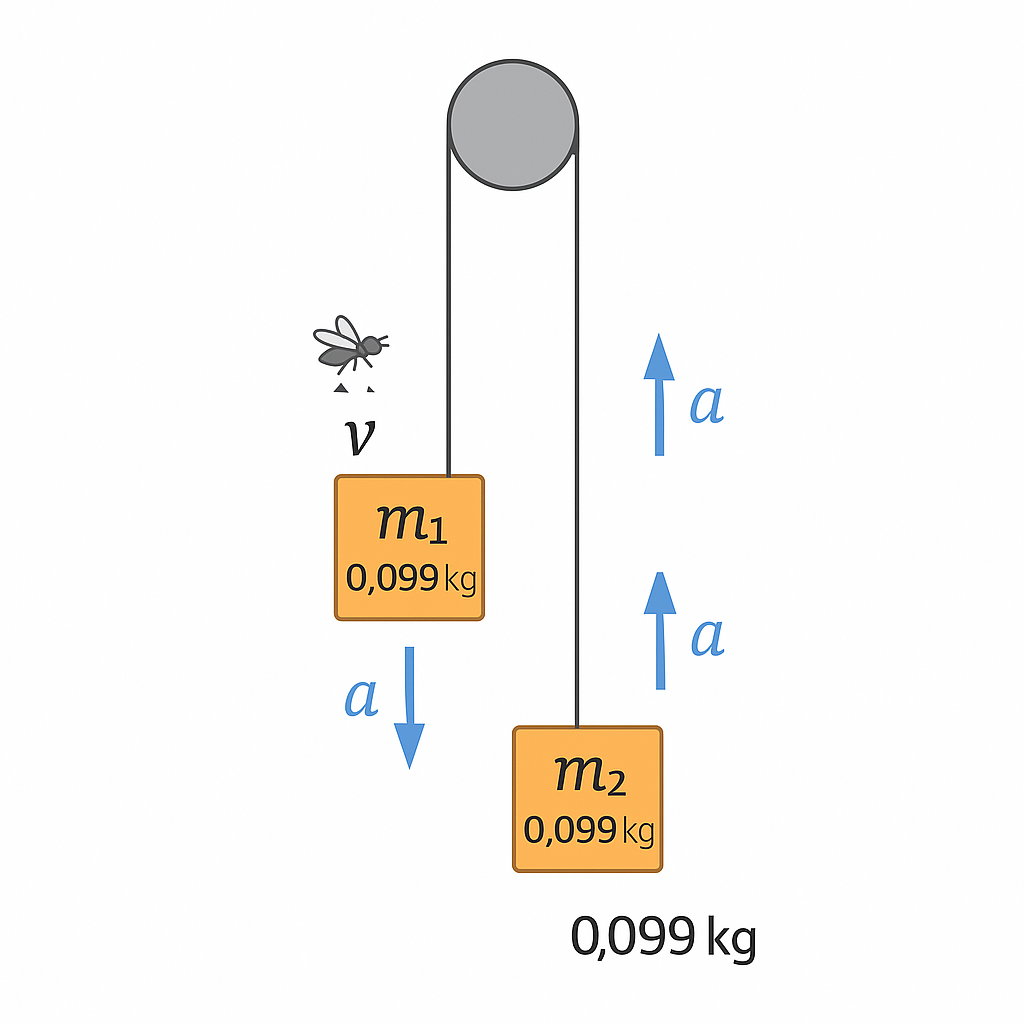
דיאגרמה בזמן נחיתת הזבוב
ציירו את המערכת בזמן $t = 0$, זמן נחיתת הזבוב על $m_1$, הוסיפו על הציור סקיצה של וקטורי המהירות והתאוצה של שתי המסות (אין צורך בחישוב).
תיאור תנועת $m_2$
תארו מילולית את תנועת המסה $m_2$ (תנועה קצובה, תאוצה קבועה, תאוצה משתנה, כיווני תנועה ותאוצה) בכל אחד משלושת פרקי הזמן:
- א) $0 \leq t < 2s$
- ב) $2s \leq t < 4s$
- ג) $t \geq 4s$
חישוב התאוצה
חשבו את התאוצה של $m_2$ בכל אחד מפרקי הזמן:
- א) $0 \leq t < 2s$
- ב) $2s \leq t < 4s$
- ג) $t \geq 4s$
כתבו את המהירות כפונקציה של הזמן של המסה $m_2$ עבור עשר השניות הראשונות של התנועה. השתמשו באותו פרמטר זמן $t$ לכל שלבי התנועה.
גרף מהירות
ציירו גרף כמותי של מהירות $m_2$ עבור עשר השניות הראשונות של התנועה.
קבלו את ההעתק הכולל של המסה $m_2$ בעשר השניות הראשונות לתנועה מבלי להיעזר במשוואות מקום-זמן.
1. דיאגרמה בזמן נחיתת הזבוב
| לפני הזבוב | הזבוב מגיע |
2. תיאור תנועת $m_2$
(א) $0 \leq t < 2s$
$m_2$ מאיצה מעלה בתאוצה קבועה ממהירות התחלתית 0.
(ב) $2s \leq t < 4s$
המערכת נמצאת בהתמדה, כלומר שקול הכוחות הפועלים עליה שווה לאפס. $m_2$ מתמידה במהירותה כלפי מעלה (החוק הראשון של ניוטון).
(ג) $t \geq 4s$
התאוצה מחליפה כיוון $-a$, כלומר שהיא בכיוון מנוגד למהירות. מצב כזה (תאוצה בכיוון מנוגד למהירות) נקרא תאוטה. בשלב מסוים יתהפך כיוון המהירות.
3. חישוב התאוצה של $m_2$
(א) $0 \leq t < 2s$
ניעזר בכל השני של ניוטון ($F = ma$). תחילה נרשום את המשוואות שפועלים על כל אחת מהמסות.
על המסה הימנית (שהזבוב נוחת עליה) - היא נעה כלפי מטה:
\[(M+m)g - T = (M+m)a \tag{1}\]על המסה השמאלית (שלא נוחת עליה הזבוב) - היא נעה כלפי מעלה:
\[T - Mg = Ma \tag{2}\]שימו לב שהכוח $T$ הוא מתיחה בחוט, והוא פועל על המסה השמאלית כלפי מעלה, ועל המסה הימנית כלפי מטה, בדומה לכוח המשיכה. מכאן ההבדל בסימנים.
נחבר את משוואות $(1)$ ו$(2)$:
\[\begin{aligned} (M+m)g - T + T - Mg &= (M+m)a + Ma \\ \cancel{Mg} + mg - \cancel{Mg} &= 2Ma + ma \\ mg &= (2M + m)a \\ a &= \frac{mg}{2M + m} \end{aligned}\]סכך הכך:
\[a = \frac{mg}{2M + m} \tag{3}\]נציב את הערכים הנתונים במשוואת התאוצה $(3)$:
\[a = \frac{0.002 \cdot 10}{0.2} = \frac{0.02}{0.2} = 0.1 \, \mathrm{m/s^2}\]סך הכל התאוצה בזמן $0 \leq t < 2s$ היא:
\[\boxed{a_{0 \leq t < 2s} = 0.1 \, \mathrm{m/s^2}}\](ב) $2s \leq t < 4s$
כאמור, בשלב הזה המערכת מתמידה. התאוצה של המסה $m_2$ היא אפס, כלומר:
\[\boxed{a_{2s \leq t < 4s} = 0 \, \mathrm{m/s^2}}\](ג) $t \geq 4s$
זה מצב סימטרי אבל עם כיוון הפוך:
\[\boxed{a_{t \geq 4s} = -0.1 \, \mathrm{m/s^2}}\]4. כתיבת המהירות כפונקציה של הזמן
אפשר להשתמש בנוסחה:
\[\boxed{v(t) = v_0 + at}\]במקרה שלנו, $v_0 = 0$ (מהירות התחלתית) ו-$a$ הוא התאוצה של המסה $m_2$ בכל אחד מהשלבים.
\[v(t) = \begin{cases} 0.1t & 0 \leq t < 2s \\ 0.2 & 2s \leq t < 4s \\ 0.2 - 0.1(t-4) & t \geq 4s \end{cases}\]אפשר גם לחשב את המהירות על ידי אינטגרציה של התאוצה $a$ לפי הזמן, כלומר:
לשלמות התמונה נכתוב את וקטור המקום כפונקציה של הזמן עבור כל אחד מהשלבים.
כאשר גוף נע בתאוצה קבועה:
\[x(t) = \cancel{x_0} + \cancel{v_0} t + \frac{1}{2}at^2 \tag{6}\]האיברים הראשונים מתבטלים מתנאי ההתחלה $x_0 = 0$ ו-$v_0 = 0$, כלומר:
\[\begin{cases} a &= 0.1 \\ v_0 &= 0 \\ \end{cases}\]נציב את הביטוי המלא של התאוצה $a$:
\[\begin{align} x(0 \leq t < 2s) &= \frac{mg}{2(2M+m) }t^2 \\ &= \frac{0.002 \cdot 10}{0.4} t^2 \\ &= \frac{0.02}{0.4} t^2 \\ &= 0.05 t^2 \tag{6} \end{align}\]ובקצרה:
\[\frac{1}{2}at^2 = \frac{1}{2} \cdot 0.1 \cdot t^2 = 0.05t^2\]הנוסחה $(6)$ נובעת מאינטגרציה של התאוצה $a$ לפי הזמן, כלומר, ולאחר מכן אינטגרציה של המהירות $v$ לפי הזמן. הצבה של תנאי ההתחלה מבטלת את האיברים הקבועים.
\[v(t) = \int a(t) dt = \int 0.1 dt = 0.1t + C\]כאשר $C$ הוא קבוע האינטגרציה, שמתקבל מתנאי ההתחלה $v(0) = 0$.
5. גרף מהירות
גרף ליניארי למקוטעין:
- עולה מ-0 ל-0.2 m/s בין $t=0$ ל-$t=2s$
- קבוע ב-0.2 m/s בין $t=2s$ ל-$t=4s$
- יורד מ-0.2 ל-(-0.4) m/s בין $t=4s$ ל-$t=10s$

6. קבלת ההעתק הכולל של המסה $m_2$
ההעתק הוא השטח מתחת לגרף מהירות-זמן:
- משולש: $\frac{1}{2} \times 2 \times 0.2 = 0.2$ m
- מלבן: $2 \times 0.2 = 0.4$ m
- טרפז: $\frac{1}{2} \times 6 \times (0.2 - 0.4) = -0.6$ m
סה”כ: $0.2 + 0.4 - 0.6 = 0 \, \mathrm{m}$
המערכת חוזרת למצבה ההתחלתי!
גליל מסתובב עם מסה (גולה) נופלת
הערה מקדימה: השאלה הצוגה במקור בשיעור התגבור עבורו מוקדש העמוד, אבל בהמשך הופיעה בבחינת הגמר של מועד א׳ 2025.
נוסח השאלה, כמו גם הפתרונות, היו שונים. להלן הגרסה האחרונה של השאלה כפי שהופיעה במבחן. ההבדל המהותי היה שבשיעור התגבור המרצה התייחס לתאוצה הכבידה, וקבע את מערכת הצירים באופן שונה.
גליל מסתובב עם כוח צנטריפוגלי בלבד
ניסוח הבעיה
גליל אופקי באורך $L$ מסתובב נגד כיוון השעון במהירות זוויתית קבועה $\omega$. מסה $m$ מתחילה במרכז הגליל (במיקום $r = L/2$) ממצב מנוחה, ונעה תחת השפעת הכוח הצנטריפוגלי בלבד.
נתונים:
תנאי התחלה:
- $r(t=0) = \frac{L}{2}$ (מיקום התחלתי במרכז הגליל)
- $\dot{r}(t=0) = 0$ (מהירות רדיאלי התחלתי אפס - ממנוחה)
הפרמטרים של המערכת:
- $\omega$ = מהירות זוויתית קבועה של הגליל
- $L$ = אורך הגליל
- $m$ = מסת הגוף
מטרה: למצוא את התנועה $r(t)$ של המסה והזמן ($t$) שבו היא מגיעה לקצה הגליל ($r = L$).
שלב 1: יישום חוק ניוטון השני במערכת ייחוס מסתובבת
במערכת ייחוס מסתובבת עם מהירות זוויתית קבועה $\omega$, הכוח הצנטריפוגלי פועל על מסה הנמצאת במרחק $r$ מהמרכז:
\[\mathbf{F}_{\text{centrifugal}} = m\omega^2 r\]הכוח מכוון החוצה ברכיב הרדיאלי $\hat{r}$.
שלב 2: משוואת התנועה
יישום החוק השני של ניוטון בכיוון הרדיאלי:
\[m\ddot{r} = m\omega^2 r\]המסה מצטמצמת:
\[\ddot{r} = \omega^2 r \tag{1}\]שלב 3: פתרון המשוואה הדיפרנציאלית
משוואה (1) היא משוואה דיפרנציאלית לינארית הומוגנית מסדר שני עם מקדמים קבועים.
המשוואה האופיינית:
\[\lambda^2 = \omega^2\]הפתרונות: $\lambda = \pm\omega$
הפתרון הכללי:
\[r(t) = A e^{\omega t} + B e^{-\omega t}\]או בצורה היפרבולית שקולה:
\[r(t) = C \cosh(\omega t) + D \sinh(\omega t) \tag{2}\]שלב 4: יישום תנאי התחלה
תנאי התחלה:
- $r(0) = \frac{L}{2}$
- $\dot{r}(0) = 0$
מהתנאי הראשון:
\[r(0) = C = \frac{L}{2}\]לכן:
\[r(t) = \frac{L}{2} \cosh(\omega t) + D \sinh(\omega t)\]מהתנאי השני:
\[\dot{r}(t) = \frac{L}{2} \omega \sinh(\omega t) + D \omega \cosh(\omega t)\] \[\dot{r}(0) = D \omega = 0\]לכן: $D = 0$
שלב 5: הפתרון הסופי
\[r(t) = \frac{L}{2} \cosh(\omega t) \tag{3}\] \[\dot{r}(t) = \frac{L \omega}{2} \sinh(\omega t) \tag{4}\] \[\ddot{r}(t) = \frac{L \omega^2}{2} \cosh(\omega t) \tag{5}\]שלב 6: חישוב זמן ההגעה לקצה הגליל
המסה מגיעה לקצה הגליל כאשר $r(t) = L$:
\[L = \frac{L}{2} \cosh(\omega t)\] \[2 = \cosh(\omega t)\] \[\omega t = \cosh^{-1}(2)\] \[\boxed{t = \frac{\cosh^{-1}(2)}{\omega}}\]הגרסה שהופיעה בתגבור
גליל מסתובב נגד כיוון השעון במהירות זוויתית קבועה. מסה $m$ מתחילה במרכז הגליל ונופלת תחת השפעת הכבידה.
נתונים
תנאי התחלה:
- $r(t=0) = 0$ (מיקום רדיאלי התחלתי)
- $v(t=0) = 0$ (מהירות התחלתית)
פרמטרי המערכת:
- $\theta(t) = \omega t$ (מיקום זוויתי של הגליל)
- $\omega$ = מהירות זוויתית קבועה של הגליל
- $m$ = מסת הגוף הנופל
מטרה: למצוא את התנועה $r(t)$ של המסה.
| מסה בגליל | מסה נופלת |
פתרון
שלב 1: יישום חוק ניוטון השני בקואורדינטות קוטביות
במערכת ייחוס מסתובבת, חוק ניוטון השני הוא:
\[m\vec{a} = \vec{F}\]התאוצה בקואורדינטות קוטביות:
\[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (r\ddot{\theta} + 2\dot{r}\dot{\theta})\hat{\theta} \tag{1}\]שלב 2: זיהוי הכוחות
כוח הכבידה במערכת קואורדינטות מסתובבת:
\[\vec{F} = mg\cos(\theta - 90°)\hat{r} - mg\sin(\theta - 90°)\hat{\theta}\]באמצעות זהויות טריגונומטריות:
- $\cos(\theta - 90°) = \sin(\theta)$
- $\sin(\theta - 90°) = -\cos(\theta)$
לכן:
\[\vec{F} = mg\sin(\theta)\hat{r} + mg\cos(\theta)\hat{\theta}\]שלב 3: הצבת ערכים ידועים
כיוון ש-$\theta(t) = \omega t$ כאשר $\omega$ קבועה:
- $\dot{\theta} = \omega$
- $\ddot{\theta} = 0$
שלב 4: משוואות לפי רכיבים
הצבה בחוק ניוטון השני ($F = ma$), כאשר $a=(1)$:
\[m[(\ddot{r} - r\omega^2)\hat{r} + (2\dot{r}\omega)\hat{\theta}] = mg\sin(\theta)\hat{r} + mg\cos(\theta)\hat{\theta}\]המסה מצטמצמת.
שלב 5: הפרדת רכיבים
רכיב רדיאלי ($\hat{r}$):
\[\begin{align} \ddot{r} - r\omega^2 &= g\sin(\theta) \\ \ddot{r} &= r\omega^2 + g\sin(\theta) \end{align}\]רכיב משיקי ($\hat{\theta}$):
\[\begin{align} 2\dot{r}\omega &= g\cos(\theta) \\ \dot{r} &= \frac{g\cos(\theta)}{2\omega} \end{align}\]שלב 6: משוואות דיפרנציאליות
הצבת $\theta = \omega t$:
\[\begin{cases} \ddot{r} = r\omega^2 + g\sin(\omega t) \\[0.5em] \dot{r} = \frac{g\cos(\omega t)}{2\omega} \end{cases}\]שתי המשוואות המצומדות האלה מתארות את התנועה של המסה הנופלת בגליל המסתובב.
הערות
- הפתרון של המשוואה הראשונה מהצורה ($\ddot{r} = r\omega^2$), הוא ב-$\cosh$ ו-$\sinh$.
- המשוואה השנייה נותנת קשר בין $\dot{r}$ לזמן
- ניתן לאמת עקביות על ידי גזירת המשוואה השנייה ובדיקה מול הראשונה
- הפתרון המלא דורש פתרון של משוואת הדיפרנציאל הלא-הומוגנית