פתיחה והיכרות
קורס הסטטיסטיקה מנוהל על ידי ד״ר יאיר דאון. בשל התחלה מאוחרת של הקורס, חלק מהחומר יושלם בהמשך.
פרטי התקשרות
- מרצה: ד״ר יאיר דאון
- אימייל: הדרך המועדפת ליצירת קשר - נבדק לפחות פעם ביום
- וואטסאפ: ניתן לשלוח הודעות במקרים דחופים במיוחד
המרצה מתמטיקאי בהכשרתו, וכיום חוקר אפידמיולוגיה ושיטות מתמטיות וחישוביות. בקורס יושם דגש חישובי שיהיה רלוונטי לעבודה העתידית של הסטודנטים.
מועדי השיעורים
- ימי רביעי: 14:15
- ימי חמישי: 8:15 (במקום 8:00)
חובות הקורס
בקורס יהיו:
- תרגילי בית: שלושה תרגילים שיוגשו דרך המודל
- עבודה חישובית: תתבצע בפייתון על נתונים אמיתיים - סטודנטים משנה שעברה ביצעו עבודות המקשרות את החומר התיאורטי לפרקטיקה רפואית אמיתית
שיתוף פעולה:
- מומלץ לעבוד בקבוצות על תרגילי הבית והעבודה החישובית
- חובה לציין עם מי בוצע שיתוף פעולה (כפי שנהוג גם בעולם המדעי)
- במבחן המסכם אסור לשתף פעולה
הגשות:
- החובה על הסטודנטים היא לוודא שהבודק יבין את הכוונה שלהם
- יש להקפיד על כתיבה ברורה, מסודרת וקריאה - רצוי מודפסת
- אם הבודק לא מבין את הכוונה, הוא רשאי להיות נדיב או שלא
מבחן מסכם: כנראה יהיה אמריקאי
תחרות מימים
בכל שבוע תתקיים תחרות מימים (memes) בנושא סטטיסטיקה:
- יש לשלוח מימים רלוונטיים לנושא שנלמד בשבוע הקודם
- יש לשלוח למייל עד יום שני
- בכותרת האימייל חובה לציין “תחרות מימים”
- ההשתתפות אינה חובה, אך מומלצת
קורלציה וסיבתיות
נושא חשוב מהשיעור הקודם הוא ההבדל בין קורלציה לסיבתיות. כפי שהודגם בדוגמה של השחף היושב על מוט ברזל:
- קורלציה: השחף נמצא על מוט הברזל
- סיבתיות שגויה: השחף כל כך כבד שהוא עיקם את מוט הברזל
- סיבתיות נכונה: בגלל שהמוט היה עקום מלכתחילה, השחף בחר לשבת דווקא באמצעו
קיים אתר המדגים קורלציות ספוריות או מקריות, כמו למשל הקשר בין צריכת שוקולד למספר הסרטים של ניקולס קייג׳, שאין סיבה הגיונית שיהיה ביניהם קשר סיבתי, אך בכל זאת במקרה יש קשר קורלטיבי.
חומרי עזר ללימוד עצמי
ניתן ללמוד באופן עצמי באמצעות:
- סרטונים ביוטיוב
- אוסמוזיס - הפקולטה משלמת על גישה לאתר זה, ויש בו סרטים על סטטיסטיקה ונושאים רפואיים נוספים
- ג׳וב - פלטפורמה נוספת שעשויה לסייע
- ספרים - רשימה מלאה נמצאת במצגת הקורס
חשיבות הסטטיסטיקה
סטטיסטיקה היא אחד המקצועות החשובים ביותר בלימודי הרפואה.
רופאים לעתיד יעבדו במגוון תחומים - חדרי ניתוח, מחלקות אף אוזן גרון, רפואת משפחה בקהילה או רפואת ילדים. בשלב מסוים עלול להתעורר שעמום כשמקרים רבים נראים דומים (למשל, ילדים עם שפעת או זיהומי אוזניים).
בנקודה זו, עשויה להתעורר סקרנות: “האם קיים קשר? האם יש כאן דפוס?” - והפתח לעולם החשיבה והמחקר הוא הסטטיסטיקה.
בעולם המדעי כיום, כמעט בלתי אפשרי לעסוק במדע ללא סטטיסטיקה. זוהי השפה של המדע והשכנוע המדעי. לא מספיק לטעון “נצפו מאתיים חולי לב ומתוכם מאה וחמישים נזקקו לצינתור, לכן כנראה שחולי לב צריכים צינתור” - נדרשת השפה המדעית, שהיא סטטיסטיקה.
מהי סטטיסטיקה?
סטטיסטיקה היא אוסף של כלים המאפשרים לקחת נתונים מספריים (דאטה) ולהסיק מסקנות. היא מסייעת:
- לנתח נתונים המוצגים בתקשורת (האם הם מוצגים בצורה נכונה?)
- להבין נתונים של ניסויים
- לבדוק השערות
- להבין איך הטבע מתנהג
שימושים בסטטיסטיקה
לרופאים, סטטיסטיקה רלוונטית מאוד. לסטטיסטיקה יש יישומים נרחבים בתחומים רבים:
- בריאות הציבור
- גנטיקה
- מחקר רפואי
- תחומים רבים נוספים
בעבודה המסכמת, הסטודנטים מעודדים לחפש שימושים סטטיסטיים בתחומים שמעניינים אותם אישית ולנתח נתונים בנושאים אלו.
מטרות הקורס
מסקנות מדעיות מתבססות תמיד על נתוני מדגם. רופאים אינם יכולים לדגום את כל חולי הלב בעולם או את כל הילדים שאי פעם נולדו - ניתן רק לבחון את המטופלים שמגיעים אליהם.
השאלה המרכזית היא: כיצד מסיקים מסקנות מתוך מדגם קטן על האוכלוסייה הגדולה? זוהי מהות הסטטיסטיקה.
הקורס יוביל בהדרגה להבנת תהליך ההסקה הסטטיסטית דרך ארבעה שלבים עיקריים:
- סטטיסטיקה תיאורית - כבר החל בווידאו ועם גיא
- הסתברות - תילמד במשך 2-3 שבועות: כיצד הנתונים מגיעים, מהי ההסתברות לקבל נתונים מסוימים, מהם מאורעות מותנים וסוגים של משתנים מקריים
- הסקה סטטיסטית - איך מסיקים מסקנות מתוך הנתונים
- כלים חישוביים - שיטות מתקדמות המתאימות למאה ה-21, שונות מהדרך שבה נלמדה סטטיסטיקה בעבר
לאורך הקורס, יוצגו דוגמאות רבות של פרדוקסים כדי להדגים מדוע הסתברות וסטטיסטיקה אינן אינטואיטיביות. המסקנות האינטואיטיביות מנתונים עלולות להיות שגויות ומפתיעות, ולכן חשוב לעצור, לחשוב, לחשב ולהיות מתודיים בגישה.
רגרסיה לינארית
בשיעור האחרון הוצג שלשני המשתנים $x$ ו-$y$ יש תפקיד סימטרי בחישוב קורלציה. אין עדיפות לאף אחד מהם כשמחשבים קורלציה - לא מחשבים קורלציה של גובה על פי BMI או להיפך. קורלציה היא תכונה המאפיינת את הזוג של המשתנים, ואין לאף אחד מהם תפקיד חשוב יותר.
משתנים תלויים ובלתי תלויים
במקרים רבים, $x$ הוא פרמטר שניתן לשלוט עליו, לדעת אותו, או לבצע עליו מניפולציה - למשל, כמות התרופה שניתנה לפציינט. לעומת זאת, $y$ הוא משתנה שאין שליטה עליו - למשל, משך הזמן שהפציינט יחיה.
במקרים כאלה יש הבדל משמעותי בתפקידים של שני המשתנים:
- אחד ניתן לשליטה (המשתנה הבלתי תלוי)
- השני לא ניתן לשליטה (המשתנה התלוי)
המטרה היא לחזות או לנבא את התוצאה (התגובה) של $y$ בהתאם ל-$x$. למשל, לדעת כמה שנים אדם יחיה על פי כמה מיליגרם של תרופה ניתנה לו באירוע תוך-ורידי.
דוגמאות נוספות:
- ציון פסיכומטרי (משתנה בלתי תלוי) וממוצע בתואר ראשון (משתנה תלוי)
- מספר שנות לימוד (משתנה בלתי תלוי) והכנסה (משתנה תלוי)
- מספר הסיגריות ליום בהריון (משתנה בלתי תלוי) ומשקל התינוק (משתנה תלוי)
חשוב לציין שהטכניקה המתמטית עצמה אינה מתייחסת לתפקידים בעולם האמיתי, אך הפרשנות צריכה להתחשב בהם. כמו שקורלציה איננה סיבתיות, גם קו רגרסיה איננו סיבתיות - אך תמיד קיים הדמיון של הכיוון הסיבתי.
ניתן לבצע:
- רגרסיה של $y$ על $x$ (הכיוון האינטואיטיבי וההגיוני ברוב המקרים)
- רגרסיה של $x$ על $y$ (פחות אינטואיטיבי ולעתים פחות הגיוני)
למשל, השאלה הרלוונטית היא בדרך כלל “אם בהריון ועישון של סיגריה נוספת, כיצד ישפיע הדבר על התינוק?” ולא “איך המשקל של התינוק ישפיע על כמות הסיגריות שנעשנו בהריון”.
מינוח מקובל
- משתנה בלתי תלוי ($x$): לא תלוי במשהו חיצוני, תלוי במניפולציה
- משתנה תלוי ($y$): תלוי במשתנה הבלתי תלוי
מונחים נוספים:
- בעולם הרפואה: חשיפה ($x$) ותגובה/תוצאה ($y$)
- בספרות באנגלית: Covariate או Exposure ($x$) ו-Outcome או Response ($y$)
איך מוצאים קו רגרסיה?
כדי לנבא את $y$ באמצעות $x$, יש לבצע את השלבים הבאים:
-
איסוף דאטה: איסוף מדגם של ערכי $x$ (למשל, מספר סיגריות או מיליגרם תרופה) וערכי $y$ הרלוונטיים להם (משקל תינוק בלידה או זמן שבו אדם חי)
-
יצירת משוואה: המטרה היא לייצר משוואה שתאפשר לחזות מה יקרה עבור ערכי $x$ שלא היו במדגם המקורי
למשל:
- אם במדגם היו נשים שעישנו 5 או 10 סיגריות ביום בהריון, מה יקרה אם אישה תעשן 8 סיגריות?
- אם הפציינטים במחלקה קיבלו 10, 20 או 30 מיליגרם תרופה, מה יקרה אם יינתנו 25 או 50 מיליגרם?
כמו כן, מודל טוב צריך להתמודד עם השונות הטבעית - למשל, אם שני פציינטים שקיבלו אותה כמות תרופה (20 מיליגרם) שרדו זמנים שונים (3 שנים ו-5 שנים), כמה זמן יחיה הפציינט הבא שיקבל אותה כמות? האם 4 שנים (ממוצע)? ומה אם פציינט אחר שרד 10 שנים?
רגרסיה לינארית פשוטה
רגרסיה באופן כללי היא חיזוי $y$ מתוך $x$ או מתוך כמה משתני $x$. במקרה של רגרסיה לינארית, ההנחה היא שהקשר בין המשתנים הוא לינארי.
כאשר הקשר לינארי, ניתן לתארו באמצעות קו ישר. למשל, בגרף של גובה האב מול גובה הבן, ניתן לראות שגובה הבן עולה בצורה יחסית מדורגת ככל שגובה האב עולה.
משמעות הקשר הלינארי:
- שינוי קבוע ב-$x$ גורם לשינוי קבוע ב-$y$
- מבחינה גרפית, לא משנה היכן על הקו נמצאים, העלייה מנקודה לנקודה במרחק קבוע של $x$ תגרום לעלייה קבועה של $y$
למשל, עלייה של אינץ’ בגובה האב שווה לעלייה של בערך חצי אינץ’ בגובה הבן בממוצע.
המשוואה המתמטית של קו ישר
משוואת קו ישר היא: $y = ax + b$, כאשר:
- $a$ הוא השיפוע - השינוי ב-$y$ כתוצאה משינוי של יחידה אחת ב-$x$
- $b$ הוא החותך - הערך של $y$ כאשר $x = 0$
דוגמה 1: משקל תינוקת
מיקה נולדה במשקל 3.5 ק”ג, ובשבועיים האחרונים משקלה עלה ב-280 גרם.
אם נתאר את משקלה של מיקה כפונקציה לינארית, נקבל:
\[\text{Weight} = a \cdot t + b\]כאשר:
- $t$ הוא הזמן בשבועות מאז הלידה
- $b$ הוא משקל הלידה = 3.5 ק”ג
- לאחר שבועיים ($t = 2$), משקלה עלה ב-280 גרם
מכאן ניתן לחשב את השיפוע $a$: בשני שבועות עלייה של 280 גרם ← בשבוע אחד עלייה של 140 גרם לכן, $a = 140$ גרם לשבוע
המשוואה הסופית:
\[\text{Weight} = 140t + 3.5\](כאשר המשקל בק”ג ו-$t$ בשבועות)
אם נמדוד את הזמן בימים במקום בשבועות:
- החותך $b$ נשאר 3.5 ק”ג
- $t = 14$ ימים (שבועיים)
- השיפוע $a$ יהיה 20 גרם ליום (280 גרם חלקי 14 ימים)
דוגמה 2: צריכת אלכוהול בהריון
נניח שנמצאה המשוואה הבאה:
\[y = -2x + 3000\]כאשר:
- $x$ הוא צריכת האלכוהול לשבוע במהלך ההריון במיליליטרים
- $y$ הוא משקל הלידה של התינוק בגרמים
המשמעות:
- שתייה של מיליליטר אלכוהול נוסף לשבוע מורידה 2 גרם ממשקל התינוק
- אם האישה לא שותה אלכוהול בהריון ($x = 0$), המשקל הממוצע של התינוק יהיה 3,000 גרם
חשוב להדגיש: רגרסיה לא קובעת מה בוודאות יקרה, אלא מהו הניחוש הטוב ביותר במובן מתמטי ספציפי.
דוגמה: אם אישה שתתה 100 מיליליטר אלכוהול לשבוע, מה יהיה משקל התינוק? נציב במשוואה:
\[y = -2 \cdot 100 + 3000 = 2800 \text{ grams}\]מציאת קו הרגרסיה הטוב ביותר
המשימה היא למצוא איזה קו ישר מתאר את הנתונים בצורה הטובה ביותר. הבעיה מנוסחת כך:
- קיימים נתונים בצורת זוגות $(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)$
- המטרה היא למצוא קו שייתן את יכולת הניבוי הטובה ביותר עבור המדגם
המטרה היא שהקו ייתן ניבוי טוב ככל האפשר לכל ערכי $y$ במדגם:
- $ax_1 + b$ יהיה קרוב ככל האפשר ל-$y_1$
- $ax_2 + b$ יהיה קרוב ככל האפשר ל-$y_2$
- וכך הלאה…
בדרך כלל לא ניתן לפגוע בדיוק בכל הנקודות, לכן נדרשת פשרה - קו שבו-זמנית יהיה הניבוי הטוב ביותר לכל ערכי $y$ יחד.
שגיאות וניבוי ברגרסיה
כאשר משתמשים במודל רגרסיה לניבוי, חשוב להבין את מושג השגיאה (השארית):
הגדרות בסיסיות
- הערך המנובא $\hat{y}_i$ (y-hat): הערך שהמודל מנבא עבור $x_i$, להבדיל מהערך האמיתי $y_i$
- השארית (error) $e_i$: ההפרש בין הערך האמיתי לערך המנובא: $e_i = y_i - \hat{y}_i$
ניבוי טוב מתאפיין בערכים קטנים של השאריות.
דוגמה לחישוב שאריות
אם יש נתונים:
| $x$ | $y$ |
|---|---|
| 1 | 2.5 |
| 2 | 4 |
| 3 | 4 |
| 4 | 7 |
וקו רגרסיה מסוים:
\[y = 1.2x + 1.5\]נחשב את הערכים המנובאים $\hat{y}$ ואת השאריות $e$:
| $i$ | $x_i$ | $y_i$ | $\hat{y}_i$ | $e_i = y_i - \hat{y}_i$ |
|---|---|---|---|---|
| 1 | 1 | 2.5 | 2.7 | -0.2 |
| 2 | 2 | 4 | 3.9 | 0.1 |
| 3 | 3 | 4 | 5.1 | -1.1 |
| 4 | 4 | 7 | 6.3 | 0.7 |
שיטת הריבועים הפחותים (Least Squares)
המטרה היא למצוא קו שנותן שגיאה כללית מינימלית. הרעיון הראשוני והנאיבי היה לחשב את סכום כל השגיאות ($E=\sum_{i=1}^n e_i$) ולמצוא קו רגרסיה שנותן סכום מינימלי. אולם, גישה זו לא יעילה מכיוון ש:
- סכום השגיאות יכול להיות אפס גם עבור קווים שאינם מתאימים היטב לנתונים
-
שגיאות חיוביות ושליליות עלולות לבטל זו את זו
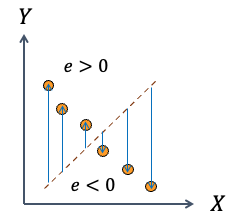
למשל, אם יש נתונים מושלמים שנמצאים על קו ישר:
- קו שעובר בדיוק דרך הנתונים ייתן סכום שגיאות אפס (כי כל השגיאות הן אפס)
- אבל גם קו אחר שחוצה את הנתונים (עם שגיאות חיוביות ושליליות) יכול לתת סכום שגיאות אפס
הפתרון: ריבועים פחותים (Least Squares)
הפתרון הוא להגדיר את השגיאה הכוללת כסכום ריבועי השגיאות (ריבועים פחותים):
\[E = \sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i - (ax_i + b))^2\]יתרונות שיטת הריבועים הפחותים:
- שגיאות שליליות וחיוביות לא מבטלות זו את זו (כי הריבוע תמיד חיובי)
- שגיאות גדולות מקבלות משקל גדול יותר (מה שגורם למודל להיות רגיש ל-
outliers) - שיטה זו מניחה שגיאות גאוסיאניות, שהן השגיאות הנפוצות ביותר בטבע
- קל לחשב אנליטית את המינימום של פונקציה זו
מציאת הפרמטרים האופטימליים
כדי למצוא את הערכים של $a$ ו-$b$ שממזערים את סכום ריבועי השגיאות, גוזרים את הפונקציה לפי $a$ ו-$b$ ומשווים לאפס:
הפתרון עבור $a$ ו-$b$ מתקבל בנוסחאות:
\[a = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}\] \[b = \bar{y} - a \cdot \bar{x}\]כאשר $\bar{x}$ ו-$\bar{y}$ הם הממוצעים של $x$ ו-$y$ בהתאמה.
דוגמה מספרית
בדוגמה המספרית שהוצגה בשיעור, התקבלו $a = 1.35$ ו-$b = 1$, אלו הם הערכים שממזערים את סכום ריבועי השגיאות. הנתונים ההתחלתיים:
| $i$ | $x_i$ | $y_i$ |
|---|---|---|
| 1 | 1 | 2.5 |
| 2 | 2 | 4 |
| 3 | 3 | 4 |
| 4 | 4 | 7 |
נחשב את $\bar{x}$ ו-$\bar{y}$:
\[\bar{x} = \frac{1 + 2 + 3 + 4}{4} = 2.5\] \[\bar{y} = \frac{2.5 + 4 + 4 + 7}{4} = 4.375\]כעת נחשב את השגיאות:
| $i$ | $x_i$ | $y_i$ | $x-\bar{x}$ | $y_i - \bar{y}$ | $(x_i - \bar{x})(y_i - \bar{y})$ | $(x_i - \bar{x})^2$ |
|---|---|---|---|---|---|---|
| 1 | 1 | 2.5 | -1.5 | -1.875 | 2.8125 | 2.25 |
| 2 | 2 | 4 | -0.5 | -0.375 | 0.1875 | 0.25 |
| 3 | 3 | 4 | 0.5 | -0.375 | -0.1875 | 0.25 |
| 4 | 4 | 7 | 1.5 | 2.625 | 3.9375 | 2.25 |
כדי לקבל את השיפוע $a$, נחשב את הסכומים:
\[\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y}) = 2.8125 + 0.1875 - 0.1875 + 3.9375 = 6.75\] \[\sum_{i=1}^{n} (x_i - \bar{x})^2 = 2.25 + 0.25 + 0.25 + 2.25 = 5\]כעת נציב בנוסחה:
\[a = \frac{6.75}{5} = 1.35\]כדי לחשב את החותך $b$, נציב בנוסחה:
\[b = \bar{y} - a \cdot \bar{x} = 4.375 - 1.35 \cdot 2.5 = 1\]המשוואה הסופית היא:
\[y = 1.35x + 1\]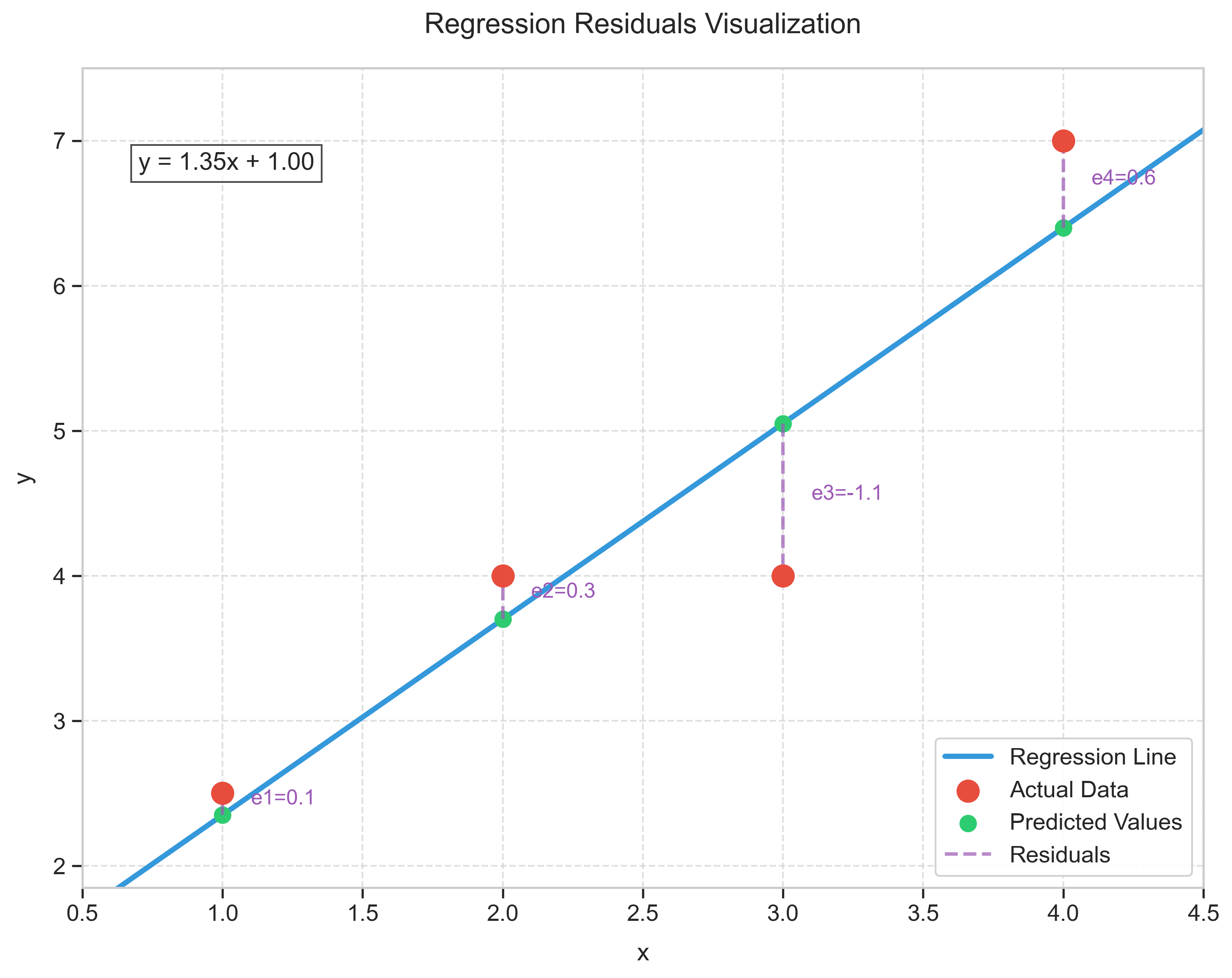
נבדוק את השגיאות:
| $i$ | $x_i$ | $\hat{y}_i$ | $y_i$ | $e_i = y_i - \hat{y}_i$ | $e_i^2$ |
|---|---|---|---|---|---|
| 1 | 1 | 2.35 | 2.5 | 0.15 | 0.0225 |
| 2 | 2 | 3.7 | 4 | 0.3 | 0.09 |
| 3 | 3 | 5.05 | 4 | -1.05 | 1.1025 |
| 4 | 4 | 6.4 | 7 | 0.6 | 0.36 |
| Total | 0 | 1.575 |
תכונות הרגרסיה הלינארית
הקשר בין שיפוע הרגרסיה ($a$) למקדם המתאם ($r$)
ניתן להראות שהשיפוע $a$ קשור למקדם המתאם $r$ באופן הבא:
\[a = r \cdot \frac{\sigma_y}{\sigma_x}\]כאשר:
- $r$ הוא מקדם המתאם בין $x$ ו-$y$
- $\sigma_y$ היא סטיית התקן של $y$
- $\sigma_x$ היא סטיית התקן של $x$
מכאן ניתן לראות ש:
- ל-$a$ ול-$r$ יש תמיד אותו סימן (חיובי או שלילי)
- ל-$a$ יש יחידות של $\frac{y}{x}$ בניגוד ל-$r$ שהוא חסר יחידות
- אם סטיות התקן של $x$ ו-$y$ זהות, אז $a = r$
רגרסיה של $x$ על $y$
אם מבצעים רגרסיה של $x$ על $y$ (כלומר, מנבאים את $x$ באמצעות $y$) במקום רגרסיה של $y$ על $x$, נקבל שיפוע שונה:
אם בביצוע רגרסיה של $y$ על $x$ התקבל $a = 10$, אז בביצוע רגרסיה של $x$ על $y$ יתקבל $a = \frac{1}{10} = 0.1$
זאת מכיוון שמקדם המתאם נשאר זהה, אך היחס בין סטיות התקן מתהפך:
\[a_{x \text{ on } y} = r \cdot \frac{\sigma_x}{\sigma_y} = r \cdot \frac{1}{\frac{\sigma_y}{\sigma_x}} = \frac{r \cdot \frac{\sigma_y}{\sigma_x}}{\frac{\sigma_y^2}{\sigma_x^2}} = \frac{a_{y \text{ on } x}}{\frac{\sigma_y^2}{\sigma_x^2}}\]מגבלות הרגרסיה הלינארית
תחום תקפות המודל
חשוב להבין שמודל הרגרסיה תקף בעיקר בטווח הנתונים שממנו נוצר. ככל שמתרחקים מהטווח הזה, אמינות המודל יורדת.
דוגמה: בנתונים של גלטון על גובה אבות ובנים, התקבלה משוואת הרגרסיה:
\[y = 0.5x + 34\]אם נציב $x = 0$ (כלומר, אב ללא גובה - דבר שאינו אפשרי במציאות), נקבל שגובה הבן הוא 34 אינץ’. תוצאה זו אינה הגיונית ומצביעה על כך שהמודל אינו תקף מחוץ לטווח הנתונים המקורי.
ביטחון במודל
ככל שנמצאים קרוב יותר לטווח הנתונים שמהם נבנה המודל, כך ניתן להיות בטוחים יותר בניבויים שלו. ככל שמתרחקים מטווח זה, הביטחון במודל יורד.
יישום רגרסיה לינארית בפייתון
ניתן ליישם רגרסיה לינארית בפייתון באמצעות חבילות כגון numpy, statsmodels או scikit-learn.
דוגמה לשימוש ב-statsmodels:
await micropip.install("statsmodels")
import numpy as np
import statsmodels.api as sm
# example data
x = np.array([1, 2, 3, 4])
y = np.array([2.5, 4, 4, 7])
# fitting the model
model = sm.OLS(y, x).fit()
print(model.summary())
ניתן לנסות להריץ את הקוד הזה ישירות באתר, בעזרת עורך הפייתון שלנו.
התוצאות מספקות מידע רב, כגון:
- מקדמי הרגרסיה (Coefficients)
- מדדי איכות ההתאמה (R-squared)
- ערכי P-value
- רווחי סמך (Confidence Intervals)
OLS Regression Results
=======================================================================================
Dep. Variable: y R-squared (uncentered): 0.974
Model: OLS Adj. R-squared (uncentered): 0.966
Method: Least Squares F-statistic: 113.8
Date: Fri, 16 May 2025 Prob (F-statistic): 0.00176
Time: 15:36:08 Log-Likelihood: -4.5176
No. Observations: 4 AIC: 11.04
Df Residuals: 3 BIC: 10.42
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 1.6833 0.158 10.666 0.002 1.181 2.186
==============================================================================
Omnibus: nan Durbin-Watson: 2.052
Prob(Omnibus): nan Jarque-Bera (JB): 0.685
Skew: -0.916 Prob(JB): 0.710
Kurtosis: 2.130 Cond. No. 1.00
==============================================================================
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
הערה חשובה
בדוגמה שהוצגה בשיעור, החסר בפלט הוא ערך החותך ($b$). בתרגילי הבית יילמד כיצד לקבל גם את השיפוע וגם את החותך באמצעות התאמת המודל.
ניתן לעבוד עם רגרסיה בפייתון ללא צורך לחשב את הפרמטרים באופן ידני, ובהמשך הקורס יילמד פירוש התוצאות המתקדמות יותר של המודל.
הערה: ניתן להתאים את המודל יחסית בקלות בעזרת יצירת מערך חדש עבור המשתנה הבלתי תלוי, למשל X עבור x, דרך הפונקציה sm.add_constant:
X = sm.add_constant(x)
לאחר מכן ניתן להתאים את המודל בעזרת $\text{sm.OLS(y, X).fit()}$, במקום $\text{sm.OLS(y, x).fit()}$. הפלט שמתקבל מהרצת הקוד המעודכן:
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.853
Model: OLS Adj. R-squared: 0.779
Method: Least Squares F-statistic: 11.57
Date: Fri, 16 May 2025 Prob (F-statistic): 0.0766
Time: 15:40:49 Log-Likelihood: -3.8117
No. Observations: 4 AIC: 11.62
Df Residuals: 2 BIC: 10.40
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.0000 1.087 0.920 0.455 -3.676 5.676
x1 1.3500 0.397 3.402 0.077 -0.358 3.058
==============================================================================
Omnibus: nan Durbin-Watson: 2.900
Prob(Omnibus): nan Jarque-Bera (JB): 0.678
Skew: -0.922 Prob(JB): 0.712
Kurtosis: 2.183 Cond. No. 7.47
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
החותך במקרה הזה הוא $b=1$, כמו שחושב קודם.
מדידת טיב ההתאמה (R-squared)
כיצד ניתן לקבוע איזה קו רגרסיה מתאר את הנתונים בצורה טובה יותר? באופן אינטואיטיבי, ניתן להסתכל על הגרף ולהעריך “בעין”, אך נדרש מדד כמותי שיאפשר להשוות בין מודלים שונים באופן אובייקטיבי.
מגבלות של סכום ריבועי השאריות
סכום ריבועי השאריות יכול לשמש כמדד לטיב ההתאמה, שכן ככל שהוא קטן יותר, כך ההתאמה טובה יותר. אולם, ישנן מספר מגבלות לשימוש בסכום ריבועי השאריות בלבד:
-
בעיית יחידות מידה שונות: כיצד להשוות בין התאמה של גיל כרונולוגי להתאמה של גובה? אלו עולמות שונים עם יחידות מידה שונות.
-
השפעת מספר התצפיות: אם למודל אחד יש 1000 תצפיות ולשני יש 20 תצפיות, האם סכום שאריות קטן יותר במודל השני בהכרח אומר שההתאמה טובה יותר? לא בהכרח.
פתרון ראשוני לבעיית מספר התצפיות הוא להסתכל על ממוצע ריבועי השאריות במקום על הסכום. זה כבר מתקנן לפי מספר התצפיות ומהווה התחלה טובה יותר.
חשיבות סקאלת הנתונים
גם כאשר בוחנים את שונות השאריות (שהיא דומה לממוצע ריבועי השאריות), עדיין נותרת בעיה מרכזית: הסקאלה של הנתונים.
לדוגמה, אם יש שני מודלים עם שונות שאריות דומה (נניח 1):
- במודל הראשון, השונות של $y$ היא כ-1 (סקאלה קטנה)
- במודל השני, השונות של $y$ היא כ-1,000,000 (סקאלה גדולה)
איזה מודל מציג התאמה טובה יותר?
במודל הראשון, השגיאה היא בסדר גודל דומה לסקאלת הנתונים (1 מתוך 1, כלומר 100%). במודל השני, השגיאה היא זניחה ביחס לסקאלת הנתונים (1 מתוך מיליון, כלומר 0.0001%).
ברור שהמודל השני מציג התאמה טובה יותר, למרות ששונות השאריות זהה בשני המקרים!
הגדרת $R^2$ (מקדם המתאם בריבוע)
כדי להתמודד עם בעיות אלה, מוגדר טיב ההתאמה כיחס בין שונות השאריות לשונות המקורית של $y$:
\[R^2 = 1 - \frac{\text{remaining variance}}{\text{original variance of } y}\]או באופן אקוויוולנטי:
\[R^2 = \frac{\text{explained variance}}{\text{original variance of } y}\]כאשר:
- שונות מוסברת היא החלק מהשונות המקורית שהמודל מצליח להסביר
- שונות השאריות היא החלק שנותר בלתי מוסבר
פירוש $R^2$
- $R^2$ קרוב ל-1: מודל מסביר את רוב השונות בנתונים, התאמה טובה
- $R^2$ קרוב ל-0: מודל מסביר מעט מאוד מהשונות בנתונים, התאמה חלשה
דוגמאות
- מודל עם התאמה חלשה:
- שונות השאריות: 1
- שונות של $y$: 1
- $R^2 = 1 - \frac{1}{1} = 0$
- המודל אינו מסביר כלל את השונות בנתונים
- מודל עם התאמה מצוינת:
- שונות השאריות: 1
- שונות של $y$: 1,000,000
- $R^2 = 1 - \frac{1}{1,000,000} = 0.999999$
- המודל מסביר כמעט את כל השונות בנתונים
הקשר בין $R^2$ למקדם המתאם $r$
כאשר מדובר ברגרסיה לינארית פשוטה (עם משתנה מסביר אחד), מתקיים קשר ישיר בין $R^2$ למקדם המתאם $r$:
\[R^2 = r^2\]חשוב לזכור:
- $r$ יכול להיות חיובי או שלילי (תלוי בכיוון הקשר)
- $R^2$ תמיד חיובי ונע בין 0 ל-1
- $R^2$ מתייחס לשונות המוסברת, בעוד $r$ מתייחס לחוזק ולכיוון הקשר הלינארי
מציאת $R^2$ בפייתון
ניתן למצוא את ערך $R^2$ בקלות באמצעות חבילת statsmodels:
import statsmodels.api as sm
# creating linear regression model
model = sm.OLS(y, x)
results = model.fit()
# printing the results including R-squared
print(results.summary())
בפלט התוצאות, statsmodels מציג את ערך ה-$R^2$ באופן אוטומטי. בדוגמה שהוצגה בהרצאה, התקבל ערך $R^2 = 0.931$, המעיד על התאמה טובה מאוד של המודל לנתונים.
סיכום
- טיב ההתאמה של מודל רגרסיה נמדד באמצעות $R^2$, שמשקף את היחס בין השונות המוסברת לשונות הכוללת
- $R^2$ מאפשר השוואה בין מודלים שונים, גם כאשר הנתונים הם בסקאלות שונות
- ככל ש-$R^2$ גבוה יותר, כך המודל מספק התאמה טובה יותר לנתונים
- ברגרסיה לינארית פשוטה, $R^2$ שווה לריבוע מקדם המתאם ($r^2$)
- בפייתון, ניתן לקבל את ערך $R^2$ באמצעות חבילת
statsmodels