חזרה מהשיעור הקודם
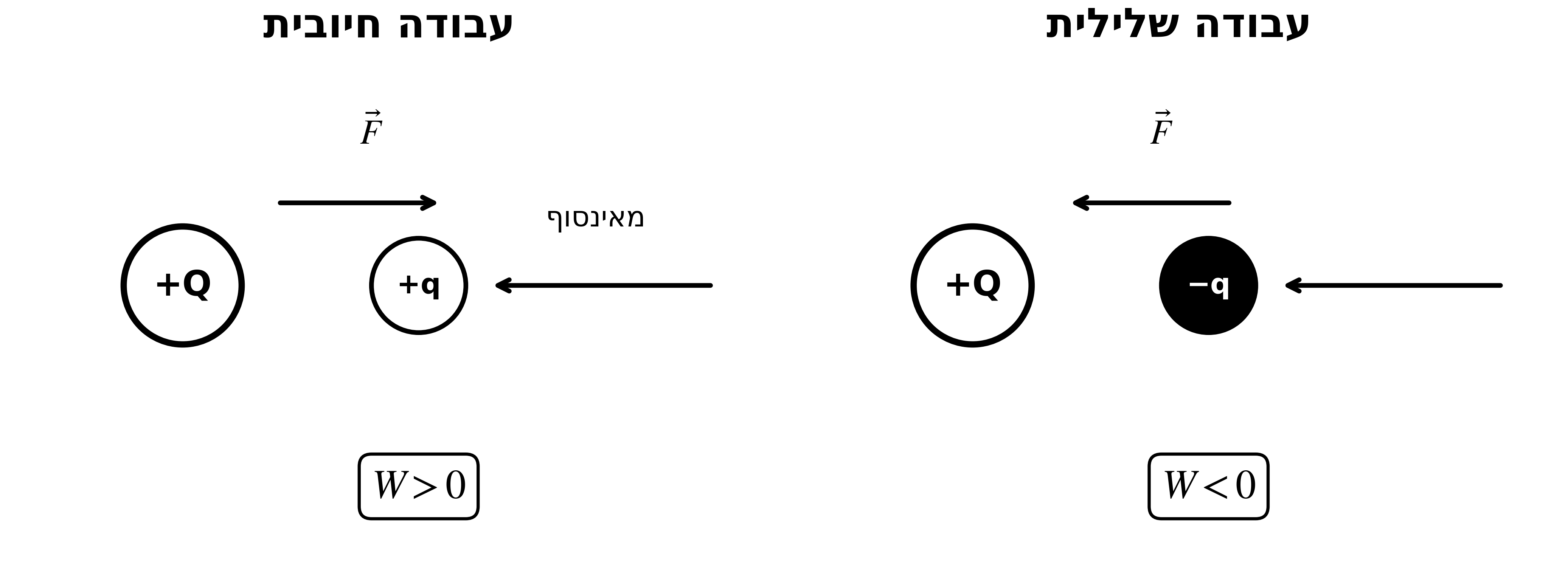
בשיעור שעבר חישבנו את העבודה שנדרשת להביא חלקיק מהאינסוף. קיבלנו:
\[W = q \cdot V(\vec{r})\]כלל חשוב:
- עבודה חיובית - כאשר המטענים הם שווי סימן (דחייה)
- עבודה שלילית - כאשר המטענים הם הפוכי סימן (משיכה)
מושג הפוטנציאל החשמלי
כוח משמר ופונקציית פוטנציאל
במכניקה דיברנו על כוח משמר. לפי הגדרה, כוח משמר הוא כוח שניתן לרשום אותו כגרדיאנט של פונקציית פוטנציאל:
\[\vec{F} = -\nabla U(\vec{r})\]העבודה של כוח משמר:
\[W = \int_{r_i}^{r_f} \vec{F} \cdot d\vec{r} = U(r_i) - U(r_f)\]חישוב העבודה של מטען $Q$ על מטען $q$
\[W = -kQq \left( \frac{1}{r} - \frac{1}{\infty} \right)\]העבודה החיצונית (נגד הכוח):
\[W_{\text{outer}} = k \frac{Qq}{r}\]הגדרת הפוטנציאל החשמלי
הפוטנציאל החשמלי של מטען נקודתי $Q$:
\[V_Q = k \frac{Q}{r}\]כאשר קבוע קולון הוא:
\[k = \frac{1}{4\pi\epsilon_0}\]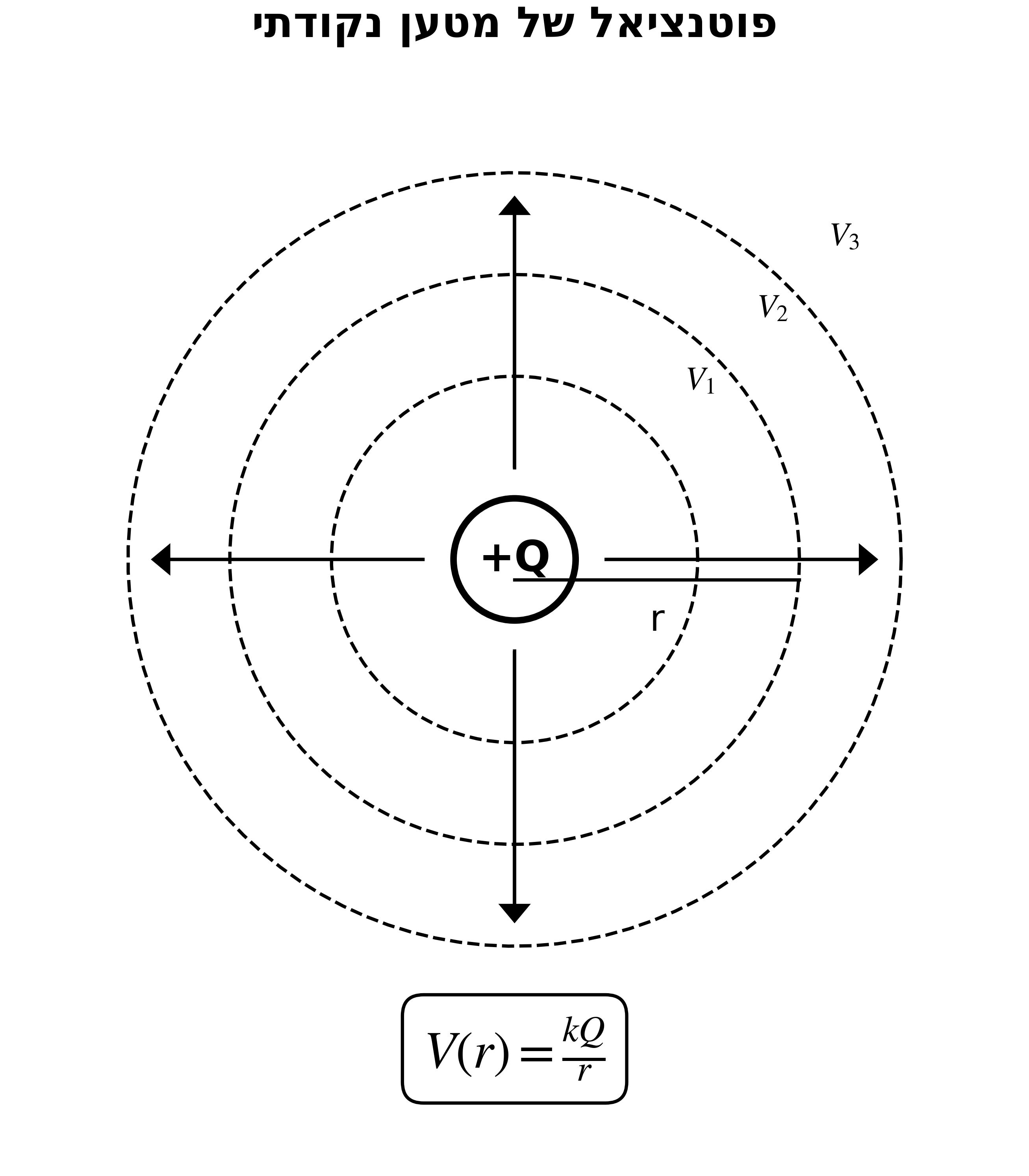
סופרפוזיציה של שדות ופוטנציאלים
כשיש קונפיגורציה של מטענים, ניתן לחשב את השדה בכל מקום במרחב באמצעות סופרפוזיציה של שדות של מטענים בודדים.
חישוב אנרגיה פוטנציאלית
האנרגיה הפוטנציאלית היא סופרפוזיציה של כל הזוגות האפשריים שניתן לבנות מהקונפיגורציה.
חישוב פוטנציאל
הפוטנציאל הוא סופרפוזיציה של הפוטנציאל שנוצר מכל המטענים שיש בסביבה.
דוגמה 1: שני מטענים חיוביים
במישור $x$-$y$, נניח שני מטענים:
- מטען $+q$ במרחק $a$ מהראשית
- מטען $+q$ במרחק $a$ מהראשית (בצד השני)
+q +q ---|---------0---------|--- |<------ 2a ------->|
השדה במרכז (בראשית)
\[\vec{E}(\vec{r}=0) = \vec{0}\]כל מטען יוצר שדה בגודל $\frac{kq}{a^2}$, אך בכיוונים הפוכים - לכן השדה הכולל הוא אפס (שני וקטורים שמבטלים זה את זה).
הערה חשובה: כותבים $\vec{E} = \vec{0}$ (וקטור האפס), לא סתם $E = 0$. וקטור האפס בתלת-ממד הוא שלושה אפסים: $(0, 0, 0)$.
הפוטנציאל במרכז
\[V(\vec{r}=0) = \frac{kq}{a} + \frac{kq}{a} = \frac{2kq}{a}\]הפוטנציאל הוא סקלר - חיבור של שני גדלים זהים. הפוטנציאל במרכז אינו אפס.
דוגמה 2: דיפול חשמלי
נתון דיפול (דו-קוטב): מטען $+q$ ומטען $-q$ במרחק $a$ מהראשית.
מהו השדה והפוטנציאל במרכז?
---•---0---•--- -q +q
השדה במרכז
מטען חיובי הוא מעיין (השדה יוצא ממנו), מטען שלילי הוא בולען (השדה נכנס אליו).
\[\vec{E}(\vec{r}=0) = \frac{2kq}{a^2}\hat{x}\]השדות מחוברים באותו כיוון.
הפוטנציאל במרכז
\[V(\vec{r}=0) = \frac{kq}{a} + \frac{k(-q)}{a} = 0\]הפוטנציאל מתאפס כי מחברים שני גדלים עם סימנים הפוכים.
כלל חשוב
פוטנציאל של מטען בודד: $V = \frac{kQ}{r}$
הסימן של המטען קובע את סימן הפוטנציאל:
- מטען חיובי ← פוטנציאל חיובי
- מטען שלילי ← פוטנציאל שלילי
פוטנציאל של התפלגות מטען רציפה
הגדרת הבעיה
במצבים רבים המטען אינו נקודתי אלא מפולג ברצף במרחב באמצעות צפיפות מטען $\rho(\vec{r})$.
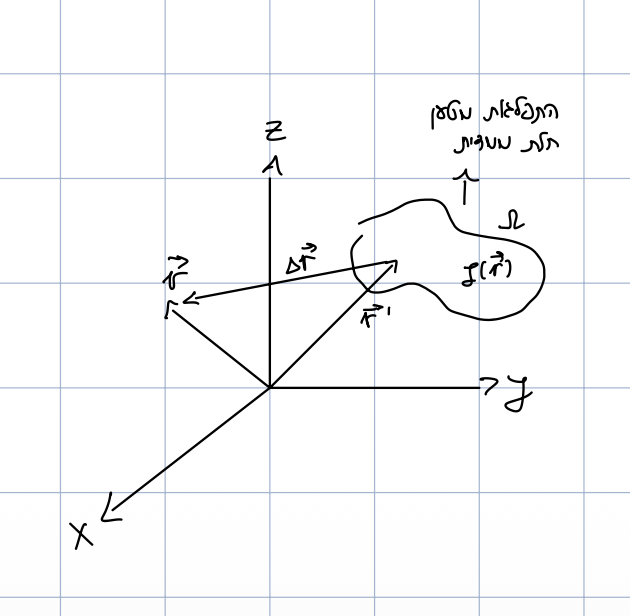
נתונה התפלגות מטען תלת-ממדית $\rho(\vec{r}’)$. נרצה למצוא את הפוטנציאל בנקודה $\vec{r}$.
הגדרות
- $\vec{r}’$ - קואורדינטת אלמנט המטען
- $\vec{r}$ - נקודת התצפית
- $\Delta \vec{r} = \vec{r} - \vec{r}’$ - וקטור המרחק
אלמנט מטען
\[dq = \rho \cdot dV = \rho(\vec{r}') \cdot d^3r'\]כאשר $d^3r’ = dx’ \cdot dy’ \cdot dz’$ הוא אלמנט נפח אינפיניטסימלי.
תרומת אלמנט המטען לפוטנציאל
\[dV = \frac{k \cdot dq}{|\vec{r} - \vec{r}'|}\]הפוטנציאל הכולל
\[V(\vec{r}) = \int_{\Omega} \frac{k \cdot \rho(\vec{r}')}{|\vec{r} - \vec{r}'|} d^3r'\]כאשר $\Omega$ הוא הנפח המכיל את צפיפות המטען.
זהו אינטגרל תלת-ממדי (שלושה אינטגרלים), אך במקרים סימטריים ניתן לרדד אותו לאינטגרל חד-ממדי.
דוגמה: כדור עם צפיפות מטען מתכלה
נתון כדור מלא ברדיוס $R$ עם צפיפות מטען:
\[\rho(r) = \rho_0 \cdot e^{-r/R}\]מה הפוטנציאל?
בדיקת גבולות
- ב-$r = 0$: $\rho(0) = \rho_0$ (בעייתי מתמטית אך סופי)
- ב-$r = R$: $\rho(R) = \rho_0 / e$
- ב-$r = 0$: יש בעיה עם $1/0^2$ אם הצפיפות הייתה $\rho_0/r^2$
חישוב הפוטנציאל על שפת הכדור
נסתכל על תרומה של קליפה כדורית ברדיוס $r$ קטן.
המטען על הקליפה:
\[dq(r) = \rho(r) \cdot dV = \rho(r) \cdot 4\pi r^2 \cdot dr\]תרומת הקליפה לפוטנציאל:
\[dV = \frac{k \cdot dq}{r} = \frac{k \cdot \rho(r) \cdot 4\pi r^2 \cdot dr}{r} = 4\pi k \cdot \rho(r) \cdot r \cdot dr\]הפוטנציאל הכולל:
\[V = \int_0^R dV(r) = \frac{1}{\epsilon_0} \int_0^R \rho(r) \cdot r \cdot dr\]כאשר $4\pi k = \frac{1}{\epsilon_0}$.
עבור $\rho(r) = \rho_0 e^{-r/R}$:
\[V = \frac{\rho_0}{\epsilon_0} \int_0^R r \cdot e^{-r/R} dr\]האינטגרל נפתר באמצעות אינטגרציה בחלקים.
כדור מוליך טעון
נתון כדור מוליך ברדיוס $R$ טעון במטען $Q$. המטען מתרכז על השפה.
מהו השדה והפוטנציאל בכל המרחב?
השדה והפוטנציאל
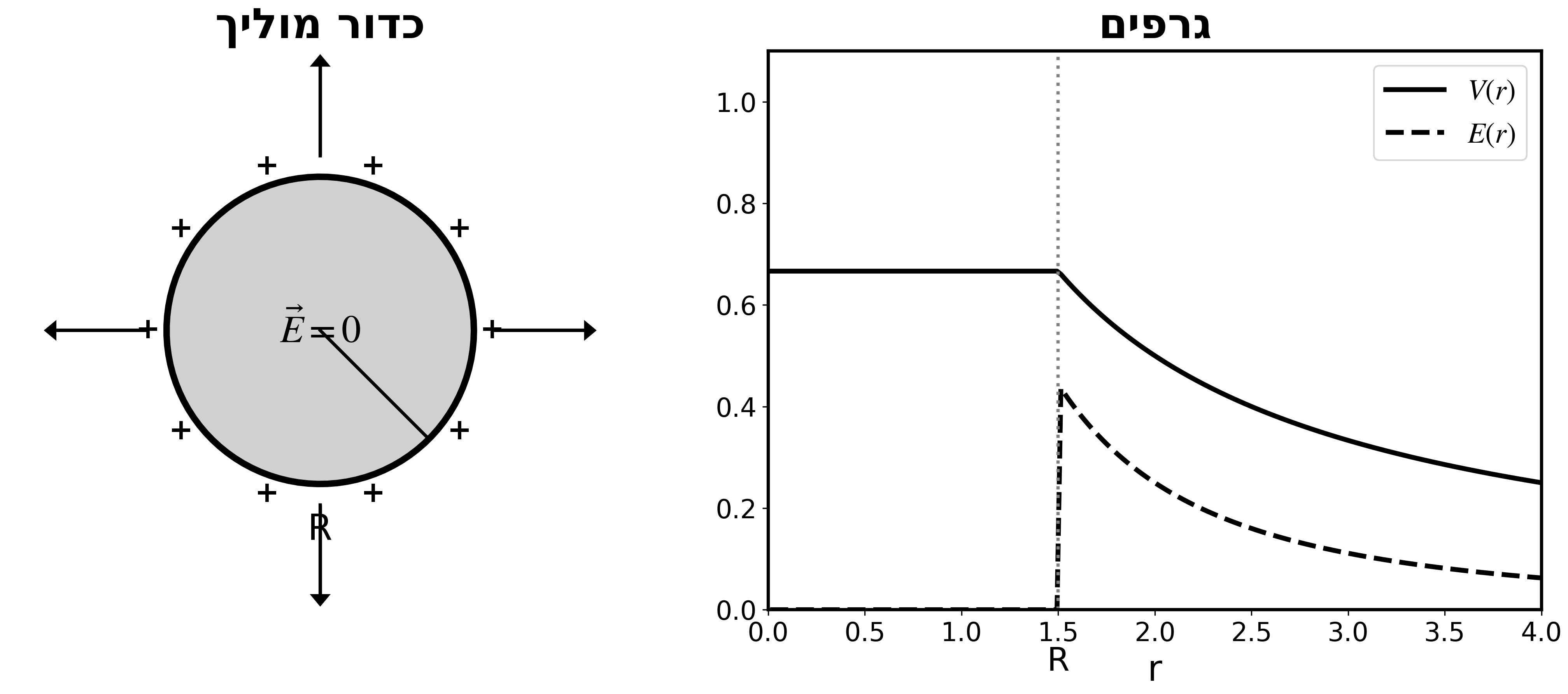
מחוץ לכדור ($r > R$):
\[V(r > R) = \frac{kQ}{r}\]בתוך הכדור ($r < R$):
השדה בתוך מוליך הוא אפס (אחרת המטענים היו זזים).
\[\vec{E} = 0 \quad \Rightarrow \quad V = \text{const}\]מכיוון ש-$\vec{E} = -\nabla V$, אם השדה אפס - הפוטנציאל קבוע.
הפוטנציאל בתוך הכדור שווה לפוטנציאל על השפה:
\[V(r < R) = \frac{kQ}{R}\]קווים שווי-פוטנציאל
- קווי השדה תמיד ניצבים לקווים שווי-פוטנציאל
- הסיבה: הגרדיאנט נותן שדה ניצב למשטחים שווי-ערך
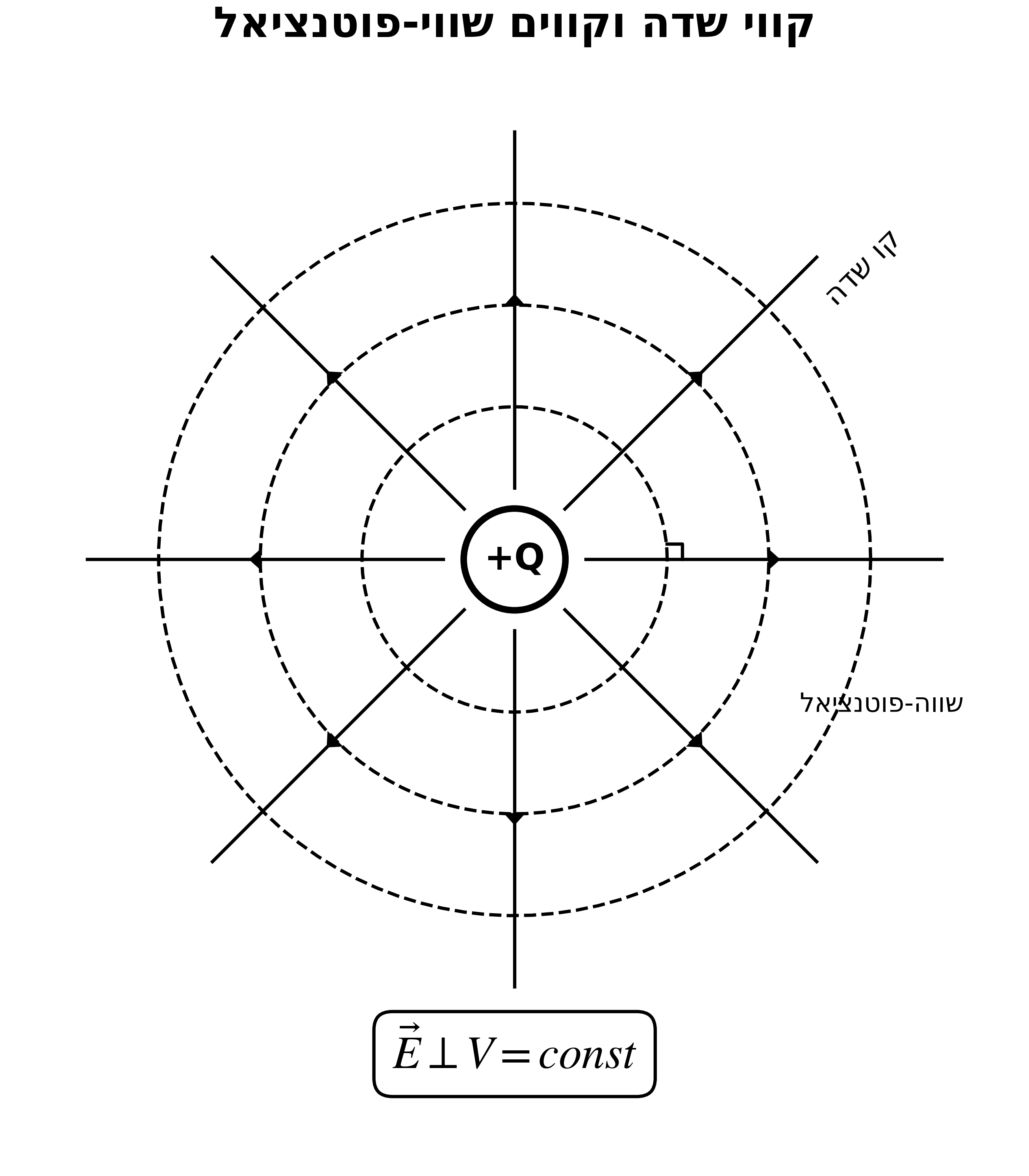
הבהרה מקלוד:
קווים שווי-פוטנציאל הם קווים (או משטחים בתלת-ממד) שעליהם הפוטנציאל החשמלי קבוע - כל הנקודות על הקו נמצאות באותו ערך של V.
תכונה חשובה: קווי השדה החשמלי תמיד ניצבים לקווים שווי-פוטנציאל.
משמעות פיזיקלית: כשמזיזים מטען לאורך קו שווה-פוטנציאל, לא מבצעים עבודה (כי אין הפרש פוטנציאל).
הארקה (Grounding)
פוטנציאל כדור הארץ
מטען כדור הארץ קטן יחסית ($\sim 10^5$ C), ורדיוס כדור הארץ גדול ($\sim 6{,}370$ km).
לכן הפוטנציאל על פני כדור הארץ קטן מאוד, וניתן לקבוע:
\[V_{\text{earth}} = 0\]משמעות הארקה
חיבור מוליך לאדמה באמצעות חוט מוליך מאלץ פוטנציאל אפס על המוליך.
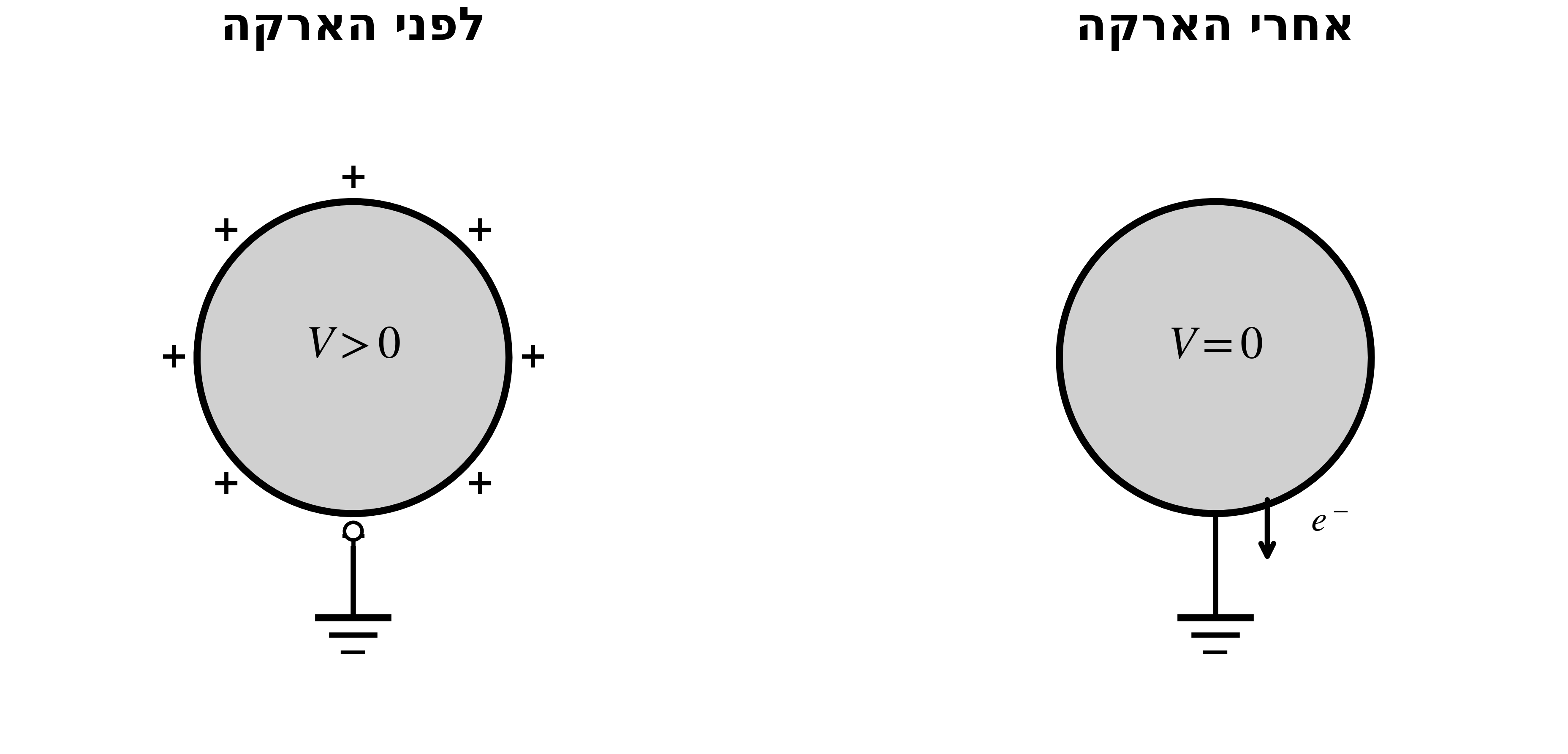
מה קורה כשמאריקים מוליך טעון?
- אם היה מטען חיובי עודף ← אלקטרונים זורמים מהאדמה ומנטרלים אותו
- אם היה מטען שלילי עודף ← אלקטרונים זורמים לאדמה
הארקה מאפסת את המטען העודף על המוליך.
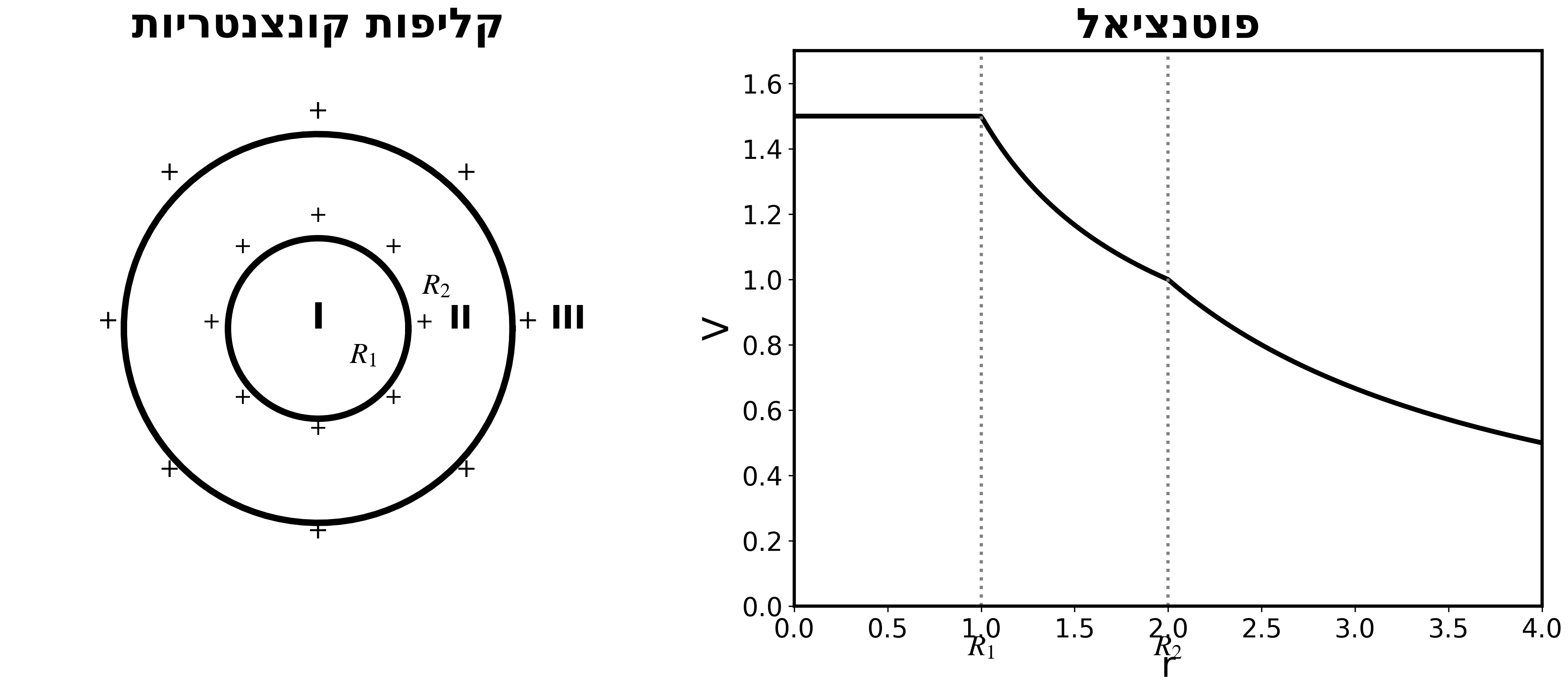
שתי קליפות קונצנטריות
נתונות שתי קליפות מוליכות קונצנטריות:
- קליפה פנימית ברדיוס $R_1$ עם מטען $Q_1$
- קליפה חיצונית ברדיוס $R_2$ עם מטען $Q_2$
מהו הפוטנציאל בכל אזור?
חישוב הפוטנציאל בכל המרחב (סופרפוזיציה)
באזור $r < R_1$:
\[V = \frac{kQ_1}{R_1} + \frac{kQ_2}{R_2}\](בתוך שתי הקליפות - כל קליפה תורמת ערך קבוע)
באזור $R_1 < r < R_2$:
\[V = \frac{kQ_1}{r} + \frac{kQ_2}{R_2}\](מחוץ לקליפה הפנימית, בתוך החיצונית)
באזור $r > R_2$:
\[V = \frac{k(Q_1 + Q_2)}{r}\](מחוץ לשתי הקליפות)
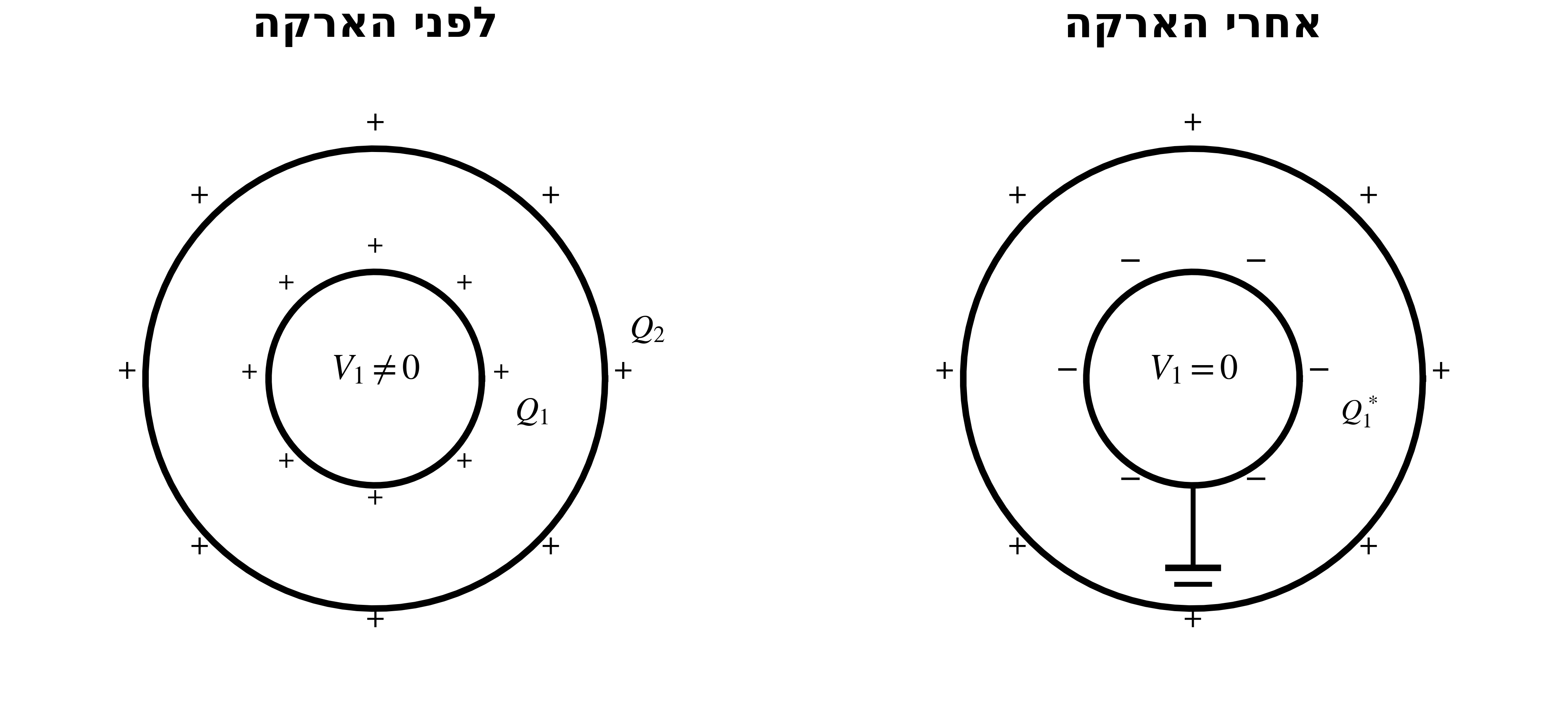
הארקת הקליפה הפנימית
השאלה
מה קורה כשמאריקים את הקליפה הפנימית (מאלצים עליה פוטנציאל אפס)?
התשובה
על הקליפה הפנימית הפוטנציאל צריך להתאפס:
\[\frac{kQ_1}{R_1} + \frac{kQ_1^*}{R_1} + \frac{kQ_2}{R_2} = 0\]כאשר $Q_1^*$ הוא המטען החדש שזורם מהאדמה.
פתרון:
\[Q_1^* = -\frac{R_1}{R_2} Q_2\]האדמה מביאה (או לוקחת) מטען כך שהפוטנציאל על הקליפה הפנימית יתאפס.
הפוטנציאל בתוך הקליפה הפנימית (אחרי הארקה)
הפוטנציאל בתוך הקליפה הפנימית הוא סופרפוזיציה:
\[V(r < R_1) = \frac{kQ_1^*}{R_1} + \frac{kQ_2}{R_2}\]שימו לב: למרות שהפוטנציאל על הקליפה הפנימית הוא אפס, הפוטנציאל בתוך הקליפה אינו בהכרח אפס - הוא שווה לתרומת הקליפה החיצונית.
סיכום נקודות חשובות
- סופרפוזיציה: הפוטנציאל הכולל הוא סכום התרומות מכל המטענים
- שדה לעומת פוטנציאל: שדה הוא וקטור (יכול להתאפס), פוטנציאל הוא סקלר
- מוליך: בתוך מוליך השדה אפס והפוטנציאל קבוע
- הארקה: מאלצת פוטנציאל אפס באמצעות זרימת מטענים מ/אל האדמה
- קווי שדה: תמיד ניצבים לקווים שווי-פוטנציאל (כי $\vec{E} = -\nabla V$)
- כלל יד ימין: $\hat{x} \times \hat{y} = \hat{z}$ - חשוב לשמור על עקביות בקואורדינטות