פתרון תרגיל 7 זרמים וכוחות מגנטיים

תוכן עניינים:

1. שאלה 1 - שלושה תיילים מקבילים (מאונכים למישור התרשים)
2. שאלה 2 - שני תיילים אינסופיים - שדה בין התיילים + מסגרת ריבועית
3. שאלה 3 - גליל אינסופי חלול עם צפיפות מטען רדיאלית + סיבוב
4. שאלה 4 - טבעת זרם ותיל ישר מעליה - שדה שקול במרכז
5. שאלה 5 - שלושה תיילים אינסופיים
6. שאלה 6 - כוחות מגנטיים על מסגרת זרם בין תיילים
7. שאלה 7 - תיל ארוך ליד סליל מעגלי דקיק (20 כריכות)
8. שאלה 8 - מסגרת מלבנית על ציר + שדה מגנטי אחיד + איזון עם משקולות
9. שאלה 9 - פרוטון וחלקיק אלפא בשדה מגנטי אחיד

שאלה 1 - שלושה תיילים מקבילים (מאונכים למישור התרשים)

נתונים שלושה תיילים ישרים, ארוכים ומקבילים $A,B,C$ מאונכים למישור התרשים. המרחק בין התיילים הוא $d = 10\,\mathrm{cm}$.

דרך שלושת התיילים זורמים זרמים חשמליים. נתון:

\[I_A = I_C = 10\,\mathrm{A}\]

כיוונו של הזרם ב-$A$ מתואר בתרשים. הזרם $I$ (בתיל המרכזי) לא ידוע.

עוד ידוע שעל התיל האמצעי פועל כוח מגנטי לכיוון תייל $A$, וגודלו של כוח זה הוא:

\[\frac{F}{L} = 4\times 10^{-4}\ \mathrm{N/m}\]

(ניוטון לכל מטר של התיל).

חשבו מהו כיוונו ומהי עוצמתו של הזרם $I$ בתיל המרכזי.

CopyRun

    A (X) . . . . . . . . . . . . . .
                          ^
                          |  d
                          v
    B ( ) . . . . . . . . . . . . . .
                          ^
                          |  d
                          v
    C ( ) . . . . . . . . . . . . . .

שלב 1 - קביעת כיוון הזרם ב-B

נתון שהכוח על B הוא לכיוון A. אנחנו צריכים לדעת שזרמים באותו כיוון נמשכים, וזרמים בכיוונים מנוגדים נדחים. תייל C נמצא מהצד השני - אז אפשר לחשוב על הכוח השקול מ-A ומ-C על B.

באיזה כיוון צריך I לזרום כדי שהשקול יהיה דווקא לכיוון A?

כדי ש-A ימשוך את B, הזרם ב-B צריך להיות באותו כיוון כמו A, כלומר גם הוא נכנס לדף (⊗).

גם חשוב: הזרם ב-C - גם משפיע על הכוח השקול. מה כיוון $I_C$? הפוך מ-A כדי ש B יידחף לכיוון A. סך הכל נקבל:

    A ⊗ . . . . . . . . . . . . . .
                          ^
                          |  d
                          v
    B ⊗ . . . . . . . . . . . . . .
                          ^
                          |  d
                          v
    C ◯ . . . . . . . . . . . . . .

לסיכום:

• A (⊗) מושך את B (⊗) - אותו כיוון ← משיכה לכיוון A ✓
• C (◯) דוחה את B (⊗) - כיוון הפוך ← דחייה מ-C, כלומר גם לכיוון A ✓

ובנוסף לכך - זאת האפשרות היחידה שנותנת כוח שקול שונה מאפס, כי אם C היה גם ⊗ כמו A, אז A היה מושך את B למעלה ו-C היה מושך את B למטה - ובגלל ש-$IA=ICI_A = I_C IA​=IC$​ והמרחקים שווים, הכוחות היו מתקזזים לאפס.

שלב 2 - חישוב הכוח לכל מטר

הנוסחה לכוח בין שני תיילים מקבילים:

נחשב בנפרד את $\frac{F_{A \to B}}{L}$ ואת $\frac{F_{C \to B}}{L}$ (המרחק מ-C ל-B הוא גם $d$), נקבע את הכיוון של כל אחד מהם, ונסכום אותם וקטורית (הם על אותו ציר).

• $\frac{F_{A \to B}}{L}$ - משיכה ← לכיוון A (למעלה) ✓

• $\frac{F_{C \to B}}{L}$ - דחייה ← הרחק מ-C, כלומר גם לכיוון A (למעלה) ✓

שני הכוחות באותו כיוון! אז הכוח השקול הוא סכום שלהם, לא הפרש:

שלב 3 - השוואה לנתון

נציב את $(1)$ ואת $(2)$ ונמצא את $I$:

נציב את הערכים של קבוע המגנטיות ושל המרחק הנתון בשאלה. תזכורת:

מכאן:

נציב גם $I_A = I_C = 10\,\mathrm{A}$:

כדי לוודא יחידות - זרם אמור לצאת ביחידות של אמפר.

אז סך הכל היחידות יצאו תקינות וקיבלנו:

בכיוון ⊗.

שאלה 2 - שני תיילים אינסופיים - שדה בין התיילים + מסגרת ריבועית

נתון המערך הבא של שני תיילים אינסופיים בהם זורם זרם זהה:

(ראו איור מטה).

נקבע את המרחק בין התיילים להיות $2a$, כאשר ציר $y$ עובר במרכז בין התיילים, וציר $z$ יוצא מהדף.

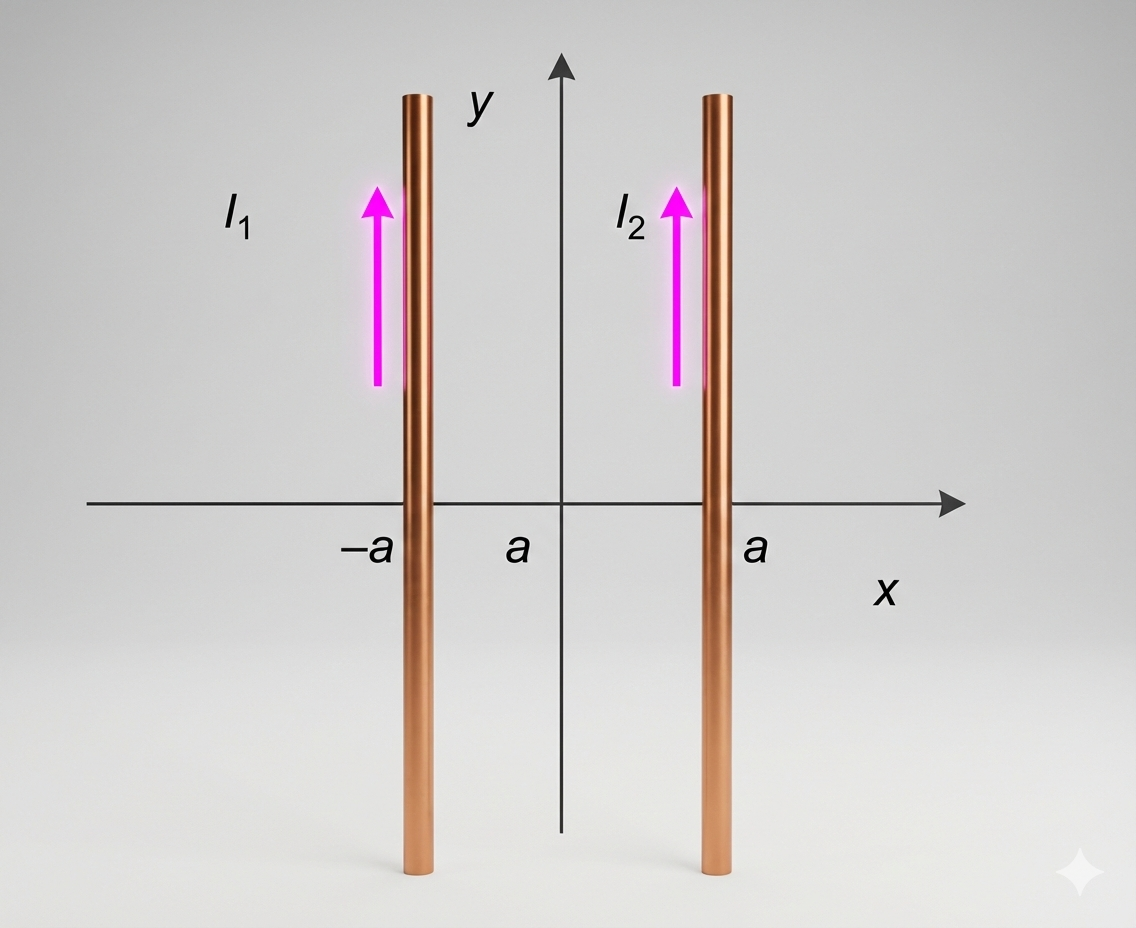
א. השדה המגנטי בין התיילים

הראו שהשדה המגנטי בין התיילים (אך לא עליהם), במרחק $x$ מהראשית, ניתן על ידי הנוסחה:

\[\vec{B}(x) = \left(\frac{\mu_0 I}{\pi}\right)\frac{x}{a^2 - x^2}\,\hat{z}\]

שלב ראשון - מציאת השדה המגנטי מכל תיל

כל תייל יוצר שדה מגנטי לפי:

כאשר $r$ הוא המרחק מהתייל.

מה המרחק מכל תייל לנקודה $x$ בין התיילים?

• מרחק מתייל 2 (ב-$x = +a$):

  \[r_2 = a - x\]

• מרחק מתייל 1 (ב-$x = -a$):

  \[r_1 = x - (-a) = x + a\]

  (כדי לא ליפול - תשומת הלב שמרחק חייב להיות חיובי).

שלב שני - מציאת הכיוון

נשתמש בכלל יד ימין כדי לקבוע את הכיוון של השדה מכל תייל בנפרד.

נשים לב לכיוון הזרמים - האם הם באותו כיוון או הפוך? זה קובע אם השדות מתחברים או מתקזזים באזור שבין התיילים.

לפי כלל יד ימין, הזרם למעלה, אז השדה המגנטי זורם נגד כיוון כיוון השעון (אם מסתכלים מלמעלה) - אבל יש הבדל ביחס לשני התיילים.

נניח שיש נקודה על ציר איקס החיובי. אז מהתייל הימני (שממקום קרוב יותר אליה, על החלק החיובי של ציר איקס), הזרם המגנטי דווקא יהיה החוצה מהדף. הזרם מהתייל השמאלי (בחלק השלילי של ציר $x$, דווקא יהיה לתוך הדף).

ניסיתי להכין ויזואליזציה נחמדה, אולי תעלה בהמשך. בשורה התחתונה, ביחס לאזור שבין שני התיילים: הזרם מהתייל הימני הוא החוצה מהדף, ואילו הזרם מהתייל השמאלי הוא לתוך הדף.

לסיכום:

שלב שלישי - סופר פוזיציה ופישוט

נחבר את שני השדות למציאת $\vec{B}_net$ (סופרפוזיציה) ונפשט.

שניהם בכיוון $\hat{z}$, אז פשוט מחברים אלגברית:

נוציא גורם משותף של $\frac{\mu_0 I}{2\pi}$:

נעשה מכנה משותף לשני השברים של $(a-x)(a+x) = a^2 - x^2$:

ב. השדה המגנטי מחוץ לתיילים

קבלו נוסחה עבור השדה המגנטי (ההשראה המגנטית?) עבור:

\[|x| > |a|\]

סופרפוזיציה

בין התיילים, השדות היו מנוגדים (חיסור). מה קורה מחוץ לתיילים? נחשוב עם כלל יד ימין - האם שני השדות עדיין מנוגדים, או שעכשיו הם באותו כיוון?

הם באותו כיוון!

נבדוק שני אזורים בנפרד:

• $x > a$: התייל הימני נכנס (מימין לו) - וגם התייל השמאלי נכנס!
• $x < -a$. התייל השמאלי יוצא - וגם התייל הימני יוצא.

נכתוב את $B_1$ ו-$B_2$ עבור נקודה ב-$x > a$ - מה המרחק מכל תייל, ומה הכיוון?

המרחק מהתייל הימני יהיה:

והמרחק מהתייל השמאלי יהיה:

הכיוון כאמור יהיה לתוך הדף ⊗.

במקרה של נקודה שקטנה ממינוס איי נקבל אותו מרחק רק בכיוון הפוך - החוצה.

נחבר, נתחיל מהמקרה החיובי:

הפעם המכנה המשותף יהיה $(x-a)(x+a)=x^2-a^2$:

דומה מאוד לסעיף הקודם רק שהביטוי במכנה שונה.

ג. כוח מגנטי על מסגרת ריבועית

מסגרת ריבועית קטנה, שאורך צלעה הוא: $d < a$ מוליכה זרם קבוע $J$ נגד כיוון השעון. (בתמונה כיוון הזרם יצא לי הפוך מהנתון, דמיינו נגד כיוון השעון).

המסגרת מונחת במישור $xy$ בין שני התיילים, כך שצלעותיה מקבילות לצירים.

מצאו ביטוי עבור הכוח המגנטי הכולל הפועל על כל המסגרת.

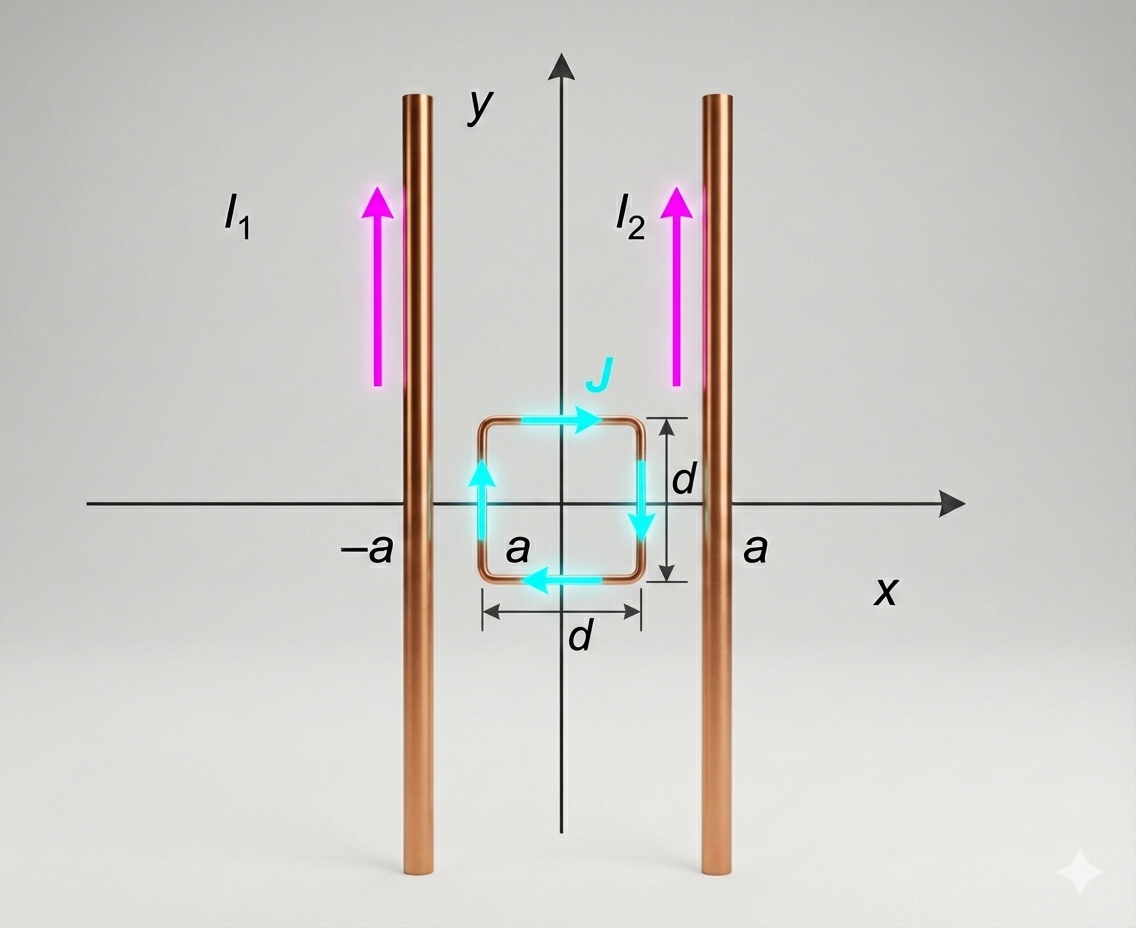
שלב 1 - כוח על כל צלע

הכוח על קטע תייל נושא זרם בשדה מגנטי הוא:

כאשר $\vec{L}$ הוא וקטור - יש לו גודל (אורך הצלע, שבמקרה הזה הוא $d$) וכיוון (כיוון הזרם באותר צלע).

נניח שמרכז המסגרת ב-$x_0$.

הבהרה מקלוד - ניסיתי להבין את המהות של איקס אפס:

$x_0$ הוא לא בהכרח ראשית הצירים. השאלה אומרת שהמסגרת מונחת בין שני התיילים, אבל לא אומרת בדיוק איפה. אז אנחנו משאירים את $x_0$ כפרמטר כללי - מרכז המסגרת יכול להיות בכל מקום בין $-a$ ל-$+a$.

לכן:

• צלע ימנית ב-$x = x_0 + d/2$
• צלע שמאלית ב-$x = x_0 - d/2$

אם המסגרת הייתה בדיוק במרכז ($x_0 = 0$), הכוח השקול היה אפס (בגלל סימטריה). דווקא כש-$x_0 \neq 0$ יש כוח שקול - וזה מה שנחשב.

כאמור, למסגרת יש 4 צלעות - נחשב את הכוח על כל אחת בנפרד.

4 הצלעות:

• ימנית (אנכית): ב-$x = x_0 + d/2$, זרם בכיוון $\hat{y}$
• שמאלית (אנכית): ב-$x = x_0 - d/2$, זרם בכיוון $-\hat{y}$
• עליונה (אופקית): ב-$y = y_0 + d/2$, זרם בכיוון $-\hat{x}$
• תחתונה (אופקית): ב-$y = y_0 + d/2$, זרם בכיוון $+\hat{x}$

(הכיוונים נובעים מזה שהזרם $J$ זורם נגד כיוון השעון.)

עכשיו, בהינתן ש-$\vec{B} = B(x)\hat{z}$ (תלוי רק ב-$x$!), נחשב $J\vec{L} \times \vec{B}$ לכל צלע. נתחיל מהצלעות האופקיות - מה יוצא מ-$\hat{x} \times \hat{z}$?

צלע אופקית עליונה

הזרם הולך שמאלה, אז:

השדה:

נציב:

עכשיו השאלה - מה זה $\hat{x} \times \hat{z}$?

נזכור את הכלל המעגלי (תודה קלוד): $\hat{x} \to \hat{y} \to \hat{z} \to \hat{x}$. מכפלה “קדימה” חיובית, “אחורה” שלילית:

אז:

ננסה עכשיו לעשות את אותו הדבר עבור הצלע התחתונה (שם $\vec{L} = d(+\hat{x})$) ונקווה לראות למה הם מתקזזים פורמאלית.

צלע אופקית תחתונה

הזרם הולך ימינה, אז:

השדה:

נציב:

מכאן:

הבהרה מ Claude Opus 4.6:

מה יש לנו?

מסגרת ריבועית עם צלע $d$, נושאת זרם $J$ נגד כיוון השעון. היא יושבת במישור $xy$. נניח שמרכז המסגרת נמצא בנקודה $x_0$ על ציר $x$.

איך נראית המסגרת?

CopyRun

        ← ← ← ← ←  (top side, current goes left)
        |           |
        |           |
   ↓    |           |    ↑
        |           |
        |           |
        → → → → →  (bottom side, current goes right)

   x₀ - d/2      x₀ + d/2

הזרם זורם נגד השעון, כלומר:

• צלע תחתונה: זרם ימינה ($+\hat{x}$)
• צלע ימנית: זרם למעלה ($+\hat{y}$)
• צלע עליונה: זרם שמאלה ($-\hat{x}$)
• צלע שמאלית: זרם למטה ($-\hat{y}$)

מה השדה המגנטי?

מסעיף א ידוע:

\[\vec{B}(x) = B(x)\,\hat{z}\]

הנקודה הקריטית: השדה תלוי רק ב-$x$, לא ב-$y$!

למה זה חשוב?

הצלע התחתונה והצלע העליונה - שתיהן עוברות מ-$x_0 - d/2$ עד $x_0 + d/2$. הן חוות בדיוק אותו שדה בכל נקודה. אבל הזרם בהן הפוך (אחת ימינה, אחת שמאלה) ← הכוחות עליהן מתקזזים!

מה שנשאר זה רק שתי הצלעות האנכיות:

• שמאלית ב-$x = x_0 - d/2$ ← חשה שדה $B(x_0 - d/2)$
• ימנית ב-$x = x_0 + d/2$ ← חשה שדה $B(x_0 + d/2)$

שדות שונים ← כוחות שונים ← יש כוח שקול!

שלב 2 - קיזוז

השדה $B(x)$ תלוי רק ב-$x$, לא ב-$y$.

חשוב: שתי הצלעות האופקיות (מקבילות ל-$\hat{x}$) נמצאות בערכי $y$ שונים אבל באותו טווח של $x$ - מה קורה לכוחות עליהן?

שלב 3 - חישוב מה שנשאר

שתי הצלעות האנכיות (מקבילות ל-$\hat{y}$) נמצאות ב-$x$ שונים: אחת ב-$x_0 - d/2$ והשנייה ב-$x_0 + d/2$. הן חשות שדה $B$ שונה - ומכאן הכוח השקול.

נכתוב את הכוח על שתי הצלעות האנכיות.

• ימנית ב-$x = x_0 + d/2$: שם $\vec{L} = d(+\hat{y})$ ו-$B = B(x_0 + d/2)$
• שמאלית ב-$x = x_0 - d/2$: שם $\vec{L} = d(-\hat{y})$ ו-$B = B(x_0 - d/2)$

צלע אנכית ימנית

מה זה $\hat{y} \times \hat{z}$?

נשתמש שוב במעגל של קלוד:

כאן הכיוון הוא קדימה - חיובי. נקבל $\hat{y} \times \hat{z} = \hat{x}$, וסך הכל:

נציב $x=x_0 + \frac{d}{2}$ ונקבל:

צלע אנכית שמאלית

הפעם הכיוון הוא למינוס וואי:

וסך הכל:

שלב 4 - חיבור והצבה

נחבר את שתי הצלעות האנכיות לכוח השקול:

עכשיו נציב את $B(x)$ מסעיף א ונפשט:

הערה: אין צורך לכלול שוב את $\hat{z}$ - התייחסנו אליו כשחישבנו את המכפלה הווקטורית בכוח של הצלעות.

להלן התשובה לאחר פישוטים שביקשתי מקלוד:

נוציא מכנה משותף. נסמן $x_+ = x_0 + \frac{d}{2}$ ו-$x_- = x_0 - \frac{d}{2}$:

\[\frac{x_+}{a^2 - x_+^2} - \frac{x_-}{a^2 - x_-^2} = \frac{x_+(a^2 - x_-^2) - x_-(a^2 - x_+^2)}{(a^2 - x_+^2)(a^2 - x_-^2)}\]

מונה:

\[= a^2(x_+ - x_-) + x_+x_-(x_+ - x_-) = (x_+ - x_-)(a^2 + x_+x_-)\]

כאשר $x_+ - x_- = d$ ו-$x_+x_- = x_0^2 - \frac{d^2}{4}$, אז:

\[= d\left(a^2 + x_0^2 - \frac{d^2}{4}\right)\]

סך הכל:

\[\boxed{\vec{F}_{net} = \frac{\mu_0 I J d^2}{\pi} \cdot \frac{a^2 + x_0^2 - \frac{d^2}{4}}{\left(a^2 - \left(x_0 + \frac{d}{2}\right)^2\right)\left(a^2 - \left(x_0 - \frac{d}{2}\right)^2\right)}\,\hat{x}}\]

זה לא דרמטית יותר פשוט, אבל לפחות הכל בשבר אחד מסודר.

זה הזכיר לי טור חזקות, שאלתי את קלוד וקיבלתי משהו שנראה כמו תשובה אפשרית במבחן. בשאלה המקורית אגב לא היה נתון $d \ll a$, זאת המצאה שלו.

בדיוק! בגלל שנתון ש-$d \ll a$, אפשר לקרב:

\[B\left(x_0 + \frac{d}{2}\right) - B\left(x_0 - \frac{d}{2}\right) \approx \frac{dB}{dx}\bigg|_{x_0} \cdot d\]

זה פשוט ההגדרה של הנגזרת כש-$d$ קטן! אז:

\[\vec{F}_{net} \approx Jd^2 \cdot \frac{dB}{dx}\bigg|_{x_0} \hat{x}\]

שים לב ש-$d^2$ זה השטח של המסגרת, מה שמקשר ישירות לדיפול מגנטי. רוצה לחשב את $\frac{dB}{dx}$ מהנוסחה של סעיף א? (כן)

צריך לגזור:

\[B(x) = \frac{\mu_0 I}{\pi} \cdot \frac{x}{a^2 - x^2}\]

נגזור $\frac{x}{a^2 - x^2}$ לפי כלל המנה:

\[\frac{d}{dx}\left[\frac{x}{a^2 - x^2}\right] = \frac{(a^2 - x^2) \cdot 1 - x \cdot (-2x)}{(a^2 - x^2)^2} = \frac{a^2 + x^2}{(a^2 - x^2)^2}\]

מכאן הכוח השקול בקירוב $d \ll a$:

\[\boxed{\vec{F}_{net} \approx \frac{\mu_0 I J d^2}{\pi} \cdot \frac{a^2 + x_0^2}{(a^2 - x_0^2)^2}\,\hat{x}}\]

הרבה יותר יפה! ושים לב - הכוח תמיד בכיוון $+\hat{x}$ (כלומר מושך את המסגרת הרחק מהמרכז, לכיוון התייל הקרוב יותר).

שאלה 3 - גליל אינסופי חלול עם צפיפות מטען רדיאלית + סיבוב

נתון גליל אינסופי חלול במרכזו, ציר הגליל מתלכד עם ציר $z$. רדיוס החלל - מציר הגליל עד לצידה הפנימי של מעטפת הגליל - הוא $R_1=b$, ועובי מעטפת הגלילית גם הוא $b$, כך שרדיוס הגליל כולו הוא $R_2=2b$.

מעטפת הגליל טעונה בהתפלגות מטען רדיאלית, וצפיפות המטען נתונה ע”י

\[\rho(r)=\frac{\alpha}{r}\sin\!\left(\frac{\pi r}{b}\right),\qquad R_1\le r\le R_2\]

כאן $\alpha$ פרמטר חיובי ו-$r$ היא הקואורדינטה הרדיאלית בהצגה הפולרית.

סעיף א׳ - נמקו בקצרה

1. מהן היחידות של $\alpha$ בשיטת SI?
2. האם המטען שבגליל חיובי או שלילי?
3. האם הגליל מבודד או מוליך?

סעיף א1 - יחידות

היחידות של צפיפות מטען נפחית הן:

סינוס הוא חסר יחידות ולרדיוס יחידות של מטר. נפתור:

א.2 - חיובי או שלילי?

$\alpha > 0$ (נתון).

בתחום $R_1 = b \leq r \leq R_2 = 2b$, מה הסימן של $\sin\left(\frac{\pi r}{b}\right)$? שלילי ובקצוות אפס.

בקצוות: כש-$r = b$ הארגומנט הוא $\pi$, וכש-$r = 2b$ הוא $2\pi$.

מה ערכי הסינוס בתחום $[\pi, 2\pi]$? בקצוות $\sin(\pi) = \sin(2\pi) = 0$ וביניהם שלילי (מעגל היחידה).

א.3 - מבודד או מוליך?

מוליך לא יכול לקיים התפלגות מטען $\rho(r)$ שמשתנה ברציפות בתוך הנפח שלו. מכאן שהגליל מבודד.

במוליך בשיווי משקל המטען נמצא רק על פני השטח, לא בנפח.

סעיף ב׳ - מהי כמות המטען הכוללת הכלואה בקטע שאורכו $\ell$?

ב. מהי כמות המטען החשמלי הכוללת הכלואה בגליל בקטע שאורכו הוא $L$?

המטען הכולל הוא אינטגרל על הנפח:

בגלל סימטריה גלילית, אלמנט הנפח הוא:

אז:

משהו נחמד: כש-$\rho(r) = \frac{\alpha}{r}\sin\left(\frac{\pi r}{b}\right)$ מוכפל ב-$r$

ה-$r$ מתקצר! אז האינטגרל נהיה פשוט:

הבהרה - עבודה עם גלילים (קלוד)

בוא נפרק את האינטגרל המשולש:

\[Q = \int_0^L dz \int_0^{2\pi} d\theta \int_b^{2b} \rho(r) \cdot r \, dr\]

אינטגרל על $z$

$\rho(r)$ לא תלוי ב-$z$ כלל, אז:

\[\int_0^L dz = L\]

אינטגרל על $\theta$

$\rho(r)$ לא תלוי ב-$\theta$ כלל (סימטריה גלילית - הגליל נראה אותו דבר מכל זווית), אז:

\[\int_0^{2\pi} d\theta = 2\pi\]

מה נשאר

רק האינטגרל הרדיאלי, שבו $\rho$ באמת משתנה:

\[Q = L \cdot 2\pi \cdot \int_b^{2b} \frac{\alpha}{r}\sin\left(\frac{\pi r}{b}\right) \cdot r \, dr\]

וכאן ה-$r$ מתקצר ונשאר:

\[Q = 2\pi \alpha L \int_b^{2b} \sin\left(\frac{\pi r}{b}\right) dr\]

זה לא שמשהו “מתבטל בגלל סימטריה” - פשוט $\rho$ תלוי רק ב-$r$, אז שני האינטגרלים האחרים הם טריוויאליים.

פתרון האינטגרל

הערה: בהתחלה הוספתי בטעות $r$ מיותר במכנה.

האנטי-נגזרת של $\sin(kx)$ היא:

\[-\frac{1}{k}\cos(kx)\]

לשלמות התמונה, האנטי נגזרת של $\cos (kx)$ היא:

\[\frac{1}{k}\sin(kx)\]

ממעגל היחידה:

מכאן:

נפשט לתוצאה סופית:

שלילי - מתאים למה שמצאנו בסעיף א.2!

סעיף ג׳ - היעזרו במשפט גאוס וקבלו את שדה העירור החשמלי $\vec{D}(r)$ בכל המרחב

ג. היעזרו במשפט גאוס וקבלו את שדה וקטור העירור החשמלי $\vec{D}(r)$ בכל המרחב (הבחינו בשלושה אזורים במרחב).

משפט גאוס לשדה העירור:

בגלל הסימטריה הגלילית, $\vec{D} = D(r)\hat{r}$ ומשטח גאוס הוא גליל ברדיוס $r$ ואורך $L$. אז:

צריך שלושה אזורים:

1. $r < b$ (חלל פנימי) - כמה מטען כלוא בפנים?
2. $b \leq r \leq 2b$ (בתוך המעטפת) - צריך לחשב $Q_{enc}(r) = 2\pi \alpha L \int_b^{r} \sin\left(\frac{\pi r’}{b}\right) dr’$
3. $r > 2b$ (מחוץ לגליל) - כל המטען כלוא, כבר חישבת ב-סעיף ב

חישוב המטען בחלל הפנימי

להבנתי הוא אפס.

חישוב המטען בתוך המעטפת

האינטגרל זהה למה שעשינו בסעיף ב, רק שהגבול העליון הוא $r$ במקום $2b$:

נציב בביטוי המלא ונפשט:

חישוב המטען מחוץ לגיל

כאמור בסעיף ב׳

מציאת שדה העירור מהמטענים

נציב ב-$Q_{enc}$ ואז נחלק ב-$2\pi r L$ כדי לקבל $D(r)$ לכל אזור:

אזור 1 ($r < b$):

אזור 2 ($b \leq r \leq 2b$):

אזור 3 ($r > 2b$):

סעיף ד׳ - קבלו ביטוי עבור צפיפות הזרם $ \vec{J}(r)$ כפי שהיא נראית לצופה במנוחה על ציר הגליל

עתה מסובבים את הגליל סביב צירו במהירות זוויתית $\vec{\omega}$ (כך שכיוון וקטור המהירות הזוויתית מכוון בכיוון ציר הסיבוב, $\vec{\omega}=\omega\hat{z}$).

ד. קבלו ביטוי עבור צפיפות הזרם $\vec{j}(r)$ כפי שהיא נראית לצופה הנמצא במנוחה על ציר הגליל.

רמז: המהירות המשיקית של כל נקודה הנמצאת במעטפת הגלילית היא $\vec{v}=\vec{\omega}\times\vec{r}$.

צפיפות זרם היא מטען שנע:

שלב 1: מה המהירות של נקודה במרחק $r$ מהציר?

רמז מקלוד: מה זה $\hat{z} \times \hat{r}$ בקואורדינטות גליליות?

בקואורדינטות גליליות יש את אותו כלל מעגלי כמו בקרטזיות:

\[\hat{r} \to \hat{\theta} \to \hat{z} \to \hat{r}\]

“קדימה” חיובי, אז:

\[\hat{z} \times \hat{r} = \hat{\theta}\]

מכאן $\vec{v} = \omega r \, \hat{\theta}$.

שלב 2: הצבת $\rho(r)$ ו $\vec{v}(r)$ ופישוט

נכפיל ב-$\rho(r)$ כדי לקבל $\vec{J}$.

סעיף ה׳ - מה ערכו של האינטגרל המסלולי של השדה המגנטי $\vec{H}$ לאורך מסילה סגורה

ה. מה ערכו של האינטגרל המסלולי של השדה המגנטי $\vec{H}$ לאורך מסילה סגורה המונחת במישור הניצב לציר הגליל, והיא מנוקבת ע”י הגליל? (חשבון או נימוק משכנע)

לא הצלחתי - להלן פתרון מתשובות של קלוד:

משפט אמפר:

כאשר $I_{enc}$ הוא הזרם החוצה את המשטח שהמסילה חוסמת.

המסילה נמצאת במישור ניצב לציר $z$, אז המשטח שלה פונה בכיוון $\hat{z}$. השאלה היא: מה רכיב ה-$\hat{z}$ של $\vec{J}$?

הרי מצאת ש-$\vec{J} = \alpha\omega\sin\left(\frac{\pi r}{b}\right)\hat{\theta}$. באיזה כיוון הזרם?

$\vec{J}$ הוא בכיוון $\hat{\theta}$ - כלומר הזרם מסתובב סביב ציר $z$, לא לאורכו.

המשטח שהמסילה חוסמת פונה בכיוון $\hat{z}$, אז רק רכיב $J_z$ תורם לזרם שחוצה אותו. אבל:

מכאן:

שאלה 4 - טבעת זרם ותיל ישר מעליה - שדה שקול במרכז

טבעת דקה שרדיוסה $a$ מונחת במישור $xy$ על שולחן אופקי. מרכז הטבעת בראשית. בטבעת עובר זרם $I_1$ (גודל/כיוון לא ידועים).

בגובה $d=2a$ מעל מרכז הטבעת ובמקביל למישורה, נמצא מוליך ישר וארוך מאוד הנושא זרם $I_2$ (גודל/כיוון לא ידועים). המוליך מתוח במקביל לציר $y$ ומוחזק בדיוק מעליו.

נמדד כי עוצמת שדה ההשראה המגנטית השקול במרכז הטבעת היא $B_0$. השדה נמצא במישור $xy$ ומכוון בזווית $45^\circ$ מעל ציר $y$ (ראו איור לא מדויק של ג׳מניי).

הערה: הניחו ששדה כדור הארץ זניח.

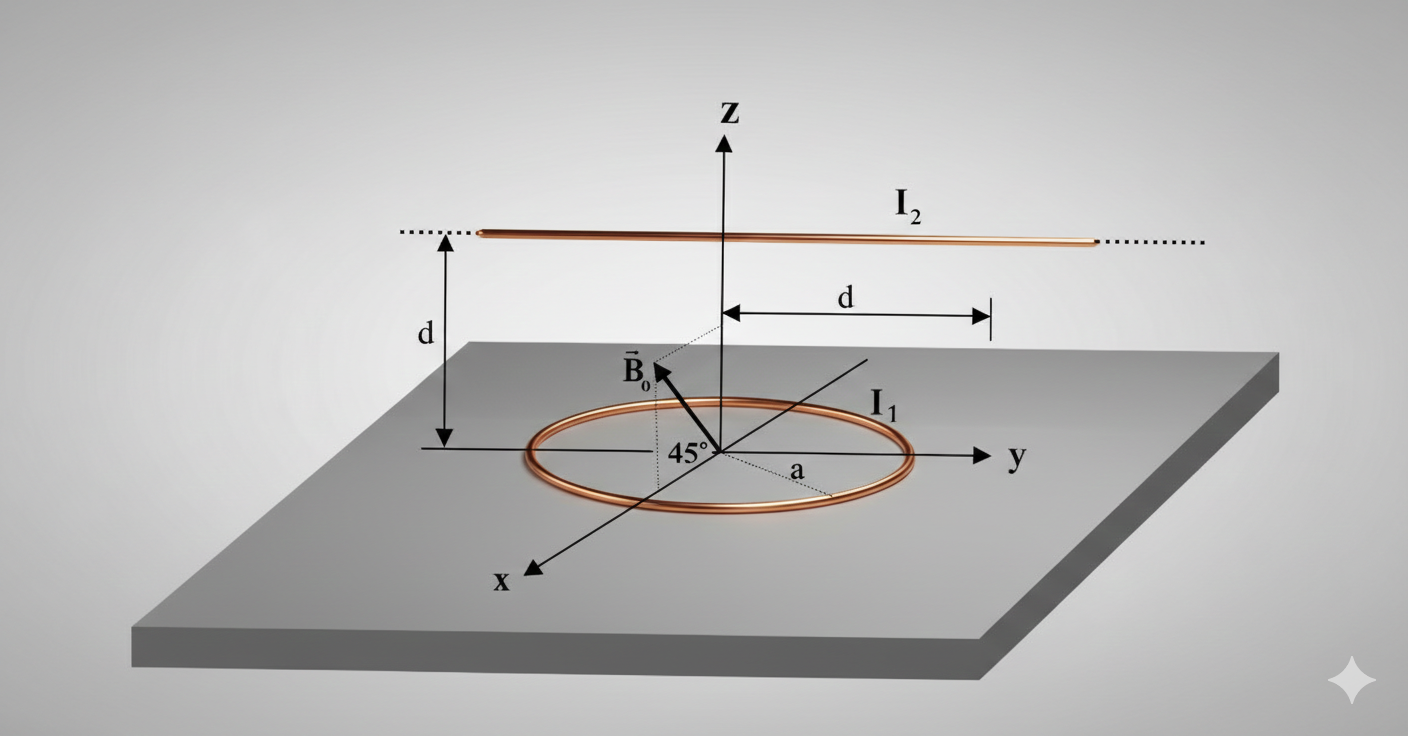
סעיף א׳ - מה כיווני הזרמים $I_1, I_2$?

שלב 1 - מציאת כיוון השדה מכל מקור

שני מקורות שדה במרכז הטבעת:

• טבעת ברדיוס $a$ במישור $xy$ ← שדה במרכזה תמיד בכיוון $\pm\hat{z}$
• תיל ישר מקביל ל-$\hat{y}$ בגובה $2a$ מעל המרכז ← שדה במרכז הטבעת בכיוון $\pm\hat{x}$

שלב 2 - שימוש בנתון על הזווית

אם השדה השקול הוא ב-$45°$, זה אומר שרכיב ה-$\hat{z}$ (מהטבעת) ורכיב ה-$\hat{x}$ (מהתיל) שווים בגודלם. הזווית $45°$ קובעת גם את הכיוון של כל רכיב - צריך להסתכל באיור ולקבוע אם $B_z$ חיובי או שלילי, ואם $B_x$ חיובי או שלילי.

שלב 3 - מכיוון השדה לכיוון הזרם

• $B_z > 0$ (מהטבעת) ← לפי כלל יד ימין, $I_1$ זורם נגד כיוון השעון כשמסתכלים מלמעלה
• $B_x > 0$ (מהתיל) ← התיל מקביל ל-$\hat{y}$ בגובה $2a$. לפי כלל יד ימין, כדי לקבל שדה בכיוון $+\hat{x}$ במרכז הטבעת, $I_2$ זורם בכיוון $-\hat{y}$

סעיף ב׳ - מהו היחס $I_1/I_2$?

כאמור, זווית $45°$ אומרת שהרכיבים שווים בגודלם:

נכתוב את הנוסחה לכל אחד:

• טבעת - שדה במרכז טבעת ברדיוס $a$:

  \[B_z = \frac{\mu_0 I_1}{2a}\]

• תיל ישר - שדה במרחק $d = 2a$ מהתיל:

  \[B_x = \frac{\mu_0 I_2}{2\pi \cdot 2a}\]

נשווה ונמצא את $I_1/I_2$:

בפתרון הרשמי פתרו מעט שונה: גם הם השתמשו ב-$d=2a$ אבל הציבו גם את הזוויות (להבנתי לא היה נדרש):

זה פשוט פירוק וקטורי של השדה הכולל $B_0$.

אנחנו יודעים שהשדה הכולל:

• גודלו $B_0$
• זוויתו $45°$

אז אפשר לפרק אותו לרכיבים:

כל רכיב מגיע ממקור אחד בלבד:

• $B_x$ מגיע רק מהתיל הישר ← $B_0\cos 45° = \frac{\mu_0 I_2}{2\pi(2a)}$
• $B_y$ מגיע רק מהטבעת ← $B_0\sin 45° = \frac{\mu_0 I_1}{2a}$

ומכיוון ש-$\cos 45° = \sin 45°$, שני הרכיבים שווים - להבנתי, הזווית הספציפית כאן לא משנה. לכל זווית פשוט מחלקים משוואה במשוואה:

$B_0$ ו-$\mu_0$ מצטמצמים, ובצד שמאל נשאר $\tan 45° = 1$. אז:

במקרה של $45°$ זה פשוט יצא נקי כי $\tan 45° = 1$, אבל השיטה עובדת לכל זווית.

סעיף ג׳ - שינויים בזווית

איזו זווית (ביחס לציר $y$) ייצור השדה השקול אם:

• מקטינים את הזרם $I_2$ פי 2
• מעלים את המוליך הישר לגובה $d=2d$ מעל השולחן

העיקרון פשוט - הזווית נקבעת לפי:

הטבעת נותנת $B_z$, התיל נותן $B_x$. בהתחלה $\tan 45° = 1$ כי הם שווים.

מקרה 1 - $I_2$ קטן פי 2

$B_x$ תלוי ישירות ב-$I_2$.

מה קורה ל-$B_x$? קטן בחצי:

ומה ל-$B_z$? כלום!

מכאן נחשב את $\tan\theta$ החדש:

נציב $\frac{I_2}{I_1} = 2\pi$ (מסעיף ב):

הזווית קטנה מ-$45°$ - הגיוני כי הקטנו את $B_x$ (מהתיל) אז השדה “מתקרב” לכיוון $\hat{z}$.

מקרה 2 - התיל עולה לגובה $2d = 4a$

$B_x = \frac{\mu_0 I_2}{2\pi r}$ כאשר $r$ הוא המרחק מהתיל למרכז הטבעת.

מה קורה ל-$r$ כשמכפילים את הגובה פי 2? הוא שוב ייקטן בשתיים כמו מקודם.

כשגם מקטינים וגם מרחיקים

ככל הנראה זאת הייתה כוונת המשורר. במקרה כזה רכיב $x$ ייקטן פי ארבע.

בפתרון הרשמי, במקום לחשב ישירות הציבו את היחס החדש ביחס המקורי:

אם $\alpha$ הזווית החדשה:

נראה אבל שיש פער בין הפתרון שלי לשלהם - אצלם:

ואצלי:

הבהרה לגבי ההבדלים: שני הפתרונות מתארים אותו כיוון בדיוק:

• אצלי: $\tan\theta = \frac{1}{4}$ ← $\theta \approx 14°$ מציר ה-$z$ (כיוון הטבעת)
• בפתרון הרשמי: $\tan\alpha = 4$ ← $\alpha \approx 76°$ מציר ה-$x$ (כיוון התיל)

תשומת הלב: $14° + 76° = 90°$ - זוויות משלימות! זה אותו כיוון, רק נמדד מציר אחר.

בדיקה פיזיקלית: הקטנו את תרומת התיל ← השדה מתקרב לכיוון הטבעת ($\hat{z}$). אכן $14°$ מ-$\hat{z}$ אומר “כמעט בכיוון הטבעת” ✓

סעיף ד׳ - כיוון כוח מגנטי של חלקיק

חלקיק נורה כלפי מעלה בכיוון ציר $z$, וחולף דרך מרכז הטבעת.

מה כיוון הכוח המגנטי שפועל עליו בנקודה זו אם החלקיק הוא: פרוטון? ניטרון? אלקטרון?

מציאת הכוח

הכוח המגנטי הוא:

הנתונים במרכז הטבעת:

• $\vec{v} = v\hat{z}$ (כלפי מעלה)
• $\vec{B} = B_x\hat{x} + B_z\hat{z}$

נחשב את המכפלות הווקטוריות של כל רכיב:

ביחס לרכיב השני:

כי מכפלה וקטורית של וקטור עם עצמו תמיד שווה אפס.

זה הגיוני פיזיקלית: הרכיב $B_z$ מקביל ל-$\vec{v}$, ומכפלה וקטורית של וקטורים מקבילים היא אפס. רק רכיב $B_x$ תורם לכוח!

אז:

מציאת הכיוון

נקבע את הכיוון עבור כל חלקיק לפי הסימן של $q$:

פרוטון ($q = +e > 0$):

ניוטרון ($q = 0$):

אלקטרון ($q = -e < 0$):

הפרוטון והאלקטרון חשים כוח בכיוונים מנוגדים (הגיוני - מטענים הפוכים), והניוטרון בכלל לא מרגיש את השדה.

שאלה 5 - שלושה תיילים אינסופיים

ראו איור המתייחס לשלושה תיילים אינסופיים בהם זורמים זרמים.

נתון שבתיילים $A,C$ זורם זרם כלפי מעלה, וכן ש-$I_A=5\,\text{A}$ ו-$I_C=3\,\text{A}$.

המרחק בין שני התיילים הללו הוא $16\,\text{cm}$.

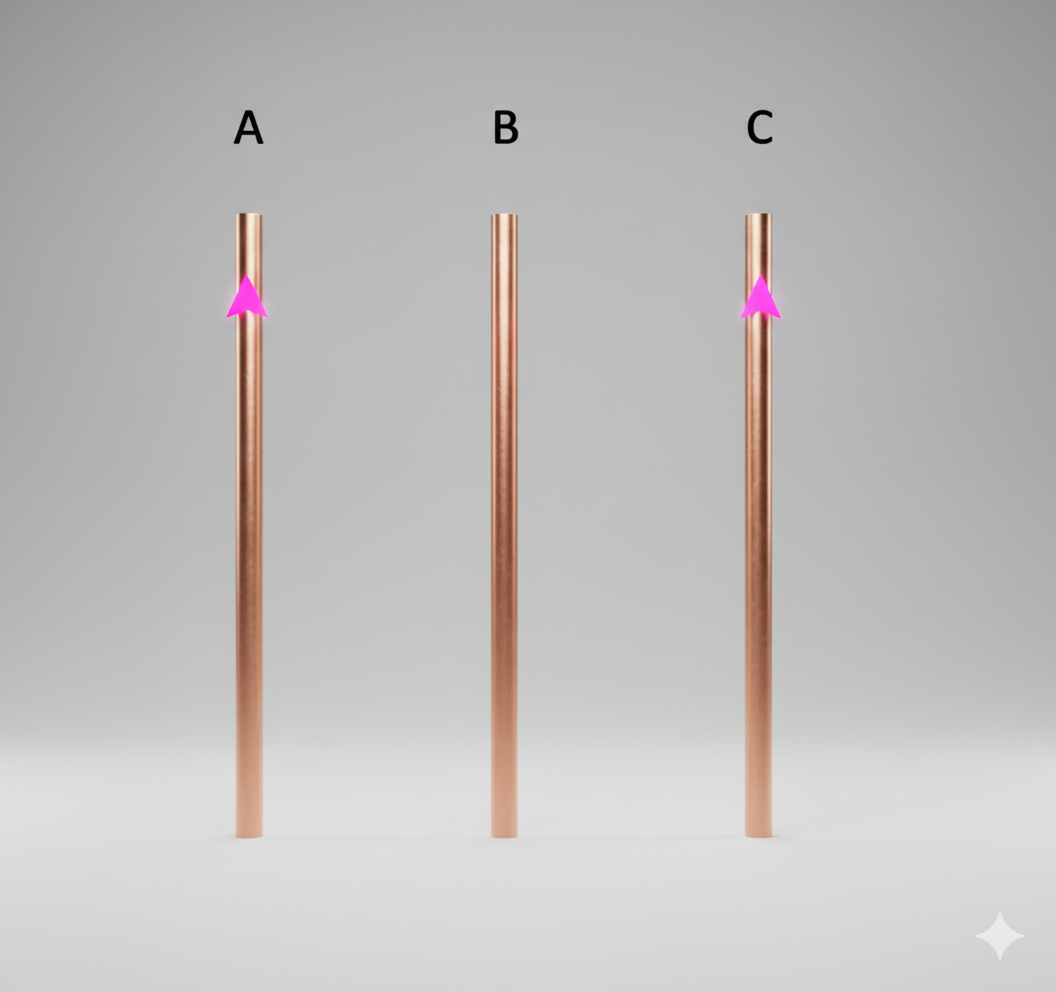
סעיף א׳ - מיקום תיל B

היכן יש למקם את התיל $B$ כך שהוא יישאר במצב שיווי משקל?

כדי ש-B יהיה בשיווי משקל, הכוחות מ-A ומ-C עליו צריכים להתקזז.

B חייב להיות בין A ל-C (למה?).

נסמן $x$ = מרחק מ-A ל-B, אז מרחק מ-C ל-B הוא $16 - x$.

תנאי שיווי משקל:

$I_B$ מצטמצמם - בהנחה שהוא לא אפס! נפשט ונפתור עבור $x$.

נציב את הזרמים:

B נמצא 10 cm מ-A ו-6 cm מ-C - קרוב יותר לזרם החלש (C), הגיוני!

סעיף ב׳ - משמעות הזרם

האם יש חשיבות לגודל של $I_B$? האם יש חשיבות לכיוון שלו?

כבר ראינו בסעיף א - $I_B$ הצטמצם מהמשוואה!

שתי שאלות:

1. גודל $I_B$: האם מיקום שיווי המשקל תלוי ב-$I_B$? לא.
2. כיוון $I_B$: האם הכיוון משפיע על מיקום שיווי המשקל, או רק על כיוון הכוחות?

לגבי הכיוון:

אם $I_B$ למעלה (כמו A ו-C), שני התיילים מושכים אותו. אם $I_B$ למטה, שניהם דוחים אותו. בשני המקרים - מה קורה לתנאי האיזון? הוא לא משתנה.

הנקודה המרכזית: שינוי כיוון $I_B$ הופך את שני הכוחות בו-זמנית, אז הם עדיין מתקזזים באותו מיקום.

סעיף ג׳ - שינויים בכיוון הזרם

מחליפים את כיוון הזרם בתיל $A$. האם במצב זה יישאר תיל $B$ בשיווי משקל?

עכשיו $I_A$ הפוך - כלפי מטה, בעוד $I_C$ עדיין כלפי מעלה.

מה כיוון הכוח של A על B, ומה כיוון הכוח של C על B?

• כשהזרמים באותו כיוון ← משיכה.
• כשהזרמים הפוכים ← דחייה.

עכשיו A ו-C בכיוונים הפוכים זה מזה - אז האם שניהם מושכים את B, שניהם דוחים אותו, או אחד מושך ואחד דוחה? שני הכוחות לאותו כיוון!

ואם שני הכוחות פועלים לאותו כיוון - האם יתכן שיווי משקל? לא!

הנקודה: בלי קשר לכיוון $I_B$, שני הכוחות תמיד דוחפים אותו לאותו צד - אין שיווי משקל אפשרי.

שאלה 6 - כוחות מגנטיים על מסגרת זרם בין תיילים

שני תיילים ארוכים ומקבילים, נושאים זרם $I$ כל אחד, במגמות המראות בציור. התיילים קבועים במישור הציור במרחק $D$ זה מזה.

מסגרת ריבועית מספר 1 ששתיים מצלעותיה מקבילות לתיילים ונושאת זרם $i$ במגמה המוראת בציור, נמצאת במישור הציור, באמצע בין התיילים בצורה סימטרית (ראה ציור).

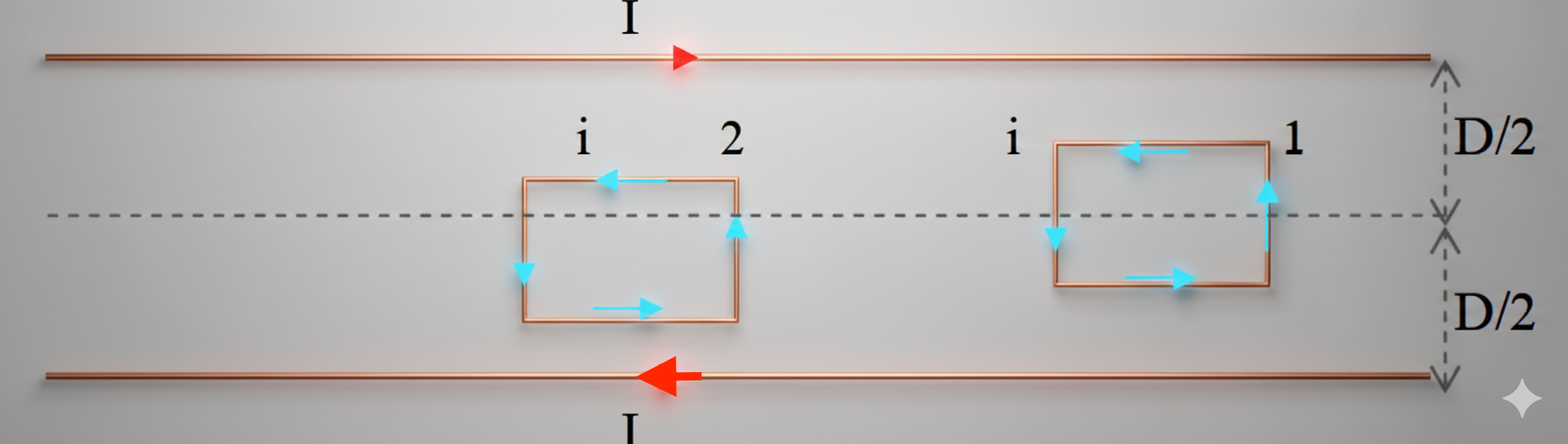
• תייל עליון: זרם ימינה →
• תייל תחתון: זרם שמאלה ←
• זרמים הפוכים!

סעיף I - מסגרת 1 (סימטרית באמצע)

הכוח המגנטי השקול הפועל על המסגרת הנ”ל (מס’ 1) מקיים:

1. אינו 0 וכיוונו כלפי מעלה, במישור הציור.
2. אינו 0 וכיוונו כלפי מטה, במישור הציור.
3. אינו 0 וכיוונו ימינה, במישור הציור.
4. אינו 0 וכיוונו ניצב למישור הציור.
5. שווה לאפס.

בגלל שהמסגרת בדיוק באמצע, לכל כוח מתייל אחד יש כוח שווה ומנוגד מהתייל השני. גם הצלעות האנכיות מתקזזות כי השדה לא תלוי ב-$x$ (תיילים אינסופיים). מה הכוח השקול? אפס!

סעיף II - מסגרת 2 (קרובה לתייל התחתון)

מסגרת ריבועית מספר 2 זהה למסגרת מספר 1 ונושאת זרם $i$ באותה מגמה, נמצאת אף היא בין התיילים, אך היא קרובה יותר לתייל התחתון (ראה ציור).

הכוח המגנטי השקול הפועל על המסגרת הנ”ל (מס’ 2) מקיים:

1. אינו 0 וכיוונו כלפי מעלה, במישור הציור.
2. אינו 0 וכיוונו כלפי מטה, במישור הציור.
3. אינו 0 וכיוונו ימינה, במישור הציור.
4. אינו 0 וכיוונו ניצב למישור הציור.
5. שווה לאפס.

נסתכל על הזרם בצלע התחתונה של המסגרת (→) לעומת הזרם בתייל התחתון (←).

הם הפוכים, לכן יש דחייה, ומכאן שהכוח שהתחתון מפעיל עליה הוא כלפי מעלה.

אותו ניתוח לצלע העליונה נותן כוח כלפי מטה, אבל חלש יותר כי היא רחוקה יותר.

לאיזה כיוון השקול? מעלה! סך הכל: אינו 0 וכיוונו כלפי מעלה, במישור הציור.

שאלה 7 - תיל ארוך ליד סליל מעגלי דקיק (20 כריכות)

תיל ארוך מאוד הנושא זרם $I_1$ מונח בצמוד לסליל מעגלי דקיק המורכב מ-20 כריכות, רדיוסו $R=10\,\text{cm}$.

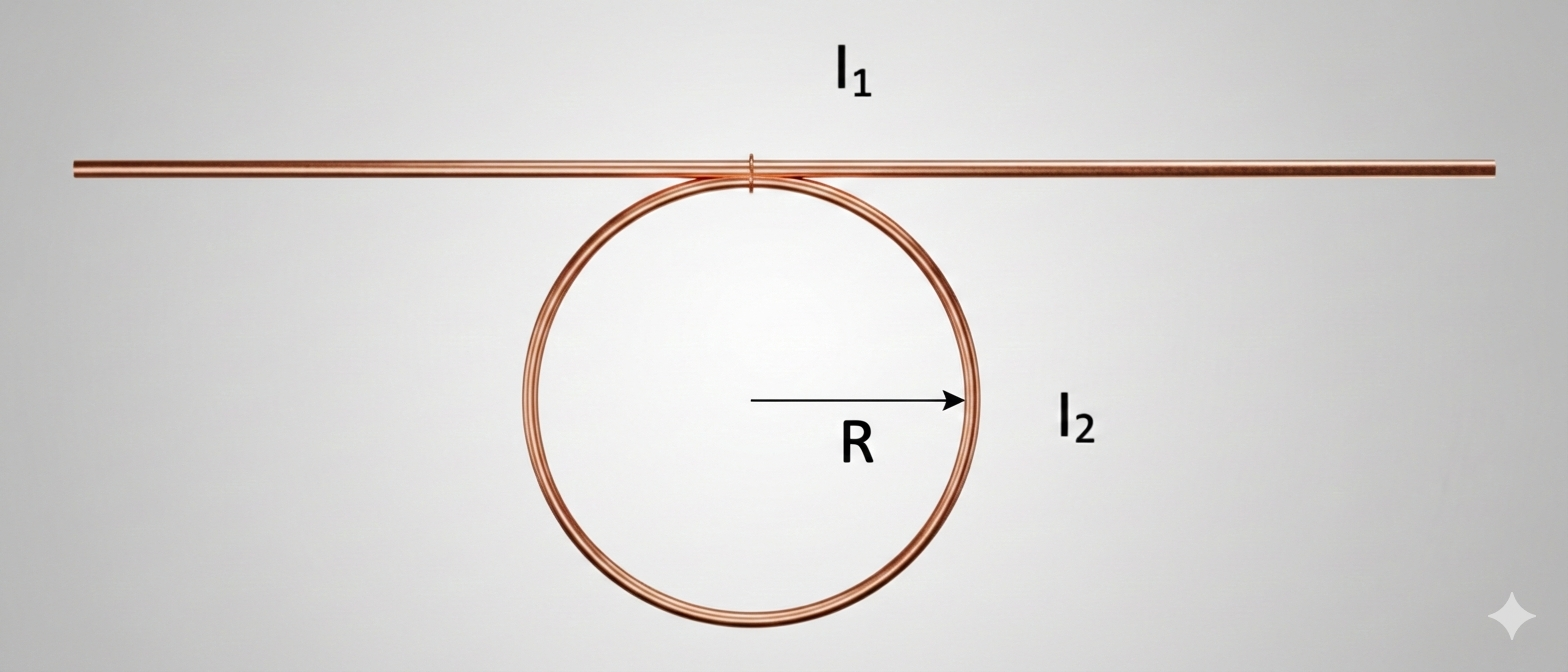
סעיף א׳ - מקרה 1 - התיל והסליל באותו מישור

כאשר זורם בסליל זרם $i_2=15\,\text{A}$ נגד כיוון השעון, מתאפסת ההשראה המגנטית במרכז הסליל.

מהו גודלו של $I_1$?

פתרון סעיף א - התיל והסליל באותו מישור

שלב 1: שני מקורות שדה במרכז הסליל:

• סליל (20 כריכות):

  \[B_{coil} = \frac{N\mu_0 i_2}{2R}\]

• תיל ישר במרחק $R$ מהמרכז (כי הוא בצמוד לסליל):

  \[B_{wire} = \frac{\mu_0 I_1}{2\pi R}\]

שלב 2: נתון שההשראה מתאפסת, כלומר:

שלב 3: נשווה ונפתור עבור $I_1$.

נצמצם גורמים - מתבטלים לא מעט.

נציב את הנתונים לגבי הזרם בסליל ומספר הכריכות:

סעיף ב׳ - מקרה 2 - התיל מאונך למישור הסליל

מסובבים את התיל כך שהוא מאונך למישור הסליל והזרם בתיל מכוון לתוך מישור הדף.

חשבו את גודלה וכיוונה של ההשראה המגנטית השקולה במרכז הכריכה.

עכשיו השדות מאונכים זה לזה במרכז הסליל:

• סליל: $B_{coil} = \frac{N\mu_0 i_2}{2R}$ - מאונך למישור הסליל
• תיל ישר: $B_{wire} = \frac{\mu_0 I_1}{2\pi R}$ - במישור הסליל

הם לא מתקזזים! מכיוון שהם מאונכים, הגודל השקול הוא:

והזווית:

תובנה: מסעיף א אנחנו כבר יודעים את היחס בין $B_{coil}$ ל-$B_{wire}$ (הם היו שווים!).

הבהרות מקלוד:

זה פשוט פיתגורס!

כשיש לך שני וקטורים מאונכים זה לזה, הגודל של הסכום שלהם הוא האלכסון של המלבן שהם יוצרים:

CopyRun

        ^
        |  B_coil
        |
        |_______ >
         B_wire

האלכסון (השקול) הוא:

\[B_{total} = \sqrt{B_{coil}^2 + B_{wire}^2}\]

זה עובד רק כשהוקטורים מאונכים. אם הם לא מאונכים צריך את חוק הקוסינוסים.

עכשיו - מסעיף א ידוע ש-$B_{coil} = B_{wire}$ (כי נתון שההשראה התאפסה), אז:

\[B_{total} = \sqrt{B^2 + B^2} = B\sqrt{2}\]

קלוד חישב צעד אחרי צעד:

שלב 1 - חישוב $B_{coil}$:

שלב 2 - מסעיף א ידוע ש:

שלב 3 - השקול (פיתגורס):

שלב 4 - הכיוון:

השדה השקול בזווית $45°$ בין כיוון השדה של הסליל לכיוון השדה של התיל.

שאלה 8 - מסגרת מלבנית על ציר + שדה מגנטי אחיד + איזון עם משקולות

מסגרת מלבנית עשויה תיל מוליך מונחת במישור אופקי על גבי ציר אופקי בשתי הנקודות $A,C$.

כל המסגרת נמצאת בשדה השראה מגנטית אופקי אחיד $\vec{B}$ אשר כיוונו מקביל לצלעות הארוכות.

כדי לאזן את המסגרת תלו משקולת שמסתה $m$ באמצע הצלע הקצרה הימנית.

כאשר מזרימים זרם $i$ במסגרת צריך להוסיף על המשקולת עוד משקולת קטנה $m^*$ כדי לאזן מחדש.

נתון:

\[i=20\,\text{A},\qquad d=l=5\,\text{cm},\qquad B=0.2\,\text{T}\]

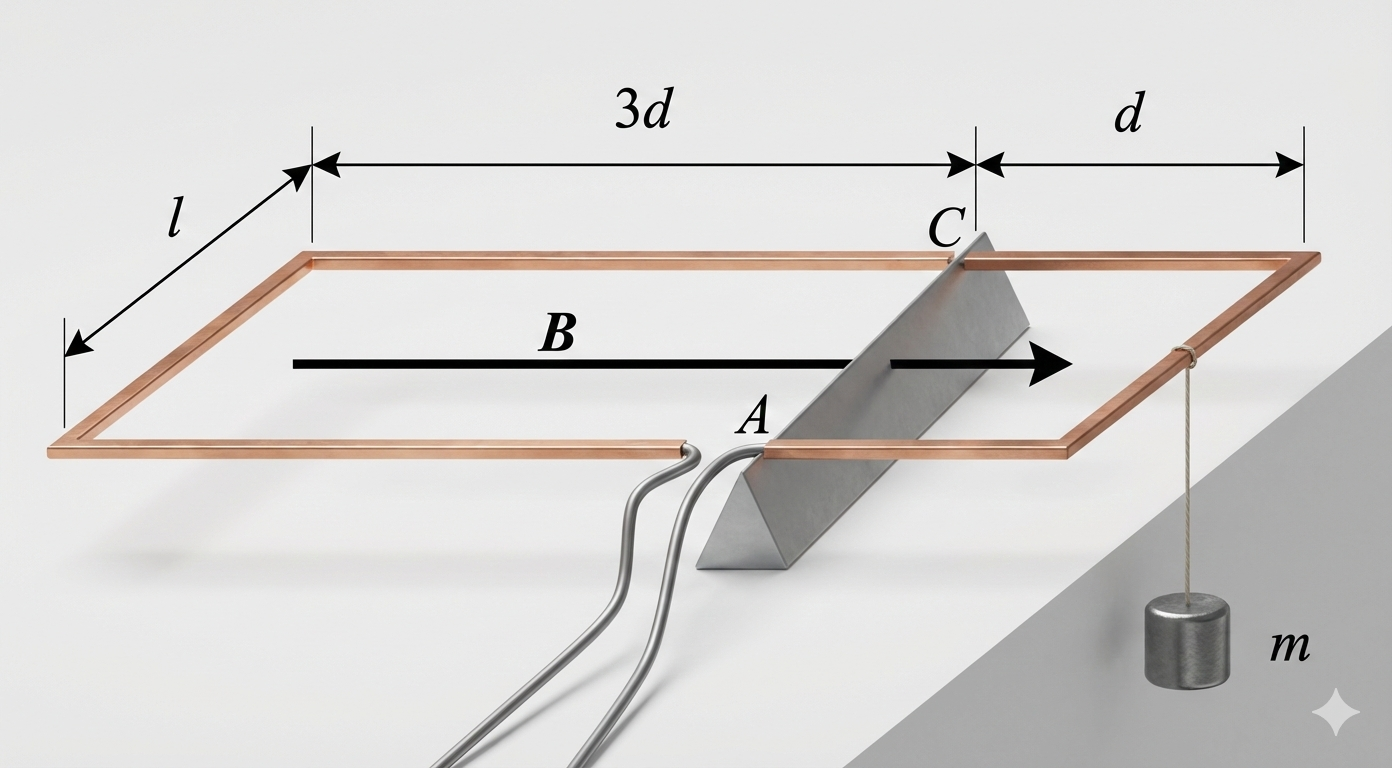
סעיף א - כיוון הזרם

סעיף א׳ - מהו כיוון הזרם במסגרת? הסבירו

תובנה: בלי זרם, המסגרת מאוזנת עם משקולת $m$ בצד ימין. כשמזרימים זרם, צריך להוסיף משקולת - כלומר, הכוח המגנטי על הצלע הימנית פועל כלפי מעלה (מקל על הצד הימני).

השאלה החדשה: באיזה כיוון צריך הזרם לזרום בצלע הימנית כדי ש-$\vec{F} = i\vec{L} \times \vec{B}$ יהיה כלפי מעלה?

מהפינה הימנית הרחוקה מאיתנו לפינה הימנית הקרובה.

אם הבנתי נכון, לפי כלל הכאפה (קרדיט ליותם):

• $\vec F$ - הכוח המגנטי על קטע תיל - כף היד
• $\vec B$ - השדה המגנטי - האצבעות
• $i$ או $I$ - הזרם בתיל (יחידות: אמפר, A) - האגודל
• $\vec L$ - וקטור באורך התיל ובכיוון של הזרם (יחידות: מטר, m)

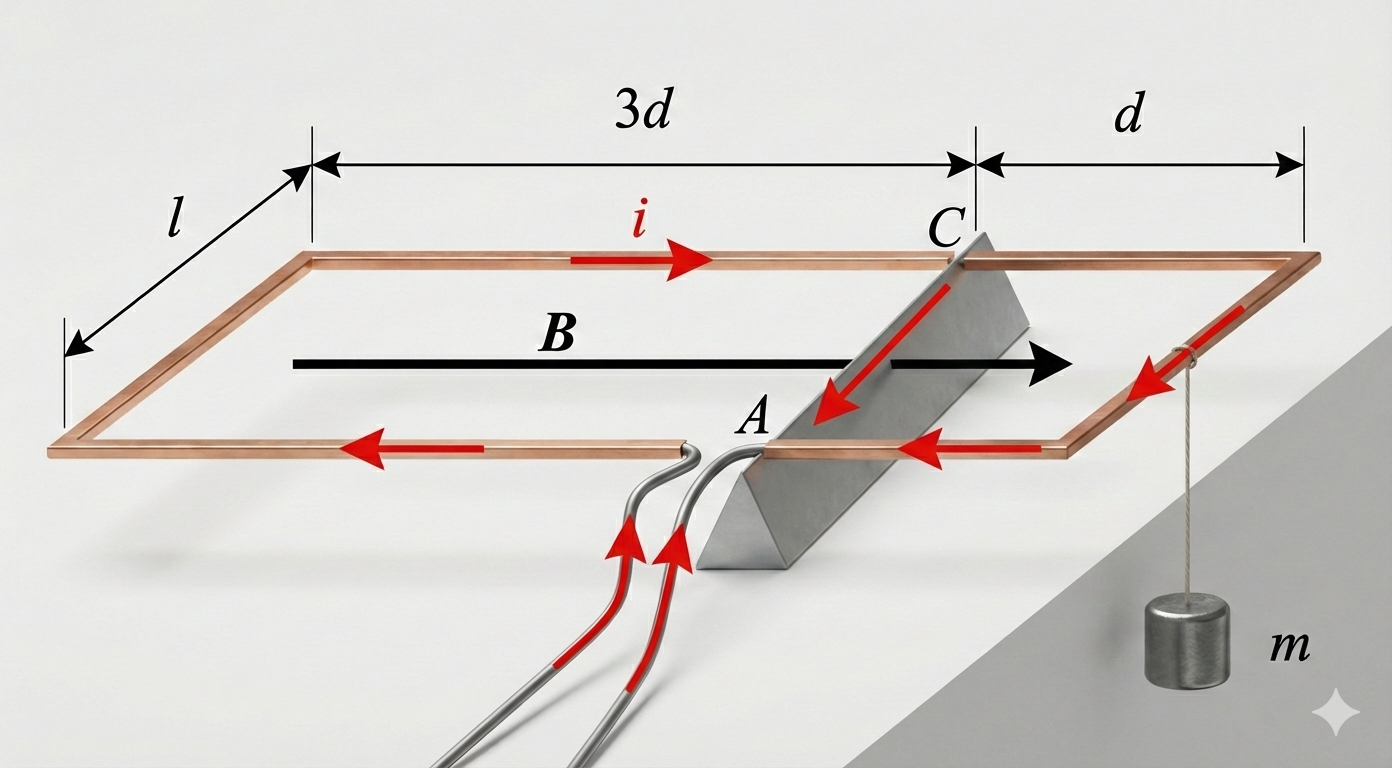
תשובה (לפי הפתרון הרשמי): עם כיוון השעון. הכוח על הצלעות הארוכות מתאפס כי שם כיוון הזרם מקביל/נוגד לשדה.

כאשר הזרם עם כיוון השעון, הכוח על הצלע הימנית כלפי מעלה ועל השמאלית כלפי מטה, ונוצר מומנט שמאזן את תוספת המשקל.

סעיף ב - כוח על כל צלע

סעיף ב׳ - חשבו את הכוח המגנטי על כל צלע של המסגרת כאשר זורם בה זרם $i$

תובנה: $\vec{F} = i\vec{L} \times \vec{B}$ לכל צלע.

נזכור ש-$\vec{B}$ מקביל לצלעות הארוכות.

מה קורה כש-$\vec{L} \parallel \vec{B}$? אין כוח מגנטי.

ומה קורה בצלעות הקצרות שמאונכות ל-$\vec{B}$?

נציב מספרים:

צלעות ארוכות ($\vec{L} \parallel \vec{B}$):

צלע ימנית קצרה ($\vec{L} \perp \vec{B}$, אורך $d = 5\,\text{cm}$):

כיוון: כלפי מעלה (מסעיף א)

צלע שמאלית קצרה - אותו גודל, כיוון הפוך (כלפי מטה).

סעיף ג - כוח שקול

סעיף ג׳ - חשבו את הכוח המגנטי השקול על המסגרת

נחשוב על הכיוון של הכוח על כל אחת משתי הצלעות הקצרות.

תשובה (לפי הפתרון): הכוח השקול על כל המסגרת הוא אפס, כי על שתי הצלעות הרלוונטיות פועלים כוחות שווים בגודלם והפוכים בכיוונם.

סעיף ד - חישוב $m^*$

סעיף ד׳ - חשבו את $m^*$

תובנה: שיווי משקל מומנטים סביב ציר $AC$.

המומנט של $m^*g$ צריך להשתוות למומנט של הכוח המגנטי. מה זרוע המומנט של כל אחד?

ביקשתי מקלוד להשלים. לא זכור לי שלמדנו את זה, לפחות לא לעומק.

שיווי משקל מומנטים סביב ציר AC:

הציר עובר באמצע הצלעות הארוכות. המרחק מהציר לכל צלע קצרה הוא $l$.

שני הכוחות המגנטיים יוצרים מומנט באותו כיוון (ימין למעלה, שמאל למטה):

המשקולת $m^*$ תלויה בצלע הימנית במרחק $l$ מהציר:

איזון:

הערה: אם $l$ מייצג חצי מהצלע הארוכה (כלומר הצלע הארוכה = $2l = 10\,\text{cm}$), אז $m^* = 0.04$. אם בציור $d$ מסמן חצי מהצלע הקצרה (כלומר הצלע הקצרה = $2d = 10\,\text{cm}$), אז $F = 0.4\,\text{N}$ ו-$m^* = 0.08\,\text{kg}$ כמו בפתרון המקורי. ללא הציור קשה לקבוע - כדאי לבדוק מה בדיוק $d$ ו-$l$ מייצגים בתרשים.

תשובה (כפי שמופיעה בקובץ):

שאלה 9 - פרוטון וחלקיק אלפא בשדה מגנטי אחיד

פרוטון (שמטענו $q = 1.6\times 10^{-19}\ \text{C}$) וחלקיק אלפא (שני פרוטונים ושני ניטרונים) נעים בכיוון ציר $x$ ונכנסים לאזור של שדה השראה מגנטית אחיד בעל עוצמה של:

\[B = 10^{-3}\ \text{T}\]

בכיוון ציר $y$.

בכניסה לשדה לשני החלקיקים אותה אנרגיה קינטית (אך לא אותה מהירות).

סעיף א - למי מהירות גדולה יותר?

למי מהירות גדולה יותר בכניסה? פי כמה?

תובנה: מהנתון על אותה אנרגיה קינטית:

מסת חלקיק אלפא: $m_\alpha = 4m_p$.

נפתור עבור $\frac{v_p}{v_\alpha}$:

כלומר, מהירות הפרוטון גדולה מזה של חלקיק האלפא פי 2.

הגיוני - חלקיק כבד (האלפא) יותר צריך מהירות קטנה יותר לאותה אנרגיה קינטית

סעיף ב - אנרגיות ביציאה

מה היחס בין האנרגיות הקינטיות ביציאה מאזור השפעת שדה ההשראה המגנטית?

שדה מגנטי לא מבצע עבודה על חלקיק טעון

תובנה: האם שדה מגנטי מבצע עבודה על חלקיק טעון?

לא - שדה מגנטי לבדו לא מבצע עבודה על חלקיק טעון.

הסיבה היא שכוח לורנץ מהמגנטיות הוא

\[\vec{F}_B = q\,\vec{v}\times \vec{B}\]

הכוח הזה מאונך תמיד למהירות $\vec v$. עבודה רגעית היא

\[dW = \vec{F}\cdot d\vec{r} = \vec{F}\cdot \vec{v}\,dt\]

ולכן עבור הכוח המגנטי:

\[\vec{F}_B\cdot \vec{v} = q(\vec{v}\times \vec{B})\cdot \vec{v}=0\]

אז:

• האנרגיה הקינטית לא משתנה בגלל $\vec B$ בלבד.
• $\vec B$ כן יכול לשנות כיוון מהירות (מסלול מעגלי/הליקלי), אבל לא את הגודל שלה.

מתי כן משתנה האנרגיה?

• כשיש שדה חשמלי: $\vec{F}_E = q\vec{E}$ והוא יכול להיות עם רכיב לאורך $\vec v$ ולכן כן עושה עבודה.
• או אם יש כוחות אחרים (גרר, התנגשויות, שדה מגנטי משתנה ש”מייצר” $\vec E$ מושרה וכו’).

הזווית בין כוח מגנטי למהירות - ישרה

שאלה חשובה - מה הזווית בין $\vec{F}$ ל-$\vec{v}$ בכוח מגנטי?

בכוח מגנטי בלבד:

לכן $\vec F$ מאונך ל-$\vec v$ (רואים את זה גם באחת הגרסאות של כלל יד ימין), כלומר:

(במילים: תמיד רבע סיבוב ביניהם, כי מכפלה וקטורית נותנת וקטור ניצב לשני הווקטורים - האגודל בכלל יד ימין).

מציאת היחס בין האנרגיות

היה נתון לנו שהחלקיקים נכנסו עם אותה אנרגיה, מכל האמור עולה שהם גם יצאו עם אותה אנרגיה.

מכאן שהיחס הוא $1$ - שדה מגנטי משנה כיוון, לא אנרגיה.

סעיף ג - רדיוסים

מהם רדיוסי המסלולים בתוך השדה?

תובנה: חלקיק טעון בשדה מגנטי נע במעגל.

אפשר להשוות כוח צנטריפטלי ($F_c = m\cdot \frac{v^2}{r}$) לכוח מגנטי ($\vec{F}=q\vec{v}\times \vec{B}$):

תזכורת:

מצאנו בסעיף א את $v_\alpha$ והשאר נתון.

רדיוס הפרוטון

נציב:

רדיוס חלקיק האלפא

הרי זה פלא - זה בדיוק $r_p$! הרדיוסים שווים:

זה לא מקרי: חלקיק אלפא כבד פי 4 (רדיוס גדול יותר) אבל איטי פי 2 (רדיוס קטן יותר) ומטענו כפול (רדיוס קטן יותר), ו-$4 \times \frac{1}{2} \times \frac{1}{2} = 1$.

סעיף ד - מרחק

נתון ששני החלקיקים נכנסו באותה נקודה. הפרוטון השלים בדיוק רבע מעגל ביציאה

מה המרחק בין הפרוטון לחלקיק האלפא ברגע זה?

שלב 1 - זמן מחזור

מצאנו ש-$r_p = r_\alpha$ אבל $v_p = 2v_\alpha$. אז:

כלומר, זמר המחזור של חלקיק אלפא כפול מזה של הפרוטון (ארוך יותר מהפרוטון).

שלב 2 - כמה השלים חלקיק אלפא

אפשר לחשב את היחסים.

בזמן שהפרוטון השלים רבע מעגל ($T_p/4$), חלקיק אלפא עם מחזור כפול השלים:

כלומר, חלקיק אלפא השלים שמינית מעגל = $45°$ (בזמן שהפרוטון רבע - הגיוני).

שלב 3 - מציאת מיקומים

שני החלקיקים נעים במעגלים עם אותו רדיוס $r$, מאותה נקודת כניסה. נחשב את המיקום של כל אחד:

• פרוטון ב-$90°$
• אלפא ב-$45°$

ונמצא את המרחק ביניהם בפיתגורס.

בשלב הזה התעייפתי וביקשתי מקלוד להשלים את החישוב.

אפשר להשאיר את התשובה כפונקציה של $r$ - זה לגיטימי לחלוטין. לא חסר נתון.

שלב 3 - מיקומים:

שניהם נכנסים בראשית בכיוון $+\hat{x}$, מעגל ברדיוס $r$. הפרמטריזציה:

• פרוטון ($\theta = 90°$): $(r,\; r)$
• אלפא ($\theta = 45°$): $\left(\frac{r}{\sqrt{2}},\; r\left(1 - \frac{1}{\sqrt{2}}\right)\right)$

שלב 4 - מרחק: