חוקי ניוטון ומערכות ייחוס
עסקנו בכתה בחוק הראשון, השני והשלישי של ניוטון, ולמדנו שבסיטואציות שבהן המערכת נמצאת בשיווי משקל, או שהיא נמצאת במצב של התמדה (כלומר, לא מורגשים בה כוחות מדומים), ושקול הכוחות שווה לאפס - בסיטואציה כזו אנחנו משתמשים בחוק הראשון של ניוטון.
לחלופין, כאשר המערכת שלנו נמצאת בתאוצה, אנחנו יכולים להשתמש בחוק השני של ניוטון.
כאשר מדובר במערכת שהיא לא מערכת התמדה (לא אינרציאלית), אנחנו יכולים להשתמש בחוק הראשון והשני, ובלבד שנכניס את העובדה שיש כוחות מדומים במערכת.
כוחות מדומים (כוחות דלמברט)
הכוחות המדומים במערכת הם מסת הגוף שאנחנו בודקים את התנועה שלו כפול תאוצת המערכת, כאשר כיוון הכוח הוא מנוגד לכיוון התאוצה.
כלומר, ביחס לכוח מדומה (נקרא לו $F_{imaginary}$ או כל שם אחר), מתקיים:
\[F_{imaginary} = -m\vec{a}\]כאשר $\vec{a}$ היא תאוצת המערכת. אנחנו צריכים להכניס את הכוח $F_{imaginary}$ לתוך מאזן הכוחות כדי שנוכל לטפל נכון בבעיה.
אגב, לכוח מדומה מהצורה הזאת יש גם שם מיוחד משלו - קוראים לו כוח דלמברט (D’Alembert).
כזכור, כוחות דלמברט הם כוחות “רפאים”, כלומר, שום דבר לא יוצר אותם מנקודת המבט של הגוף שנמצא במערכת המאיצה. הם פשוט מופיעים “משום מקום”, ומקורם בהתמדה של הגוף. המערכת של הגוף נמצאת בתאוצה ולכן היא “בורחת” ממנו, והבריחה הזאת מבטאת את העובדה שהוא מרגיש כאילו פועל עליו איזשהו כוח שדוחף אותו לאחת הפינות.
דוגמה: בעיית גליל על טריז
קיבלנו בשיעורי הבית כל מיני דוגמאות, למשל מקרה של גוף שמונח על מסה שמחליקה או דבר דומה. ראינו שאנחנו צריכים להוסיף את כוחות דלמברט כדי לפתור את הבעיה מתוך המערכת המאיצה. אם אנחנו לא בתוך המערכת המאיצה, אז אנחנו לא צריכים להוסיף את כוחות דלמברט, אלא התאוצה פשוט באה לידי ביטוי בתאוצת הגוף.
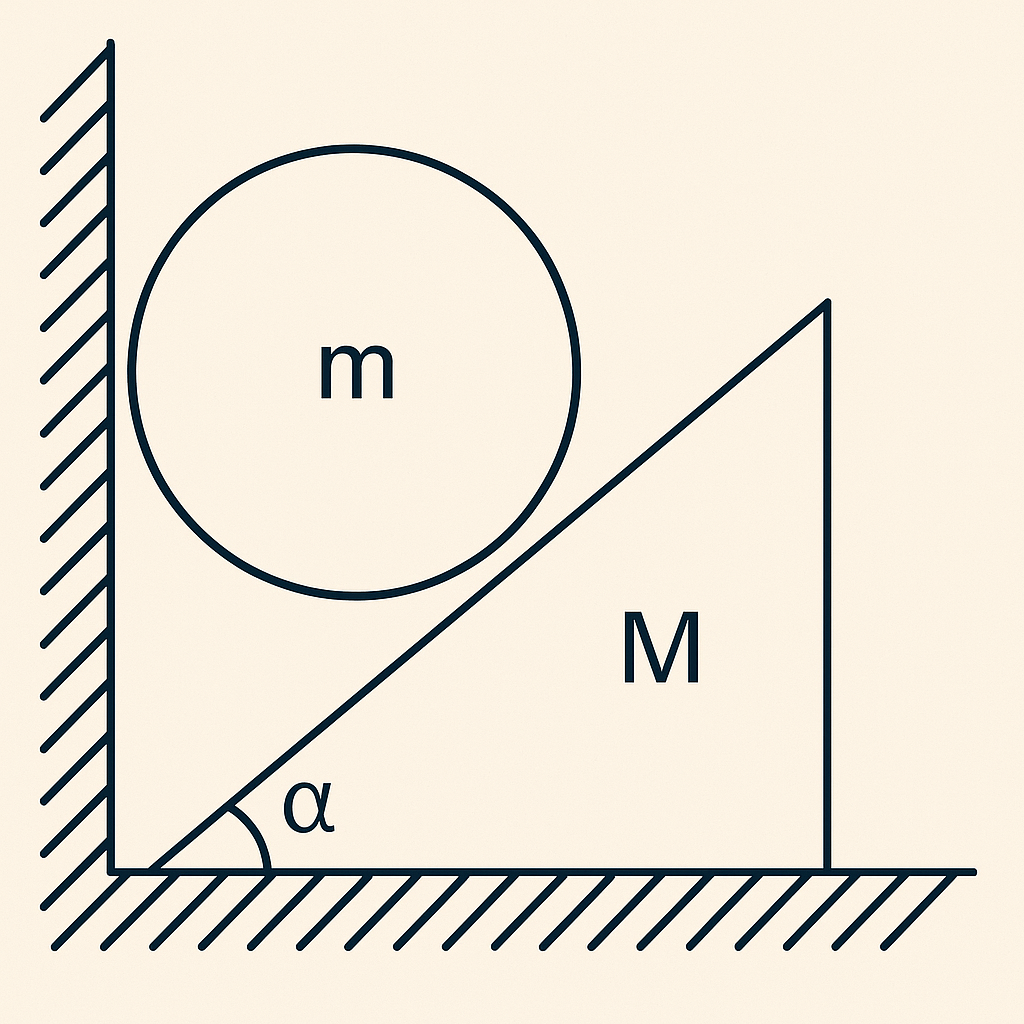
ניתוח המערכת
נסתכל על בעיה שבה יש לנו גליל (מסה קטנה $m$) על טריז (מסה גדולה $M$). נבחר מערכת צירים כך שציר $x$ פונה ימינה, וציר $y$ פונה כלפי מעלה.
הטריז נמצא בזווית $\alpha$ ביחס למישור האופקי, כאשר הגליל נמצא עליו.
הכוחות על המסה הגדולה ($M$)
נסתכל תחילה על המסה הגדולה (הטריז). הכוחות הפועלים עליה:
- כוח נורמלי $N_1$ מהגליל (המסה הקטנה) על הטריז
- כוח המשיכה $Mg$ הפועל כלפי מטה
- כוח נורמלי $\tilde{N}$ מהרצפה על הטריז
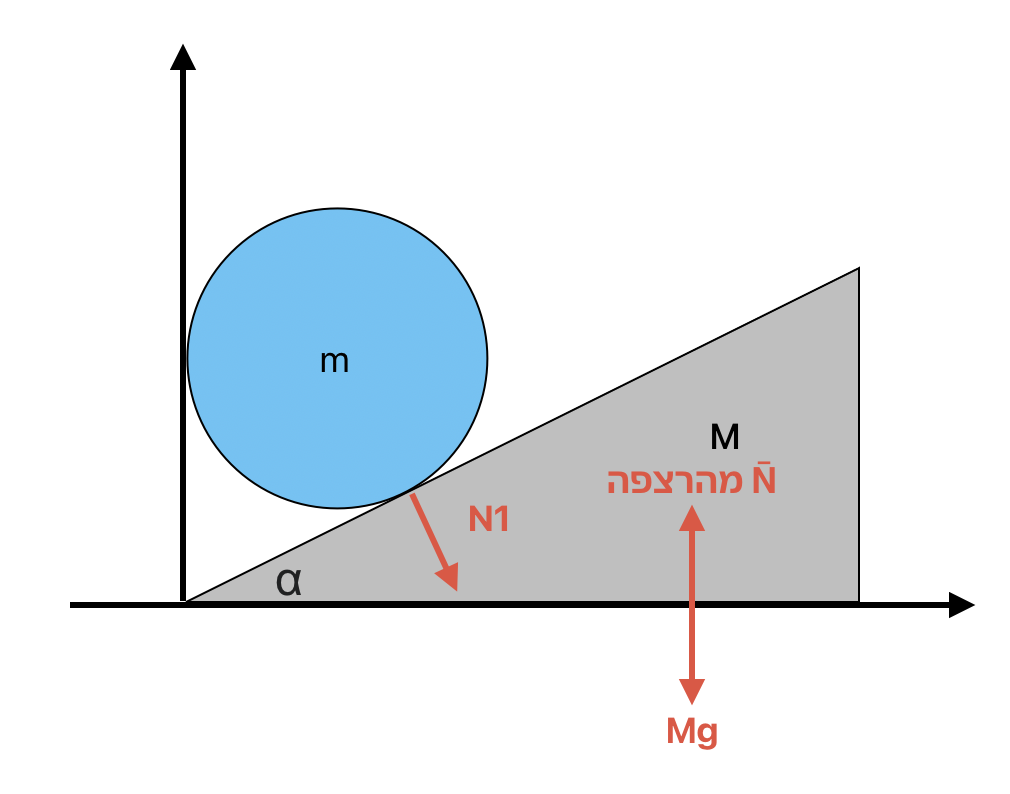
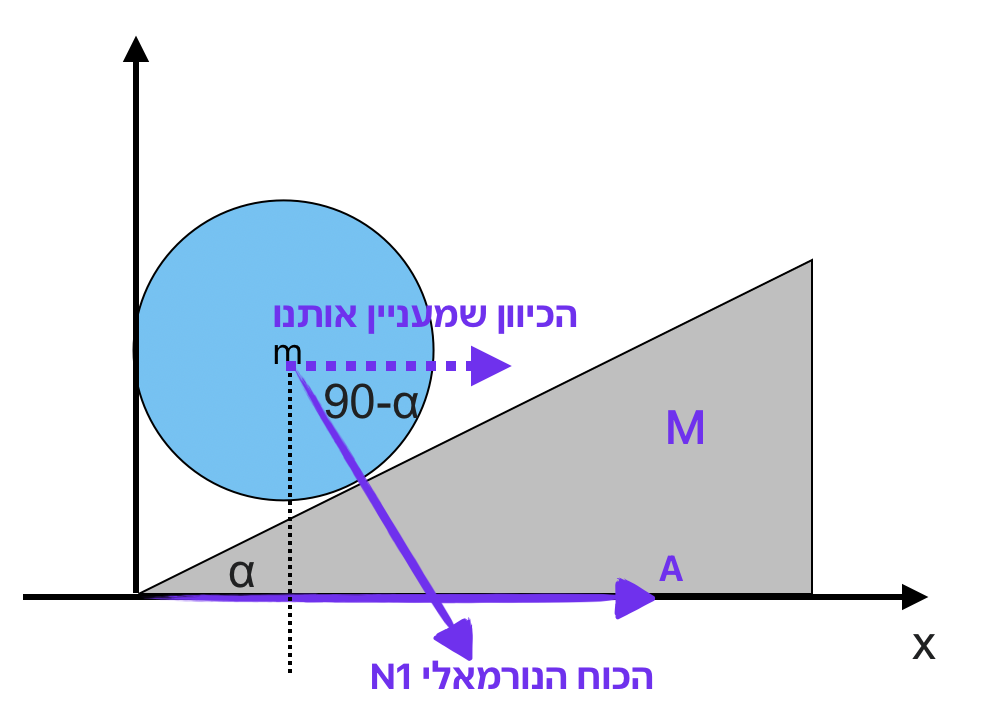
לפי החוק השני של ניוטון, בכיוון ציר $x$:
\[N_1 \sin \alpha = MA\]כאשר $A$ היא התאוצה של הטריז בכיוון ציר $x$ החיובי.
בכיוון ציר $y$, אין תאוצה (הטריז לא מתרומם), ולכן לפי החוק הראשון של ניוטון:
\[N_1 \cos \alpha + Mg = \tilde{N}\]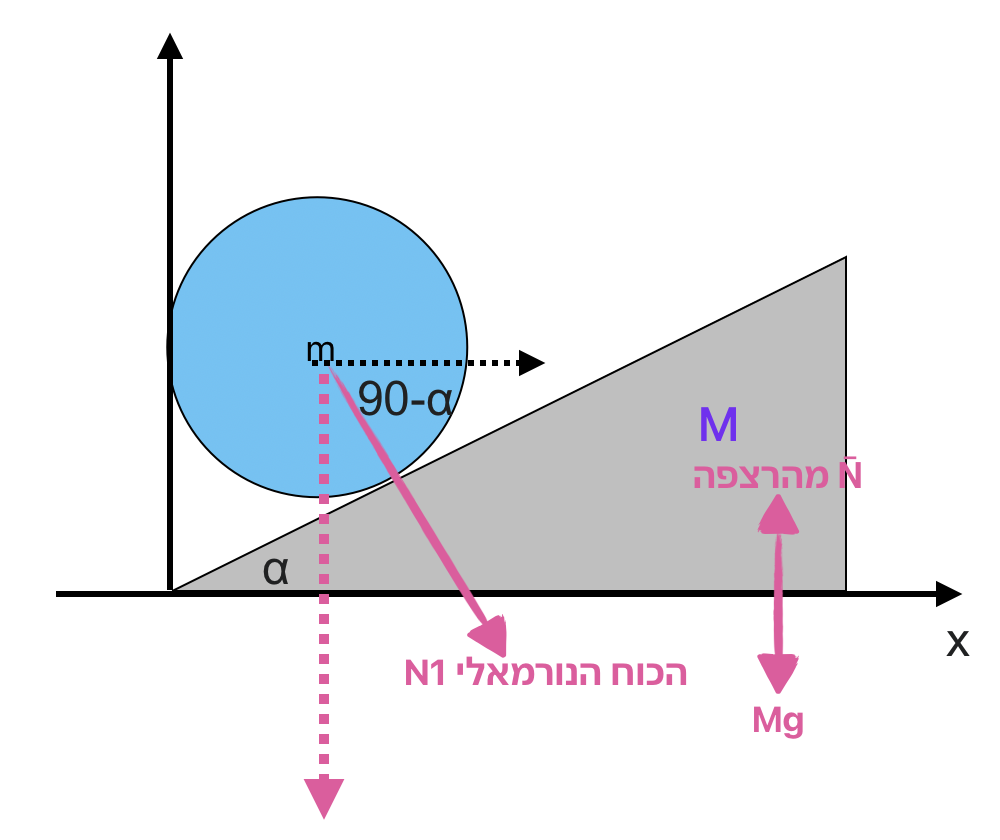
הכוחות על המסה הקטנה ($m$)
עכשיו נסתכל על המסה הקטנה (הגליל). הכוחות הפועלים עליה:
- כוח נורמלי $N_1$ מהטריז על הגליל (בכיוון הפוך לכוח שהגליל מפעיל על הטריז)
- כוח המשיכה $mg$ כלפי מטה
- כוח נורמלי $N_2$ מהקיר על הגליל
שימו לב שהגליל נלחץ בין הטריז לבין הקיר, ולכן מרגיש את הכוח הנורמלי $N_2$ מהקיר.
מכיוון שהגליל צמוד לקיר ולא מבצע תנועה בכיוון ציר $x$, מתקיים לפי החוק הראשון של ניוטון:
\[N_1 \sin \alpha = N_2\]בכיוון ציר $y$, לפי החוק השני של ניוטון (אם נגדיר את הכיוון החיובי כלפי מטה):
\[mg - N_1 \cos \alpha = ma\]כאשר $a$ היא התאוצה של הגליל כלפי מטה.
אילוץ גיאומטרי
מהגיאומטריה של הבעיה, ניתן להסיק שהיחס בין התאוצה בציר $y$ לבין התאוצה בציר $x$ חייב להיות קבוע ושווה לטנגנס של הזווית $\alpha$:
\[\frac{a}{A} = \tan \alpha\]כלומר, $a = A \tan \alpha$.
פתרון הבעיה
יש לנו שלוש משוואות בשלושה נעלמים ($N_1$, $A$, $a$):
- $N_1 \sin \alpha = MA$ (מהניתוח של הטריז)
- $mg - N_1 \cos \alpha = ma$ (מהניתוח של הגליל)
- $a = A \tan \alpha$ (מהאילוץ הגיאומטרי)
מהמשוואה הראשונה, נקבל:
\[A = \frac{N_1 \sin \alpha}{M}\]מהמשוואה השנייה, נקבל:
\[a = \frac{mg - N_1 \cos \alpha}{m}\]כעת נשתמש במשוואה השלישית ונציב:
\[\frac{mg - N_1 \cos \alpha}{m} = \frac{N_1 \sin \alpha}{M} \tan \alpha\]נפשט את המשוואה:
\[\frac{mg - N_1 \cos \alpha}{N_1 \sin \alpha} \cdot \frac{M}{m} = \tan \alpha\] \[\frac{mg}{N_1 \sin \alpha} \cdot \frac{M}{m} - \frac{N_1 \cos \alpha}{N_1 \sin \alpha} \cdot \frac{M}{m} = \tan \alpha\] \[\frac{Mg}{N_1 \sin \alpha} - \frac{M \cos \alpha}{m \sin \alpha} = \tan \alpha\] \[\frac{Mg}{N_1 \sin \alpha} - \frac{M}{m} \cdot \frac{1}{\tan \alpha} = \tan \alpha\]מכאן ניתן לחלץ את $N_1$:
\[\frac{Mg}{N_1 \sin \alpha} = \tan \alpha + \frac{M}{m} \cdot \frac{1}{\tan \alpha}\] \[\frac{Mg}{N_1 \sin \alpha} = \tan \alpha + \frac{M}{m \tan \alpha}\] \[N_1 = \frac{Mg}{\sin \alpha \left(\tan \alpha + \frac{M}{m \tan \alpha}\right)}\]לאחר שמצאנו את $N_1$, ניתן להציב חזרה במשוואות ולמצוא את $A$ ואת $a$.
הערות נוספות
- החישוב הזה הוא אלגברי בלבד, ואינו דורש שימוש במספרים.
- אם היינו רוצים למצוא את $N_2$, היינו משתמשים במשוואה $N_1 \sin \alpha = N_2$.
- הביטויים שקיבלנו מכילים פרמטרים פיזיקליים ($m$, $M$, $\alpha$, $g$) שמאפיינים את המערכת ואינם משתנים עם הזמן.
- בקורס זה, בדרך כלל נפתור בעיות באופן פרמטרי, ללא הצבת מספרים.
צניחה חופשית עם התנגדות אוויר
הבעיה הפיזיקלית
הבעיה שנתתי בתרגיל הבית עסקה בצנחנית (או צונחת) הנמצאת בצניחה חופשית. על פי נתוני הבעיה, פועל עליה כוח גרר שמתכונתי לריבוע המהירות שלה. נבחן את הכוחות הפועלים על הצנחנית ואת התנועה שלה כפונקציה של הזמן.
הכוחות הפועלים
אם אנחנו מדמים את הצנחנית כנקודה חומרית, הכוחות הפועלים עליה הם:
- כוח הכבידה כלפי מטה: $mg$
- כוח הגרר (התנגדות האוויר) כלפי מעלה: $\beta v^2$
כאשר הצנחנית מתחילה את הצניחה ממהירות אפס, ברור ש-$mg > \beta v^2$ בהתחלה, ולכן היא מאיצה כלפי מטה. אולם, ככל שהמהירות גדלה, כוח הגרר ($\beta v^2$) גדל גם הוא.
מהירות טרמינלית
התהליך של הגדלת המהירות נמשך עד שמגיעים למצב שבו $\beta v^2 = mg$. ברגע זה, שקול הכוחות שווה לאפס, חל תנאי ההתמדה (החוק הראשון של ניוטון), והצנחנית תתמיד במהירות קבועה - זוהי המהירות הטרמינלית.
המהירות הטרמינלית ($v_T$) ניתנת על ידי:
\[\beta v_T^2 = mg\]ומכאן:
\[v_T = \sqrt{\frac{mg}{\beta}}\]במקרה של צונחת רגילה, $\beta$ הוא בסדר גודל של 6, והמהירות הטרמינלית היא בסביבות 200 קמ”ש (בגבהים נמוכים). בגבהים גבוהים יותר (כמו 10 ק”מ), צפיפות האוויר נמוכה יותר, כוח הגרר קטן יותר, ולכן המהירות הטרמינלית גבוהה יותר.
המשוואה הדיפרנציאלית
כעת נבנה את המשוואה הדיפרנציאלית המתארת את התנועה. לפי החוק השני של ניוטון:
\[m \frac{dv}{dt} = mg - \beta v^2\]נחלק את שני האגפים ב-$m$:
\[\frac{dv}{dt} = g - \frac{\beta}{m} v^2\]לשם נוחות, נגדיר פרמטר חדש:
\[\alpha^2 = \frac{\beta}{m}\]כך שהמשוואה הופכת ל:
\[\frac{dv}{dt} = g - \alpha^2 v^2\]פתרון המשוואה הדיפרנציאלית
שלב 1: הפרדת משתנים
נפריד את המשתנים במשוואה:
\[\frac{dv}{g - \alpha^2 v^2} = dt\]שלב 2: ביצוע האינטגרציה
נבצע אינטגרציה משני צדי המשוואה:
\[\int \frac{dv}{g - \alpha^2 v^2} = \int dt = t + C\]לפתרון האינטגרל בצד שמאל, נעשה טריק אלגברי. נכפול ונחלק את האינטגרל ב-$\alpha$:
\[\int \frac{dv}{g - \alpha^2 v^2} = \frac{1}{\alpha} \int \frac{\alpha \, dv}{g - \alpha^2 v^2}\]נגדיר $y = \alpha v$, כך ש-$dy = \alpha \, dv$, ונקבל:
\[\frac{1}{\alpha} \int \frac{dy}{g - y^2}\]שלב 3: פתרון בעזרת פונקציות היפרבוליות
נעשה החלפת משתנים נוספת: $y = \sqrt{g} \tanh \phi$, כאשר $\phi$ משתנה חדש.
נבדוק מה המכנה במונחים של $\phi$:
\[g - y^2 = g - g \tanh^2 \phi = g(1 - \tanh^2 \phi) = \frac{g}{\cosh^2 \phi}\]כעת נחשב את $dy$:
\[dy = \sqrt{g} \cdot \frac{d(\tanh \phi)}{d\phi} \cdot d\phi = \frac{\sqrt{g}}{\cosh^2 \phi} \, d\phi\]נציב במשוואה:
\[\frac{1}{\alpha} \int \frac{dy}{g - y^2} = \frac{1}{\alpha} \int \frac{\frac{\sqrt{g}}{\cosh^2 \phi} \, d\phi}{\frac{g}{\cosh^2 \phi}} = \frac{1}{\alpha \sqrt{g}} \int d\phi = \frac{\phi}{\alpha \sqrt{g}} + C\]שלב 4: חזרה למשתנה המקורי
מהגדרת $\phi$ אנחנו יודעים ש:
\[\frac{\alpha v}{\sqrt{g}} = \tanh \phi\]לכן:
\[\phi = \tanh^{-1}\left(\frac{\alpha v}{\sqrt{g}}\right)\]נציב בפתרון:
\[\frac{1}{\alpha \sqrt{g}} \tanh^{-1}\left(\frac{\alpha v}{\sqrt{g}}\right) = t + C\]נכפול את שני הצדדים ב-$\alpha \sqrt{g}$:
\[\tanh^{-1}\left(\frac{\alpha v}{\sqrt{g}}\right) = \alpha \sqrt{g} \, t + C'\]שלב 5: קביעת קבוע האינטגרציה
נשתמש בתנאי ההתחלה: בזמן $t = 0$, המהירות $v = 0$.
\[\tanh^{-1}\left(\frac{\alpha \cdot 0}{\sqrt{g}}\right) = \alpha \sqrt{g} \cdot 0 + C'\]מכיוון ש-$\tanh^{-1}(0) = 0$, נקבל $C’ = 0$.
שלב 6: המהירות כפונקציה של הזמן
כעת נוציא את $v$ מהמשוואה על ידי הפעלת פונקציית $\tanh$ על שני צדי המשוואה:
\[\frac{\alpha v}{\sqrt{g}} = \tanh(\alpha \sqrt{g} \, t)\]ומכאן:
\[v(t) = \frac{\sqrt{g}}{\alpha} \tanh(\alpha \sqrt{g} \, t)\]בדיקת יחידות
נבדוק אם היחידות במשוואה הסופית הגיוניות:
מהמשוואה $\frac{dv}{dt} = g - \alpha^2 v^2$, נובע ש-$\alpha^2 v^2$ חייב להיות בעל יחידות של תאוצה (מטר לשנייה בריבוע). כלומר:
\[[\alpha^2 v^2] = [\alpha^2] \cdot [v^2] = [\alpha^2] \cdot \frac{m^2}{s^2} = \frac{m}{s^2}\]מכאן:
\[[\alpha^2] = \frac{1}{m}\] \[[\alpha] = \frac{1}{\sqrt{m}}\]בפתרון הסופי:
\[v(t) = \frac{\sqrt{g}}{\alpha} \tanh(\alpha \sqrt{g} \, t)\]היחידות של $\sqrt{g}$ הן $\sqrt{\frac{m}{s^2}} = \frac{\sqrt{m}}{s}$. כשמחלקים ב-$\alpha$ שיחידותיו $\frac{1}{\sqrt{m}}$, מקבלים $\frac{m}{s}$, שהן אכן יחידות של מהירות, כנדרש.
התנהגות המהירות לאורך זמן
-
בזמן $t = 0$:
\[v(0) = \frac{\sqrt{g}}{\alpha} \tanh(0) = 0\]כמצופה, המהירות ההתחלתית היא אפס.
-
כאשר $t \to \infty$:
\[v(t) \to \frac{\sqrt{g}}{\alpha} \tanh(\infty) = \frac{\sqrt{g}}{\alpha} \cdot 1 = \frac{\sqrt{g}}{\alpha}\]מכיוון ש-$\alpha^2 = \frac{\beta}{m}$, נקבל:
\[v(t) \to \frac{\sqrt{g}}{\sqrt{\frac{\beta}{m}}} = \sqrt{\frac{mg}{\beta}}\]וזוהי בדיוק המהירות הטרמינלית שחישבנו קודם.
הערה חשובה על כיוון המהירות
חשוב לציין שהפתרון שמצאנו מניח שהצנחנית נעה כלפי מטה (בכיוון החיובי של ציר ה-$y$). אם היא הייתה קופצת כלפי מעלה בתחילת התנועה, אז כוח הגרר היה פועל בכיוון מנוגד, וצריך היה לשנות את סימנו במשוואה עד לנקודה שבה המהירות משנה כיוון.
סיכום
פתרנו את המשוואה הדיפרנציאלית המתארת את תנועת הצנחנית בנוכחות כוח גרר הפרופורציונלי לריבוע המהירות. הפתרון מראה כיצד המהירות גדלה עם הזמן ומתקרבת בהדרגה למהירות הטרמינלית.
הגרפים של המהירות כפונקציה של הזמן יראו עקומה העולה במהירות בתחילה, ואז מתמתנת בהדרגה ומתקרבת אסימפטוטית למהירות הטרמינלית.
דור פסקל