תוכן עניינים:
- שאלה באלקטרוסטטיקה: חשיבה לפני חישוב
- שאלה 2: חוט מוליך אידיאלי
- שאלה 3: תייל ישר אינסופי
- שאלה 4: זרם דרך רדיוס דיסקה
- חלק א’: משוואות מקסוול – התמונה הגדולה
- חלק ב’: מי מייצר מה ועל מי פועל כוח
- חלק ג’: כוח לורנץ – המשוואה החמישית
- חלק ד’: שדה מגנטי של תיל – חוק אמפר
- חלק ה’: מהו זרם? (הגדרות חשובות)
- חלק ו’: שאלות מהשיעור
- חלק ז’: סיכום – מה צריך לדעת?
שאלה באלקטרוסטטיקה: חשיבה לפני חישוב
כדור מבודד ברדיוס $R$, הטעון בצפיפות מטען נפחית המשתנה לפי הפונקציה
\[\rho(r) = \rho_0 \left(1 - \frac{4r}{3R}\right) \, , \quad r < R\]קלפיה מוליכה מוארקת ($V=0$) ברדיוס $2R$ המקיפה את הכדור.
כוח חיצוני מעביר מטען נקודתי חיובי $q$ מהקליפה מוארקת $(r=2R)$ אל מרכז הכדור ($r=0$).
מה העבודה $W$ שביצע הכוח החיצוני?
- $W=0$
- $W = \frac{\rho_0 R^2 q}{18 \epsilon_0}$
- $W = \frac{\rho_0 R^2 q}{6 \epsilon_0}$
- $W = \frac{\rho_0 R^2 q}{12 \epsilon_0} \ln 2$
תזכורת:
\[W_{2R \to 0} = \int \vec{F} \cdot d\vec{r} = \int q\vec{E} \cdot d\vec{r} = q \int_{2R}^{0} E(r) \, dr\]נפתור את השאלה:
שלב 1: מציאת השדה החשמלי בתוך הכדור
נשתמש בחוק גאוס:
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{\text{enc}}}{\epsilon_0}\]נחשב את המטען הכולל של הכדור (עבור $r = R$):
\[Q_{\text{total}} = \int_0^R \rho(r') \cdot 4\pi r'^2 \, dr' = 4\pi \rho_0 \int_0^R \left(1 - \frac{4r'}{3R}\right) r'^2 \, dr'\] \[= 4\pi \rho_0 \left[\frac{r'^3}{3} - \frac{r'^4}{3R}\right]_0^R = 4\pi \rho_0 \left(\frac{R^3}{3} - \frac{R^3}{3}\right) = 0\]מכאן נקבל את השדה החשמלי בין $R$ ל-$2R$:
\[\vec{E}(R<r<2R) = 0\]נחשב את המטען הכלוא בתוך כדור רדיוס $r < R$:
\[4\pi r^2 \cdot E(r<R) = \frac{Q_{\text{enc}}}{\epsilon_0} = \frac{1}{\epsilon_0} \int_0^r \rho(r') \cdot 4\pi r'^2 \, dr'\] \[= \frac{4\pi \rho_0}{\epsilon_0} \int_0^r \left(1 - \frac{4r'}{3R}\right) r'^2 \, dr' = \frac{4\pi \rho_0}{\epsilon_0} \left[\frac{r'^3}{3} - \frac{r'^4}{3R}\right]_0^r = \frac{4\pi \rho_0}{\epsilon_0} \left(\frac{r^3}{3} - \frac{r^4}{3R}\right)\]מכאן נקבל את השדה החשמלי בתוך הכדור:
\[\vec{E}(r<R) = \frac{\rho_0 r}{3 \epsilon_0} \left(1 - \frac{r}{R}\right) \hat{r}\]שלב 2: חישוב העבודה
\[W_{2R \to 0} = q \int_{2R}^{0} E(r) \, dr = q \int_{2R}^{R} \underbrace{0}_{E(R\leq r \leq 2R)=0} \, dr + q \int_{R}^{0} \frac{\rho_0 r}{3 \epsilon_0} \left(1 - \frac{r}{R}\right) dr\] \[= \frac{q \rho_0}{3 \epsilon_0} \int_{R}^{0} \left(r - \frac{r^2}{R}\right) dr = \frac{q \rho_0}{3 \epsilon_0} \left[\frac{r^2}{2} - \frac{r^3}{3R}\right]_R^0\] \[= \frac{q \rho_0}{3 \epsilon_0} \left(0 - \frac{R^2}{2} + \frac{R^2}{3}\right) = \frac{q \rho_0}{3 \epsilon_0} \cdot \left(-\frac{R^2}{6}\right) = -\frac{\rho_0 R^2 q}{18 \epsilon_0}\]מכיוון שהעבודה של כוח חיצוני שווה למינוס העבודה של השדה:
\[W_{\text{ext}} = -W_{\text{field}} = \frac{\rho_0 R^2 q}{18 \epsilon_0}\]שאלה 2: חוט מוליך אידיאלי
\[\varepsilon = \frac{-\partial \Phi_B}{\partial t} = -\frac{\partial (B \cdot A)}{\partial t} = -B \frac{\partial \overset{\star}{A}}{\partial t}\]חוט מוליך אידיאלי אידיאלי ובעל מסה זניחה, עשוי בצורת $V$ שמשוואתו היא \(y=\|x\|\) מונח במישור הדף (מישור $xy$). במרחב פועל שדה מגנטי אחיד $B$ המכוון כלפי פנים הדף.
מוט מוליך ארוך מאוד בעל צפיפות התנגדות אורכית $\lambda \left[\frac{\Omega}{m}\right]$ מוסע במהכירות קבועה נתונה (בכיוון החיובי של ציר ה-$y$) כאשר בתחילה הוא היה מונח במנוחה על גבי ציר $X$ ובמהלך תנועתו המוט נשאר מקביל לציר $X$.
התלות בזמן של הכא״מ במושרה במוט היא:
- א. $\varepsilon(t) = - 2 B V^2 t$
- ב. $\varepsilon(t) = - B V^2 t $
- ג. $\varepsilon(t) = - 4 BV^2 t$
- ד. $\varepsilon(t) = - BV^2 t^2$
גודלו וכיוונו של הזרם במוט היא:
- א. $I(t) = \frac{Bv}{\lambda}$ שמאלה
- ב. $I(t) = \frac{2B V^2 t}{\lambda}$ ימינה
- ג. $I(t) = \frac{4 B V^2 t}{\lambda}$ ימינה
- ד. $I(t) = \frac{B V^2}{\lambda}$ שמאלה
גודלו וכיוונו של הכוח החיצוני המופעל בכדי לקיים את המהירות הקבועה של המוט האופקי הוא (מהירות מטעני הזרם מקיימת את המשוואה: $qv_x = IL$):
- א. $\vec{F}_{\text{ext}} = -2\frac{B^2 V^3}{\lambda} t$ למעלה
- ב. $\vec{F}_{\text{ext}} = -\frac{B V^2 t}{\lambda}$ למעלה
- ג. $\vec{F}_{\text{ext}} = -\frac{4B}{\lambda}$ למטה
- ד. $\vec{F}_{\text{ext}} = -\frac{B V^2}{\lambda}$ למעלה
כאשר $\star$ מסמן שטח חתך של המעגל החשמלי המשולשי.
\[\overset{\star}{A} = \frac{1}{2} \cdot \text{base} \cdot \text{height} = \frac{1}{2} \cdot (2 V t) \cdot (V t) = V^2 t^2\] \[\Rightarrow \varepsilon = -B \frac{\partial (V^2 t^2)}{\partial t} = -2 B V^2 t\] \[I = \frac{\varepsilon}{R} = \frac{-2 B V^2 t}{\lambda \cdot (2 V t)} = \frac{-B V}{\lambda}\]לגבי הכיוון - באמצעות כלל יד ימין, נקבל שהזרם הוא שמאלה.
\[q V_x \times B = I \cdot (2 V t) \cdot B \hat{z} = \frac{-B V}{\lambda} \cdot (2 V t) \cdot B \hat{z} = \frac{-2 B^2 V^2 t}{\lambda} \hat{z}\]
שאלה 3: תייל ישר אינסופי
נתון תייל ישר אינסופי הנושא זרם $I$ לאורכו. מכניסים אלקטרון בנקודה $P$ עם מהירות התחלתית $v_0$, בכיוון המאונך לתייל והרחק ממנו. ראו איור.
I ↑ | P | -------------> v_0 | | |מהו כיוון הכוח המגנטי הפועל על האלקטרון בנקודה זו?
- לתוך הדך $\otimes$
- ימינה $\rightarrow$
- למעלה $\uparrow$
- שמאלה $\leftarrow$
- למטה $\downarrow$
נשתמש בכלל יד ימין:
- כיוון הזרם: למעלה
- כיוון מהירות האלקטרון: ימינה
- כיוון המטען: שלילי (האלקטרון)
- כיוון השדה המגנטי: לתוך הדף $\otimes$
- כיוון הכוח המגנטי: למטה $\downarrow$
- תשובה נכונה: 5. למטה $\downarrow$
F אגודל V אצבע B אצבע אמצעית
בגלל שזה אלקטרון הופכים את כיוון הכוח (שלילי).
\[\vec{F} = q(\vec{v} \times \vec{B})\]השדה המגנטי יוצר שדה פנימה כי הזרם למעלה. יוצר שדה מגנטי סיבובי לפי כלל יד ימין (הנוסף).
שאלה 4: זרם דרך רדיוס דיסקה
דיסקה ברדיוס $R$ טעונה בצפיפות מטען משטחית אחידה $\sigma$. הדיסקה מסתובבת במהירות זוויתית $\omega$. מהו הזרם העובר דרך רדיוס הדסקה?
- $I = \frac{\sigma \omega R^2}{2}$
- $I = \sigma \omega R^2$
- $I = \frac{\sigma \omega R}{2}$
- $I = 0$
- תלוי בזמן
ω
↻
-----
| |
| | σ
| |
-----
נחשב את המטען הכולל על הדיסקה:
\[Q = \sigma \cdot A = \sigma \cdot \pi R^2\]מהירות אופקית (ניצבת ל-$R$) בנקודה ברדיוס $r$:
\[v = \omega r\]הזרם הוא מטען ליחידת זמן:
\[I = \frac{dQ}{dt}\]נחשב את המטען שעובר דרך הרדיוס $R$:
\[I = \sigma \cdot (2 \pi r) \cdot v = \ \sigma \cdot (2 \pi r) \cdot (\omega r) = 2 \pi \sigma \omega r^2\]נחשב את הזרם הכולל על כל הדיסקה על ידי אינטגרציה מ-$0$ עד $R$:
\[I_{\text{total}} = \int_0^R 2 \pi \sigma \omega r^2 \, dr = 2 \pi \sigma \omega \left[\frac{r^3}{3}\right]_0^R = \frac{2 \pi \sigma \omega R^3}{3}\]תשובה נכונה: 1. $I = \frac{\sigma \omega R^2}{2}$
להלן גרסת התרגול של יותם:
חלק א’: משוואות מקסוול – התמונה הגדולה
לפני שנכנס לשאלות, בואו נבין את הסיפור השלם. יש לנו שני שדות בטבע – שדה חשמלי $\vec{E}$ ושדה מגנטי $\vec{B}$ – והם משפיעים אחד על השני. משוואות מקסוול הן ארבע משוואות שמתארות הכל על השדות האלה.
מושגים בסיסיים – שטף וקונטור
לפני שנכתוב את המשוואות, צריך להבין שני כלים מתמטיים:
שטף (Flux) דרך משטח סגור $\oint \vec{F} \cdot d\vec{A}$: דמיינו שיש לכם קופסה סגורה (או ספירה). שטף זה כמה “חיצים” של השדה יוצאים מהקופסה. אם יותר יוצאים מאשר נכנסים – השטף חיובי. אם הכל מתקזז – השטף אפס.
קונטור (Contour) $\Gamma$: קונטור זה קו סגור – כמו מעגל או ריבוע. כשכותבים $\oint_\Gamma \vec{F} \cdot d\vec{l}$ הכוונה היא: הולכים לאורך הקו הסגור $\Gamma$ וסוכמים את תרומת השדה לאורך המסלול. זה נקרא אינטגרל קווי סגור (circulation).
המשוואה הראשונה – חוק גאוס לשדה חשמלי
\[\oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\varepsilon_0}\]מה זה אומר בעברית: שטף השדה החשמלי דרך משטח סגור = כמות המטען שבתוך המשטח חלקי $\varepsilon_0$.
בקיצור: מטענים מייצרים שדה חשמלי. יש מטען בפנים? יוצא שדה חשמלי.
המשוואה השנייה – חוק גאוס לשדה מגנטי
\[\oint \vec{B} \cdot d\vec{A} = 0\]מה זה אומר בעברית: שטף השדה המגנטי דרך משטח סגור הוא תמיד אפס.
למה? כי אין “מטען מגנטי” (מונופול מגנטי). כל קו שדה מגנטי שיוצא מהקופסה – חייב גם לחזור אליה. לכן הסך תמיד אפס.
חשוב להבין: דרך שטח פתוח (כמו דיסקה, מעגל) כן אפשר למצוא שטף מגנטי! רק דרך משטח סגור (כמו ספירה, קופסה) השטף תמיד אפס.
המשוואה השלישית – חוק פאראדיי (קונטור של $\vec{E}$)
\[\oint_\Gamma \vec{E} \cdot d\vec{l} = -\frac{d\Phi_B}{dt}\]מה זה אומר בעברית: אם עושים קונטור $\Gamma$ (מעגל סגור) ומחשבים את האינטגרל הקווי של השדה החשמלי – מקבלים שזה שווה לשינוי בשטף המגנטי דרך השטח שהקונטור תוחם.
בקיצור: שדה מגנטי משתנה בזמן ← נוצר שדה חשמלי.
מתי יש שדה חשמלי דרך קונטור?
- ❌ שדה מגנטי קבוע ← לא מספיק!
- ✅ שדה מגנטי משתנה בזמן ← כן! נוצר שדה חשמלי
המשוואה הרביעית – חוק אמפר-מקסוול (קונטור של $\vec{B}$)
\[\oint_\Gamma \vec{B} \cdot d\vec{l} = \mu_0 I_{enc} + \mu_0 \varepsilon_0 \frac{d\Phi_E}{dt}\]מה זה אומר בעברית: קונטור $\Gamma$ של השדה המגנטי שווה לזרם שעובר דרך השטח שהקונטור תוחם, או לשדה חשמלי משתנה בזמן.
מתי יש שדה מגנטי דרך קונטור $\Gamma$?
- ✅ יש זרם $I$ שעובר בפנים
- ✅ יש שדה חשמלי משתנה בזמן בפנים
- אחד מהם או שניהם ביחד
סיכום משוואות מקסוול – טבלה
| משוואה | מה מחשבים | מה צריך שיהיה כדי לקבל תוצאה לא-אפס |
|---|---|---|
| גאוס ל-$\vec{E}$ (שטף) | $\oint \vec{E} \cdot d\vec{A}$ | מטען בפנים |
| גאוס ל-$\vec{B}$ (שטף) | $\oint \vec{B} \cdot d\vec{A}$ | תמיד אפס! |
| פאראדיי (קונטור $\Gamma$ של $\vec{E}$) | $\oint_\Gamma \vec{E} \cdot d\vec{l}$ | שדה מגנטי משתנה בזמן |
| אמפר (קונטור $\Gamma$ של $\vec{B}$) | $\oint_\Gamma \vec{B} \cdot d\vec{l}$ | זרם או שדה חשמלי משתנה בזמן |
חלק ב’: מי מייצר מה ועל מי פועל כוח
שדה חשמלי
| תשובה | |
|---|---|
| מי מייצר שדה חשמלי? | מטען |
| על מי השדה החשמלי מפעיל כוח? | על מטען אחר |
מטען מייצר שדה חשמלי סביבו. אם שמים מטען אחר בתוך השדה – הוא מרגיש כוח.
שדה מגנטי
| תשובה | |
|---|---|
| מי מייצר שדה מגנטי? | מטענים בתנועה (= זרם) |
| על מי השדה המגנטי מפעיל כוח? | על מטענים בתנועה (= זרם) |
דוגמה: אם יש תיל עם זרם $I$ – הוא מייצר שדה מגנטי סביבו (בעיגולים). גם מטען בודד שנע – מייצר שדה מגנטי!
הערה חשובה על מטען נע: אם מחזיקים מטען ביד ורצים – מנקודת המבט של אדם שעומד: המטען נע, אז יש גם שדה חשמלי (כי יש מטען) וגם שדה מגנטי (כי המטען בתנועה). השדה החשמלי “עוקב” אחרי המטען.
מנקודת המבט שלכם (שרצים עם המטען): המטען נראה קבוע (מהירות אפס!), אז אין שדה מגנטי. זה הסיפור ה”קריפי” של יחסות!
חלק ג’: כוח לורנץ – המשוואה החמישית
כל חמש המשוואות של הקורס הן ארבע משוואות מקסוול + כוח לורנץ:
\[\boxed{\vec{F} = q\vec{E} + q\vec{v} \times \vec{B}}\]שני חלקים:
- כוח חשמלי: $\vec{F}_E = q\vec{E}$ – פועל על כל מטען, גם אם הוא עומד במקום
- כוח מגנטי: $\vec{F}_B = q\vec{v} \times \vec{B}$ – פועל רק על מטען בתנועה
אם יש גם שדה חשמלי וגם מגנטי ← המטען מרגיש את שניהם ביחד.
צורות שימושיות
| מצב | נוסחה | מתי משתמשים |
|---|---|---|
| מטען בודד | $\vec{F} = q\vec{v} \times \vec{B}$ | מטען בודד נע בתוך שדה מגנטי |
| תיל נושא זרם | $\vec{F} = I\vec{L} \times \vec{B}$ | תיל עם זרם בתוך שדה מגנטי |
כלל יד ימין לכוח
כדי למצוא כיוון $\vec{v} \times \vec{B}$:
- תמיד עושים יד ימין (גם למטען שלילי!)
- אצבעות מצביעות בכיוון $\vec{v}$
- מסלסלים לכיוון $\vec{B}$
- האגודל מצביע לכיוון $\vec{v} \times \vec{B}$
- אם המטען שלילי (כמו אלקטרון) ← הופכים את הכיוון
חשוב: כשבודקים כיוון הכוח – בודקים לפי מי שמופעל עליו הכוח, לא לפי מי שמייצר את השדה. אם אלקטרון מייצר שדה מגנטי ומטען אחר נמצא בו – עושים יד ימין עבור המטען האחר.
חלק ד’: שדה מגנטי של תיל – חוק אמפר
דוגמה קלאסית: תיל אינסופי ישר
תיל אינסופי נושא זרם $I$. מה השדה המגנטי סביבו?
כלל יד ימין (מלפפת): האגודל בכיוון הזרם ← האצבעות מלפפות בכיוון השדה המגנטי.
השדה המגנטי עוטף את התיל בעיגולים:
\[\boxed{B = \frac{\mu_0 I}{2\pi r}}\]- $r$ – המרחק מהתיל
- כיוון: עיגולים סביב התיל (לפי יד ימין)
- $\mu_0 = 4\pi \times 10^{-7} \; T \cdot m / A$
מאיפה זה בא? מחוק אמפר! לוקחים קונטור $\Gamma$ מעגלי ברדיוס $r$ סביב התיל:
\[\oint_\Gamma \vec{B} \cdot d\vec{l} = B \cdot 2\pi r = \mu_0 I\]ומקבלים $B = \frac{\mu_0 I}{2\pi r}$.
הערה: גליל סופי (סולנואיד), כשמתקרבים אליו מאוד, נראה כמו תיל אינסופי – אז אפשר להשתמש באותה נוסחה.
חלק ה’: מהו זרם? (הגדרות חשובות)
הגדרה בסיסית
\[\boxed{I = \frac{dQ}{dt}}\]זרם = כמה מטען עובר בנקודה מסוימת ליחידת זמן. יחידות: אמפר $[A] = [C/s]$
צפיפות זרם $\vec{J}$
צפיפות זרם = כמה זרם עובר ליחידת שטח:
\[\boxed{\vec{J} = \sigma_q \vec{v}}\]- $\sigma_q$ – צפיפות מטען (מטען ליחידת שטח/נפח)
- $\vec{v}$ – מהירות המטענים
הקשר בין זרם לצפיפות זרם:
\[I = \int \vec{J} \cdot d\vec{A}\]זרם = אינטגרל של צפיפות הזרם על השטח שדרכו עוברים המטענים.
אינטואיציה: דמיינו צינור מים. צפיפות הזרם $\vec{J}$ אומרת כמה מים זורמים בכל נקודה. הזרם $I$ הכולל הוא הסכום על כל החתך של הצינור.
חלק ו’: שאלות מהשיעור
שאלה 1: זרם בדיסקה מסתובבת
דיסקה ברדיוס $R$ טעונה בצפיפות מטען משטחית $\sigma$ אחידה. הדיסקה מסתובבת במהירות זוויתית $\omega$.
מהו הזרם שעובר דרך חתך רדיאלי של הדיסקה?

פתרון – דרך אינטגרל
שלב 1: מציאת צפיפות הזרם
צפיפות זרם = צפיפות מטען × מהירות:
\[J = \sigma \cdot v\]המהירות של נקודה במרחק $r$ מהמרכז:
\[v = \omega r\]לכן:
\[J(r) = \sigma \omega r\]שימו לב: צפיפות הזרם תלויה ב-$r$. ככל שמתרחקים מהמרכז – המהירות גדלה ← צפיפות הזרם גדלה.
שלב 2: אינטגרציה על החתך
עושים חתך רדיאלי (קו מהמרכז לשפה). דרך כל פיסת $dr$ קטנה ברדיוס $r$ עובר זרם:
\[dI = J(r) \cdot dr = \sigma \omega r \, dr\]סוכמים מ-$0$ עד $R$:
\[I = \int_0^R \sigma \omega r \, dr = \sigma \omega \frac{r^2}{2}\Bigg|_0^R = \frac{\sigma \omega R^2}{2}\]פתרון – דרך חשיבה פיזיקלית
כמה מטען עובר דרך החתך בסיבוב שלם?
כל המטענים בדיסקה עוברים דרך הקו הרדיאלי פעם אחת בכל סיבוב. כמות המטען הכוללת על הדיסקה:
\[Q = \sigma \cdot \pi R^2\]כמה זמן לוקח סיבוב שלם?
\[T = \frac{2\pi}{\omega}\](כי $\omega$ ברדיאנים לשנייה, וסיבוב שלם = $2\pi$ רדיאנים)
הזרם:
\[I = \frac{Q}{T} = \frac{\sigma \pi R^2}{\frac{2\pi}{\omega}} = \frac{\sigma \omega R^2}{2} \checkmark\]שאלה 2: כוח על תיל אינסופי בשדה מגנטי
נתון תיל אינסופי עם צפיפות מטען קווית $\lambda$ (קבועה) לאורך ציר ה-$Z$.
התיל נמצא בשדה מגנטי אחיד חיצוני $\vec{B} = B_0 \hat{x}$ (בכיוון $\hat{x}$).
מניעים את התיל במהירות $\vec{v} = v\hat{z}$.
מהו הכוח ליחידת אורך הפועל על התיל?
- $\vec{F}/L = B_0 \lambda v \hat{x}$
- $\vec{F}/L = B_0 \lambda v \hat{y}$
- $\vec{F}/L = - B_0 \lambda v \hat{x}$
- $\vec{F}/L = - B_0 \lambda v \hat{y}$
- $\vec{F}/L = 0$
מערכת הצירים:
\[\hat{x}\text{ – into the page}, \quad \hat{y}\text{ – up}, \quad \hat{z}\text{ – to the right (along the wire)}\]פתרון
שלב 1: כיוון הכוח
\[\vec{F} = q\vec{v} \times \vec{B}\]כיוון: $\hat{z} \times \hat{x} = \hat{y}$ ← הכוח כלפי מעלה (בכיוון $\hat{y}$)
שלב 2: גודל הכוח
\[|\vec{F}| = |q| \cdot v \cdot B \cdot \sin\theta\]הזווית בין $\vec{v}$ (כיוון $\hat{z}$) לבין $\vec{B}$ (כיוון $\hat{x}$) היא $90°$:
\[\sin 90° = 1\]המטען על קטע באורך $L$:
\[Q = \lambda \cdot L\]הכוח על קטע $L$:
\[F = \lambda L \cdot v \cdot B \cdot 1 = \lambda L v B\]הכוח ליחידת אורך:
\[\boxed{\frac{\vec{F}}{L} = \lambda v B \; \hat{y}}\]הערה על כיוון: זה הכיוון בהנחה שהמטענים חיוביים. אם $\lambda < 0$ (מטענים שליליים), הכוח מתהפך.
שאלה 3: שדה מגנטי של שני תילים מקבילים
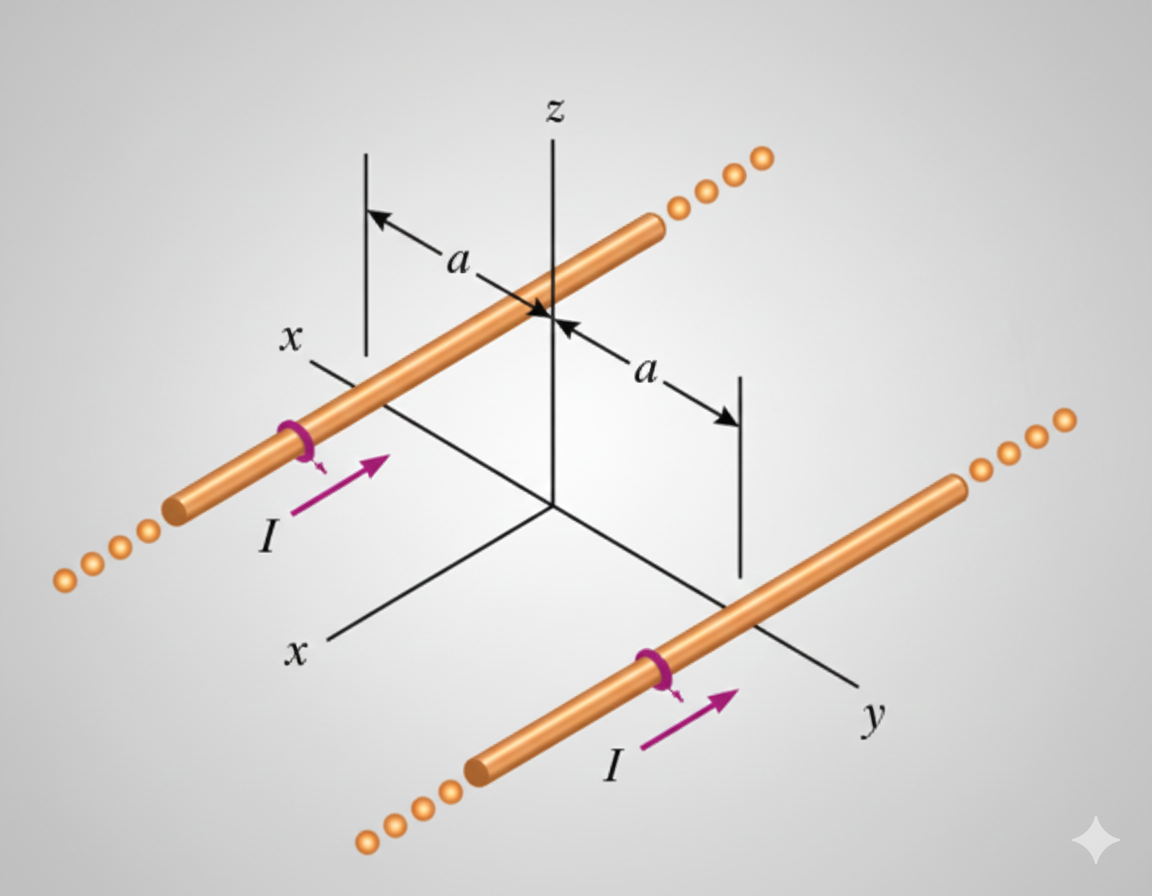
נתונים שני תילים אינסופיים מקבילים, כל אחד נושא זרם $I$ באותו כיוון (מינוס איקס), והם נמצאים במרחק $2d$ זה מזה (סימטרית סביב ציר ה-$Z$). (באיור $2a$ במקום $2d$).
- מצא את רכיבי השדה המגנטי ואת גודלו $B$ על הציר $z$ כפונקציה של $z$.
- עבור איזה ערך של הקואורדינטה $z$ יגיע גודל השדה המגנטי $B$ למקסימום?
פתרון
שלב 1: שדה של כל תיל בנפרד
כל תיל מייצר שדה מגנטי:
\[B_1 = B_2 = \frac{\mu_0 I}{2\pi r}\]כאשר $r$ = המרחק מהתיל לנקודה:
\[r = \sqrt{d^2 + z^2}\]שלב 2: כיוון – וביטול רכיבים
השדה של כל תיל מאונך לקו שמחבר את התיל לנקודה. בגלל הסימטריה:
- רכיבי $\hat{x}$ (אופקיים) – מבטלים זה את זה! (שווים בגודל, הפוכים בכיוון)
- רכיבי $\hat{y}$ (אנכיים) – מצטברים!
נשאר רק כיוון $\hat{y}$.
שלב 3: חישוב
הרכיב ב-$\hat{y}$ של כל תיל:
\[B_{y} = B \cos\alpha = \frac{\mu_0 I}{2\pi r} \cdot \cos\alpha\]כאשר $\cos\alpha = \frac{z}{r} = \frac{z}{\sqrt{d^2 + z^2}}$
סכום שני התילים:
\[B_{total} = 2 \cdot \frac{\mu_0 I}{2\pi r} \cdot \frac{z}{r} = \frac{\mu_0 I z}{\pi(d^2 + z^2)}\] \[\boxed{\vec{B}_{total} = \frac{\mu_0 I z}{\pi(d^2 + z^2)} \; \hat{y}}\]ניתוח: איפה השדה מקסימלי?
- כש-$z = 0$: $B = 0$ (הרכיבים מבטלים)
- כש-$z \to \infty$: $B \to 0$ (רחוק מדי)
- ביניהם יש מקסימום – גוזרים ומשווים לאפס ← המקסימום ב-$z = d$
שאלה 4: שדה מגנטי בתוך גליל עם צפיפות זרם אחידה
נתון גליל אינסופי ברדיוס $R$ עם צפיפות זרם $\vec{J}$ אחידה בכיוון $\hat{\varphi}$ (היקפי):
\[\vec{J} = J_0 \hat{\varphi}\]מה ניתן לומר על השדה המגנטי בתוך הגליל?
- כיוונו אורכי $\hat{z}$, והוא גדל עם המרחק הרדיאלי $r$.
- כיוונו היקפי $\hat{\varphi}$, והוא גדל עם המרחק הרדיאלי $r$.
- כיוונו אורכי $\hat{z}$, והוא קטן עם המרחק הרדיאלי $r$.
- כיוונו היקפי $\hat{\varphi}$, והוא קטן עם המרחק הרדיאלי $r$.
- כיוונו היקפי $\hat{\varphi}$, והוא לא תלוי במרחק הרדיאלי $r$.
ניתוח סימטריה
למה השדה תלוי רק ב-$r$?
בגלל הסימטריה הגלילית:
- אם זזים לאורך $\hat{z}$ – התמונה לא משתנה ← $B$ לא תלוי ב-$z$
- אם מסתובבים סביב הציר ($\hat{\varphi}$) – התמונה לא משתנה ← $B$ לא תלוי ב-$\varphi$
- רק אם זזים רדיאלית ($\hat{r}$) – רואים שינוי ← $B$ תלוי ב-$r$ בלבד
חוק אמפר – לולאת $\Gamma$
לוקחים קונטור $\Gamma$ מלבני: צלע אחת בגובה $z$ מסוים וברדיוס $r$, והצלעות האחרות סוגרות את הלולאה מבחוץ (שם $B = 0$).
\[\oint_\Gamma \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}\]ככל ש-$r$ קטן יותר ← הלולאה מקיפה פחות זרם ← השדה קטן יותר.
מסקנה: השדה המגנטי קטן ככל שמתקרבים למרכז הגליל.
אינטואיציה: חשבו על זרם מעגלי כמו לולאת זרם. כל לולאה מייצרת שדה שנכנס מצד אחד ויוצא מצד שני. כשאתם בפנים – השדה פנימה, בחוץ – השדה החוצה.
שאלה 5: כא”מ מושרה – חוט V עם מוט נע
נתון חוט מוליך ארוך בצורת V, כך ש-$y = |x|$ (זווית 45° מכל צד).
לחוט צפיפות התנגדות $\rho$ (התנגדות ליחידת אורך), ביחידות $[\Omega/m]$.
מוט מוליך ישר, מקביל לציר $X$, מונח על שני זרועות ה-V.
המוט נע כלפי מעלה ($+\hat{y}$) במהירות קבועה $v$.
שדה מגנטי אחיד $\vec{B} = -B\hat{z}$ (פנימה לדף).
בזמן $t = 0$ המוט על ראשית הצירים.
מצאו:
- כא”מ מושרה
- כיוון הזרם
- ההתנגדות
- הזרם
- הכוח על המוט
הבנת הסיטואציה
יש לנו לולאה מוליכה שנוצרת מה-V (שתי זרועות) + המוט (בסיס). ככל שהמוט עולה – הלולאה גדלה ← השטח גדל ← השטף המגנטי גדל ← יש כא”מ מושרה!
הסיפור של כא”מ מושרה:
\[\text{Changing magnetic flux} \rightarrow \text{EMF (induced voltage)} \rightarrow \text{Current} \rightarrow \text{Force}\]כלומר, שטף משתנה גורר כא״מ שגורם לזרם שגורם לכוח.
א. כא”מ מושרה
שלב 1: מציאת השטח כפונקציה של הזמן
השטח הוא משולש שווה שוקיים. כשהמוט בגובה $y$:
- בגלל ש-$y = |x|$, רוחב הבסיס = $2y$ (כי $x$ הולך מ-$-y$ עד $+y$)
- הגובה = $y$
המוט נע במהירות קבועה $v$, אז:
\[y = vt\] \[S(t) = v^2 t^2\]שלב 2: שטף מגנטי
\[\Phi_B = B \cdot S = B v^2 t^2\](כי $\vec{B}$ אחיד ומאונך לשטח)
שלב 3: גזירה
\[\mathcal{E} = -\frac{d\Phi_B}{dt} = -\frac{d}{dt}(Bv^2 t^2) = -2Bv^2 t\] \[\boxed{|\mathcal{E}| = 2Bv^2 t}\]ב. כיוון הזרם – חוק לנץ
חוק לנץ: הזרם המושרה מתנגד לשינוי בשטף (לא לשטף עצמו!).
- השדה המגנטי פנימה לדף ←
- השטח גדל ← השטף גדל ←
- כדי להתנגד לגידול ← הזרם צריך לייצר שדה מגנטי החוצה מהדף ←
- לפי כלל יד ימין ← זרם נגד כיוון השעון
דגש: אם המוט היה יורד (השטח קטן) – הזרם היה בכיוון השעון כדי להוסיף שטף ולהתנגד לקיטון.
ג. ההתנגדות
$\rho$ = התנגדות ליחידת אורך. צריך למצוא את אורך הלולאה הכולל:
אורך המוט (בסיס): $l_{base} = 2x = 2y = 2vt$
אורך כל שוק של ה-V: הזווית היא 45°, אז:
\[l_{arm} = \frac{y}{\sin 45°} = y\sqrt{2} = vt\sqrt{2}\]אורך כולל:
\[L_{total} = 2vt + 2 \cdot vt\sqrt{2} = 2vt(1 + \sqrt{2})\]ההתנגדות:
\[\boxed{R = \rho \cdot 2vt(1 + \sqrt{2})}\]ד. הזרם
\[I = \frac{|\mathcal{E}|}{R} = \frac{2Bv^2 t}{\rho \cdot 2vt(1 + \sqrt{2})}\]ה-$t$ מצטמצם! ה-$v$ מצטמצם חלקית:
\[\boxed{I = \frac{Bv}{\rho(1 + \sqrt{2})}}\]תוצאה מעניינת: הזרם קבוע בזמן! למרות שהכא”מ גדל עם הזמן, גם ההתנגדות גדלה באותו קצב.
ה. כוח על המוט
\[F = I \cdot l_{base} \cdot B = \frac{Bv}{\rho(1+\sqrt{2})} \cdot 2vt \cdot B\] \[\boxed{F = \frac{2B^2 v^2 t}{\rho(1+\sqrt{2})}}\]כיוון: כלפי מטה (מתנגד לתנועה – חוק לנץ!).
כוח חיצוני: כדי שהמוט ינוע במהירות קבועה, צריך כוח חיצוני שווה בגודל והפוך בכיוון ← כלפי מעלה באותו גודל.
שימו לב: הכוח על המוט גדל עם הזמן (למרות שהזרם קבוע), כי אורך המוט גדל עם הזמן.
חלק ז’: סיכום – מה צריך לדעת?
סוגי השאלות בנושא מגנטיות
| סוג שאלה | מה עושים | כלי |
|---|---|---|
| למצוא שדה מגנטי שזרם מייצר | חוק אמפר: $\oint_\Gamma \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}$ | בוחרים לולאת $\Gamma$ חכמה |
| למצוא כוח על מטען/זרם בשדה | כוח לורנץ: $\vec{F} = q\vec{v} \times \vec{B}$ | או $\vec{F} = I\vec{L} \times \vec{B}$ |
| למצוא כא”מ מושרה | חוק פאראדיי: $\mathcal{E} = -\frac{d\Phi_B}{dt}$ | + חוק לנץ לכיוון |
| למצוא זרם | $I = dQ/dt$ או $I = \int \vec{J} \cdot d\vec{A}$ | הגדרת זרם |
חמש המשוואות של הקורס
- $\oint \vec{E} \cdot d\vec{A} = \frac{Q_{enc}}{\varepsilon_0}$ (גאוס)
- $\oint \vec{B} \cdot d\vec{A} = 0$ (אין מונופולים)
- $\oint_\Gamma \vec{E} \cdot d\vec{l} = -\frac{d\Phi_B}{dt}$ (פאראדיי)
- $\oint_\Gamma \vec{B} \cdot d\vec{l} = \mu_0 I + \mu_0\varepsilon_0\frac{d\Phi_E}{dt}$ (אמפר-מקסוול)
- $\vec{F} = q\vec{E} + q\vec{v} \times \vec{B}$ (לורנץ)
מה לא נכלל בקורס (לא הספיקו)
קבלים, משרנים, גלים אלקטרומגנטיים, מעגלי זרם חילופין, אלקטרודינמיקה.
דור פסקלהערה לגבי המבחן: השאלות דורשות בעיקר הבנה. החישוב עצמו לא ארוך – אינטגרלים פשוטים. חשוב מאוד לצייר סקיצות!