סיכום אלגוריתם לפתרון בעיות מכניקה

סיימנו חזרה פה, והיה כאן גם אלגוריתם על איך אנחנו ניגשים לבעיה במכניקה:

  1. שלב אפס: לקבל פרפרים בבטן
  2. שלב ראשון: לרשום תרשים כוחות לכל גוף - זה שלב קשה שדורש להזיע
  3. שלב שני: בחירת מערך צירים ופירוק הכוחות לרכיבים - חשוב לבחור אותם בצורה חכמה כדי לא להסתבך
  4. שלב שלישי: רישום משוואות התנועה בהתאם למה שנדרש בשאלה

החשוב ביותר הוא השלב הראשון - הפירוט של הכוחות. אם עשיתם אותו כמו שצריך, אז “יש לכם את השאלה ביד”.

הבעיה

יש לנו מסה קטנה $m$ שצמודה לעגלה (קרונית). בין המסה לבין העגלה פועל כוח חיכוך, עם מקדם חיכוך סטטי $\mu_s$.

נשאל:

  • מה צריכה להיות התאוצה של העגלה על מנת שהמסה לא תחליק למטה?
  • מה הערכים האפשריים של המהירות?

ניתוח הכוחות

כוחות על המסה הקטנה $m$

  1. כוח הכבידה ($mg$) - פועל כלפי מטה
  2. כוח נורמלי ($N$) - פועל מהעגלה על המסה בכיוון אופקי
  3. כוח חיכוך סטטי ($F_s$) - פועל כלפי מעלה

הערה לגבי כיוון החיכוך: החיכוך תמיד פועל בכיוון הפוך למה שהכוח השני “רוצה”. במקרה זה, המסה “רוצה” ליפול למטה בגלל כוח הכבידה, ולכן החיכוך פועל כלפי מעלה.

בחירת מערכת צירים

נבחר מערכת צירים סטנדרטית:

  • ציר $y$ כלפי מעלה
  • ציר $x$ לימין

משוואות התנועה

נסתכל על הגוף הקטן (המסה) וננתח את הכוחות הפועלים עליו:

בכיוון ציר $y$ (אנכי)

סכום הכוחות בכיוון $y$: $F_s - mg = 0$

כלומר: $F_s = mg$

בכיוון ציר $x$ (אופקי)

סכום הכוחות בכיוון $x$: $N = ma$

כאשר $a$ היא התאוצה האופקית (תאוצת העגלה).

תנאי על כוח החיכוך הסטטי

אנחנו יודעים שכוח החיכוך הסטטי מוגבל: $F_s \leq \mu_s \cdot N$

מכיוון ש-$F_s = mg$ ו-$N = ma$, נקבל: $mg \leq \mu_s \cdot ma$

נחלק ב-$m$ משני הצדדים: $g \leq \mu_s \cdot a$

לכן: $a \geq \frac{g}{\mu_s}$

התשובה

  1. התאוצה המינימלית הנדרשת כדי שהמסה לא תחליק למטה היא: $a \geq \frac{g}{\mu_s}$

  2. הערכים האפשריים של המהירות: כאשר תנאי התאוצה מתקיים, אין מגבלה על המהירות. המהירות יכולה לקבל כל ערך אפשרי.

הערות מהדיון בכיתה

לגבי מקדם החיכוך $\mu_s$

  • מקדם החיכוך $\mu_s$ הוא חסר יחידות.
  • זהו מספר טהור (סקלר) שמתאר את היחס בין כוח החיכוך המקסימלי לכוח הנורמלי.

לגבי הקשר בין כוח החיכוך למשטח

  • החיכוך אינו תלוי בשטח המגע, רק בכוח הנורמלי.
  • אפילו אם יש לנו שני גופים מאותו חומר, אחד עם שטח קטן ואחד עם שטח גדול, שניהם יתחילו להחליק באותו זווית של שיפוע - זה מפתיע ולא אינטואיטיבי.

לגבי ההגיון הפיזיקלי

  • אם העגלה לא מאיצה מספיק, המסה תיפול כלפי מטה.
  • ככל שהעגלה מאיצה יותר, כוח הנורמל גדל וכך גם כוח החיכוך המקסימלי, מה שמאפשר למסה להישאר צמודה לעגלה.
  • כאשר התאוצה מספיק גדולה, החיכוך הסטטי מצליח להתנגד לכוח הכבידה ולמנוע החלקה של המסה.

לגבי התאוצה והמהירות

  • אין הגבלה על המהירות - כל עוד התאוצה גדולה או שווה ל-$\frac{g}{\mu_s}$.
  • המהירות יכולה לגדול ולגדול “עד 300 מיליון ק”מ לשעה” (קירוב לא יחסותי).

בעיית שיווי משקל - מטפסת הדוחפת קיר

תיאור הבעיה

ברוח התקופה, אנו בוחנים מקרה של מטפסת (ולא מטפס) הדוחפת קיר בכוח $F$.

נתון:

  • מקדם החיכוך בין הגב לקיר הוא $\mu_s$
  • מקדם החיכוך בין הרגליים לקיר הוא גם $\mu_s$ (אותו מקדם חיכוך סטטי)

השאלה: מה הכוח $F$ שהיא צריכה להפעיל בשביל לשמור על שיווי משקל?

ניתוח הכוחות

אנחנו צריכים לסרטט את הסיטואציה ולנתח את הכוחות שפועלים על המטפסת.

הערה: אנחנו מעוניינים רק בכוחות שפועלים על המטפסת.

כוחות שפועלים על המטפסת

באזור הגב
  • $F_1$: הכוח שהמטפסת מפעילה על הקיר (כלפי חוץ)
  • $N_1$: כוח נורמלי שהקיר מפעיל על המטפסת בתגובה (מכיוון שאין תנועה, בגלל החוק השלישי של ניוטון)
  • $f_{חיכוך_1}$: כוח חיכוך שפועל כלפי מעלה
באזור הרגליים
  • $F_2$: כוח נוסף שהמטפסת מפעילה על הקיר (אינטואיטיבית היינו רוצים להגיד שזהו אותו $F_1$, אך תכף נראה מתוך המשוואות)
  • $N_2$: כוח נורמלי שהקיר מפעיל על המטפסת באזור הרגליים
  • $f_{חיכוך_2}$: כוח חיכוך שפועל כלפי מעלה באזור הרגליים
כוח נוסף
  • $mg$: כוח הכבידה שפועל על המטפסת כלפי מטה

דיון על היחס בין הכוחות

תלמיד/ה: האם אנחנו נצטרך לחבר את שני ה-$F$ (כלומר את $F_1$ ואת $F_2$) או שמספיק אחד?

מרצה: אני חושב שהם יוצאים זהים, אבל באופן כללי לא. כי נניח שהנעליים שלה יש להן כוח חיכוך אחר מאשר המכנסיים, ובמיוחד אם היא דרכה על שמן לפני זה. זה לא בהכרח אותו כוח חיכוך, אבל פה עשו הפשטה. עדיין, אותו כוח שתפעיל החוצה.

תלמיד/ה: כן, נכון.

מרצה: זאת אומרת, תכל’ס, ה-$F_1$ שווה ל-$N_1$ בגלל החוק השלישי של ניוטון, ואותו דבר $N_2$ שווה ל-$F_2$.

משוואות שיווי משקל

בחירת צירים

נעשה בחירה של צירים, ונגדיר את ציר ה-$x$ בכיוון אופקי.

סכום הכוחות בציר $x$

$\sum F_x = 0$

תלמיד/ה: שווה ל-$N_1$ ועוד $N_2$?

מרצה: $N_1$ ועוד $N_2$ פחות…

תלמיד/ה: גם אני הייתי רוצה להגיד פה… [מתבלבל/ת קצת] זה מה שפועל על הקיר, לא עליה?

מרצה: בסדר, הקיר מפעיל עליה בחזרה, זה ה-$N$.

אז בעצם $N_1$ שווה ל-$N_2$, אז זה נחמד. ומכיוון שיש לנו חוק שלישי, אז זה גם כן: $F_1 = N_1 = N_2 = F_2$

שאלה על נוטציה

תלמיד/ה: סתם שאלה, למה אתה קורא לזה $N$?

מרצה: $N$ מ”נורמל”, לא בגלל משהו מיוחד.

תלמיד/ה: כי זה כאילו אמור להיות שווה ל-$\mu \cdot N$?

מרצה: נכון.

תלמיד/ה: כאילו אני פתאום מבינה כי בהגדרה נורמל זה $F$ שווה $\mu \cdot N$.

מרצה: נכון.

תלמיד/ה: איך $F$ שווה…? [נראה כי התלמיד/ה מתבלבל/ת בין החוק השני של ניוטון לבין הקשר בין כוח החיכוך לכוח הנורמלי]

מרצה: אני מבין מה את שואלת. שאלה ממש טכנית. לא, סופר ל-$N$… [נראה שהוא מנסה להסביר את הקשר בין הנוטציות]

בעיית האוסצילטור - תנועת מסה בין שני קפיצים

תיאור הבעיה - אוסצילטור עם שני קפיצים

נתונה מסה הנמצאת בין שני קפיצים על משטח אופקי. המסה מחוברת לשני קפיצים, אחד מצד שמאל ואחד מצד ימין.

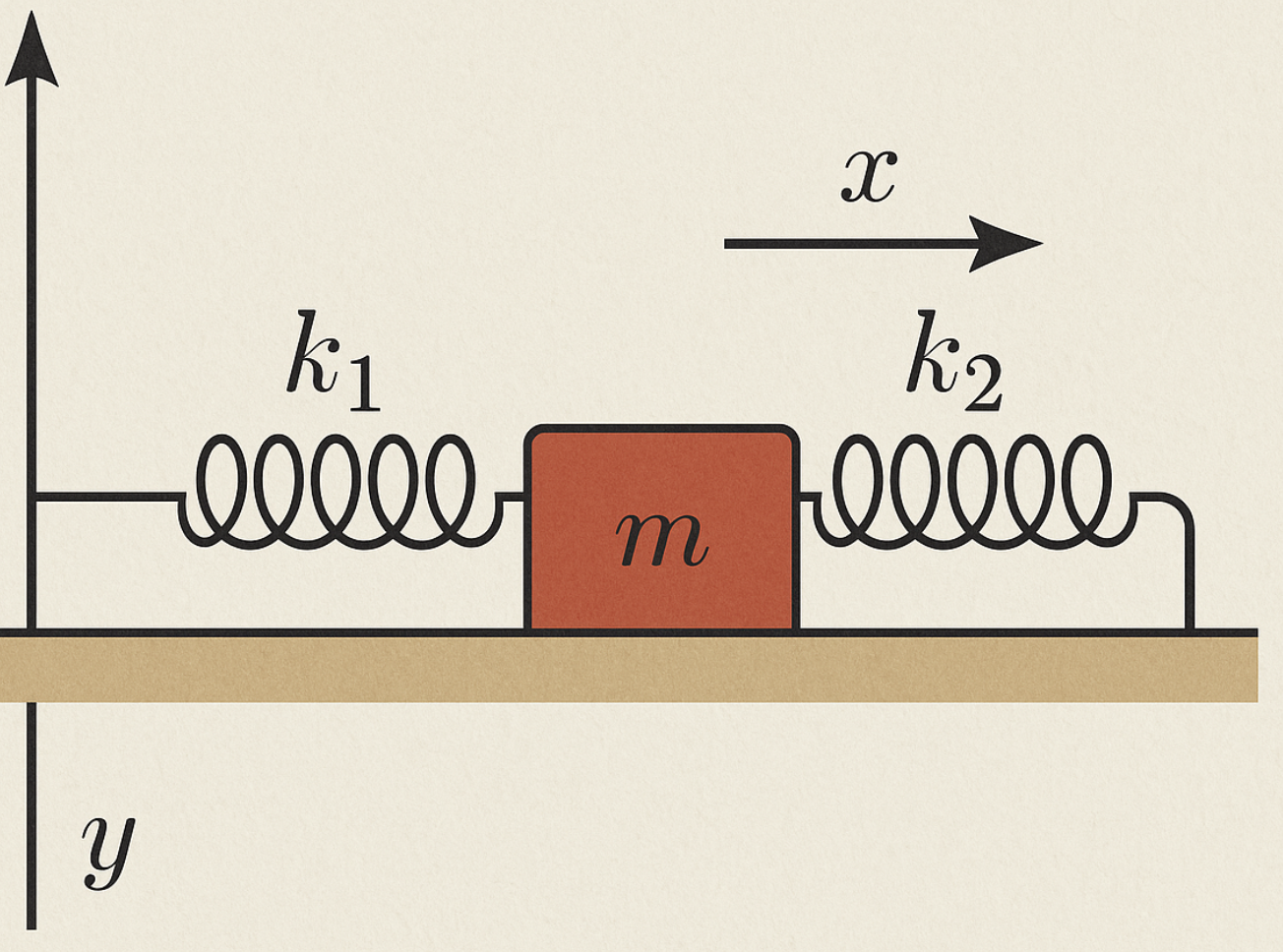
אנחנו בוחרים את מערכת הצירים כך שציר ה-$x$ מכוון ימינה, וציר ה-$y$ מכוון כלפי מעלה. נקודת שיווי המשקל של המערכת (כאשר שני הקפיצים במצב לא מתוח) נקבעת כמקור הצירים: $x_0 = 0$.

הבעיה: מושכים את המסה למרחק $A$ (חיובי) מנקודת שיווי המשקל ומשחררים אותה ממנוחה. מבקשים למצוא:

  1. את מיקום המסה כפונקציה של הזמן
  2. את הזמן הדרוש למסה לחזור לראשונה לנקודת שיווי המשקל

ניתוח הכוחות

נסמן:

  • $m$ - מסת הגוף
  • $k_1$ - קבוע הקפיץ השמאלי
  • $k_2$ - קבוע הקפיץ הימני
  • $x(t)$ - מיקום המסה בזמן $t$
  • $A$ - המיקום ההתחלתי (מרחק מנקודת שיווי המשקל)

כאשר המסה נמצאת במיקום $x$, הכוחות הפועלים עליה הם:

  1. כוח הקפיץ השמאלי: $F_1 = -k_1 \cdot x$
    • אם $x > 0$ (המסה נמצאת מימין לנקודת שיווי המשקל), הכוח מושך שמאלה
    • אם $x < 0$ (המסה נמצאת משמאל לנקודת שיווי המשקל), הכוח דוחף ימינה
  2. כוח הקפיץ הימני: $F_2 = -k_2 \cdot x$
    • אם $x > 0$, הקפיץ הימני נדחס ודוחף את המסה שמאלה
    • אם $x < 0$, הקפיץ הימני נמתח ומושך את המסה ימינה

המשוואה הדיפרנציאלית

לפי החוק השני של ניוטון:

\[\sum F = m \cdot a\]

סכום הכוחות בכיוון $x$ הוא:

\[F_1 + F_2 = -k_1 \cdot x - k_2 \cdot x = -(k_1 + k_2) \cdot x\]

המשוואה הדיפרנציאלית המתקבלת:

\[m \cdot \ddot{x} = -(k_1 + k_2) \cdot x\]

או:

\[\ddot{x} = -\frac{k_1 + k_2}{m} \cdot x\]

נסמן $\omega^2 = \frac{k_1 + k_2}{m}$, ונקבל:

\[\ddot{x} = -\omega^2 \cdot x\]

זוהי משוואה דיפרנציאלית מסדר שני. הפתרון הכללי של משוואה זו הוא:

\[x(t) = c_1 \cdot \sin(\omega t) + c_2 \cdot \cos(\omega t)\]

כאשר $c_1$ ו-$c_2$ הם קבועים שנקבעים לפי תנאי ההתחלה.

פתרון המשוואה הדיפרנציאלית

נשתמש בתנאי ההתחלה כדי למצוא את $c_1$ ו-$c_2$:

  1. המיקום ההתחלתי: $x(0) = A$
\[A = c_1 \cdot \sin(0) + c_2 \cdot \cos(0) = c_2\]

מכאן $c_2 = A$

  1. המהירות ההתחלתית: $\dot{x}(0) = 0$
\[\dot{x}(t) = c_1 \cdot \omega \cdot \cos(\omega t) - c_2 \cdot \omega \cdot \sin(\omega t)\] \[0 = c_1 \cdot \omega \cdot \cos(0) - c_2 \cdot \omega \cdot \sin(0) = c_1 \cdot \omega\]

מכאן $c_1 = 0$

לכן הפתרון הוא:

\[x(t) = A \cdot \cos(\omega t)\]

כאשר $\omega = \sqrt{\frac{k_1 + k_2}{m}}$

חישוב הזמן לחזרה לנקודת שיווי המשקל

נקודת שיווי המשקל היא בנקודה $x = 0$. אנחנו מחפשים את הזמן $t^*$ הראשון (שגדול מאפס) כך ש-$x(t^*) = 0$.

\[A \cdot \cos(\omega t^*) = 0\]

פתרון המשוואה הזו הוא:

\[\omega t^* = \frac{\pi}{2}\]

מכאן:

\[t^* = \frac{\pi}{2\omega} = \frac{\pi}{2\sqrt{\frac{k_1 + k_2}{m}}} = \frac{\pi}{2} \cdot \sqrt{\frac{m}{k_1 + k_2}}\]

זהו הזמן הדרוש למסה לחזור לראשונה לנקודת שיווי המשקל.

התנהגות המערכת לאורך זמן

התנועה של המסה היא תנועה הרמונית פשוטה, שבה המסה נעה בין $+A$ ל-$-A$ ובחזרה. כשהמסה נמצאת במיקום $x = 0$ (נקודת שיווי המשקל), המהירות שלה מקסימלית. כשהמסה נמצאת בנקודות הקיצון ($x = \pm A$), המהירות שלה אפס.

מכיוון שאין חיכוך במערכת, התנועה תמשיך לנצח בלי לדעוך. בעולם האמיתי, כמובן, יש תמיד חיכוך וכוחות אחרים שגורמים לדעיכה של התנודות עם הזמן.

הערות נוספות מהדיון בכיתה

  • המערכת נעה בצורה סינוסואידלית עם הזמן
  • זמן המחזור המלא של התנועה הוא $T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k_1 + k_2}}$
  • אם היינו מתחילים עם מהירות התחלתית שונה מאפס, היינו מקבלים גם את האיבר עם הסינוס בפתרון
  • ניתן גם לכתוב את הפתרון בצורה $x(t) = C \cos(\omega t + \phi)$ כאשר $C$ ו-$\phi$ הם קבועים שתלויים בתנאי ההתחלה
  • בתוך גרעינים אטומיים וברמה המיקרוסקופית של החומר, תנודות מסוג זה מתרחשות כמעט ללא דעיכה (בטמפרטורה נמוכה מאוד)
דור פסקל
חזור לשיעור 4
חזרה לעמוד הראשי