שאלה 1
מצאו את הכוח הקבוע הדרוש כדי להאיץ מסה של 10 טון מ־54 קמ״ש ל־108 קמ״ש לאורך קו ישר, במשך 5 דקות.
שלב 1: המרת יחידות
- נמיר את המסה מטונות לק”ג: 10 טון = 10,000 ק”ג
- נמיר את המהירויות ממ”ש לק”מ:
- $54$ ק”מ/שעה = $54 \times \frac{1000}{3600} = 15$ מ’/שנייה
- $108$ ק”מ/שעה = $108 \times \frac{1000}{3600} = 30$ מ’/שנייה
- נמיר את הזמן מדקות לשניות: 5 דקות = $5 \times 60 = 300$ שניות
שלב 2: חישוב התאוצה
התאוצה היא קצב השינוי במהירות. נשתמש בנוסחה:
\[a = \frac{v_f - v_i}{t}\]כאשר:
- $v_f$ היא המהירות הסופית
- $v_i$ היא המהירות ההתחלתית
- $t$ הוא הזמן שעבר
נציב:
\[a = \frac{30 - 15}{300} = \frac{15}{300} = 0.05 \left[\frac{\text{m}}{\text{s}^2}\right]\]שלב 3: חישוב הכוח
לפי החוק השני של ניוטון, הכוח שווה למסה כפול התאוצה:
\[F = m \times a\]נציב:
\[F = 10,000 \times 0.05 = 500 \left[\text{N}\right]\]הסבר: הכוח הדרוש הוא 500 ניוטון. כוח זה צריך להיות מופעל באופן קבוע במשך 5 דקות כדי להגדיל את מהירות העצם מ-54 קמ״ש ל-108 קמ״ש. בפיזיקה, כוח הוא מה שגורם לשינוי במצב התנועה של גוף. ככל שהמסה גדולה יותר, יש צורך בכוח גדול יותר כדי לייצר את אותה התאוצה.
שאלה 2: נושאת מטוסים מול זבוב
א. איזה כוח נדרש לעצור נושאת מטוסים של 100,000 טון מ־40 קמ״ש לעצירה תוך 10 דקות?
שלב 1: המרת יחידות לנושאת המטוסים
- נמיר את המסה מטונות לק”ג: 100,000 טון = 100,000,000 ק”ג
- נמיר את המהירות מק”מ/שעה למ’/שנייה: $40$ ק”מ/שעה = $40 \times \frac{1000}{3600} \approx 11.11$ מ’/שנייה
- נמיר את הזמן מדקות לשניות: 10 דקות = $10 \times 60 = 600$ שניות
שלב 2: חישוב התאוצה של נושאת המטוסים
מכיוון שאנחנו מעוניינים לעצור את נושאת המטוסים, המהירות הסופית היא אפס:
\[a = \frac{v_f - v_i}{t} = \frac{0 - 11.11}{600} = \frac{-11.11}{600} \approx -0.01852 \left[\frac{\text{m}}{\text{s}^2}\right]\]הסימן השלילי מציין האטה (תאוצה שלילית).
שלב 3: חישוב הכוח לעצירת נושאת המטוסים
\[F = m \times a = 100,000,000 \times (-0.01852) = -1,852,000 \left[\text{N}\right]\]מכיוון שאנחנו מחפשים את גודל הכוח, נתייחס לערך המוחלט: 1,852,000 ניוטון.
הסבר: נדרש כוח של כ-1.85 מיליון ניוטון כדי לעצור נושאת מטוסים ענקית. זהו כוח עצום! דמיינו כאילו אתם דוחפים 185,000 ק”ג (משקל של כ-185 מכוניות) כנגד כוח הכבידה.
ב. כמה זמן ייקח לעצור זבוב של גרם אחד באותה מהירות, עם אותו כוח?
שלב 1: המרת יחידות לזבוב
- נמיר את מסת הזבוב מגרמים לק”ג: 1 גרם = 0.001 ק”ג
שלב 2: חישוב התאוצה של הזבוב
כאשר אותו כוח (1,852,000 ניוטון) פועל על הזבוב, התאוצה תהיה:
\[a = \frac{F}{m} = \frac{1,852,000}{0.001} = 1,852,000,000 \left[\frac{\text{m}}{\text{s}^2}\right]\]שלב 3: חישוב הזמן לעצירת הזבוב
\[t = \frac{v_f - v_i}{a} = \frac{0 - 11.11}{1,852,000,000} \approx -6 \times 10^{-9} \left[\text{s}\right]\]הסימן השלילי מציין את כיוון התנועה. לכן, הזמן הנדרש הוא כ-6 ננו-שניות.
הסבר: עם אותו כוח שנדרש לעצור נושאת מטוסים, זבוב קטן ייעצר כמעט מיידית - תוך פחות מאחד חלקי מיליארד של שנייה! זוהי המחשה מדהימה של החוק השני של ניוטון: $F = ma$. ככל שהמסה קטנה יותר, התאוצה גדולה יותר כאשר מפעילים אותו כוח.
שאלה 3: סכום כוחות
נתון חלקיק עליו פועלים שלושת הכוחות:
\[\begin{align*} \vec{F}_1 &= 3\hat{x} - 2\hat{y} + 4\hat{z} \\ \vec{F}_2 &= -5\hat{x} + 3\hat{y} - 3\hat{z} \\ \vec{F}_3 &= -2\hat{x} + 4\hat{y} - 5\hat{z} \end{align*}\]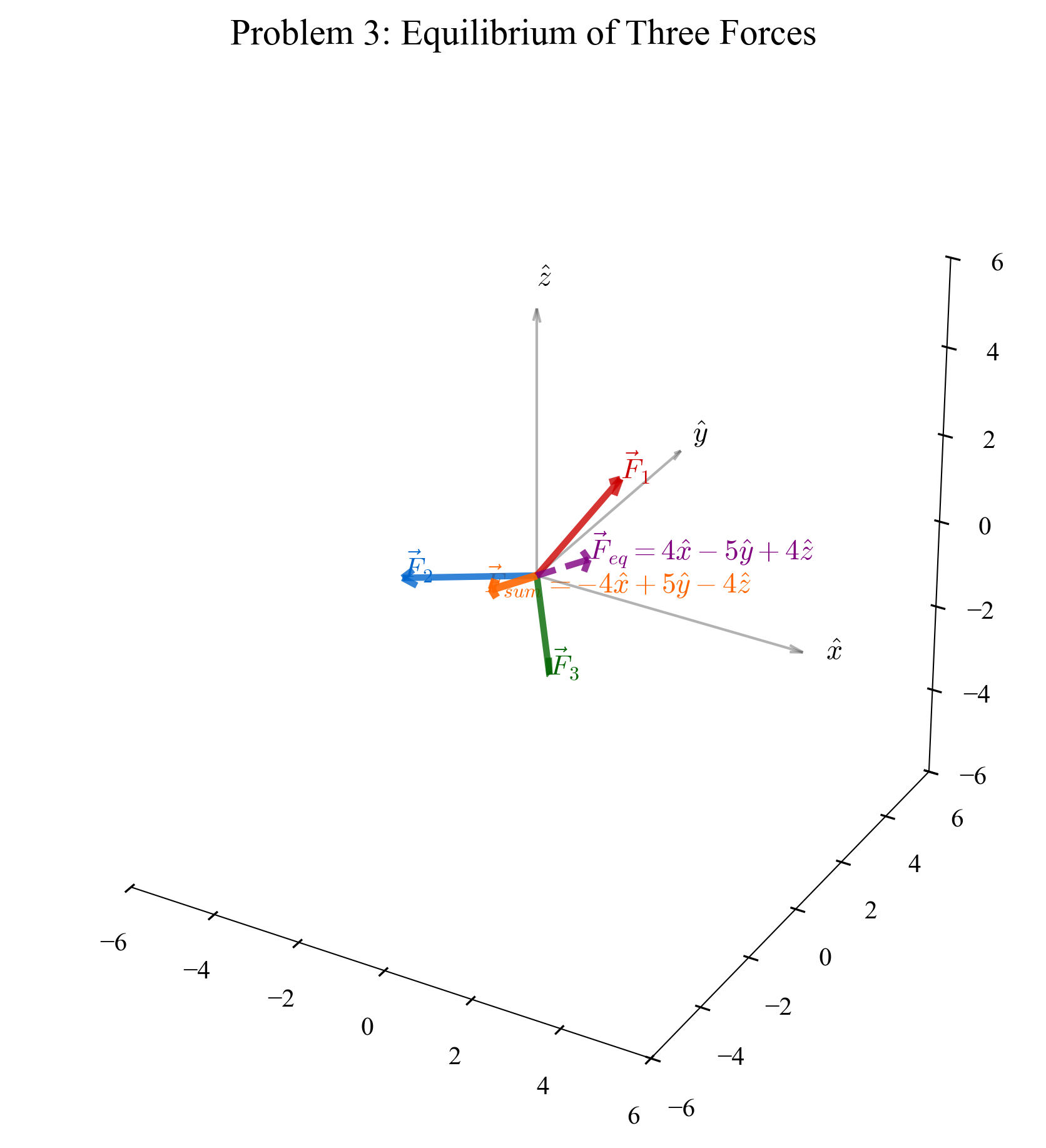
- א. איזה כוח יש להפעיל על החלקיק כדי שוקטור המהירות שלו יישאר קבוע?
- ב. בהנחה שהכוח הזה לא מופעל, מה יהיה וקטור התאוצה של החלקיק? ומה גודלו?
שלב 1: הבנת העיקרון הפיזיקלי
לפי החוק הראשון של ניוטון, אם החלקיק נע במהירות קבועה (כלומר, וקטור המהירות שלו אינו משתנה), סכום הכוחות הפועלים עליו חייב להיות אפס.
שלב 2: חישוב סכום הכוחות הנתונים
נחשב את סכום שלושת הכוחות הנתונים:
\[\vec{F}_{sum} = \vec{F}_1 + \vec{F}_2 + \vec{F}_3\]נחבר את המרכיבים בכל אחד מהכיוונים בנפרד:
- בכיוון $\hat{x}$: $3 + (-5) + (-2) = 3 - 5 - 2 = -4$
- בכיוון $\hat{y}$: $(-2) + 3 + 4 = -2 + 3 + 4 = 5$
- בכיוון $\hat{z}$: $4 + (-3) + (-5) = 4 - 3 - 5 = -4$
מכאן:
\[\vec{F}_{sum} = -4\hat{x} + 5\hat{y} - 4\hat{z}\]שלב 3: מציאת הכוח הנדרש
כדי שסכום הכוחות יהיה אפס, עלינו להפעיל כוח שהוא ההופכי של סכום הכוחות הנתונים:
\[\begin{align*} \vec{F}_{neended} &= -\vec{F}_{sum} \\ &= -(-4\hat{x} + 5\hat{y} - 4\hat{z}) \\ &= 4\hat{x} - 5\hat{y} + 4\hat{z} \end{align*}\]הסבר: כדי לשמור על מהירות קבועה, עלינו להפעיל כוח שיבטל בדיוק את השפעת כל הכוחות האחרים. זהו יישום ישיר של החוק הראשון של ניוטון, הקובע שגוף ישמור על מצב התנועה שלו אלא אם כן פועל עליו כוח חיצוני.
הפתרון לחלק ב’
שלב 1: הבנת העיקרון הפיזיקלי
אם הכוח שמצאנו בחלק א’ אינו מופעל, אז לפי החוק השני של ניוטון, סכום הכוחות יגרום לתאוצה של החלקיק.
שלב 2: חישוב וקטור התאוצה
בהנחה שמסת החלקיק היא $m$, וקטור התאוצה יהיה: $\vec{a} = \frac{\vec{F}_{sum}}{m} = \frac{-4\hat{x} + 5\hat{y} - 4\hat{z}}{m}$
במקרה זה, אם לא נתונה המסה, נניח $m = 1$ ק”ג לשם פשטות:
\[\vec{a} = -4\hat{x} + 5\hat{y} - 4\hat{z} \left[\frac{\text{m}}{\text{s}^2}\right]\]שלב 3: חישוב גודל וקטור התאוצה
גודל וקטור התאוצה מחושב לפי נוסחת המרחק במרחב תלת-ממדי:
\[\begin{align*} |\vec{a}| &= \sqrt{a_x^2 + a_y^2 + a_z^2} \\ &= \sqrt{(-4)^2 + 5^2 + (-4)^2} \\ &= \sqrt{16 + 25 + 16} = \sqrt{57} \approx 7.55 \left[\frac{\text{m}}{\text{s}^2}\right] \end{align*}\]הסבר: אם לא נפעיל את הכוח המאזן, החלקיק יאיץ בכיוון שנקבע על ידי סכום הכוחות. התאוצה תהיה בעוצמה של כ-7.55 מ’/שנייה². זה אומר שבכל שנייה, מהירות החלקיק תשתנה ב-7.55 מ’/שנייה בכיוון שחישבנו. אפשר לדמיין זאת כמו מכונית שמאיצה מ-0 ל-100 קמ״ש בכ-3.7 שניות - זוהי תאוצה משמעותית!
שאלה 4: תנועה בנפילה חופשית
נניח גוף נופל בתאוצה קבועה בקרבת פני כדור הארץ:
\[g \approx 10~\left[\frac{\text{m}}{\text{s}^2}\right]\]נבחר את ציר x להיות אנכי כלפי מטה.
-
א. הראו:
\[v(t) = v_0 + g(t - t_0)\]כאשר:
- $v_0 = v(t_0)$
- $\frac{\Delta v}{\Delta t} = g$
-
ב. הראו:
\[x(t) = x_0 + v_0(t - t_0) + \frac{1}{2}g(t - t_0)^2\]כאשר:
- $x_0 = x(t_0)$
- $\frac{dx}{dt} = v(t)$
-
ג. לתוך פיר בעומק 500 מטר, הושלכה אבן במהירות התחלתית של שני מטר לשנייה. בשעה 10:00 בבוקר (נניח $t_0 = 0$). חשבו:
- מהי מהירות האבן בשנייה השלישית?
- איפה היא נמצאת בזמן זה?
- מה הדרך שהיא עברה בין השנייה הרביעית לחמישית?
- כמה זמן ייקח לה להגיע לתחתית?
א. הוכחת נוסחת המהירות $v(t)=v_0 + g(t - t_0)$
שלב 1: הבנת ההגדרות הבסיסיות
תאוצה מוגדרת כקצב השינוי של המהירות ביחס לזמן:
\[a = \frac{\Delta v}{\Delta t}\]במקרה של נפילה חופשית, התאוצה קבועה ושווה ל-$g$:
\[\frac{\Delta v}{\Delta t} = g\]שלב 2: ניסוח משוואה דיפרנציאלית ואינטגרציה
אם התאוצה קבועה, נוכל לכתוב:
\[\frac{dv}{dt} = g\]נבצע אינטגרציה על שני צדי המשוואה:
\[\int_{t_0}^{t} \frac{dv}{dt} dt = \int_{t_0}^{t} g dt\]מימין נקבל:
\[\int_{t_0}^{t} g dt = g(t - t_0)\]משמאל נקבל:
\[\int_{t_0}^{t} \frac{dv}{dt} dt = \int_{v_0}^{v(t)} dv = v(t) - v_0\]נשלב את התוצאות:
\[v(t) - v_0 = g(t - t_0)\] \[v(t) = v_0 + g(t - t_0)\]הסבר: נוסחה זו מראה כיצד המהירות משתנה עם הזמן תחת תאוצה קבועה. היא אומרת לנו שהמהירות בזמן $t$ שווה למהירות ההתחלתית $v_0$ בתוספת המהירות שנוספה כתוצאה מהתאוצה. המהירות הנוספת היא מכפלה של התאוצה $g$ בזמן שחלף $(t - t_0)$.
ב. הוכחת נוסחת המיקום $x(t)=x_0 + v_0(t - t_0) + \frac{1}{2}g(t - t_0)^2$
שלב 1: שימוש בקשר בין מהירות למיקום
לפי ההגדרה, מהירות היא קצב השינוי של המיקום ביחס לזמן:
\[v(t) = \frac{dx}{dt}\]שלב 2: הצבת נוסחת המהירות ואינטגרציה
נציב את הנוסחה שמצאנו בחלק א’:
\[\frac{dx}{dt} = v_0 + g(t - t_0)\]נבצע אינטגרציה על שני צדי המשוואה:
\[\int_{t_0}^{t} \frac{dx}{dt} dt = \int_{t_0}^{t} [v_0 + g(t - t_0)] dt\]משמאל נקבל:
\[\int_{t_0}^{t} \frac{dx}{dt} dt = \int_{x_0}^{x(t)} dx = x(t) - x_0\]מימין נקבל:
\[\begin{align*} \int_{t_0}^{t} [v_0 + g(t - t_0)] dt &= v_0 \int_{t_0}^{t} dt + g \int_{t_0}^{t} (t - t_0) dt \\ &= v_0 (t - t_0) + g \int_{t_0}^{t} (t - t_0) dt \end{align*}\]נחשב את האינטגרל השני:
\[\begin{align*} \int_{t_0}^{t} (t - t_0) dt &= \int_{t_0}^{t} t dt - t_0 \int_{t_0}^{t} dt = \left[\frac{t^2}{2}\right]_{t_0}^{t} - t_0 (t - t_0) \\ &= \frac{t^2}{2} - \frac{t_0^2}{2} - t_0 (t - t_0) = \frac{t^2 - t_0^2}{2} - t_0 (t - t_0) \\ &= \frac{(t + t_0)(t - t_0)}{2} - t_0 (t - t_0) = (t - t_0) \left[\frac{t + t_0}{2} - t_0 \right] \\ &= (t - t_0) \frac{t + t_0 - 2t_0}{2} = (t - t_0) \frac{t - t_0}{2} = \frac{(t - t_0)^2}{2} \end{align*}\]נשלב את התוצאות:
\[x(t) - x_0 = v_0 (t - t_0) + g \frac{(t - t_0)^2}{2}\] \[x(t) = x_0 + v_0 (t - t_0) + \frac{1}{2} g (t - t_0)^2\]הסבר: נוסחה זו מתארת את המיקום של גוף בזמן $t$ כתלות במיקום ההתחלתי $x_0$, המהירות ההתחלתית $v_0$, והתאוצה $g$. היא מורכבת משלושה חלקים: המיקום ההתחלתי, המרחק שהיה נעבר במהירות קבועה $v_0$, והתוספת עקב התאוצה הקבועה.
ג. פתרון הבעיה המעשית
נתונים:
- עומק הפיר: $500$ מטר
- מהירות התחלתית: $v_0 = 2$ מ’/שנייה (כלפי מטה)
- זמן התחלתי: $t_0 = 0$
- תאוצת הכבידה: $g = 10$ מ’/שנייה²
- מיקום התחלתי: $x_0 = 0$ (נקבע את ראשית הצירים בפתח הפיר)
1. מהירות האבן בשנייה השלישית
נשתמש בנוסחה מחלק א’ כדי למצוא את המהירות בזמן $t = 3$ שניות:
\[v(3) = v_0 + g(3 - 0) = 2 + 10 \cdot 3 = 2 + 30 = 32 \text{m/s}\]הסבר: האבן מתחילה עם מהירות של 2 מ’/שנייה ומאיצה עקב הכבידה. לאחר 3 שניות, היא צברה 30 מ’/שנייה נוספים, כך שהמהירות הכוללת היא 32 מ’/שנייה.
2. מיקום האבן בשנייה השלישית
נשתמש בנוסחה מחלק ב’ כדי למצוא את המיקום בזמן $t = 3$ שניות:
\[\begin{align*} x(3) &= x_0 + v_0(3 - 0) + \frac{1}{2}g(3 - 0)^2 \\ &= 0 + 2 \cdot 3 + \frac{1}{2} \cdot 10 \cdot 3^2 \\ &= 6 + 5 \cdot 9 = 6 + 45 = 51 \text{meter} \end{align*}\]הסבר: לאחר 3 שניות, האבן נמצאת במרחק של 51 מטר מפתח הפיר. מתוך זה, 6 מטרים הם תוצאה של המהירות ההתחלתית, ו-45 מטרים נוספים הם תוצאה של התאוצה עקב הכבידה.
3. הדרך שנעברה בין השנייה הרביעית לחמישית
נמצא את המיקום בזמן $t = 4$ שניות:
\[x(4) = 0 + 2 \cdot 4 + \frac{1}{2} \cdot 10 \cdot 4^2 = 8 + 5 \cdot 16 = 8 + 80 = 88 \left[\text{m}\right]\]נמצא את המיקום בזמן $t = 5$ שניות:
\[x(5) = 0 + 2 \cdot 5 + \frac{1}{2} \cdot 10 \cdot 5^2 = 10 + 5 \cdot 25 = 10 + 125 = 135 \left[\text{m}\right]\]הדרך שנעברה בין השנייה הרביעית לחמישית היא:
\[\Delta x = x(5) - x(4) = 135 - 88 = 47 \left[\text{m}\right]\]הסבר: בין השנייה הרביעית לחמישית, האבן עברה מרחק של 47 מטר. זה יותר מהמרחק שהיא עברה בשנייה הקודמת, כי האבן מאיצה ונעה מהר יותר עם כל שנייה שחולפת.
4. הזמן שייקח לאבן להגיע לתחתית הפיר
נרצה למצוא את הזמן $t$ כך שהמיקום $x(t) = 500$ (עומק הפיר):
$500 = 0 + 2t + \frac{1}{2} \cdot 10 \cdot t^2 = 2t + 5t^2$
$5t^2 + 2t - 500 = 0$
נפתור את המשוואה הריבועית באמצעות נוסחת השורשים:
$t = \frac{-2 \pm \sqrt{4 + 4 \cdot 5 \cdot 500}}{2 \cdot 5} = \frac{-2 \pm \sqrt{4 + 10000}}{10} = \frac{-2 \pm \sqrt{10004}}{10}$
$t = \frac{-2 \pm 100.02}{10} \approx \frac{-2 + 100.02}{10} \approx 9.8 \text{s}$
(הפתרון השני, עם הסימן שלילי, אינו פיזיקלי כי אנחנו מחפשים זמן חיובי.)
הסבר: ייקח לאבן כ-9.8 שניות להגיע לתחתית הפיר בעומק 500 מטר. בזמן זה, האבן תאיץ בהדרגה עקב הכבידה ותגביר את מהירותה, עד שתגיע לתחתית.
שאלה 5: קשר בין העתק למהירות
הראו שאם גוף נע בתאוצה קבועה, מתקיים:
\[v^2(t) = v_0^2 + 2g\Delta x\]זהו קשר שימושי כאשר אין מידע על הזמן, אלא רק על מהירויות והעתקים.
שלב 1: שימוש בנוסחאות הקיימות
מהשאלה הקודמת, יש לנו את הנוסחאות הבאות:
- מהירות: $v(t) = v_0 + g(t - t_0)$
- מיקום: $x(t) = x_0 + v_0(t - t_0) + \frac{1}{2}g(t - t_0)^2$
לשם פשטות, נניח $t_0 = 0$. אז הנוסחאות הופכות ל:
\[v(t) = v_0 + gt\] \[x(t) = x_0 + v_0t + \frac{1}{2}gt^2\]שלב 2: הגדרת ההעתק
ההעתק $\Delta x$ הוא השינוי במיקום:
\[\Delta x = x(t) - x_0 = v_0t + \frac{1}{2}gt^2\]שלב 3: מציאת הזמן $t$ מנוסחת המהירות
מהנוסחה של המהירות, אנחנו יכולים לבטא את הזמן $t$:
\[v(t) = v_0 + gt\] \[t = \frac{v(t) - v_0}{g}\]שלב 4: הצבת הזמן בנוסחת ההעתק
נציב את $t$ בנוסחת ההעתק:
\[\begin{align*} \Delta x &= v_0 \cdot \frac{v(t) - v_0}{g} + \frac{1}{2}g \cdot \left(\frac{v(t) - v_0}{g}\right)^2 \\ &= \frac{v_0(v(t) - v_0)}{g} + \frac{1}{2} \cdot \frac{(v(t) - v_0)^2}{g} \\ &= \frac{1}{g} \left[v_0(v(t) - v_0) + \frac{1}{2}(v(t) - v_0)^2\right] \end{align*}\]שלב 5: פיתוח האלגברי
נפתח את הסוגריים בביטוי האחרון:
\[\begin{align*} \Delta x &= \frac{1}{g} \left[v_0v(t) - v_0^2 + \frac{1}{2}v(t)^2 - v_0v(t) + \frac{1}{2}v_0^2\right] \\ &= \frac{1}{g} \left[\frac{1}{2}v(t)^2 - \frac{1}{2}v_0^2\right]\\ &= \frac{1}{2g} \left[v(t)^2 - v_0^2\right] \end{align*}\]שלב 6: אלגברה סופית
נכפיל את שני הצדדים ב-$2g$:
\[2g \cdot \Delta x = v(t)^2 - v_0^2\] \[v(t)^2 = v_0^2 + 2g\Delta x\]הסבר: נוסחה זו מקשרת בין ריבוע המהירות, ריבוע המהירות ההתחלתית, וההעתק (השינוי במיקום). היא מאפשרת לנו לחשב את המהירות הסופית ללא צורך לדעת את הזמן שעבר. זוהי נוסחה שימושית במיוחד בבעיות מעשיות, כמו חישוב מהירות גוף לאחר שנפל ממגדל בגובה ידוע, או מהירות רכב לאחר שעבר מרחק מסוים בתאוצה קבועה.
יתרונה הגדול של נוסחה זו הוא שהיא מאפשרת לנו לקשר ישירות בין מהירויות והעתקים, ללא התייחסות לזמן. במקרים רבים, קל יותר למדוד מרחקים ומהירויות מאשר זמנים מדויקים, ולכן זוהי נוסחה פרקטית מאוד בפיזיקה יישומית ובהנדסה.
שאלה 6: תנועה אנכית כלפי מעלה
זורקים אבן כלפי מעלה במהירות התחלתית של $v_0 = 17~$ מטר לשנייה.
- א. מהי התאוצה בנקודת שיא הגובה?
- ב. מהי המהירות בנקודת שיא הגובה?
- ג. לאיזה גובה תגיע האבן?
- ד. באיזו מהירות תחזור האבן לידיו של הזורק?
- ה. אם היא פוגעת בקרקע מטר אחד מתחת לידו — באיזו מהירות היא פוגעת?
הפתרון
א. התאוצה בנקודת שיא הגובה
שלב 1: הבנת הכוחות הפועלים
כאשר זורקים אבן כלפי מעלה, הכוח היחיד הפועל עליה הוא כוח הכבידה. כוח זה פועל תמיד כלפי מטה, ללא קשר למיקום האבן או למהירותה.
שלב 2: יישום החוק השני של ניוטון
לפי החוק השני של ניוטון, התאוצה שווה לכוח חלקי מסה:
\[a = \frac{F}{m} = \frac{mg}{m} = g\]כיוון שגוף הנמצא בקרבת פני כדור הארץ חווה תאוצת כבידה של כ-10 מ’/שנייה² כלפי מטה, התאוצה של האבן בכל נקודה, כולל נקודת שיא הגובה, היא:
\[a = -g = -10~\left[\frac{\text{m}}{\text{s}^2}\right]\](הסימן השלילי מציין שהתאוצה פועלת בכיוון ההפוך לציר החיובי, שהוא כלפי מעלה במקרה זה)
הסבר: גם כאשר האבן מגיעה לשיא הגובה ו”עוצרת” לרגע, כוח הכבידה ממשיך לפעול עליה. לכן התאוצה אינה משתנה ונשארת -10 מ’/שנייה² לאורך כל המסלול.
ב. המהירות בנקודת שיא הגובה
שלב 1: הבנת מה מאפיין את נקודת שיא הגובה
בנקודת שיא הגובה, האבן מגיעה למצב שבו היא משנה את כיוון תנועתה - מתנועה כלפי מעלה לתנועה כלפי מטה. בנקודה זו, המהירות האנכית חייבת להיות אפס.
שלב 2: המסקנה לגבי המהירות
\[v = 0~\text{m/s}\]הסבר: במצב של תנועה אנכית, בנקודת שיא הגובה האבן “עוצרת” באופן רגעי לפני שהיא מתחילה לרדת. זהו מצב שבו המהירות האנכית שווה לאפס. אם הייתה לאבן מהירות שאינה אפס בנקודה זו, היא הייתה ממשיכה לעלות גבוה יותר.
ג. הגובה שאליו תגיע האבן
שלב 1: שימוש בנוסחת הקשר בין מהירות להעתק
נשתמש בנוסחה שהוכחנו בשאלה 5:
\[v^2 = v_0^2 - 2g\Delta x\](הסימן התחלף מ”+” ל”-“ כי התאוצה היא בכיוון ההפוך לתנועה ההתחלתית)
שלב 2: הצבת הנתונים וחישוב הגובה
בנקודת שיא הגובה, המהירות היא אפס ($v = 0$). נציב:
\[\begin{align*} 0 &= v_0^2 - 2g\Delta x \\ 2g\Delta x &= v_0^2 \\ \Delta x &= \frac{v_0^2}{2g} = \frac{17^2}{2 \cdot 10} = \frac{289}{20} = 14.45~\text{meter} \end{align*}\]הסבר: כאשר זורקים אבן כלפי מעלה, האנרגיה הקינטית (שקשורה למהירות) הופכת לאנרגיה פוטנציאלית (שקשורה לגובה). נוסחה זו מבטאת את שימור האנרגיה - האבן תעלה עד לגובה שבו כל האנרגיה הקינטית ההתחלתית שלה הפכה לאנרגיה פוטנציאלית.
ד. מהירות האבן בחזרה לידיו של הזורק
שלב 1: שימוש בעקרון שימור האנרגיה
במערכת שבה אין חיכוך או התנגדות אוויר, האנרגיה המכנית נשמרת. זה אומר שכאשר האבן חוזרת לגובה ההתחלתי, מהירותה (בערך מוחלט) תהיה זהה למהירות ההתחלתית.
שלב 2: קביעת הכיוון
מכיוון שהאבן חוזרת לידיו של הזורק, היא נעה כלפי מטה, כלומר בכיוון ההפוך למהירות ההתחלתית.
שלב 3: המסקנה
המהירות שבה האבן תחזור לידיו של הזורק היא:
\[v = -v_0 = -17~\text{m/s}\](הסימן השלילי מציין שהמהירות היא בכיוון ההפוך לציר החיובי)
הסבר: בתנועה אנכית תחת השפעת הכבידה בלבד (ללא התנגדות אוויר), המהירות בחזרה לנקודת המוצא תהיה שווה בגודלה למהירות ההתחלתית אך בכיוון הפוך. זוהי תוצאה ישירה של שימור האנרגיה.
ה. מהירות הפגיעה בקרקע מטר אחד מתחת ליד
שלב 1: שימוש בנוסחת הקשר בין מהירות להעתק
נשתמש שוב בנוסחה:
\[v^2 = v_0^2 + 2g\Delta x\]הפעם הסימן הוא חיובי כי התאוצה והתנועה הן באותו כיוון (כלפי מטה).
שלב 2: הצבת הנתונים
- $v_0 = 17~\text{מ/ש}$ (המהירות ההתחלתית)
- $g = 10~\left[\frac{\text{m}}{\text{s}^2}\right]$ (תאוצת הכבידה)
- $\Delta x = 1~\text{מ’}$ (העתק נוסף מתחת לנקודת הזריקה)
$v^2 = 17^2 + 2 \cdot 10 \cdot 1 = 289 + 20 = 309$ $v = \sqrt{309} \approx 17.58~\text{מ/ש}$
מכיוון שהאבן נעה כלפי מטה, המהירות היא שלילית:
\[v \approx -17.58~\text{m/s}\]הסבר: כאשר האבן ממשיכה מעבר לנקודת הזריקה, היא צוברת אנרגיה קינטית נוספת עקב הכבידה, ולכן מהירותה גדלה. ככל שהאבן נופלת למרחק גדול יותר, מהירותה תגדל בהתאם.
שאלה 7: תנועה היפרבולית במישור
השאלה
וקטור המהירות:
\[\vec{v}(t) = 2\cosh(3t)\hat{i} + 2\sinh(3t)\hat{j}\]- א. מהי מהירותו ההתחלתית של הגוף ותאוצתו בזמן $t = 0$?
- ב. הניחו כי: $\vec{r}(0) = 3\hat{i} + 3\hat{j}$ מצאו ביטוי לוקטור המקום $\vec{r}(t)$.
- ג. מה גודלו של הכוח בכל רגע? \(\|\vec{F}(t)\| = m\|\vec{a}(t)\|\), \(m = 10~\text{kg}\)
- ד. מה כיוון הכוח בכל רגע?
הפתרון
א. המהירות ההתחלתית והתאוצה בזמן $t = 0$
שלב 1: חישוב המהירות ההתחלתית
המהירות ההתחלתית היא וקטור המהירות בזמן $t = 0$:
\[\vec{v}(0) = 2\cosh(3 \cdot 0)\hat{i} + 2\sinh(3 \cdot 0)\hat{j}\]נזכור כי:
- $\cosh(0) = 1$
- $\sinh(0) = 0$
לכן:
\[\vec{v}(0) = 2 \cdot 1 \cdot \hat{i} + 2 \cdot 0 \cdot \hat{j} = 2\hat{i}\]שלב 2: חישוב התאוצה
התאוצה היא הנגזרת של וקטור המהירות ביחס לזמן:
$\vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{d}{dt}[2\cosh(3t)\hat{i} + 2\sinh(3t)\hat{j}]$
נגזור כל רכיב:
$\frac{d}{dt}[2\cosh(3t)] = 2 \cdot 3 \cdot \sinh(3t) = 6\sinh(3t)$ $\frac{d}{dt}[2\sinh(3t)] = 2 \cdot 3 \cdot \cosh(3t) = 6\cosh(3t)$
לכן:
$\vec{a}(t) = 6\sinh(3t)\hat{i} + 6\cosh(3t)\hat{j}$
שלב 3: חישוב התאוצה בזמן $t = 0$
$\vec{a}(0) = 6\sinh(0)\hat{i} + 6\cosh(0)\hat{j} = 6 \cdot 0 \cdot \hat{i} + 6 \cdot 1 \cdot \hat{j} = 6\hat{j}$
הסבר: בזמן $t = 0$, הגוף נע במהירות של 2 מטר לשנייה בכיוון ציר ה-$x$ החיובי. באותו רגע, התאוצה שלו היא 6 מטר לשנייה בריבוע בכיוון ציר ה-$y$ החיובי. זה מצביע על כך שהגוף יתחיל לשנות את כיוון התנועה שלו, עם נטייה גוברת בכיוון ציר ה-$y$.
ב. מציאת וקטור המקום $\vec{r}(t)$
שלב 1: הכרת הקשר בין מהירות למיקום
המהירות היא הנגזרת של המיקום ביחס לזמן:
\[\vec{v}(t) = \frac{d\vec{r}}{dt}\]שלב 2: אינטגרציה של וקטור המהירות
כדי למצוא את וקטור המקום, עלינו לאינטגרל את וקטור המהירות:
$\vec{r}(t) = \vec{r}(0) + \int_{0}^{t} \vec{v}(s) ds$ $= \vec{r}(0) + \int_{0}^{t} [2\cosh(3s)\hat{i} + 2\sinh(3s)\hat{j}] ds$
שלב 3: חישוב האינטגרלים
נחשב בנפרד עבור כל רכיב: $\int \cosh(ax) dx = \frac{1}{a} \sinh(ax) + C$ $\int \sinh(ax) dx = \frac{1}{a} \cosh(ax) + C$
עבור הרכיב בכיוון $\hat{i}$:
\[\int_{0}^{t} 2\cosh(3s) ds = 2 \int_{0}^{t} \cosh(3s) ds = 2 \cdot \frac{1}{3}[\sinh(3s)]_{0}^{t} = \frac{2}{3}[\sinh(3t) - \sinh(0)] = \frac{2}{3}\sinh(3t)\]עבור הרכיב בכיוון $\hat{j}$:
\[\int_{0}^{t} 2\sinh(3s) ds = 2 \int_{0}^{t} \sinh(3s) ds = 2 \cdot \frac{1}{3}[\cosh(3s)]_{0}^{t} = \frac{2}{3}[\cosh(3t) - \cosh(0)] = \frac{2}{3}[\cosh(3t) - 1]\]שלב 4: חיבור הרכיבים והצבת $\vec{r}(0)$
\[\begin{align*} \vec{r}(t) &= \vec{r}(0) + \frac{2}{3}\sinh(3t)\hat{i} + \frac{2}{3}[\cosh(3t) - 1]\hat{j} \\ &= 3\hat{i} + 3\hat{j} + \frac{2}{3}\sinh(3t)\hat{i} + \frac{2}{3}[\cosh(3t) - 1]\hat{j} \\ &= (3 + \frac{2}{3}\sinh(3t))\hat{i} + (3 + \frac{2}{3}\cosh(3t) - \frac{2}{3})\hat{j} \\ &= (3 + \frac{2}{3}\sinh(3t))\hat{i} + (3 - \frac{2}{3} + \frac{2}{3}\cosh(3t))\hat{j} \\ &= (3 + \frac{2}{3}\sinh(3t))\hat{i} + (\frac{7}{3} + \frac{2}{3}\cosh(3t))\hat{j} \end{align*}\]הסבר: וקטור המקום $\vec{r}(t)$ מתאר את מיקום הגוף בכל רגע. הביטוי שקיבלנו מראה כיצד הגוף נע במישור, עם רכיבים שמשתנים באופן היפרבולי עם הזמן. התנועה מתחילה מהנקודה $(3,3)$ ומתפתחת בהתאם לפונקציות היפרבוליות $\sinh$ ו-$\cosh$.
ג. גודל הכוח בכל רגע
שלב 1: חישוב גודל וקטור התאוצה
ראינו כי וקטור התאוצה הוא:
$\vec{a}(t) = 6\sinh(3t)\hat{i} + 6\cosh(3t)\hat{j}$
גודלו של וקטור התאוצה הוא:
\[|\vec{a}(t)| = \sqrt{(6\sinh(3t))^2 + (6\cosh(3t))^2} = 6\sqrt{\sinh^2(3t) + \cosh^2(3t)}\]נזכור את הזהות ההיפרבולית:
\[\cosh^2(x) - \sinh^2(x) = 1\]לכן:
\[\sinh^2(x) + \cosh^2(x) = 2\cosh^2(x) - 1\]נציב:
\[|\vec{a}(t)| = 6\sqrt{2\cosh^2(3t) - 1}\]שלב 2: חישוב גודל הכוח
לפי החוק השני של ניוטון:
\[\begin{align*} |\vec{F}(t)| &= m|\vec{a}(t)| \\ &= 10 \cdot 6\sqrt{2\cosh^2(3t) - 1} \\ &= 60\sqrt{2\cosh^2(3t) - 1}~\left[\text{N}\right] \end{align*}\]הסבר: גודל הכוח גדל עם הזמן, כיוון שהפונקציה $\cosh(3t)$ גדלה עם $t$. ככל שהזמן חולף, הגוף חווה כוח הולך וגדל, מה שגורם לו להאיץ בקצב גובר.
ד. כיוון הכוח בכל רגע
שלב 1: התבוננות בקשר בין כוח לתאוצה
לפי החוק השני של ניוטון, וקטור הכוח ווקטור התאוצה נמצאים באותו כיוון:
\[\vec{F} = m\vec{a}\]שלב 2: מציאת כיוון התאוצה
כיוון התאוצה נקבע על ידי הווקטור היחידה בכיוון התאוצה:
\[\hat{a}(t) = \frac{\vec{a}(t)}{|\vec{a}(t)|} = \frac{6\sinh(3t)\hat{i} + 6\cosh(3t)\hat{j}}{6\sqrt{\sinh^2(3t) + \cosh^2(3t)}} = \frac{\sinh(3t)\hat{i} + \cosh(3t)\hat{j}}{\sqrt{\sinh^2(3t) + \cosh^2(3t)}}\]שלב 3: מסקנה לגבי כיוון הכוח
כיוון שהכוח והתאוצה הם באותו כיוון, כיוון הכוח בכל רגע יהיה:
\[\hat{F}(t) = \hat{a}(t) = \frac{\sinh(3t)\hat{i} + \cosh(3t)\hat{j}}{\sqrt{\sinh^2(3t) + \cosh^2(3t)}}\]הסבר: כיוון הכוח משתנה עם הזמן, מתחיל בכיוון ציר ה-$y$ החיובי (כאשר $t = 0$) ומשנה את עצמו בהתאם ליחס בין הפונקציות $\sinh(3t)$ ו-$\cosh(3t)$. ככל ש-$t$ גדל, הרכיב בכיוון $\hat{i}$ גדל, והכוח נוטה יותר לכיוון הראשון של המישור (צפון-מזרח).
שאלה 8: טריז וגליל
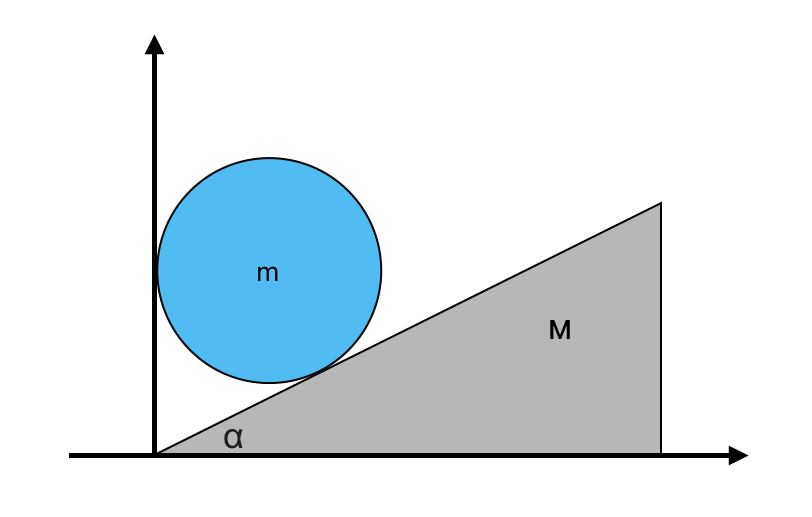
טריז מסה $M$, גליל מסה $m$, שיפוע $\alpha = 30^\circ$, אין חיכוך.
א. כאשר הטריז מקובע:
- מהם הכוחות הנורמליים על הגליל? על הטריז?
ב. כאשר הטריז חופשי לנוע:
- הגליל מחליק, הטריז מאיץ ימינה. מצאו את התאוצות $a$ ו־$A$ בהתחשב בקשר: $a = A \tan(\alpha)$
הפתרון
א. כאשר הטריז מקובע - כוחות נורמליים
שלב 1: ניתוח הכוחות על הגליל
על הגליל פועלים הכוחות הבאים:
- כוח הכבידה $\vec{W}_g = m\vec{g} = mg\hat{j}$, כלפי מטה בכיוון הציר השלילי של $y$
- כוח נורמלי $\vec{N}$ מהטריז, בכיוון ניצב למשטח השיפוע
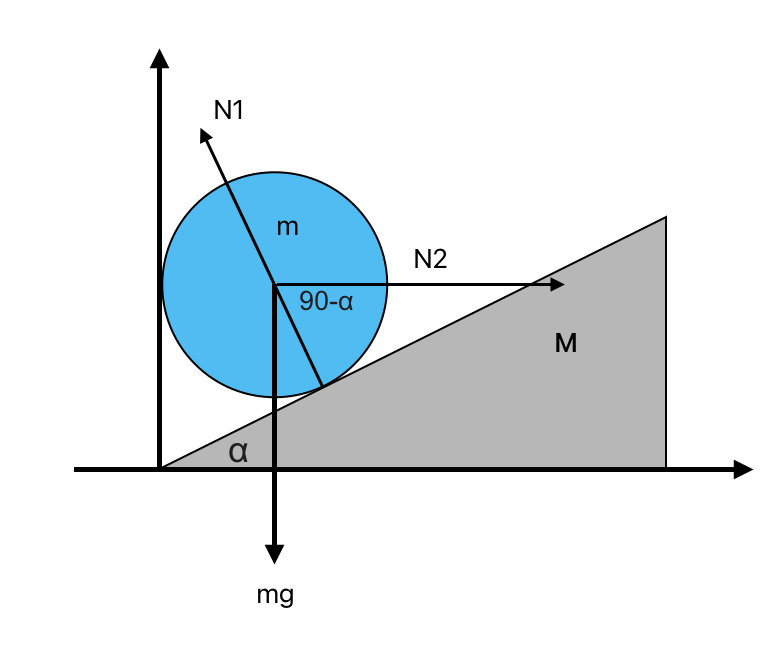
שלב 2: פירוק הכוחות לרכיבים במערכת צירים מתאימה
נגדיר מערכת צירים כך ש:
- ציר $x’$ מקביל למשטח השיפוע
- ציר $y’$ ניצב למשטח השיפוע
פירוק כוח הכבידה:
- הרכיב במקביל למשטח: $mg\sin\alpha$
- הרכיב בניצב למשטח: $mg\cos\alpha$
שלב 3: יישום החוק השני של ניוטון
כאשר הטריז מקובע, הגליל ינוע במורד המדרון בתאוצה. בכיוון הניצב למשטח, אין תאוצה:
$N - mg\cos\alpha = 0$ $N = mg\cos\alpha = mg\cos(30^\circ) = mg \cdot \frac{\sqrt{3}}{2} \approx 0.866mg$
שלב 4: כוח נורמלי על הטריז על פי החוק השלישי של ניוטון, הכוח שהגליל מפעיל על הטריז שווה בגודלו והפוך בכיוונו לכוח שהטריז מפעיל על הגליל:
$N_{\text{על הטריז}} = N = mg\cos\alpha \approx 0.866mg$
הסבר: הכוח הנורמלי על הגליל הוא הכוח שמונע ממנו לחדור לתוך משטח הטריז. גודלו שווה לרכיב כוח הכבידה הניצב למשטח. לפי החוק השלישי של ניוטון, כוח התגובה הזה פועל גם על הטריז, בכיוון ההפוך.
ב. כאשר הטריז חופשי לנוע - מציאת התאוצות
שלב 1: ניתוח הכוחות והתנועה
כאשר הטריז חופשי לנוע:
- הגליל מחליק במורד השיפוע בתאוצה $a$ (בכיוון $x’$ היחסי לטריז)
- הטריז נע ימינה בתאוצה $A$ (בכיוון $x$ הגלובלי)
נתון שיש קשר בין התאוצות: $a = A \tan(\alpha)$
שלב 2: יישום החוק השני של ניוטון לגליל
בכיוון המקביל למשטח השיפוע, הכוח היחיד הוא רכיב הכבידה:
$mg\sin\alpha = m(a_{\text{יחסי}} + A\cos\alpha)$
כאן $a_{\text{יחסי}}$ היא התאוצה של הגליל ביחס לטריז, ו-$A\cos\alpha$ היא התאוצה הנובעת מתנועת הטריז.
שלב 3: שימוש בקשר בין התאוצות מהנתון: $a_{\text{יחסי}} = a = A\tan\alpha$
נציב:
$mg\sin\alpha = m(A\tan\alpha + A\cos\alpha)$ $mg\sin\alpha = mA(\tan\alpha + \cos\alpha)$ $g\sin\alpha = A(\tan\alpha + \cos\alpha)$ $g\sin\alpha = A(\frac{\sin\alpha}{\cos\alpha} + \cos\alpha)$ $g\sin\alpha = A(\frac{\sin\alpha + \cos^2\alpha}{\cos\alpha})$ $g\sin\alpha = A\frac{\sin\alpha + 1 - \sin^2\alpha}{\cos\alpha}$ $g\sin\alpha \cdot \cos\alpha = A(\sin\alpha + 1 - \sin^2\alpha)$
שלב 4: פתרון המשוואה
\[\begin{align*} A &= \frac{g\sin\alpha \cdot \cos\alpha}{\sin\alpha + 1 - \sin^2\alpha} \\ &= \frac{g\sin\alpha \cdot \cos\alpha}{1 + \sin\alpha - \sin^2\alpha} \\ &= \frac{g\sin\alpha \cdot \cos\alpha}{1 + \sin\alpha(1 - \sin\alpha)} \end{align*}\]לערך המספרי של $\alpha = 30^\circ$:
\[\sin(30^\circ) = 0.5\] \[\cos(30^\circ) = \frac{\sqrt{3}}{2} \approx 0.866\] \[A = \frac{g \cdot 0.5 \cdot 0.866}{1 + 0.5(1 - 0.5)} = \frac{0.433g}{1 + 0.25} = \frac{0.433g}{1.25} \approx 0.346g\]שלב 5: חישוב תאוצת הגליל
מהקשר הנתון:
\[a = A\tan\alpha = 0.346g \cdot \tan(30^\circ) = 0.346g \cdot 0.577 \approx 0.2g\]הסבר: כאשר הטריז חופשי לנוע, חלק מאנרגיית התנועה של הגליל מועברת לטריז, ולכן הגליל מאיץ בקצב איטי יותר בהשוואה למקרה שבו הטריז מקובע. תאוצת הגליל ביחס לקרקע היא סכום וקטורי של תאוצתו ביחס לטריז ותאוצת הטריז עצמו.
שאלה 9: תנועה בקואורדינטות קוטביות
א. מהן קואורדינטות קוטביות?
- $r(t)$: מרחק מהראשית.
- $\theta(t)$: הזווית עם ציר $x$.
ב. וקטורי היחידה:
\[\hat{r}(t) = \cos\theta\hat{i} + \sin\theta\hat{j}\] \[\hat{\theta}(t) = -\sin\theta\hat{i} + \cos\theta\hat{j}\]הראו כי זוהי מערכת אורתונורמלית.
ג. וקטור המהירות והתאוצה:
\[\vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta}\] \[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta}\]ד. אם שקול הכוחות הוא:
$\vec{F} = F_r\hat{r} + F_\theta\hat{\theta}$
אז לפי חוק שני של ניוטון:
\[F_r\hat{r} + F_\theta\hat{\theta} = m\vec{a}\]ה. מה קורה כשמסת הגוף משתנה בזמן?
הפתרון
א. הסבר קואורדינטות קוטביות
שלב 1: הגדרת קואורדינטות קוטביות
קואורדינטות קוטביות הן שיטה אלטרנטיבית לתיאור מיקום של נקודה במישור, באמצעות:
- $r(t)$ - המרחק מהראשית (נקודת המקור של מערכת הצירים)
- $\theta(t)$ - הזווית בין הקו המחבר את הנקודה לראשית לבין הציר האופקי החיובי (ציר $x$)
שלב 2: הקשר לקואורדינטות קרטזיות
אם נסמן את הקואורדינטות הקרטזיות של נקודה כ-$(x, y)$, אז הקשר לקואורדינטות הקוטביות $(r, \theta)$ הוא:
\[x = r \cos\theta , \qquad y = r \sin\theta\]לחילופין:
\[r = \sqrt{x^2 + y^2} , \qquad \theta = \tan^{-1}(\frac{y}{x})\]הסבר: קואורדינטות קוטביות שימושיות במיוחד כאשר מתארים תנועה מעגלית או תנועה שבה המרחק מנקודה מרכזית משחק תפקיד חשוב, כגון בבעיות הקשורות לכבידה, תנועה פלנטרית, או תנועה בשדות כוח מרכזיים.
ב. הוכחת המערכת האורתונורמלית
שלב 1: הגדרת מערכת אורתונורמלית
מערכת אורתונורמלית של וקטורים מורכבת מווקטורים יחידה שניצבים זה לזה. עלינו להוכיח ששני וקטורי היחידה בקואורדינטות קוטביות - $\hat{r}$ ו-$\hat{\theta}$ - מקיימים:
- הם וקטורי יחידה: \(\|\hat{r}\| = \|\hat{\theta}\| = 1\)
- הם ניצבים זה לזה: \(\hat{r} \cdot \hat{\theta} = 0\)
שלב 2: בדיקת תנאי וקטורי יחידה
לבדוק אם $\hat{r}$ הוא וקטור יחידה:
\[|\hat{r}|^2 = (\cos\theta)^2 + (\sin\theta)^2 = \cos^2\theta + \sin^2\theta = 1\]מכאן
\[|\hat{r}| = 1\]לבדוק אם $\hat{\theta}$ הוא וקטור יחידה:
\[|\hat{\theta}|^2 = (-\sin\theta)^2 + (\cos\theta)^2 = \sin^2\theta + \cos^2\theta = 1\]מכאן
\[|\hat{\theta}| = 1\]שלב 3: בדיקת תנאי הניצבות
\[\begin{align*} \hat{r} \cdot \hat{\theta} &= \cos\theta \cdot (-\sin\theta) + \sin\theta \cdot \cos\theta \\ &= -\cos\theta \sin\theta + \sin\theta \cos\theta = 0 \end{align*}\]הסבר: הוכחנו שזוהי מערכת אורתונורמלית. וקטור $\hat{r}$ מצביע תמיד בכיוון היוצא מהראשית לנקודה, כלומר בכיוון הרדיאלי, בעוד שווקטור $\hat{\theta}$ ניצב לו ומצביע בכיוון התנועה המעגלית סביב הראשית.
ג. הסבר וקטור המהירות והתאוצה
שלב 1: וקטור המהירות בקואורדינטות קוטביות
\[\vec{v} = \dot{r}\hat{r} + r\dot{\theta}\hat{\theta}\]הביטוי הזה מורכב משני רכיבים:
- $\dot{r}\hat{r}$ - רכיב רדיאלי של המהירות, המייצג את קצב השינוי של המרחק מהראשית
- $r\dot{\theta}\hat{\theta}$ - רכיב טנגנציאלי של המהירות, המייצג את התנועה הסיבובית סביב הראשית
שלב 2: וקטור התאוצה בקואורדינטות קוטביות
\[\vec{a} = (\ddot{r} - r\dot{\theta}^2)\hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta}\]הביטוי מורכב משני רכיבים:
- רכיב רדיאלי: $(\ddot{r} - r\dot{\theta}^2)\hat{r}$
- $\ddot{r}$ - תאוצה רדיאלית ישירה (שינוי בקצב השינוי של $r$)
- $-r\dot{\theta}^2$ - תאוצה צנטריפטלית (הנובעת מהתנועה הסיבובית)
- רכיב טנגנציאלי: $(2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta}$
- $2\dot{r}\dot{\theta}$ - אפקט קוריוליס (הנובע משינוי בו-זמני של $r$ ו-$\theta$)
- $r\ddot{\theta}$ - תאוצה זוויתית (שינוי בקצב הסיבוב)
הסבר: יתרון גדול בשימוש בקואורדינטות קוטביות הוא שהן מאפשרות לבטא באופן ישיר וטבעי תנועה מעגלית או ספירלית. הביטויים שקיבלנו למהירות ולתאוצה כוללים את כל האפקטים הדינמיים החשובים, כמו תאוצה צנטריפטלית ואפקט קוריוליס, שקשה יותר לראות בקואורדינטות קרטזיות.
ד. יישום החוק השני של ניוטון
שלב 1: הצגת וקטור הכוח בקואורדינטות קוטביות
\[\vec{F} = F_r\hat{r} + F_\theta\hat{\theta}\]כוח ניתן לפרק לרכיב רדיאלי $F_r$ (בכיוון $\hat{r}$) ורכיב טנגנציאלי $F_\theta$ (בכיוון $\hat{\theta}$).
שלב 2: יישום החוק השני של ניוטון
$\vec{F} = m\vec{a}$
$(F_r\hat{r} + F_\theta\hat{\theta}) = m((\ddot{r} - r\dot{\theta}^2)\hat{r} + (2\dot{r}\dot{\theta} + r\ddot{\theta})\hat{\theta})$
שלב 3: השוואת רכיבים
מכיוון ש-$\hat{r}$ ו-$\hat{\theta}$ הם וקטורים עצמאיים, אנו יכולים להשוות את הרכיבים משני צדי המשוואה:
רכיב רדיאלי:
\[F_r = m(\ddot{r} - r\dot{\theta}^2)\]רכיב טנגנציאלי:
\[F_\theta = m(2\dot{r}\dot{\theta} + r\ddot{\theta})\]הסבר: משוואות אלו מתארות את הדינמיקה של גוף הנע במישור בקואורדינטות קוטביות. הן מאפשרות לנו לחשב את תנועת הגוף כאשר ידועים הכוחות הפועלים עליו, או לחילופין לקבוע את הכוחות הדרושים כדי לייצר תנועה מסוימת.
ה. משמעות שינוי המסה עם הזמן
שלב 1: הצגת בעיה עם מסה משתנה
כאשר מסת הגוף $m(t)$ משתנה עם הזמן, החוק השני של ניוטון בצורתו הפשוטה $\vec{F} = m\vec{a}$ אינו תקף יותר.
שלב 2: עדכון החוק השני של ניוטון
הניסוח הכללי יותר של החוק השני של ניוטון הוא:
\[\vec{F} = \frac{d\vec{p}}{dt}\]כאשר $\vec{p} = m\vec{v}$ הוא התנע של הגוף.
במקרה של מסה משתנה:
\[\vec{F} = \frac{d(m\vec{v})}{dt} = \frac{dm}{dt}\vec{v} + m\frac{d\vec{v}}{dt} = \dot{m}\vec{v} + m\vec{a}\]שלב 3: השלכות על התנועה בקואורדינטות קוטביות
הרכיב הרדיאלי:
\[F_r = \dot{m}v_r + m(\ddot{r} - r\dot{\theta}^2)\]כאשר $v_r = \dot{r}$ הוא רכיב המהירות בכיוון $\hat{r}$.
הרכיב הטנגנציאלי:
\[F_\theta = \dot{m}v_\theta + m(2\dot{r}\dot{\theta} + r\ddot{\theta})\]כאשר $v_\theta = r\dot{\theta}$ הוא רכיב המהירות בכיוון $\hat{\theta}$.
הסבר: כאשר מסת הגוף משתנה, יש לקחת בחשבון גם את קצב שינוי המסה. דוגמה מעשית היא תנועת רקטה, שמסתה פוחתת ככל שהיא צורכת דלק. השינוי במסה תורם לכוח נוסף, הנקרא “תגובת סילון” (jet reaction), המשפיע על תנועת הגוף. ניתוח התנועה במקרה כזה דורש את הצורה הכללית יותר של החוק השני של ניוטון, שלוקחת בחשבון את שינוי התנע במלואו.
דור פסקלחזרה לעמוד הראשי