שאלה 1 - וקטורים תלת-ממדיים וזווית ביניהם
נתונים שני הווקטורים:
\[\vec{a} = \hat{x} + (\sqrt{2})\hat{y} - (\sqrt{3})\hat{z}\] \[\vec{b} = (\sqrt{3})\hat{x} - (\sqrt{2})\hat{y} + \hat{z}\]
- היעזרו במחשבון בלבד כדי למצוא את הזווית בין שני הווקטורים.
- קבלו וקטור יחידה המצביע בכיוון השקול הווקטורי של שני הווקטורים.
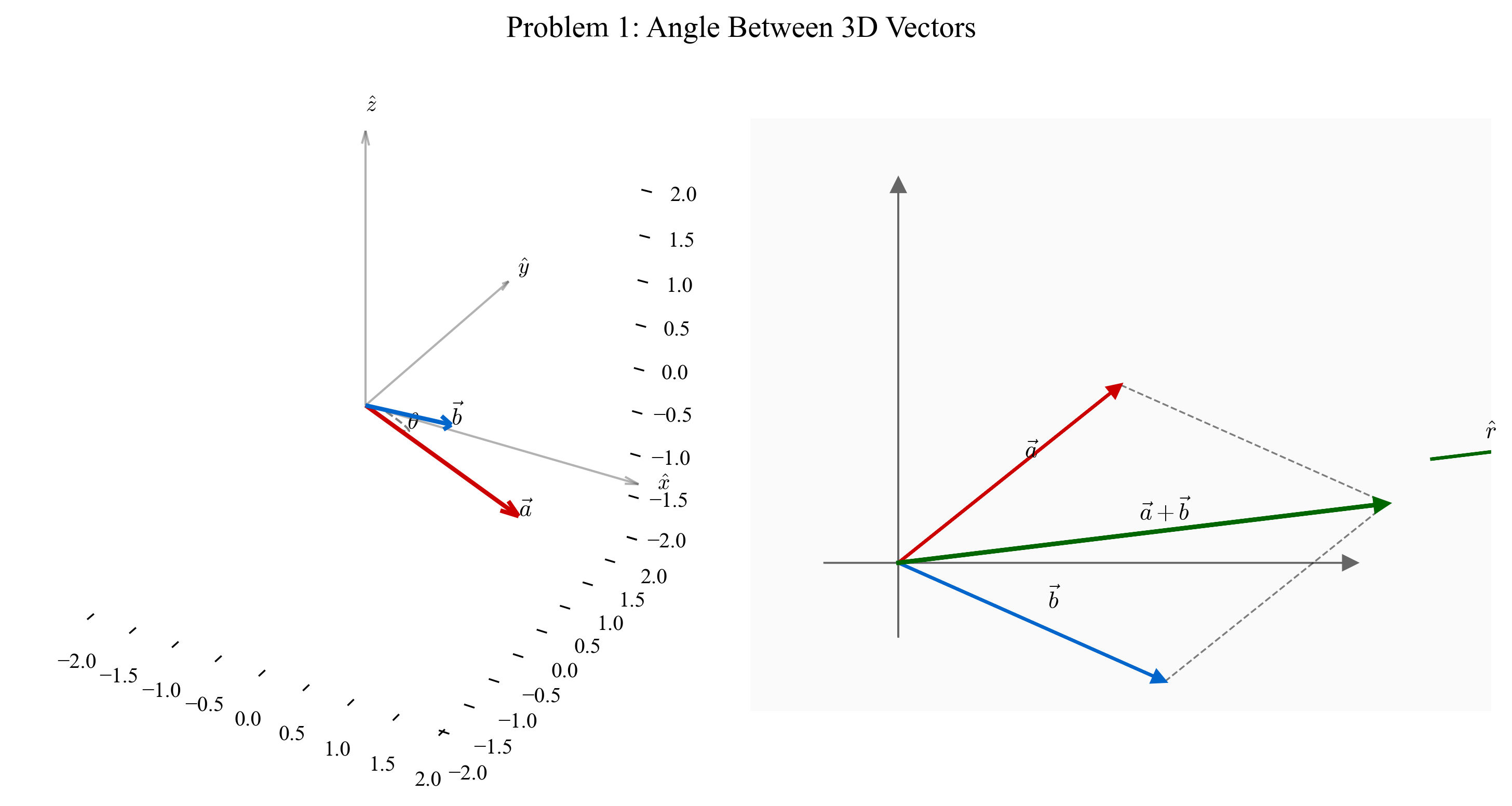
סעיף א: זווית בין וקטורים
הזווית בין שני וקטורים מחושבת באמצעות המכפלה הסקלרית:
\[\cos\theta = \frac{\vec{a} \cdot \vec{b}}{\vert \vec{a}|\vert \vec{b}\vert}\]שלב 1: חישוב המכפלה הסקלרית
\[\vec{a} \cdot \vec{b} = (1)(\sqrt{3}) + (\sqrt{2})(-\sqrt{2}) + (-\sqrt{3})(1)\] \[= \sqrt{3} - 2 - \sqrt{3} = -2\]שלב 2: חישוב גודל הווקטורים
\[\vert \vec{a}\vert = \sqrt{1^2 + (\sqrt{2})^2 + (-\sqrt{3})^2} = \sqrt{1 + 2 + 3} = \sqrt{6}\] \[\vert \vec{b}\vert = \sqrt{(\sqrt{3})^2 + (-\sqrt{2})^2 + 1^2} = \sqrt{3 + 2 + 1} = \sqrt{6}\]שלב 3: חישוב הזווית
\[\cos\theta = \frac{-2}{\sqrt{6} \cdot \sqrt{6}} = \frac{-2}{6} = -\frac{1}{3}\] \[\boxed{\theta = \arccos\left(-\frac{1}{3}\right) \approx 109.47^\circ}\]הערה: זווית גדולה מ-90° מעידה על כך שהווקטורים יוצרים זווית קהה ביניהם. המכפלה הסקלרית השלילית מאששת זאת.
סעיף ב: וקטור יחידה בכיוון השקול
שלב 1: מציאת השקול
\[\begin{aligned} \vec{a} + \vec{b} &= (1 + \sqrt{3})\hat{x} + (\sqrt{2} - \sqrt{2})\hat{y} + (-\sqrt{3} + 1)\hat{z} \\[10pt] &= (1 + \sqrt{3})\hat{x} + 0\hat{y} + (1 - \sqrt{3})\hat{z} \end{aligned}\]שלב 2: חישוב גודל השקול
\[\vert \vec{a} + \vec{b}\vert = \sqrt{(1 + \sqrt{3})^2 + 0^2 + (1 - \sqrt{3})^2}\]פיתוח הביטויים:
\[(1 + \sqrt{3})^2 = 1 + 2\sqrt{3} + 3 = 4 + 2\sqrt{3}\] \[(1 - \sqrt{3})^2 = 1 - 2\sqrt{3} + 3 = 4 - 2\sqrt{3}\]לכן:
\[\vert \vec{a} + \vec{b}\vert = \sqrt{4 + 2\sqrt{3} + 4 - 2\sqrt{3}} = \sqrt{8} = 2\sqrt{2}\]שלב 3: וקטור היחידה
\[\begin{aligned} \hat{r} &= \frac{\vec{a} + \vec{b}}{\vert \vec{a} + \vec{b}\vert} \\[10pt] &= \frac{1}{2\sqrt{2}}[(1 + \sqrt{3})\hat{x} + (1 - \sqrt{3})\hat{z}] \\[10pt] &= \frac{1 + \sqrt{3}}{2\sqrt{2}}\hat{x} + \frac{1 - \sqrt{3}}{2\sqrt{2}}\hat{z} \end{aligned}\]שאלה 2: פעולות על וקטורים דו-ממדיים
נתונים שני וקטורים דו-ממדיים:
\[\vec{a} = 3\hat{x} - 3\hat{y}, \quad \vec{b} = -2\hat{x} + \hat{y}\]
- קבלו את הסינוס והקוסינוס של הזווית של הווקטור $2\vec{a} - 3\vec{b}$ ביחס לציר האיקס (אין צורך לחשב את הזווית עצמה).
- נתון הווקטור $\vec{c} = \pi\hat{x} + e\hat{y}$. קבלו את כל הווקטורים שבעולם הניצבים לו.
- רישמו את הווקטור $\vec{c}$ בבסיס שנפרש ע”י הווקטורים $\vec{a}, \vec{b}$.
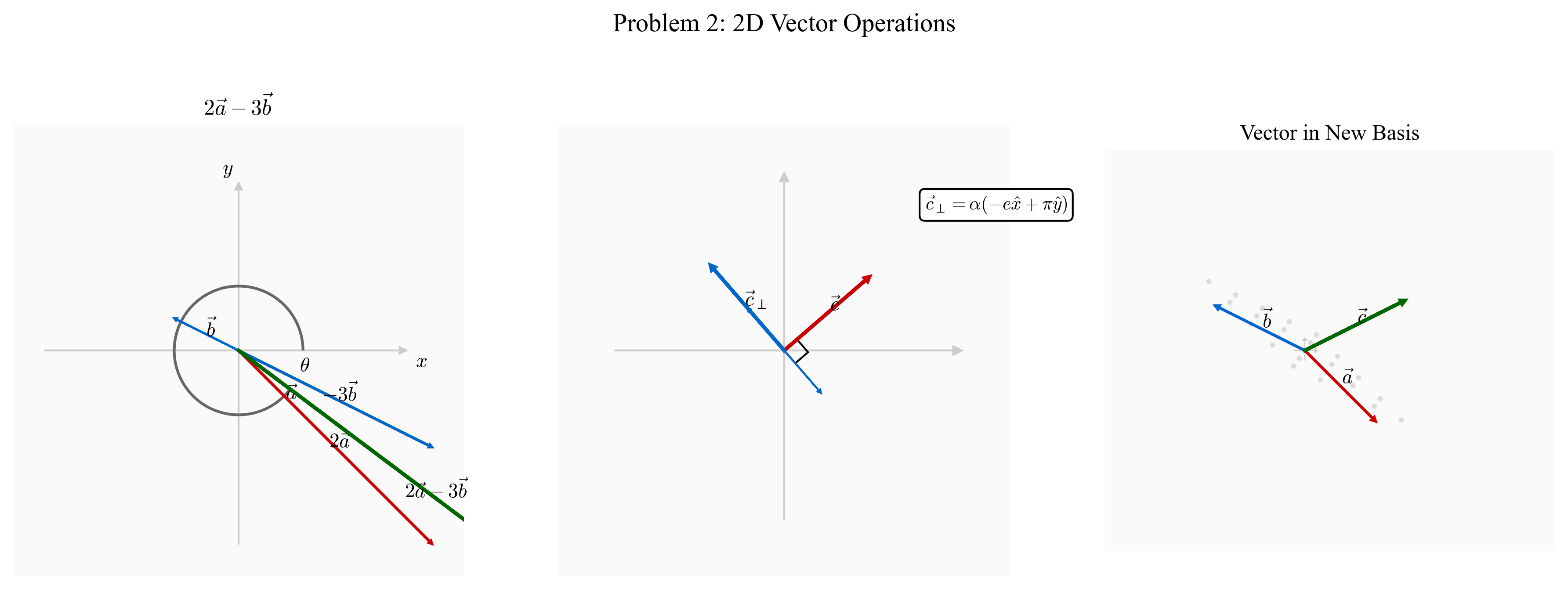
סעיף א: סינוס וקוסינוס של זווית
שלב 1: חישוב הווקטור
\[2\vec{a} - 3\vec{b} = 2(3\hat{x} - 3\hat{y}) - 3(-2\hat{x} + \hat{y})\] \[= 6\hat{x} - 6\hat{y} + 6\hat{x} - 3\hat{y}\] \[= 12\hat{x} - 9\hat{y}\]שלב 2: גודל הווקטור
\[|2\vec{a} - 3\vec{b}\vert = \sqrt{12^2 + (-9)^2} = \sqrt{144 + 81} = \sqrt{225} = 15\]שלב 3: הסינוס והקוסינוס
עבור וקטור $\vec{v} = v_x\hat{x} + v_y\hat{y}$:
- $\cos\theta = \frac{v_x}{\vert \vec{v}\vert }$ (רכיב x מנורמל)
- $\sin\theta = \frac{v_y}{\vert \vec{v}\vert }$ (רכיב y מנורמל)
לכן:
\[\cos\theta = \frac{12}{15} = \frac{4}{5}\] \[\sin\theta = \frac{-9}{15} = -\frac{3}{5}\]הערה: שימו לב שמתקיים $\cos^2\theta + \sin^2\theta = \frac{16}{25} + \frac{9}{25} = 1$ כנדרש.
סעיף ב: וקטורים ניצבים
עיקרון: וקטור $\vec{v}$ ניצב ל-$\vec{c}$ אם ורק אם $\vec{v} \cdot \vec{c} = 0$.
אם $\vec{v} = x\hat{x} + y\hat{y}$, אז:
\[\vec{v} \cdot \vec{c} = x\pi + ye = 0\]מכאן:
\[x\pi = -ye\] \[x = -\frac{e}{\pi}y\]התשובה: כל הווקטורים הניצבים ל-$\vec{c}$ הם מהצורה:
\[\vec{v}_\perp = \alpha(-e\hat{x} + \pi\hat{y})\]כאשר $\alpha$ הוא סקלר כלשהו.
בדיקה:
\(\vec{v}_\perp \cdot \vec{c} = \alpha(-e\pi + \pi e) = 0\) ✓
סעיף ג: ייצוג בבסיס חדש
מטרה: למצוא סקלרים $\lambda, \mu$ כך ש:
\[\vec{c} = \lambda\vec{a} + \mu\vec{b}\]הצבה:
\[\pi\hat{x} + e\hat{y} = \lambda(3\hat{x} - 3\hat{y}) + \mu(-2\hat{x} + \hat{y})\]השוואת רכיבים:
- רכיב x: $\pi = 3\lambda - 2\mu$
- רכיב y: $e = -3\lambda + \mu$
פתרון מערכת המשוואות:
מהמשוואה השנייה: $\mu = e + 3\lambda$
הצבה בראשונה:
\[\pi = 3\lambda - 2(e + 3\lambda) = 3\lambda - 2e - 6\lambda = -3\lambda - 2e\] \[\lambda = -\frac{\pi + 2e}{3}\] \[\mu = e + 3\left(-\frac{\pi + 2e}{3}\right) = e - \pi - 2e = -\pi - e\]התשובה:
\[\vec{c} = -\frac{\pi + 2e}{3}\vec{a} - (\pi + e)\vec{b}\]שאלה 3: הוכחת משפט הקוסינוסים
נתון משולש עם צלעות a, b, c וזווית γ מול הצלע c. הוכיחו את משפט הקוסינוסים:
\[c^2 = a^2 + b^2 - 2ab\cos\gamma\]באמצעות שימוש טריוויאלי במכפלה הסקלרית.
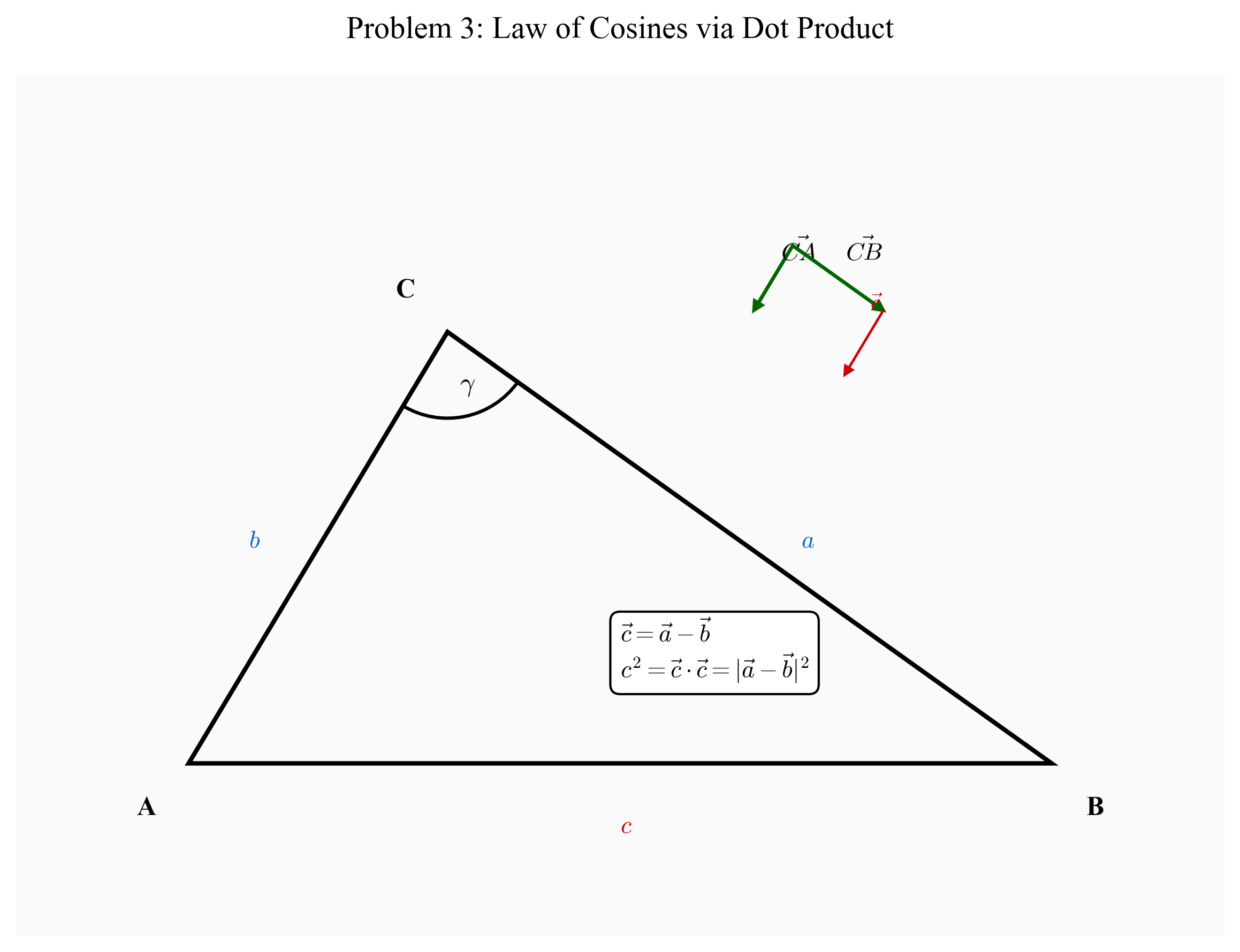
רעיון מרכזי: נייצג את צלעות המשולש כווקטורים ונשתמש בתכונות המכפלה הסקלרית.
שלב 1: הגדרת הווקטורים
נסמן את קודקודי המשולש כ-A, B, C. נגדיר:
- $\vec{a}$ = וקטור מ-C ל-B (אורכו a)
- $\vec{b}$ = וקטור מ-C ל-A (אורכו b)
- $\vec{c}$ = וקטור מ-A ל-B (אורכו c)
שלב 2: קשר בין הווקטורים מסגירת המשולש:
\[\vec{c} = \vec{a} - \vec{b}\]שלב 3: חישוב $c^2$ באמצעות מכפלה סקלרית
\[c^2 = \vert \vec{c}|^2 = \vec{c} \cdot \vec{c}\]הצבת הקשר מצעד 2:
\[c^2 = (\vec{a} - \vec{b}) \cdot (\vec{a} - \vec{b})\]שלב 4: פיתוח המכפלה הסקלרית
תכונת הדיסטריביוטיביות של המכפלה הסקלרית:
\[c^2 = \vec{a} \cdot \vec{a} - \vec{a} \cdot \vec{b} - \vec{b} \cdot \vec{a} + \vec{b} \cdot \vec{b}\]מכיוון שהמכפלה הסקלרית קומוטטיבית: $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$
\[c^2 = \vert \vec{a}|^2 - 2\vec{a} \cdot \vec{b} + \vert \vec{b}|^2\]שלב 5: שימוש בהגדרת המכפלה הסקלרית
\[\vec{a} \cdot \vec{b} = \vert \vec{a}|\vert \vec{b}|\cos\gamma\]כאשר γ היא הזווית בין $\vec{a}$ ו-$\vec{b}$ (שהיא הזווית בקודקוד C).
שלב 6: הצבה וסיום
\[c^2 = a^2 - 2ab\cos\gamma + b^2\] \[c^2 = a^2 + b^2 - 2ab\cos\gamma\]✓
תובנה: ההוכחה הווקטורית אלגנטית יותר מההוכחה הגיאומטרית הקלאסית ומדגישה את הקשר בין אלגברה וגיאומטריה.
שאלה 4: קואורדינטות כדוריות
הביטו באיור בנקודה P אשר מרחקה מהראשית הוא r. הווקטור היוצא מהראשית ומצביע אל הנקודה נתון בביטוי:
\[\vec{r} = x\hat{x} + y\hat{y} + z\hat{z}\]כאשר (x, y, z) הם הקואורדינטות של הנקודה P. תהיינה (r, θ, φ) קואורדינטות חדשות כמוראה באיור. שלושה זו מכונה קואורדינטות כדוריות.
א. הראו שמתקיים:
\[x = r\sin\theta\cos\varphi, \quad y = r\sin\theta\sin\varphi, \quad z = r\cos\theta\]ב. עשו שימוש בביטויים מעלה וקבלו במפורש:
\[x^2 + y^2 + z^2 = r^2\]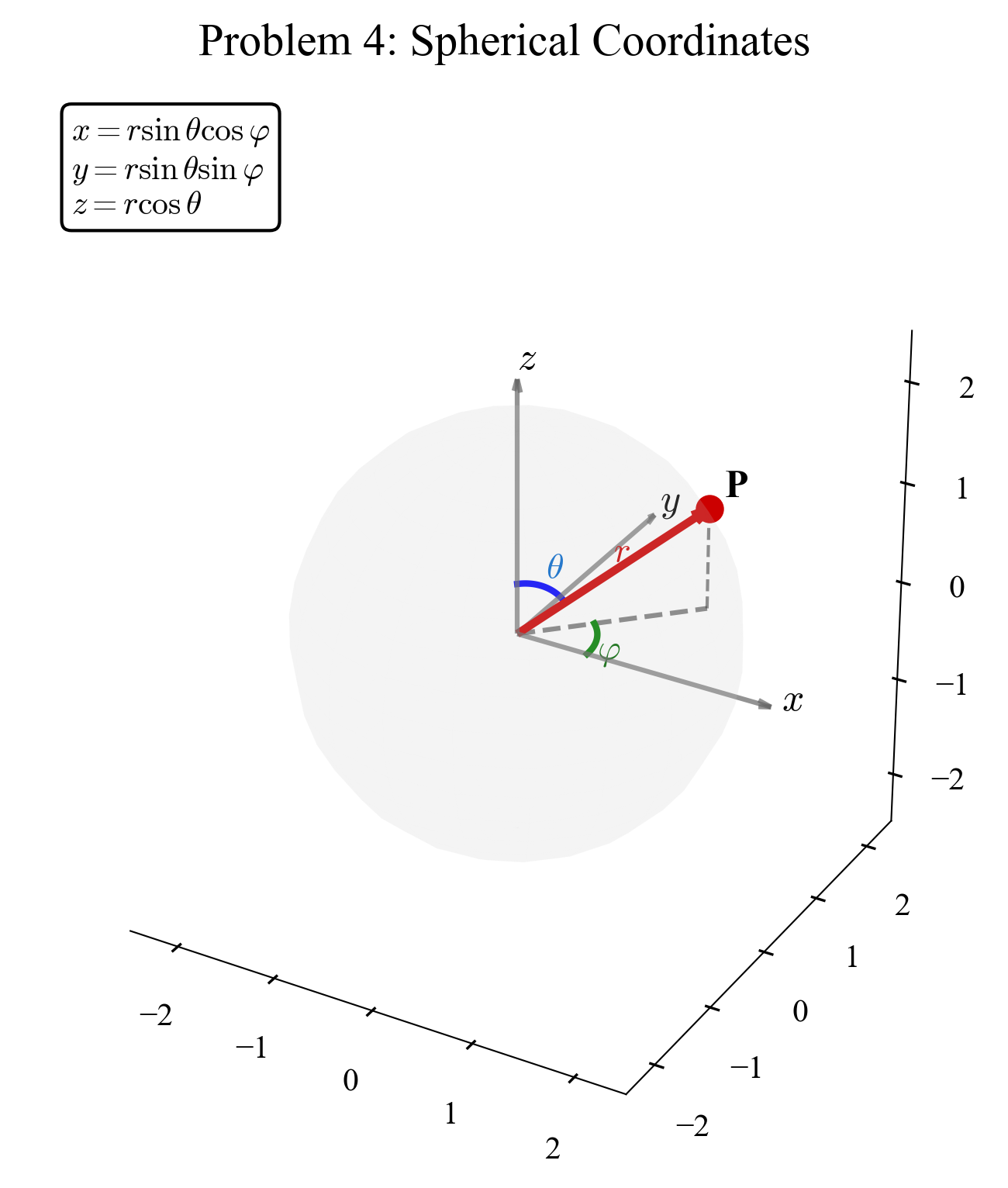
סעיף א: נוסחאות ההמרה
הבנת המערכת:
- r: המרחק מהראשית לנקודה P
- θ: הזווית מציר z החיובי (זווית קוטבית, 0 ≤ θ ≤ π)
- φ: הזווית בהיטל על מישור xy מציר x החיובי (זווית אזימוטלית, 0 ≤ φ < 2π)
גזירת הנוסחאות:
שלב 1: רכיב z
מהגדרת θ כזווית מציר z:
\[z = r\cos\theta\]שלב 2: היטל על מישור xy
אורך ההיטל של $\vec{r}$ על מישור xy:
\[\rho = r\sin\theta\]שלב 3: רכיבי x ו-y
בהיטל על מישור xy, הזווית φ נמדדת מציר x:
\[x = \rho\cos\varphi = r\sin\theta\cos\varphi\] \[y = \rho\sin\varphi = r\sin\theta\sin\varphi\]סעיף ב: אימות הקשר
חישוב ישיר:
\[\begin{aligned} x^2 + y^2 + z^2 &= (r\sin\theta\cos\varphi)^2 + (r\sin\theta\sin\varphi)^2 + (r\cos\theta)^2 \\[10pt] &= r^2\sin^2\theta\cos^2\varphi + r^2\sin^2\theta\sin^2\varphi + r^2\cos^2\theta \\[10pt] &= r^2\sin^2\theta(\cos^2\varphi + \sin^2\varphi) + r^2\cos^2\theta \end{aligned}\]מהזהות הטריגונומטרית $\cos^2\varphi + \sin^2\varphi = 1$:
\[= r^2\sin^2\theta + r^2\cos^2\theta\] \[= r^2(\sin^2\theta + \cos^2\theta)\]\(= r^2 \cdot 1 = r^2\) ✓
משמעות פיזיקלית: התוצאה מאשרת שהמרחק מהראשית נשמר בהמרה בין מערכות הקואורדינטות.
שאלה 5: תנועה סינוסואידלית משולבת
וקטור המקום של גוף מסוים המבצע תנועה כלשהי מתואר באמצעות:
\[\vec{r}(t) = \vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)\]כאשר $\vec{a}, \vec{b}$ הם וקטורים קבועים.
- קבלו את המרחק של הגוף מהראשית כפונקציה של הזמן.
- קבלו ביטוי עבור וקטור המהירות של הגוף.
- קבלו ביטוי עבור וקטור היחידה תלוי-הזמן המתאר את כיוון תנועתו של הגוף.
- קבלו את המכפלה $\vec{r}(t) \cdot \vec{v}(t)$.
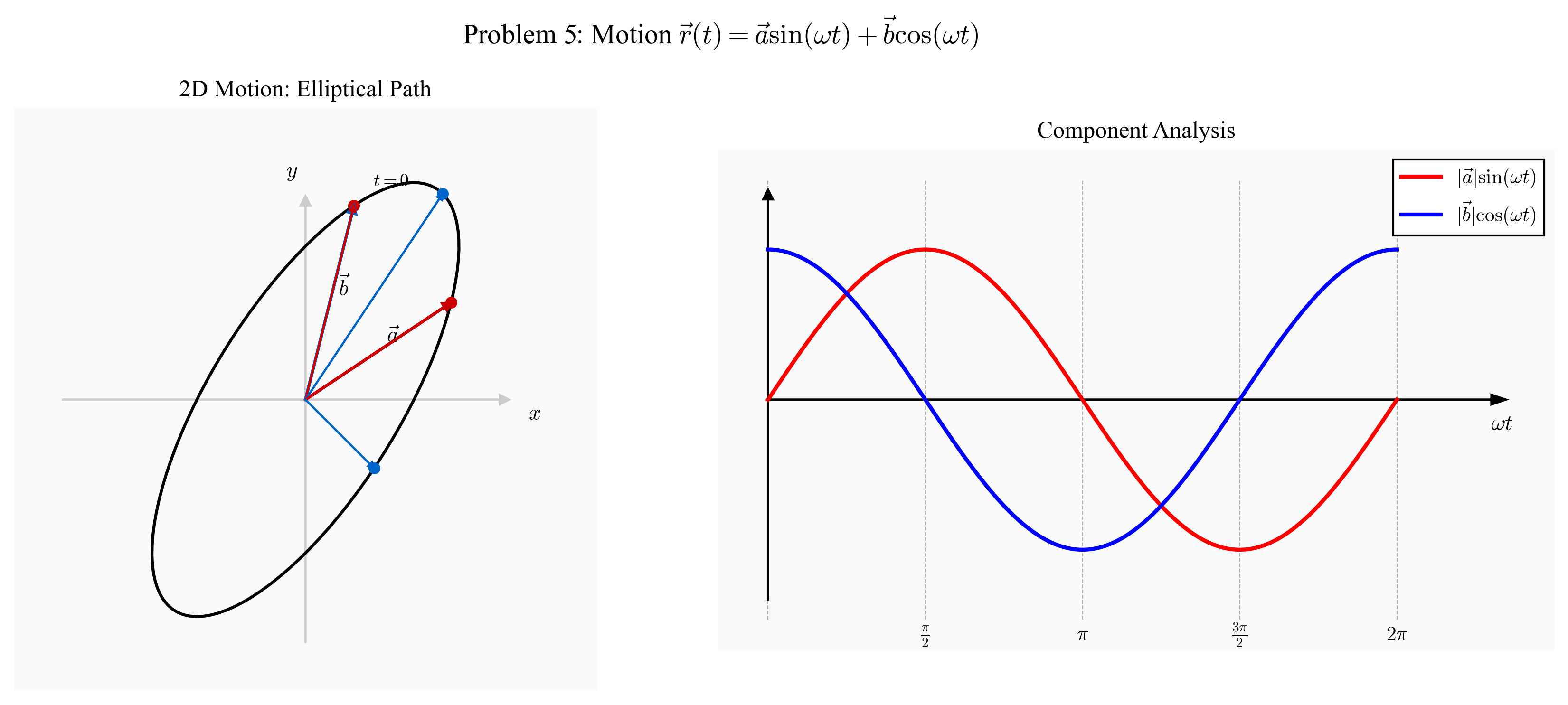
הערה: השאלה הופיעה בבלוג של המרצה, עם החלפה בין $\sin$ ל-$\cos$, וסקאלרים $a, b$ במקום וקטורים. הפתרון כאן מתייחס לגרסה המקורית עם וקטורים.
סעיף א: מרחק מהראשית
\[\begin{aligned} \vert \vec{r}(t)| &= \sqrt{(\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)) \cdot (\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t))} \\[10pt] &= \sqrt{\vert \vec{a}|^2\sin^2(\omega t) + 2(\vec{a} \cdot \vec{b})\sin(\omega t)\cos(\omega t) + \vert \vec{b}|^2\cos^2(\omega t)} \end{aligned}\] \[= \vert \vec{a}|^2\sin^2(\omega t) + 2(\vec{a} \cdot \vec{b})\sin(\omega t)\cos(\omega t) + \vert \vec{b}|^2\cos^2(\omega t)\]שימוש בזהות: $\sin(\omega t)\cos(\omega t) = \frac{1}{2}\sin(2\omega t)$
\[\vert \vec{r}(t)|^2 = \vert \vec{a}|^2\sin^2(\omega t) + \vert \vec{b}|^2\cos^2(\omega t) + (\vec{a} \cdot \vec{b})\sin(2\omega t)\]המרחק:
\[\boxed{\vert \vec{r}(t)| = \sqrt{\vert \vec{a}\vert ^2\sin^2(\omega t) + \vert \vec{b}\vert ^2\cos^2(\omega t) + (\vec{a} \cdot \vec{b})\sin(2\omega t)}}\]מקרה פרטי: אם $\vec{a} \perp \vec{b}$ (כלומר $\vec{a} \cdot \vec{b} = 0$) ו-$\vert \vec{a}\vert = \vert \vec{b}\vert = R$, אז:
\[\boxed{\vert \vec{r}(t)| = R}\]והתנועה היא מעגלית ברדיוס קבוע.
סעיף ב: וקטור המהירות
\[\vec{v}(t) = \frac{d\vec{r}}{dt} = \frac{d}{dt}[\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)]\] \[= \vec{a}\omega\cos(\omega t) - \vec{b}\omega\sin(\omega t)\] \[= \omega[\vec{a}\cos(\omega t) - \vec{b}\sin(\omega t)]\]סעיף ג: וקטור יחידה בכיוון התנועה
וקטור היחידה בכיוון המהירות:
\[\hat{v}(t) = \frac{\vec{v}(t)}{\vert \vec{v}(t)|}\]תחילה נחשב את גודל המהירות:
\[\vert \vec{v}(t)|^2 = \omega^2[\vert \vec{a}|^2\cos^2(\omega t) - 2(\vec{a} \cdot \vec{b})\cos(\omega t)\sin(\omega t) + \vert \vec{b}|^2\sin^2(\omega t)]\] \[= \omega^2[\vert \vec{a}|^2\cos^2(\omega t) + \vert \vec{b}|^2\sin^2(\omega t) - (\vec{a} \cdot \vec{b})\sin(2\omega t)]\]לכן:
\[\hat{v}(t) = \frac{\vec{a}\cos(\omega t) - \vec{b}\sin(\omega t)}{\sqrt{\vert \vec{a}|^2\cos^2(\omega t) + \vert \vec{b}|^2\sin^2(\omega t) - (\vec{a} \cdot \vec{b})\sin(2\omega t)}}\]סעיף ד: מכפלה סקלרית
\[\vec{r}(t) \cdot \vec{v}(t) = [\vec{a}\sin(\omega t) + \vec{b}\cos(\omega t)] \cdot \omega[\vec{a}\cos(\omega t) - \vec{b}\sin(\omega t)]\] \[= \omega[\vert \vec{a}|^2\sin(\omega t)\cos(\omega t) - (\vec{a} \cdot \vec{b})\sin^2(\omega t) + (\vec{a} \cdot \vec{b})\cos^2(\omega t) - \vert \vec{b}|^2\sin(\omega t)\cos(\omega t)]\] \[= \omega\sin(\omega t)\cos[\omega t](\vert \vec{a}|^2 - \vert \vec{b}|^2) + \omega[\vec{a} \cdot \vec{b}](\cos^2(\omega t) - \sin^2(\omega t))\]שימוש בזהויות:
\[\cos^2(\omega t) - \sin^2(\omega t) = \cos(2\omega t)\]ובזהות הטריגונומטרית:
\[\sin(\omega t)\cos(\omega t) = \frac{1}{2}\sin(2\omega t)\] \[\vec{r}(t) \cdot \vec{v}(t) = \frac{\omega}{2}[\vert \vec{a}|^2 - \vert \vec{b}|^2]\sin(2\omega t) + \omega(\vec{a} \cdot \vec{b})\cos(2\omega t)\]תובנה פיזיקלית: כאשר $\vert \vec{a}\vert = \vert \vec{b}\vert $ ו-$\vec{a} \perp \vec{b}$, מתקבל $\vec{r}(t) \cdot \vec{v}(t) = 0$, כלומר המהירות תמיד ניצבת למיקום - תנועה מעגלית!
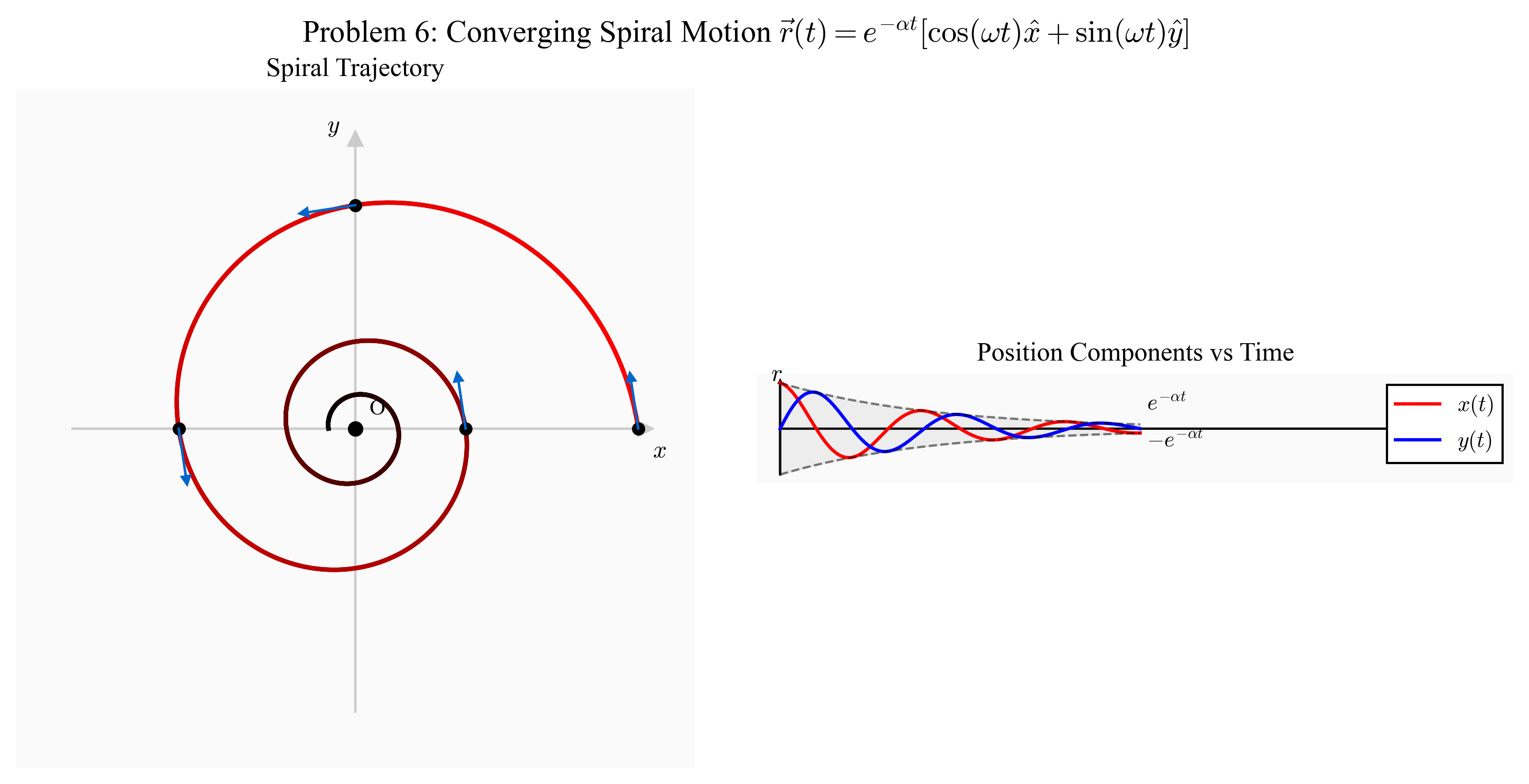
שאלה 6: תנועה ספירלית מתכנסת
וקטור המקום של חלקיק כלשהו הנע במישור נתון ע”י:
\[\vec{r}(t) = e^{-\alpha t}\cos(\omega t)\hat{x} + e^{-\alpha t}\sin(\omega t)\hat{y}\]כאשר α, ω הם פרמטרים כלשהם.
- מהן היחידות של הפרמטרים α, ω?
- הראו שהחלקיק נע בספירלה מעגלית שמתכנסת לעבר המרכז.
- קבלו את וקטור המהירות של החלקיק כתלות בזמן.
- מהו גודל וקטור המהירות של החלקיק כתלות בזמן?
סעיף א: יחידות הפרמטרים
עקרון: הארגומנט של פונקציות אקספוננציאליות וטריגונומטריות חייב להיות חסר יחידות.
-
עבור $e^{-\alpha t}$: הביטוי $\alpha t$ חייב להיות חסר יחידות. מכיוון ש-$[t] = \text{s}$ (שניות), נדרש: $[\alpha] = \text{s}^{-1}$
-
עבור $\cos(\omega t)$ ו-$\sin(\omega t)$: הביטוי $\omega t$ חייב להיות חסר יחידות (רדיאנים). לכן: $[\omega] = \text{rad/s} = \text{s}^{-1}$
משמעות פיזיקלית:
- $\alpha$: קצב הדעיכה (decay rate)
- $\omega$: תדירות זוויתית של הסיבוב
סעיף ב: הוכחת תנועה ספירלית מתכנסת
שלב 1: מרחק מהראשית
\[\begin{aligned} \vert \vec{r}(t)| &= \sqrt{(e^{-\alpha t}\cos(\omega t))^2 + (e^{-\alpha t}\sin(\omega t))^2} \\[10pt] &= e^{-\alpha t}\sqrt{\cos^2(\omega t) + \sin^2(\omega t)} \\[10pt] &= e^{-\alpha t} \cdot 1 = e^{-\alpha t} \end{aligned}\]מכיוון ש-$\alpha > 0$ (פיזיקלית), המרחק דועך אקספוננציאלית עם הזמן.
שלב 2: זווית הקוטב
\[\tan\phi = \frac{y}{x} = \frac{e^{-\alpha t}\sin(\omega t)}{e^{-\alpha t}\cos(\omega t)} = \tan(\omega t)\]לכן: $\phi = \omega t$
הזווית גדלה ליניארית עם הזמן - החלקיק מסתובב.
מסקנה: החלקיק נע על ספירלה המתלפפת פנימה, כאשר המרחק מהראשית דועך אקספוננציאלית והזווית גדלה ליניארית - ספירלה לוגריתמית מתכנסת.
סעיף ג: וקטור המהירות
\[\vec{v}(t) = \frac{d\vec{r}}{dt}\]נגזור כל רכיב בנפרד באמצעות כלל המכפלה:
רכיב x:
\[\begin{aligned} v_x &= \frac{d}{dt}[e^{-\alpha t}\cos(\omega t)] \\[10pt] &= -\alpha e^{-\alpha t}\cos(\omega t) - \omega e^{-\alpha t}\sin(\omega t) \\[10pt] &= -e^{-\alpha t}[\alpha\cos(\omega t) + \omega\sin(\omega t)] \end{aligned}\]רכיב y:
\[v_y = \frac{d}{dt}[e^{-\alpha t}\sin(\omega t)]\] \[= -\alpha e^{-\alpha t}\sin(\omega t) + \omega e^{-\alpha t}\cos(\omega t)\] \[= e^{-\alpha t}[\omega\cos(\omega t) - \alpha\sin(\omega t)]\]וקטור המהירות:
\[\vec{v}(t) = e^{-\alpha t}[-(\alpha\cos(\omega t) + \omega\sin(\omega t))\hat{x} + (\omega\cos(\omega t) - \alpha\sin(\omega t))\hat{y}]\]סעיף ד: גודל המהירות
\[\vert \vec{v}(t)|^2 = v_x^2 + v_y^2\] \[= e^{-2\alpha t}[(\alpha\cos(\omega t) + \omega\sin(\omega t))^2 + (\omega\cos(\omega t) - \alpha\sin(\omega t))^2]\]פיתוח הסוגריים:
\[= e^{-2\alpha t}[\alpha^2\cos^2(\omega t) + 2\alpha\omega\cos(\omega t)\sin(\omega t) + \omega^2\sin^2(\omega t)\] \[+ \omega^2\cos^2(\omega t) - 2\alpha\omega\cos(\omega t)\sin(\omega t) + \alpha^2\sin^2(\omega t)]\]האיברים המעורבים מתבטלים:
\[\begin{aligned} \vert \vec{v}(t)|^2 &= e^{-2\alpha t}[\alpha^2(\cos^2(\omega t) + \sin^2(\omega t)) + \omega^2(\cos^2(\omega t) + \sin^2(\omega t))] \\[10pt] &= e^{-2\alpha t}[\alpha^2 + \omega^2(\cos^2(\omega t) + \sin^2(\omega t))] \\[10pt] &= e^{-2\alpha t}[\alpha^2 + \omega^2] \end{aligned}\]גודל המהירות:
\[\vert \vec{v}(t)| = e^{-\alpha t}\sqrt{\alpha^2 + \omega^2}\]תובנות פיזיקליות:
- המהירות דועכת באותו קצב כמו המרחק מהראשית
-
היחס בין גודל המהירות למרחק קבוע:
\[\frac{\vert \vec{v}(t)|}{\vert \vec{r}(t)|} = \sqrt{\alpha^2 + \omega^2}\] - במקרה הגבולי $\alpha = 0$, מתקבלת תנועה מעגלית במהירות קבועה