שאלה 1 וקטורים דו-מימדיים
נתונים שני וקטורים דו-מימדיים:
\[\begin{aligned} \vec{a} &= 3\hat{x} - 3\hat{y} \\[10pt] \vec{b} &= -2\hat{x} + \hat{y} \end{aligned}\]נתון:
\[\vec{c} = -2\vec{a} + 3\vec{b}\]
א. חישוב וקטור $\vec{c}$
נציב את הערכים:
\[\begin{aligned} \vec{c} &= -2(3\hat{x} - 3\hat{y}) + 3(-2\hat{x} + \hat{y}) \\[10pt] &= (-6\hat{x} + 6\hat{y}) + (-6\hat{x} + 3\hat{y}) \\[10pt] &= -12\hat{x} + 9\hat{y} \end{aligned}\]ב. חישוב וקטורי היחידה
וקטור יחידה מוגדר כוקטור בעל אותו כיוון כמו הוקטור המקורי, אך באורך 1. כדי לחשב וקטור יחידה, מחלקים את הוקטור באורכו (נורמה).
עבור $\vec{a}$:
\[\vert \vec{a}\vert = \sqrt{3^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} = 3\sqrt{2}\]וקטור היחידה:
\[\begin{aligned} \hat{a} = \frac{\vec{a}}{\vert \vec{a}\vert} &= \frac{3\hat{x} - 3\hat{y}}{3\sqrt{2}} \\[10pt] &= \frac{1}{\sqrt{2}}\hat{x} - \frac{1}{\sqrt{2}}\hat{y} \end{aligned}\]עבור $\vec{b}$:
\[\vert \vec{b}\vert = \sqrt{(-2)^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}\]וקטור היחידה:
\[\begin{aligned} \hat{b} = \frac{\vec{b}}{\vert \vec{b}\vert} &= \frac{-2\hat{x} + \hat{y}}{\sqrt{5}} \\[10pt] &= -\frac{2}{\sqrt{5}}\hat{x} + \frac{1}{\sqrt{5}}\hat{y} \end{aligned}\]עבור $\vec{c}$:
\[\vert \vec{c}\vert = \sqrt{(-12)^2 + 9^2} = \sqrt{144 + 81} = \sqrt{225} = 15\]וקטור היחידה:
\[\hat{c} = \frac{\vec{c}}{\vert \vec{c}\vert} = \frac{-12\hat{x} + 9\hat{y}}{15} = -\frac{4}{5}\hat{x} + \frac{3}{5}\hat{y}\]ג. ציור הוקטור השקול ווקטור ההפרש
הוקטור השקול $\vec{a} + \vec{b}$:
\[\vec{a} + \vec{b} = (3\hat{x} - 3\hat{y}) + (-2\hat{x} + \hat{y}) = \hat{x} - 2\hat{y}\]וקטור ההפרש $\vec{a} - \vec{b}$:
\[\begin{aligned} \vec{a} - \vec{b} &= (3\hat{x} - 3\hat{y}) - (-2\hat{x} + \hat{y}) \\[10pt] &= 3\hat{x} - 3\hat{y} + 2\hat{x} - \hat{y} \\[10pt] &= 5\hat{x} - 4\hat{y} \end{aligned}\]לציור הוקטורים על נייר משבצות, יש לסמן את מערכת הצירים ולשרטט:
- את $\vec{a}$ מראשית הצירים לנקודה $(3, -3)$
- את $\vec{b}$ מראשית הצירים לנקודה $(-2, 1)$
- את $\vec{a} + \vec{b}$ מראשית הצירים לנקודה $(1, -2)$
- את $\vec{a} - \vec{b}$ מראשית הצירים לנקודה $(5, -4)$
ד. ציור הוקטור השקול $\vec{a} + \vec{b} + \vec{c}$
נחשב תחילה את הסכום:
\[\begin{aligned} \vec{a} + \vec{b} + \vec{c} &= (3\hat{x} - 3\hat{y}) + (-2\hat{x} + \hat{y}) + (-12\hat{x} + 9\hat{y}) \\[10pt] &= (3 - 2 - 12)\hat{x} + (-3 + 1 + 9)\hat{y} \\[10pt] &= -11\hat{x} + 7\hat{y} \end{aligned}\]לציור הוקטור השקול, יש לסמן את מערכת הצירים ולשרטט את הוקטור מראשית הצירים לנקודה $(-11, 7)$.
ה. חישוב הזוויות
הזווית שוקטור יוצר עם ציר ה-$x$ (נגד כיוון השעון) ניתנת על ידי הביטוי: $\theta = \tan^{-1}(\frac{y}{x})$
כאשר צריך לקחת בחשבון את הרביע שבו נמצא הוקטור:
עבור $\vec{a} = 3\hat{x} - 3\hat{y}$:
מכיוון שהוקטור נמצא ברביע הרביעי ($x > 0$, $y < 0$), נחשב:
\[\theta_a = \tan^{-1}(\frac{-3}{3}) = \tan^{-1}(-1) = -45°\]ומכיוון שאנו מודדים נגד כיוון השעון, נוסיף $360°$:
\[\theta_a = 360° - 45° = 315°\]עבור $\vec{b} = -2\hat{x} + \hat{y}$:
מכיוון שהוקטור נמצא ברביע השני ($x < 0$, $y > 0$), נחשב:
\[\theta_b = \tan^{-1}(\frac{1}{-2}) = \tan^{-1}(-0.5) \approx -26.57°\]ונוסיף $180°$:
\[\theta_b = 180° - 26.57° = 153.43°\]עבור $\vec{c} = -12\hat{x} + 9\hat{y}$:
מכיוון שהוקטור נמצא ברביע השני ($x < 0$, $y > 0$), נחשב:
\[\theta_c = \tan^{-1}(\frac{9}{-12}) = \tan^{-1}(-0.75) \approx -36.87°\]ונוסיף $180°$:
\[\theta_c = 180° - 36.87° = 143.13°\]שאלה 2: וקטורים תלת-מימדיים
נתונים שלושת הוקטורים התלת-מימדיים:
\[\begin{aligned} \vec{a} &= (2,2,0) \\[10pt] \vec{b} &= (2,0,2) \\[10pt] \vec{c} &= (0,2,2) \end{aligned}\]
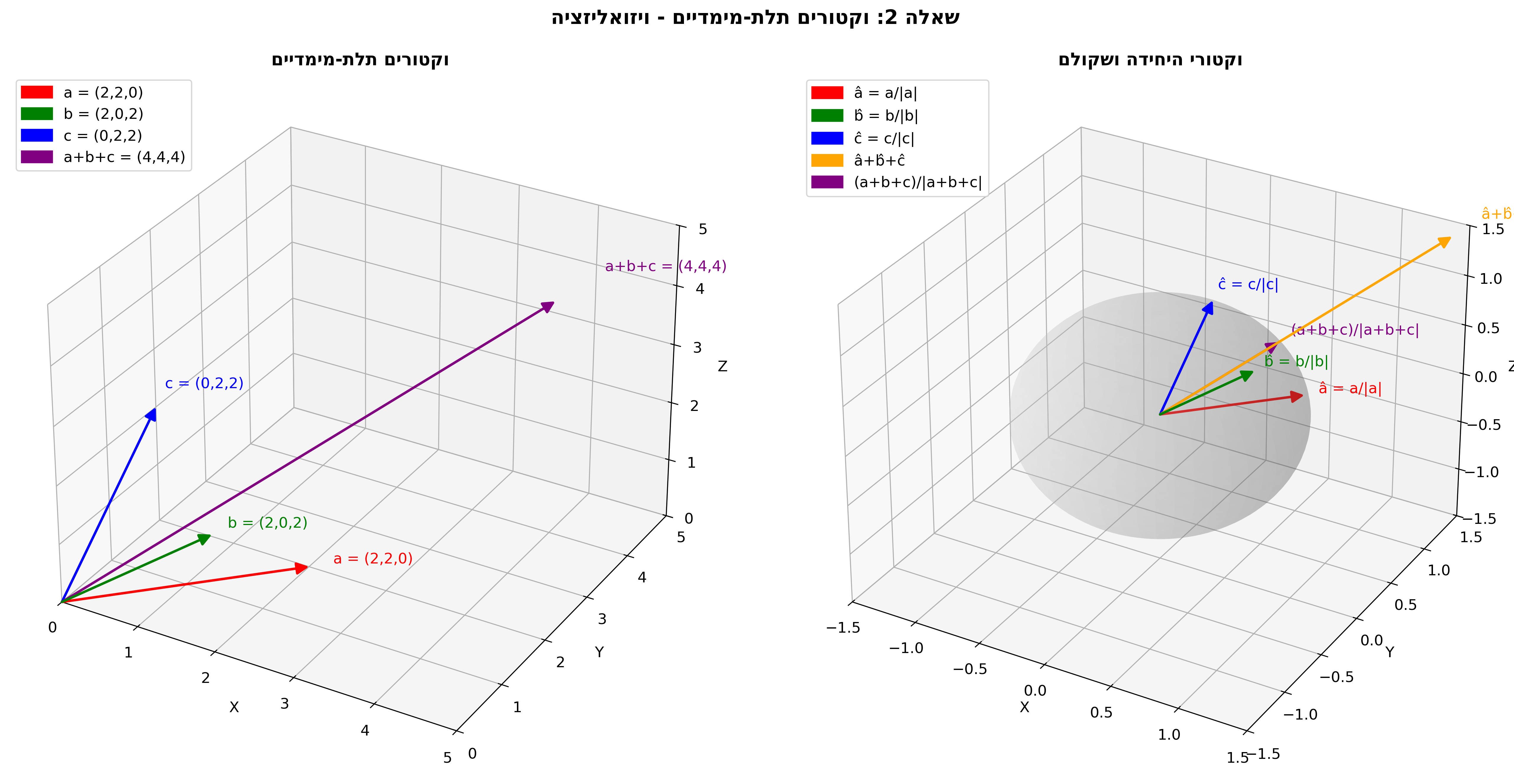
א. ציור הוקטורים במערכת צירים קרטזית
לציור וקטורים תלת-מימדיים, יש לסמן מערכת צירים תלת-מימדית ולשרטט:
- את $\vec{a}$ מראשית הצירים לנקודה $(2, 2, 0)$
- את $\vec{b}$ מראשית הצירים לנקודה $(2, 0, 2)$
- את $\vec{c}$ מראשית הצירים לנקודה $(0, 2, 2)$
 |  |
|---|---|
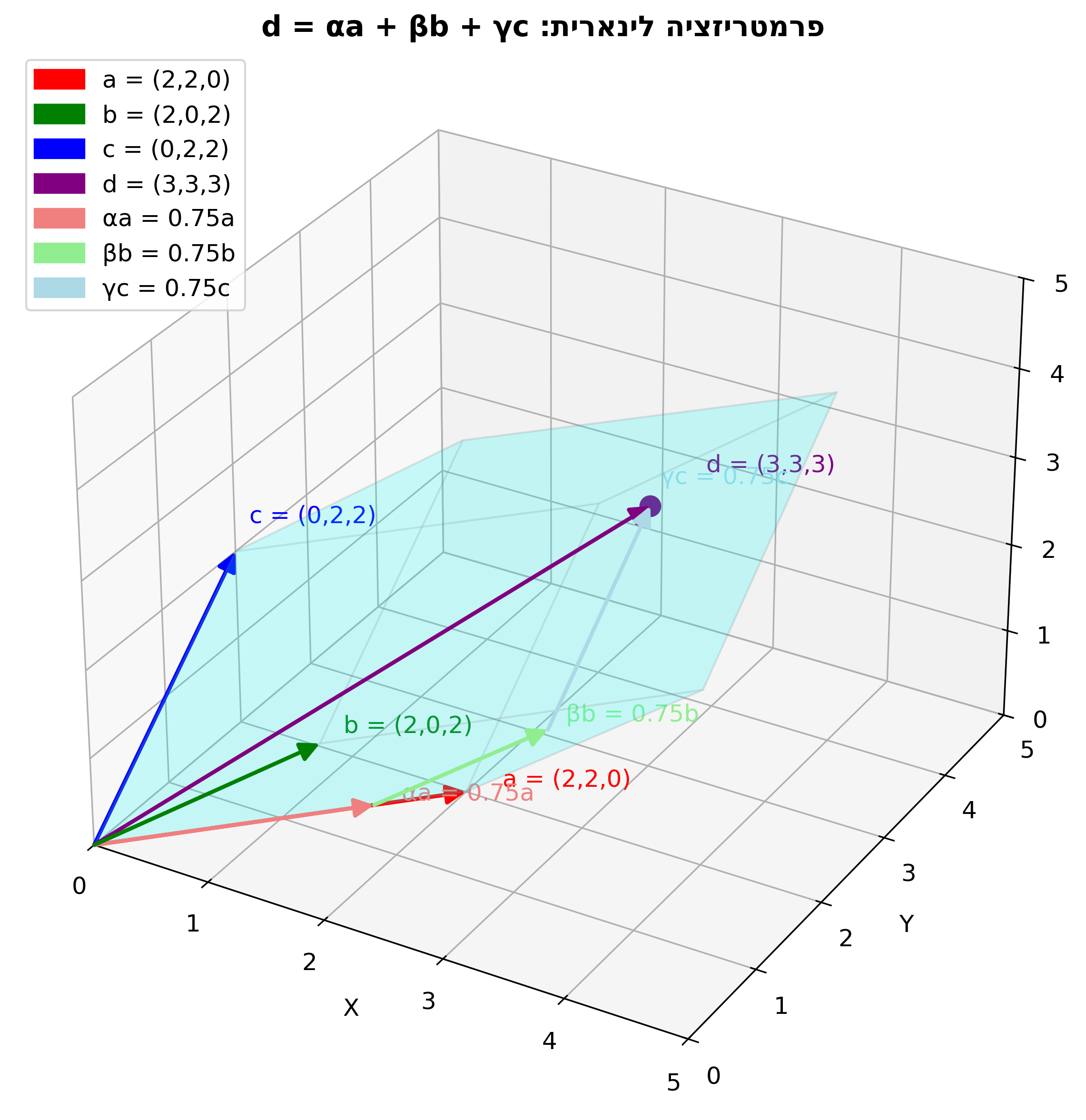
| איור של הוקטורים במערכת צירים תלת-מימדית | הדמיה של הפרמטריזציה הלינארית של שלושת הוקטורים |
ב. ציור השקול הוקטורי
השקול הוקטורי של שלושת הוקטורים הוא:
\[\begin{aligned} \vec{a} + \vec{b} + \vec{c} &= (2,2,0) + (2,0,2) + (0,2,2) \\[10pt] &= (2+2+0, 2+0+2, 0+2+2) \\[10pt] &= (4, 4, 4) \end{aligned}\]לציור השקול הוקטורי, יש לשרטט וקטור מראשית הצירים לנקודה $(4, 4, 4)$.
ג. נרמול הוקטורים
נרמול וקטור פירושו חישוב וקטור היחידה בכיוון הוקטור המקורי.
עבור $\vec{a}$:
\[\vert \vec{a}\vert = \sqrt{2^2 + 2^2 + 0^2} = \sqrt{8} = 2\sqrt{2}\]הוקטור המנורמל:
\[\hat{a} = \frac{\vec{a}}{\vert \vec{a}\vert} = \frac{(2,2,0)}{2\sqrt{2}} = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0)\]עבור $\vec{b}$:
\[\vert \vec{b}\vert = \sqrt{2^2 + 0^2 + 2^2} = \sqrt{8} = 2\sqrt{2}\]הוקטור המנורמל:
\[\hat{b} = \frac{\vec{b}}{\vert \vec{b}\vert} = \frac{(2,0,2)}{2\sqrt{2}} = (\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}})\]עבור $\vec{c}$:
\[\vert \vec{c}\vert = \sqrt{0^2 + 2^2 + 2^2} = \sqrt{8} = 2\sqrt{2}\]הוקטור המנורמל:
\[\hat{c} = \frac{\vec{c}}{\vert \vec{c}\vert} = \frac{(0,2,2)}{2\sqrt{2}} = (0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})\]ד. בדיקת התלכדות
נבדוק האם השקול של שלושת הוקטורים המנורמלים מתלכד עם וקטור היחידה של השקול הוקטורי.
סכום הוקטורים המנורמלים:
\[\hat{a} + \hat{b} + \hat{c} = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0) + (\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}) + (0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})\] \[\begin{aligned} &= (\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} + 0, \frac{1}{\sqrt{2}} + 0 + \frac{1}{\sqrt{2}}, 0 + \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}) \\[10pt] &= (\frac{2}{\sqrt{2}}, \frac{2}{\sqrt{2}}, \frac{2}{\sqrt{2}}) \\[10pt] &= \sqrt{2} \cdot (1, 1, 1) \end{aligned}\]וקטור היחידה של השקול:
השקול הוקטורי:
\[\vec{a} + \vec{b} + \vec{c} = (4, 4, 4)\]האורך שלו:
\[\vert \vec{a} + \vec{b} + \vec{c}\vert = \sqrt{4^2 + 4^2 + 4^2} = \sqrt{48} = 4\sqrt{3}\]וקטור היחידה:
\[\frac{\vec{a} + \vec{b} + \vec{c}}{\vert \vec{a} + \vec{b} + \vec{c}\vert} = \frac{(4, 4, 4)}{4\sqrt{3}} = \frac{1}{\sqrt{3}} \cdot (1, 1, 1)\]מכיוון ש-$\hat{a} + \hat{b} + \hat{c} = \sqrt{2} \cdot (1, 1, 1)$ והוקטור היחידה של השקול הוא $\frac{1}{\sqrt{3}} \cdot (1, 1, 1)$, הם אינם מתלכדים. הסכום של הוקטורים המנורמלים גדול פי $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$ מוקטור היחידה של השקול.
ה. מציאת המקדמים בצרוף הלינארי
נתון הוקטור
\[\vec{d} = (3, 3, 3)\]ואנו מחפשים את הערכים $\alpha, \beta, \gamma$ כך ש:
\[\vec{d} = \alpha\vec{a} + \beta\vec{b} + \gamma\vec{c}\]נציב את הוקטורים הנתונים:
\[\vec{d} = \alpha(2,2,0) + \beta(2,0,2) + \gamma(0,2,2)\]נפרק לרכיבים:
\[\begin{aligned} 3 &= 2\alpha + 2\beta \\[10pt] 3 &= 2\alpha + 2\gamma \\[10pt] 3 &= 2\beta + 2\gamma \end{aligned}\]מהשוואת המשוואה הראשונה והשנייה, מקבלים: $\beta = \gamma$
נסכם את שלוש המשוואות:
\[9 = 4\alpha + 4\beta + 4\gamma\]מכיוון ש-$\beta = \gamma$, מקבלים:
\[9 = 4\alpha + 8\beta\] \[\frac{9}{4} = \alpha + 2\beta\]מהמשוואה הראשונה:
\[\frac{3}{2} = \alpha + \beta\]נפתור את המערכת:
\[\alpha + 2\beta = \frac{9}{4}\] \[\alpha + \beta = \frac{3}{2}\]נחסר את המשוואה השנייה מהראשונה:
\[\beta = \frac{9}{4} - \frac{3}{2} = \frac{9 - 6}{4} = \frac{3}{4}\]נציב בחזרה:
\[\alpha + \frac{3}{4} = \frac{3}{2}\] \[\alpha = \frac{3}{2} - \frac{3}{4} = \frac{6 - 3}{4} = \frac{3}{4}\]כיוון ש-$\beta = \gamma$, מקבלים: $\alpha = \beta = \gamma = \frac{3}{4}$
נבדוק את התוצאה:
\[\alpha\vec{a} + \beta\vec{b} + \gamma\vec{c} = \frac{3}{4}(2,2,0) + \frac{3}{4}(2,0,2) + \frac{3}{4}(0,2,2)\] \[= \frac{3}{4}(4, 4, 4) = (3, 3, 3) = \vec{d}\]הערה: יש שיטה מתודולוגית יותר לפתור את הבעיה של מציאת מקדמים בצירוף לינארי באמצעות מטריצות. זוהי למעשה השיטה הסטנדרטית בעולם האלגברה הלינארית. יש שיטות נוספות לפתרון, כמו מטריצה הפוכה.
שאלה 3: קואורדינטות גליליות
קואורדינטות גליליות מורכבות משלושה מרכיבים: $(ρ, \theta, z)$, כאשר:
- $ρ$ הוא המרחק מציר ה-$z$ (ולא מהראשית)
- $\theta$ היא הזווית במישור $x$-$y$, הנמדדת מציר ה-$x$ (נגד כיוון השעון)
- $z$ היא הקואורדינטה לאורך ציר ה-$z$
א. נוסחאות המעבר
המעבר מקואורדינטות קרטזיות לגליליות:
$ρ = \sqrt{x^2 + y^2}$ (המרחק מציר ה-$z$) $\theta = \tan^{-1}(y/x)$ (הזווית במישור $x$-$y$) $z$ נשאר זהה
המעבר מקואורדינטות גליליות לקרטזיות:
$x = ρ \cos \theta$ $y = ρ \sin \theta$ $z$ נשאר זהה
ב. הקשר הפיתגוראי
המרחק של נקודה מהראשית בקואורדינטות קרטזיות הוא:
\[r = \sqrt{x^2 + y^2 + z^2}\]בקואורדינטות גליליות, הקשר הפיתגוראי הוא:
\[r^2 = ρ^2 + z^2 = x^2 + y^2 + z^2\]דור פסקלשאלה 4: יישומי וקטורים בגיאומטריה
בשאלה זו מובאות דוגמאות לשימושים של וקטורים לפתרון בעיות גיאומטריות:
הוכחה שאלכסוני מקבילית חוצים זה את זה:
במקבילית ABCD עם אלכסונים הנפגשים בנקודה P, ניתן לייצג את הוקטורים מהראשית:
- $\vec{P} = \frac{1}{2}(\vec{A} + \vec{C}) = \frac{1}{2}(\vec{B} + \vec{D})$
כלומר, P היא נקודת האמצע של שני האלכסונים, מה שמוכיח שהם חוצים זה את זה.
הוכחת משפט על קו המחבר את נקודות האמצע של שתי צלעות במשולש:
במשולש ABC, אם D היא נקודת האמצע של AB ו-E היא נקודת האמצע של AC, אז:
- $\vec{DE} = \vec{E} - \vec{D} = \frac{1}{2}\vec{C} - \frac{1}{2}\vec{B} = \frac{1}{2}(\vec{C} - \vec{B}) = \frac{1}{2}\vec{BC}$
מכאן, הקו DE מקביל לצלע BC ואורכו מחצית מאורך BC.