שתי משוואות מקסוול הראשונות
\[\vec{\nabla} \cdot \vec{D} = \rho\] \[\vec{\nabla} \times \vec{H} = \vec{J} + \frac{\partial \vec{D}}{\partial t}\]נציב את קשרי המבנה (Constitutive Relations):
\[\vec{H} = \frac{1}{\mu_0} \vec{B}\] \[\vec{D} = \epsilon_0 \vec{E}\]נציב במשוואה השנייה:
\[\vec{\nabla} \times \frac{1}{\mu_0} \vec{B} = \vec{J} + \epsilon_0 \frac{\partial \vec{E}}{\partial t}\] \[\vec{\nabla} \times \vec{B} = \mu_0 \vec{J} + \mu_0 \epsilon_0 \frac{\partial \vec{E}}{\partial t}\]נשתמש בקשר $c = \frac{1}{\sqrt{\mu_0 \epsilon_0}}$:
\[\vec{\nabla} \times \vec{B} = \mu_0 \vec{J} + \frac{1}{c^2} \frac{\partial \vec{E}}{\partial t}\]מתי נופל האיבר השני? במקרים קוואזי-סטטיים (quasi-static), כלומר כאשר השדות משתנים לאט מספיק כך שניתן להזניח את קצב השינוי של השדה החשמלי. זה מתקיים במוליכים עם זרם יציב (DC) או בתדרים נמוכים מספיק. במקרים אלו נקבל את חוק אמפר:
\[\vec{\nabla} \times \vec{B} = \mu_0 \vec{J}\]זוהי הצורה הדיפרנציאלית של חוק אמפר: הרוטור של השדה המגנטי פרופורציונלי לצפיפות הזרם החשמלי.
חוק גאוס בצורה דיפרנציאלית
משוואה נוספת חשובה - הדיברגנץ של השדה החשמלי פרופורציונלי לצפיפות המטען:
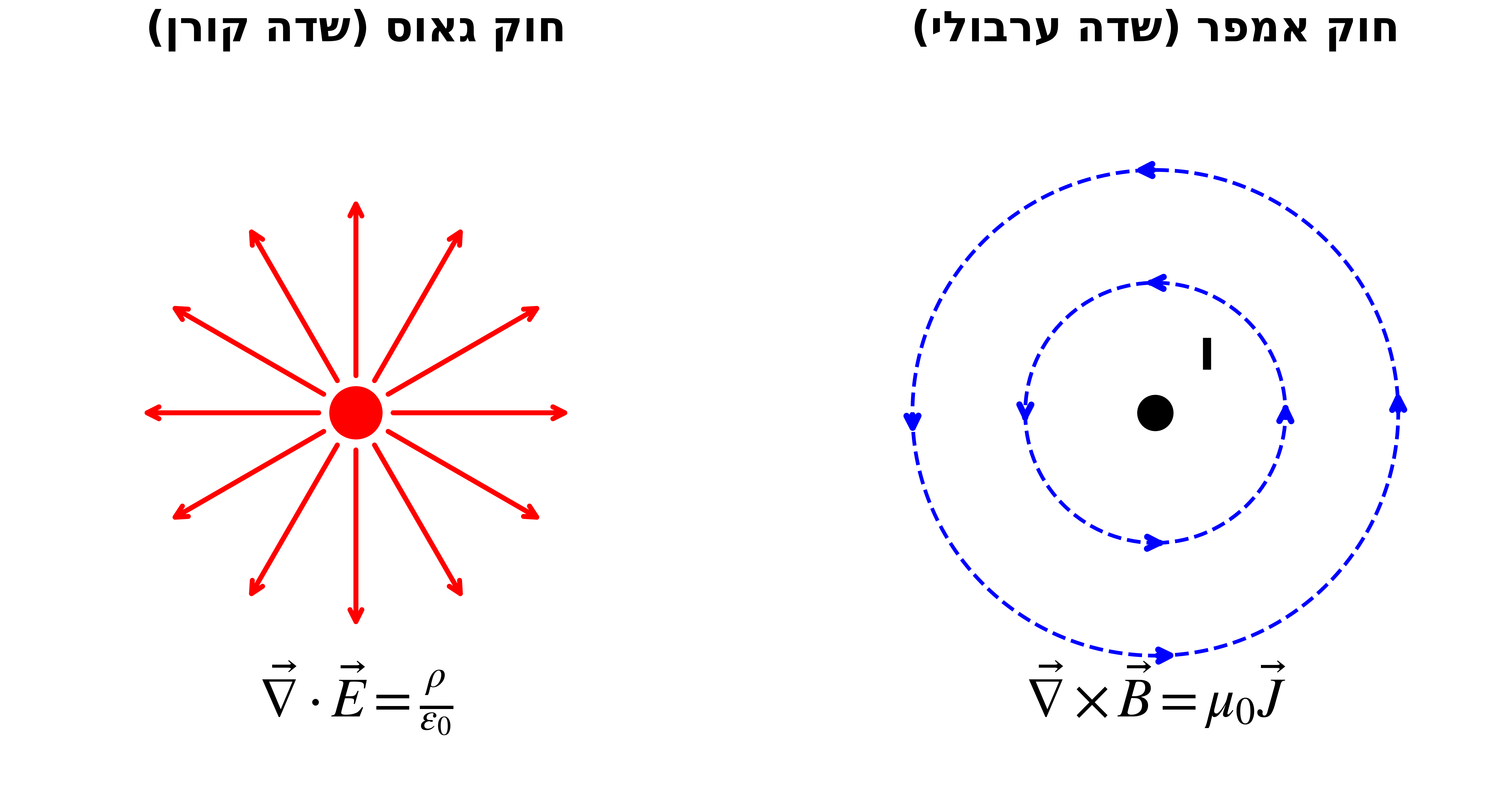
\[\vec{\nabla} \cdot \vec{E} = \frac{\rho}{\epsilon_0}\]זהו חוק גאוס בצורה דיפרנציאלית. המשוואה מתארת כיצד מטענים חשמליים (מקורות) יוצרים שדה חשמלי מתפשט (קורן).
הבדל מהותי בין שני החוקים:
- חוק גאוס: שדה חשמלי הוא שדה קורן (divergent) - יש לו מקורות ובולענים (מטענים)
- חוק אמפר: שדה מגנטי הוא שדה ערבולי (solenoidal) - קווי השדה נסגרים על עצמם
חוק אמפר האינטגרלי - אינטגרל על מסלול סגור
עבור שדה חשמלי אלקטרוסטטי (שדה משמר):
\[\oint \vec{E} \cdot d\vec{l} = 0\]האינטגרל הקווי של שדה חשמלי סטטי על מסלול סגור שווה לאפס - זוהי תכונה של שדה משמר. (בכתה דווקא נכתב שוויון שונה $=\frac{Q}{\epsilon_0}$).
עבור שדה מגנטי (חוק אמפר האינטגרלי):
\[\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}\]האינטגרל הקווי של השדה המגנטי על מסלול סגור שווה ל-$\mu_0$ כפול הזרם הכלוא בתוך המסלול.
פיתוח מתמטי - ממשוואה דיפרנציאלית לאינטגרלית (משפט סטוקס)
נתחיל מחוק אמפר הדיפרנציאלי:
\[\vec{\nabla} \times \vec{B} = \mu_0 \vec{J}\]נעשה אינטגרל על משטח $S$ לשני האגפים:
\[\int_S (\vec{\nabla} \times \vec{B}) \cdot d\vec{a} = \int_S \mu_0 \vec{J} \cdot d\vec{a}\]נשתמש במשפט סטוקס באגף שמאל (האינטגרל של הרוטור על משטח שווה לאינטגרל הקווי על השפה):
\[\oint_C \vec{B} \cdot d\vec{l} = \mu_0 \int_S \vec{J} \cdot d\vec{a}\]האינטגרל באגף ימין הוא הזרם הכולל העובר דרך המשטח:
\[\oint_C \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}\]דוגמה: שדה מגנטי של תיל אינסופי נושא זרם
נתון: תיל אינסופי נושא זרם $I$.
מצאו: את השדה המגנטי במרחק $r$ מהתיל.
פתרון:
מסימטריה גלילית, השדה המגנטי חייב להיות בכיוון $\hat{\phi}$ (משיקי למעגלים סביב התיל) ותלוי רק במרחק $r$:
\[\vec{B} = B(r) \hat{\phi}\]נבחר מסלול אמפרי - מעגל ברדיוס $r$ במישור ניצב לתיל ומרוכז עליו.
נשתמש בחוק אמפר האינטגרלי:
\[\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}\]מכיוון ש-$\vec{B}$ מקביל ל-$d\vec{l}$ לאורך כל המסלול, וגודלו קבוע על המעגל:
\[B(r) \cdot 2\pi r = \mu_0 I\]נבודד את השדה המגנטי:
\[\boxed{\vec{B}(r) = \frac{\mu_0 I}{2 \pi r} \hat{\phi}}\]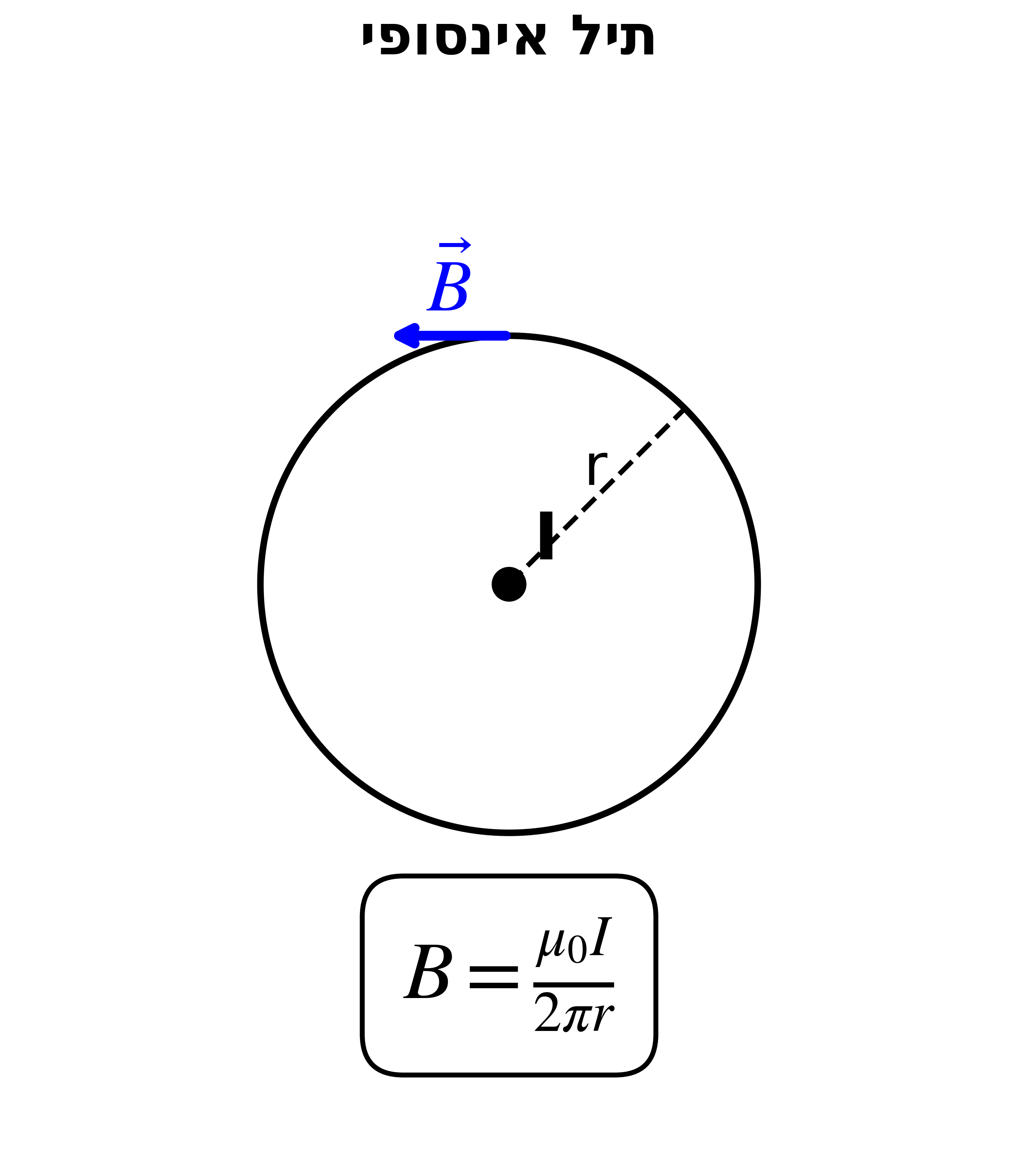
שאלת בחינה לדוגמה - מוליך גלילי עם צפיפות זרם משתנה
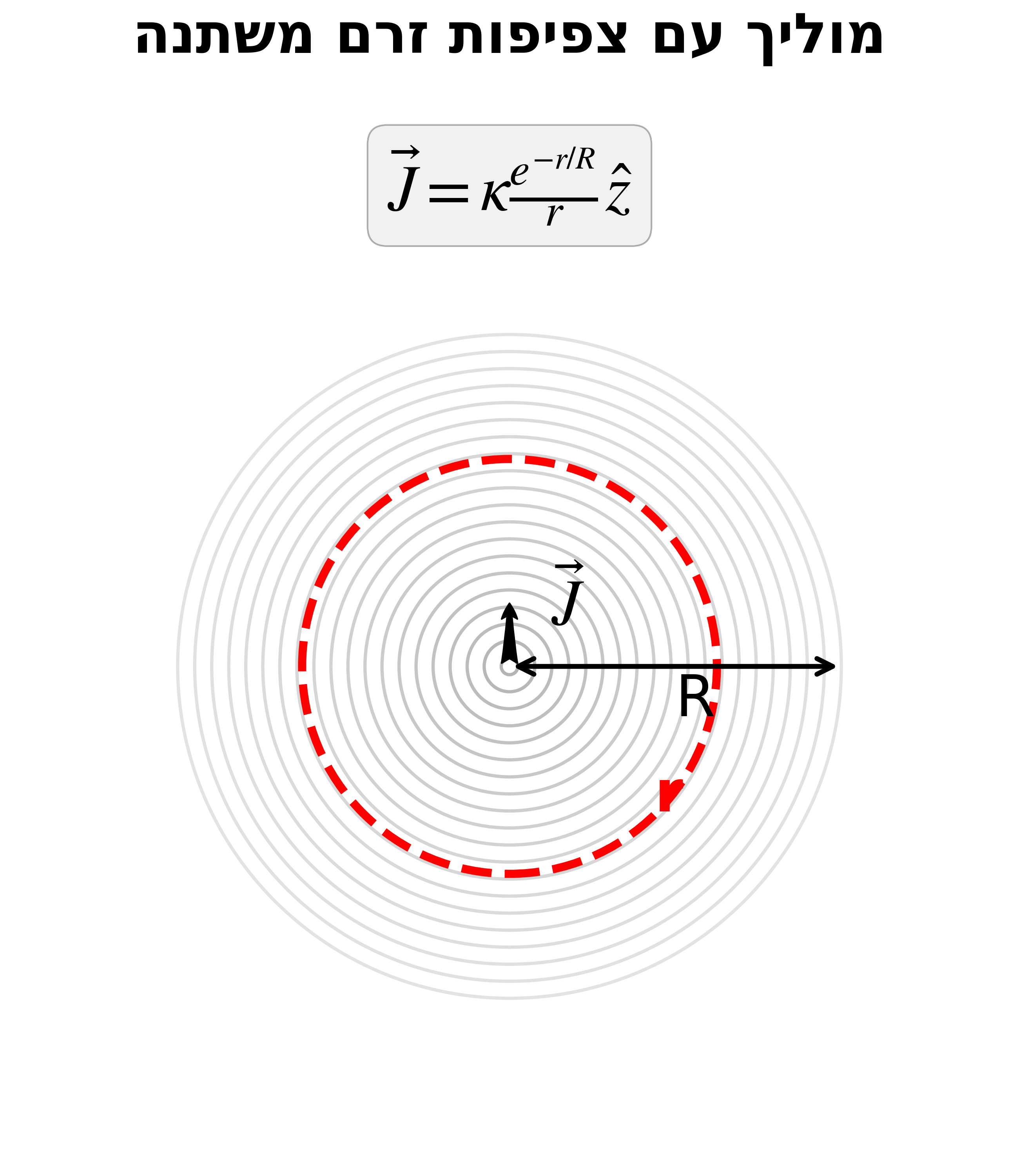
נתון: מוליך גלילי (כבל) אינסופי עם רדיוס $R$, נושא צפיפות זרם:
\[\vec{J} = \kappa \frac{e^{-r/R}}{r} \hat{z}\]כאשר $r$ הוא המרחק מציר הגליל.
הערה פיזיקלית: מודל זה מתאר התפלגות זרם שבה הזרם מרוכז בעיקר במרכז המוליך ודועך אקספוננציאלית החוצה. זוהי אנלוגיה טובה לזרימת יונים בנוירון (אקסון).
א. מה היחידות של $\kappa$?
צפיפות זרם $\vec{J}$ מוגדרת כזרם ליחידת שטח:
\[[\vec{J}] = \frac{[I]}{[A]} = \frac{\mathrm{A}}{\mathrm{m}^2} = \frac{\mathrm{C}}{\mathrm{s} \cdot \mathrm{m}^2}\](ניתן להגיע לזה גם מההגדרה $\vec{J} = \rho \vec{v}$, כאשר $\rho$ צפיפות מטען ו-$\vec{v}$ מהירות)
מהנוסחה הנתונה:
\[[\vec{J}] = [\kappa] \cdot \frac{1}{[r]} = [\kappa] \cdot \frac{1}{\mathrm{m}}\](האקספוננט הוא חסר יחידות)
לכן:
\[\boxed{[\kappa] = \frac{\mathrm{A}}{\mathrm{m}} = \frac{\mathrm{C}}{\mathrm{s} \cdot \mathrm{m}}}\]זוהי יחידה של זרם ליחידת אורך.
ב. מהו השדה המגנטי בתוך המוליך ($r < R$)?
שלב 1: חישוב הזרם הכלוא
נשתמש בחוק אמפר האינטגרלי עם מעגל אמפרי ברדיוס $r < R$:
\[\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}(r)\]תחילה נחשב את הזרם העובר דרך המעגל. אלמנט השטח בקואורדינטות גליליות הוא טבעת ברדיוס $r’$ ועובי $dr’$:
\[dA = 2\pi r' \, dr'\]הזרם דרך הטבעת:
\[dI = \vec{J} \cdot d\vec{A} = \kappa \frac{e^{-r'/R}}{r'} \cdot 2\pi r' \, dr' = 2\pi \kappa e^{-r'/R} dr'\]שימו לב: ה-$r’$ מצטמצם! זה אומר שלמרות שצפיפות הזרם סינגולרית ב-$r=0$, הזרם עצמו מוגדר היטב (סינגולריות אינטגרבילית).
הזרם הכולל עד רדיוס $r$:
\[I_{enc}(r) = \int_0^r 2\pi \kappa e^{-r'/R} dr' = 2\pi \kappa \left[-R e^{-r'/R}\right]_0^r = 2\pi \kappa R \left(1 - e^{-r/R}\right)\]שלב 2: חישוב השדה המגנטי
מסימטריה, $\vec{B} = B(r)\hat{\phi}$, ולכן:
\[B(r) \cdot 2\pi r = \mu_0 \cdot 2\pi \kappa R \left(1 - e^{-r/R}\right)\] \[\boxed{B(r) = \frac{\mu_0 \kappa R \left(1 - e^{-r/R}\right)}{r} \quad \text{for } r < R}\]ג. מהו השדה המגנטי מחוץ למוליך ($r > R$)?
מחוץ למוליך, כל הזרם כלוא בתוך מסלול האמפר:
\[I_{total} = 2\pi \kappa R \left(1 - e^{-1}\right)\]לכן:
\[\boxed{B(r) = \frac{\mu_0 \kappa R \left(1 - e^{-1}\right)}{r} \quad \text{for } r > R}\]ד. התנהגות השדה כאשר $r \to 0$
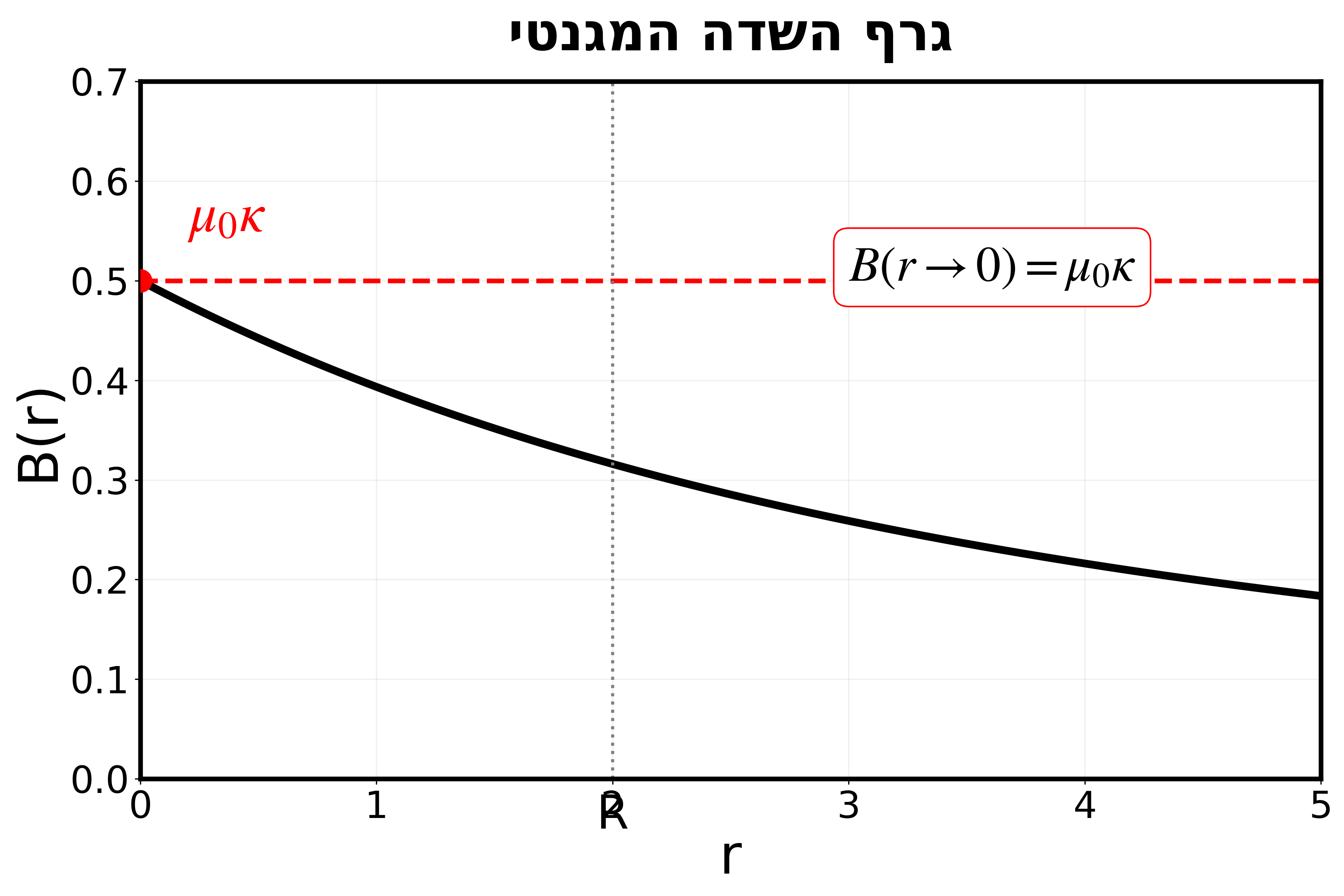
נבדוק שהשדה מוגדר היטב במרכז למרות הסינגולריות של $\vec{J}$.
נפתח את האקספוננט בטור טיילור:
\[e^{-r/R} \approx 1 - \frac{r}{R} + \frac{1}{2}\left(\frac{r}{R}\right)^2 - \ldots\]נציב בביטוי לשדה:
\[B(r) = \frac{\mu_0 \kappa R \left(1 - \left(1 - \frac{r}{R} + \frac{r^2}{2R^2} - \ldots\right)\right)}{r}\] \[= \frac{\mu_0 \kappa R \left(\frac{r}{R} - \frac{r^2}{2R^2} + \ldots\right)}{r}\] \[= \mu_0 \kappa \left(1 - \frac{r}{2R} + \ldots\right)\]לכן:
\[\boxed{\lim_{r \to 0} B(r) = \mu_0 \kappa}\]מסקנה: למרות שצפיפות הזרם $\vec{J}$ מתפוצצת ב-$r=0$, השדה המגנטי מוגדר היטב ושווה לערך סופי $\mu_0 \kappa$.
הערות חשובות - אינטגרלים בסימטריות שונות
| סימטריה | אלמנט שטח/נפח | הסבר |
|---|---|---|
| גלילית | $dA = 2\pi r \, dr$ | היקף מעגל כפול עובי הטבעת |
| כדורית | $dV = 4\pi r^2 \, dr$ | שטח פני כדור כפול עובי הקליפה |
כלל אצבע: בקואורדינטות גליליות משתמשים ב-$2\pi r$, בכדוריות ב-$4\pi r^2$.
סיכום נוסחאות
| חוק | צורה דיפרנציאלית | צורה אינטגרלית |
|---|---|---|
| גאוס | $\vec{\nabla} \cdot \vec{E} = \dfrac{\rho}{\epsilon_0}$ | $\oint \vec{E} \cdot d\vec{a} = \dfrac{Q_{enc}}{\epsilon_0}$ |
| אמפר | $\vec{\nabla} \times \vec{B} = \mu_0 \vec{J}$ | $\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}$ |
שדה מגנטי של תיל אינסופי:
\[\vec{B}(r) = \frac{\mu_0 I}{2\pi r} \hat{\phi}\] דור פסקל