פתרון משוואות דיפרנציאליות בבעיות דינמיות
כאשר אנו פותרים בעיות דינמיות מורכבות, עלינו להיות מסוגלים לטפל במשוואות דיפרנציאליות מהצורות הבסיסיות הבאות. אם נתבקש לפתור משוואות דיפרנציאליות, הפתרונות יגיעו מתוך ארבע האפשרויות העיקריות שנלמדו, כולל האפשרות של הזזה בקבוע.
לדוגמה, עבור משוואת האוסילטור ההרמוני:
\[\ddot{x} = -\omega^2 x\]ייתכן שנקבל משוואה מהצורה:
\[\ddot{x} = -\omega^2 x + \lambda\]כאשר $\lambda$ הוא גודל קבוע. במקרה כזה, עלינו להעביר את המשוואה לצורה:
\[\ddot{x} = -\omega^2 \left(x - \frac{\lambda}{\omega^2}\right)\]נגדיר משתנה חדש $y = x - \frac{\lambda}{\omega^2}$, ונקבל משוואה מהצורה:
\[\ddot{y} = -\omega^2 y\]שהפתרונות שלה הם:
\[y(t) = C\cos(\omega t + \phi)\]מכיוון ש-$y = x - \frac{\lambda}{\omega^2}$, נוכל לכתוב:
\[x(t) = C\cos(\omega t + \phi) + \frac{\lambda}{\omega^2}\]המשוואות הדיפרנציאליות הרלוונטיות
המשוואות הבסיסיות שעלינו להכיר הן:
- אוסילטור הרמוני: $\ddot{x} = -\omega^2 x$ עם פתרונות סינוסיים וקוסינוסיים
- אוסילטור הפוך: $\ddot{x} = \omega^2 x$ עם פתרונות אקספוננציאליים (בשיעור ובכתה התייחסנו לפתרונות בצורות $x(t) = A\cosh(\omega t) + B\sinh(\omega t)$, אבל ניתן גם לכתוב את הפתרונות בצורות אקספוננציאליות פשוטות כמו $x(t) = C e^{\omega t} + D e^{-\omega t}$)
- דעיכה אקספוננציאלית: $\dot{x} = -\gamma x$ עם פתרון $x(t) = x_0 e^{-\gamma t}$ - למשל בשאלות של קליע, להבנתי.
- צורה נוספת: $\dot{v} = -\beta^2 v$ או משוואות דומות
ניתוח מערכת של שתי מסות מצומדות
תיאור המערכת
נבחן מערכת המורכבת משתי מסות: מסה קטנה $m$ ומסה גדולה $M$, המחוברות באמצעות קפיץ. המסה הקטנה נמצאת על משטח משופע בזווית $\alpha$, והמסה הגדולה יכולה לנוע אופקית. קבוע הקפיץ הוא $k$, ואורך הקפיץ במצב מנוחה הוא $L$ (ייתכן שהיה נוח לבחור $L=0$).
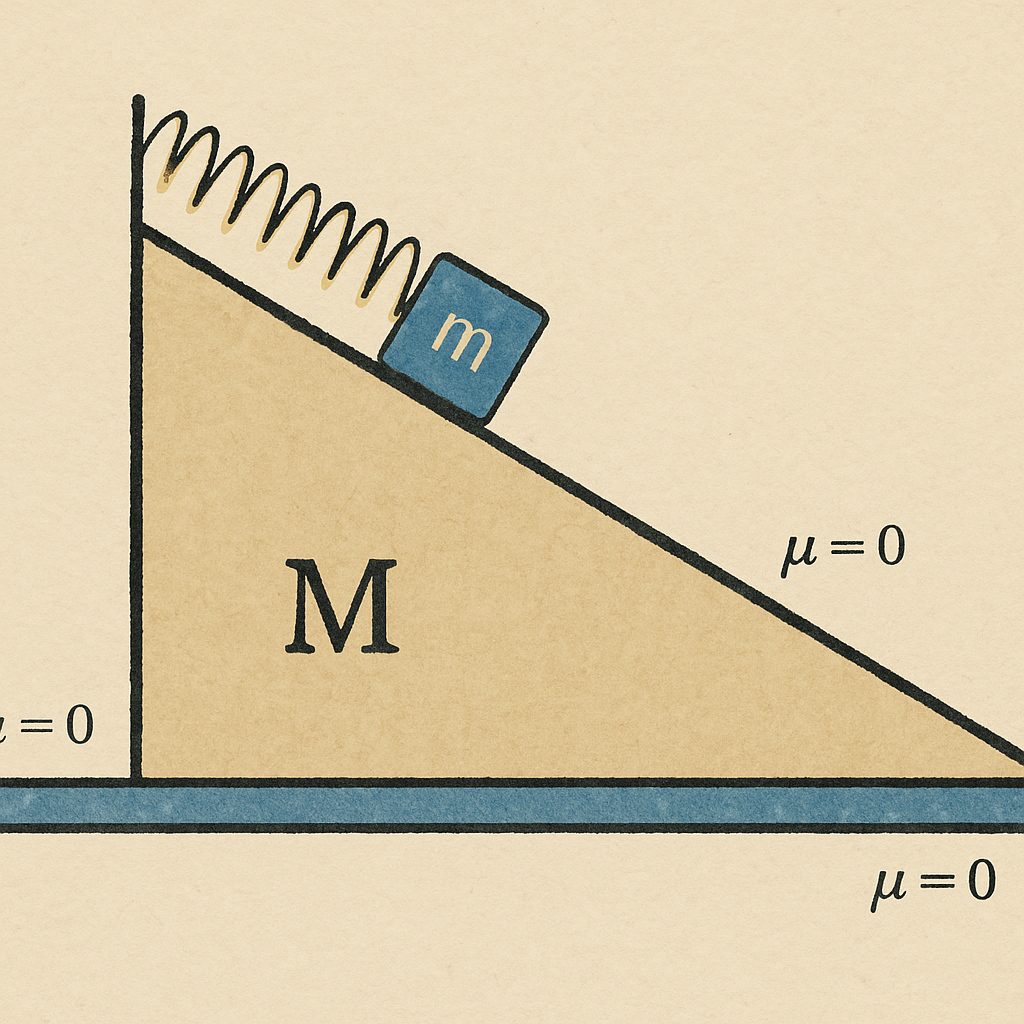
כוחות במערכת
במערכת פועלים מספר סוגי כוחות:
כוח מחזיר של קפיץ: מבחינה וקטורית, כוח מחזיר תמיד מתואר על ידי:
\[\vec{F} = -k\vec{r}\]כאשר $\vec{r}$ הוא וקטור המקום מנקודת השיווי. הכוח תמיד מנוגד לוקטור המקום ומתכונתי לו בגודלו.
נסמן ב-$A$ את התאוצה של המסה הגדולה שמאלה, וב-$x$ את המקום של המסה הקטנה על המשטח המשופע. מכאן שתאוצת המסה הקטנה היא $\ddot{x}$.
מערכת לא אינרציאלית
חשוב להבין שהמסה הקטנה נמצאת במערכת ייחוס לא אינרציאלית, מכיוון שהיא מחוברת למסה הגדולה הנעה בתאוצה. לכן עלינו להתחשב בכוחות מדומים. זה דומה למצב של נוסע באוטובוס המאיץ - הנוסע מרגיש כוח “מדומה” בכיוון הפוך לתאוצה.
המסה הגדולה, לעומת זאת, נמצאת במערכת אינרציאלית ולא מרגישה כוחות מדומים.
ניתוח הכוחות על המסה הקטנה
ניתוח הכוחות בכיוון המקביל למשטח המשופע (↘)
עבור המסה הקטנה $m$ הנמצאת על המשטח המשופע, נבחר ציר חיובי לכיוון מטה לאורך המשטח. הכוחות הפועלים בכיוון זה הם:
- רכיב כוח הכבידה: $mg\sin\alpha$ כלפי מטה.
- כוח מדומה: $mA\cos\alpha$ (בשל תאוצת המסה הגדולה). לפי הפתרון בבלוג, המסה הגדולה מאיצה שמאלה, ולכן הכוח המדומה פועל בכיוון ההפוך לתאוצה של המסה הגדולה (כלומר ימינה).
- כוח הקפיץ: $-k(x - L)$ (כוח מחזיר), במעלה המישור המשופע (ומכאן שלילי).
המשוואה הדינמית למסה הקטנה, מהחוק השני של ניוטון ביחס לציר המקביל למשטח המשופע, היא:
\[mg\sin\alpha + mA\cos\alpha - k(x - L) = m\ddot{x} \tag{1}\]ניתוח הכוחות בכיוון הניצב למשטח (↗)
במערכת הלא אינרציאלית של המסה הקטנה, בכיוון הניצב למשטח המשופע (ציר $y$), המסה תמיד צמודה לפני המשטח. המשמעות היא ש-$y = 0$ בכל זמן, ולכן אין תאוצה בכיוון זה. במצב הזה ניתן להפעיל את החוק הראשון של ניוטון (שיווי משקל של כוחות $\sum F_y = 0$), שכן בתוך המערכת המאיצה אין דינמיקה בציר $y$.
הכוחות הפועלים על המסה הקטנה בכיוון הניצב למשטח הם:
- הכוח הנורמלי: $N$ פועל בכיוון הניצב למשטח, אך יש לו רכיב בכיוון התנועה של המסה הקטנה. למעלה וימינה.
- רכיב כוח הכבידה: $mg\cos\alpha$
- רכיב הכוח המדומה: $mA\sin\alpha$ (כי $\cos(90° - \alpha) = \sin\alpha$)
משוואת שיווי המשקל בכיוון הניצב למשט, לפי החוק הראשון של ניוטון, היא:
\[N + mA\sin\alpha = mg\cos\alpha \tag{2}\]מכאן נקבל:
\[\boxed{N = mg\cos\alpha - mA\sin\alpha}\]ניתוח הכוחות על המסה הגדולה
המסה הגדולה $M$ נעה אופקית תחת השפעת:
- כוח המשיכה $Mg$ (כלפי מטה, אך אין לו רכיב אופקי).
- רכיב הכוח הנורמלי: $N\sin\alpha$ (בכיוון התנועה של המסה הגדולה, כלומר שמאלה ומטה). מדובר בכוח שהמסה הקטנה מפעילה על המסה הגדולה.
- כוח הקפיץ: $-k(x - L)\cos\alpha$ בשמו הפורמאלי - הכוח המחזיר של הקפיץ.
- הכוח הנורמאלי $N’$ של המסה הגדולה, הפועל בכיוון הניצב למשטח המשופע (כלפי מעלה).
המשוואה הדינמית למסה הגדולה:
\[N\sin\alpha - k(x - L)\cos\alpha = MA \tag{3}\]פתרון המערכת המצומדת
אסטרטגיית הפתרון
יש לנו מערכת של שלוש נעלמים: $x$, $A$, ו-$N$. כעת נוכל לפתור את מערכת המשוואות המצומדות בשיטה הבאה:
- נציב את הביטוי עבור $N$ במשוואה של המסה הגדולה (משוואה 3).
- נקבל משוואה דיפרנציאלית יחידה במשתנה $x$
- נפתור אותה כאוסילטור הרמוני עם איבר קבוע
האסטרטגיה היא להתנער מהנעלמים $N$ ו-$A$, ולהשאיר רק את $x$ ונגזרותיו.
הצבה ופיתוח המשוואה
מהמשוואה של המסה הגדולה:
\[N\sin\alpha - k(x-L)\cos\alpha = MA\]נציב את הביטוי עבור $N$:
\[\left(mg\cos\alpha - mA\sin\alpha\right)\sin\alpha - k(x-L)\cos\alpha = MA\]פיתוח הביטוי:
\[mg\cos\alpha\sin\alpha - mA\sin^2\alpha - k(x-L)\cos\alpha = MA\]העברת האיברים ואיסוף:
\[mg\cos\alpha\sin\alpha - k(x-L)\cos\alpha = MA + mA\sin^2\alpha\]מכאן נוכל להוציא את $A$:
\[A = \frac{mg\cos\alpha\sin\alpha - k(x-L)\cos\alpha}{M + m\sin^2\alpha}\]הצבה במשוואה של המסה הקטנה
נציב את הביטוי עבור $A$ במשוואה של המסה הקטנה (משוואה 1):
\[mg\sin\alpha + m\left(\frac{mg\cos\alpha\sin\alpha - k(x-L)\cos\alpha}{M + m\sin^2\alpha}\right)\cos\alpha - k(x-L) = m\ddot{x}\]נפתח את הביטוי:
\[mg\sin\alpha + \frac{m^2g\cos^2\alpha\sin\alpha}{M + m\sin^2\alpha} - \frac{mk(x-L)\cos^2\alpha}{M + m\sin^2\alpha} - k(x-L) = m\ddot{x}\] \[mg\sin\alpha + \frac{m^2g\cos^2\alpha\sin\alpha}{M + m\sin^2\alpha} - \left(1 + \frac{m\cos^2\alpha}{M + m\sin^2\alpha}\right)k(x-L) = m\ddot{x}\]נחלק את המשוואה ב-$m$:
\[\ddot{x} = g\sin\alpha + \frac{mg\cos^2\alpha\sin\alpha}{M + m\sin^2\alpha} - \left(\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}\right)(x-L)\] \[\ddot{x} = g\sin\alpha \left(1 + \frac{m\cos^2\alpha}{M + m\sin^2\alpha}\right) - \left(\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}\right)(x-L)\]נגדיר משתנה מוזז $\tilde{x} = x - L$, ונקבל כך ש-$ֿ\ddot{\tilde{x}} = \ddot{x}$:
\[\ddot{\tilde{x}} = - \underbrace{\left(\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}\right)}_{\omega^2} \tilde{x} + \underbrace{g\sin\alpha \left(1 + \frac{m\cos^2\alpha}{M + m\sin^2\alpha}\right)}_{\tilde{x_0}}\]הפתרון הכללי
הפתרון הכללי למשוואה זו הוא:
\[x(t) = A\cos(\omega t) + B\sin(\omega t) + \frac{\tilde{x_0}}{\omega^2}\]התאמה לתנאי התחלה
בהנחה שהמערכת מתחילה ממנוחה בזמן $t=0$ עם $x(0) = L$ ו-$\dot{x}(0) = 0$:
מתנאי המקום ההתחלתי:
\[L = A\cos(0) + B\sin(0) + \frac{\tilde{x_0}}{\omega^2} = A + \frac{\tilde{x_0}}{\omega^2}\]לכן:
\[A = L - \frac{\tilde{x_0}}{\omega^2}\]מתנאי המהירות ההתחלתית:
\[\dot{x}(t) = -A\omega\sin(\omega t) + B\omega\cos(\omega t)\] \[\dot{x}(0) = B\omega = 0\]לכן:
\[B = 0\]הסיבה ש-$B = 0$ היא שהתחלנו ממהירות אפס - שחררנו את המסה ממנוחה.
הפתרון הסופי
הפתרון הסופי עם תנאי ההתחלה הוא:
\[x(t) = \left(L - \frac{\tilde{x_0}}{\omega^2}\right)\cos(\omega t) + \frac{\tilde{x_0}}{\omega^2}\]ניתוח התנועה
זמן הגעה לנקודת שיווי המשקל
המסה הקטנה תגיע לנקודת שיווי המשקל החדשה לראשונה בזמן $t^*$ המקיים:
\[t^* = \frac{T}{4} = \frac{\pi}{2\omega}\]כאשר $T = \frac{2\pi}{\omega}$ הוא זמן המחזור של התנודה.
הסיבה לכך היא שבתנועה קוסינוסואידית, אנו מתחילים מנקודת השיווי, יורדים למטה (זה רבע זמן מחזור), מגיעים לנקודה מקסימלית, חוזרים לנקודת השיווי (חצי זמן מחזור), עולים למעלה (שלושת רבעי זמן מחזור), וחוזרים שוב לנקודת השיווי (זמן מחזור שלם).
התדירות המותאמת
חשוב לציין שהתדירות $\omega$ במערכת זו אינה התדירות הפשוטה $\sqrt{k/m}$ של קפיץ בודד, אלא תדירות מותאמת התלויה במסות שתי הגופים ובזווית המשטח:
\[\omega = \sqrt{\frac{k}{m} + \frac{k\cos^2\alpha}{M + m\sin^2\alpha}}\]בגבול שבו $M \to \infty$, התדירות מתקרבה ל-$\sqrt{k/m}$ (עד כדי איבר זווית), מכיוון שאז חוזרים למצב של משטח משופע קבוע שעליו מתנדנדת מסה.
בהמשך עלתה דוגמה מורכבת עם חיכוך.
דור פסקל